The Cahn–Hilliard model of coherent lamellar microstructure: application to alkali feldspar

Abstract

The temporal evolution of coherent lamellar microstructures is significantly influenced by their elastic properties, particularly when the exsolved phases are coherent. This research utilizes the Cahn–Hilliard model to examine the morphological and energetic evolution of binary alkali feldspar, integrating anisotropic elastic energy into the Gibbs energy equation. The Cahn–Hilliard model successfully simulated the orientation of lamellae observed in natural samples and the elastic strain was consistent with previous research. We also computed the coherent solvus from the annealing simulation of various precursor compositions and temperatures. The temperature difference ($\Delta T$) between the strain-free solvus and the coherent solvus was $\Delta T = 85\,{}^\circ \text {C}$, which is slightly lower than previously reported values obtained from similar parameters. This discrepancy is likely due to the presence of non-planar lamellae at the onset of phase separation, which are more stable than planar ones. We also simulated the binodal curves of the coherent solvi for different precursor phase compositions. The computed solvi were not unique but varied depending on the precursor composition. Our model is flexible because it does not assume any specific shapes for the lamellar interfaces and is applicable to various coherent binary systems.

Introduction

Elastic properties, determined by their structural and bonding characteristics, control macroscopic physical properties and exert a significant influence on the free energy. This affects nucleation, lattice orientation, and phase separation processes (Abart et al. 2009; Angel et al. 2014; Hess and Ague 2023; Hobbs and Ord 2016). These elastic effects are particularly notable in binary solid solutions when the exsolved microstructure is coherent and the lattice misfit is significant (McCallister and Yund 1977; Petrishcheva and Abart 2012; Petrishcheva et al. 2023; Tullis and Yutrp 1979). In this context, coherence refers to the continuous lattice between host and precipitated phases. In this study, we focused on Na–K alkali feldspar, a well-known coherent binary system, characterized by a submicron lamella microstructure that can develop when the feldspar is cooled under subsolvus conditions.

Alkali feldspar has large cavities within a structural framework composed of $[\text {SiO}_{4}]^{2-}$ and $[\text {AlO}_{4}]^{-}$ tetrahedra which are occupied by $\text {Na}^+$ and $\text {K}^+$ ions (Angel et al. 2012). This configuration causes chemical strain due to Na–K interdiffusion and together with the significant difference in ionic radii, results in elastic energy. Consequently, the elasticity suppresses phase separation, because elastic energy contributes to an increase in Gibbs energy during phase separation. The effect of elastic energy on phase separation has been examined in various experimental and theoretical studies (Petrishcheva et al. 2023; Robin 1974; Sipling and Yund 1976; Tullis and Yutrp 1979). The recent theoretical study by Petrishcheva et al. (2023) indicates that the temperature of the coherent solvus in binary alkali feldspar is approximately ca. 100 $^{\circ }\text {C}\,$ lower than the strain-free solvus. Here, strain-free solvus is computed purely on thermodynamic parameters without incorporating elastic parameters.

The influence of elastic energy caused by chemical strain becomes significant in coherent intergrowths, as the system tends to arrange precipitated phases to minimize the chemical strain energy. Simplifications are often applied in calculating these elastic energies. Robin (1974) and Williame and Brown (1974) calculated the elastic energy on the assumption that the total strain at lamellar interfaces is negligible. Petrishcheva et al. (2023) pointed out that this assumption is only applicable for vanishingly thin lamellae. They further refined the model to include the effect of strain parallel to lamellar interfaces, assuming infinitely planar lamellae. However, the exact morphology of lamellae formed at the onset of phase separation from a uniform phase is unclear in both experimental and natural settings. The morphology of these lamellae, whether planar or not, influences the elastic energy, and consequently, could affect the temperature of the coherent solvus. Therefore, the coherent solvus should be recalculated without relying on morphological presumptions.

Abart et al. (2009) and Petrishcheva and Abart (2012), authors of a pioneering work in the application of diffuse interface modeling to petrology, adopted an alternative approach using a 2D Cahn–Hilliard model to characterize the morphological evolution of alkali feldspar lamellae during cooling. They simplified the analysis to a 2D system, focusing on the (010) plane, and this successfully simulate the lamellae’s morphological evolution, but does not account for the elastic energy of lamellar planes observed in coherent binary system. To overcome this limitation, we developed a 3D Cahn–Hilliard model in this paper. This model incorporates the anisotropy of the stiffness coefficient and chemical strain into the Gibbs energy calculation. As a result, the model can predict the stress or elastic strain in the system as well as the morphological and compositional evolution of microstructures.

Basic equations for spinodal decomposition

We first formulate a basic equation that governs the spinodal decomposition of alkali feldspar binary using a Cahn–Hilliard model (Cahn and Hilliard 1958) incorporating the elastic effect of the system. To confirm the validity of the simulation, we checked its consistency against well-known thermodynamic research on the coherent lamellae of feldspar (Petrishcheva et al. 2023). We used the same elastic parameters as those in the referenced research: the stiffness coefficients from Haussiihl (1993) and the lattice parameters from Kroll et al. (1986).

Assumption of crystal symmetry

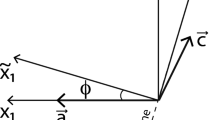
The elastic term in the Cahn–Hilliard equation is derived under the assumption of monoclinic symmetry of the alkali feldspar. This assumption is valid above the temperature of the monoclinic to triclinic symmetry breaking transition (Brown and Parsons 1989). The primitive translation vectors of alkali feldspar are represented by $\varvec{a}$, $\varvec{b}$ and $\varvec{c}$, with the orientation such that $\varvec{a} \perp \varvec{b}$ and $\varvec{c} \perp \varvec{b}$. The lattice parameters of $\varvec{a}$, $\varvec{b}$ and $\varvec{c}$ are denoted as a, b and c, respectively. The angle between $\varvec{a}$ and $\varvec{c}$ is denoted as $\beta$. Additionally, an orthogonal coordinate system is defined as $\varvec{x_1} \parallel \varvec{a}$, $\varvec{x_2} \parallel \varvec{b}$ and $\varvec{x_3}$ perpendicular to both $\varvec{x_1}$ and $\varvec{x_2}$ where $\varvec{x_1}$ ,$\varvec{x_2}$ and $\varvec{x_3}$ are unit vector (Fig. 1). The coordinates of the lattice vectors in an orthogonal system are given by,

$$\begin{aligned} (\varvec{a} \, \varvec{b} \, \varvec{c}) = \begin{pmatrix} a &{} 0 &{} c\cos \beta \\ 0 &{} b &{} 0 \\ 0 &{} 0 &{} c\sin \beta \\ \end{pmatrix}. \end{aligned}$$

(1)

Fig. 1

The coordinate system used in this study. Vectors $\varvec{x_2}$ or $\varvec{b}$ are perpendicular to both $\varvec{x_1}$ and $\varvec{x_3}$ pointing into the page

Chemical strain

We used the lattice parameters Kroll et al. (1986) to estimate the chemical strain. The compositional dependencies of the lattice parameters are calculated as a linear function of K-feldspar mole fraction X, which is determined on the basis of a linear regression of cell parameter data. The slope of the linear function gives the derivative relation of the lattice parameter and X,

$$\begin{aligned}{} & {} \frac{1}{a} \frac{\partial a}{\partial X} = 0.0540, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \frac{1}{b} \frac{\partial b}{\partial X} = 0.0115, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \frac{1}{c} \frac{\partial c}{\partial X} = 0.00893,\end{aligned}$$

(4)

$$\begin{aligned}{} & {} \frac{\partial \beta }{\partial X} = -0.008. \end{aligned}$$

(5)

As the mole fraction of the solid solution changes from $X_0$ to $X_0 + \Delta X$, the primitive translation vectors change from $\varvec{a}$, $\varvec{b}$ and $\varvec{c}$ to $\varvec{a}+\Delta \varvec{a}$, $\varvec{b}+\Delta \varvec{b}$ and $\varvec{c}+\Delta \varvec{c}$, respectively. The chemical strain is quantified by the lattice parameter gradients in the orthogonal basis $<\varvec{x}_1, \varvec{x}_2, \varvec{x}_3>$. This allows for the calculation of the chemical strain tensor,

$$\begin{aligned} \epsilon _{ij}^* = \frac{ (\Delta \varvec{a})_i(\varvec{a^*})_j + (\Delta \varvec{b})_i(\varvec{b^*})_j +(\Delta \varvec{c})_i(\varvec{c^*})_j }{2} + (i \leftrightarrow j). \end{aligned}$$

(6)

In this context, $\varvec{a^*}$, $\varvec{b^*}$, and $\varvec{c^*}$ denote the reciprocal basis vectors of the lattice (Petrishcheva et al. 2023). The notation $(i \leftrightarrow j)$ means the interchange of indices in the preceding term. This formulation gives chemical strain as a function of mole fraction X,

$$\begin{aligned} \epsilon ^*_{ij} = \eta _{ij}(X - X_0), \end{aligned}$$

(7)

where

$$\begin{aligned} \eta = \begin{pmatrix} 0.0540 &{} 0 &{} 0.0153\\ 0 &{} 0.0115 &{} 0 \\ 0.0153 &{} 0 &{} 0.0131\\ \end{pmatrix}. \end{aligned}$$

(8)

The mole fraction of $X$ is denoted by $X = X(\varvec{r})$ because $X$ can be expressed as a function of spatial coordinates $\varvec{r} = (x_1, x_2, x_3)$ in a non-uniform system. Therefore, if we explicitly rewrite Eq. 7 as a spatial function, the chemical strain $\epsilon ^*_{ij}$ is expressed as $\epsilon ^*_{ij}(\varvec{r}) = \eta _{ij}(X(\varvec{r}) - X_0)$.

In this paper, we assume that only the chemical strain contributes to the non-elastic components of the strain or, in other words, we disregard the effects of dislocations and other lattice defects. As a result, the relationships among the elastic strain $\epsilon ^{el}_{ij}(\varvec{r})$, the total strain $\epsilon ^{t}_{ij}(\varvec{r})$, and the chemical strain $\epsilon ^{*}_{ij}(\varvec{r})$ are expressed as,

$$\begin{aligned} \epsilon ^{t}_{ij}(\varvec{r}) = \epsilon ^{el}_{ij}(\varvec{r}) + \epsilon ^{*}_{ij}(\varvec{r}). \end{aligned}$$

(9)

Stiffness tensor

We utilized the stiffness tensor from Haussiihl (1993) for both endmembers of alkali feldspars (Model 1) to compare the simulation results with Petrishcheva et al. (2023). Meanwhile, in Sect. 4.5, we employed the stiffness tensor from Haussiihl (1993) for K-feldspar and from Brown et al. (2006) for Na-feldspar (Model 2) to evaluate the effect of an compositionally dependent stiffness tensor. The coefficients of the stiffness tensor are transformed to $x_1 || \varvec{a}$, $x_2 || \varvec{b}$, and $x_3 || \varvec{c^*}$ coordinates (Petrishcheva et al. 2023).

Elastic energy

The coherent interface assumption for two adjacent phases results in lattice parameter mismatches between the phases. These mismatches lead to nonhydrostatic stresses and non-uniform elastic energy. In such coherent systems, it is essential to include elastic energy in the Gibbs energy. Because the elastic energy term is always greater than zero, it suppresses phase separation. As a result, the temperature of the coherent solvus is lower than that of the strain-free solvus.

However, the elastic energy cannot be expressed by a simple function of $X$; it is complexly influenced by the shapes of the phases and their distribution. Therefore, numerical methods are required to estimate the elastic energy density $E(\varvec{r})$ from a given $X(\varvec{r})$. The key step in incorporating elastic energy into Gibbs energy is computing the total strain $\epsilon ^t_{ij}(\varvec{r})$ from the mole fraction $X(\varvec{r})$ because the elastic energy density is calculated from $\epsilon ^t_{ij}(\varvec{r})$ as,

$$\begin{aligned} \begin{aligned} E(\varvec{r}) &= \frac{1}{2} C_{ijkl} \epsilon ^{el}_{ij} \epsilon ^{el}_{kl} \\&= \frac{1}{2} C_{ijkl}\{e^{t}_{ij} - \eta _{ij}(X-X_0)\} \{e^{t}_{kl} - \eta _{kl}(X-X_0)\}. \end{aligned} \end{aligned}$$

(10)

The second equality follows from Eqs. 7, 9. For the numerical computation of the total strain $\epsilon ^t_{ij}{(\varvec{r})}$ from $X(\varvec{r})$, we implemented the algorithm proposed by Moulinec and Suquet (1998) because of its easy and simple implementation. An implementation is introduced in Biner (2017) of a 2D case. The Eq. 10 computation is updated at each time step of the Cahn–Hilliard simulation, as discussed in Sect. 3.2.

Gibbs energy

The Cahn–Hilliard model assumes a continuous distribution of atomic density, represented by the number of atoms per unit volume $n_\alpha$ for each component ($\alpha = A, B, \ldots$) across different phases. This distribution is modeled as a smoothly varying function, $n_\alpha (\textbf{r})$. A fundamental assumption of this approach is local equilibrium. Under this assumption, the Gibbs energy for the entire system can be defined from local Gibbs energy,

$$\begin{aligned} \int n(\varvec{r})G(\textbf{r}) \, d\textbf{r}. \end{aligned}$$

(11)

Here, $n = n_{\text {K}} + n_{\text {Na}}$ represents the total local number of atoms per unit volume, with $n_{\text {K}}$ and $n_{\text {Na}}$ denoting the contributions of K- and Na-feldspar, respectively. G is the Gibbs energy per mole at point $\varvec{r}$, which can be expressed as a sum of three distinct components,

$$\begin{aligned} {G} = {G}^\text {chem} + {E}^\text {grad} + {E}^\text {str}. \end{aligned}$$

(12)

In this equation, ${G}^\text {chem}$ represents the Gibbs energy per mole associated with a specific solid solution composition,

$$\begin{aligned} \begin{aligned} {G}^\text {chem} = \left\{ \begin{gathered} RT(X \ln X + (1 - X) \ln (1 - X)) \\ + X(1-X)(W_{\text {Na}}X + W_{\text {K}}(1-X)) \end{gathered} \right\} , \end{aligned} \end{aligned}$$

(13)

where R is the gas constant, T is the temperature. ${E}^\text {grad}$ is the gradient energy term where,

$$\begin{aligned} {E}^\text {grad} = \kappa (\nabla X)^2. \end{aligned}$$

(14)

This term imposes an energy penalty where the gradient of the mole fraction in the solid solution is significant such as, for example, near the interface between two different phases. The coefficient $\kappa$ in this expression is related to the isotropic interface free energy (Petrishcheva and Abart 2009). The formulation of the first two terms in Eq. 12 is follow the strategy of Cahn and Hilliard (1958). To applying their theory to the feldspar solid solution system, we introduced $W_{\text {K}}$ and $W_{\text {Na}}$ Margules parameters, $W_{\text {K}}[\text {J/mol}] = 22820 - 6.3T[\text {K}] + 0.461P[\text {bar}]$ and $W_{\text {Na}}[\text {mol}] = 19550 - 10.5T[\text {K}] + 0.327P[\text {bar}]$, respectively (Hovis et al. 1991). We used the pressure $P=1$ bar for the parameter estimation.

The last term in Eq. 12, elastic energy ${E}^\text {str}$, is defined as Eq. 10 divided by n,

$$\begin{aligned} E^{\text{str}} = \frac{1}{2n} C_{ijkl} \epsilon ^{el}_{ij} \epsilon ^{el}_{kl}. \end{aligned}$$

(15)

Evolution equation

Compositional changes in a non-uniform binary system can be described by the Cahn–Hilliard equation

$$\begin{aligned} \frac{\partial X}{\partial t} = \nabla \cdot \left[ M(X)\nabla (\mu _\text {K} - \mu _\text {Na}) \right] , \end{aligned}$$

(16)

where $M(X) = {const.}$ in the linear scenario, and $M(X) = D_{\text {Na-K}}(X,T)X(1-X)/(RT)$ in the nonlinear scenario. This formulation is valid under the assumption that the particle density is conserved everywhere. Here, $D_{\text {Na-K}}(X,T)$ represents the interdiffusion coefficient, defined by,

$$D_\text{Na-K}(X,T)=\begin{aligned} \frac{D^*_{\text {Na}} D^*_{\text {K}}}{(1-X)D^*_{\text {Na}} + X D^*_{\text {K}}}, \end{aligned}$$

(17)

where $D^*_{\text {Na}} = D^*_{\text {Na}}(X,T)$ and $D^*_{\text {K}} = D^*_{\text {K}}(X,T)$ are tracer diffusion coefficients that depends on temperature $T$ and composition $X$. We used the tracer diffusion coefficient of Foland (1982) for Na-feldspar and Kasper (1975) for K-feldspar. Both temperature and composition dependencies of these coefficients are approximated using the Arrhenius relationship (see Brady and Yund 1983). The difference between the chemical potential of K-feldspar ($\mu _\text {K}$) and Na-feldspar ($\mu _\text {Na}$) in the Eq. 16 is formulated as,

$$\begin{aligned} \mu _\text {K} - \mu _\text {Na} = \Delta \mu ^\text {chem} + \Delta \mu ^\text {grad} + \Delta \mu ^\text {str}, \end{aligned}$$

(18)

where $\Delta \mu ^{\text {chem}}$, $\Delta \mu ^{\text {grad}}$ and $\Delta \mu ^{\text {str}}$ are

$$\begin{aligned} \begin{aligned} \Delta \mu ^\text {chem}&= \frac{\delta }{\delta X} \int G^{\text {chem}} d\varvec{r}\\&= RT\ln \left( \frac{X}{1-X}\right) + (1 - 2X)\{W_{\text {Na}}X + W_{\text {K}}(1-X)\} \\&\quad + X(1-X)(W_{\text {Na}} - W_{\text {K}}),\\ \Delta \mu ^\text {grad}&= \frac{\delta }{\delta X} \int E^{\text {grad}} d\varvec{r}= -2\kappa \nabla ^2 X, \\ \Delta \mu ^\text {str}&= \frac{1}{n} \frac{\delta }{\delta X} \int E^{\text{str}} d\varvec{r}= -\frac{C_{ijkl}}{n}(e^{t}_{ij} - \eta _{ij}(X-X_0)) \eta _{kl}. \end{aligned} \end{aligned}$$

(19)

A derivation of these equations is provided in the Appendix of this article. In particular, the derivation of the $\Delta \mu ^{\text {chem}} + \Delta \mu ^{\text {grad}}$ term is comprehensively reviewed in Petrishcheva and Abart (2009). Here, we used the experimentally determined gradient parameter, $\kappa = 6.2 \times 10^{-15} \text { Jm}^2$ (Petrishcheva et al. 2020), for the Cahn–Hilliard simulation. This gradient parameter is estimated by linear extrapolation of the average wavelength of the lamellae intergrowth to $t=0$, which is the minimal estimate of the gradient parameter. This value is expected to depend on temperature, and the experimental conditions in Petrishcheva et al. (2020) were estimated to be at 550 $^{\circ }\text {C}\,$. However, there is a lack of knowledge about the temperature dependencies of $\kappa$, and there are no consistent experimental results. Therefore, we assumed that the parameter is independent of temperature.

Simulation of Cahn–Hilliard model

Nondimensionalization of Gibbs energy

For the numerical analysis of the Cahn–Hilliard equation in a binary system, we introduce nondimensionalization for various physical parameters and operators,

$$\begin{aligned} \begin{aligned} \bar{x} = \frac{x}{l}, \,\, \bar{y} = \frac{y}{l}, \,\, \bar{z} = \frac{z}{l}, \,\, \bar{t} = \frac{t}{\tau }, \,\, \bar{\nabla } = \nabla l, \,\, \\ \bar{W}_{\text {K}} = \frac{W_{\text {K}}}{e}, \,\, \bar{W}_{\text {Na}} = \frac{W_{\text {Na}}}{e}, \,\, \bar{C}_{ijkl} = \frac{C_{ijkl}}{ne}, \end{aligned} \end{aligned}$$

(20)

where the nondimensional units are defined as follows: $e = RT$ (unit energy per mole), $l = \sqrt{\frac{\kappa }{RT}}$ (unit length), and $\tau = \frac{\kappa }{LRT}$ (unit time). Here, L is introduced to have same dimension as M(X). The nondimensionalized parameter $\bar{M}(X)$ is expressed as,

$$\begin{aligned} \bar{M}(X) = \frac{\tau M(X)}{l^2} = \frac{M(X)}{L}. \end{aligned}$$

(21)

We choose $L = \max _X M(X)$, although this selection is arbitrary and does not affect the computational outcomes. Specifically, in the scenario where the Cahn–Hilliard equation is linear (i.e., $M(X) = \text{const.}$), $\bar{M}(X) = 1$. The nondimensional coefficient for gradient energy $\bar{\kappa }$ is given by:

$$\begin{aligned} \bar{\kappa } = \frac{\kappa }{l^2RT} = 1. \end{aligned}$$

(22)

Using these nondimensional parameters, the Cahn–Hilliard equation is (Eq. 16) reformulated as,

$$\begin{aligned} \frac{\partial X}{\partial \bar{t}} = \bar{\nabla } \cdot \left[ \bar{M}(X) \bar{\nabla } \left\{ \begin{aligned}&\ln \frac{X}{1-X} + (1 - 2 X)\{\bar{W}_{\text {Na}}X + \bar{W}_{\text {K}}(1-X)\}\\&\quad +X(1-X)(\bar{W}_{\text {K}} - \bar{W}_{\text {Na}}) - 2\bar{\nabla }^2X \\&\quad -\bar{C}_{ijkl}(e^{t}_{ij} - \eta _{ij}(X-X_0)) \eta _{kl} \end{aligned} \right\} \right] . \end{aligned}$$

(23)

Implementation of Cahn–Hilliard model simulation

We solved Eq. 23 using the Fourier spectrum-based Cahn–Hilliard model (Biner 2017; Hu and Chen 2001; Wang et al. 2013). Specifically, Biner (2017) implemented and demonstrated minimal code for a 2D coherent exsolution system in a cubic crystal. Our implementation extended this work to a monoclinic system, thereby, developing a 3D diffusion simulation and incorporating a nonlinear algorithm. In the simulation, we used periodic boundary condition. We employed two types of algorithms: a non-linear algorithm and a linear algorithm. The nonlinear algorithm simulations were computed by inconstant mobility, $M(X) = D_{\text{Na-K}}X(1-X)/(RT)$ with an explicit Euler time integration scheme. We adopted the pseudo-spectrum method (Orszag 1972) to manage these nonlinear aspects. The computational domain was discretized using a mesh size of $100 \times 100 \times 100$. The nonlinear simulation was computationally intensive, requiring several days to complete. Although contrary to the nonlinear algorithm, the linear algorithm is not accurate at the exact timing of phase separation, it is much more efficient than the nonlinear algorithm and computations typically complete within a few minutes. Therefore, we used linear algorithm when simulating the Cahn–Hilliard model repeatedly, such as when computing phase diagrams (Sect. 4.5) or when comparing the compositional evolution (Figs. 5 and  6). The linear algorithm was simulated by $M(x) = \text {const.}$ The implementation relies on an semi-implicit Euler algorithm, and the computational domain is discretized using a mesh size of $64 \times 64 \times 64$. We added initial Gaussian noise with a standard deviation of 0.01 to $X(\varvec{r})=X_0$ to promote the spinodal decomposition. In our simulations, the temperature was kept constant throughout the computational process and, as such, our simulations were imitating with the conditions of annealing experiments. The entire computation was developed using the Python programming language, implementing a simulation of Cahn–Hilliard model package called coLamB (https://github.com/Tan-Furukawa/coLamB/; Furukawa 2024).

Results and discussion

Morphological evolution of lamellae

The Cahn–Hilliard model was implemented under the conditions of $T = 500$ $^{\circ }\text {C}\,$ and $X_0 = 0.35$, as illustrated in Fig. 2. Initial noise dissipated rapidly within $t < 0.01$ d, followed by a slow phase separation process ($t \lesssim 2$ d). Subsequently, a periodic microstructure emerged between $2 \lesssim t \lesssim 4$ d (Fig. 3) and a significant decrease in Gibbs energy occurred. After $t \gtrsim 2$ d, the free energy or phase composition remained nearly stable. On the other hand, $E^\text {str}$, which potentially suppresses phase separation, exhibited a gradual increase throughout the computed period. The gradient energy $E^\text {grad}$ also increased and acted to suppress phase separation. After $t = 5.2$ d, $E^\text {grad}$ began to slightly decrease but remained almost stable between $2 \lesssim t \lesssim 4$ d.

The simulated lamellar wavelength was 13.8 nm at $t = 4$ d, which is smaller than the experimental result of 17.5 nm at $t = 4$ d reported by Petrishcheva et al. (2020). However, their experiment was conducted at $T = 550$ $^{\circ }\text {C}\,$, whereas our simulation was at $T = 500$ $^{\circ }\text {C}\,$. The interdiffusion coefficient at $T = 550$ $^{\circ }\text {C}\,$and $X = 0.35$ was approximately seven times larger, and this may have caused the lamellae wavelength that was inconsistent with the Petrishcheva et al. (2020) experiment.

Fig. 2

Evolution of lamellar microstructure from exsolution of alkali feldspar, where the composition of the homogeneous precursor phase is X₀ = 0.35, at $T = 500$ ºC when a t = 1 d, b t = 2 d, c t = 3 d and d t = 5 d

Fig. 3

a Evolution of mean elastic energy density ($E^\text {str}$), gradient energy density ($E^\text {grad}$), and the free energy density ($G^\text {chem}$), with the initial value of $G^\text {chem}$ set to 0. b Evolution of lamellar compositions of K-feldspar

Fig. 4

Lamellar microstructures viewed parallel to the [010] axis at t = 2.8 to t = 3.9. The color map corresponds to mole fraction of K-feldspar. The pink arrows indicate the $\text {K}^+$ flux vector field. At t = 2.8, the direction of the flow vectors exhibit a rhythmical pattern. However, the flux is gradually getting smaller except around the “Y-junctions”. The two Y-junctions are merged into a single lamella and the microstructural evolution almost stops til t = 3.9 d

We found that the lamellae coarsening process is characterized by “Y-junctions,” where Y-shaped cross-sections form in the lamellae plane (see Fig. 4, $t = 3.0$ d). The evolution is driven by the flow of $\text {K}^{+}$ cations and the inverse flow of $\text {Na}^{+}$ cations (see Fig. 4). From the onset of phase separation to $t = 2.8$ d, flow exists around the phase interface which exhibit a rhythmic change of the flow direction. At $t = 3.0$ d, flow near the Y-junctions persists, while the flow around the planer interfaces is decreasing in speed. This trend continues at $t = 3.1$ d, with the two Y-junctions gradually approaching each other. By $t = 3.9$ d, the Y-junctions have completely merged into a single lamellar and if no Y-junctions are present in the computed space, the flow is significantly slows and the morphological evolution nearly ceases.

These Y-junctions, which drive morphological evolution, have been discussed in the context of a physical model by Brady (1987). According to this research, the interfacial energy at the wedge-shaped end of the Y-junction is higher than that of a normal lamellae plane, thus causing a chemical potential gradient and cation flow. In our simulation, it is challenging to estimate the local interfacial energy around the Y-junction because its shape is not easily quantified. However, the similarity in the flow directions between our model and Brady’s research suggests the presence of a similar coarsening mechanism. Observations of similar microstructures in some natural cryptoperthite (Kontonikas-Charos et al. 2018; Robin 1974) suggest that these mechanisms are common in alkali feldspar coarsening.

Evolution dependencies with different $X_0$ and $T$

Figure 5 illustrates the evolution paths of phase compositions under constant $X_0$ with varying $T$, measured by normalized time $t^*$ (Fig. 5a) and real time $t$ (Fig. 5b). In Fig. 5a, the compositions are calculated using a nondimensional timescale to ignore the effects of interdiffusion dependencies on temperature. The evolution rate of the lamellar microstructure is influenced by the composition and significantly decelerates as the annealing temperature approaches the coherent solvus temperature ($555$ °C). No phase separation observed above this threshold. This phenomenon can be qualitatively explained by the initial wavelength of the lamellae, as suggested by Kuhl and Schmid (2007):

$$\begin{aligned} \lambda \approx \sqrt{\frac{2\kappa }{-G''(X_0)}}. \end{aligned}$$

(24)

Near the spinodal point, where $G''(X_0) \rightarrow 0$, an initial wavelength of the lamellae gets larger, indicating that the diffusion length is significant in achieving equilibrium composition.

However, even though the evolution proceeds sluggishly near the spinodal temperature, diffusion accelerates significantly at high temperatures. This phenomenon is illustrated in real-time plot (Fig. 5b). For instance, the interdiffusion coefficient at $T = 550\,^\circ \text {C}$ is 70 times greater than at $T = 450\,^\circ \text {C}$ for $X_0=0.35$. Consequently, the rate of exsolution at high temperatures on a real-time scale is still greater than that observed at lower temperatures.

In Fig. 6, the trends closely resemble those in Fig. 5, where the compositional evolution is notably sluggish near the spinodal compositions ($X_0 = 0.25$ and $X_0 = 0.46$). The stable compositions at near the end of the simulation are different for each $X_0$. This trend is particularly clear for the K-rich feldspar phase. According to Petrishcheva et al. (2023), the volume fractions of the Na-rich and the K-rich lamellae depend on $X_0$, which influences the elastic energy and the stable compositions.

The composition trends observed in our simulation for K-rich feldspar are consistent with the results of $X_0 = 0.3, 0.35, 0.4$ reported by Petrishcheva et al. (2023). On the other hand, in the Na-rich phase, our simulations reveal no clear trend between the equilibrium composition and the precursor composition $X_0$. The exact reason for this remains unclear, but as Petrishcheva et al. (2023) described, it is a fact that the solvi estimated from different $X_0$ for the Na-rich phase are more concentrated than those for the K-rich phase. We can postulate that this trend makes it difficult to estimate the equilibrium composition of the Na-rich phase.

Fig. 5

Composition evolution at $X_0 = 0.35$ as a function of nondimensional time (a) and real time (b) at different temperatures T. The evolution is sluggish near the spinodal temperature, and remains rapid at elevated temperatures due to the significantly larger diffusion coefficients at higher temperatures compared to lower temperatures

Fig. 6

Composition evolution at $T = 500\,^\circ \text {C}$ as a function of real time for various initial compositions, $X_0$. Similar to Fig. 5, the evolution is sluggish near the spinodal composition. The equilibrium composition depends on the initial composition, $X_0$, which is consistent with the results computed by Petrishcheva et al. (2023)

Lamellae orientation

The orientation of the lamellae is selected to minimize the total elastic energy of the system. In the case of alkali feldspar lamellae, both empirical observations from natural samples and theoretical analyses indicate that the orientation of feldspar lamellae varies between the $(\bar{6}01)$ and $(\bar{8}01)$ planes (Petrishcheva et al. 2023; Robin 1974). At $t = 6$ d, a Fourier transformation of $X(\varvec{r})$ showed that the simulated lamellar planes were inclined approximately 71.6 $^{\circ }$ towards the $(100)$ plane, corresponding to a Miller index of approximately $(\bar{6}01)$.

Our simulations did not account for the anisotropy of gradient energy. However, the lamellae orientations observed in experimental or natural samples were effectively replicated in our model. This observation suggests that the impact of the anisotropy of gradient energy on the coherent system is minimal. On the other hand, Abart et al. (2009) discusses a 2D Cahn–Hilliard model for the alkali feldspar $2 \times 2$ tensor $\kappa$ to address anisotropic gradient energy. The principal difference between our study and Abart et al. (2009) is that our simulations assume coherency within the system while Abart et al. (2009) does not. Because this research ignores the elastic term in Gibbs energy, their simulation should used for incoherent interfaces where the anisotropy of interfacial energy plays a more significant role.

Distribution of strain and elastic energy

We estimated the volumetric strain $\text {Tr}[\epsilon ] = \epsilon _{11} + \epsilon _{22} + \epsilon _{33}$ for elastic strain ($\epsilon ^{el}$), total strain ($\epsilon ^{t}$), and chemical strain ($\epsilon ^{*}$) as depicted in Fig. 7. Here, the volumetric strain is the relative variation of the volume ($\Delta V/V$) under the assumption of infinitesimal strain. According to the volumetric strain of $\text {Tr}[\epsilon ^{el}]$, the K-feldspar phase undergoes compression while the Na-feldspar phase expands, balancing at the interface such that the elastic strain is nullified. The elastic energy is mainly stored in the interior of the lamellae, whereas it is almost zero at the interface. One explanation for the low strain energy density along the lamellar interfaces is that there are smooth compositional transitions between lamellae that create regions where the chemical and elastic strains are low or nonexistent. When the elastic strain vanishes, the elastic energy vanishes as well.

Fig. 7

Volumetric strain of a elastic strain ($\epsilon ^{el}$), b total strain ($\epsilon ^t$) and c chemical strain ($\epsilon ^*$). The elastic energy density estimated by Eq. 10 is illustrated in d

Coherent phase diagram

We applied the Cahn–Hilliard model repeatedly using various initial compositions $X_0$ and temperatures $T$ and constructed a coherent phase diagram for the spinode (Fig. 8a) and binode (Fig. 8b), by checking whether or not phase separation occurred in every simulation run. In Fig. 8, the points marked with upward-pointing triangles represent the conditions under which phase separation occurs, and the points marked with downward-pointing triangles represent the conditions under which no separation occurs. For the computation of the spinode, two models were implemented: Model 1 utilizes a constant stiffness tensor (Haussiihl 1993), and Model 2 employs a composition-dependent stiffness tensor defined as $C(X) = (1-X) C_\text {Na} + XC_{\text {K}}$, where Brown et al. (2006) is referenced for $C_\text {Na}$ and Haussiihl (1993) is referenced for $C_\text {K}$.

The spinodal curves (Fig. 8a) were fitted by the function $f(X) = X(1-X)(aX + b(1-X)) + c$. The coefficients were estimated as $a = 9.1 \times 10^2$, $b = 3.9 \times 10^3$, $c = -99$ for Model 1, and $a = 5.4 \times 10^2$, $b = 4.0 \times 10^3$, $c = -86$ for Model 2. The maximum temperature for the coherent solvus in Model 1 was 555 $^{\circ }\text {C}\,$ at $X = 0.35$, which is 85 $^{\circ }\text {C}\,$ lower than the strain-free solvus. For Model 2, the maximum temperature was 545 $^{\circ }\text {C}\,$ at $X = 0.35$ with a differential $\Delta T = 96$ $^{\circ }\text {C}\,$.

The critical temperature of Model 1 was 15 $^{\circ }\text {C}\,$ higher than that reported by Petrishcheva et al. (2023), despite using identical parameters for computation. This discrepancy is likely due to overestimation of the elastic energy in Petrishcheva et al. (2023) at the initial stage of phase separation, which would be caused by their assumption of infinitely planar lamellae. Contrary to previous assumptions, our simulation does not assume any specific shape of the initially precipitated phase. Through simulation, our study identified disjointed small microstructures at the onset of phase separation (Fig. 9), which are more energetically favorable than planar microstructures. Accordingly, the estimated two-phase coexistence region was larger and the solvus temperature was higher than in the previous model.

In previous research, the stiffness tensor was assumed to be constant due to the small compositional dependencies of the stiffness tensor (Petrishcheva et al. 2023; Robin 1974). However, estimating the phase diagram from compositionally dependent stiffness is challenging because of the difficulties of mathematical analysis. On the other hand, our simulation-based phase diagram can easily estimate this effect. For example, we estimated the solvus in Model 2 (Fig. 8a), which was approximately 10 $^{\circ }\text {C}\,$ lower than that in Model 1.

In Fig. 8b, we estimated the binodal composition from the K- and Na-rich feldspar compositions after a long simulation run for various $X_0$ and $T$. We used the composition of each phase after $t^*=600$ as a proxy for binodal composition and carefully excluded data where the Gibbs energy did not appear constant at $t^*=600$. As a result, we observed a clear trend in the limb of the solvus on K-rich side. Specifically, the precursor phase composition $X_0$ was positively correlated with the binodal composition of the K-rich phase.

On the other hand, we cannot find a clear trend in the Na-rich feldspar solvi. The overall trend of the K-rich feldspar phase is consistent with the findings of Petrishcheva et al. (2023). As highlighted in their study, the shift of solvi does not appear if the elastic model of exsolution lamellae disregards the non-zero strain at the lamellar interfaces. Our simulation did not assume any constraints about interface strain, and this allowed us to successfully simulate the effects. However, our simulation-based approach for solvi estimation have some limitations and uncertainties. One problem is the lack of solvi information near the composition of the spinodal curve because phase separation does not complete within the timeframe if $(X_0, T)$ is close to the spinodal curve, as discussed in Sect. 4.2 (see Fig. 6). Additionally, sometimes Y-junctions did not disappear within the simulated time interval, potentially resulting in non-equilibrium compositions of phases.

Fig. 8

a Phase diagram computed using the Cahn–Hilliard model. When the precursor phase composition and annealing temperature correspond to an upward-pointing triangle, the growth of lamellae will proceed, and downward-pointing triangles correspond to conditions, where lamellae do not evolve. b Binodal compositions for different compositions of the precursor phase. The binodal compositions of the K-rich lamellae are clearly correlated when the precursor phase composition is K-rich, whereas the relation for the Na-rich feldspar phase is unclear

Fig. 9

The initial stage of phase separation at $t = 0.1$ d under the conditions of $X_0 = 0.35$ and $T=500$ $^{\circ }\text {C}\,$. The elastic energy does not exhibit a repeated lamellae microstructure, but rather shows small disjointed microstructure

New insights

The influence of elastic energy associated with the coherent lamellar intergrowth of Na-rich and K-rich alkali feldspar has been studied. This study advances our understanding of the morphological evolution of coherent alkali feldspar lamellae by evaluating the elastic energy contribution to the phase separation and the formation of lamellar microstructures by utilizing the Cahn–Hilliard model. The simulation successfully gives results consistent with previous research on orientation of lamellae, elastic strain in crystals and the coherent solvus of the binary system, and it predicts the dynamics and morphological evolution of the phase separation process. Notably, our study emphasizes the importance of the initial stage of phase separation, which often does not remain in natural rock records but has the potential to affect the overall behavior of solid solutions.

The simulation is also applicable to other coherent binary solid solutions because it does not assume any specific shapes for the lamellar interfaces. This flexibility enables the computation of the coherent solvus or phase separation dynamics for minerals that have complex lamellar interfaces.

Appendix A Derivation of evolution equation

A.0.1 Chemical potential

We assume that the chemical potential of the non-uniform A–B binary system $\mu _\alpha$ consists of three terms,

$$\begin{aligned} \mu _\alpha = \mu _\alpha ^{\text {chem}} + \mu _\alpha ^{\text {grad}} + \mu _\alpha ^{\text {str}}, \end{aligned}$$

(A1)

which are defined as variational derivatives,

$$\begin{aligned} \begin{aligned} \mu _\alpha&= \frac{\delta }{\delta n_\alpha }\int nG d\varvec{r},\\ \mu _\alpha ^{\text {chem}}&= \frac{\delta }{\delta n_\alpha }\int (n_A + n_B) G^{\text {chem}},\\ \mu _\alpha ^{\text {grad}}&= \frac{\delta }{\delta n_\alpha }\int (n_A + n_B) E^{\text {grad}},\\ \mu _\alpha ^{\text {str}}&= \frac{\delta }{\delta n_\alpha }\int E^{\text {str}},\\ \end{aligned} \end{aligned}$$

(A2)

for each component $\alpha = A, B$. The sum of the chemical potentials of first and second terms ($\mu _\alpha ^{\text {chem}} + \mu _\alpha ^{\text {grad}}$) in Eq. A1 is,

$$\begin{aligned} \begin{aligned} \mu _A^{\text {chem}} + \mu _A^{\text {grad}}&= G^{\text {chem}} + E^{\text {grad}} + (1 - X) \frac{\delta }{\delta X}\int G^{\text {chem}} + E^{\text {grad}} d\varvec{r}, \\ \mu _B^{\text {chem}} + \mu _B^{\text {grad}}&= G^{\text {chem}} + E^{\text {grad}} - X \frac{\delta }{\delta X}\int G^{\text {chem}} + E^{\text {grad}} d\varvec{r}, \end{aligned} \end{aligned}$$

(A3)

with mole fraction $X = n_A / (n_A + n_B)$ (Petrishcheva and Abart 2009). The difference in chemical potential at both endmembers is summarized as,

$$\begin{aligned} \begin{aligned} \Delta \mu ^{\text {chem}}&:= \mu _A^{\text {chem}}-\mu _B^{\text {chem}} = \frac{\delta }{\delta X}\int G^{\text {chem}} d\varvec{r}, \\ \Delta \mu ^{\text {grad}}&:= \mu _A^{\text {grad}}-\mu _B^{\text {grad}} = \frac{\delta }{\delta X}\int E^{\text {chem}} d\varvec{r}. \end{aligned} \end{aligned}$$

(A4)

On the other hand, the last term $\mu _\alpha ^{\text {str}}$ in Eq. A1 is given by,

$$\begin{aligned} \begin{aligned} \mu _A^{\text {str}}&= \frac{\partial X}{\partial n_A} \frac{\delta }{\delta X}\int E^{\text {str}} d\varvec{r}= \frac{1-x}{n}\int E^{\text {str}} d\varvec{r},\\ \mu _B^{\text {str}}&= \frac{\partial X}{\partial n_B} \frac{\delta }{\delta X}\int E^{\text {str}} d\varvec{r}= \frac{-x}{n}\int E^{\text {str}} d\varvec{r}, \end{aligned} \end{aligned}$$

(A5)

and the difference of chemical potential in both endmembers are,

$$\begin{aligned} \Delta \mu ^{\text {str}} := \mu _A^{\text {str}}-\mu _B^{\text {str}} = \frac{\delta }{n\delta X}\int E^{\text {str}} d\varvec{r}. \end{aligned}$$

(A6)

A.0.2 Free energy density

From this definition, the diffusion potential, $\mu ^\text {chem}$, which depends solely on the mole fraction, can be derived directly as,

$$\begin{aligned} \begin{aligned} \Delta \mu ^\text {chem}&= \frac{\delta }{\delta X} \int G^\text {chem}d\varvec{r}\\&= \frac{\partial G^\text {chem}(X)}{\partial X} \\&= RT\ln \left( \frac{X}{1-X}\right) + (1 - 2X)(W_{\text{Na}}X + W_{\text{K}}(1-X)) \\&\quad + X(1-X)(W_{\text{Na}} - W_{\text{K}}). \end{aligned} \end{aligned}$$

(A7)

A.0.3 Gradient energy

When analyzing of gradient energy, we consider the effect of an infinitesimal change in the mole fraction $X$ as transitioning from $X$ to $X + \delta X$. The change of gradient energy, $\delta E^\text {grad}$, is given by,

$$\begin{aligned} \begin{aligned} \delta E^\text {grad}&= \int \kappa (\nabla (X + \delta X))^2 d\varvec{r} - \int \kappa (\nabla X)^2 d\varvec{r} \\&= \int 2\kappa \nabla X \cdot \nabla \delta X d\varvec{r} \\&= \int 2\kappa \nabla \cdot (\delta X \nabla X)d\varvec{r} - \int 2\kappa \delta X \nabla ^2 X d\varvec{r}. \end{aligned} \end{aligned}$$

(A8)

By applying Gauss’s divergence theorem, the first term on the right-hand side of the last equality can be expressed as a surface integral,

$$\begin{aligned} \int 2\kappa \nabla \cdot (\delta X \nabla X)d\varvec{r} = \int _{S} 2\kappa (\delta X \nabla X) \cdot d\varvec{S}, \end{aligned}$$

(A9)

where the integral over $S$ represents the surface contribution. In the macroscopic limit, this surface term becomes negligible and, thus, our attention is focused solely on the volumetric changes. Hence, based on the definition of the variational derivative, the diffusion potential attributed to the interfacial energy is succinctly given by,

$$\begin{aligned} \Delta \mu ^\text {grad} = -2\kappa \nabla ^2 X. \end{aligned}$$

A.0.4 Elastic energy

If the displacement vector $\varvec{u}(\varvec{r}) = (u_1(\varvec{r}), u_2(\varvec{r}), u_3(\varvec{r}))$ is sufficiently small, it is appropriate to apply linear elasticity theory to describe the strain behavior in the material (Nye 1985). Under this condition, the total strain, $\epsilon ^t_{ij}(\varvec{r})$ can be expressed in terms of the displacement field,

$$\begin{aligned} \epsilon ^t_{ij} = \frac{1}{2} \left( \partial _j u_i + \partial _i u_j \right) , \end{aligned}$$

(A10)

where $\partial _j u_i := \partial u_i / \partial x_j$. The relationship between elastic strain $\epsilon ^{el}_{ij}$ and stress within the material (Mura 1987) is described by Hooke’s law, given by

$$\begin{aligned} \sigma ^{el}_{ij}(\varvec{r}) = C_{ijkl} \epsilon ^{el}_{kl}(\varvec{r}) = C_{ijkl}\left\{ e^{t}_{kl}(\varvec{r}) - \eta _{kl}(X(\varvec{r})-X_0) \right\} , \end{aligned}$$

(A11)

where the Einstein summation convention is employed for shorthand notation. The mechanical equilibrium condition in the absence of external volumetric forces is

$$\begin{aligned} \frac{\partial \sigma ^{el}_{ij}}{\partial x_j} = 0. \end{aligned}$$

(A12)

Combining this equilibrium condition with the Eqs. A10, A11, A12 allows for the determination of a unique displacement field $\varvec{u}$ within the material. The combination of Eqs. A10, A11 and substitution of them into Eq. A12 gives us the equilibrium equation,

$$\begin{aligned} \begin{aligned} \frac{1}{2}C_{ijkl} \left( \frac{\partial ^2 u_k}{\partial x_j \partial x_l} + \frac{\partial ^2 u_l}{\partial x_j \partial x_k}\right)&= C_{ijkl}\left( \frac{\partial ^2 u_k}{\partial x_j \partial x_l} \right) \\&= C_{ijkl}\eta _{kl} \frac{\partial X}{\partial x_j}. \end{aligned} \end{aligned}$$

(A13)

We redefine the elastic strain tensor $\epsilon ^{el}_{ij}(\varvec{u}, X)$ in terms of the displacement field $\varvec{u}$ and mole fraction $X$, incorporating Eqs. 7, A10,

$$\begin{aligned} \epsilon ^{el}_{ij} = \frac{1}{2}(\partial _j u_i + \partial _i u_j) - \eta _{ij}(X-X_0). \end{aligned}$$

The elastic energy density $E(\varvec{u}, X)$ is then expressed by

$$\begin{aligned} \begin{aligned} E(\varvec{u}, X)&:= \frac{1}{2} C_{ijkl} \epsilon ^{el}_{ij} \epsilon ^{el}_{kl} \\&= \frac{1}{2} C_{ijkl} \left\{ \frac{1}{2}(\partial _j u_i + \partial _i u_j) - \eta _{ij}(X-X_0) \right\} \times \\&\left\{ \frac{1}{2}(\partial _k u_l + \partial _l u_k) - \eta _{kl}(X-X_0) \right\} , \end{aligned} \end{aligned}$$

(A14)

utilizing the symmetries of the stiffness tensor, $C_{ijkl} = C_{jikl} = C_{ijlk}$. The variation of elastic energy with respect to the displacement field $\varvec{u}(\varvec{r})$ at a fixed mole fraction $X$ yields:

$$\begin{aligned} \begin{aligned} \delta E^\text {str}&= \int _{\varvec{r}} \frac{1}{2}C_{ijkl}\{\partial _j (u_i+\delta u_i)- \eta _{ij}(X-X_0)\}\\&\quad\times\{\partial _l (u_k+\delta u_k) - \eta _{kl}(X-X_0)\} d\varvec{r}\\&\quad -\int _{\varvec{r}}\frac{1}{2}C_{ijkl}\{\partial _j u_i - \eta _{ij}(X-X_0)\}\{\partial _l u_k - \eta _{kl}(X-X_0)\} d\varvec{r}\\&=\int _{\varvec{r}} C_{ijkl}\{\partial _j \delta u_i\partial _l u_k - \partial _j \delta u_i \eta _{kl}(X-X_0)\} d\varvec{r}\\&=-\int _{\varvec{r}} \partial _j C_{ijkl}\{\partial _l u_k - \eta _{kl}(X-X_0)\} \delta u_i d\varvec{r}\\&=-\int _{\varvec{r}} \partial _j C_{ijkl}\{1/2(\partial _l u_k + \partial _k u_l) - \eta _{kl}(X-X_0)\} \delta u_i d\varvec{r}\\&=-\int _{\varvec{r}} \partial _j C_{ijkl}\epsilon ^{el}_{kl} \delta u_i d\varvec{r}\\&=-\int _{\varvec{r}} (\partial _j \sigma ^{el}_{ij}) \delta u_i d\varvec{r}\\&= 0, \end{aligned} \end{aligned}$$

(A15)

leveraging $C_{ijkl} = C_{klij}$ and Eq. A12. This demonstrates that the change in elastic energy due to displacement variations is strictly zero, suggesting that energy changes are primarily influenced by variations in $X(\varvec{r})$, as discussed in prior studies (Koyama and Miyazaki 1998; Onuki 2002). Thus, the diffusion potential of elastic energy, $\mu ^\text {str}$, is derived as

$$\begin{aligned} \Delta \mu ^\text {str} = \frac{\delta }{\delta X}\int E^\text {str} d\varvec{r}= \frac{\partial E^\text {str}(\varvec{u}, X)}{\partial X} = -C_{ijkl}(e^{t}_{ij} - \eta _{ij}(X-X_0)) \eta _{kl}. \end{aligned}$$