1 Introduction

Canopy flows are common in the atmospheric boundary layer and can be roughly divided into natural vegetative canopies (e.g. forests), urban canopies (large cities), and agricultural canopies (e.g. maize fields). During the last decades, the flow over canopies has been extensively studied and the general picture of canopy flows with regard to momentum, mass, and heat transfer over idealized conditions, i.e. homogeneous canopies on flat terrain, has become clear (see reviews by Finnigan 2000; Brunet 2020). The focus of recent research efforts has shifted towards elucidating the effects of spatial heterogeneities, e.g. due to landscape fragmentation, on transfer properties. In particular, much research has been done on cases where the governing flow direction is either perpendicular to the canopy’s edge leading to the formation of internal boundary layers, or parallel leading to the onset of secondary circulations (see review and references herein by Bou-Zeid et al. 2020). Vegetative canopies constantly exchange heat, momentum, and mass with the outside flow through strong shear layers that develop at the canopy’s edges. However, at present, little detailed information is available on the flow field characteristics across a spanwise vegetative canopy edge. Of particular interest are the momentum, heat, and mass transfer processes that occur across the spanwise canopy edge as their understanding may aid in mitigating desertification and/or in applying smart irrigation techniques.

It is well-known that for horizontally homogeneous canopies, transfer processes are driven by large-scale coherent structures (sweeps and ejections) generated as a result of Kelvin-Helmholtz instabilities at canopy height (Finnigan 2000). At the spanwise canopy edges of vegetative canopies, similar transfer mechanisms may be expected. However, as far as we are aware, the effect of spanwise heterogeneity has only been studied for vegetated river banks, flood plains, and estuarine channels with fringing mangroves (e.g. and references herein, Li et al. 2022; Nezu and Onitsuka 2002; White and Nepf 2008; Yan et al. 2016; Unigarro Villota et al. 2023), where the vegetation usually emerges from the water. These studies indicated that as a result of an inflection point of the transverse profile of the mean streamwise velocity across the canopy edge, coherent vortices were generated. These were responsible for the momentum exchange across the spanwise edge. White and Nepf (2008) proposed a model for predicting the distributions of velocity and shear stress across a spanwise edge of an emergent model canopy in a shallow water channel. Their model is based on distinguishing two regions within the high shear layer and predicts the width of the momentum penetration into the vegetation due to vortex-induced exchange.

The most commonly applied methodology for analyzing turbulent transport processes across interfaces is applying statistical ensemble averaging techniques in an Eulerian frame of reference. This approach is hereafter termed the “conventional ensemble average (CEA)” approach. A disadvantage of this approach is that it leads to smearing of the “jumps” of flow quantities across sharp interfaces, in particular when the instantaneous interface is constantly changing such as in jets, wakes and mixing layers (da Silva et al. 2014). Therefore in recent years, research has focused on extracting instantaneous interface dynamics and on understanding their effect on ensemble averaged flow statistics (Saxton-Fox and McKeon 2017; McKeon 2019; Bautista et al. 2019). This approach employs conditional sampling to determine the change of flow properties across instantaneous interfaces between turbulent and non-turbulent interfaces and within turbulent flows, and is hereafter termed the “conditionally sampled instantaneous interface (CSII)” approach. The nature and the properties of the sharp interfaces that demarcate turbulent from non-turbulent flow, as well as those demarcating uniform momentum zones (UMZs) within turbulent flows, have been studied extensively. Corrsin and Kistler (1955) provided the first empirical evidence of the existence of a convoluted thin layer connecting the turbulent rotational region and the external region characterized by weak fluctuations, nowadays referred to as the turbulent/non-turbulent interface (TNTI) (Anand et al. 2009; Westerweel et al. 2009). In the past few decades, several studies have focused on the detection of TNTIs, (i) by thresholding based on vorticity and enstrophy (Bisset et al. 2002; Westerweel et al. 2009; Long et al. 2023), TKE (Chauhan et al. 2014; Kwon et al. 2016; Saxton-Fox and McKeon 2017), velocity magnitude (Holzner et al. 2006), or combined velocity-vorticity (Anand et al. 2009), and (ii) by using a passive scalar approach, in the form of dye in experiments (Mistry et al. 2016; Kohan and Gaskin 2020) or scalars in numerical simulations (Watanabe et al. 2015). A common characteristic of TNTIs is that they are highly dynamic and govern entrainment and transport processes of momentum and scalars by engulfing and nibbling motions (Westerweel et al. 2005; da Silva et al. 2014).

Compared to TNTIs, less is known about thin internal interfacial layers (hereafter termed “internal interfaces”) that demarcate between flow regions in a turbulent flow with nearly constant streamwise momentum, broadly referred to as UMZs. The presence of internal interfaces within wall-bounded turbulent flows was established through the research of Meinhart and Adrian (1995), who based interface detection on a histogram modal velocity analysis of vector maps acquired by planar particle image velocimetry (PIV). After detection of the instantaneous (internal) interfaces in the PIV snapshots, conditionally sampled, average properties across the interface can be determined (CSII approach). In the last decade, internal interfaces and associated UMZs in turbulent flows have been investigated by several research groups (Eisma et al. 2015; de Silva et al. 2016, 2017; Gul et al. 2020; Hearst et al. 2021) and more recently in atmospheric boundary layer flows (Heisel et al. 2023; Ehsani et al. 2024). Their results showed that large jumps in velocity, Reynolds stresses and vorticity occur between adjacent UMZs, making these interfaces hot spots of transfer processes. These zones are thought to be associated with hairpin packets in turbulent boundary layers (e.g. Eisma et al. 2015) and have also been observed in modeling of large-scale coherence in turbulent boundary layers (Saxton-Fox and McKeon 2017; McKeon 2019). In addition, Bautista et al. (2019) have used UMZs to model boundary layer statistics up to fourth order.

As is clear from the above, internal interfaces have been studied in detail for turbulent wall-bounded flows. However, UMZs and associated internal interfaces that govern instantaneous mass, momentum, and heat transfer, are also expected to be important across a spanwise canopy edge. However, flow field characteristics across spanwise vegetative canopy edges have not been studied much. The aim of this research was to analyze the three-dimensional (3D) flow field across a spanwise canopy edge applying the CEA and the CSII approaches. The analysis is based on data collected within and above a wind tunnel vegetative canopy model, obtained by stereoscopic image velocimetry (SPIV) in wall-parallel planes in between canopy elements. By comparing these two approaches, an improved understanding is achieved of how the instantaneous interface dynamics affect the ensemble averaged flow statistics. The experimental setup including the model canopy and the SPIV system is described in Sect. 2. Instantaneous interface detection is described in Sect. 3 after which the results are presented in Sect. 4. Section 5 provides a short summary and conclusions.

2 Experimental Setup

Fig. 1
figure 1

Schematic of the a heterogeneous model canopy layout (top view), b field of view (FOV) of the SPIV measurements (top view) at canopy height (\(x_3/h\) = 1), c canopy element, d spanwise cross-section of the SPIV setup. Not to scale, all dimensions are in cm

Full size image

The experiments were performed in the Environmental Wind Tunnel at the Civil and Environmental Engineering Faculty at the Technion-IIT. The tunnel has a 16.1 m long, square (1.95 \(\times \) 1.95 m\(^2\)) test section, and for more specific details the reader is referred to Winiarska et al. (2023). A model canopy with a streamwise length of 4.8 m and consisting of triangular-shaped, perforated canopy elements (height, h = 200 mm, Fig. 1c) was assembled inside the wind tunnel. The canopy elements were perforated with 18 and 20 mm diameter holes spaced evenly over three levels (see Fig. 1c). The elements were designed to match the vertical distribution of the projected frontal area index (PFAI) defined as the total frontal area of canopy elements per unit ground area, of corn canopies (Wilson et al. 1982; Boedhram et al. 2001; van Hout et al. 2007). The canopy elements were mounted on the tunnel floor in an inline configuration (see Fig. 1), transverse to the streamwise velocity component. The streamwise distance between the canopy elements was 10 ± 0.5 cm giving PFAI = 0.61, i.e. lower than those in actual maize crops (van Hout et al. 2007; Wilson et al. 1982), but still characteristic of relatively dense artificial vegetative canopies (Finnigan 2000; Pietri et al. 2009; Zhu et al. 2006).

The experiments were performed on both a homogeneous and a heterogeneous canopy layout as discussed in detail by Winiarska et al. (2023). A spanwise heterogeneity was created by clearing the middle section of the canopy model (open patch, width S = 63 cm) at the center of the wind tunnel (Fig. 1). Two right-handed, orthogonal coordinate systems are used. One positioned at the start of the canopy field with its origin at the center of the open patch, \(x^*_i\) (i = 1–3) (Fig. 1a), where i = 1, 2 and 3 denote the streamwise, transverse and wall-normal directions, and the other, \(x_i\) (i = 1–3), with its origin positioned at the edge of the canopy element projected onto the bottom of the wind tunnel (see Fig. 1b, d). Corresponding instantaneous flow velocities are denoted by \(U_i\), fluctuating velocity components (Reynolds decomposed) by \(u_i\) (i = 1–3). Ensemble averaged values, denoted by an overbar, were calculated as averages over all statistically independent measurements at each height. Note that statistically independent measurements imply that the measurements were spaced at least one integral timescale apart as was validated by hot-wire measurements just above canopy. Spatial averages are indicated by angle brackets, and |..| denotes the magnitude.

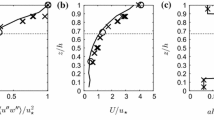
In the first stage of this study, the wind tunnel floor was fully covered by the model canopy (homogeneous layout). In order to ensure fully developed conditions at the measurement position, wall-normal profiles of the mean streamwise flow velocity above canopy were obtained at various streamwise and spanwise locations in the wind tunnel, using an array of pitot tubes mounted on a 3-axis traverse system. The wall-normal profiles of \({\overline{U}}_1/U_\infty \) at different \(x_1^*/h\) depicted in figure 2a, show that at \(x_1^*/h\) = 15 and 17.5, profiles of \({\overline{U}}_1/U_\infty \) collapse, indicating that a fully developed mean velocity profile is obtained. The normalized 99% boundary layer thickness was \(\delta /h\) = 3.5 (based on the pitot tube measurements), while the friction velocity for the homogeneous layout was \(u_\tau = \sqrt{-\overline{u_1u_3}}\) = 0.24 m/s based on average peak values of the Reynolds shear stress components, \(\overline{u_1u_3}\), between 1 \(\le x_3/h \le \) 1.5, extracted from SPIV measurements (see Winiarska et al. 2023). In the heterogeneous layout, \(u_\tau \) reduced from 0.27 m/s between two canopy elements to 0.26 m/s and 0.25 m/s at the canopy edge and in the open patch, respectively (Winiarska et al. 2023). The canopy Reynolds numbers \(\hbox {Re}_h\) = \(u_\tau \) \(h\)/\(\nu \) (Brunet et al. 1994), where \(\nu \) represents the air kinematic viscosity, were \(\hbox {Re}_h\) = 3200 and 3467 in the homogeneous and heterogeneous (at \(x_2/h\) = 0) layout, respectively. Further note that when the middle section was removed (heterogeneous layout), the ratio between the open patch width and the boundary layer thickness equaled, S/\(\delta \approx \) 0.85, indicating that large-scale secondary motions may arise (Vanderwel and Ganapathisubramani 2015). However, resolving these secondary flows is beyond the scope of the present investigation.

Fig. 2
figure 2

Wall normal profiles of the normalized, mean streamwise velocity a along the model wind tunnel canopy, and at different spanwise locations (at \(x_1^*/h\) = 16.5) for the b homogeneous and c heterogeneous canopy layout. Markers in (a) are displayed at reduced spatial resolution (every 14th data point) but lines connect between all data points explaining the raggedness

Full size image

Three components of the velocity field across the spanwise canopy edge, within and above the heterogeneous canopy layout were measured using a SPIV setup (Fig. 1). The measurements were performed at \(x_1^*/h\) = 16.5 and the spanwise variation of \({\overline{U}}_1/U_\infty \) in the homogeneous and heterogeneous layouts based on the pitot tube measurements is shown in Fig. 2b, c, respectively. As can be observed in Fig. 2b, the spanwise variation of \({\overline{U}}_1\) in the homogeneous layout is about 0.1\({\overline{U}}_\infty \) between 1 \(< x_3/h<\) 2, as a result of the non-homogeneous flow structure in the model canopy as will be discussed in the following. In contrast, for the heterogeneous layout (Fig. 2c), the wall-normal gradients of \({\overline{U}}_\infty \) strongly reduce upon moving across the canopy edge. At \(x_3/h\) = 2, the spread in \({\overline{U}}_\infty \) is similar as measured in the homogeneous layout indicating that the canopy edge effect is “felt” only up to twice the canopy height.

The SPIV setup consisted of two CCD cameras (2048 \(\times \) 2048, 7.4 \(\times \) 7.4 \(\upmu \)m\(^2\) pixels), a pulsed, dual-head Nd: YAG laser (Litron, 200 mJ/pulse max output at 15Hz), laser sheet optics and data acquisition and processing software (DaVis10, LaVision GmbH). The laser sheet was centered between two rows of canopy elements (see Fig. 1a) passing through the test section parallel with the bottom similar as Nezu and Onitsuka (2002) in an aquatic environment. Vaporized glycerol-water solution particles (1–2 \(\upmu \)m) were introduced at the inlet of the wind tunnel just before the honeycomb using a fog machine (Antari FT-100). Two cameras spaced 1.35 m apart, were mounted on top of the wind tunnel (Fig. 1d). They were equipped with lenses (Nikon MicroNikkor, 200 mm, \(\hbox {f}_\#\) = 5.6) and Scheimpflug adapters to achieve focus over the whole field of view (FOV) (Adrian and Westerweel 2011). The laser sheet thickness at the position of the FOV was about 3 mm. Calibration was done using a dual-plane calibration target aligned with the laser light sheet and the mapping function for each camera was determined by a third-order polynomial fit. This resulted in a FOV of approximately 13 \(\times \) 13 cm\(^2\) that crossed the spatial heterogeneity as illustrated in Fig 1b at canopy height (\(x_3/h\) = 1). Note that due to laser light reflections close to the canopy elements, especially near canopy height (\(x_3/h\) = 0.95 and 0.85), vectors could not be accurately determined. As a result, data in these regions are blanked out in the plots.

Velocity field measurements were conducted at one bulk flow rate, corresponding to a free stream air velocity of \(U_\infty \) = 3 m/s, resulting in a boundary layer Reynolds number, \(Re_\delta \) = \(U_\infty \) \(\delta \)/\(\nu \) = 1.4 \(\times 10^5\), where \(\nu \) represents the air kinematic viscosity. Measurements were performed in 13 wall-parallel planes positioned between \(x_3/h\) = 0.7 and 1.3 (spaced at \(\varDelta x_3/h\) = 0.05) and in an additional three wall-parallel planes positioned at \(x_3/h\) = 0.5, 0.975 and 1.5. However, internal interfaces (see Sect. 3) were only detected below canopy (\(x_3/h \le \) 0.95), and here we present only data acquired at \(x_3/h\) = 0.5, 0.7, 0.85, and 0.95. For each height, 3000 statistically independent PIV image pairs per camera were acquired at 1 Hz. 2D velocity distributions were calculated for each camera separately, using multi-pass cross-correlation based on fast Fourier transforms as implemented in DaVis 10 (LaVision GmbH). The interrogation window size was reduced from 64 \(\times \) 64 pixels to 24 \(\times \) 24 pixels with 50% overlap leading to a vector spacing ranging between 0.728 mm and 0.773 mm, depending on the measurement height. In between passes and in the final post-processing step, a vector validation and a robust, universal outlier median filter (Adrian and Westerweel 2011) were applied to remove outliers. The average percentage of outliers did not exceed 3% of the total number of vectors. Removed outliers were replaced by linear interpolation as implemented in DaVis10 (LaVision GmbH). Taking advantage of the different camera perspectives, the 2D velocity components were used to determine all three velocity components in the laser sheet plane (Raffel et al. 2018) using DaVis10 software (LaVision GmbH).

The out-of-plane vorticity component (hereafter termed “vorticity”) was determined by \(\omega _3 = \frac{\partial U_1}{\partial x_2} - \frac{\partial U_2}{\partial x_1}\), where the velocity gradients were determined by central difference schemes. In addition, the directional swirling strength (hereafter termed “swirling strength”), \(\varLambda _{ci} = \lambda _{ci}\frac{\omega _3}{|\omega _3|}\) (Adrian et al. 2000), was calculated, where \(\lambda _{ci}\) denotes the complex imaginary eigenvector of the velocity gradient tensor evaluated for a 2D vector field. Note that in contrast to the vorticity that displays both shear as well as rotational motion, the swirling strength isolates rotational motion.

Statistical uncertainties of the SPIV measurements were evaluated assuming uncorrelated and normally distributed velocities (Benedict and Gould 1996). Under these constraints and for 95% confidence intervals, the uncertainty of \({\overline{U}}_i\) was less than ±3%. The uncertainty of the Reynolds shear stress components \(\overline{u_1u_2}\) and \(\overline{u_1u_3}\) did not exceed ±11.5%, while that of the triple correlation term was within ±32%. The uncertainty associated with the measurement height was \(\pm 0.01\) h.

3 Detection of Instantaneous Interfaces

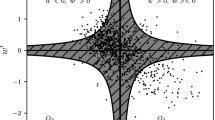
The detection of the instantaneous interface demarcating between different UMZs follows the quantitative modal maxima method proposed by Adrian et al. (2000). The methodology is based on examining histograms of the instantaneous streamwise velocities for each PIV snapshot (see also de Silva et al. 2016, 2017; Gul et al. 2020) and is illustrated for one snapshot in Figs. 3a, d. When UMZs are present in the flow field, the histogram is characterized by distinct peaks (“modes”), and each local maximum is termed a “modal velocity” (indicated by the red circles in Figs. 3d). The arithmetic mean of the two modal velocities, \(U_1^i\) (the superscript “i” denotes interface), is indicated by a vertical red dashed line in Fig. 3d, and sets the boundary of the instantaneous interface between the detected UMZs. In the particular example of Figs. 3a, d, a single interface was detected based on the two detected modal velocities in the histogram of \(U_1/U_\infty \) (Fig. 3d). The interface is superposed as isolines of \(U_1^i/U_\infty \) (magenta curves) on the corresponding surface plot of \(U_1/U_\infty \) in Fig. 3a. It can be seen that in addition to the interface between two UMZs, also some small “blobs” are demarcated. These blobs were removed in a subsequent processing step by applying an area-based threshold. Furthermore, the final interface between the two UMZs superposed in black on the original detected interface (magenta curve) in Fig. 3a, was taken as the smallest \(x_2/h\) position and no multiple interface positions for a given \(x_1/h\) location were recorded, similar as applied by Westerweel et al. (2009). The final interface position is denoted by \(x_2^i\) and flow field characteristics were conditionally sampled with respect to it. At each side of \(x_2^i\), a maximum of seven data points were taken into account, i.e. a thin strip between -0.03 \(\le \left( x_2-x_2^i\right) /h \le \) 0.03. Note that based on the nature of the flow across the spanwise canopy edge, the applied interface detection was constrained to the assumption that only one significant interface exists. Therefore, in case more than two interfaces were detected, the interface velocity, \(U^i_1\), between the two modal velocities having the highest counts, was identified as the instantaneous interface.

Fig. 3
figure 3

Example of the modal maxima method applied to detect instantaneous interfaces between UMZs, and the effect of increasing the number of bins. Upper row: surface plots at \(x_3/h=0.85\) of \(U_1/U_\infty \) including the preliminary interface (magenta curve) according to \(U^i_1/U_\infty \) and the final interface location (black curve). Gray rectangles indicate the canopy elements. The modal maxima method was applied using a, d 10, b, e 20, and c, f 30 bins. Red circles and vertical dashed lines indicate detected modal velocities and values of \(U_1^i/U_\infty \) are depicted in red in the bottom row

Full size image
Fig. 4
figure 4

The effect of the number of bins on flow parameters conditionally sampled with respect to \(x_2^i\) (at \(x_3/h = 0.85\)). a \(\langle {\overline{U}}_1^i\rangle /U_{\infty }\), b \(\langle {\overline{U}}_2^i\rangle /U_{\infty }\), c \(-\langle \overline{u_1u_2}^i\rangle /U_{\infty }^2\), d \(\langle {{\overline{\omega }}}_3^i\rangle h/U_{\infty }\). Numbers in the legend correspond to the number of bins

Full size image

Two different averaging approaches are applied here. The first is the CEA approach in which conventional ensemble averages of the acquired PIV vector maps are calculated and Reynolds decomposition (Pope 2000) is applied. Quantities based on this approach are denoted by the superscript “c”. The second one is the CSII approach in which ensemble averages are calculated based on the conditionally sampled interface data. Subsequently, Reynolds decomposition is performed with respect to the conditionally averaged flow velocities. Flow field parameters based on this approach are denoted by the superscript “i”.

The probability of detecting more than two modal velocities increases as the number of histogram bins is increased. This is illustrated in Fig. 3d–f, where histograms of \(U_{1}/U_\infty \) are depicted for an increasing number of bins. As can be seen, using 10 bins (Fig. 3d), only two modal velocities are detected, whereas for 20 and 30 bins depicted in Fig. 3e, f, respectively, four modal velocities are present. As can be seen, \(U_1^i/U_\infty \) increases with the number of bins for this particular example which slightly affects the instantaneous final boundaries that are depicted in black in the upper row of Fig. 3. However, as a result of the strong spanwise gradients of \(U_1\) at the interface, the effect on the conditionally sampled statistics is small as is discussed in the following.

In order to evaluate the effect of the number of bins on the flow field characteristics across the interface, the transverse profiles of the normalized mean velocities, \(\langle {\overline{U}}_1^i\rangle /U_\infty \), \(\langle {\overline{U}}_2^i\rangle /U_\infty \), Reynolds shear stress component, \(-\langle \overline{u_1u_2}^i\rangle /U_\infty ^2\), and the vorticity \(\langle {{\overline{\omega }}}_3^i\rangle h/U_\infty \), across the interface were determined for bin numbers ranging between eight to twenty. The flow parameters were ensemble averaged as well as spatially averaged over the streamwise direction. Results depicted in Fig. 4 indicate that as expected, significant “jumps” of the investigated quantities exist across the thin interface. The effect of changing the number of bins is minor for \(\langle {\overline{U}}_1^i\rangle /U_\infty \) and \(\langle {{\overline{\omega }}}_3^i\rangle h/U_\infty \) depicted in Fig. 4a, d, respectively, while a more significant effect is observed in \(\langle {\overline{U}}_2^i\rangle /U_\infty \) and \(\langle -\overline{u_1u_2}^i\rangle /U_\infty ^2\) depicted in Fig. 4b, c, respectively. However, upon close scrutiny, it can be seen that in most of the cases, the difference between using 8 to 12 bins is relatively small. Note that although Reynolds stresses (see Fig. 4c) exhibit slightly larger changes in magnitude, the underlying trends remain preserved. Therefore based on this, all data sets were processed using 10 bins. Note that for this number of bins, in the majority of snapshots, only two modal velocities (one interface) were detected.

The interface detection procedure was applied to data recorded at all heights, but distinct interfaces were only detected below canopy (\(x_3/h \le 0.95\)). Furthermore, interfaces were not detected in all instantaneous snapshots, and the ratio of snapshots with interfaces to the total number of snapshots increased with decreasing height: 0.73, 0.78, 0.80, and 0.84 for \(x_3/h\) = 0.95, 0.85, 0.70 and 0.50, respectively. Joint probability density functions (JPDFs) of the instantaneous interface location at the different heights are displayed in Fig. 5. The results show that for \(x_3/h \le \) 0.85 (Fig. 5a–c) and \(x_1/h \le \) 0.05, the interface is predominantly the result of the canopy element obstruction. At \(x_3/h\) = 0.95 (Fig. 5d), interfaces were also detected close to the perforations in the canopy elements. At all heights, instantaneous interface positions were predominantly detected for \(x_2/h \le \) 0, indicating the inward incursion of the interface. In the following, the flow field characteristics across the CSII will be compared to those obtained by the CEA approach.

Fig. 5
figure 5

JPDFs of the instantaneous spanwise location of the detected interface at \(x_3/h\) = a 0.50, b, 0.70, c 0.85, and d 0.95. Gray rectangles indicate canopy elements

Full size image

4 Results

4.1 Mean Velocities and Reynolds Stresses

Fig. 6
figure 6

Examples of contour plots (\(x_3/h\) = 0.85) of a \({\overline{U}}_1^i/U_\infty \), b \({\overline{U}}_2^i/U_\infty \), c \({\overline{U}}_1^c/U_\infty \), and d \({\overline{U}}_2^c/U_\infty \). Vertical white dashed lines indicate streamwise positions \(x_1/h\) = 0.05, 0.25, and 0.40. Note constant level spacing in (a) and (c) equals and in (b) and (d)

Full size image

Examples of contour plots of the normalized, ensemble averaged streamwise and spanwise velocities, \({\overline{U}}_1/U_\infty \) and \({\overline{U}}_2/U_\infty \), respectively, are depicted in Fig. 6 at \(x_3/h\) = 0.85. Results are shown for the CSII (upper row in Fig. 6), and the CEA (bottom row in Fig. 6). Results at different heights (\(x_3/h \le \) 0.95) showed similar trends and are not shown here. For clarity, the y-axes are scaled differently in the upper and the bottom rows of Fig. 6. As expected, a clear “jump” in \({\overline{U}}_1\) is observed both for the CSII (Fig. 6a) and the CEA (Fig. 6c). However, this jump is much more pronounced across the CSII (Fig. 6a) in agreement with literature results in turbulent boundary layers (Eisma et al. 2015; Hearst et al. 2021) and turbulent jets (Westerweel et al. 2005). In all cases, the spanwise gradients of \({\overline{U}}_1\) across the CSII strongly exceed those of the CEA (not shown). For example, for this particular height, the value of the maximum spanwise gradient of \({\overline{U}}_1^i/U_\infty \) at \(x_1/h\) = 0.25 equals \(\partial {\overline{U}}_1^i/\partial x_2\) = 127.4 s\(^{-1}\), which is one order of magnitude larger than the maximum gradient of \(\partial {\overline{U}}_1^c/\partial x_2\) = 16.2 s\(^{-1}\) at this location. These high values of the shear across the conditionally sampled instantaneous interface indicate the disproportionate (with respect to the area it occupies) contribution of the CSII to the conventional mean shear and emphasize the well-known intermittent nature of turbulent flows and transport.

Fig. 7
figure 7

Spanwise profiles of \({\overline{U}}_1^i/U_\infty \) (top row) and \({\overline{U}}_1^c/U_\infty \) (bottom row) for \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Columns from left to right correspond to streamwise positions, \(x_1/h\) = 0.05, 0.25, 0.40, respectively, indicated by the vertical white dashed lines in Fig. 6. Data points in the bottom row are depicted at half the actual spatial resolution

Full size image

The contour plots of \({\overline{U}}_2^i/U_\infty \) and \({\overline{U}}_2^c/U_\infty \) that are depicted in Fig. 6b, d, respectively, indicate that spanwise gradients of \({\overline{U}}_2\) are small compared to those of \({\overline{U}}_1\), except for small \(x_1/h\) close to the canopy element. However, \({\overline{U}}_2^i/U_\infty \) (Fig. 6b) changes sign and becomes negative for \(x_1/h \ge \) 0.08 with increasing \(x_1/h\) along \((x_2-x^i_2)/h = 0\). This indicates that just downstream of the first canopy element (\(x_1/h \le \) 0.08), the instantaneous interface moves on average outward into the open patch while moving inward further downstream. Note that the contour plot of \({\overline{U}}_2^c/U_\infty \) (Fig. 6d) shows a similar distribution along \(x_2/h\) = 0 with increasing \(x_1/h\).

Fig. 8
figure 8

Spanwise profiles of \({\overline{U}}_2^i/U_\infty \) (top row) and \({\overline{U}}_2^c/U_\infty \) (bottom row) for \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Columns from left to right correspond to streamwise positions, \(x_1/h\) = 0.05, 0.25, 0.40, respectively, indicated by the vertical white dashed lines in Fig. 6. Data points in the bottom row are depicted at half the actual spatial resolution

Full size image

In order to analyze the effect of changing height, spanwise profiles of \({\overline{U}}_1^i/U_\infty \) and \({\overline{U}}_1^c/U_\infty \) at streamwise locations \(x_1/h\) = 0.05, 0.25 and 0.40 (see dashed vertical white lines in Fig. 6) are shown in Fig. 7 for different heights below canopy. Similar plots for \({\overline{U}}_2/U_\infty \) are plotted in Fig. 8. Both for the CSII and the CEA, \({\overline{U}}_1/U_\infty \) is the highest close to the canopy height at \(x_3/h\) = 0.95. However, \({\overline{U}}_1^c/U_\infty \) (bottom row in Fig. 7) does not decrease with decreasing height and \({\overline{U}}_1^c/U_\infty \) at \(x_3/h\) = 0.5 exceeds \({\overline{U}}_1^c/U_\infty \)at \(x_3/h\) = 0.7. This is likely the result of the triangular shape of the canopy elements that leads to a lower pressure drop with decreasing height. Note that for the CSII (upper row in Fig. 7), this is not observed. At all heights, spanwise profiles of \({\overline{U}}_1^i/U_\infty \) and \({\overline{U}}_1^c/U_\infty \) (Fig. 8) show a strong increase of \({\overline{U}}_1/U_\infty \) upon moving from the canopy into the open patch. The increase in \({\overline{U}}_1/U_\infty \) is most pronounced just downstream of the canopy element at \(x_1/h\) = 0.05 (Fig. 7a, d) while further downstream spanwise gradients decrease for both \({\overline{U}}_1^i/U_\infty \) as well as for \({\overline{U}}_1^c/U_\infty \) (Fig. 7b, c, e, f).

The normalized jump in streamwise velocity (upper row in Fig. 7) across the CSII can be defined as \(\varDelta {\overline{U}}_1^i/U_\infty \), where \(\varDelta {\overline{U}}^i_1\) is the streamwise velocity difference given by the “plateau” values at the edges of the considered interface (see Fig. 7a). Based on \(\varDelta {\overline{U}}_1^i\), the vorticity thickness defined as \(\delta _\omega ^i = \varDelta {\overline{U}}_1^i/\left( \partial {\overline{U}}_1^i/\partial x_2\right) ^{max}\), can be used to characterize the shear layer’s thickness across the CSII. Values of \(\varDelta {\overline{U}}_1^i/U_\infty \) and \(\delta _\omega ^i/h\) are plotted in Fig. 9a, b, respectively, as a function of \(x_1/h\). Values of \(\varDelta {\overline{U}}_1^i/U_\infty \) peak at \(x_3/h\) = 0.85 close to the canopy element (\(\varDelta {\overline{U}}_1^i/U_\infty \) = 0.29 at \(x_1/h \approx \) 0.07), and for all heights, values decrease to a minimum of \(\varDelta {\overline{U}}_1^i/U_\infty \approx \) 0.15 at \(x_1/h \approx \) 0.4. Values of \(\delta _\omega ^i/h\) (Fig. 9b) range between 0.015 \(< \delta _\omega ^i/h<\) 0.0175, just downstream of the canopy element, while further downstream, values increase with decreasing height to \(\delta _\omega ^i/h \approx \) 0.0275 at \(x_3/h\) = 0.50. These small values indicate thin, strong shear layers that play an important role in transverse transport as will be discussed in the following. Note that corresponding values for the CEA are not easily obtained from the present results as the velocity “jump” is not clearly defined in this case. However, since \(\left( \partial {\overline{U}}_1^c/\partial x_2\right) ^{max} \ll \left( \partial {\overline{U}}_1^i/\partial x_2\right) ^{max}\), associated vorticity thicknesses are expected to be at least an order of magnitude higher. Further note that for turbulent/non-turbulent interfaces, the thickness of the turbulent sublayer or vorticity layer is of the order of the Taylor micro-scale (da Silva et al. 2014). The same scaling was found for internal interfaces between UMZs in turbulent boundary layers where the shear layer thickness scales with the Taylor micro-scale (Eisma et al. 2015; de Silva et al. 2017). We can observe in Fig. 9b that \(\delta _\omega ^i/h\) is smallest just below canopy height (\(x_3/h\) = 0.95) where the turbulence is strongest and the Taylor micro-scale is expected to be smallest as the TKE dissipation rate peaks near canopy height (van Hout et al. 2007).

Fig. 9
figure 9

Streamwise distributions of a \(\varDelta {\overline{U}}_1^i/U_\infty \) and b \(\delta _\omega ^i/h\) along the detected interface at for \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Data points are depicted at half the actual spatial resolution

Full size image
Fig. 10
figure 10

Streamwise profiles of a \({\overline{U}}_1^i/U_\infty \) and b \({\overline{U}}_2^i/U_\infty \) along the detected interface at for \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Data points are depicted at half the actual spatial resolution

Full size image

In contrast to \({\overline{U}}_1/U_\infty \) (Fig. 7), changes of \({\overline{U}}_2^i/U_\infty \) (top row in Fig. 8) are much less abrupt while the shape of the profiles of \({\overline{U}}_2^c/U_\infty \) (bottom row in Fig. 8) strongly depends on the streamwise position. The sign of \({\overline{U}}^c_2/U_\infty \) depends on the height. At \(x_3/h\) = 0.50, \({\overline{U}}^c_2/U_\infty \) is predominantly negative, especially for \(x_2/h>\) 0, while at \(x_3/h\) = 0.70, \({\overline{U}}^c_2/U_\infty \) is predominantly positive. This hints at a complex transverse flow across the spanwise heterogeneity. Since values of \({\overline{U}}_2^i/U_\infty \) are mostly negative, whereas those of \({\overline{U}}_2^c/U_\infty \) are mainly positive (except at \(x_3/h\) = 0.5), this means that on average the instantaneous interface tends to move towards the canopy whereas the ensemble averaged velocity field mainly indicates outward directed flow.

The normalized streamwise and transverse interface velocities, \({\overline{U}}^i_1/U_{\infty }\) and \({\overline{U}}^i_2/U_{\infty }\), respectively, along \(\left( x_2-x_2^i\right) /h\) = 0 (see top row in Fig. 6), are plotted as a function of \(x_1/h\) in Fig. 10 for different heights. The results for \({\overline{U}}_1^i/U_\infty \) indicate a strong wall normal gradient as \({\overline{U}}^i_1/U_{\infty }\) drops from \({\overline{U}}^i_1/U_{\infty } \approx \) 0.25 at \(x_3/h\) = 0.95 to values of about 0.19 for \(x_3/h\le \) 0.85. Such a strong wall-normal gradient is usually observed above homogeneous canopies (Finnigan 2000) and is here also obtained for the CSII. Values of \({\overline{U}}^i_2/U_{\infty }\) (Fig. 10b) are one order of magnitude lower than those of \({\overline{U}}^i_1/U_{\infty }\) and are mostly directed towards the canopy (\({\overline{U}}_2^i/U_\infty<\) 0) emphasizing the importance of the instantaneous interface in mean transport from the open patch into the canopy.

Since the sign of \({\overline{U}}_2\) dictates the direction of the mean spanwise convective transport of TKE, it is of interest to look at the probability of \(U_2<\) 0, i.e. of “inward” (into canopy) transport \(P(U_2<0)\). Results are depicted in the left and right columns of Fig. 11 for \(x_3/h\) = 0.5 and 0.95, respectively, for both the CSII (upper row) and the CEA (bottom row) results. These two heights illustrate the trend of \(P(U_2<0)\) with increasing height. Surprisingly, values of \(P^i(U_2<0)\) (upper row in Fig. 11) are mostly lower than 0.5, with values that decrease with increasing height. However as seen in Fig. 10b, on average, \({\overline{U}}_2^i/U_\infty<\) 0 (0.1 \(\le x_1/h \le \) 0.4), which indicates that inward moving instantaneous interfaces have transverse velocity magnitudes that exceed those of the outward directed ones illustrating the strong intermittency of the instantaneous interfaces. This will be further discussed when presenting the results of the Quadrant-Hole analysis (Sect. 4.4). In contrast, for the conventional average, \(P^c(U_2<0)\) mostly exceeds 0.5 at \(x_3/h\) = 0.5 (Fig. 11c) and 0.95 (Fig. 11d). This is in agreement with the results of \({\overline{U}}_2^c/U_\infty \) displayed in the bottom row of Fig. 8.

Fig. 11
figure 11

Probabilities, P(\(U_2<0\)), across the CSII (upper row) and for the CEA (bottom row) depicted at \(x_3/h=0.50\) and 0.95 in the left and right columns, respectively

Full size image
Fig. 12
figure 12

Examples of contour plots (at \(x_3/h\) = 0.85) of a \(\overline{u_1u_2}^i/U_\infty ^2\) and b \(k^i/U_{\infty }^2\) for the CSII, and c \(\overline{u_1u_2}^c/U_\infty ^2\) and d \(k^c/U_{\infty }^2\) for the CEA. Note constant level spacing in (a) and (c) equals \(1 \times 10^{-3}\) and \(2.5 \times 10^{-3}\) in (b) and (d)

Full size image
Fig. 13
figure 13

Spanwise profiles of \(\overline{u_1u_2}^i/U_\infty ^2\) and \(\overline{k}^i/U_\infty ^2\)(top row), and \(\overline{u_1u_2}^c/U_\infty ^2\) and \(\overline{k}^c/U_\infty ^2\) (bottom row) for \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Each column corresponds to a streamwise position \(x_1/h\) = 0.05, 0.25, 0.40, respectively. Values of \(\overline{u_1u_2}/U_\infty ^2\) and \(\overline{k}/U_\infty ^2\) can be distinguished based on their sign, negative and positive, respectively. Data points in the bottom row are depicted at half the actual spatial resolution

Full size image

Turbulent momentum transport across the spanwise heterogeneity is governed by the Reynolds shear stresses. The present measurements resolve all three components, \(\overline{u_1u_2}\), \(\overline{u_1u_3}\), and \(\overline{u_2u_3}\). However, our results indicated that \(|\overline{u_1u_2}|\) is one order of magnitude larger than \(|\overline{u_1u_3}|\) and \(|\overline{u_2u_3}|\), and hence we present only results for \(\overline{u_1u_2}\). Example contour plots of \(\overline{u_1u_2}^i/U_\infty ^2\) and \(\overline{u_1u_2}^c/U_\infty ^2\) at \(x_3/h\) = 0.85 presented in Fig. 12a, c, respectively, indicate strong spanwise gradients for the CEA (Fig. 12c) associated with the strong shear layer extending from the edge of the upstream canopy element. These spanwise gradients clearly exceed those across the CSII (Fig. 12a). In addition to the Reynolds shear stress, contour plots of TKE, \(k = \frac{1}{2}\overline{u_iu_i}\) (i = 1, 2, 3), are plotted in Fig. 12b, d, for the CSII and the CEA, respectively. Significant transverse jumps in TKE can be observed, mainly associated with the high shear layer (CEA, Fig. 12d), while those associated with the CSII (Fig. 12b) are less pronounced.

The variation of \(\overline{u_1u_2}/U_\infty ^2\) and \(k/U_\infty ^2\) with height is illustrated by plotting their transverse profiles in Fig. 13 at \(x_1/h\) = 0.05, 0.25, and 0.40. Note that \(k/U_\infty ^2\) (> 0) and \(\overline{u_1u_2}/U_\infty ^2\) (< 0) can be distinguished based on their sign. As can be observed, changes in \(\overline{u_1u_2}/U_\infty ^2\) across the CSII (top row of Fig. 13) are small as are differences with height, although magnitudes of \(\overline{u_1u_2}/U_\infty ^2\) slightly increase with decreasing height. Strong jumps in \(\overline{u_1u_2}/U_\infty ^2\) are only observed for the CEA, close to the upstream canopy element (\(x_1/h\) = 0.05, Fig. 13d) at the spanwise position of the strong shear layer. The present results indicate that Reynolds stresses and TKE do not indicate strong pronounced “jumps” at the CSII and display magnitudes that are close to zero, especially for \(\left( x_2-x_2^i\right) /h<\) 0. The turbulent flow structure will be analyzed by a Quadrant-Hole analysis in Sect. 4.4 where the contribution of different quadrants to \(\overline{u_1u_2}\) will be discussed.

4.2 Vorticity and Directional Swirling Strength

As shown in the previous sections, the flow across spanwise heterogeneity is characterized by the development of a strong shear layer, and it is therefore of interest to examine in detail the vorticity, \(\omega _3\), and the swirling strength, \(\varLambda _{ci}\), both across the CSII as well as for the CEA. The swirling strength will be shown separately for counterclockwise and clockwise rotating vortices as denoted by the superscripts “+” and “−”, respectively.

Fig. 14
figure 14

Example contour plots (\(x_3/h\) = 0.85) of \({{\overline{\omega }}}_3h/U_\infty \) (left column), \({{\overline{\varLambda }}}_{ci}^-h^2/U_\infty ^2\) (middle column), and \({{\overline{\varLambda }}}_{ci}^+h^2/U_\infty ^2\) (right column). Results are plotted in the upper and bottom rows for the CSII and for the CEA, respectively. Note constant level spacing equals 1 (1st column), 0.02 (2nd column), and 0.005 (3rd column)

Full size image

Example contour plots of \({{\overline{\omega }}}_3\), \({{\overline{\varLambda }}}_{ci}^+\), and \({{\overline{\varLambda }}}_{ci}^-\) depicted in Fig. 14, indicate strikingly different distributions across the CSII and for the CEA. Whereas across the CSII (upper row in Fig. 14), a “ridge” like pattern emerges along \(x_1/h\), for the CEA (bottom row in Fig. 14) high magnitudes of \({{\overline{\omega }}}_3^c\) and \({{\overline{\varLambda }}}_{ci}^{c}\) are confined to the region close to the edge of the upstream canopy element where the flow separates. This striking difference between spanwise distributions across the CSII and the CEA shows that the CSII samples regions of high \(|\omega _3|\) as the interface position fluctuates (Fig. 5).

Furthermore, the instantaneous interface is not only a “hot spot” of high vorticity governed by high transverse shear, \(\partial U_1/\partial x_2\), but is also densely populated by clockwise rotating vortices indicated by the large magnitudes of \({{\overline{\varLambda }}}_{ci}^{-i}\) (Fig. 14b) while being devoid of counterclockwise rotating vortices, \({{\overline{\varLambda }}}_{ci}^{+i} \approx \) 0 (Fig. 14c). Mixing layer characteristics along the instantaneous conditionally sampled interface are the reason for the observed population of negative sign (clockwise rotating) vortices. The conditionally sampled interface is characterized by high momentum flow for \(\left( x_2-x_2^i\right) /h>\) 0 and low momentum flow for \(\left( x_2-x_2^i\right) /h<\) 0. As we will show in Sect. 4.4, the spanwise momentum transport has similar characteristics as the wall-normal turbulent transport and is governed by sweep-ejection cycles.

Fig. 15
figure 15

Spanwise profiles of \({\overline{\omega }}_3^ih/U_\infty \) (top row) and \({\overline{\omega }}_3^ch/U_\infty \) (bottom row) for \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Columns from left to right correspond to streamwise positions \(x_1/h\) = 0.05, 0.25, and 0.40, respectively

Full size image
Fig. 16
figure 16

Spanwise profiles of \({\overline{\varLambda }}_{ci}^ih^2/U_\infty ^2\)(top row) and \({\overline{\varLambda }}_{ci}^ch^2/U_\infty ^2\) (bottom row) for \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). \({\overline{\varLambda }}_{ci}^+\) and \({\overline{\varLambda }}_{ci}^-\) can be distinguished based on their sign. Columns from left to right correspond to streamwise positions \(x_1/h\) = 0.05, 0.25, and 0.40, respectively

Full size image

The impact of changing the height on the spanwise profiles of \({{\overline{\omega }}}_3\) and \({{\overline{\varLambda }}}_{ci}\) at \(x_1/h\) = 0.05, 0.25, and 0.40 is depicted in Figs. 15 and 16 for both the CSII as well as for the CEA. For all heights, both \({{\overline{\omega }}}_3^i\) and \({{\overline{\varLambda }}}_{ci}^{-i}\) peak strongly at \(\left( x_2-x_2^i\right) /h\) = 0, indicating strong “coherence” of the instantaneous interface across the investigated heights (0.5 \(\le x_3/h \le \) 0.95). Peak magnitudes of \({{\overline{\omega }}}_3^i\) and \({{\overline{\varLambda }}}_{ci}^{-i}\) are highest closest to the canopy element (Figs. 15a and 16a) but remain high along the streamwise measurement range (Figs. 15b, c and 16b, c). In contrast, corresponding values of the CEAs are mostly close to zero with the exception of those close to the canopy element depicted in Figs. 15d and 16d. However, even there, peak magnitudes are much lower than those for the CSII. Note that counterclockwise rotating vortices are absent at the interface at all heights (\({{\overline{\varLambda }}}_{ci}^{+i}\), upper row in Fig. 16).

The results up till now provide strong evidence that applying the CEA is not sufficient for capturing the interface flow dynamics occurring in the flow across a spanwise heterogeneity.

4.3 Terms of the TKE transport equation

Spanwise-wall normal heterogeneity has been shown to induce large-scale secondary flow patterns as a result of an imbalance between the production and dissipation of TKE (Anderson et al. 2015) as appearing in the Reynolds averaged TKE transport equation (invoking Einstein’s summation convention):

$$\begin{aligned} \frac{\partial k}{\partial t} + {\overline{U}}_j\frac{\partial k}{\partial x_j} = \frac{\partial }{\partial x_j}\left[ -\frac{\overline{pu_j}}{\rho }-\frac{1}{2}\overline{u_iu_iu_j} +2\nu \overline{s_{ij}u_i}\right] -\overline{u_iu_j}\frac{\partial {\overline{U}}_i}{\partial x_j} - \epsilon , \end{aligned}$$
(1)

where \(s_{ij}\) denotes the strain rate tensor of the fluctuating velocity gradients, p and \(\epsilon \) denote pressure and TKE dissipation rate, respectively. The present measurements enable to determine the advection term of TKE (2nd term on the left hand side of Eq. 1), the turbulent and viscous transport terms (2nd and 3rd terms within square brackets), as well as all production terms \(P_{ij}\) (using also the continuity equation for incompressible flow, \(\frac{\partial {\overline{U}}_i}{\partial x_i}\) = 0). Note that the viscous transport term was negligible in this high Reynolds number flow (Hinze 1967; Pope 2000), while the turbulent transport term may be significant especially near the top of the canopy (Brunet et al. 1994). In the present case, since the flow is inhomogeneous in all directions, none of the production terms were a-priori neglected. However, results showed that \(P_{12}\) and \(P_{21}\) governed, and example contour plots of these two terms at \(x_3/h\) = 0.85 are depicted in Fig. 17. It is clear that for the CEA (bottom row of Fig. 17), \(P_{12}\) is only significant close to the upstream canopy element in the thin high shear layer, whereas \(P_{21}\) displays values close to zero throughout the FOV. In contrast, across the conditionally sampled interface, slightly enhanced values of \(P_{12}\) can be observed along the full extent of \(x_1/h\) (Fig. 17a), while values of \(P_{21}\) (Fig. 17b) are low everywhere. \(P_{12}\) and \(P_{21}\) have opposite sign, indicating that \(P_{12}\) acts as a source of TKE and \(P_{21}\) as a sink. Magnitudes of \(P_{12}\) and \(P_{21}\) are especially significant close to the upstream canopy element up to \(x_1/h \approx \) 0.15, and decrease farther downstream. The sum of \(P_{12}\) and \(P_{21}\) plotted in Fig. 17c, clearly indicates that \(P_{12}\) dominates over \(P_{21}\).

Values of the turbulent transport terms, \(T_{ij}=-\frac{1}{2}\frac{\partial }{\partial x_j}\overline{u_iu_iu_j}\), were distributed similarly as the production terms, and were only significant for the CEA just downstream of the canopy elements in the strong shear layers, as illustrated in the bottom row of Fig. 18 for \(x_3/h\) = 0.95. Three terms, \(T_{11}\), \(T_{22}\), and \(T_{12}\) governed and their sum is plotted in the 4th column of Fig. 18. As can be seen, for the CEA (Fig. 18h), magnitudes of the sum of \(T_{ij}\) are only significant close to the canopy element, while for the CSII (Fig. 18d), magnitudes are close to zero everywhere.

The changes in transverse profiles of \(P_{12}\) and \(P_{21}\) and those of \((T_{11}+T_{22}+T_{12}\)) at different heights are shown in Figs. 19 and 20, respectively, at \(x_1/h\) = 0.05, 0.25, and 0.40 for both the CSII (upper rows) and the CEA (bottom rows). The results indicate that the shape of the profiles of the production terms as well as their magnitudes, do not change much with height. This illustrates the strong coherence of the obtained CSII characteristics at least across half the canopy height (0.5 \(\le x_3/h \le \) 0.95). Note that peak values of \(|P_{12}|\) and \(|P_{21}|\) for the CEA are comparable to those obtained by the CSII. Profiles of the sum of the turbulent transport terms show that the main contributions having high magnitudes occur just below canopy height at \(x_3/h\) = 0.95 and 0.85, downstream of the canopy element at \(x_1/h\) = 0.05 (CEA, Fig. 20d). Note that in all other cases, magnitudes are small with relatively large uncertainties (see Sect. 2), displaying considerable scatter.

Fig. 17
figure 17

Example contour plots (\(x_3/h\) = 0.85) of \(P_{12}h/U_\infty ^3\) (1st column), \(P_{21}h/U_\infty ^3\) (2nd column) and their sum (3rd column) for the CSII (upper row) and the CEA (bottom row), respectively. Note constant level spacing equals 2.5 \(\times \) 10\(^{-3}\)

Full size image
Fig. 18
figure 18

Example contour plots (\(x_3/h\) = 0.95) of \(T_{11}\) (1st column), \(T_{12}\) (2nd column), \(T_{22}\) (3rd column) and their sum (4th column) for the CSII (upper row) and the CEA (bottom row), respectively. Note constant level spacing equals a, e , b, f , c, g , and d, h 0.01

Full size image
Fig. 19
figure 19

Spanwise profiles of production terms \(P_{12}h/U_\infty ^3\) and \(P_{21}h/U_\infty ^3\) both for the CSII (upper row) and the CEA (bottom row). \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Filled symbols represent \(P_{21}h/U_\infty ^3\), and empty symbols represent \(P_{12}h/U_\infty ^3\). Columns from left to right correspond to streamwise positions, \(x_1/h\) = 0.05, 0.25, 0.40, respectively

Full size image
Fig. 20
figure 20

Spanwise profiles of the sum of \(T_{11}+T_{22}+T_{12}\), both for the CSII (upper row) and the CEA (bottom row). \(x_3/h\) = 0.95 (blue diamond), 0.85 (red square), 0.70 (green upward pointing triangle), 0.50 (black circle). Columns from left to right correspond to streamwise positions, \(x_1/h\) = 0.05, 0.25, 0.40, respectively

Full size image

In addition to the production terms, two advection terms, \({\overline{U}}_1\frac{\partial k}{\partial x_1}\) and \({\overline{U}}_2\frac{\partial k}{\partial x_2}\) were calculated. The magnitudes of both terms (not shown here) were one order of magnitude lower than those of \(P_{12}h/U^3_\infty \), hinting that the imbalance between TKE production rate and TKE dissipation rate might be small across the spanwise heterogeneity. However, more detailed 3D measurements are needed to corroborate this statement.

4.4 Quadrant–Hole Analysis

In order to investigate the turbulence structure and in particular the relative importance of ejections and sweeps across the spanwise heterogeneity, Quadrant–Hole (Q–H) analysis (Lu and Willmarth 1973; Zhu et al. 2007b) was performed. It is well-known that coherent turbulent structures called “ejections” and “sweeps” are responsible for the bulk of turbulent momentum transport into and out of canopies. This has been mostly studied for vertical transport over homogeneous canopies (Zhu et al. 2007a, b; van Hout et al. 2007) as well as recently for a two-height canopy wind tunnel model (Shig et al. 2023), but relatively little is known about their importance across a spanwise canopy edge (Winiarska et al. 2023).

Fig. 21
figure 21

Results of Q–H analysis on \(u_1\) and \(u_2\) at \(x_1/h\) = 0.25. JPDFs of \(u_1\) and \(u_2\) at \(x_3/h\) = 0.5 and 0.85 are depicted in the 1st and 2nd columns, respectively. Fractional contributions of each quadrant at \(x_3/h\) = 0.50 and 0.85 are depicted in the 3rd and 4th column, respectively. Data in the 1st, 2nd, and 3rd rows are at S1, S2, and S3, respectively. Red solid curves indicate hole sizes for H = 1, 3, 5, 7, 9

Full size image
Fig. 22
figure 22

Results of Q–H analysis on \(u_1\) and \(u_3\) at \(x_1/h\) = 0.25. JPDFs of \(u_1\) and \(u_3\) at \(x_3/h\) = 0.5 and 0.85 are depicted in the 1st and 2nd columns, respectively. Fractional contributions of each quadrant at \(x_3/h\) = 0.50 and 0.85 are depicted in the 3rd and 4th column, respectively. Data in the 1st, 2nd, and 3rd rows are at S1, S2, and S3, respectively. Red solid curves indicate hole sizes for H = 1, 3, 5, 7, 9

Full size image

Here, Q–H analysis was performed on the \(u_1 - u_2\) as well as on \(u_1 - u_3\) velocity fluctuations, shedding light on both the spanwise and wall-normal turbulent transport across the canopy edge. The fraction of measurements of \(u_1u_j\) (j = 2 or 3) exceeding a predefined threshold, \(u_1u_j \ge H |\overline{u_1u_j}|\), is described by the duration fraction in quadrant k (= 1–4):

$$\begin{aligned} D^k_{u_1u_j}|H = \frac{1}{N}\sum _{n=1}^N I^k_{H,n}, \end{aligned}$$
(2)

where H denotes the “hole” size, n denotes a specific vector map, and N is the total ensemble size; \(I^k_{H,n}\) = 1 when \(u_1u_j \ge H |\overline{u_1u_j}|\) and \(I^k_{H,n}\) = 0 when \(u_1u_j < H |\overline{u_1u_j}|\); Note that \(\sum D^k_{u_1u_j}|0\) = 1 (for k = 1–4). The stress fraction of each quadrant provides the fractional contribution to the total Reynolds shear stress component:

$$\begin{aligned} \phi ^k_{\overline{u_1u_j}}|H = \frac{\overline{(u_1u_j)}^k_H}{\overline{u_1u_j}} D^k_{u_1u_j}|H. \end{aligned}$$
(3)
Fig. 23
figure 23

Q–H analysis of \(u_1^i\) and \(u_2^i\) (1st row) and on \(u_1^i\) and \(u_3^i\) (2nd row) across the CSII. JPDFs at \(x_3/h\) = 0.5 and 0.85 are depicted in the 1st and 2nd columns, respectively. Fractional contributions of each quadrant at \(x_3/h\) = 0.50 and 0.85 are depicted in the 3rd and 4th columns respectively. Red solid curves indicate hole sizes for H = 1, 3, 5, 7, 9

Full size image

Q–H analysis was applied both across the CSII as well as for the CEA. In the latter case, due to spatial inhomogeneity, Q–H analysis was performed at a streamwise location centered between the canopy elements (\(x_1/h\) = 0.25) on small patches (7 \(\times \) 7 vectors) at three spanwise positions, \(x_2/h\) = −0.2 (S1), 0 (S2), and 0.2 (S3), i.e. sheltered between the canopy elements, exactly at the canopy-open patch interface, and out in the open patch (“exposed”), respectively. Note that these results are representative for the bulk of the FOV, but due to streamwise inhomogeneity, close to the canopy elements, results were different (not shown here).

Focusing first on the transverse transport, the JPDFs of \(u_1\) and \(u_2\) as well as the corresponding fractional contributions at \(x_3/h\) = 0.50 and 0.85, are depicted in Figs. 21, and 23 for the CEA and the CSII, respectively. Note that changes with height were continuous and consistent, and are well observed at \(x_3/h\) = 0.50 and 0.85 that are presented here. For the CEA, in most cases, the JPDFs of \(u_1\) and \(u_2\) (1st and 2nd columns in Figs. 21 and 23a, b) resemble elliptical distributions with a clear preference for sweep and ejection quadrants except for S1 at \(x_3/h\) = 0.85 (CEA, Fig. 21b) that indicates more or less equal stress fractions for all quadrants. For the CSII (1st and 2nd columns in Fig. 23a, b) the JPDFs of \(u_1\) and \(u_2\) are more equally distributed over the different quadrants resulting in values of \(\overline{u_1u_2}^i\) that are close to zero (see Figs. 12 and 13). Fractional contributions of the quadrants are different depending on height and spanwise position. For example, for the CEA at \(x_3/h\) = 0.85 (4th column in Fig. 21), \(\phi ^4_{\overline{u_1u_j}}|H > \phi ^2_{\overline{u_1u_j}}|H\) at S1 and S2 for all H (Fig. 21d, h) but \(\phi ^2_{\overline{u_1u_j}}|H > \phi ^4_{\overline{u_1u_j}}|H\) at S3 (Fig. 21l). At \(x_3/h\) = 0.50, this “switch” between ejections (k = 2) and sweeps (k = 4) occurs already at S2 (3rd column in Fig. 21). Note that in terms of duration fractions (not shown here), for H = 0, ejections govern within canopy (S1) and sweeps in the open patch (S3). These results indicate that moving across the spanwise canopy edge into the open patch, the turbulent momentum transfer changes from being governed by sweeps (Fig. 21c, d) to being governed by ejections (Fig. 21k, l). In contrast, across the CSII (1st row in Fig. 23) sweeps (k = 4) and ejections (k = 2) almost equally contribute to \(\overline{u_1u_2}^i\). Furthermore, in contrast to the CEA results (Fig. 21), the CSII results depicted in Fig. 23 indicate that contributions of quadrants k = 1 and 3 (outward and inward interactions) significantly contribute to \(\overline{u_1u_2}^i\). Since these contributions are positive, they essentially lead to small amplitudes of \(\overline{u_1u_2}^i\). In terms of duration fractions (not shown), ejections and sweeps govern, with those of ejections being slightly higher than those of sweeps.

Next, we focus on the wall-normal turbulent momentum transport across the spanwise canopy edge, and the JPDFs of \(u_1\) and \(u_3\) for both the CEA and the CSII are depicted in Figs. 22 and 23 (bottom row), respectively. For homogeneous canopy layouts, it is well known that sweeps are dominant, whereas for turbulent boundary layers on hydraulically smooth surfaces, ejections govern turbulent momentum transport (Lu and Willmarth 1973). The present results at \(x_3/h\) = 0.85 (CEA, 2nd and 4th columns in Fig. 22) show that at S1, \(\phi ^4_{\overline{u_1u_3}}|H > \phi ^2_{\overline{u_1u_3}}|H\) (Fig. 22d). However, the difference becomes smaller as we move across the canopy edge into the open patch and at S3 (Fig. 22l), \(\phi ^4_{\overline{u_1u_3}}|H \approx \phi ^2_{\overline{u_1u_3}}|H\). Surprisingly, at \(x_3/h\) = 0.50 (1st and 3rd columns in Fig. 22), at S1 (Fig. 22a, c), it can be observed that inward (k = 3) and outward (k = 1) interactions govern. This means that the sign of \(\overline{u_1u_3}\) that was negative at \(x_3/h\) = 0.85 has become positive at \(x_3/h\) = 0.50. Note that this flip of the sign was not observed within a homogeneous canopy (not shown) for which the picture sketched for \(x_3/h\) = 0.85 (Fig. 22d) was consistent at all heights. This indicates that as a result of the spanwise heterogeneity, the sweeps and ejections just inside the canopy do not penetrate as strongly and coherently into the lower canopy regions as for a homogeneous canopy, at least close to the spanwise canopy-open patch boundary. Note that as we move out of the canopy into the open patch at this height (Fig. 22e, i, g, k), the sign of \(\overline{u_1u_3}\) flips again at S3, however, the fractional contribution of all quadrants is similar (Fig. 22b).

In the case of the CSII (bottom row in Fig. 23), it can be observed that the JPDFs of \(u_1\) and \(u_3\) (Fig. 23e, f) are more or less circular with almost equal duration fractions (not shown), and all quadrants contribute to \(\overline{u_1u_3}^i\). Also in this case, we observe a change in sign of \(\overline{u_1u_3}^i\) and \(\overline{u_1u_3}^i>\) 0 at \(x_3/h\) = 0.50, indicating that the instantaneous interface preferentially samples regions deep within the canopy as shown in Fig. 5, where \(u_1u_3>\) 0 at this height.

5 Summary and Conclusions

Turbulent flow characteristics developing across a spanwise edge in a canopy field were investigated through the analysis of detailed SPIV experiments. A comparison between conditionally sampled flow quantities across instantaneous internal interfaces (CSII approach) to those determined by a conventional ensemble average (CEA approach) was performed. The instantaneous, internal interfaces were detected using a modal analysis commonly used to determine the boundaries between high and low uniform momentum zones in turbulent boundary layers. The measurements were performed across the spanwise edge of a canopy model set up in a large atmospheric, open loop wind tunnel. Canopy elements were modeled by triangular (small at the bottom) shaped canopy elements, perforated at the top, that matched the vertical distribution of the PFAI of an actual corn canopy. SPIV measurements of the three air velocity components were conducted in wall-parallel planes crossing the spanwise canopy edge, providing information on spanwise transport processes. Of particular interest in this study was to understand if internal interfaces existed at the canopy edge and what is their contribution to the ensemble averaged statistics.

As expected, results showed that the change in mean velocity, vorticity, and swirling strength was almost stepwise across the detected, conditionally sampled internal interfaces. In contrast, the change in the same quantities across the canopy edge after applying a conventional ensemble average (CEA approach) was much more gradual, as the strong gradients across the instantaneous interface were smeared, emphasizing the importance of the instantaneous interface dynamics in transverse transport. Note that the Reynolds stress values across the internal interfaces did not indicate a strong jump. This is likely the result of the vortical structures concentrated at the internal interfaces that equally contributed to the Reynolds stresses on both sides of them. The present SPIV measurements allowed us to determine the turbulent transport terms, production rate terms as well as advection terms in the TKE transport equation based on both the CEA as well as the CSII approach. Significant advection would hint at large-scale secondary flows (not resolved in the present measurements) that are known to occur at spanwise heterogeneities (e.g. Anderson et al. 2015). Our results indicated that \(\hbox {P}_{{12}}\) \(\left( = \overline{u_1u_2}\frac{\partial {\overline{U}}_1}{\partial x_2}\right) \) governed TKE production in both CSII and CEA approaches. In the latter approach, \(P_{12}\) was only significant in the thin shear layer extending from the upstream canopy element. Furthermore, in the CSII approach, \(P_{21}\) acted as a sink across the instantaneously detected interface, whereas it was negligible in the CEA approach. All other production terms were negligible. For the CEA, calculated turbulent transport terms were only significant just downstream of the canopy elements. Estimated magnitudes of TKE advection terms were one order of magnitude smaller than peak magnitudes of production, suggesting only a small imbalance between dissipation and production rates across the spanwise canopy edge, which would mean that secondary flows were weak in the current model canopy configuration. Further measurements outside the scope of the present investigation, are needed to corroborate this.

In order to unravel the turbulence flow structure and turbulent momentum transport across the spanwise canopy edge, Q–H analysis for both the CEA and CSII approaches was performed. In the CEA approach, wall-normal turbulent transport near the canopy top (\(x_3/h>\) 0.70) and just within the canopy (S1) was governed by sweeps similar as for homogeneous canopies (e.g. van Hout et al. 2007; Zhu et al. 2006, 2007a). However, upon moving into the open patch, ejections gained importance at the expense of sweeps, showing that smooth boundary layer characteristics were recovered upon moving away from the canopy edge. Note that in contrast to homogeneous canopies, at the canopy edge just within canopy (S1, \(x_3/h \le \) 0.70), the sign of \(\overline{u_1u_3}\) changed from negative to positive, and fractional contributions of outward (k = 1) and inward (k = 3) interactions became equally important as those of the sweeps and ejections. Upon moving away from the canopy edge into the open patch, smooth boundary layer characteristics were again recovered as was the case when \(x_3/h>\) 0.70. Similar observations were made for the CSII approach. The change of sign of \(\overline{u_1u_3}\) at the spanwise canopy edge when \(x_3/h \le \) 0.7, is absent within homogeneous canopies, and indicates that the turbulence structure significantly changes close to a spanwise canopy edge. These changes are expected to strongly affect the turbulent momentum transfer as well as impact turbulent heat and mass transfer across a spanwise canopy edge.

The present investigation has revealed the importance of the instantaneous interface dynamics between UMZs across a spanwise canopy edge. Although currently, we are not aware of specific canopy models that incorporate CSII statistics, a possible way forward could be to pursue along the lines of the models proposed by Saxton-Fox and McKeon (2017) and Bautista et al. (2019). The latter showed that by incorporating UMZs and their interfaces (so-called “vortical fissures”), statistical moments up to the fourth order were well predicted in turbulent boundary layers. Perhaps a similar approach may be successful in reproducing canopy edge flow statistics without fully resolving the complex flow field. Needless to add that turbulent transport processes across canopy edges play a significant role in the process of desertification by contributing to soil erosion, sediment transport, and the degradation of land in arid and semi-arid regions, and addressing these processes will be crucial for sustainable land management.