1 Introduction

In recent years black holes have been very much at the center of interest in gravity and astrophysics, with achievements ranging from the observation of gravitational waves by the LIGO/VIRGO collaboration [1,2,3,4], and the imaging of the shadows of the supermassive black holes at the center of M87 and the Milky Way, Sgr \(\hbox {A}^*\) by the Event Horizon Collaboration [5, 6] to the increased accuracy of the measurements of the stars orbiting Sgr \(\hbox {A}^*\) [7,8,9,10].

Black holes arise in General Relativity (GR) as solutions of the field equations. The static Schwarzschild black holes and the rotating Kerr black holes represent amazingly simple objects, since only two quantities, their mass and their spin, are sufficient to fully characterize their surrounding spacetime [11]. In particular, the Kerr black holes are considered to be most relevant from an astrophysical point of view, and up to now all observations involving black holes are in agreement with the Kerr paradigm, that astrophysical black holes are indeed properly described by this solution [12].

While being scrutinized thoroughly since many decades, GR has passed all observational tests so far [13]. However, general expectations based to a large extent on the incompatibility of GR and Quantum Mechanics and the current riddles of cosmology like dark matter and dark energy, consider GR as an approximate theory that will be superseded by a more complete theory. Towards this goal, in particular, numerous alternative gravity theories have been considered (see e.g. [14,15,16]). Among these the family of Einstein-scalar–Gauss–Bonnet (EsGB) theories has stood out as a very attractive testing ground.

On the one hand EsGB theories are theoretically well motivated, since they arise, for instance, in the low energy limit of string theory [17, 18]. The EsGB action contains terms that are higher order in curvature, representing thus a subset of so-called quadratic gravity theories. In EsGB theories the higher order terms enter in the form of the Gauss–Bonnet invariant, which necessitates the coupling to a dynamical field, a scalar field, in order to lead to non-trivial modifications of the field equations. EsGB theories yield in fact second order field equations, which makes them a subclass of Horndeski theories [19] and importantly, they do not feature ghosts.

EsGB theories represent a valuable tool for black hole physics, since they feature black holes with scalar hair (for a recent review see [20]). Depending on the type of coupling of the scalar field to the Gauss–Bonnet (GB) invariant and the coupling strength, the properties of the resulting black holes can vary widely and be rather distinct from those of GR black holes. Here we will address the emergence of scalarized black holes for the various types of coupling functions and focus on their stability properties as far as they are known.

The study of scalarized black holes in EsGB theories started basically with the work of Kanti et al. [21], where the string theory motivated dilatonic coupling of the scalar field to the Gauss–Bonnet invariant was employed. For this coupling function the GR black holes are no longer solutions of the field equations, but all resulting black holes carry scalar hair [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. A variant of this case is given by so-called shift symmetric EsGB theories, where a linear coupling is taken [37, 38].

In contrast, for other types of coupling functions the GR black holes may remain solutions of the generalized field equations, while at the same time scalarized black holes may emerge in certain parameter regions. Here a major discovery was the occurrence of curvature induced spontaneous scalarization of black holes [39,40,41], possibly inspired by matter induced spontaneous scalarization of neutron stars [42]. Here the coupling of the scalar field to the GB invariant triggers a tachyonic instability, when the GB source term in the scalar field equation is sufficiently strong, and scalarized black holes arise [39,40,41, 43,44,45,46,47,48,49,50,51,52,53,54,55,56].

Besides spontaneous scalarization of black holes also non-linear scalarization of black holes may arise [57]. Again, GR black holes remain solutions of the generalized field equations, but these do not feature tachyonic instabilities, since there are no linear source terms in the scalar field equation. In this case it is the non-linearities that give rise to scalarized black holes in certain parameter regions [57,58,59].

Another interesting EsGB type theory was suggested in order to deal with potential problems for some EsGB theories arising in the context of cosmology [68]. Indeed, theories with spontaneous scalarization are expected to lead to a non-negligible scalar field in the early universe, that would remain present today, when no fine-tuning is invoked. Therefore an additional coupling of the scalar field to the Ricci scalar was taken into account, resulting in Einstein-scalar–Gauss–Bonnet–Ricci (EsGBR) theories. These EsGBR theories may then feature GR as a cosmic attractor, and allow for curvature-induced spontaneous scalarization of black holes [68,69,70,71].

Here we first give a brief introduction to EsGB theories and to quasi-normal modes (QNMs) including linear stability analysis. Next we review the properties of scalarized black holes obtained with dilatonic coupling functions, and with coupling functions giving rise to spontaneous and non-linear scalarization. We then review the properties of scalarized black holes in EsGBR theories, focusing on their surprising multipolar instabilities, and finally present our conclusions.

2 Einstein-scalar–Gauss–Bonnet black holes

2.1 Action and equations

We consider the EsGB action

$$\begin{aligned} S=\frac{1}{16 \pi }\int d^4x \sqrt{-g} \left[ R - \frac{1}{2} (\partial _\mu \varphi )^2 + \alpha f(\varphi ) R^2_\textrm{GB} \right] , \end{aligned}$$
(1)

with Ricci scalar R, real scalar field \(\varphi \), GB coupling constant \(\alpha \), coupling function \(f(\varphi )\), and Gauss–Bonnet invariant

$$\begin{aligned} R^2_\textrm{GB} = R_{\mu \nu \rho \sigma } R^{\mu \nu \rho \sigma } - 4 R_{\mu \nu } R^{\mu \nu } + R^2. \end{aligned}$$
(2)

Variation of the action leads to the coupled set of equations of motion, which are of second order [19]. The generalized Einstein equations read

$$\begin{aligned} G_{\mu \nu }= & -\frac{1}{4}g_{\mu \nu }\partial _\rho \varphi \partial ^\rho \varphi +\frac{1}{2} \partial _\mu \varphi \partial _\nu \varphi \nonumber \\ & \quad -\frac{\alpha }{2}\left( g_{\rho \mu }g_{\lambda \nu }+g_{\lambda \mu }g_{\rho \nu }\right) \eta ^{\kappa \lambda \alpha \beta }\tilde{R}^{\rho \gamma }_{\ \ \, \alpha \beta }\nabla _\gamma \partial _\kappa f(\varphi ) , \end{aligned}$$
(3)

with \(\tilde{R}^{\rho \gamma }_{\ \ \, \alpha \beta }=\eta ^{\rho \gamma \sigma \tau } R_{\sigma \tau \alpha \beta }\), while the scalar equation is given by

$$\begin{aligned} \nabla _\mu \nabla ^\mu \varphi + \alpha \frac{df}{d\varphi } R^2_\textrm{GB} =0. \end{aligned}$$
(4)

Clearly, the choice of the coupling function \(f(\varphi )\) is crucial for the resulting black holes, and we would like to distinguish the following main cases:

  • GR black hole solutions do not remain solutions of the coupled set of field equations. Since \(\displaystyle \frac{df}{d\varphi }(0) \ne 0\) there will be a non-vanishing source term for the scalar field and only hairy black holes result.

  • GR black hole solutions do remain solutions of the coupled set of field equations. With \(\displaystyle \frac{df}{d\varphi }(0) = 0\) the scalar field \(\varphi =0\) leads to vacuum solutions of the equations. Under appropriate conditions, however, in addition scalarized black holes emerge.

2.2 Linear perturbations

We now briefly recall some relevant features of linear perturbation theory, addressing damped gravitational and scalar oscillations and unstable runaway modes. The metric and the scalar field are assumed to consist of the background solution denoted by the superscript (0) and small fluctuations around this solution

$$\begin{aligned} g_{\mu \nu }= & g_{\mu \nu }^{(0)}(r) + \epsilon h_{\mu \nu }(t,r,\theta ,\phi ), \end{aligned}$$
(5)
$$\begin{aligned} \varphi= & \varphi _0(r) + \epsilon \delta \varphi (t,r,\theta ,\phi ), \end{aligned}$$
(6)

denoted by \(h_{\mu \nu }(t,r,\theta ,\phi )\) for the metric and \(\delta \varphi (t,r,\theta ,\phi )\) for the scalar field. The perturbation parameter is denoted by \(\epsilon \).

Here we focus on the QNMs of static spherically symmetric GR and scalarized black holes. In that case, the even parity perturbations and the odd parity perturbations decouple, leading to distinct sets of equations for both. The even parity perturbations are called the polar modes, and an adequate ansatz for the metric perturbations is given by [60]

$$\begin{aligned}&h_{\mu \nu }=\left[ \begin{array}{cccc} H_0(r) & H_1(r) & 0 & 0 \\ H_1(r) & H_2(r) & 0 & 0\\ 0 & 0 & r^2 T(r) & 0\\ 0 & 0 & 0 & r^2 \sin ^2\theta T(r) \end{array}\right] Y^{lm}(\theta ,\phi ) e^{i\omega t} , \end{aligned}$$
(7)

where \(\omega \) is a complex frequency, and the functions \(H_i(r)\) and T(r) depend on the multipole number l of the spherical harmonics \(Y^{lm}(\theta ,\phi )\). The scalar field enters only in the polar modes, its corresponding ansatz being given by

$$\begin{aligned} \delta \varphi (t,r,\theta ,\phi ) = \varphi _1(r) Y^{lm}(\theta ,\phi ) e^{i\omega t}. \end{aligned}$$
(8)

The odd or axial perturbations yield pure space-time modes and are parameterized by

$$\begin{aligned}&h_{\mu \nu }=\left[ \begin{array}{cccc} 0 & 0 & 0 & \sin \theta ~ h_0(r)\partial _\theta \\ 0 & 0 & 0 & \sin \theta ~ h_1(r)\partial _\theta \\ 0 & 0 & 0 & 0\\ \sin \theta ~ h_0(r)\partial _\theta & \sin \theta ~ h_1(r)\partial _\theta & 0 & 0 \end{array}\right] \,Y^{lm}(\theta ,\phi ) e^{i\omega t} . \end{aligned}$$
(9)

Inserting these perturbations into the field equations leads to distinct coupled systems of equations for the polar and the axial modes, that may often be simplified to a single master equation, a Schrödinger-like eigenvalue equation for the complex frequency \(\omega =\omega _R + i \omega _I\). Here the real part \(\omega _R\) corresponds to the frequency of the gravitational waves, while the imaginary part \(\omega _I\) encodes the decay time \(\tau = 1/\omega _I\) of the damped oscillations, when \(\omega _I>0\). When \(\omega _I<0\), on the other hand, an instability is detected since the mode grows exponentially in time.

2.3 Dilatonic scalarization

We start with considering scalarized black holes obtained with the string theory motivated dilatonic coupling function

$$\begin{aligned} \displaystyle f(\varphi )=\frac{1}{4} e^{-{\gamma } \varphi }, \end{aligned}$$
(10)

with Gauss–Bonnet coupling constant \(\alpha \) and dilaton coupling constant \(\gamma \). We note that the string theory value of \(\gamma \) is given by \(\gamma = 1\), however, other values of \(\gamma \) have also been considered.

Recalling the scalar field equation (4) and inserting the dilatonic coupling function yields

$$\begin{aligned} \nabla _\mu \nabla ^\mu \varphi - \alpha \gamma \frac{1}{4} e^{-{ \gamma } \varphi } R^2_\textrm{GB} = 0. \end{aligned}$$
(11)

Clearly, the coupling to the GB invariant always represents a source term for the scalar field. Thus GR black holes that require \(\varphi =0\) are no longer solutions of the field equations and only hairy black holes can be present.

Static spherically symmetric hairy black holes were first obtained in Ref. [21]. When for a given GB coupling constant \(\alpha \) these black holes are large their properties tend toward those of the Schwarzschild black holes. As they get smaller though they deviate increasingly from the Schwarzschild black holes until they reach a minimal value of their mass. Thus, for a given \(\alpha \), mass M and horizon radius \(r_H\) of the hairy black holes cannot become arbitrarily small. For dilaton coupling \(\gamma =1\) a critical configuration appears, where a horizon expansion revealed the reason: a square root appears and the radicand vanishes at the critical configuration with minimal mass [21]

$$\begin{aligned} \sqrt{ 1-6 \frac{\alpha ^2}{r_H^4} e^{2 \varphi _H}}. \end{aligned}$$
(12)

As pointed out in Ref. [22] at the critical solution a very short second branch of solutions arises, that extends toward still smaller horizon radii but again larger masses, and that soon ends in a curvature singularity.

This behavior is demonstrated in Fig. 1a, where the scaled horizon area \(A_H/16 \pi M^2\) is shown versus the scaled GB coupling constant \(\zeta ={\alpha }/{M^2}\). In these dimensionless quantities, the family of Schwarzschild black holes resides at \(A_H/16 \pi M^2=1\), \(\zeta =0\). The critical configuration is marked in the inset with a green dot, while the singular configuration is shown by the blue dot. The black dot only signifies that for a given \(\zeta \) there will be two solutions beyond, and thus uniqueness is lost. As the dilaton coupling \(\gamma \) is varied the short branch increases in length towards larger values of \(\gamma \), whereas it disappears towards smaller values of \(\gamma \) around \(\gamma = 0.9130\) (see Fig. 1b) [36].

Fig. 1
figure 1

Static dilatonic black holes: a Scaled horizon area \(A_H/16 \pi M^2\) versus scaled GB coupling constant \(\zeta ={\alpha }/{M^2}\) for \(\gamma =1\). b Scaled horizon area \(A_H/16 \pi M^2\) versus scaled coupling constant \(\gamma \zeta \) for \(\gamma =1, 2, 3\), and for the linear coupling case

Full size image

Linear stability of these hairy black holes has been studied in Refs. [33, 36] for the low-lying modes, focusing on the string theory value of the dilatonic coupling \(\gamma =1\). For the physically most relevant quadrupole (\(l=2\)) and octupole (\(l=3\)) modes no instabilities were found. We recall, that there are three sets of branches for these modes representing the polar gravity-led mode, the polar scalar-led mode and the axial mode. However, inspection of the radial \(l=0\) mode along the long (fundamental) hairy black hole branch and the second short branch confirmed that the solutions along the short branch are unstable as pointed out in Ref. [22]. Indeed, along the short branch a family of modes is present, whose real part of the frequency \(\omega _R\) vanishes, while its imaginary part is negative. This is demonstrated in Fig. 2, where the scaled real part of the frequency \(\omega _R M\) and imaginary part \(\omega _I M\) are shown versus the scaled coupling \(\zeta \).

Fig. 2
figure 2

Static dilatonic black holes: a Scaled real frequency part \(\omega _R M\) of the radial (\(l=0\)) modes versus scaled GB coupling constant \(\zeta ={\alpha }/{M^2}\) close to its maximum value (\(\gamma =1\)). b Scaled imaginary part \(\omega _I M\) versus \(\zeta \)

Full size image

These calculations strongly indicate linear stability of the static spherically symmetric dilatonic hairy black holes. While instabilities of higher modes have not been fully excluded, also the analysis performed in Ref. [61] has not found any sign of instabilities for such black holes. Here the angular propagation speeds of odd and even parity perturbations have been investigated in the large l limit. In particular, for black holes in theories with no \(Z_2\) symmetric coupling function a gradient instability was not found.

From an astrophysical point of view rotating black holes are most important. Rapidly rotating dilatonic black holes (for \(\gamma \!=\!1\)) were considered in Refs. [26, 30, 32]. We exhibit the domain of existing of these black holes in Fig. 3a, where the scaled horizon area \(a_\textrm{H}\!=\!A_\textrm{H}/16 \pi M^2\) is shown versus the scaled angular momentum \(j=J/M^2\). The domain of solutions is bounded by the Kerr black holes, by the static black holes, by the critical black holes, and by extremal black holes. The inset highlights the large j region, showing that the Kerr bound \(J/M^2=1\) is slightly violated.

Fig. 3
figure 3

Rotating dilatonic black holes: a Scaled horizon area \(a_\textrm{H}=A_\textrm{H}/16 \pi M^2\) versus scaled angular momentum \(j=J/M^2\) for fixed values of the scaled horizon angular velocity \(\Omega _\textrm{H} \alpha ^{1/2}\). b Scaled entropy \(s=S/16 \pi M^2\) versus j. The shaded area indicates the domain of existence (\(\gamma =1\))

Full size image

Figure 3b shows the scaled entropy of the solutions versus the scaled angular momentum. Clearly, these hairy black holes possess higher entropy than the GR black holes. They also feature higher horizon temperatures and quadrupole moments, and their geodesics show deviating ISCOs and orbital periods. Concerning their linear mode stability not much is known currently, however work towards this goal is underway [62,63,64,65,66].

2.4 Spontaneous scalarization

The phenomenon of spontaneous scalarization was first observed for static neutron stars in certain scalar-tensor theories [42]. In this case, for a sufficiently strong matter source term in the scalar field equation and an adequate coupling function a tachyonic instability would occur, and scalarized neutron stars would arise beside the GR neutron stars. For the Schwarzschild and Kerr black holes, however, analogous spontaneous scalarization seemed not possible due to a lack of source term.

However, as realized in parallel in Refs. [39,40,41] spontaneous scalarization can also be curvature induced. Employing EsGB theories with \(Z_2\) even coupling functions static spherically symmetric hairy black holes were obtained, that were generated by the mechanism of curvature induced spontaneous scalarization.

When the coupling function satisfies \(\displaystyle \frac{df(\varphi )}{d\varphi }=0\) for \(\varphi =0\) the GR solutions remain solutions. When the coupling function satisfies in addition \(\displaystyle \frac{d^2 f(\varphi )}{d\varphi ^2} \ne 0\) for \(\varphi =0\) the coupling term in the scalar field Eq. (4) contains an effective mass

$$\begin{aligned} m^2_\textrm{eff} \sim - \alpha R^2_\textrm{GB} \,. \end{aligned}$$
(13)

Insertion of the Schwarzschild Gauss–Bonnet yields for the Gauss–Bonnet invariant

$$\begin{aligned} R^2_\textrm{GB} = \frac{48 M^2}{r^6}> 0 \,, \end{aligned}$$
(14)

i.e., a negative \(m^2_\textrm{eff}\) for \(\alpha >0\). For sufficiently strong curvature this then leads to a tachyonic instability of the Schwarzschild black holes for positive GB coupling \(\alpha \) [39,40,41]. In fact, independent of the precise choice of the coupling function \(f(\varphi )\) not only a single branch of scalarized black holes arises, but a countable number of branches, representing the fundamental scalarized black holes and their excitations.

A rather attractive choice for the coupling function was made in [39]

$$\begin{aligned} f(\varphi )= \frac{1}{12} \left( 1- e^{-6\varphi ^2}\right) , \end{aligned}$$
(15)

following the neutron star case [42]. In Fig. 4a the fundamental branch, denoted \(n=0\), is shown together with the first few radially excited branches, \(n=1\), 2, 3. In particular, for these scalarized black holes the scaled scalar charge \(D/\lambda \) is shown versus the scaled mass \(M/\lambda \), where \(\lambda \sim \sqrt{\alpha }\) [39]. The scalarized solutions branch off symmetrically from the Schwarzschild solution, signifying the \(Z_2\) symmetry of the coupling function.

Fig. 4
figure 4

Static spontaneously scalarized black holes: a Scaled scalar charge \(D/\lambda \) versus scaled mass \(M/\lambda \) for the fundamental branch \(n=0\) and the first radially excited branches, \(n=1\), 2, 3 for the exponential coupling function (15). b Function \(\left( 1-\frac{r_H}{r}\right) ^2 g^2\) signalling loss of hyperbolicity versus scaled radial coordinate \(1-r_H/r\) for a set of black holes (\(n=0\), \(\lambda =1\)) and several values of the horizon radius \(r_H\)

Full size image

Linear mode stability for the black hole solutions of this theory was investigated in Refs. [39, 44, 50, 51]. The Schwarzschild black holes possess zero modes at the onsets of the scalarized black hole branches, that give rise to branches of unstable radial modes. Thus with each radial excitation the Schwarzschild solution collects one more unstable radial mode. To investigate the radial (in)stability of the scalarized black hole branches one has to consider the perturbation equations in the background of the scalarized solutions instead of the Schwarzschild background. We note, that an indication for the stability of the black holes on the fundamental branch was already obtained before by showing that their entropy is larger than the corresponding entropy of the Schwarzschild black holes [39].

Introducing functions g(r), \(C_1(r)\) and U(r) as abbreviations of rather lengthy expressions the radial perturbation equations can be reduced to the following master equation [44]

$$\begin{aligned} g^2(r) \ddot{\varphi }_1 - \varphi _1'' + C_1(r) \varphi _1' + U(r) \varphi _1=0 \,, \end{aligned}$$
(16)

where the dot and the prime denote differentiation with respect to the time and the radial coordinate, respectively.

Importantly, the fundamental branch of scalarized black holes is radially stable until hyperbolicity of the equation is lost at small \(M/\lambda \). In Fig. 4a the line style along the fundamental branch then changes. The loss of hyperbolicity happens, since the coefficient \(g^2(r)\) of the first term in equation (16) changes sign, and thus the equation is no longer a wave equation. This change of sign is illustrated in Fig. 4b, where the scaled coefficient \((1-\frac{r_H}{r})^2 g^2\) is shown versus the scaled radial coordinate \(1-r_H/r\) for a set of fundamental scalarized black holes with decreasing horizon radius \(r_H\). We note, that the loss of hyperbolicity was observed earlier in higher dimensional Gauss–Bonnet gravity and Lovelock theories [72, 73].

Unlike the fundamental scalarized black holes (along most of the branch) the radially excited black holes are radially unstable. In fact, with every node of the scalar field a further unstable mode arises. Their radial instability is, of course, expected. An immediate visual indication of the different stability properties of the fundamental branch and the radial excitations is their different dependence on \(M/\lambda \): the fundamental branch extends to smaller values of mass (for fixed coupling) \(M/\lambda \) and is thus easily reachable with respect to the instability onset of the Schwarzschild solution, whereas the excited branches extend to larger values of \(M/\lambda \).

Investigation of the fundamental branch with respect to higher multipole perturbations (but still small l) in the axial and the polar sector did not lead to any further instabilities. Thus the fundamental branch of scalarized black holes in this theory was considered to be stable up to the loss of hyperbolicity [50, 51]. However, recent calculations of the angular propagation speeds came to the conclusion that these become imaginary for the even-parity perturbations in the large l limit for this theory, and that all its static spherically symmetric scalarized black holes should therefore suffer from a gradient instability [61].

Fig. 5
figure 5

Static spontaneously scalarized black holes: a Scaled scalar charge \(D/\lambda \) versus scaled mass \(M/\lambda \) for the fundamental branch \(n=0\) and the first radially excited branches, \(n=1\), 2, 3 for the quadratic coupling function (17). b Scaled frequencies \(\omega _I M^2 /\lambda \) versus \(M/\lambda \) for \(n=0\) and 1. For comparison, the first unstable modes of Schwarzschild and of the \(n=1\) branch with exponential coupling (15) are also shown

Full size image

The simplest coupling function giving rise to spontaneously scalarized black holes is, of course, a quadratic coupling function

$$\begin{aligned} f(\varphi ) = \frac{\varphi ^2}{2}. \end{aligned}$$
(17)

Whereas the radially excited branches are very similar to those of the exponential coupling function, the fundamental branch is quite distinct, since it now extends toward larger masses \(M/\lambda \). Not surprisingly, this signals its instability to radial perturbations as demonstrated in Fig. 5.

The first branches of scalarized solutions are seen in Fig. 5a, where the scaled scalar charge \(D/\lambda \) is shown versus the scaled mass \(M/\lambda \), while the corresponding unstable modes are seen in Fig. 5b [44]. Here the scaled imaginary frequency \(\omega _I M^2 /\lambda \) is shown versus the scaled mass \(M/\lambda \) for the branches \(n=0\) and \(n=1\). Also shown are the first unstable modes of the Schwarzschild black holes, starting at the onset of the scalarized branches, and the unstable mode of the \(n=1\) branch for the exponential coupling (15).

Thus all static spherically symmetric scalarized black holes are unstable when the quadratic coupling function is employed. To evade or at least alleviate the radial instability of the fundamental branch of these black holes it was suggested to include a potential term for the scalar field in the action [46]

$$\begin{aligned} V(\varphi ) = \frac{1}{2} \mu ^2 \varphi ^2 + \frac{1}{8} \lambda \varphi ^4. \end{aligned}$$
(18)

In this case for small scalar field mass and large self-interaction indeed the fundamental branch would first extend toward smaller masses, until at some minimal value of the mass the branch would extend backwards again toward larger masses. Investigating the radial perturbations showed, that the fundamental branch is radially stable between its onset and that minimal value of the mass. According to the reasoning on the gradient instability, however, all static spherically symmetric scalarized black holes with a \(Z_2\) symmetric coupling function would be unstable [61].

We now turn to the rotating spontaneously scalarized black holes considered first in Refs. [47, 48, 52]. We therefore recall the scalar equation (4) with the resulting effective mass (13), \( m^2_\textrm{eff}(r) \sim - \alpha R^2_\textrm{GB}\). The new features now are caused by the different source term, since the GB invariant in the Kerr background reads

$$\begin{aligned} R^2_\textrm{GB} = \frac{48 M^2}{(r^2 + \chi ^2)^6} \left( r^6 - 15 r^4 \chi ^2 + 15 r^2 \chi ^4 - \chi ^6 \right) , \end{aligned}$$
(19)

where \(\chi =a \cos \theta \) with \(a=J/M\).

Obviously, rotation influences the occurrence of spontaneous scalarization. In particular, we distinguish two cases:

  • \( \alpha > 0\): spin suppresses scalarization,

  • \( \alpha < 0\): spin induces scalarization.

In the first case (for \(\alpha >0\)) the rotating scalarized black holes are simply obtained by starting from the static spherically symmetric solutions and increasing slowly the spin. This was done for the fundamental scalarized solutions and the exponential coupling function (15) in Ref. [47]. The obtained domain of existence indeed decreases with increasing spin, and, as expected, the entropy of these scalarized rotating black holes is larger than the entropy of the Kerr black holes. Interestingly, the size of the black hole shadow can differ quite strongly from the shadow of a comparable Kerr black hole [47].

Fig. 6
figure 6

Rotating spontaneously scalarized black holes: a Scaled horizon area \(a_\textrm{H}=A_\textrm{H}/16 \pi M^2\) versus scaled angular momentum \(j=J/M^2\) for quadratic coupling function (17) and \(\alpha >0\). The inset shows the scaled entropy \(s=S/16 \pi M^2\) vs j. b Scaled horizon area \(a_\textrm{H}\) vs scaled angular momentum j for \(\alpha <0\) with scaled entropy s versus scaled angular momentum j in the inset

Full size image

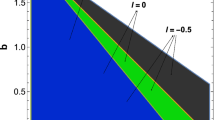
For the quadratic coupling function (17) the branch of fundamental solutions is already small in the static case, and the entropy along this branch is smaller than the Schwarzschild entropy. The domain of existence of the rotating scalarized black holes associated with the static ones is then small and decreasing with increasing spin, as illustrated in Fig. 6a [48]. The domain is bounded by the static black holes, the Kerr black holes, and the critical black holes. The entropy is shown in the inset in Fig. 6a, and it is always smaller than the entropy of the Kerr black holes [48].

In the second case (for \(\alpha \!<\!0\)) the spontaneous scalarization is referred to as being spin-induced. This possibility was first considered in Ref. [52], where the onset of spin-induced scalarization was demonstrated. To induce a tachyonic instability of the Kerr black holes fast rotation is needed, with \(j\!=\!0.5\) being the limiting value [52, 53]. We note that the occurrence of spontaneous scalarization for a negative value of the coupling constant was already demonstrated earlier in the case of neutron stars [67].

Subsequently the domain of existence of spin-induced rotating black holes was obtained for both the exponential coupling function (15) [55] and the quadratic coupling function (17) [56]. Whereas the exponential coupling function did not yield any surprises, this was different for the quadratic coupling function. As seen in Fig. 6b, where the scaled area \(a_H\) is shown versus the scaled angular momentum j and in the inset the scaled entropy s versus j, the entropy of the spin-induced scalarized rotating black holes is larger than the entropy of the Kerr black holes. Thus these scalarized solutions are entropically preferred. However, up to now investigation of their stability still needs to be done.

2.5 Non-linear scalarization

We now briefly turn to the non-linear scalarization of black holes obtained in Ref. [57]. Here the conditions for the GR black holes to remain solutions of the field equations are retained. However, the condition giving rise to a tachyonic instability of the GR solutions is discarded. Instead it is required that \(\displaystyle \frac{d^2 f(\varphi )}{d\varphi ^2} = 0\) for \(\varphi =0\) such that the source term in the scalar field Eq. (4) does not contain an effective mass and is of higher order in \(\varphi \).

Fig. 7
figure 7

Static non-linearly scalarized black holes: a Scaled scalar charge \(D/\lambda \) versus scaled mass \(M/\lambda \) for the non-linear coupling function (20) and \(\kappa =1000\). b Scaled scalar charge \(D/\lambda \) versus scaled mass \(M/\lambda \) for the non-linear coupling function (20) and \(\kappa =100\). The radially stable branch parts are denoted b2 (solid)

Full size image
Fig. 8
figure 8

Static spontaneously scalarized black holes with Ricci coupling: a Scaled scalar charge \(D/\sqrt{\alpha }\) versus scaled mass \(M/\sqrt{\alpha }\) for the fundamental branch for Ricci coupling \(\beta =2\), 5. The black dots signal die onset of the static \(l=2\) branches, shown in the insets. b Scaled scalar charge \(D/\sqrt{\alpha }\) versus scaled mass \(M/\sqrt{\alpha }\) for the fundamental branch for Ricci coupling \(\beta =2\) together with the \(l=2\) and \(l=4\) branches, highlighted in the insets

Full size image

The resulting non-linear scalarization of static spherically symmetric black holes was demonstrated for coupling function

$$\begin{aligned} f(\varphi )= \frac{1}{4\kappa }\left( 1-e^{-\kappa \varphi ^4}\right) \, \end{aligned}$$
(20)

and further higher order ones [57]. Their radial stability was investigated subsequently [58]. We exhibit in Fig. 7 the branches of static spherically symmetric black holes for the coupling function (20) and two values of \(\kappa \), \(\kappa =1000\) in Fig. 7a and \(\kappa =100\) in Fig. 7b. Here, as before, the scaled scalar charge \(D/\lambda \) is shown versus the scaled mass \(M/\lambda \). For large values of \(\kappa \) the set of non-linearly scalarized black holes forms a loop, starting from the origin (Fig. 7a). However, for smaller values of \(\kappa \), the loop develops a gap (Fig. 7b), while further decrease leads to a disconnected loop and a single branch emerging from the origin [58].

Fig. 9
figure 9

Static spontaneously scalarized black holes with Ricci coupling: a 3-dimensional horizon embedding for \(l=2\), \(\beta =2\) and 3 values of \(\alpha \). b 3-dimensional horizon embedding for \(l=4\), \(\beta =2\) and 3 values of \(\alpha \). c 2-dimensional slice for \(l=2\), d 2-dimensional slice for \(l=4\)

Full size image

The figure also shows the radially stable parts for these values of \(\kappa \) and the various unstable parts as well as the parts where hyperbolicity is lost. For very small \(\kappa \), in contrast, no radially stable part is found any more [58]. The radially stable branch parts suggest, that for the larger \(\kappa \) indeed linearly stable static spherically symmetric black holes exist for the case of non-linear scalarization. We note, however, that the gradient instability was also studied for the case of non-linear scalarization, and again the even perturbations of the static spherically symmetric scalarized black holes were found to feature imaginary propagation speeds in the large l limit [61].

3 Einstein-scalar–Gauss–Bonnet–Ricci black holes

When EsGB theories allowing for spontaneous scalarization are considered in the early universe, a non-negligible scalar field is generated. Surviving till today its presence should preclude spontaneous scalarization of black holes, unless strong fine-tuning is applied in the early universe [68]. As shown in Ref. [68] such fine-tuning can be avoided, when an additional term is included in the action, where the scalar field is coupled to the Ricci scalar. Considering the same quadratic coupling function (17) with two independent coupling constants, \(\alpha \) and \(\beta \), GR then becomes a cosmic attractor, allowing again for spontaneous scalarization of black holes in the current epoch [68].

Accordingly, we now consider the action of EsGBR theory containing the additional coupling of the scalar field to the Ricci scalar

$$ S=\frac{1}{16 \pi }\int d^4x \sqrt{-g} \left[ R - \frac{1}{2} (\partial _\mu \varphi )^2 + \frac{\varphi ^2}{2} \left( \alpha R^2_\textrm{GB} - \frac{\beta }{2} R \right) \right] \, , $$

with the quadratic coupling function (17) [69, 70]. Since the contribution from the additional term to the effective mass vanishes for GR vacuum solutions (\(R=0\))

$$\begin{aligned} m^2_\textrm{eff} = \frac{\beta }{2} R - \alpha R^2_\textrm{GB} \,, \end{aligned}$$
(21)

the tachyonic instability and the onset of the branches of scalarized black holes is not affected.

As demonstrated in Refs. [69, 70], for small values of the Ricci coupling constant \(\beta \) the fundamental branch of spontaneously scalarized black holes still extends toward larger values of the mass \(M/\sqrt{\alpha }\), as it does for vanishing \(\beta \). However, beyond a critical value of \(\beta \) it starts to first extend toward smaller values of the mass, until it reaches a minimal value of the mass, where it extends backwards or ends. A linear stability analysis for the radial modes then showed, that the fundamental branches are indeed radially stable between the onset and the minimal mass [69, 70].

While this suggested again that these scalarized black holes would be linearly stable, a surprising phenomenon appeared. During the study of their rotating generalizations, more scalarized black hole solutions appeared than had been expected. Extending some of these rotating solutions to their static limits then revealed the existence of branches of static only axially (and not spherically) symmetric scalarized black holes, bifurcating from the static spherically symmetric scalarized black holes [71]. Thus the branches of static spherically symmetric black holes are only radially stable, but possess a quadrupole (\(l=2\)) instability. Moreover, as realized subsequently, they also feature a hexadecupole (\(l=4)\) instability, where additional branches of static axially symmetric scalarized black holes bifurcate.

We exhibit the fundamental branch of static spherically symmetric black holes together with the static axially symmetric branches in Fig. 8. In Fig. 8a the scaled scalar charge \(D/\sqrt{\alpha }\) is shown versus the scaled mass \(M/\sqrt{\alpha }\) for Ricci couplings \(\beta =2\) and 5 between their common onset and their minimal masses. At the black dots the spherically symmetric black holes possess a zero mode of quadrupole type, where two branches of static scalarized black holes with quadrupole deformation bifurcate from the fundamental branch [71]. These \(l=2\) branches are highlighted in the insets for \(\beta =2\) and 5.

In Fig. 8b we restrict to Ricci coupling \(\beta =2\), zooming into the region with the quadrupole and hexadecupole instabilities. Here the branching off of the deformed branches from the fundamental branch is clearly visible. Still we highlighted the \(l=2\) branches and the \(l=4\) branches in the insets. In order to demonstrate the corresponding deformations of these black holes, we show examples for the embeddings of their horizons in Euclidean space. Full 3-dimensional embeddings are shown in Fig. 9a and b, while 2-dimensional ones are seen in Fig. 9c and d. For comparison the spherical configuration at the bifurcation point is always included. In particular, for the quadrupole solutions it is clearly visible, that one of the branches features prolate horizons, and the other oblate horizons. Evaluation of their entropy is hinting that oblate scalarized black holes might be entropically preferred.

The presence of the \(l=2\) and \(l=4\) instabilities of the radially stable fundamental branch immediately begs the question, whether there would be further higher l instabilities: \(l=6\), \(l=8\), \(\dots \) [61, 71]. A linear stability analysis for higher l should yield an answer. In any case, a recent investigation of the gradient instability for the theory with Ricci coupling found imaginary propagation speeds in the large l limit, thus indicating instability also for large l [74].

4 Conclusion

When going beyond General Relativity typically new degrees of freedom enter. Here we addressed alternative theories of gravity with an additional scalar field coupled to curvature invariants, mainly the Gauss–Bonnet term but also additionally the Ricci scalar. The black holes in these theories exhibit a much richer set of properties than the Schwarzschild and Kerr black holes of GR. In particular, black holes with scalar hair arise, and the scalar degree of freedom enhances the spectrum of QNMs, allowing for monopole and dipole radiation, doubling the polar modes, which can be gravity-led and scalar-led, as well as breaking of the isospectrality of GR black holes.

The coupling functions of the scalar field to the invariants are decisive for the type of scalarization that is realized. Dilatonic coupling functions, motivated by string theory, allow only for scalarized black holes. GR black holes no longer solve the generalized field equations. In contrast, coupling functions with \(Z_2\) symmetry let the GR black holes persist as solutions of the field equation, while at the same time allowing, in addition, for scalarized black holes in certain parts of the parameter space. Moreover, the scalarization may be spontaneous or non-linear, depending on the presence or absence of a tachyonic effective mass.

So far the stability of these black holes has been addressed basically only in perturbative schemes and only for static spherically symmetric black holes. Investigations of linear mode stability concluded that dilatonic black holes should be linearly stable, in agreement with results based on investigations of the gradient instability. In contrast, for scalarized black holes with \(Z_2\) symmetric coupling functions linear mode stability (with respect to the lower multipolar modes) might be obtained, but would be refuted when considering the propagation speed of certain perturbations in the large l limit. Interestingly, the fundamental branch of scalarized black holes can be radially stable, but suffer from quadrupole and hexadecupole instabilities, giving rise to static black holes with multipolar horizon deformation.

Besides the many studies of static and stationary black holes, numerous time-dependent numerical relativity studies were performed in recent years. Such calculations feature processes of dynamical scalarization and descalarization, and may reveal the dynamical stability or instability of the various types of scalarized black holes in the future. Moreover, gravitational wave templates will be obtained, that will allow for direct comparison with future more accurate observations, allowing to put stringent bounds or even exclude certain alternative gravity theories.