Abstract
A novel fatalistic argument that combines elements of modal, temporal, and epistemic logic to prove that the fixed past is not compatible with the open future has recently been presented by Lampert (Analysis 82(3):426–434, 2022). By the construction of a countermodel, it is shown that his line of reasoning is defective. However, it is also explained how Lampert’s argument could be corrected if it were supported with an extra premise regarding the temporal status of a priori knowledge. This additional assumption—which was tacit in the original presentation—is shown to be the weakest link, and it is argued that, despite Lampert’s assurance, it can be plausibly rejected in a roughly Ockhamist framework. Thus, it is concluded that the fixed past poses no threat to the open future; however, a few different lessons about knowledge, necessity, and time are drawn from careful reflection on this novel argument.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Everyone has heard of theological fatalism: roughly, it is the idea that divine foreknowledge precludes human freedom. But arguments in support of such a fatalistic conclusion rely on some controversial assumptions, not least of which is that there is an omniscient and infallible epistemic agent. In view of this, a recent article by Lampert (2022) offers an astonishing improvement as it aims to show that far weaker premises are sufficient to establish the fatalistic conclusion. In particular, his proof requires an epistemic agent who merely knows some elementary a priori truths. Thus, the mysterious powers that allow God to epistemically infiltrate the future are no longer required to prove that nothing happens by chance. This is obviously a concerning result as it speaks against the deeply held intuition that the future is ours to create, and it demands that we re-examine the relations between freedom, possibility, knowledge, and time. Hold your horses, though. My plan is to argue that there are lessons to be learned from Lampert’s argument, but they are different from those he suggested. In particular, his suggestion that an open future requires an open past is premature.
My claim is that Lampert’s argument, which is recounted in Sect. 1, is not conclusive. This is established by the consistency proof presented in Sect. 2, in which a model is offered that verifies all the supposedly inconsistent assumptions. Section 3 identifies the false step in the original line of reasoning, while Sect. 4 offers an improvement which involves an additional premise that was implicit in the original presentation. In Sect. 5, it is argued that the tacit premise—which states that knowing something a priori is a temporally local affair—is in fact the weakest link of the entire line of reasoning and should be rejected. Some alternative reactions to the argument are discussed in Sect. 6.
1 The argument
The original presentation of Lampert’s argument relies on six assumptions, which I categorize into three groups:
-
Logical:
- 1.:
-
(L1) Classical logic holds.
- 2.:
-
(L2) \(@\phi \rightarrow \Box @\phi \). "If Actually \(\phi \), then necessarily, actually \(\phi \)" is universally true. This is a thesis of the classical modal logic of actuality.
-
Epistemic:
- 3.:
-
(E1) \(\Box ({\mathcal {K}}\phi \rightarrow \phi )\). A priori knowledge is necessarily factive.
- 4.:
-
(E2) \({\mathcal {K}}(@\phi \rightarrow \phi )\). The implication "If actually A, then A" is known a priori. For the classical discussion, cf. (Davies & Humberstone, 1980).
-
Metaphysical:
- 5.:
-
(M1) The future is contingent; that is, not everything that will actually happen is determined to happen by the present state of the world (for some \(\phi \),
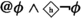 ).
). - 6.:
-
(M2) The past is fixed. This assumption is the hardest to capture formally. Some suggestions will be offered in the next section.
Before we begin the reconstruction, let us observe that L1, L2, and E1 jointly imply (in logic K) what Lampert calls a knowledge lemma: \(@\phi \rightarrow \Box ({\mathcal {K}}(@\phi \rightarrow \phi )\rightarrow \phi )\). Those interested in a (valid) proof should consult the original paper.
To focus the debate, I present below a sketch of Lampert’s line of thought; a precise reconstruction of (a version of) the argument in purely formal language will be given in Sect. 4. For now let us assume, in the spirit of M1, that the future is open and that it is only contingently true that S (S may stand for "There will be a sea battle tomorrow"). Then, we can reason as follows:
-
1.
In the actual world, S. (M1)
-
2.
In some world that is like the actual world up to now, not S. (M1)
-
3.
If actually S, then necessarily, if it is known at any time that actually S implies S, then S. (the knowledge lemma, based on L1, L2, and E1)
-
4.
Necessarily, if it is known at any time that actually S implies S, then S. (follows from 1 and 3)
-
5.
In the actual world, it is known at some past time that actually S implies S. (E2)
-
6.
In all worlds that are like the actual world up to now, it is known at some past time that actually S implies S. (follows from 5 and M2)
-
7.
In all worlds that are like the actual world up to now, S. (follows from 4 and 6, contradicts 2)
Hence, some rudimentary assumptions about classical and modal logic, supplemented with relatively widely accepted views on a priori knowledge, apparently imply that the open future is not compatible with the fixed past. This means that given how things have been up to now, there is only one possible future path; thus, as Aristotle put it, "everything that happens happens of necessity" (De Interpretatione, 18b26–19a7).
Lampert’s argument relies on numerous assumptions, so there are alternative possible reactions. He discusses several of them and conjectures that relaxing assumption M2 is the most reasonable solution. Thus, his proof may be seen as a challenge to all those who believe that the past is fixed, immutable, inevitable, etc. As I have signaled, this is a premature conclusion, and there is no reason to despair. We shall see in a moment that all Lampert’s assumptions are jointly consistent, and there must be a mistake in his line of reasoning.
2 Consistency proof
In what follows, a simple model is presented that validates L1, L2, E1, E2, M1, M2, which constitutes proof of their internal consistency. Before we turn to formal details, let us look at a pictorial representation of the model.

In this picture, \(w_1\) represents the actual world. Worlds \(w_1\) and \(w_2\) overlap up to time \(t_1\), indicating that these two worlds are indistinguishable up to this time (we may even assume that they are partially identical). Thus, the world at \(t_1\) has only one possible past. We shall see that within this model, at point \(\langle t_1,w_1\rangle \), all the assumptions listed in the previous section are true: it is known that p will happen tomorrow if it actually will; knowledge is necessarily factive; and standard modal logic is preserved. Nevertheless, the past of \(t_1\) is clearly fixed, while its future is clearly open. Thus, Lampert’s assumptions are not internally inconsistent.
For the sake of formal uniformity, I chose a tensed modal language for my reconstruction. This requires a slight reformulation of Lampert’s premises, but nothing substantial hangs on this because the same essential points can be stated in a purely tenseless language, as the interested reader may witness in Appendix 8.2.
A language rich enough to capture Lampert’s argument needs to contain propositional constants \(p,q,r,\dots \) that express atomic propositions like "There is a sea battle"; the classical Boolean operators \(\lnot ,\wedge ,\rightarrow \); an operator of universal modality \(\Box \); an a priori knowledge operator \({\mathcal {K}}\); a future tense operator \(F_1\) ("in a day, it will be the case that"); and an operator of "historic" modality  , which expresses the temporal, circumstance-specific notion of necessity: "given how things have been, it is settled that".
, which expresses the temporal, circumstance-specific notion of necessity: "given how things have been, it is settled that".
The branching-time (BT) model \({\mathfrak {M}}\) for this language consists of a quintuple \(\langle W,T,\approx ,V,t_c\rangle \) in which:
-
W is the set of possible worlds.
-
T is a linearly ordered set of times. For simplicity, T will be identified with the set of real numbers \({\mathbb {R}}\), but for our purposes even a finite subset of natural numbers would do.
-
\(\approx \) is a three-place relation, where \({\approx }(w_1,w_2,t)\), or \(w_1{\approx _t} w_2\), indicates that \(w_1\) is indistinguishable from \(w_2\) at t. For any given t, \(\approx _t\) is an equivalence relation on W. This relation is needed to express the time-dependent notion of necessity.
-
V is the valuation function that maps propositional constants to subsets of \(W\times T\) (world-time pairs). Thus, the semantic values of sentences of our language are temporal propositions (see Appendix 8.2 for the eternal variant). The truth of atomic propositions is meant to be "temporally local": whether p is true at a \(\langle w,t\rangle \) pair depends uniquely on what happens in w at t. To capture this, we assume that if \(w_1{\approx _t} w_2\), then \(\langle w_1,t\rangle \in V(p)\) iff \(\langle w_2,t\rangle \in V(p)\), i.e., all worlds indistinguishable at t assign the same truth value to an atomic p.Footnote 1
-
Finally, \(t_c\in T\) is the distinguished time of the model (the present time, if you wish). It is not essential that the model contains the distinguished time, as it could be added as a contextual parameter. I decided to build it into the model, since adding \(t_c\) as an additional semantic parameter would further complicate the presentation.Footnote 2
A crucial feature of any BT model—highly relevant for our investigations—is that it is required that the past of each possible world is fixed at each time:
- Fixity of the past (FP):
-
\(\forall {t,t',w,w'}\big (\textit{If\ }(t{\le }t'{} \textit{ and }w{\approx _{t'}}w')\textit{, then\ } w{\approx _{t}}w'\big )\).
This means that if two worlds are indistinguishable at any time, they are indistinguishable at all earlier times. This feature is sometimes described as the "no-backward-branching" requirement on the set of possible worlds. This structural fact is clearly reflected at the semantic level: if \(w_1{\approx _t}w_2\), then for every \(t'\) such that \({t'\le t}\) and every propositional constant p, \(\langle w_1,t'\rangle \in V(p)\) iff \(\langle w_2,t'\rangle \in V(p)\). Thus, in BT models, the past is as fixed as it gets, and if any formula \(\phi \) differs in truth value between two worlds indistinguishable at t, its truth value cannot depend on what happens up to t; instead, it needs to be "about the future" of time t—the future in which the two worlds diverge. You should keep this in mind when we come back to whether all knowledge ascriptions are "temporally local" and thus whether they are a part of the fixed past.
Sentences of our language are evaluated at quadruples \(\langle {\mathfrak {M}},w_c,w,t\rangle \), in which \({\mathfrak {M}}\) is a BT model, \(w_c\in W\) is the world of context, \(w\in W\) is the world of evaluation, and \(t\in T\) is the time of evaluation. The world of context is needed to interpret the modal indexical @ and to offer a partial analysis of the aprioricity operator. This analysis is sufficient to capture the argument, so we do not need an independent "epistemic" semantic parameter (such as an epistemically possible world). Finally, we are ready to introduce the recursive definition of truth.
Definition 1
A sentence is true in BT model \({\mathfrak {M}}\), at the world of the context \(w_c\), at the world of evaluation w, and at the time of evaluation t:
- 1.:
-
\({\mathfrak {M}},w_c,w,t\models p\) iff \(\langle w,t\rangle \in V(p)\);
- 2.:
-
standard definitions of the Boolean connectives;
- 3.:
-
\({\mathfrak {M}},w_c,w,t\models \Box \phi \) iff \(\forall w'\forall t' \,{\mathfrak {M}},w_c,w',t'\models \phi \);
- 4.:
-
\({\mathfrak {M}},w_c,w,t\models @\phi \) iff \({\mathfrak {M}},w_c,w_c,t_c\models \phi \);
- 5.:
-
If \({\mathfrak {M}},w_c,w,t\models {\mathcal {K}}\phi \), then \({\mathfrak {M}},w_c,w,t\models \phi \);
- 6.:
-
If \(\forall {w}\, {\mathfrak {M}},w,w,t_c\models \phi \), then \(\forall {w'}\, {\mathfrak {M}},w',w',t_c\models {\mathcal {K}}\phi \);
- 7.:
-
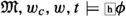 iff \(\forall {w'}(\)if \(w'{\approx _t}w\), then \({\mathfrak {M}},w_c,w',t\models \phi )\);
iff \(\forall {w'}(\)if \(w'{\approx _t}w\), then \({\mathfrak {M}},w_c,w',t\models \phi )\); - 8.:
-
\({\mathfrak {M}},w_c,w,t\models F_1\phi \) iff \({\mathfrak {M}},w_c,w,t{+}1\models \phi \).
The operators of universal and historical possibility are dual to those of universal and historical necessity: \(\Diamond {:}{=}\lnot \Box \lnot \),  .
.
These definitions are rather orthodox in philosophical formal semantics; they are merely adjusted to the language of the discussed argument. However, a few comments may help. First, since a tensed language was chosen, the universal modality \(\Box \) is analyzed as both a modal and a temporal necessity (that could be captured as "necessarily always"); as a consequence, the actuality operator @ assumes partly temporal meaning as well (in this instance, I follow the ideas of Belnap et al., 2001, pp. 245–246); the temporal aspect of necessity could be discarded at the cost of complicating the presentation (see Appendix 8.2). Second, point 1.5 is meant to capture the factivity of a priori knowledge. Third, point 1.6 states that if \(\phi \) is true regardless of the context in which it is used, it is an a priori truth (even if it happens to be contingent).Footnote 3 This is obviously an idealized and oversimplified (partial) definition of aprioricity. In particular, it abstracts from peculiar human epistemic subjects as it implies that all validities are always known.Footnote 4 This definition is in line, however, with Chalmers’ definition of aprioricity within the two-dimensional framework (a sentence is a priori iff its primary intention is true in all scenarios, see Chalmers, 2005), and I believe that this idealized version is sufficiently close to Lampert’s original meaning.
We now have all that is needed to prove the consistency of Lampert’s assumptions. Let \({\mathfrak {N}}\) be a BT model corresponding to the depiction on page 3. In this model \(W{=}\{w_1,w_2\}\), \(T{=}\{t_1,t_2\}\), \(t_c{=}t_1\), \(t_2=t_1+1\), and \(w_1{\approx _{t_1}} w_2\), while \(w_1{\not \approx _{t_2}}w_2\). Let us now take the atomic formula p, such that \(\langle w_1,t_2\rangle \in V(p)\) and \(\langle w_2,t_2\rangle \notin V(p)\).Footnote 5 Then, all Lampert’s assumptions are satisfied at \(\langle {\mathfrak {N}},w_1,w_1,t_1\rangle \):
-
Logical:
- 1.:
-
\({\mathfrak {N}},w_1,w_1,t_1\models \) classical logic (due to Definition 1.2, all the truths of classical logic are true at all indexes).
- 2.:
-
\({\mathfrak {N}},w_1,w_1,t_1\models @F_1p\rightarrow \Box @F_1p\) (due to Definitions 1.2–1.4, all sentences of the form \(@\phi \rightarrow \Box @\phi \) are true at all indexes).
-
Epistemic:
- 3.:
-
\({\mathfrak {N}},w_1,w_1,t_1\models \Box ({\mathcal {K}}F_1p\rightarrow F_1p)\) (due to Definitions 1.2, 1.3, 1.5, all sentences of the form \(\Box ({\mathcal {K}}\phi \rightarrow \phi )\) are true at all indexes).
- 4.:
-
\({\mathfrak {N}},w_1,w_1,t_1\models {\mathcal {K}}(@F_1p\rightarrow F_1p)\). First, observe that any sentence of the form \(@\phi \rightarrow \phi \) is true at any index of the form \({\mathfrak {M}},w,w,t_c\) (due to Definition 1.4). Then, notice that index \({\mathfrak {N}},w_1,w_1,t_1\) is of this form and apply Definition 1.6.Footnote 6
-
Metaphysical
- 5.:
-
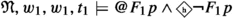 . This is the libertarian precondition of freedom. It holds because \({\mathfrak {N}},w_1,w_1,t_1\models F_1p\) and \({\mathfrak {N}},w_1,w_2,t_1\models \lnot F_1p\).
. This is the libertarian precondition of freedom. It holds because \({\mathfrak {N}},w_1,w_1,t_1\models F_1p\) and \({\mathfrak {N}},w_1,w_2,t_1\models \lnot F_1p\). - 6.:
-
The past is fixed. This condition is built into the very notion of the BT model. All worlds that are indistinguishable at one time are indistinguishable at all earlier times. In particular, worlds \(w_1\) and \(w_2\) of our model are completely indistinguishable/identical up to \(t_1\).
Hence, model \({\mathfrak {N}}\) demonstrates that Lampert’s assumptions are jointly consistent, therefore there must be a mistake in his argument to the contrary. We could end at this point as the alleged problem with the fixed past has been dismissed. Nonetheless, it is instructive to learn why Lampert’s argument seems flawless. This will further our understanding of the relations between aprioricity, possibility, and time.
3 What went wrong?
Let us return to the original argument to identify the misstep. I claim that the unjustified move is the transition from step 5 to step 6 of my reconstruction above (the transition from steps 7 and 9 to 11 in Lampert, 2022, pp. 427–428). Notice what happens there: in world \(w_1\), at time \(t_1\), it is known a priori that actually S only if S. Since the past is assumed to be fixed, and worlds \(w_1\) and \(w_2\) share the same past until \(t_1\), the author concludes that it "clearly follows" (Lampert, 2022, p. 428) that the same proposition is also known in \(w_2\). This observation naturally leads to a contradiction and concludes the proof.
However, the inference above is far from evident. Given the formal resources developed so far, we can clarify this step and ask whether the assumptions:
-
\({\mathfrak {M}},w_c,w_c,t_c\models {\mathcal {K}}(@\phi \rightarrow \phi )\) and \(w_c{\approx _{t_c}} w'\) justify the conclusion that
-
\({\mathfrak {M}},w_c,w',t_c\models {\mathcal {K}}(@\phi \rightarrow \phi )\).
And the answer is that they clearly do not! Observe that in model \({\mathfrak {N}}\):
-
\({\mathfrak {N}},w_1,w_1,t_1\models {\mathcal {K}}(@F_1 p\rightarrow F_1 p)\) and \(w_1{\approx _{t_1}} w_2\), while
-
\({\mathfrak {N}},w_1,w_2,t_1\not \models {\mathcal {K}}(@F_1p\rightarrow F_1p)\).
The truth of \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) at \(\langle {\mathfrak {N}},w_1,w_1,t_1\rangle \) is guaranteed by Definition 1.6, while \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) is false at \(\langle {\mathfrak {N}},w_1,w_2,t_1\rangle \) because \(@F_1p\rightarrow F_1p\) is false at \(\langle {\mathfrak {N}},w_1,w_2,t\rangle \) and a priori knowledge is assumed to be factive (see Definition 1.5).
Thus, the fact that proposition A is known a priori in world \(w_1\) at time \(t_1\), taken jointly with the fact that world \(w_1\) overlaps with world \(w_2\) at \(t_1\), does not justify the claim that proposition A is also known a priori at time \(t_1\) in world \(w_2\). Beware that there might be a different proposition B, known a priori in world \(w_2\) at \(t_1\), which happens to be expressed in world \(w_2\) by the same sentence which expresses proposition A in world \(w_1\) at \(t_1\). Case in point: the sentence \(@F_1p\rightarrow F_1p\) expresses a different proposition depending on which world, \(w_1\) or \(w_2\), is the world of the context (this is spelled out formally in Sect. 5). Therefore, we must be extra careful to ensure that the world of context does not change during the evaluation process. Otherwise, \(@\phi \) might not be univocal.
To use a familiar example, the sentence "I exist" expresses a true proposition in every world in which it is used. Nonetheless, we cannot conclude on this ground, as stressed by Kaplan (1989), that my existence implies my necessary existence. By analogy, we should be careful not to argue that \(\Box {\mathcal {K}}(@F_1p\rightarrow F_1p)\) is true because \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) (or \(@F_1p\rightarrow F_1p\)) expresses a true proposition in every world in which it is used. I do not claim that Lampert makes this very mistake in his argument. Instead, he is best understood as using an additional assumption (which is explicated in the next section). However, this extra assumption appears unjustified unless this very mistake is made.
4 Fixing the argument
The extra assumption I have in mind is the claim that some epistemic facts are "temporally local". This means that whether an agent knows something a priori is a temporally intrinsic state of affairs. In particular, it does not depend on what happens in the future. Then, since the past (and the present) is fixed, we can conclude that if an agent knows a priori that \(\phi \), it is a settled fact that she does.
- Fixed knowledge (FK):
-
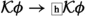 .
.
This principle needs to be true—at least with respect to a priori knowledge—for (a version of) Lampert’s argument to succeed. This is attested by the formal piece of reasoning based on Lampert’s assumptions that is presented below. The proof requires that we postulate a natural interaction between the universal and the historical modality: if something is necessary—in the broadest sense of the word—it is also historically necessary:
- (IM):
-
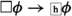 .
.
This assumption is implicitly made by Lampert and I find it completely uncontroversial.
Now, let us prove that the orthodox modal and epistemic assumptions invoked by Lampert, supplemented with FK, are sufficient to show (in logic K) that \(@\phi \) and  cannot be jointly true.
cannot be jointly true.
-
1.
\(@\phi \) (M1)
-
2.
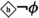 (M1)
(M1) -
3.
\(@\phi \rightarrow \Box @\phi \) (L2)
-
4.
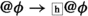 (from 3 and IM)
(from 3 and IM) -
5.
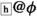 (from 1 and 4)
(from 1 and 4) -
6.
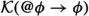 (E2)
(E2) -
7.
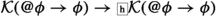 (FK)
(FK) -
8.
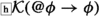 (from 6 and 7)
(from 6 and 7) -
9.
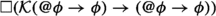 (E1)
(E1) -
10.
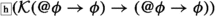 (from 9 and IM)
(from 9 and IM) -
11.
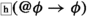 (from 8 and 10, by distribution of
(from 8 and 10, by distribution of 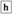 )
) -
12.
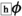 (from 5 and 11, by distribution of
(from 5 and 11, by distribution of 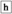 ; contradicts 2).
; contradicts 2).
Thus, the relatively uncontroversial logical and epistemic principles (L1, L2, E1, E2, IM), together with FK, imply that nothing ever happens by chance. What will actually happen is already inevitable. Thus, we have derived, following in Lampert’s footsteps, a completely novel argument for fatalism.
Lampert presents his argument as a dilemma between fatalism and FP. An argument which establishes—very much in the spirit of the Master Argument of Diodorus Cronus—that the open future is not compatible with the fixed past. The reconstruction above shows that he is not quite right. The dilemma is rather between fatalism and FK, and it could be transformed into Lampert’s dilemma only if we assume that FP implies FK. However, this step should be questioned. It turns out that the open future is very much compatible with the fixed past, assuming that we accept that a priori knowledge is not always temporally local. This means that what happens in the future might partly determine whether something is presently known a priori, because what happens in the future determines whether what is presently believed on a priori grounds is also true. I suggest that this is the most reasonable exit route from Lampert’s maze; it is much less costly than scarifying the open future, the fixed past, or some basic principles of epistemic or modal logic.Footnote 7
5 The Ockhamist response
Let us examine FK more carefully. First, observe that sentences of the form  are not universally true. For example, \(F_1p\) is true and
are not universally true. For example, \(F_1p\) is true and  is false at \(\langle {\mathfrak {N}},w_1,w_1,t_1\rangle \). The implication
is false at \(\langle {\mathfrak {N}},w_1,w_1,t_1\rangle \). The implication  is valid only if \(\phi \) contains "no trace of futurity" (i.e., it is "about" what is and has been the case). An extra argument is required to justify that any sentence of the form \({\mathcal {K}}\phi \) is "wholly about the present" and the transition from \({\mathcal {K}}\phi \) to
is valid only if \(\phi \) contains "no trace of futurity" (i.e., it is "about" what is and has been the case). An extra argument is required to justify that any sentence of the form \({\mathcal {K}}\phi \) is "wholly about the present" and the transition from \({\mathcal {K}}\phi \) to  is valid.
is valid.
Indeed, an assumption along these lines is not alien to philosophical debate. It is the central point of contention in the conversation related to divine foreknowledge. After all, if God already knows at present what will happen, and if what God presently knows is intrinsic to how the world presently is (and thus—already settled), it is hard to escape the conclusion that the future is predetermined. In this form, the concept of fixed knowledge reoccurs through the history of philosophy and theology.Footnote 8
However, there is a well-known response to this line of thinking that is commonly attributed to William of Ockham. According to Ockham, whether God currently knows that something will happen is not an already settled fact. It is a "soft fact" whose present occurrence depends on a contingent future turn of events. A similar idea could be applied in our case: whether an agent knows that \(@\phi \rightarrow \phi \) might not be a settled fact. After all, it is not settled whether the known proposition is true, and since knowledge is a factive attitude, it is equally unsettled whether this proposition is known. Thus, we may argue that \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) corresponds to a "soft" fact; this is an essentially future-oriented proposition whose "futurity" is disguised by its grammatical form. I believe that this is the most reasonable reaction to Lampert’s argument, especially as it requires, as we shall see, a rather weak variant of Ockhamism.
Interestingly, Lampert himself discusses and rejects the Ockhamist response to his argument:
[C]onsider the following fact about t:
(16) Smith knows at t that Alice will actually offer him the job in a week only if she will offer him the job in a week.
Does (16) depend on the future in order to obtain? It might seem so on the surface. Yet, on closer inspection, (16) tells us nothing about Smith’s career prospects. Whether it is a fact that Smith knows that a priori truth at t does not depend on whether he gets offered the job or not. (...), it is not in virtue of how the future turns out that (16) counts as a fact at the time in question, for Smith does not count as knowing that a priori truth at t in virtue of what happens at a later time. (16), therefore, seems to display no dependence on the future. (Lampert, p. 432)
I respectfully disagree. Admittedly, it is hard to give a precise criterion that distinguishes a proposition which depends on the future from another one which does not.Footnote 9 Fortunately, the semantic resources developed in Sect. 2 make it possible to delineate this notion somewhat more precisely. The core idea is simple: if two worlds are indistinguishable until t and the proposition A is true in one of them and false in the other, then the truth value of that proposition depends on the future of t. To put it more precisely, let \(W_{wt}^\approx \) be the set of worlds indistinguishable from w until t:
Definition 2
\(W_{wt}^\approx {:}{=}\{w'\in W|w'\approx _t w\}\).
Also, let \(\llbracket \phi \rrbracket ^{w_c}\) be the (eternal) proposition expressed by sentence \(\phi \) used in the context of world \(w_c\) in model \({\mathfrak {M}}\):
Definition 3
\(\llbracket \phi \rrbracket ^{w_c}{:}{=}\{w\in W|{\mathfrak {M}},w_c,w,t_c\models \phi \}\).
Then, we can state a sufficient condition for a proposition to be "about" the future:
Definition 4
The truth of the proposition expressed by sentence \(\phi \) in context \(w_c\) depends on the future if \(W_{w_ct_c}^\approx \cap \llbracket \phi \rrbracket ^{w_c}\not =W_{w_ct_c}^\approx \) and \(W_{w_ct_c}^\approx \cap \llbracket \phi \rrbracket ^{w_c}\not =\emptyset \).
This means that if proposition \(\llbracket \phi \rrbracket ^{w_c}\) is true in some but not all worlds indistinguishable from \(w_c\) at \(t_c\), then this proposition is about the future. This should be rather uncontroversial: clearly, if two worlds are indistinguishable at \(t_c\), it is what happens after \(t_c\) (i.e., in the future) that accounts for the difference in truth value across these worlds.
Now, let us return to the toy model \({\mathfrak {N}}\) and assume that \(w_1\) is the world of the context (that is, the actual world). Then, \(W_{w_ct_c}^\approx =\{w_1,w_2\}\), while \(\llbracket {\mathcal {K}}(@F_1p\rightarrow F_1p)\rrbracket ^{w_c}=\{w_1\}\).Footnote 10 Thus, in accordance with Definition 4, the proposition \(\llbracket {\mathcal {K}}(@F_1p\rightarrow F_1p)\rrbracket ^{w_c}\) does depend on the future! Then, it is no surprise that the principle of the fixity of the past does not apply here. In fact, it is easy to calculate that  . This is yet another way to realize that the transition from step 5 to 6 in my reconstruction of Lampert’s argument is the weakest link of the entire line of reasoning. Therefore, an Ockhamist can show that the (epistemic and modal) logic itself does not threaten the open future, even if the past is fixed.
. This is yet another way to realize that the transition from step 5 to 6 in my reconstruction of Lampert’s argument is the weakest link of the entire line of reasoning. Therefore, an Ockhamist can show that the (epistemic and modal) logic itself does not threaten the open future, even if the past is fixed.
A caveat is required before proceeding. One could object that I did not read Lampert’s response to Ockhamism charitably enough. I read him as trying to say that the proposition expressed in the actual world by \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) is true with respect to every world indistinguishable from the actual world until now. This turned out to be incorrect. What he might be trying to say is that regardless of which of the worlds happens to be the actual one, the proposition expressed by \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) is true (with respect to that world). This is certainly true! Our semantic definitions guarantee that \(\forall {w_c}\,w_c{\in }\llbracket {\mathcal {K}}(@F_1p\rightarrow F_1p)\rrbracket ^{w_c}\). This is in part because for any \({\mathfrak {M}}\) and \(w_c\), \({\mathfrak {M}},w_c,w_c,t_c\models @F_1p\rightarrow F_1p\). This might be what convinced Lampert that \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) is temporally local and, therefore, historically necessary. However, this is the mistake I already mentioned. We cannot rely on the observation that a sentence expresses a true proposition in every (indistinguishable) context to justify that the proposition actually expressed by this very sentence is true with respect to every indistinguishable world (and is thus historically necessary). This is not dissimilar to arguing that "I exist" expresses a necessary proposition because it expresses a true proposition in every context in which it is used.
In conclusion, FK is not an innocent assumption, nor is it a consequence of FP. The discussion above demonstrates that a sentence of the form \({\mathcal {K}}\phi \) may well depend on the future and, therefore, the general rule  should not be accepted. In particular, the proposition \(\llbracket {\mathcal {K}}(@F_1p\rightarrow F_1p)\rrbracket ^{w_c}\) does depend on the future. Therefore, the mere fact that it is true at t at one world does not imply that it needs to be true at t at another world, even if this second world is indistinguishable from the first until t. This suggestion might not be obvious straight away, but neither is it excessively extravagant, especially if acceptance of logical fatalism is the alternative. Also, we should stress that the assumption that one could possess a priori knowledge of a future contingent \(@F_1p\rightarrow F_1p\) strikes me as significantly less controversial than the traditional Ockhamist assumption that it could be known that Peter will sin tonight. In particular, justification of the latter requires a somewhat mysterious epistemic capacity—a sort of sense that detects the contingent future events. In contrast, justification of the former is achieved through purely a priori means by intellectual insight into what the words mean. Thus, a relatively uninvolved variant of Ockhamism is sufficient to block Lampert’s proof. We then have a solution to the alleged problem with the fixed past (or the open future). Before I conclude, however, let me inspect some alternative reactions.
should not be accepted. In particular, the proposition \(\llbracket {\mathcal {K}}(@F_1p\rightarrow F_1p)\rrbracket ^{w_c}\) does depend on the future. Therefore, the mere fact that it is true at t at one world does not imply that it needs to be true at t at another world, even if this second world is indistinguishable from the first until t. This suggestion might not be obvious straight away, but neither is it excessively extravagant, especially if acceptance of logical fatalism is the alternative. Also, we should stress that the assumption that one could possess a priori knowledge of a future contingent \(@F_1p\rightarrow F_1p\) strikes me as significantly less controversial than the traditional Ockhamist assumption that it could be known that Peter will sin tonight. In particular, justification of the latter requires a somewhat mysterious epistemic capacity—a sort of sense that detects the contingent future events. In contrast, justification of the former is achieved through purely a priori means by intellectual insight into what the words mean. Thus, a relatively uninvolved variant of Ockhamism is sufficient to block Lampert’s proof. We then have a solution to the alleged problem with the fixed past (or the open future). Before I conclude, however, let me inspect some alternative reactions.
6 Alternative responses
Lampert himself ponders on several reactions to his argument, and there is no point repeating the discussion here. Let me just mention that I agree with him that stopping his argument by rejecting (i) classical logic, (ii) the standard modal logic of actuality, or (iii) the factivity of knowledge would be an unjustified overreaction.
If the fatalistic conclusion is to be avoided, however, we have a few more possibilities to explore. Firstly, we can deny premise M1 on semantic rather than metaphysical grounds. That is, we can insist that the sentence  can never be true for semantic reasons. This idea is adopted by Belnap et al. (2001, p. 246) and MacFarlane (2008, p. 99), who define operator @ as an indexical variant of historical necessity—"given the present, actual state of the world, it is inevitable that." This definition would block Lampert’s argument from the outset as it would prevent premise M1 from being true in any context. M1 could not be true, not because the future is determined but because ’actually’ is read as a form of historical necessity which renders
can never be true for semantic reasons. This idea is adopted by Belnap et al. (2001, p. 246) and MacFarlane (2008, p. 99), who define operator @ as an indexical variant of historical necessity—"given the present, actual state of the world, it is inevitable that." This definition would block Lampert’s argument from the outset as it would prevent premise M1 from being true in any context. M1 could not be true, not because the future is determined but because ’actually’ is read as a form of historical necessity which renders  false in every context in which it is used.Footnote 11 I do not recommend this solution as it enforces a rather artificial reading of ‘actually’, but I signal this as an unexplored possibility (some controversial consequences of such a semantic decision are discussed in Wawer, 2014, Sect. 4.4).
false in every context in which it is used.Footnote 11 I do not recommend this solution as it enforces a rather artificial reading of ‘actually’, but I signal this as an unexplored possibility (some controversial consequences of such a semantic decision are discussed in Wawer, 2014, Sect. 4.4).
An alternative reaction to the argument would be to deny that the proposition expressed by \(@F_1p\rightarrow F_1p\), where \(F_1p\) is a future contingent, can be known a priori. Observe that if two worlds are indistinguishable until t, this sentence may well express different propositions (when used at time t), depending on which of these worlds is the world of context (i.e., the actual world). Case in point: \(\llbracket @F_1p\rightarrow F_1p\rrbracket ^{w_1}=\{w_1\}\), while \(\llbracket @F_1p\rightarrow F_1p\rrbracket ^{w_2}=\{w_1,w_2\}\) in model \({\mathfrak {N}}\). This is problematic since no data available to any (human) subject at \(t_1\) can determine whether \(w_1\) or \(w_2\) is the actual world. After all, these worlds are completely indistinguishable until t. Thus, the subject has no way of knowing at t which proposition she expresses when she utters \(@F_1p\rightarrow F_1p\), and one could reasonably argue that if a subject cannot know, in principle, which proposition is being expressed by the sentence she utters, she cannot hold beliefs (let alone possess knowledge) with respect to this proposition. It could be said, at most, that what the subject knows a priori is that the proposition expressed by the sentence \(@F_1p\rightarrow F_1p\) is true (regardless of which proposition it happens to be), but the proposition itself is not known. I do not want to explore this option any further here, but it should be stressed that when future contingents are concerned, the a priori status of \(@A\rightarrow A\) could be called into question, and premise E2 of Lampert’s argument could be rejected (more on relationships between aprioricity and contingency in Wawer, 2016).
Lastly, we could modify the constraints on \({\mathcal {K}}\) in a way that ensures the truth of  . For this purpose, we should replace points 5 and 6 of Definition 1 with the following postulate:
. For this purpose, we should replace points 5 and 6 of Definition 1 with the following postulate:
Thus, if the sentence \(\phi \) is true regardless of which of the indistinguishable worlds happens to be the actual one, then it is known a priori that \(\phi \) is true in all indistinguishable worlds. This attempt seems in line with the fragment of Lampert’s text cited above: "whether it is a fact that Smith knows that a priori truth at t does not depend on whether he gets offered the job or not." (Lampert, 2022, p. 432). The author observes that regardless of which of the currently indistinguishable worlds happens to be the actual one (the working world or the jobless world), the proposition expressed by \(@\phi \rightarrow \phi \) is true, and he concludes that the truth of this proposition does not depend on the future.
This reaction is indeed relatively straightforward and natural as it embodies the idea that the evaluation of the knowledge claims requires that we assume the perspective of the knower. Nevertheless, this move undermines another tenet endorsed by the author, namely the factivity of knowledge. Going back again to model \({\mathfrak {N}}\), observe that the new condition on a priori knowledge renders the result that
- 1.:
-
\({\mathfrak {N}},w_1,w_2,t_1\models {\mathcal {K}}(@F_1p\rightarrow F_1p)\), and
- 2.:
-
\({\mathfrak {N}},w_1,w_2,t_1\not \models @F_1p\rightarrow F_1p\).
Thus, FK could be traded for factivity of knowledge (Lampert’s argument would be stopped either way). Personally, I do not consider this a fair trade, but this is a different matter for a different occasion.
7 Conclusion
To conclude, anyone who appreciates future-oriented indeterminism can breathe a sigh of relief. Lampert’s argument does not establish that the fixed past forecloses the open future. However, it provokes more careful reflection on the relationship between possibility, knowledge, and time. It reveals, in particular, that an agent’s knowing something a priori might presently be a "soft" fact whose present occurrence depends on what happens in the future. Lampert’s argument also helps to recognize that a priori truths that involve future contingents are particularly controversial: it is not obvious whether these truths can even be believed, let alone known. The argument also reveals that the necessary factivity of a priori knowledge is not completely innocent when indexicals are involved. These are just a few avenues that are opened by careful reflection on this argument, which shows that even though the argument is not logically valid, it is far from futile.
Notes
Technically, this requires a transition from Kripke frames to generalized Kripke frames since not all subsets of \(W\times T\) are eligible values of the valuation function, see (Blackburn et al., 2001, ch. 5).
The in-built parameter \(t_c\) surfaces twice in what follows: it is used to interpret "actually" and to define tenseless propositions expressed in a tensed language.
We run into the problem that \(\phi \) could be true at every context of a given model due not to its a priori character but the peculiar features of the model (e.g., if the model represents the physically possible scenarios uniquely, the laws of nature are true at every context and are thus supposed to be known a priori). This problem could be avoided by generalizing the clause and quantifying over all models.
A somewhat more realistic principle that every in-context valid \(\phi \) is known if believed (for a priori reasons) would suffice for our purposes, but this would complicate the presentation as we would need to constantly repeat a contingent assumption that some particular person did form (for a priori reasons) the belief "There actually will be a sea-battle tomorrow only if there will be one" at some point in the past. Alternatively, and more contentiously, we could replace "known" in clause 1.6 with "a priori justified" and assume that a priori justification is necessarily factive.
We can assume that p states that there is a sea battle.
An important side note: even though \({\mathcal {K}}(@F_1p\rightarrow F_1p)\) is true at every context, it is not an axiom of our modal system, and it should not be used as such in Lampert’s argument. If it were, the rule of necessitation would apply, and we would easily derive a controversial theorem \(@\phi \rightarrow \Box \phi \). For an easy proof, consult the appendix.
It is worth noting that the fixity assumption is somewhat more plausible with respect to belief than with respect to knowledge. However, belief is not necessarily factive, so the argument is not threatening in the case of belief either. It might regain its power if one assumes that an epistemic agent, e.g., God, possesses necessarily factive (i.e., infallible) beliefs. However, this is not the place to dwell on this (interesting) variant of the argument.
The connection between divine knowledge and predetermination was recently elucidated and heavily exploited in (Todd, 2021). A simple formal argument that establishes the deterministic consequence of the assumption of foreknowledge can be found in (Belnap et al., 2001, p. 55–58); a more elaborate but clearly related line of thought is developed in (Rönnedal, 2021).
For example, even if a sentence contains a future-tensed sub-sentence, this does not yet imply that the proposition it expresses depends on the future. The proposition expressed by \(P_2F_1p\), where \(P_2\) stands for “two days ago” and \(F_1\) for “one day hence”, is clearly about the past. Furthermore, the proposition expressed by \(F_1p\rightarrow F_1p\) cannot be reasonably qualified as future-dependent, despite the occurrence of a future tense operator in the sentence that expresses it.
As was already discussed, \(w_2\not \in \llbracket {\mathcal {K}}(@F_1p\rightarrow F_1p)\rrbracket ^{w_c}\) because knowledge is necessarily factive, while \({\mathfrak {N}},w_1,w_2,t_1\not \models @F_1p\rightarrow F_1p\).
A variant of this response may be recognized in the semantic project originating in (Todd, 2016).
References
Aristotle. (1991). In Barnes, J. (Eds.), Complete works of Aristotle: The revised Oxford translation, (Vol. 2). Princeton University Press.
Belnap, N., Perloff, M., & Xu, M. (2001). Facing the future: Agents and choices in our indeterministic world. Oxford University Press.
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal logic. Volume 53 of Cambridge Tracts in Theoretical Computer Science. Cambridge University Press.
Chalmers, D. J. (2005). The foundations of two-dimensional semantics. In García-Carpintero, M., & Macià, J. (Eds.), Two-dimensional semantics: Foundations and applications. Oxford University Press.
Davies, M., & Humberstone, L. (1980). Two notions of necessity. Philosophical Studies, 38(1), 1–31.
Kaplan, D. (1989). Demonstratives: An essay on the semantics, logic, metaphysics, and epistemology of demonstratives and other indexicals. In J. Almog, J. Perry, & H. Wettstein (Eds.), Themes from Kaplan, chapter 17 (pp. 481–563). Oxford University Press.
Lampert, F. (2022). A puzzle about the fixity of the past. Analysis, 82(3), 426–434.
MacFarlane, J. (2008). Truth in the garden of forking paths. In M. García-Carpintero & M. Kölbel (Eds.), Relative truth, chapter 4 (pp. 81–102). Oxford University Press.
Rönnedal, D. (2021). The aporia of future directed beliefs. Acta Analytica, 36(2), 249–261.
Todd, P. (2016). Future contingents are all false! On behalf of a Russellian open future. Mind, 125(499), 775–798.
Todd, P. (2021). The open future: Why future contingents are all false. Oxford University Press.
Wawer, J. (2014). The truth about the future. Erkenntnis, 79, 365–401.
Wawer, J. (2016). How contingent and how a priori are contingent a priori truths? Studia Semiotyczne-English Supplement, 28, 25–56.
Acknowledgements
I would like to thank Allard Tamminga and Fabio Lampert for numerous conversations that helped me to clarify the ideas presented here, for the valuable feedback they offered on the initial version of the paper, and for their hospitality during my visit to the University of Greifswald. The author acknowledges that this research was funded by the National Science Centre, Poland, project no. 2020/39/D/HS1/00810.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflicts of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
8 Appendix
8 Appendix
1.1 8.1 Actually \(\phi \) implies necessarily \(\phi \)
-
1.
\({\mathcal {K}}(@\phi \rightarrow \phi )\) (E2)
-
2.
\(\Box {\mathcal {K}}(@\phi \rightarrow \phi )\) (from 1, by necessitation)
-
3.
\(\Box ({\mathcal {K}}(@\phi \rightarrow \phi )\rightarrow (@\phi \rightarrow \phi ))\) (E1)
-
4.
\(\Box (@\phi \rightarrow \phi )\) (from 2 and 3, by distribution of necessity)
-
5.
\(@\phi \rightarrow \Box @\phi \) (L2)
-
6.
\(@\phi \rightarrow \Box \phi \) (from 4 and 5, by classical logic and distribution of necessity)
1.2 8.2 Tenseless formulation
Tenseless formulation renders syntax slightly more cumbersome, but it admits simpler semantics as the temporal semantic index can be discarded. The previously introduced formal language requires two adjustments. Firstly, propositional constants, \(\Phi ^1_{t_1},\Phi ^2_{t_1},\dots \), \(\Phi ^1_{t_2},\Phi ^2_{t_2},\dots \), need to express atomic, time-specific propositions like "John is playing the piano at \(t_1\)"; secondly, the time-sensitive historic modalities are replaced with time-insensitive variants,  , which can be read as "given how things have been up to t, it is settled that."
, which can be read as "given how things have been up to t, it is settled that."
The eternalist branching time model \(BT^E\) no longer requires the time of the context, so it is a quadruple \(\langle W,T,\approx ,V\rangle \) which satisfies the condition FP. All the elements of the model are defined as before, except for the valuation function:
-
V maps propositional constants to subsets of W. Thus, the semantic values of sentences are sets of possible worlds, i.e., traditional propositions. The truth of (tenseless) atomic propositions remains "temporally local": whether \(\Phi _t\) is true depends uniquely on what happens at t. This is expressed with the condition that if \(w_1{\approx _t} w_2\), then \(w_1\in V(\Phi _t)\) iff \(w_2\in V(\Phi _t)\), i.e., all the worlds indistinguishable at t assign the same truth value to the atomic \(\Phi _t\).
Sentences of our language are evaluated at \(\langle {\mathfrak {M}},w_c,w\rangle \) triples in which \({\mathfrak {M}}{:}{=}\langle W,T,\approx ,V\rangle \) is a \(BT^E\) model, \(w_c\in W\) is the world of the context, and \(w\in W\) is the world of evaluation. Observe that the time of evaluation is no longer required. The tenseless truth is defined as follows:
Definition 5
A sentence is true in model \({\mathfrak {M}}\), at the world of context \(w_c\) and the world of evaluation w:
-
1.
\({\mathfrak {M}},w_c,w\models \Phi _t\) iff \(w\in V(\Phi _t)\);
-
2.
standard definition of Boolean connectives;
-
3.
\({\mathfrak {M}},w_c,w\models \Box \phi \) iff \(\forall {w'}\, {\mathfrak {M}},w_c,w'\models \phi \);
-
4.
\({\mathfrak {M}},w_c,w\models @\phi \) iff \({\mathfrak {M}},w_c,w_c\models \phi \);
-
5.
If \({\mathfrak {M}},w_c,w\models {\mathcal {K}}\phi \), then \({\mathfrak {M}},w_c,w\models \phi \);
-
6.
If \(\forall w\, {\mathfrak {M}},w,w\models \phi \), then \(\forall w'\, {\mathfrak {M}},w',w'\models {\mathcal {K}}\phi \);
-
7.
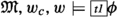 iff \(\forall {w'}(\)if \(w'{\approx _{t_1}}w\), then \({\mathfrak {M}},w_c,w'\models \phi )\).
iff \(\forall {w'}(\)if \(w'{\approx _{t_1}}w\), then \({\mathfrak {M}},w_c,w'\models \phi )\).
The operators of universal and historical possibility are dual to those of universal and historical necessity: \(\Diamond {:}{=}\lnot \Box \lnot \),  .
.
Model \({\mathfrak {N}}\) is defined as above, with the necessary adjustment: we choose a tenseless sentence \(\Phi _{t_2}\) such that \(w_1\in V(\Phi _{t_2})\) and \(w_2\notin V(\Phi _{t_2})\). This sentence may express the tenseless proposition that Lampert used in his original formulation of the argument: "Agent S \(\Phi \)-s at time \(t_2\)".
Then, all Lampert’s assumptions are satisfied at \({\mathfrak {N}},w_1,w_1\):
-
Logical:
-
1.
\({\mathfrak {N}},w_1,w_1\models \) classical logic (due to Definition 5.2, all truths of classical logic are true at all indexes).
-
2.
\({\mathfrak {N}},w_1,w_1\models @\Phi _{t_2}\rightarrow \Box @\Phi _{t_2}\) (due to Definitions 5.2–5.4, all sentences of the form \(@\phi \rightarrow \Box @\phi \) are true at all indexes).
-
1.
-
Epistemic:
-
3.
\({\mathfrak {N}},w_1,w_1\models \Box ({\mathcal {K}}\Phi _{t_2}\rightarrow \Phi _{t_2})\) (due to Definitions 5.2, 5.3, 5.5, all sentences of the form \(\Box ({\mathcal {K}}\phi \rightarrow \phi )\) are true at all indexes).
-
4.
\({\mathfrak {N}},w_1,w_1\models {\mathcal {K}}(@\Phi _{t_2}\rightarrow \Phi _{t_2})\). First, observe that any sentence of the form \(@\phi \rightarrow \phi \) is true at any index of the form \({\mathfrak {M}},w,w\) (due to Definition 5.4). Then, notice that index \({\mathfrak {N}},w_1,w_1\) is of this form and apply Definition 5.6.
-
3.
-
Metaphysical
-
5.
. This holds because \({\mathfrak {N}},w_1,w_1\models \Phi _{t_2}\) and \({\mathfrak {N}},w_1,w_2\models \lnot \Phi _{t_2}\)
-
6.
The past is fixed. Semantically: \(\forall {\Phi _{t_1}}\forall t_2,t_1(\)If \(t_2\ge t_1\), then
 .
.
-
5.
Observe that  , because \({\mathfrak {N}},w_1,w_1\models {\mathcal {K}}(@\Phi _{t_2}\rightarrow \Phi _{t_2})\), while \({\mathfrak {N}},w_1,w_2\not \models {\mathcal {K}}(@\Phi _{t_2}\rightarrow \Phi _{t_2})\) (due to the falsity of \(@\Phi _{t_2}\rightarrow \Phi _{t_2}\) at \(\langle {\mathfrak {N}},w_1,w_2\rangle \)). Therefore, the step from point 5 to point 6 of Lampert’s argument (see Sect. 1) is, once again, unjustified—just as an Ockhamist would have us believe.
, because \({\mathfrak {N}},w_1,w_1\models {\mathcal {K}}(@\Phi _{t_2}\rightarrow \Phi _{t_2})\), while \({\mathfrak {N}},w_1,w_2\not \models {\mathcal {K}}(@\Phi _{t_2}\rightarrow \Phi _{t_2})\) (due to the falsity of \(@\Phi _{t_2}\rightarrow \Phi _{t_2}\) at \(\langle {\mathfrak {N}},w_1,w_2\rangle \)). Therefore, the step from point 5 to point 6 of Lampert’s argument (see Sect. 1) is, once again, unjustified—just as an Ockhamist would have us believe.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wawer, J. A problem with the fixed past fixed. Synthese 202, 154 (2023). https://doi.org/10.1007/s11229-023-04345-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04345-6




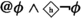 ).
).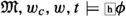 iff
iff 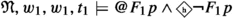 . This is the libertarian precondition of freedom. It holds because
. This is the libertarian precondition of freedom. It holds because 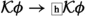 .
.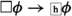 .
.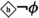 (M1)
(M1)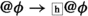 (from 3 and IM)
(from 3 and IM)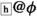 (from 1 and 4)
(from 1 and 4)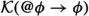 (E2)
(E2)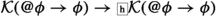 (FK)
(FK)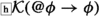 (from 6 and 7)
(from 6 and 7)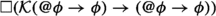 (E1)
(E1)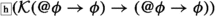 (from 9 and IM)
(from 9 and IM)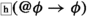 (from 8 and 10, by distribution of
(from 8 and 10, by distribution of 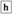 )
)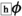 (from 5 and 11, by distribution of
(from 5 and 11, by distribution of 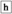 ; contradicts 2).
; contradicts 2).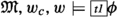 iff
iff 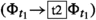 .
.