Introduction

Spectral methods (see, for instance [1–6]) are one of the principal methods of discretization for the numerical solution of differential equations. The main advantage of these methods lies in their accuracy for a given number of unknowns. For smooth problems in simple geometries, they offer exponential rates of convergence/spectral accuracy. In contrast, finite difference and finite-element methods yield only algebraic convergence rates. The three spectral methods, namely, the Galerkin, collocation, and tau methods are used extensively in the literature. Collocation methods [7, 8] have become increasingly popular for solving differential equations, since they are very useful in providing highly accurate solutions to nonlinear differential equations. Petrov–Galerkin method is widely used for solving ordinary and partial differential equations; see for example [9–13]. The Petrov–Galerkin methods [14] have generally come to be known as “stablized” formulations, because they prevent the spatial oscillations and sometimes yield nodally exact solutions where the classical Galerkin method would fail badly. The difference between Galerkin and Petrov–Galerkin methods is that the test and trial functions in Galerkin method are the same, while in Petrov–Galerkin method, they are not.

The subject of nonlinear differential equations is a well-established part of mathematics and its systematic development goes back to the early days of the development of calculus. Many recent advances in mathematics, paralleled by a renewed and flourishing interaction between mathematics, the sciences, and engineering, have again shown that many phenomena in applied sciences, modeled by differential equations, will yield some mathematical explanation of these phenomena (at least in some approximate sense).

Even order differential equations have been extensively discussed by a large number of authors due to their great importance in various applications in many fields. For example, in the sequence of papers [12, 15–17], the authors dealt with such equations by the Galerkin method. They constructed suitable basis functions which satisfy the boundary conditions of the given differential equation. For this purpose, they used compact combinations of various orthogonal polynomials. The suggested algorithms in these articles are suitable for handling one- and two-dimensional linear high even-order boundary value problems. In this paper, we aim to give some algorithms for handling both of linear and nonlinear second-order boundary value problems based on introducing a new operational matrix of derivatives, and then applying Petrov–Galerkin method on linear equations and collocation method on nonlinear equations.

Of the important high-order differential equations are the singular and singular perturbed problems (SPPs) which arise in several branches of applied mathematics, such as quantum mechanics, fluid dynamics, elasticity, chemical reactor theory, and gas porous electrodes theory. The presence of a small parameter in these problems prevents one from obtaining satisfactory numerical solutions. It is a well-known fact that the solutions of SPPs have a multi-scale character, that is, there are thin layer(s) where the solution varies very rapidly, while away from the layer(s) the solution behaves regularly and varies slowly.

Also, among the second-order boundary value problems is the one-dimensional Bratu problem which has a long history. Bratu’s own article appeared in 1914 [19]; generalizations are sometimes called the Liouville–Gelfand or Liouville–Gelfand–Bratu problem in honor of Gelfand [20] and the nineteenth century work of the great French mathematician Liouville. In recent years, it has been a popular testbed for numerical and perturbation methods [21–27].

Simplification of the solid fuel ignition model in thermal combustion theory yields an elliptic nonlinear partial differential equation, namely the Bratu problem. Also due to its use in a large variety of applications, many authors have contributed to the study of such problem. Some applications of Bratu problem are the model of thermal reaction process, the Chandrasekhar model of the expansion of the Universe, chemical reaction theory, nanotechnology and radiative heat transfer (see, [28–32]).

The Bratu problem is nonlinear (BVP) and extensively used as a benchmark problem to test the accuracy of many numerical methods. It is given by:

$$\begin{aligned} y''(x)+\lambda \,\displaystyle e^{y(x)}=0,\quad y(0)=y(1)=0,\quad 0\leqslant x\leqslant 1, \end{aligned}$$
(1)

where \(\lambda >0\). The Bratu problem has the following analytical solution:

$$\begin{aligned} y(x)=-2\ln \bigg [\displaystyle \frac{\cosh \big (\frac{\theta }{4}(2x-1)\big )}{\cosh \left( \frac{\theta }{4}\right) }\bigg ], \end{aligned}$$
(2)

where \(\theta\) is the solution of the nonlinear equation \(\theta =\sqrt{2\lambda }\cosh \theta\).

Our main objectives in the present paper are:

  • Introducing a new operational matrix of derivatives based on using shifted Legendre polynomials and harmonic numbers.

  • Using Petrov–Galerkin matrix method (PGMM) to solve linear second-order BVPs.

  • Using collocation matrix method (CMM) to solve a class of nonlinear second-order BVPs, including singular, singularly perturbed and Bratu-type equations.

The outlines of the paper is as follows. In "Some properties and relations of Shifted Legendre polynomials and harmonic numbers", some relevant properties of shifted Legendre polynomials are given. Some properties and relations of harmonic numbers are also given in this section. In "A shifted Legendre matrix of derivatives", and with the aid of shifted Legendre polynomials polynomials, a new operational matrix of derivatives is given in terms of harmonic numbers. In "Solution of second-order linear two point BVPs", we use the introduced operational matrix for reducing a linear or a nonlinear second-order boundary value problems to a system of algebraic equations based on the application of Petrov–Galerkin and collocation methods, and also we state and prove a theorem for convergence. Some numerical examples are presented in "Numerical results and discussions" to show the efficiency and the applicability of the suggested algorithms. Some concluding remarks are given in "Concluding remarks".

Some properties and relations of shifted Legendre polynomials and harmonic numbers

Shifted Legendre polynomials

The shifted Legendre polynomials \(L^{*}_k(x)\) are defined on [a, b] as:

$$\begin{aligned} L^{*}_{k}(x)=L_{k}\left( \frac{2x-a-b}{b-a}\right) ,\qquad k=0,1,\ldots , \end{aligned}$$

where \(L_{k}(x)\) are the classical Legendre polynomials. They may be generated by using the recurrence relation

$$\begin{aligned} (k+1)\,L^{*}_{k+1}(x)=(2k+1)\,\left( \frac{2x-b-a}{b-a}\right) \,L^{*}_{k}(x)-k\,L^{*}_{k-1}(x),\qquad k=1, 2,\dots , \end{aligned}$$
(3)

with \(L^{*}_0(x)=1,\,L^{*}_1(x)=\displaystyle \frac{2x-b-a}{b-a}.\)These polynomials are orthogonal on [a, b],  i.e.,

$$\begin{gathered} \int \limits _{a}^{b}L^{*}_{m}(x)\,L^{*}_{n}(x)\ dx=\left\{ \begin{array}{ll} \displaystyle \frac{b-a}{2n+1},\quad &{} m=n,\\ 0,\quad &{} m\not =n. \end{array} \right. \end{gathered}$$
(4)

The polynomials \(L^{*}_{k}(x)\) are eigenfunctions of the following singular Sturm–Liouville equation:

$$\begin{aligned} -D\big[ (x-a)(x-b)\,D\, \phi _{k}(x)\big ]+k(k+1)\ \phi _{k}(x)=0, \end{aligned}$$

where \(D\equiv \frac{d}{dx}\).

Harmonic numbers

The nth harmonic number is the sum of the reciprocals of the first n natural numbers, i.e.,

$$\begin{aligned} H_{n}=\displaystyle \sum _{i=1}^{n}\frac{1}{i}. \end{aligned}$$
(5)

The numbers \(H_{n}\) satisfy the recurrence relation

$$\begin{aligned} H_{n}-H_{n-1}=\displaystyle \frac{1}{n},\quad n=1,2,\ldots , \end{aligned}$$

and have the integral representation

$$\begin{aligned} H_{n}=\displaystyle \int _{0}^{1}\displaystyle \frac{1-x^n}{1-x}\, dx. \end{aligned}$$

The following Lemma is of fundamental importance in the sequel.

Lemma 1

The harmonic numbers satisfy the following three-term recurrence relation:

$$\begin{aligned} (2 i-1)\, H_{i-1}-(i-1)\, H_{i-2}=i\, H_{i},\qquad i\ge 2. \end{aligned}$$
(6)

Proof

The recurrence relation (6) can be easily proved with the aid of the relation (5). \(\square.\)

A shifted Legendre matrix of derivatives

Consider the space (see, [33])

$$\begin{aligned} L_0^2[a, b]=\{\phi (x)\in \,L^2[a,b]: \phi (a)=\phi (b)=0\}, \end{aligned}$$

and choose the following set of basis functions:

$$\begin{aligned} \phi _i(x)=(x-a)(b-x)\,L^{*}_i(x),\quad i=0,1,2,\ldots . \end{aligned}$$
(7)

It is not difficult to show that the set of polynomials \(\{\phi _k(x):\, k=0,1,2,\dots \}\) are linearly independent and orthogonal in the complete Hilbert space \(L_0^2[a, b],\) with respect to the weight function \(w(x)=\displaystyle \frac{1}{(x-a)^2\, (b-x)^2}\), i.e.,

$$\begin{gathered} \int _{a}^{b}\frac{\phi _{i}(x)\ \phi _{j}(x)\, dx}{(x-a)^2\, (b-x)^2}= {\left\{ \begin{array}{ll} 0,\quad &{}i\not =j,\\ \displaystyle \frac{b-a}{2\, i+1},\quad &{}i=j. \end{array}\right. } \end{gathered}$$

Any function \(y(x)\in L_0^2[a,b]\) can be expanded as

$$\begin{aligned} y(x)=\displaystyle \sum _{i=0}^{\infty }c_i\,\phi _{i}(x), \end{aligned}$$
(8)

where

$$\begin{aligned} c_i=\frac{2i+1}{b-a}\displaystyle \int _a^b\frac{y(x)\, \phi _{i}(x)}{(x-a)^2(b-x)^2}\ dx=\bigg (y(x),\phi _i(x)\bigg )_{w(x)}. \end{aligned}$$

If the series in Eq. (8) is approximated by the first \((N+1)\) terms, then

$$\begin{aligned} y(x)\simeq y_{N}(x)=\displaystyle \sum _{i=0}^{N}c_i\,\phi _{i}(x)={\varvec{C}}^T\,{\varvec{\Phi }}(x), \end{aligned}$$
(9)

where

$$\begin{aligned} {\varvec{C}}^T=[c_0, c_1,\dots ,c_N],\quad {\varvec{\Phi }(x)}=[\phi _{0}(x), \phi _{1}(x),\dots , \phi _{N}(x)]^{T}. \end{aligned}$$
(10)

Now, we state and prove the basic theorem, from which a new operational matrix can be intoduced.

Theorem 1

Let \(\phi _{i}(x)\) be as chosen in (7). Then for all \(i\ge 1\), one has

$$\begin{aligned} D\, \phi _{i}(x)=\displaystyle \frac{2}{b-a}\displaystyle \sum _{\begin{array}{c} j=0\\ (i+j)\, \text {odd}\end{array}}^{i-1}(2\, j+1)\left( 1+2\, H_{i}-2\, H_{j}\right) \, \phi _{j}(x)+\delta _{i}(x), \end{aligned}$$
(11)

where \(\delta _{i}(x)\) is given by

$$\begin{aligned} \delta _{i}(x)= {\left\{ \begin{array}{ll} a+b-2\, x,&{}\quad i\ \text {even},\\ a-b,&{}\quad i\ \text {odd}. \end{array}\right. } \end{aligned}$$
(12)

Proof

We proceed by induction on i. For \(i=1,\) it is clear that the left hand side of (11) is equal to its right-hand side, which is equal to: \(\displaystyle a-b+\frac{6\, (x-a) (b-x)}{b-a}\). Assuming that relation (11) is valid for \((i-2)\) and \((i-1)\), we want to prove its validity for i. If we multiply both sides of (3) by \((x-a)(x-b)\) and make use of relation (7), we get

$$\begin{aligned} \phi _i(x)=\left( \frac{2\, i-1}{i}\right) \left( \frac{2\, x-b-a}{b-a}\right) \phi _{i-1}(x)-\left( \frac{i-1}{i}\right) \phi _{i-2}(x),\quad i=2,3,\dots , \end{aligned}$$
(13)

which immediately gives

$$\begin{aligned} D\phi _i(x)=\left( \frac{2\, i-1}{i(b-a)}\right) \bigg [(2x-b-a)D\phi _{i-1}(x)+2\, \phi _{i-1}(x)\bigg ] -\left( \frac{i-1}{i}\right) D\phi _{i-2}(x). \end{aligned}$$
(14)

Now, application of the induction step on \(D\phi _{i-1}(x)\) and \(D\phi _{i-2}(x)\) in (14), yields

$$\begin{aligned} D\phi _{i}(x)= & {} \displaystyle \frac{2(2\, i-1)(2x-b-a)}{i(b-a)^2}\displaystyle \sum _{\begin{array}{c} j=0\\ (i+j)\, {\text {even}} \end{array}}^{i-2}(2\, j+1)\left( 1+2\, H_{i-1}-2\, H_{j}\right) \, \phi _{j}(x)\nonumber \\&-\displaystyle \frac{2(i-1)}{i(b-a)}\displaystyle \sum _{\begin{array}{c} j=0\\ (i+j)\, \text{odd} \end{array}}^{i-3}(2\, j+1)\left( 1+2\, H_{i-2}-2\, H_{j}\right) \, \phi _{j}(x)\nonumber \\&+\displaystyle \frac{2(2i-1)}{i(b-a)}\phi _{i-1}(x)+\xi _i(x), \end{aligned}$$
(15)

where

$$\begin{aligned} \xi _i(x)= & {} \displaystyle \frac{(2i-1)(2x-b-a)}{i(b-a)}\, \delta _{i-1}(x)-\displaystyle \frac{i-1}{i}\, \delta _{i-2}(x)\nonumber \\=& \left\{ \begin{array}{ll} a+b-2x,\quad {} & {i \; \text {even},} \\ \displaystyle \frac{(2\, i-1)(2x-b-a)^2}{i(a-b)}-\displaystyle \frac{i-1}{i}(a-b),\quad {} & {i \;\text {odd}.}\\ \end{array} \right. \end{aligned}$$
(16)

Substitution of the recurrence relation (13) in the form

$$\begin{aligned} \left( \frac{2x-a-b}{b-a}\right) \phi _j(x)=\displaystyle \frac{j+1}{2j+1}\left[ \phi _{j+1}(x)+\displaystyle \frac{j}{j+1}\phi _{j-1}(x)\right] , \end{aligned}$$

into relation (15), and after performing some rather lenghthy algebraic manipulations, give

$$\begin{aligned} D\phi _i(x)= & {} \displaystyle \sum _{\begin{array}{c} j=1\\ (i+j)\, \text{odd} \end{array}}^{i-3}m_{ij}\,\phi _j(x)+\displaystyle \frac{2(2i-1)}{(b-a)} \left[ 1+\displaystyle \frac{2(i-1)}{i}\left( H_{i-1}-H_{i-2}\right) \right] \phi _{i-1}(x)\nonumber \\- & {} \displaystyle \frac{2\, c_i}{(b-a)}\left[ \displaystyle \frac{2(i-1)}{i}H_{i-2} -\displaystyle \frac{2(2i-1)}{i}H_{i-1}+\displaystyle \frac{3i-2}{i}\right] \phi _0(x)+\xi _i(x), \end{aligned}$$
(17)

where

$$\begin{aligned} m_{ij}= & {} \displaystyle \frac{2(2j+1)}{(b-a)}\left[ 1-\displaystyle \frac{2(2i-1)j}{i(2j+1)}H_{j-1}+\displaystyle \frac{2(i-1)}{i}H_{j} -\displaystyle \frac{2(2i-1)(j+1)}{i(2j+1)}H_{j+1}\right. \nonumber \\&\left. -\displaystyle \frac{2(i-1)}{i}H_{i-2}+\displaystyle \frac{2(2i-1)}{i}H_{i-1}\right] , \end{aligned}$$
(18)
$$\begin{aligned} c_i=\left\{ \begin{array}{ll} 1,\quad &{} \hbox {i odd,} \\ 0,\quad &{} \hbox {i even.}\\ \end{array} \right. \end{aligned}$$

Now, the elements \(m_{ij}\) in (18) can be written in the alternative form

$$\begin{aligned} m_{ij}= & {} \displaystyle \frac{2(2j+1)}{(b-a)}\left[ 1+\displaystyle \frac{2}{i}\left\{ (2i-1)H_{i-1}-(i-1)H_{i-2}\right\} \right. \nonumber \\&\left. -\displaystyle \frac{2(2i-1)}{i(2j+1)}\left\{ j\,H_{j-1}+(j+1)H_{j+1}\right\} +\displaystyle \frac{2(i-1)}{i}H_j\right] , \end{aligned}$$
(19)

which can be simplified with the aid of Lemma 1, to take the form

$$\begin{aligned} m_{ij}=\displaystyle \frac{2(2j+1)}{(b-a)}\left( 1+2H_i-2H_j\right) . \end{aligned}$$

Repeated use of Lemma 1 in (17), and after performing some manipulation, leads to

$$\begin{aligned} D\phi _i(x)= & {} \displaystyle \frac{2}{b-a}\left[ \displaystyle \sum _{\begin{array}{c} j=0\\ (i+j)\,\text{odd} \end{array}}^{i-1}(2j+1)\left( 1+2H_i-2H_j\right) \phi _j(x)\right. \nonumber \\&\left. -\displaystyle \frac{2(2i-1)}{i}c_i(x-a)(b-x)\right] +\xi _i(x), \end{aligned}$$
(20)

and by noting that

$$\begin{aligned} \xi _i(x)-\displaystyle \frac{4(2i-1)}{i(b-a)}c_i(x-a)(b-x)=\delta _i(x), \end{aligned}$$

then

$$\begin{aligned} D\phi _i(x)=\displaystyle \frac{2}{b-a}\displaystyle \sum _{\begin{array}{c} j=0\\ (i+j)\,\text{odd} \end{array}}^{i-1}(2j+1)\left( 1+2H_i-2H_j\right) \phi _j(x)+\delta _i(x), \end{aligned}$$
(21)

and this completes the proof of Theorem 1. \(\square\)

Corollary 1

Let \(x\in [-1,1]=[a,b],\, \psi _i(x)=(1-x^2)L_i(x).\) Then for all \(i\geqslant 1,\) one has

$$\begin{aligned} D\psi _i(x)=\displaystyle \sum _{\begin{array}{c} j=0\\ (i+j)\,\text{odd} \end{array}}^{i-1}(2j+1)\left( 1+2H_i-2H_j\right) \psi _j(x)+\gamma _i(x), \end{aligned}$$
(22)

where

$$\begin{aligned} \gamma _i(x)=\left\{ \begin{array}{ll} -2x,\quad {i \; \text {even},} \\ -2,\quad {i\; \text {odd}.}\\ \end{array} \right. \end{aligned}$$

Now, and based on Theorem 1, it can be easily shown that the first derivative of the vector \({\varvec{\Phi} (x)}\) defined in (10) can be expressed in the matrix form:

$$\begin{aligned} \displaystyle \frac{d{\varvec{\Phi }(x)}}{dx}={M}\,{\varvec{\Phi (x)}} +{\varvec{\delta }}, \end{aligned}$$
(23)

where

$$\begin{aligned} {\varvec{\delta }}=\left( \delta _{0}(x),\delta _{1}(x),\dots ,\delta _{N}(x)\right) ^T,\qquad \delta _i=\left\{ \begin{array}{ll} a+b-2x,\quad &{} {i \; \text {even},} \\ a-b,\quad &{} {i \;\text {odd},}\\ \end{array} \right. \end{aligned}$$

and \(M=\big (m_{ij}\big )_{0\leqslant i,j\leqslant N}\), is an \((N+1)\times (N+1)\) matrix whose nonzero elements can be given explicitly from relation (11) as:

$$\begin{aligned} m_{i,j}= {\left\{ \begin{array}{ll} \displaystyle \frac{2}{b-a}(2\, j+1)\left( 1+2\, H_{i}-2\, H_{j}\right) ,&{} \quad i>j,\ (i+j)\ \text{odd},\\ 0,&{} \quad \text{otherwise}. \end{array}\right. } \end{aligned}$$

For example, for \(N=5\), we have

$$\begin{aligned} M=\frac{2}{b-a}\left( \begin{array}{cccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 3 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 6 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \frac{14}{3} &{}\quad 0 &{}\quad \frac{25}{3} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \frac{19}{2} &{}\quad 0 &{}\quad \frac{21}{2} &{}\quad 0 &{}\quad 0 \\ \frac{167}{30} &{}\quad 0 &{}\quad \frac{77}{6} &{}\quad 0 &{}\quad \frac{63}{5} &{}\quad 0 \end{array} \right) . \end{aligned}$$

Remark 1

The second derivative of the vector \(\varvec{\Phi }(x)\) is given by

$$\begin{aligned} \displaystyle \frac{d^2 {\varvec{\Phi }(x)}}{dx^2}={M}^2\,\varvec{\Phi (x)}+{M}\, {\varvec{\delta }}+{\varvec{\delta }}', \end{aligned}$$
(24)

where

$$\begin{aligned} {\varvec{\delta '}}=\left( \delta '_0,\delta '_1,\dots ,\delta '_N\right) ^T,\qquad \delta '_i=\left\{ \begin{array}{ll} -2,\quad &{} {i \; \text{even},} \\ 0,\quad &{} {i\;\text{odd}.} \\ \end{array} \right. \end{aligned}$$

Solution of second-order linear two-point BVPs

In this section, both of linear and nonlinear second-order two-point BVPs are handled. For linear equations, a Petrov–Galerkin method is applied, while for nonlinear equations, the typical collocation method is applied.

Linear second-order BVPs subject to homogenous boundary conditions

Consider the linear second-order boundary value problem

$$\begin{aligned} y''(x)+f_1(x)\,y'(x)+f_2(x)\,y(x)=g(x),\quad x\in (a, b), \end{aligned}$$
(25)

subject to the homogenous boundary conditions

$$\begin{aligned} y(a)=y(b)=0. \end{aligned}$$
(26)

If we approximate y(x) as in (9), making use of relations (23) and (24), we have the following approximations for y(x), \(y'(x)\) and \(y''(x)\):

$$\begin{aligned}&y(x)\simeq {\varvec{C}}^T\,{\varvec{\Phi }(x)},\end{aligned}$$
(27)
$$\begin{aligned}&y'(x)\simeq {\varvec{C}}^T\, M\, {\varvec{\Phi }(x)}+{\varvec{C}}^T\,{\varvec{\delta }},\end{aligned}$$
(28)
$$\begin{aligned}&y''(x)\simeq {\varvec{C}}^T\, M^2\, {\varvec{\Phi }(x)}+{\varvec{C}}^T\, M\,{\varvec{\delta }}+{\varvec{C}}^T\,{\varvec{\delta '}}. \end{aligned}$$
(29)

If we substitute the relations (27), (28) and (29) into Eq. (25), then the residual R(x),  of this equation is given by:

$$\begin{aligned} R(x)= & {} {\varvec{C}}^T\, M^2{\varvec{\Phi }(x)}+{\varvec{C}}^T\, M\, {\varvec{\delta }}+{\varvec{C}}^T\,\varvec{\delta '}+f_1(x)\,\left( {\varvec{C}}^T\, M\, {\varvec{\Phi }(x)}+{\varvec{C}}^T\, \varvec{\delta }\right) \nonumber \\&\quad +f_2(x)\,\left( {\varvec{C}}^T\,{\varvec{\Phi }(x)}\right) -g(x). \end{aligned}$$
(30)

The application of Petrov Galerkin method (see, [1]) yields the following \((N+1)\) linear equations in the unknown expansion coefficients, \(c_i,\) namely,

$$\begin{aligned} \displaystyle \int _{a}^{b}R(x)\,L^*_i(x)\,dx=0, \quad i=0,1,\dots ,N. \end{aligned}$$
(31)

Thus, Eq. (31) generates a set of \((N+1)\) linear equations which can be solved for the unknown components of the vector \({\varvec{C}}\), and hence the approximate spectral solution \(y_{N}(x)\) given in (9) can be obtained.

Linear second-order BVPs subject to nonhomogeneous boundary conditions

Consider the following one-dimensional second-order equation:

$$\begin{aligned} u''(x)+f_1(x)\,u'(x)+f_2(x)\,u(x)=g_1(x),\quad x\in (a, b), \end{aligned}$$
(32)

subject to the nonhomogeneous boundary conditions:

$$\begin{aligned} u(a)=\alpha ,\quad u(b)=\beta . \end{aligned}$$
(33)

It is clear that the transformation

$$\begin{aligned} u(x)=y(x)+\frac{\alpha \,(b-x)+\beta \,(x-a)}{b-a}, \end{aligned}$$

turns the nonhomogeneous boundary conditions (33) into the homogeneous boundary conditions:

$$\begin{aligned} y(a)=y(b)=0. \end{aligned}$$
(34)

Hence it suffices to solve the following modified one-dimensional second-order equation:

$$\begin{aligned} y''(x)+f_1(x)\,y'(x)+f_2(x)\,y(x)=g(x),\quad x\in (a,b), \end{aligned}$$
(35)

subject to the homogeneous boundary conditions (34), where

$$\begin{aligned} g(x)=g_1(x)-\frac{\beta -\alpha }{b-a}\,f_1(x)- \frac{\alpha \,(b-x)+\beta \,(x-a)}{b-a}\,f_2(x). \end{aligned}$$

Solution of second-order nonlinear two-point BVPs

Consider the nonlinear differential equation

$$\begin{aligned} y''(x)=F\left( x,y(x),y'(x)\right) , \end{aligned}$$
(36)

subject to the homogenous conditions

$$\begin{aligned} y(a)=y(b)=0. \end{aligned}$$

If we follow the same procedure of "Linear second-order BVPs subject to homogenous boundary conditions", and approximate y(x) as in (27), then after making use of the two relations (23) and (24), then we get the following nonlinear equation in the unknown vector \(\mathbf C\)

$$\begin{aligned} {{\varvec{C}}^T}\mathbf M ^2{\varvec{\Phi }(x)}+{\varvec{C}}^T\, M\,\varvec{\delta }+ {\varvec{C}}^T\,{\varvec{\delta '}}=F\left( x, {\varvec{C}}^T\,{\varvec{\Phi }(x)}, {\varvec{C}}^T\, M\, {\varvec{\Phi }(x)}+{\varvec{C}}^T\,\varvec{\delta }\right) . \end{aligned}$$
(37)

To find the numerical solution \(y_{N}(x)\), we enforce (37) to be satisfied exactly at the first \((N+1)\) roots of the polynomial \(L^{*}_{N+1}(x)\). Thus a set of \((N+1)\) nonlinear equations is generated in the expansion coefficients, \(c_{i}\). With the aid of the well-known Newton’s iterative method, this nonlinear system can be solved, and hence the approximate solution \(y_{N}(x)\) can be obtained.

Remark 2

Following a similar procedure to that given in "Linear second-order BVPs subject to nonhomogeneous boundary conditions", the nonlinear second-order Eq. (36) subject to the nonhomogeneous boundary conditions given as in (33) can be tackled.

Convergence analysis

In this section, we state and prove a theorem for convergence of the proposed method.

Theorem 2

The series solutions of Eqs. (25) and (36) converge to the exact ones.

Proof

Let

$$\begin{aligned} y(x)= & {} \displaystyle \sum _{i=0}^{\infty }c_{i}\phi _i(x),\\ y_M(x)= & {} \displaystyle \sum _{i=0}^{M}c_{i}\phi _i(x),\\ y_N(x)= & {} \displaystyle \sum _{i=0}^{N}c_{i}\phi _i(x), \end{aligned}$$

be the exact and approximate solutions (partial sums) to Eqs. (25) and (36) with \(N\geqslant M\). Then we have

$$\begin{aligned} \bigg (y(x), y_{N}(x)\bigg )_{w(x)}= & {} \bigg (y(x),\displaystyle \sum _{i=0}^{N}c_{i}\, \phi _i(x)\bigg )_{w(x)}=\displaystyle \sum _{i=0}^{N}\bar{c}_{i} \,\bigg (y(x), \phi _i(x)\bigg )_{w(x)}\\&\quad =\displaystyle \sum _{i=0}^{N}\bar{c}_{i}\,c_{i} =\displaystyle \sum _{i=0}^{N}|c_{i}|^2. \end{aligned}$$

We show that \(y_{N}(x)\) is a Cauchy sequence in the complete Hilbert space \(L_0^2[a,b]\) and hence converges.

Now,

$$\begin{aligned} \big \Vert y_{N}(x)-y_{M}(x)\big \Vert _{w(x)}^2=\displaystyle \sum _{i=M+1}^{N}|c_{i}|^2. \end{aligned}$$

From Bessel’s inequality, we have \(\displaystyle \sum _{i=0}^{\infty }|c_{i}|^2\) is convergent, which yields \(\big \Vert y_{N}(x)-y_{M}(x)\big \Vert _{w(x)}^2\rightarrow 0\) as \(M, N\rightarrow \infty\) and hence \(y_{N}(x)\) converges to say b(x). We prove that \(b(x)=y(x),\)

$$\begin{aligned} \bigg (b(x)-y(x), \phi _i(x)\bigg )_{w(x)}= & {} \bigg (b(x), \phi _i(x)\bigg )_{w(x)} -\bigg (y(x), \phi _i(x)\bigg )_{w(x)}\\= & {} \bigg (\displaystyle \lim _{N\rightarrow \infty }y_{N}, \phi _i(x)\bigg )_{w(x)} -c_{i}\\= & {} \displaystyle \lim _{N\rightarrow \infty }\bigg (y_{N}, \phi _i(x)\bigg )_{w(x)} -c_{i}\\= & {} 0. \end{aligned}$$

This proves \(\displaystyle \sum _{i=0}^{\infty }c_{i}\phi _i(x)\) converges to y(x). \(\square\)

As the convergence has been proved, then consistency and stability can be easily deduced.

Numerical results and discussions

In this section, the presented algorithms in "Solution of second-order linear two point BVPs" are applied to solve regular, singular as well as singularly perturbed problems. As expected, the accuracy increases as the number of terms of the basis expansion increases.

Example 1

Consider the second-order nonlinear equation (see, [34]).

$$\begin{aligned} 2\,y''=\left( y+x+1\right) ^3,\quad 0<x<1,\quad y(0)=y(1)=0. \end{aligned}$$
(38)

The exact solution of (38) is

$$\begin{aligned} y(x) =\frac{2}{2-x}-x-1. \end{aligned}$$

In Table 1, the maximum absolute error E is listed for various values of N, while in Table 2 a comparison between the numerical solution of problem (38) obtained by the application of CMM with the two numerical solutions obtained by using a sinc-collocation and a sinc-Galerkin methods in [34] is given.

Table 1 Maximum absolute error E for Example 1
Full size table
Table 2 Comparison between different solutions for Example 1
Full size table

Example 2

Consider the second-order nonlinear singular equation (see, [34]).

$$\begin{aligned}&(4+x^s)\left( x^{\sigma }\,y'\right) '=s\,x^{\sigma +s-2}\left( s\,x^s\,e^y-\sigma -s+1\right) ,\quad 0<x<1,\\&y(0)=\ln \left( \frac{1}{4}\right) ,\quad y(1)=\ln \left( \frac{1}{5}\right) ,\qquad s=3-\sigma ,\quad \sigma \in (0, 1), \end{aligned}$$

with the exact solution

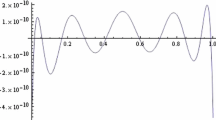
$$\begin{aligned} y(x) =-\ln \left( 4+x^s\right) . \end{aligned}$$

In Table 3, the maximum absolute error E is listed for various values of \(\sigma\) and N, while in Table 4 a comparison between the solution of Example 2 obtained by our method (CMM) with the two numerical solutions obtained in [34] is given for the case \(\sigma =\frac{1}{4}\). In addition, Fig. 1 illustrates the absolute error resulting from the application of CMM for the two cases corresponding to \(N=10,\, \sigma =\frac{1}{4}\) and \(N=15,\, \sigma =\frac{1}{4}\).

Table 3 Maximum absolute error E for Example 2
Full size table
Table 4 Comparison between different solutions for Example 2, \(\sigma =\frac{1}{4}\)
Full size table
Fig. 1
figure 1

The absolute error of Example 2 for \(\sigma =\frac{1}{4}\)

Full size image

Example 3

Consider the following singularly perturbed linear second-order BVP (see, [35])

$$\begin{aligned}&\epsilon \,y''(x)+y'(x)-y(x)=0;\qquad \qquad 0<x<1,\\&y(0)=\frac{2\bar{\epsilon }\,e^{\frac{1+\bar{\epsilon }}{2\epsilon }}}{(\bar{\epsilon }+2\epsilon +1) e^{\frac{\bar{\epsilon }}{\epsilon }}+\bar{\epsilon }-2\epsilon -1},\quad y(1)=1, \end{aligned}$$

where \(\bar{\epsilon }=\sqrt{4\epsilon +1},\) with the exact solution

$$\begin{aligned} y(x)=e^{\frac{\left( \bar{\epsilon }+1\right) (1-x) }{2\epsilon }}\displaystyle \frac{ \left( \bar{\epsilon }+2 \epsilon +1\right) e^{\frac{x \bar{\epsilon }}{\epsilon }}+\bar{\epsilon }-2 \epsilon -1}{\left( \bar{\epsilon }+2\epsilon +1\right) e^{\frac{\bar{\epsilon }}{\epsilon }}+\bar{\epsilon }-2 \epsilon -1}. \end{aligned}$$

In Table 5, the maximum absolute error E is listed for various values of \(\epsilon\) and N, while in Table 6, we give a comparison between the solution of Example 3 obtained by our method (PGMM) with the solution obtained by the shooting method given in [35].

Table 5 Maximum absolute error E for Example 3
Full size table
Table 6 Comparison between the best errors for Example 3
Full size table

Example 4

Consider the following nonlinear second-order boundary value problem:

$$\begin{aligned} y''(x)- \big (y'(x)\big )^2+ 16\,y(x)=2 - 16\,x^6;\quad -1<x<1,\quad \quad y(-1)=y(1)=0, \end{aligned}$$
(39)

with the exact solution \(y(x)=x^2-x^4.\) Making use of (9) with \(N=2\) yields

$$\begin{aligned} y_{N}(x)={\varvec{C}}^T\,{\varvec{\Phi (x)}}=(1-x^2)\, \big (c_0\,L_{0}(x)+c_1\,L_{1}(x)+c_2\,L_{2}(x)\big ). \end{aligned}$$

Moreover, in this case the two matrices M and \(M^2\) take the forms

$$\begin{aligned} M=\left( \begin{array}{lll} 0 &{} \quad 0 &{} \quad 0 \\ 3 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 6 &{} \quad 0 \end{array} \right) , \quad M^2=\left( \begin{array}{lll} 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 \\ 18&{} \quad 0 &{} \quad 0 \end{array} \right) . \end{aligned}$$

Now, with the aid of Eq. (37), we have

$$\begin{aligned}&c_0(2x^2-1)+c_1(6x^3-5x)+c_2(6x^4+5x^2-1)\nonumber \\&\qquad +\frac{1}{2}\big (2 c_0\,x-c_1+3\,c_1\,x^2+6\,c_2\,x^3-4 c_2\,x\big )^2=8x^6-1. \end{aligned}$$
(40)

We enforce (40) to be satisfied exactly at the roots of \(L_3(x)\), namely, \(-\sqrt{\frac{3}{5}},\,0,\,\sqrt{\frac{3}{5}}.\) This immediately yields three nonlinear algebraic equations in the three unknowns, \(c_0, c_1\) and \(c_2\). Solving these equations, we get

$$\begin{aligned} c_0=\frac{1}{3},\quad c_1=0,\quad c_2=\frac{2}{3}, \end{aligned}$$

and hence

$$\begin{aligned} y(x)=\left( \frac{1}{3},\,\, 0,\,\,\frac{2}{3}\right) \left( \begin{array}{c} 1-x^2 \\ x-x^3 \\ -\frac{1}{2}+2 x^2-\frac{3}{2} x^4 \\ \end{array} \right) =x^2-x^4, \end{aligned}$$

which is the exact solution.

Example 5

Consider the following Bratu Equation (see, [28–31]).

$$\begin{aligned} y''(x)+\lambda \,\displaystyle e^{y(x)}=0,\qquad y(0)=y(1)=0,\qquad 0\leqslant x\leqslant 1. \end{aligned}$$
(41)

With the analytical solution

$$\begin{aligned} y(x)=-2\ln \bigg [\displaystyle \frac{\cosh \big (\frac{\theta }{4}(2x-1)\big )}{\cosh \left( \frac{\theta }{4}\right) }\bigg ], \end{aligned}$$
(42)

where \(\theta\) is the solution of the nonlinear equation \(\theta =\sqrt{2\lambda }\cosh \theta\). The presented algorithm in Section 4.3 is applied to numerically solve Eq. (41), for the three cases corresponding to \(\lambda =1,\,2\) and 3.51 which yield \(\theta =1.51716,\,2.35755\) and 4.66781, respectively. In Table 7, the maximum absolute error E is listed for various values of N, and in Table 8, we give a comparison between the best errors obtained by various methods used to solve Example 5. This table shows that our method is more accurate compared with the methods developed in [28–31]. In addition, Fig. 2 illustrates a comparison between different solutions obtained by our algorithm (CMM) in case of \(\lambda =1\) and \(N=1,2,3\).

Table 7 Maximum absolute error E for Example 5
Full size table
Table 8 Comparison between the best errors for Example 5 for \(\lambda =1\)
Full size table
Fig. 2
figure 2

Different solutions of Example 5

Full size image

Concluding remarks

In this paper, a novel matrix algorithm for obtaining numerical spectral solutions for second-order boundary value problems is presented and analyzed. The derivation of this algorithm is essentially based on choosing a set of basis functions satisfying the boundary conditions of the given boundary value problem in terms of shifted Legendre polynomials. The two spectral methods, namely, Petrov–Galerkin and collocation methods, are used for handling linear second-order and nonlinear second-order boundary value problems, respectively. One of the main advantages of the presented algorithms is their availability for application on both linear and nonlinear second-order boundary value problems including some important singular perturbed equations and also a Bratu-type equation. Another advantage of the developed algorithms is that high accurate approximate solutions are achieved by using a few number of terms of the suggested expansion. The obtained numerical results are comparing favorably with the analytical ones. We do believe that the proposed algorithms in this article can be extended to treat other types of problems including some two-dimensional problems.