Comparison of a finite-element and finite-volume scheme for a degenerate cross-diffusion system for ion transport

Abstract

A structure-preserving implicit Euler finite-element scheme for a degenerate cross-diffusion system for ion transport is analyzed. The scheme preserves the nonnegativity and upper bounds of the ion concentrations, the total relative mass, and it dissipates the entropy (or free energy). The existence of discrete solutions to the scheme and their convergence towards a solution to the continuous system are proved. Numerical simulations of two-dimensional ion channels using the finite-element scheme with linear elements and an alternative finite-volume scheme are presented. The advantages and drawbacks of both schemes are discussed in detail.

1 Introduction

Ion channels are pore-forming proteins that create a pathway for charged ions to pass through the cell membrane. They are of great biological importance since they contribute to processes in the nervous system, the coordination of muscle contraction, and the regulation of secretion of hormones, for instance. Ion-channel models range from simple systems of differential equations (Hodgkin and Huxley 1952) as well as Brownian and Langevin dynamics (Im et al. 2000; Nadler et al. 2005) to the widely used Poisson–Nernst–Planck model (Eisenberg 1998). The latter model fails in narrow channels since it neglects the finite size of the ions. Finite-size interactions can be approximately captured by adding suitable chemical potential terms (Gillespie et al. 2005; Nonner et al. 2000), for instance. In this paper, we follow another approach. Starting from a random walk on a lattice, one can derive in the diffusion limit an extended Poisson–Nernst–Planck model, taking into account that ion concentrations might saturate in the narrow channel. This leads to the appearance of cross-diffusion terms in the evolution equations for the ion concentrations (Burger et al. 2010; Simpson et al. 2009). These nonlinear cross-diffusion terms are common in diffusive multicomponent systems (Jüngel 2016, Chapter 4). A lattice-free approach, starting from stochastic Langevin equations, can be found in Bruna and Chapman (2014). The scope of this paper is to present a new finite-element discretization of the degenerate cross-diffusion system and to compare this scheme to a previously proposed finite-volume method (Cancès et al. 2019).

The dynamics of the ion concentrations $u=(u_1,\ldots ,u_n)$ is governed by the evolution equations

$$\begin{aligned} \partial _t u_i + {\text {div}}{{\mathcal {F}}}_i = 0, \quad {{\mathcal {F}}}_i = -D_i\big (u_0\nabla u_i - u_i\nabla u_0 + u_0u_i\beta z_i\nabla \Phi \big )\quad \text{ in } \Omega ,\ t>0, \end{aligned}$$

(1)

where $u_{0}=1-\sum _{i=1}^{n}u_i$ denotes the solvent concentration, $D_i>0$ is the diffusion constant, $z_i$ the ion charge, and $\beta$ a mobility parameter. To be precise, $u_i$ is the mass fraction of the ith ion, and we refer to $\sum _{i=0}^n u_i=1$ as the total relative mass, just meaning that the ion-solvent mixture is saturated. The electric potential $\Phi$ is self-consistently given by the Poisson equation

$$\begin{aligned} -\lambda ^2\Delta \Phi = \sum _{i=1}^nz_iu_i + f \quad \text{ in } \Omega , \end{aligned}$$

(2)

with the permanent charge density $f=f(x)$ and the scaled permittivity constant $\lambda ^2$. The equations are solved in a bounded domain $\Omega \subset {{\mathbb {R}}}^d$ with smooth boundary $\partial \Omega$. Equations (1) are equipped with initial data $u(0)=u^I$ satisfying $0<\sum _{i=1}^n u_i^I<1$. The boundary $\partial \Omega$ consists of an insulating part $\Gamma _\mathrm{N}$ and the union $\Gamma _\mathrm{D}$ of contacts with external reservoirs:

$$\begin{aligned} {{\mathcal {F}}}_i\cdot \nu =0\quad \text{ on } \Gamma _\mathrm{N},&\quad u_i={\overline{u}}_i\quad \text{ on } \Gamma _\mathrm{D}, \quad i=1,\ldots ,n, \end{aligned}$$

(3)

$$\begin{aligned} \nabla \Phi \cdot \nu =0\quad \text{ on } \Gamma _\mathrm{N},&\quad \Phi ={\overline{\Phi }}\quad \text{ on } \Gamma _\mathrm{D}. \end{aligned}$$

(4)

System (1)–(2) can be interpreted as a generalized Poisson–Nernst–Planck model. The usual Poisson–Nernst–Planck equations (Eisenberg 1998) follow from (1) by setting $u_0=\text{ const }$. In the literature, there are several generalized versions of the standard model. For instance, adding a term involving the relative velocity differences in the entropy production leads to cross-diffusion expressions different from (1) (Hsieh et al. 2015). This model, however, does not take into account effects from the finite ion size. Thermodynamically consistent Nernst–Planck models with cross-diffusion terms were suggested in Dreyer et al. (2013), but the coefficients differ from (1). The model at hand was derived in Burger et al. (2010) and Simpson et al. (2009) from a lattice model taking into account finite-size effects.

Model (1)–(4) contains some mathematical difficulties. First, its diffusion matrix $A(u)=(A_{ij}(u))\in {{\mathbb {R}}}^{n\times n}$, given by $A_{ij}(u)=D_iu_i$ for $i\ne j$ and $A_{ii}(u)=D_i(u_0+u_i)$ for $i=1,\ldots ,n$ is generally neither symmetric nor positive definite. Second, it degenerates in regions where the concentrations vanish. Third, the standard maximum principle cannot be applied to achieve $0\le u_i\le 1$ for $i=1,\ldots ,n$. In the following, we explain how these issues can be solved.

The first difficulty can be overcome by introducing so-called entropy variables $w_i$ defined from the entropy (or, more precisely, free energy) of the system,

$$\begin{aligned} H(u) = \int _\Omega h(u)\mathrm{d}x, \quad \text{ where } h(u) = \sum _{i=0}^n\int _{{\overline{u}}_i}^{u_i}\log \frac{s}{{\overline{u}}_i}\mathrm{d}s + \frac{\beta \lambda ^2}{2}|\nabla (\Phi -{\overline{\Phi }})|^2. \end{aligned}$$

(5)

Indeed, writing Eq. (1) in terms of the entropy variables $w_1,\ldots ,w_n$, given by

$$\begin{aligned}&\frac{\partial h}{\partial u_i} = w_i - {\overline{w}}_i, \quad \text{ where } \nonumber \\&w_i = \log \frac{u_i}{u_0} + \beta z_i\Phi , \quad {\overline{w}}_i = \log \frac{{\overline{u}}_i}{{\overline{u}}_0} + \beta z_i{\overline{\Phi }}, \quad i=1,\ldots ,n, \end{aligned}$$

(6)

it follows that

$$\begin{aligned} \partial _t u_i(w,\Phi ) = {\text {div}}\bigg (\sum _{j=1}^n B_{ij}(w,\Phi )\nabla w_j\bigg ), \end{aligned}$$

(7)

where the new diffusion matrix $B=(B_{ij}(w,\Phi ))\in {{\mathbb {R}}}^{n\times n}$ with

$$\begin{aligned} B_{ij}(w,\Phi ) = D_iu_0(w,\Phi )u_i(w,\Phi )\delta _{ij}, \quad i,j=1,\ldots ,n, \end{aligned}$$

is symmetric and positive semidefinite (in fact, it is even diagonal). This procedure has a thermodynamical background: the quantities $\partial h/\partial u_i$ are known as the chemical potentials, and B is the so-called mobility or Onsager matrix [de Groot and Mazur (1984)].

The transformation to entropy variables also solves the third difficulty. Solving the transformed system (7) for $w=(w_1,\ldots ,w_n)$, the concentrations are given by

$$\begin{aligned} u_i(w,\Phi ) = \frac{\exp (w_i-\beta z_i\Phi )}{1+\sum _{j=1}^n \exp (w_j-\beta z_j\Phi )}, \quad i=1,\ldots ,n, \end{aligned}$$

(8)

showing that $u_i$ is positive and bounded from above:

$$\begin{aligned} u(w,\Phi )\in {\mathcal {D}} := \bigg \{u\in (0,1)^n:\sum _{i=1}^n u_i < 1\bigg \}. \end{aligned}$$

(9)

Moreover, the entropy structure leads to gradient estimates via the entropy inequality

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}t} + \frac{1}{2}\int _\Omega \sum _{i=1}^n D_iu_0u_i|\nabla w_i|^2 \mathrm{d}x \le C, \end{aligned}$$

where the constant $C>0$ depends on the Dirichlet boundary data.

Still, we have to deal with the second difficulty, the degeneracy. It is reflected in the entropy inequality since we lose the gradient estimate if $u_i=0$ or $u_0=0$. This problem is overcome using the “degenerate” Aubin–Lions lemma of Jüngel 2015, Appendix C or its discrete version in Cancès et al. 2019, Lemma 10.

These ideas were employed in Burger et al. (2010) for $n=2$ ion species and without electric potential to show the global existence of weak solutions. The existence result was extended to an arbitrary number of species in Jüngel (2015), Zamponi and Jüngel (2017), still excluding the potential. A global existence result for the full problem (1)–(4) was established in Gerstenmayer and Jüngel (2018).

We are interested in devising a numerical scheme which preserves the structure of the continuous system, like nonnegativity, upper bounds, and the entropy structure, on the discrete level. A first result in this direction was presented in Cancès et al. (2019), analyzing a finite-volume scheme preserving the aforementioned properties. However, the scheme preserves the nonnegativity and upper bounds only if the diffusion coefficients $D_i$ are all equal, and the discrete entropy is dissipated only if additionally the potential term vanishes. In this paper, we propose a finite-element scheme for which the structure preservation holds under natural conditions.

Before we proceed, we briefly discuss some related literature. While there are many results for the classical Poisson–Nernst–Planck system, see for example Lu et al. (2010), Prohl and Schmuck (2009), there seems to be no numerical analysis of the ion-transport model (1)–(4) apart from the finite-volume scheme in Cancès et al. (2019) and simulations of the stationary equations in Burger et al. (2012). Let us mention some other works on finite-element methods for related cross-diffusion models. In Barrett and Blowey (2004), a convergent finite-element scheme for a cross-diffusion population model was presented. The approximation is not based on entropy variables, but a regularization of the entropy itself that is used to define a regularized system. The same technique was also employed in Galiano and Selgas (2014). A lumped finite-element method was analyzed in Frittelli et al. (2017) for a reaction-cross-diffusion equation on a stationary surface with positive definite diffusion matrix. In Jüngel and Leingang (2018), an implicit Euler Galerkin approximation in entropy variables for a Poisson–Maxwell–Stefan system was shown to converge. Recently, an abstract framework for the numerical approximation of evolution problems with entropy structure was presented in Egger (2018). The discretization is based on a discontinuous Galerkin method in time and a Galerkin approximation in space. When applied to cross-diffusion systems, this approach also leads to an approximation in entropy variables that preserves the entropy dissipation. However, neither the existence of discrete solutions nor the convergence of the scheme are discussed.

Our main results are as follows:

• We propose an implicit Euler finite-element scheme for (1)–(4) in entropy variables with linear finite elements (Sect. 2). The scheme preserves the nonnegativity of the concentrations and the upper bounds, the total relative mass, and it dissipates the discrete entropy associated to (5) if the boundary data are in thermal equilibrium; see the Remark 1.

• We prove the existence of discrete solutions (Lemma 1) and their convergence to the solution to (1)–(4) when the approximation parameters tend to zero (Theorem 3). The convergence rate can be only computed numerically and is approximately of second order (with respect to the $L^2$ norm).

• The finite-element scheme and the finite-volume scheme of Cancès et al. (2019) (recalled in Sect. 3) are applied to two test cases in two space dimensions: a calcium-selective ion channel and a bipolar ion channel (Sect. 4). Static current–voltage curves show the rectifying behavior of the bipolar ion channel.

• The advantages and drawbacks of both schemes are discussed (Sect. 5). The finite-element scheme allows for structure-preserving properties under natural assumptions, while the finite-volume scheme can be analyzed only under restrictive conditions. On the other hand, the finite-volume scheme allows for vanishing initial concentrations and faster algorithms compared to the finite-element scheme due to the highly nonlinear structure of the latter formulation.

2 The finite-element scheme

2.1 Notation and assumptions

Before we define the finite-element discretization, we introduce our notation and make precise the conditions assumed throughout this section. We assume:

• (H1) Domain: $\Omega \subset {{\mathbb {R}}}^d$ ($d=2$ or $d=3$) is an open, bounded, polygonal domain with $\partial \Omega =\Gamma _\mathrm{D}\cup \Gamma _\mathrm{N}\in C^{0,1}$, $\Gamma _\mathrm{D}\cap \Gamma _\mathrm{N}=\emptyset$, $\Gamma _\mathrm{N}$ is open in $\partial \Omega$, and $\text{ meas }(\Gamma _\mathrm{D})>0$.

• (H2) Parameters: $T>0$, $D_i>0$, $\beta >0$, and $z_i\in {{\mathbb {R}}}$, $i=1,\ldots ,n$.

• (H3) Background charge: $f\in L^\infty (\Omega )$.

• (H4) Initial and boundary data: $u_i^{I}\in H^2(\Omega )$ and ${\overline{u}}_i\in H^2(\Omega )$ satisfy $u_i^{I} > 0$, ${\overline{u}}_i > 0$ for $i=1,\ldots ,n$, $1-\sum _{i=1}^n u_i^{I} > 0$, $1-\sum _{i=1}^n {\overline{u}}_i > 0$ in $\Omega$, and ${\overline{\Phi }}\in H^2(\Omega )\cap L^\infty (\Omega )$.

The $H^2$ regularity of the initial and boundary data ensures that the standard interpolation converges to the given data, see (10) below.

We consider equations (1) on a finite time interval (0, T) with $T>0$. For simplicity, we use a uniform time discretization with time step $\tau >0$ and set $t^k=k\tau$ for $k=1,\ldots ,N$, where $N\in {{\mathbb {N}}}$ is given and $\tau =T/N$.

For the space discretization, we introduce a family ${{\mathcal {T}}}_h$ ($h>0$) of triangulations of $\Omega$, consisting of open polygonal convex subsets of $\Omega$ (the so-called cells) such that ${\overline{\Omega }}=\cup _{K\in {{\mathcal {T}}}_h}{\overline{K}}$ with maximal diameter $h=\max _{K\in {{\mathcal {T}}}_h}\text {diam}(K)$. We assume that the corresponding family of edges ${{\mathcal {E}}}$ can be split into internal and external edges, ${{\mathcal {E}}}={{\mathcal {E}}}_{\mathrm{int}}\cup {{\mathcal {E}}}_{\mathrm{ext}}$ with ${{\mathcal {E}}}_{\mathrm{int}} = \{\sigma \in {{\mathcal {E}}}:\sigma \subset \Omega \}$ and ${{\mathcal {E}}}_{\mathrm{ext}}=\{\sigma \in {{\mathcal {E}}}:\sigma \subset \partial \Omega \}$. Each exterior edge is assumed to be an element of either the Dirichlet or Neumann boundary, i.e., ${{\mathcal {E}}}_{\mathrm{ext}}={{\mathcal {E}}}_{\mathrm{ext}}^D\cup {{\mathcal {E}}}_{\mathrm{ext}}^N$. For given $K\in {{\mathcal {T}}}_h$, we define the set ${{\mathcal {E}}}_K$ of the edges of K, which is the union of internal edges and edges on the Dirichlet or Neumann boundary, and we set ${{\mathcal {E}}}_{K,\mathrm int}={{\mathcal {E}}}_K\cap {{\mathcal {E}}}_{\mathrm{int}}$.

In the finite-element setting, the triangulation is completed by the set of nodes $\{p_j:j\in J\}$. We impose the following regularity assumption on the mesh. There exists a constant $\gamma \ge 1$ such that

$$\begin{aligned} \rho _K \le h_K \le \gamma \rho _K \quad \text{ for } \text{ all } K\in {{\mathcal {T}}}_h, \end{aligned}$$

where $\rho _K$ is the radius of the incircle and $h_K$ is the diameter of K.

We associate with ${{\mathcal {T}}}_\mathrm{h}$ the usual conforming finite-element spaces

$$\begin{aligned} {{\mathcal {S}}}({{\mathcal {T}}}_\mathrm{h})&:= \{ \xi \in C^0({\overline{\Omega }}): \xi |_K \text { is linear for all } K\in {{\mathcal {T}}}_h \}\subset H^1(\Omega ), \\ {{\mathcal {S}}}_D({{\mathcal {T}}}_\mathrm{h})&:= {{\mathcal {S}}}({{\mathcal {T}}}_\mathrm{h})\cap H^1_\mathrm{D}(\Omega ), \end{aligned}$$

and $H_D^1(\Omega )$ is the set of $H^1(\Omega )$ functions that vanish on $\Gamma _D$ in the weak sense. Let $\{\chi _j\}_{j\in J}$ be the standard basis functions for ${{\mathcal {S}}}({{\mathcal {T}}}_h)$ with $\chi _j(p_i)=\delta _{ij}$ for all $i,j\in J$. We define the nodal interpolation operator $I_h:C^0({\overline{\Omega }})\rightarrow {{\mathcal {S}}}({{\mathcal {T}}}_h)$ via $(I_h v)(p_j)=v(p_j)$ for all $v\in {{\mathcal {S}}}({{\mathcal {T}}}_h)$ and $j\in J$. Due to the regularity assumptions on the mesh, $I_h$ has the following approximation property [(see, e.g., (Ciarlet 1978, Chapter 3)]:

$$\begin{aligned} \lim _{h\rightarrow 0}\Vert \phi -I_h\phi \Vert _{H^1(\Omega )} = 0 \quad \text {for all }\phi \in H^2(\Omega ). \end{aligned}$$

(10)

2.2 Definition of the scheme

To define the finite-element scheme, we need to approximate the initial and boundary data. We set $w^0_i=I_h(\log (u_i^I/u_0^I))+\beta z_i\Phi ^0$, where $\Phi ^0$ is the standard finite-element solution to the linear equation (2) with $u_i^I$ on the right-hand side. Furthermore, we set ${\overline{w}}_h=I_h(\log ({\overline{u}}_i/{\overline{u}}_0)+\beta z_i{\overline{\Phi }})$ and ${\overline{\Phi }}_h=I_h({\overline{\Phi }})$.

The finite-element scheme is now defined as follows. Given $w^{k-1}\in {{\mathcal {S}}}({{\mathcal {T}}}_h)^n$ and $\Phi ^{k-1}\in {{\mathcal {S}}}({{\mathcal {T}}}_h)$, find $w^k-{\overline{w}}_h\in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_h)^n$ and $\Phi ^k-{\overline{\Phi }}_h\in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_h)$ such that

$$\begin{aligned}&\frac{1}{\tau }\int _\Omega \big (u(w^k,\Phi ^k) - u(w^{k-1},\Phi ^{k-1}) \big )\cdot \phi \, \mathrm{d}x \nonumber \\&\quad + \int _\Omega \nabla \phi :B(w^k,\Phi ^k)\nabla w^k\mathrm{d}x + \varepsilon \int _\Omega (w^k-{\overline{w}}_h)\cdot \phi \,\mathrm{d}x = 0, \end{aligned}$$

(11)

$$\begin{aligned}&\lambda ^2\int _\Omega \nabla \Phi ^k\cdot \nabla \theta \mathrm{d}x = \int _\Omega \bigg (\sum _{i=1}^n z_i u_i(w^k,\Phi ^k)+f\bigg )\theta \mathrm{d}x, \end{aligned}$$

(12)

for all $\phi \in {{\mathcal {S}}}_D({{\mathcal {T}}}_h)^n$ and $\theta \in {{\mathcal {S}}}_D({{\mathcal {T}}}_h)$. The symbol “:” signifies the Frobenius matrix product; here, the expression reduces to

$$\begin{aligned} \nabla \phi :B(w^k,\Phi ^k)\nabla w^k = \sum _{i=1}^n D_iu_i\left( w^k,\Phi ^k \right) u_0\left( w^k,\Phi ^k \right) \nabla \phi _i\cdot \nabla w_i^k. \end{aligned}$$

The term involving the parameter $\varepsilon >0$ is only needed to guarantee the coercivity of (11), (12). Indeed, the diffusion matrix $B(w^k,\Phi ^k)$ degenerates when $w^k_i\rightarrow -\infty$, and the corresponding bilinear form is only positive semidefinite. To emphasize the dependence on the mesh and $\varepsilon$, we should rather write $w^{(h,\varepsilon ,k)}$ instead of $w^k$ and similarly for $\Phi ^k$; however, for the sake of presentation, we will mostly omit the additional superscripts. The original variables are recovered by computing $u^{k}=u(w^{k},\Phi ^{k})$ according to (8). Setting $u^{(\tau )}(x,t)=u^k(x)$ for $x\in \Omega$, $t\in ((k-1)\tau ,k\tau ]$, $k=1,\ldots ,N$, and $u^{(\tau )}(\cdot ,0)=I_hu^I$ as well as similarly for $\Phi ^{(\tau )}$, we obtain piecewise constant in time functions.

2.3 Existence of discrete solutions

The first result concerns the existence of solutions to the nonlinear finite-element scheme (11), (12).

Lemma 1

(Existence of solutions and discrete entropy inequality) There exists a solution to scheme (11), (12) that satisfies the following discrete entropy inequality:

$$\begin{aligned} H(u^k) + \tau \int _\Omega \nabla (w^k-{\overline{w}}_h):B\left( w^k,\Phi ^k \right) \nabla w^k \mathrm{d}x + \varepsilon \tau \Vert w^k-{\overline{w}}_h\Vert _{L^2(\Omega )}^2 \le H\left( u^{k-1}\right) , \nonumber \\ \end{aligned}$$

(13)

where H is defined in (5) and $u^k=u\left( w^k,\Phi ^k \right)$, $u^{k-1}=u\left( w^{k-1},\Phi ^{k-1}\right)$ are defined in (8).

The proof of the lemma is similar to the proof of Theorem 1 in Gerstenmayer and Jüngel (2018). The main difference is that in Gerstenmayer and Jüngel (2018), a regularization term of the type $\varepsilon \left( (-\Delta )^m w^k+w^k \right)$ has been added to achieve via $H^m(\Omega )\hookrightarrow L^\infty (\Omega )$ for $m>d/2$ compactness and $L^\infty$ solutions. In the finite-dimensional setting, this embedding is not necessary but we still need the regularization $\varepsilon w^k$ to conclude coercivity. We conjecture that this regularization is just technical but currently, we are not able to remove it. Note, however, that we can use arbitrarily small values of $\varepsilon$ in the numerical simulations such that the additional term does not affect the solution practically.

Proof of Lemma 1

Let $y\in {{\mathcal {S}}}({{\mathcal {T}}}_h)^n$ and $\delta \in [0,1]$. There exists a unique solution $\Phi ^k$ to (12) with $w^k$ replaced by $y+{\overline{w}}_h$, satisfying $\Phi ^k-{{\overline{\Phi }}}_h\in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_h)$, since the function $\Phi \mapsto z_iu_i(y,\Phi )$ is bounded and nonincreasing. Indeed, let $\Phi _1$ and $\Phi _2$ be two solutions with the same initial datum. Then, taking the difference of the corresponding weak formulations (12) and using the test function $\Phi _1-\Phi _2$, we find that

$$\begin{aligned} \lambda ^2\int _\Omega |\nabla (\Phi _1-\Phi _2)|^2 \mathrm{d}x \!=\! \int _\Omega \sum _{i\!=\!1}^n z_i\big (u_i(y\!+\!{\overline{w}}^h,\Phi _1) - u_i(y+{\overline{w}}^h,\Phi _2)\big )(\Phi _1-\Phi _2)\mathrm{d}x \le 0. \end{aligned}$$

Moreover, the estimate

$$\begin{aligned} \Vert \Phi ^k\Vert _{H^1(\Omega )} \le C\left( 1+\Vert {\overline{\Phi }}_h\Vert _{H^1(\Omega )}\right) , \end{aligned}$$

(14)

holds for some constant $C>0$.

Next, we consider the linear problem

$$\begin{aligned} a(v,\phi )=F(\phi )\quad \text{ for } \text{ all } \phi \in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n, \end{aligned}$$

(15)

where

$$\begin{aligned} a(v,\phi )&= \int _\Omega \nabla \phi :B\left( y+{\overline{w}}_\mathrm{h},\Phi ^k \right) \nabla v\, \mathrm{d}x + \varepsilon \int _\Omega v\cdot \phi \,\mathrm{d}x, \\ F(\phi )&= -\frac{\delta }{\tau }\int _\Omega \big (u(y+{\overline{w}}_\mathrm{h},\Phi ^k) - u\left( w^{k-1},\Phi ^{k-1}\right) \big )\cdot \phi \mathrm{d}x \\&\quad - \delta \int _\Omega \nabla \phi :B(y+{\overline{w}}_\mathrm{h},\Phi ^k)\nabla {\overline{w}}_h \mathrm{d}x. \end{aligned}$$

The bilinear form a and the linear form F are continuous on ${{\mathcal {S}}}_D({{\mathcal {T}}}_\mathrm{h})^n$. The equivalence of all norms on the finite-dimensional space ${{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})$ implies the coercivity of a,

$$\begin{aligned} a(v,v) \ge \varepsilon \Vert v\Vert _{L^2(\Omega )}^2 \ge \varepsilon C\Vert v\Vert _{H^1(\Omega )}^2. \end{aligned}$$

By the Lax–Milgram lemma, there exists a unique solution $v\in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n$ to this problem. This defines the fixed-point operator $S:{{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n\times [0,1]\rightarrow {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n$, $S(y,\delta )=v$. The inequality

$$\begin{aligned} \varepsilon C\Vert v\Vert _{H^1(\Omega )}^2 \le a(v,v) = F(v) \le C(\tau )\Vert v\Vert _{H^1(\Omega )} \end{aligned}$$

shows that all elements v are bounded independent of y and $\delta$ and thus, all fixed points $v=S(v,\delta )$ are uniformly bounded. Furthermore, $S(y,0)=0$ for all $y\in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n$. The continuity of S follows from standard arguments and the compactness comes from the fact that ${{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n$ is finite-dimensional. By the Leray–Schauder fixed-point theorem, there exists $v^k\in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n$ such that $S(v^k,1)=v^k$, and $w^k:=v^k+{\overline{w}}_\mathrm{h}$ is a solution to (11).

The discrete entropy inequality (13) is proven using $\tau (w^k-{\overline{w}}_\mathrm{h})\in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n$ as a test function in (11) and exploiting the convexity of H,

$$\begin{aligned} \int _\Omega (u^k-u^{k-1})\cdot \left( w^k-{\overline{w}}_h\right) \mathrm{d}x = \int _\Omega (u^k-u^{k-1})\cdot \nabla h(u^k)\mathrm{d}x \ge H(u^k)-H\left( u^{k-1}\right) , \end{aligned}$$

which concludes the proof. $\square$

Remark 1

(Structure preservation of the scheme) Lemma 1 shows that if the boundary data are in thermal equilibrium, i.e., $\nabla {\overline{w}}_\mathrm{h}=0$, then the finite-element scheme (11), (12) dissipates the entropy (5), i.e., $H\left( u^k \right) \le H\left( u^{k-1} \right)$. Moreover, it preserves the invariant region ${\mathcal {D}}$, i.e., $u^k\in {\mathcal {D}}$, and the mass fraction $u_i^k$ is nonnegative and bounded by one. The scheme conserves the total relative mass, i.e., $\sum _{i=1}^n \Vert u_i^k\Vert _{L^1(\Omega )}=1$, which is a direct consequence of the definition of $u_0^k$. $\square$

2.4 Uniform estimates

The next step is the derivation of a priori estimates uniform in the parameters $\varepsilon$, $\tau$, and h. To this end, we transform back to the original variable $u^k$ and exploit the discrete entropy inequality (13).

Lemma 2

(A priori estimates) For the solution to the finite-element scheme from Lemma 1, the following estimates hold:

$$\begin{aligned} \Vert u_i^k\Vert _{L^\infty (\Omega )} + \varepsilon \tau \sum _{j=1}^k\Vert w_i^j-{\overline{w}}_{i,h}\Vert _{L^2(\Omega )}^2&\le C, \end{aligned}$$

(16)

$$\begin{aligned} \tau \sum _{j=1}^k\Big (\Vert (u_0^j)^{1/2}\Vert _{H^1(\Omega )}^2 + \Vert u_0^j\Vert _{H^1(\Omega )}^2 + \Vert (u_0^j)^{1/2}\nabla (u_i^j)^{1/2}\Vert _{L^2(\Omega )}^2\Big )&\le C, \end{aligned}$$

(17)

for $i=1,\ldots ,n$, where here and in the following, $C>0$ is a generic constant independent of $\varepsilon$, $\tau$, and h.

Proof

As the proof is similar to that one in the continuous setting, we give only a sketch. Note that our finite-element space is a subset of $H^1(\Omega )$, so the computations can be done as in Gerstenmayer and Jüngel (2018), and in particular, the chain rule holds. Observe that the definition of the entropy variables implies that $0<u_i^k<1$ in $\Omega$ for $i=1,\ldots ,n$ and $k=1,\ldots ,N$. It is shown in the proof of Lemma 6 of Gerstenmayer and Jüngel (2018) that

$$\begin{aligned} \nabla (w^k-{\overline{w}}_h):B(w^k,\Phi ^k)\nabla w^k&\ge \frac{D_{\mathrm{min}}}{4}\sum _{i=1}^n u_i^k u_0^k \bigg |\nabla \log \frac{u_i^k}{u_0^k}\bigg |^2 - \frac{D_{\mathrm{min}}}{2}\sum _{i=1}^n|\beta z_i\nabla \Phi ^k|^2 \\&\quad - \frac{D_{\mathrm{max}}}{2}\sum _{i=1}^n|\nabla {\overline{w}}_i|^2, \end{aligned}$$

where $D_{\mathrm{min}}=\min _{i=1,\ldots ,n}D_i$ and $D_{\mathrm{max}}=\max _{i=1,\ldots ,n}D_i$. Then (13) gives

$$\begin{aligned}&H(u^k) + \tau \frac{D_{\mathrm{min}}}{4}\int _\Omega \sum _{i=1}^n u_i^k u_0^k \bigg |\nabla \log \frac{u_i^k}{u_0^k}\bigg |^2 \mathrm{d}x + \varepsilon \tau \Vert w^k-{\overline{w}}_\mathrm{h}\Vert _{L^2(\Omega )}^2 \\&\quad \le H(u^{k-1}) + \tau \frac{D_{\mathrm{min}}}{2}\sum _{i=1}^n|\beta z_i\nabla \Phi ^k|^2 \mathrm{d}x + \tau \frac{D_{\mathrm{max}}}{2}\int _\Omega \sum _{i=1}^n|\nabla {\overline{w}}_{i,h}|^2 \mathrm{d}x. \end{aligned}$$

We resolve this recursion to find that

$$\begin{aligned}&H(u^k) + \tau \frac{D_{\mathrm{min}}}{4}\sum _{j=1}^k \int _\Omega \sum _{i=1}^n u_i^ju_0^j \bigg |\nabla \log \frac{u_i^j}{u_0^j}\bigg |^2 \mathrm{d}x + \varepsilon \tau \sum _{j=1}^k \Vert w^j-{\overline{w}}_{\mathrm{h}}\Vert _{L^2(\Omega )}^2 \\&\quad \le H(u^0) + \tau \frac{D_{\mathrm{min}}}{2}\sum _{j=1}^k\int _\Omega \sum _{i=1}^n |\beta z_i\nabla \Phi ^j|^2 \mathrm{d}x + \tau k\frac{D_{\mathrm{max}}}{2}\int _\Omega \sum _{i=1}^n|\nabla {\overline{w}}_{i,h}|^2 \mathrm{d}x. \end{aligned}$$

The right-hand side is bounded because of (14), $\tau k\le T$, and the boundedness of the interpolation operator. Inserting the identity

$$\begin{aligned} \sum _{i=1}^n u_i^ju_0^j\bigg |\nabla \log \frac{u_i^j}{u_0^j}\bigg |^2 = 4u_0^j\sum _{i=1}^n|\nabla (u_i^j)^{1/2}|^2 + |\nabla u_0^j|^2 + 4|\nabla (u_0^j)^{1/2}|^2, \end{aligned}$$

the estimates follow. $\square$

2.5 Convergence of the scheme

The a priori estimates from the previous lemma allow us to formulate our main result, the convergence of the finite-element solutions to a solution to the continuous model (1)–(4).

Theorem 3

(Convergence of the finite-element solution) Let $(u^{(h,\varepsilon ,\tau )},\Phi ^{(h,\varepsilon ,\tau )})$ be an approximate solution constructed from scheme (11), (12). Set $u^{(h,\varepsilon ,\tau )}_0=1-\sum _iu^{(h,\varepsilon ,\tau )}_i$. Then there exist functions $u_0$, $u=(u_1,\ldots ,u_n)$, and $\Phi$, satisfying $u(x,t)\in {{\overline{{{\mathcal {D}}}}}}$ (${{\mathcal {D}}}$ is defined in (9)), $u_0=1-\sum _{i=1}^n u_i$ in $\Omega$, the regularity

$$\begin{aligned} u_0^{1/2},\, u_0^{1/2}u_i,\, \Phi \in L^2\left( 0,T;H^1(\Omega )\right) ,\quad \partial _tu_i \in L^2\left( 0,T;H^1_D(\Omega )'\right) , \end{aligned}$$

for $i=1,\ldots ,n$, such that as $(h,\varepsilon )\rightarrow 0$ and then $\tau \rightarrow 0$,

$$\begin{aligned} (u^{(h,\varepsilon ,\tau )}_{0})^{1/2}\rightarrow u_0^{1/2},\ (u^{(h,\varepsilon ,\tau )}_{0})^{1/2}u_{i}^{(h,\varepsilon ,\tau )}\rightarrow u_0^{1/2}u_i&\quad \text{ strongly } \text{ in } L^2 \left( \Omega \times (0,T)\right) , \\ \Phi ^{(h,\varepsilon ,\tau )}\rightarrow \Phi&\quad \text{ strongly } \text{ in } L^2\left( \Omega \times (0,T)\right) , \end{aligned}$$

and $(u,\Phi )$ are weak solutions to (1)–(4). In particular, for all $\phi \in L^2(0,T;H^1_D(\Omega ))$ and $i=1,\ldots ,n$, it holds that

$$\begin{aligned}&\int _0^T\langle \partial _t u_i,\phi \rangle \, \mathrm{d}t + D_i\int _0^T\int _\Omega u_0^{1/2}\big (\nabla (u_0^{1/2}u_i) - 3u_i\nabla u_0^{1/2}\big )\cdot \nabla \phi \, \mathrm{d}x\mathrm{d}t \nonumber \\&\phantom {xx}{} + D_i\int _0^T\int _\Omega u_i u_0\beta z_i\nabla \Phi \cdot \nabla \phi \, \mathrm{d}x\mathrm{d}t = 0, \end{aligned}$$

(18)

$$\begin{aligned}&\lambda ^2\int _0^T\int _\Omega \nabla \Phi \cdot \nabla \phi \, \mathrm{d}x\mathrm{d}t = \int _0^T\int _\Omega \bigg (\sum _{i=1}^n z_iu_i + f\bigg )\phi \, \mathrm{d}x\mathrm{d}t, \end{aligned}$$

(19)

where $\langle \cdot ,\cdot \rangle$ is the duality pairing in $H^1_D(\Omega )'$ and $H_D^1(\Omega )$, and the boundary and initial conditions are satisfied in a weak sense.

Proof

We pass first to the limit $(\varepsilon ,h)\rightarrow 0$ and then $\tau \rightarrow 0$, since the latter limit can be performed as in the proof of Theorem 1 in Gerstenmayer and Jüngel (2018). Fix $k\in \{1,\ldots ,N\}$ and let $u_i^{(\varepsilon ,h)}=u_i^{(\varepsilon ,h,k)}$ and $\Phi ^{(\varepsilon ,h)}=\Phi ^{(\varepsilon ,h,k)}$ be the approximate solution from Lemma 1. We set $u_0^{(\varepsilon ,h)}=1-\sum _{i=1}^n u_i^{(\varepsilon ,h)}$. Using the compact embedding $H^1(\Omega )\hookrightarrow L^2(\Omega )$ and the a priori estimates from Lemma 2, it follows that there exists a subsequence which is not relabeled such that, as $(\varepsilon ,h)\rightarrow 0$,

$$\begin{aligned} u_i^{(\varepsilon ,h)} \rightharpoonup ^* u_i^k&\qquad \text{ weakly* } \text{ in } L^\infty (\Omega ), \ i=1,\ldots ,n, \end{aligned}$$

(20)

$$\begin{aligned} (u_0^{(\varepsilon ,h)})^{1/2}\rightharpoonup (u_0^k)^{1/2}, \quad \Phi ^{(\varepsilon ,h)}\rightharpoonup \Phi ^k&\qquad \text{ weakly } \text{ in } H^1(\Omega ), \end{aligned}$$

(21)

$$\begin{aligned} u_0^{(\varepsilon ,h)}\rightarrow u_0^k, \quad \Phi ^{(\varepsilon ,h)}\rightarrow \Phi ^k&\qquad \text{ strongly } \text{ in } L^2(\Omega ), \end{aligned}$$

(22)

$$\begin{aligned} \varepsilon (w_i^{(\varepsilon ,h)}-{\overline{w}}_{i,h})\rightarrow 0&\qquad \text{ strongly } \text{ in } L^2(\Omega ). \end{aligned}$$

(23)

Combining (17) and (21), we infer that (up to a subsequence)

$$\begin{aligned} u_i^{(\varepsilon ,h)}(u_0^{(\varepsilon ,h)})^{1/2}\rightharpoonup u_i^k(u_0^k)^{1/2} \quad \text{ weakly } \text{ in } H^1(\Omega ) \text{ and } \text{ strongly } \text{ in } L^2(\Omega ). \end{aligned}$$

(24)

Next, let $\phi \in (H^2(\Omega )\cap H_D^1(\Omega ))^n$. As we cannot use $\phi _i$ directly as a test function in (11), we take $I_h\phi \in {{\mathcal {S}}}_\mathrm{D}({{\mathcal {T}}}_\mathrm{h})^n$, where $I_h$ is the interpolation operator, see (10). To pass to the limit in (11), we rewrite the integral involving the diffusion matrix:

$$\begin{aligned}&\int _\Omega \nabla (I_h\phi ):B(w^{(\varepsilon ,h)},\Phi ^{(\varepsilon ,h)})\nabla w^{(\varepsilon ,h)} \mathrm{d}x = \int _\Omega \sum _{i=1}^n D_i u_i^{(\varepsilon ,h)}u_0^{(\varepsilon ,h)}\nabla w_i^{(\varepsilon ,h)} \cdot \nabla (I_h\phi _i) \mathrm{d}x \nonumber \\&\quad = \int _\Omega \sum _{i=1}^n D_i\Big ((u_0^{(\varepsilon ,h)})^{1/2}\nabla \big (u_i^{(\varepsilon ,h)} (u_0^{(\varepsilon ,h)})^{1/2}\big ) - 3u_i^{(\varepsilon ,h)}(u_0^{(\varepsilon ,h)})^{1/2}\nabla (u_0^{(\varepsilon ,h)})^{1/2} \nonumber \\&\qquad + \beta z_i u_i^{(\varepsilon ,h)} u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)}\Big ) \cdot \nabla ( I_h\phi _i) \mathrm{d}x. \end{aligned}$$

(25)

We estimate each of the above summands separately. For the last term, we proceed as follows:

$$\begin{aligned}&\bigg | \int _{\Omega } u_i^{(\varepsilon ,h)} u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)} \cdot \nabla (I_h\phi _i)\mathrm{d}x - \int _{\Omega }u_i^k u_0^k\nabla \Phi ^k\cdot \nabla \phi _idx\bigg | \nonumber \\&\quad \le \bigg | \int _{\Omega }u_i^{(\varepsilon ,h)} u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)} \cdot \nabla ( I_h\phi _i -\phi _i)\mathrm{d}x \bigg | \nonumber \\&\qquad + \bigg | \int _{\Omega }(u_i^{(\varepsilon ,h)} u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)} -u_i^k u_0^k\nabla \Phi ^k)\cdot \nabla \phi _i\mathrm{d}x \bigg | \nonumber \\&\quad \le \Vert u_i^{(\varepsilon ,h)} u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)}\Vert _{L^2(\Omega )} \Vert \nabla ( I_h\phi _i -\phi _i)\Vert _{L^2(\Omega )} \nonumber \\&\qquad + \bigg | \int _{\Omega }(u_i^{(\varepsilon ,h)} u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)} -u_i^k u_0^k\nabla \Phi ^k)\cdot \nabla \phi _i\mathrm{d}x \bigg |. \end{aligned}$$

(26)

Similarly as for (24), it follows that

$$\begin{aligned} u_i^{(\varepsilon ,h)}u_0^{(\varepsilon ,h)}\rightarrow u_i^ku_0^k \quad \text{ strongly } \text{ in } L^2(\Omega ). \end{aligned}$$

Then, together with the weak convergence of $\nabla \Phi ^{(\varepsilon ,h)}$, we infer that

$$\begin{aligned} u_i^{(\varepsilon ,h)}u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)} \rightharpoonup u_i^ku_0^k\nabla \Phi ^k \quad \text{ weakly } \text{ in } L^1(\Omega ). \end{aligned}$$

Since $(u_i^{(\varepsilon ,h)}u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)})$ is bounded in $L^2(\Omega )$, this weak convergence also holds in $L^2(\Omega )$. Because of the interpolation property (10) and estimate (26),

$$\begin{aligned} \int _{\Omega }u_i^{(\varepsilon ,h)} u_0^{(\varepsilon ,h)}\nabla \Phi ^{(\varepsilon ,h)} \cdot \nabla ( I_h\phi _i)\mathrm{d}x \rightarrow \int _{\Omega }u_i^k u_0^k\nabla \Phi ^k\cdot \nabla \phi _i\mathrm{d}x. \end{aligned}$$

Following the arguments of Step 3 in Gerstenmayer and Jüngel (2018), Section 2, [using (24)], we have

$$\begin{aligned}&(u_0^{(\varepsilon ,h)})^{1/2}\nabla \big (u_i^{(\varepsilon ,h)}(u_0^{(\varepsilon ,h)})^{1/2}\big ) - 3u_i^{(\varepsilon ,h)}(u_0^{(\varepsilon ,h)})^{1/2}\nabla \big ((u_0^{(\varepsilon ,h)})^{1/2}\big ) \\&\quad \rightharpoonup (u_0^k)^{1/2}\nabla \big (u_0^k(u_0^k)^{1/2}\big ) - 3u_i^k(u_0^k)^{1/2}\nabla ((u_0^k)^{1/2}) \quad \text{ weakly } \text{ in } L^2(\Omega ). \end{aligned}$$

Thus, the limit $(\varepsilon ,h)\rightarrow 0$ in (25) gives

$$\begin{aligned}&\lim _{(\varepsilon ,h)\rightarrow 0}\int _\Omega \nabla (I_h\phi ):B(w^{(\varepsilon ,h)},\Phi ^{(\varepsilon ,h)})\nabla w^{(\varepsilon ,h)} \mathrm{d}x = \int _\Omega \sum _{i=1}^n D_i\Big ((u_0^k)^{1/2}\nabla \big (u_0^k(u_0^k)^{1/2}\big ) \\&\quad - 3u_i^k(u_0^k)^{1/2}\nabla ((u_0^k)^{1/2}) + \beta z_iu_i^ku_0^k\nabla \Phi ^k\Big )\cdot \nabla \phi _i \mathrm{d}x. \end{aligned}$$

Furthermore, we deduce from (23) that

$$\begin{aligned} \bigg |\varepsilon \int _\Omega (w_i^{(\varepsilon ,h)}-{\overline{w}}_{i,h})(I_h\phi _i)\mathrm{d}x\bigg | \le \varepsilon \Vert w_i^{(\varepsilon ,h)}-{\overline{w}}_{i,h}\Vert _{L^2(\Omega )} \Vert I_h\phi _i\Vert _{L^2(\Omega )} \rightarrow 0. \end{aligned}$$

Thus, passing to the limit $(\varepsilon ,h)\rightarrow 0$ in scheme (11), (12) leads to

$$\begin{aligned}&\frac{1}{\tau }\int _\Omega (u^k-u^{k-1})\cdot \phi \mathrm{d}x + \int _\Omega \sum _{i=1}^n D_i(u_0^k)^{1/2} \big (\nabla (u_i^k(u_0^k)^{1/2}) - 3u_i^k\nabla (u_0^k)^{1/2}\big )\cdot \nabla \phi _i \mathrm{d}x \\&\quad + \int _\Omega \sum _{i=1}^n D_i\beta z_i u_i^ku_0^k\nabla \Phi ^k \cdot \nabla \phi _i \mathrm{d}x = 0, \\&\lambda ^2\int _\Omega \nabla \Phi ^k\cdot \nabla \theta \mathrm{d}x = \int _\Omega \bigg (\sum _{i=1}^n z_iu_i^k + f\bigg )\theta \mathrm{d}x, \end{aligned}$$

for all $\phi _i$, $\theta \in H^2(\Omega )\cap H_D^1(\Omega )$. A density argument shows that we can take test functions $\phi _i$, $\theta \in H_D^1(\Omega )$. The a priori estimates from Lemma 2 remain valid in the weak limit.

Now the limit $\tau \rightarrow 0$ can be done exactly as in Gerstenmayer and Jüngel (2018), Theorem 1, Step 4, which concludes the proof. $\square$

3 The finite-volume scheme

We briefly recall the finite-volume scheme from Cancès et al. (2019) and summarize the assumptions and results, as this is necessary for the comparison of the finite-element and finite-volume scheme in Sect. 5.

We assume that Hypotheses (H1)–(H4) from the previous section hold and we use the same notation for the time and space discretizations. For a two-point approximation of the discrete gradients, we require additionally that the mesh is admissible in the sense of Eymard et al. (2000), Definition 9.1. This means that a family of points $(x_K)_{K\in {{\mathcal {T}}}}$ is associated to the cells and that the line connecting the points $x_K$ and $x_L$ of two neighboring cells K and L is perpendicular to the edge K|L. For $\sigma \in {{\mathcal {E}}}_{\mathrm{int}}$ with $\sigma =K|L$, we denote by ${\mathrm {d}}_\sigma ={\mathrm {d}}(x_K,x_L)$ the Euclidean distance between $x_K$ and $x_L$, while for $\sigma \in {{\mathcal {E}}}_{\mathrm{ext}}$, we set ${\mathrm {d}}_\sigma ={\mathrm {d}}(x_K,\sigma )$. For a given edge $\sigma \in {{\mathcal {E}}}$, the transmissibility coefficient is defined by $\tau _\sigma = \text {m}(\sigma )/{\mathrm {d}}_\sigma$, where $\text {m}(\sigma )$ denotes the Lebesgue measure of $\sigma$.

For the definition of the scheme, we approximate the initial, boundary, and given functions on the elements $K\in {{\mathcal {T}}}$ and edges $\sigma \in {{\mathcal {E}}}$:

$$\begin{aligned} u^{I}_{i,K}&= \frac{1}{\text {m}(K)}\int _{K}u^{I}_i(x)\mathrm{d}x,&f_K&= \frac{1}{\text {m}(K)}\int _{K}f(x)\mathrm{d}x, \\ {\overline{u}}_{i,\sigma }&= \frac{1}{\text {m}(\sigma )}\int _{\sigma }{\overline{u}}_i\mathrm{d}s,&{\overline{\Phi }}_{\sigma }&= \frac{1}{\text {m}(\sigma )}\int _{\sigma }{\overline{\Phi }}\mathrm{d}s, \end{aligned}$$

and we set $u_{0,K}^I= 1-\sum _{i=1}^n u_{i,K}^I$ and ${\overline{u}}_{0,\sigma }=1-\sum _{i=1}^n{\overline{u}}_{i,\sigma }$. Furthermore, we introduce the discrete gradients

$$\begin{aligned}&\text {D}_{K,\sigma }(u_i) = u_{i,K,\sigma }-u_{i,K},&\text{ where }\quad u_{i,K,\sigma } = {\left\{ \begin{array}{ll} u_{i,L} \quad &{}\text { for }\sigma \in {{\mathcal {E}}}_{\mathrm{int}},\ \sigma =K|L,\\ {\overline{u}}_{i,\sigma } \quad &{}\text { for }\sigma \in {{\mathcal {E}}}^D_{\mathrm{ext},K},\\ u_{i,K} &{}\text { for }\sigma \in {{\mathcal {E}}}^N_{\mathrm{ext},K}. \end{array}\right. } \end{aligned}$$

The numerical scheme is now defined as follows. Let $K\in {{\mathcal {T}}}$, $k\in \{1,\ldots ,N\}$, $i\in \{1,\ldots ,n\}$, and $u_{i,K}^{k-1}\ge 0$ be given. Then the values $u_{i,K}^k$ are determined by the implicit Euler scheme

$$\begin{aligned} \text {m}(K)\frac{u_{i,K}^k-u_{i,K}^{k-1}}{\Delta t} + \sum _{\sigma \in {{\mathcal {E}}}_K}{{\mathcal {F}}}_{i,K,\sigma }^k = 0, \end{aligned}$$

(27)

where the fluxes ${{\mathcal {F}}}_{i,K,\sigma }^k$ are given by the upwind scheme

$$\begin{aligned} {{\mathcal {F}}}_{i,K,\sigma }^k = -\tau _\sigma D_i\Big (u_{0,\sigma }^k\text {D}_{K,\sigma }(u_i^k) - u_{i,\sigma }^k\big (\text {D}_{K,\sigma }(u_0^k) - {\widehat{u}}_{0,\sigma ,i}^k \beta z_i\text {D}_{K,\sigma }(\Phi ^k)\big )\Big ). \end{aligned}$$

Here, we have set

$$\begin{aligned}&u_{0,K}^k=1-\sum _{i=1}^n u_{i,K}^k, \quad u_{0,\sigma }^k = \max \left\{ u_{0,K}^k,u_{0,L}^k \right\} , \\&u^k_{i,\sigma } = {\left\{ \begin{array}{ll} u^k_{i,K} \quad &{} \text {if } {{\mathcal {V}}}^k_{i,K,\sigma }\ge 0, \\ u^k_{i,K,\sigma } &{} \text {if }{{\mathcal {V}}}^k_{i,K,\sigma }< 0, \end{array}\right. }, \quad {\widehat{u}}_{0,\sigma ,i}^k = {\left\{ \begin{array}{ll} u^k_{0,K} \quad &{} \text {if }z_i\text {D}_{K,\sigma }\left( \Phi ^k \right) \ge 0, \\ u^k_{0,K,\sigma } &{} \text {if }z_i\text {D}_{K,\sigma }\left( \Phi ^k \right) < 0, \end{array}\right. }, \end{aligned}$$

and ${{\mathcal {V}}}_{i,K,\sigma }^k$ is the “drift part” of the flux,

$$\begin{aligned} {{\mathcal {V}}}_{i,K,\sigma }^k = \text {D}_{K,\sigma }(u_0^k) - {\widehat{u}}_{0,\sigma ,i}^k \beta z_i\text {D}_{K,\sigma }\left( \Phi ^k \right) , \end{aligned}$$

for $i=1,\ldots ,n$. Observe that we employed a double upwinding: one related to the electric potential, defining ${\widehat{u}}_{0,\sigma ,i}^k$, and another one related to the drift part of the flux, ${{\mathcal {V}}}_{i,K,\sigma }^k$. The potential is computed via

$$\begin{aligned} -\lambda ^2\sum _{\sigma \in {{\mathcal {E}}}_K}\tau _\sigma \text {D}_{K,\sigma }(\Phi ^k) = \text {m}(K)\left( \sum _{i=1}^n z_iu_{i,K}^k + f_K\right) . \end{aligned}$$

The finite-volume scheme preserves the structure of the continuous equations only under certain assumptions:

• (A1) $\partial \Omega =\Gamma _N$, i.e., we impose no-flux boundary conditions on the whole boundary.

• (A2) The diffusion constants are equal, $D_i=D>0$ for $i=1,\ldots ,n$.

• (A3) The drift terms are set to zero, $\Phi \equiv 0$.

Without these assumptions, we can only assure the nonnegativity of the discrete concentrations $u_i$, $i=1,\ldots ,n$. Since we lack a maximum principle for cross-diffusion systems, the upper bounds can only be proven if we assume equal diffusion constants (A2). Under this assumption, the solvent concentration satisfies

$$\begin{aligned} \partial _t u_0 = D{\text {div}}\left( \nabla u_0 - u_0 w\nabla \Phi \right) , \quad \text{ where } w = \beta \sum _{i=1}^n z_iu_i, \end{aligned}$$

for which a discrete maximum principle can be applied. The $L^\infty$ bounds on the concentrations then ensure the existence of solutions for the scheme. If additionally the drift term vanishes (A3), a discrete version of the entropy inequality, the uniqueness of discrete solutions and most importantly, the convergence of the scheme can be proven (under an additional regularity assumption on the mesh). For details, we refer to Cancès et al. (2019).

4 Numerical experiments

4.1 Implementation

The finite-element discretization is implemented within the finite-element library NGSolve/Netgen, see Schöberl (1997, 2014). The nonlinear equations are solved in every time step by Newton’s method in the variables $w_i$ and $\Phi$. The Jacobi matrix is computed using the NGSolve function AssembleLinearization. The finite-volume scheme is implemented in Matlab. Also here, the nonlinear equations are solved by Newton’s method in every time step, using the variables u, $\Phi$, and $u_0$. The integrals appearing in scheme (11), (12) are computed using a Gauß quadrature implemented in NGSolve that computes the trial functions exactly. Because of the nonlinear functions appearing in the integrals, the quadrature yields only approximate values.

We remark that the finite-volume scheme also performs well when we use a simpler semi-implicit scheme, where we compute u from Eq. (27) with $\Phi$ taken from the previous time step via Newton’s method and subsequently only need to solve a linear equation to compute the update for the potential. It turned out that this approach is not working for the finite-element discretization. Furthermore, the computationally cheaper implementation used in Jüngel and Leingang (2018) for a similar scheme in one space dimension, where a Newton and Picard iteration are combined, did not work well in the two-dimensional test cases presented in this paper.

4.2 Test case 1: calcium-selective ion channel

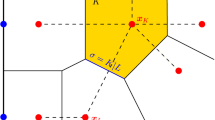
Our first test case models the basic features of an L-type calcium channel (the letter L stands for “long-lasting”, referring to the length of activation). This type of channel is of great biological importance, as it is present in the cardiac muscle and responsible for coordinating the contractions of the heart (Carafoli et al. 2001). The selectivity for calcium in this channel protein is caused by the so-called EEEE-locus made up of four glutamate residues. We follow the modeling approach of Nonner et al. (2001), where the glutamate side chains are each treated as two half-charged oxygen ions, accounting for a total of eight $O^{1/2-}$ ions confined to the channel. In contrast to Nonner et al. (2001), where the oxygen ions are described by hard spheres that are free to move inside the channel region, we make a further reduction and simply consider a constant density of oxygen in the channel that decreases linearly to zero in the baths (see Fig. 1),

$$\begin{aligned} u_{\mathrm{ox}}(x,y) = u_{\mathrm{ox},\max }\times {\left\{ \begin{array}{ll} 1 \quad &{}\quad \text {for }0.45 \le x \le 0.55, \\ 10(x-0.35) \quad &{}\quad \text {for }0.35 \le x \le 0.45,\\ 10(0.65-x) \quad &{}\quad \text {for }0.55 \le x \le 0.65, \\ 0 \quad &{}\quad \text {else}, \end{array}\right. } \end{aligned}$$

where the scaled maximal oxygen concentration equals $u_{\mathrm{ox},\max }=(N_A/u_{\mathrm{typ}})\times 52\,\,$mol/L. Here, $N_A\approx 6.022\times 10^{23}\,$mol$^{-1}$ is the Avogadro constant and $u_{\mathrm{typ}}=3.7037\times 10^{25} L^{-1}$ the typical concentration [taken from (Burger et al. 2012, Table 1)]. In addition to the immobile oxygen ions, we consider three different species of ions, whose concentrations evolve according to model equations (1): calcium (Ca$^{2+}$, $u_1$), sodium (Na$^+$, $u_2$), and chloride (Cl$^-$, $u_3$). We assume that the oxygen ions not only contribute to the permanent charge density $f=-u_{\mathrm{ox}}/2$, but also take up space in the channel, so that we have $u_0=1-\sum _{i=1}^3 u_i-u_{\mathrm{ox}}$ for the solvent concentration.

For the simulation domain, we take a simple geometric setup resembling the form of a channel; see Fig. 1. The boundary conditions are as described in the introduction, with constant values for the ion concentrations and the electric potential in the baths. The physical parameters used in our simulations are taken from (Burger et al. 2012, Table 1). The simulations are performed with a constant (scaled) time step size $\tau =2\times 10^{-4}$. The initial concentrations are simply taken as linear functions connecting the boundary values. An admissible mesh consisting of 74 triangles was created with Matlab’s initmesh command, which produces Delauney triangulations. Four finer meshes were obtained by regular refinement, dividing each triangle into four triangles of the same shape.

Fig. 1

Schematic picture of the ion channel $\Omega$ used for the simulations. Dirichlet boundary conditions are prescribed on $\Gamma _D$ (blue), homogeneous Neumann boundary conditions are given on $\Gamma _N$ (black). The red color represents the density of confined $O^{1/2-}$ ions (colour figure online)

We remark that the same test case was already used in Cancès et al. (2019) to illustrate the efficiency of the finite-volume approximation. Furthermore, numerical simulations for a one-dimensional approximation of the calcium channel can be found in Burger et al. (2012) for stationary solutions and in Gerstenmayer and Jüngel (2018) for transient solutions.

Figures 2 and 3 present the solution to the ion-transport model in the original variables u and $\Phi$ at two different times; the first one after only 600 time steps and the second one after 6000 time steps, which is already close to the equilibrium state. The results are computed on the finest mesh with 18,944 elements. In the upper panel, the concentration profiles and electric potential as computed with the finite-element scheme are depicted. In the lower panel, the difference between the finite-volume and finite-element solutions is plotted. We have omitted the plots for the third ion species (Cl$^-$), since it vanishes almost immediately from the channel due to its negative charge. While absolute differences are relatively small, we can still observe that the electric potential in the finite-element case is always smaller compared to the finite-volume solution, while the peaks of the concentration profiles are more distinctive for the finite-element than for the finite-volume solution.

Fig. 2

Solution after 600 time steps computed from the finite-element scheme (top) and difference between the finite-volume (FV) and finite-element (FE) solutions (bottom)

Fig. 3

Solution after 6000 time steps (close to equilibrium) computed from the finite-element scheme (top) and difference between the finite-volume (FV) and finite-element (FE) solutions (bottom)

To compare the two numerical methods, we test the convergence of the schemes with respect to the mesh diameter. Since an exact solution to our problem is not available, we compute a reference solution both with the finite-volume and the finite-element scheme on a very fine mesh with 18,944 elements and maximal cell diameter $h\approx 0.01$. The differences between these reference solutions in the discrete $L^1$ and $L^\infty$ norms are given in Table 1 for the various unknowns. Since the finite-element and finite-volume solutions are found in different function spaces, one has to be careful how to compare them. The values in Table 1 are obtained by projecting the finite-element solution onto the finite-volume space of functions that are constant on each cell in NGSolve, thereby introducing an additional error. However, the difference between the reference solutions is still reasonably small, especially when the simulations are already close to the equilibrium state.

To avoid the interpolation error in the convergence plots, we compare the approximate finite-element or finite-volume solutions on coarser nested meshes with the reference solutions computed with the corresponding method. In Fig. 4, the errors in the discrete $L^1$ norm between the reference solution and the solutions on the coarser meshes at the two fixed time steps $k=600$ and $k=6000$ are plotted. For the finite-volume approximation, we clearly observe the expected first-order convergence in space, whereas for the finite-element method, the error decreases, again as expected, with $h^2$. These results serve as a validation for the theoretical convergence result proven for the finite-element scheme and show the efficiency of the finite-volume method even in the general case of ion transport, which is not covered by the convergence theorem in Cancès et al. (2019).

Table 1 Difference between the finite-volume and finite-element reference solutions after 600 and after 6000 time steps

Fig. 4

$L^1$ error relative to the reference solution after 600 time steps (black) and 6000 time steps (red) plotted over the mesh size h. Dashed lines are used for the finite-element solution, full lines for the finite-volume solution

In Table 2, the average time needed to compute one time step with the finite-element or finite-volume scheme for the five nested meshes is given. Clearly, the finite-volume scheme is much faster than the finite-element method. This is mostly due to the computationally expensive assembly of the finite-element matrices.

Table 2 Average time needed to compute one time step (in s)

In addition to the convergence analysis, we also study the behavior of the discrete entropy for both schemes. We consider in both cases the entropy relative to the steady state $(u^\infty _{i},\Phi ^\infty )$, which is computed from the corresponding discretizations of the stationary equations with the same parameters and boundary data. Figure 5 shows the relative entropy [see (Cancès et al. 2019, Section 6)] and the $L^1$ error compared to the equilibrium state for the finite-element and finite-volume solutions on different meshes. Whereas for the coarsest mesh the convergence rates differ notably, we can observe a similar behavior when the mesh is reasonably fine. In Fig. 6, we investigate the convergence of the relative entropy with respect to the mesh size. As before, we observe second-order convergence for the finite-element scheme and a first-order rate for the finite-volume method.

Fig. 5

Relative entropy (left) and sum of $L^1$ differences of u and $\Phi$ relative to the equilibrium state (right) over time for various meshes. Mesh 1 has 74 triangles, mesh 4 has 18,944 elements

Fig. 6

Error for the relative entropy with respect to mesh size

4.3 Test case 2: bipolar ion channel

The second example models a pore with asymmetric charge distribution, which occurs naturally in biological ion channels but also in synthetic nanopores. Asymmetric pores typically rectify the ion current, meaning that the current measured for applied voltages of positive sign is higher than the current for the same absolute value of voltage with negative sign. The setup is similar to that of an N–P semiconductor diode. The N-region is characterized by the fixed positive charge. The anions are the counter-ions and thus the majority charge carriers, while the cations are the co-ions and minority charge carriers. In the P-region, the situation is exactly the other way around. In the on-state, the current is conducted by the majority carriers, while in the off-state, the minority carriers are responsible for the current, which leads to the rectification behavior.

Often, bipolar ion channels are modeled with asymmetric surface charge distributions on the channel walls. However, to fit these channels into the framework of our model, we follow the approach described in Ható et al. (2016). Similar to the first test case, we assume that there are eight confined molecules inside the channel, but this time four molecules are positively charged ($+\,\,0.5$e) and the other four molecules are negatively charged ($-\,\,0.5$e). The simulation domain $\Omega \subset {{\mathbb {R}}}^2$ is depicted in Fig. 7. The shape of the domain and the parameters used for the simulations are taken from Ható et al. (2016) and are summarized in Table 3. The mesh (made up of 2080 triangles) was created with NGSolve/Netgen. We consider two mobile species of ions, one cation (Na$^+$, $u_1$) and one anion (Cl$^-$, $u_2$). The confined ions are modeled as eight fixed circles of radius 1.4, where the concentration $c\equiv c_{\max }$ is such that the portion of the channel occupied by these ions is the same as in the simulations in Ható et al. (2016). The solvent concentration then becomes $u_0=1-u_1-u_2-c$.

Fig. 7

Simulation domain with triangulation for the bipolar ion channel. The blue circles represent positively charged confined ions, the red circles negatively charged ions. The black (blue) part of the boundary is equipped with Neumann (Dirichlet) boundary conditions (colour figure online)

Table 3 Dimensionless parameters used for the simulation of the bipolar ion channel and values used for the scaling

By changing the boundary value ${\overline{\Phi }}_\text {right}$ for the potential $\Phi$ on the right part of the Dirichlet boundary (on the left side, it is fixed to zero), we can apply an electric field in forward bias (on-state, ${\overline{\Phi }}_\text {right}=1$) or reverse bias (off-state, ${\overline{\Phi }}_\text {right}=-1$). Figures 8 and 9 show the stationary state computed with the finite-element method in the on- and off-state, respectively. Evidently, the ion concentrations in the on-state are much higher than in the off-state. In comparison with the results from Ható et al. (2016), where the Poisson–Nernst–Planck equations with linear diffusion (referred to as the linear PNP model) were combined with Local Equilibrium Monte–Carlo simulations, we find that with the Poisson–Nernst–Planck equations with cross-diffusion (referred to as the nonlinear PNP model), the charged ions in the channel attract an amount of ions higher than the bath concentrations even in the off-state.

Fig. 8

Stationary solution in the on-state (channel region)

Fig. 9

Stationary solution in the off-state (channel region)

From a modeling point of view, it is an important question whether the nonlinear PNP model reproduces the rectification mechanism described above. For this purpose, we need to calculate the electric current I flowing through the pore, given by

$$\begin{aligned} I = -\sum _{i}z_i\int _{A}{{\mathcal {F}}}_i\cdot \nu \mathrm{d}s, \end{aligned}$$

(28)

where A is the cross section of the pore and $\nu$ the unit normal to A. In the finite-element setting, we can use the representation of the fluxes in entropy variables, ${{\mathcal {F}}}_i = D_i u_i(w,\Phi )u_0(w,\Phi )\nabla w_i$ and compute the integrals in (28) using a quadrature formula along the line $x=10$.

Fig. 10

Current–voltage curves and rectification. First row: the parameters are as in Table 3; second row: with $c_{\max }=0.7$

Figure 10 shows the current–voltage curves obtained with the finite-element solutions. In addition, the rectification is depicted, which is calculated for voltages $U\ge 0$ according to

$$\begin{aligned} r(U) = \bigg | \frac{I(U)}{I(-U)} \bigg |. \end{aligned}$$

We also compute the current–voltage curve for the linear PNP model, which is obtained from the model equations by setting $u_0\equiv 1$, such that

$$\begin{aligned} \partial _t u_i = {\text {div}}\big (D_i\nabla u_i + D_i\beta z_iu_i\nabla \Phi \big ). \end{aligned}$$

We expect from the simulations done in Burger et al. (2012) for the calcium channel that the current of the nonlinear PNP model is lower than that one from the linear PNP model. This expectation is also confirmed in this case. As Fig. 10 shows, the rectification is stronger in the nonlinear PNP model. The difference between the two models is even more pronounced when we increase the concentration of the confined ions to $c_{\max }=0.7$. In that case, the channel gets more crowded and size exclusion has a bigger effect. We observe a significantly lower current and higher rectification for the nonlinear PNP model.

5 Conclusions

In this work, we have presented a finite-element discretization of a cross-diffusion Poisson–Nernst–Planck system and recalled a finite-volume scheme that was previously proposed and analyzed (Cancès et al. 2019). In the following, we summarize the differences between both approaches from a theoretical viewpoint and our findings from the numerical experiments.

• Structure of the scheme The finite-element scheme strongly relies on the entropy structure of the system and is formulated in the entropy variables. From a thermodynamic viewpoint, the entropy variables are related to the chemical potentials, which gives a clear connection to nonequilibrium thermodynamics. On the other hand, the finite-volume scheme exploits the drift-diffusion structure that the system displays in the original variables.

• $L^\infty$ bounds Due to the formulation in entropy variables, the $L^\infty$ bounds for the finite-element solutions follow immediately from (8) without the use of a maximum principle. In other words, the lower and upper bounds are inherent in the entropy formulation. In the case of the finite-volume scheme, we can apply a discrete maximum principle, but only under the (restrictive) assumption that the diffusion coefficients $D_i$ are the same.

• Convergence analysis The entropy structure used in the finite-element scheme allows us to use the same mathematical techniques for the convergence proof as for the continuous system, but a regularizing term has to be added to ensure the existence of discrete solutions. The convergence of the finite-volume solution requires more restrictive assumptions: in addition to the equal diffusion constants necessary for proving the existence and $L^\infty$ bounds, we can only obtain the entropy inequality and gradient estimates for vanishing potentials.

• Initial data Since the initial concentrations have to be transformed to entropy variables via (6), the finite-element scheme can only be applied for initial data strictly greater than zero. The finite-volume scheme, on the other hand, can handle exactly vanishing initial concentrations.

• Experimental convergence rate In the numerical experiments, both schemes exhibit the expected order of convergence with respect to mesh size (even if we cannot prove any rates analytically): first-order convergence for the finite-volume scheme and second-order convergence for the finite-element scheme.

• Performance The numerical experiments done for this work suggest that the finite-element algorithm needs smaller time steps for the Newton iterations to converge than for the finite-volume scheme, especially when the solvent concentration is close to zero. Furthermore, the assembly of the finite-element matrices is computationally quite expensive resulting in longer running times compared to the finite-volume scheme.

• Mesh requirements A finite-volume mesh needs to satisfy the admissibility condition. This might be a disadvantage for simulations in three space dimensions.