Introduction

Suppose Covid testing positivity rate is 6.25%. That is, on average, one specimen would test positive and the other fifteen would test negative. Oftentimes, we find most of the Covid tests are negative, for instance, when we run screening tests for asymptomatic patients, workers, or students. Therefore, more efficient testing strategies were developed. One strategy was to pool specimens together [1,2,3,4]. Since pooling negative specimens together produces a negative test result, one single test would potentially eliminate many specimens. Thus, we present a theoretical approach to the Covid testing strategy, using sixteen specimens as an example. We will show how to pool specimens together, run the testing on different groups simultaneously, and identify the positive one(s) with binary encoding and decoding. This approach can be applied to different Covid testing positivity rates and any number of specimens.

Method

Suppose there are sixteen specimens, and all of them have enough sample for more than one test. We first present the strategy for a hypothetical scenario, then the strategy for the real world.

  1. 1)

    Assuming there is one and only one Covid positive specimen.

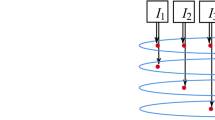
We pool eight specimens together to form a single new specimen for testing. Four groups will be formed according to the following strategy (Table 1).

Table 1 Four groups of new specimens are formed, as marked in blue. The specimens in each group are listed below
Full size table

All four pooled specimens are then submitted for PCR Covid testing simultaneously. A test would turn out positive if any one of the eight initial specimens is positive; otherwise, if all of them are negative, the result will be negative. Each group will either test positive or negative. The combination of positive and negative results will then identify which patient is Covid positive. Two scenarios are given below as examples:

In the first scenario, suppose group 1 is positive, group 2 negative, group 3 negative and group 4 positive (Table 2). Let positive results be given a value 1 and negative be given 0. Describe the overall test results in 0 and 1 combination from left to right, with left-most being group 1 and right-most group 4. Then, we can identify the Covid positive patient to be patient number 1001, in binary, i.e., patient number 9 in decimal. The conversion from binary to decimal is computed as follows:

$$ 1 \cdot 2^{3} + 0 \cdot 2^{2} + 0 \cdot 2^{1} + 1 \cdot 2^{0} = 9 $$
Table 2 Positive (in red) and negative (in green) combinations identify the Covid patient. Of note, the pooled specimen can test either positive or negative. Under the assumption that one and only one patient is Covid positive, we know if the pooled specimen tests positive, then the second half of untested specimens must be negative and vice versa. Because group 1 tested positive in this scenario, we know that the positive specimen is present in specimens 8 to 15. Since group 2 tested negative, we can rule out specimens 12 to 15. Similarly, we further rule out specimens 10 and 11 from group 3 testing. Now only specimens 8 and 9 are left. Since group 4 tested positive, we know that specimen 9 is positive
Full size table

In the second scenario, suppose group 1 is negative, group 2 positive, group 3 negative and group 4 positive (shown in Table 3). Again, let positive results be given a value 1 and negative be given 0. Describe the overall test results in 0 or 1 combinations from left to right, with left-most being group 1 and right-most group 4. Then, we can identify the Covid positive patient to be patient number 0101, in binary, i.e., patient number 5 in decimal. The conversion from binary to decimal is computed as follows:

$$ 0 \cdot 2^{3} + 1 \cdot 2^{2} + 0 \cdot 2^{1} + 1 \cdot 2^{0} = 5 $$
Table 3 The test results of scenario 2. Negative group 1 testing rules out specimens 8 to 15 and rules in specimens 0 to 7; positive group 2 testing rules in specimens 4 to 7; negative group 3 testing rules in specimens 4 to 5; positive group 4 testing rules in specimen 5
Full size table

As we can see from the above examples, the combinations of test results in 0 or 1 actually encode the positive specimen in binary (See supplement 4 for proof). With this strategy, we only need to run four PCR tests on four pooled specimens instead of the conventional sixteen PCR tests. In addition, since we can run four PCR tests simultaneously, we can save both resources and time.

  1. 2)

    Without the knowledge of how many specimens are positive.

In a real-world scenario, we cannot assume there is only one positive covid specimen. However, a similar strategy could apply to the grouping and testing. In this new strategy, we still pool 8 specimens together, but we evaluate only 15 patients at a time, patient 1 to 15 (Table 4). We don’t include patient number 0 this time. Because, in the first strategy, we never test patient number 0, we will never know if he/she is positive or negative.

Table 4 Four groups of new specimens are formed, as marked in blue. The specimens in each group are listed below
Full size table

With this strategy, there are five test results from which we can draw a final conclusion. Let positive be 1 and negative be 0. (1) When the result is 0000, all patients are Covid negative. (2) When the result is 0001 (Table 5), patient number 1 is positive. (3) When the result is 0010, patient number 2 is positive. (4) When the result is 0100, patient number 4 is positive. (5) When the result is 1000, patient number 8 is positive. Test result of 0001 is illustrated in Table 5.

Table 5 An example of one positive. Three negatives rule out specimens 2 to 15. The positive rules in specimen 1
Full size table

When the test result has two positives and two negatives, we can rule out 12 specimens and we might need up to 3 additional tests to find the positive specimen(s) (Table 6). This way, the total number of tests is 4 + 3 = 7, which is still much less than the conventional 15 tests.

Table 6 An example of two positive specimens. Two negatives rule out specimens 4 to 15. Specimens 1 to 3 need further testing. If specimen 3 tests negative, then we know both specimens 1 and 2 are positive. Otherwise, further testing is needed
Full size table

When the test result has three positives and one negative (Table 7), we can rule out 8 patients and we might need up to 7 additional tests. This way, the total number of tests is 4 + 7 = 11, still less than the conventional 15 tests.

Table 7 An example of three positives. The negative test rules out specimens 8 to 15. Specimens 1 to 7 need more testing
Full size table

When the test results are all positive, no conclusion can be drawn. All positive results suggest specimen 1111, or specimen 15, could be the culprit. However, many other possibilities would produce the same result. For example, positive specimens 13 and 14 will cause all pooled specimens to be positive. The most efficient strategy at this point is yet to be determined.

Discussion

Since Covid-19 erupted, many papers described group testing to save resources. Armendáriz et al. found when the prevalence is 0.02, “the mean number of tests required to screen 100 individuals is 20” [5]. Žilinskas et al. described “under mild assumptions, a 13-time average reduction of tests can be achieved compared to individual testing” [6]. Many papers investigated the optimal pool size [4, 7,8,9]. Ayazv et al. found that “a pool size of 20 is recommended for mass RT-PCR testing” [7]. Nguyen et al. stated “accurate prevalence estimation is crucial for preventing and mitigating emerging and seasonal diseases” [10]. Ma et al. suggested “under normal circumstances, the optimal combination number of samples for nucleic acid detection is about 10” [9]. However, all these papers employed sequential testing and therefore needed many time cycles.

Algorithms Saving Only Resources

The Covid testing positivity rate varies from time to time and from city to city. The strategy presented here was developed for a positivity rate of 6.25%, i.e., one in sixteen. With the assumption of only one positive specimen out of sixteen, the following traditional strategy saves only resources. Pool eight specimens together. If eight together is positive, then test four. If four together is positive, then test two. If two is positive, then test one. During the process, a negative result will lead to the testing of half of the untested half. This way, four tests are needed to find the positive specimen. However, this strategy, although it saves resources, requires sequential testing, and therefore will take four time-cycles. In contrast, our strategy potentially needs only one or two-time cycles and thus saves both resources and time.

Binary Encoding

The four groups in our strategy can be formed by binary encoding. In binary, sixteen specimens will run from 0000 to 1111, (or from 0001 to 1111 in the case of fifteen specimens). The first group, 8 to 15 group, is made up of all specimens whose fourth digit is 1, i.e., in the form of 1xxx, x being 0 or 1. The second group is made up of all specimens whose third digit is 1, i.e., in the form of x1xx, x being 0 or 1. So on, so forth. The beauty of the strategy is that the combinations of positive and negative test results in binary directly encodes the Covid positive patient’s number as shown above.

Probability

In the real-world scenario, the probabilities of getting zero, one, two, three and four positive group-test results are \(37.98\%, 10.13\%, 18.30\%, 19.78\%\mathrm{ and} 13.81\% \mathrm{respectively}.\) (See supplement 1, 2 and 3.) Therefore, our strategy returns an answer \(48\%, \left(37.98\%+10.13\%\approx 48\%\right),\) of the time, after four tests and one time cycle. \(18.3\%\) of the time, up to three additional tests are needed. \(19.78\%\) of the time, up to seven additional tests are needed. Only \(13.81\%\) of the time does the testing result in 1111, and the best testing strategy from here is yet to be determined, needing possibly up to additional 15 tests. Overall, the average number of tests is 8, by weighted averaging as shown below:

$$ 0.3798 \cdot 4 + 0.1013 \cdot 4 + 0.1830 \cdot 7 + 0.1978 \cdot 11 + 0.1381 \cdot 19 = 8.0051 $$

The overall number of time cycles is 1.5.

$$ 0.3798 \cdot 1 + 0.1013 \cdot 1 + 0.1830 \cdot 2 + 0.1978 \cdot 2 + 0.1381 \cdot 2 = 1.5189 $$

Therefore, in a real-life situation, our strategy remains valid and efficient.

Although there exist more sophisticated strategies to decipher the results of two, three or four positives, the additional saving of resources and time is limited. The average number of tests saved would be 1, dropping from 8 to 7. (See supplement 3) For practical purpose, the easiest way is to test each of undetermined specimens.

Generalizing to \({2}^{n}\) Patients

Suppose we have 2n patients and one of them is Covid positive. Then n groups are formed according to the following n-digit binary notations: 1xx…x, x1x…x, xx1…x, …………, xxx…1. These n groups will be tested simultaneously and produce a combination of positive and negative results that encode the ID of the positive patient. The number of tests would be n and the time cycle would be 1. In contrast, the traditional testing would need 2n tests. The traditional grouping strategy would need n tests and n time cycles.

When the number of specimens is between 2 and 2n−1, n groups are still formed with similar binary strategy. For example, there are twenty patients and one of them is positive. These 20 patients will be grouped as follows: 1xxxx, x1xxx, xx1xx, xxx1x, xxxx1, where the first group consists of five patients: patient 16, 17, 18, 19 and 20 or, in binary, patient 10,000, 10,001, 10,010, 10,011 and 10,100. In this case, 5 tests and 1 time cycle are needed.

Different Positivity Rates

In real world testing, we don’t know how many positive samples there will be in a batch of specimens. However, the current Covid testing positivity rate will provide good guidance for the grouping strategy, assuming those specimens are randomly selected. At different positivity rates, the size of the pooled specimen needs to be modified accordingly. For instance, when the positive rate is 12.5% or one in eight, our strategy is to take seven patients at a time and test three pooled specimens. Similarly, when the positive rate is 3.125% or one in thirty-two, our strategy is to take 31 patients at a time and pool 16 specimens together.

When the positivity rate is less than 1 in 16, the average numbers of tests and time cycles to identify the positive patients will need to be determined by future research. It would be mathematically challenging to compute the average numbers of tests and time cycles. A brute force approach and computer simulation would be most likely needed.

Limitations and Error Analysis

The grouping by hand does result in errors. However, the process can be computerized and/or automated. Other errors involve false positives and false negatives. False negative rate depends on the sensitivity and specificity of the test itself.

Pooling dilutes samples, and therefore, might further decrease the sensitivity of the test. Specimens are diluted in the process of pooling. A pooled specimen may contain less genetic material for PCR testing and, therefore, return a false negative result. Clinical validation is needed. For this strategy to work, it may require a test with higher sensitivity. Another limitation is that not all tests return a definite positive or negative result. When the result is intermediate, or indeterminate, more tests are needed [2].

Conclusion

Since most Covid tests are negative, it is wasteful of resources and time to test all specimens. Our strategy allows for pooling specimens together and testing different groups of pooled specimens simultaneously. Our strategy is applicable to different stages of the pandemic when the testing positivity rates are different. The binary encoding and decoding process during the testing is convenient and intuitive. In a hypothetical situation where only one in sixteen specimens is positive, our strategy needs only four tests and one time cycle to identify the positive one. For real world application, our strategy will return an answer 48% of the time in four tests and one time cycle when the positivity rate is 6.25%. Overall, the average number of tests is seven or eight and the average time cycle is around one and a half.