1 Introduction

The presumption that economic agents are rational is one of the pillars of economic analysis. Among other things, rational assumptions imply that agents make objective predictions about their prospects and update those forecasts in a Bayesian way. However, tons of evidence in the psychological field refutes this notion (Lewinsohn et al. 1980; Taylor and Brown 1988). In fact, humans frequently make social cognitive biases, such as systematic mistakes in predicting the prevalence of cooperative conduct in communities. Monin and Norton (2003) gave the example of asking students to take fewer showers more frequently during a field study when there was a water shortage. People regularly lack the capability to evaluate other people’s pro-social actions (Krueger and Funder 2004). According to the survey, students revealed common social cognitive biases including false consensus, false uniqueness, pluralistic ignorance, and others. Beliefs regarding climate change are affected by cognitive biases (West and Kenny 2011; Taddicken et al. 2019; Garrett and Daw 2020), which go beyond local public goods (Vuolevi and van Lange 2010; Leviston et al. 2013; Castro Santa et al. 2018). In general, these biased opinions can be used as proxies for participation (or non-participation) in climate action, even though they cannot be immediately translated into acts of cooperation or defection (Krueger and Funder 2004). All of the previously mentioned biases are well-known in social psychology (Geiger and Swim 2016; Weber 2017): for instance, false uniqueness or uniqueness bias corresponds to situations in which people mistakenly believe that their opinions or behavior are different from others (Miller and McFarland 1987; Suls and Wan 1987; Goethals et al. 1991; Prentice and Miller 1993; Miller and Prentice 2016); false consensus refers to the tendency to overestimate the proportion of one's opinion or behavior in a group (Ross et al. 1977; Shamir and Shamir 1997). Given the connection between thoughts about other people's cooperative conduct and cooperation in the aforementioned issue (McAuliffe and Dunham 2016), it seems plausible that this bias affects collective action as a whole (Milinski et al. 2008; Johnson and Fowler 2011; Nyborg et al. 2016; Ackermann and Murphy 2019; McNamara et al. 2021).

Public goods games (PGG) have widely been utilized as a paradigm to examine such conundrums marked by conflicts between individual and group interests (Fehr and Gächter 2002; Hauert et al. 2002; Szolnoki et al. 2011; Sasaki and Uchida 2013, 2014; Wang et al. 2019). Cognitive biases often do not significantly affect the results of collective actions in common linear PGG because the payoff structure is linear and proportional to the number of cooperators (Evans 1989; Frey and Meier 2004). However, the influence of cognitive bias may be magnified in nonlinear PGG when considering the possibility of group failure. A typical illustration of this is the PGG with a threshold, in which the advantages of cooperation would be attained only when a specific percentage of cooperators is present (Santos and Pacheco 2011; Tavoni et al. 2011). In certain situations, an incorrect estimation of the percentage of people intending to cooperate may hinder cooperation; on the other hand, it may generate false cognition that the required number of cooperators is higher than the real number, thus encouraging individuals to cooperate.

We closely follow the work of (Santos et al. 2021), but unlike in the past, we set the cognitive biases to be heterogeneous, and the bias values of cooperators and defectors in the initial stage follow a certain distribution. Obviously, the individual’s level of cognitive bias will directly affect his judgment on the expected payoff of the PGG, thus making individuals who pursue short-term profit maximization consider whether to change their original strategies (Fudenberg and Levine 1998; Santos et al. 2006). Conversely, when individuals update their cognition, they would also be affected by the real payoff in the previous round. We employ Monte Carlo methods to simulate the evolution process due to the complexity of this interaction mechanism. The main goal of this study is to explore how much the inherent parameters of TPGG, the initial distribution of bias, and the updating process of cognition affect the cooperation density when the system reaches a steady state after introducing the heterogeneous bias with an updating process, as opposed to the unbiased traditional version.

The rest of the paper is organized as follows. Section 2 reviews the related literature. The third part introduces the TPGG model with cognitive bias, evolutionary dynamics, and updating rules of bias. The simulation results are presented and further analyzed in Sect. 4. The last section summarizes the previous conclusions and gives an outlook on possible future directions.

2 Related literature

2.1 Research on cognitive bias and cooperation

In the past, the research that combined cognitive bias (or belief) and cooperation can be roughly divided into two categories: one discussed the evolution of cognitive bias in the game theory scenarios, and the other discussed the changes in cooperation with preset bias. Regarding the first question, the earlier evidence of Nyarko and Schotter (2002) on the evolution of beliefs in constant-sum games showed that there may be completely different behaviors behind the evolution of people’s beliefs in different environments. Duan and Stanley (2010) proposed a benefit-oriented belief updating mechanism under the ultimatum game. Simulations showed that belief updating may induce the emergence of fair behavior. Guazzini et al. (2019) adopted a behavioral model based on the ultimatum game to illustrate how altruistic behavior based on in-group bias is stabilized. Leimar and McNamara (2019) studied the evolution of cognitive biases under repeated games. Individuals could decide the amount of investments through costs and benefits, and empirical research showed that overestimation of investment costs can evolve, but also lead to reduced investment. Further research demonstrated that there were cognitive limitations in belief updating and that the evolution of biases can compensate for this situation (McNamara et al. 2021).

For the latter research path, Fischbacher et al. used empirical methods to study the role of social preferences and beliefs on voluntary cooperation in the early days (Fischbacher et al. 2001; Fischbacher and Gächter 2010). The results showed that the frequency of conditional cooperation remained stable. However, the free-riding phenomenon gradually increased, while a steady decline in cooperation strategies was observed in another series of experiments, and a considerable number of subjects became unconditional defectors (Andreozzi et al. 2020). Ackermann and Murphy (2019) extended previous empirical research on public goods problems by eliciting beliefs at the individual level and testing individuals’ performance in one-shot and repeated games. Research showed that people’s decisions, beliefs, and even social preferences would change as the game progresses.

Simulation methods were employed to explore the cooperative behavior with belief as well. Based on a one-shot and repeated prisoner’s dilemma, Delton et al. (2011) proved that the generous belief is a necessary by-product of decision-making system selection that regulates binary reciprocity under uncertainty, and a fundamental reason for its evolutionary stability is that it's inherently a high-payoff strategy. Ellingsen and Robles (2002) explored the theoretical basis of the stranded problem through the bargaining model of the evolution process of beliefs and strategies. Tang et al. (2014) used the prisoner’s dilemma game to study how structural dynamics affect the cooperation of two interdependent groups. The results showed that intra-group bias is usually beneficial to cooperation, but larger biases sometimes inhibit cooperation. Johnson and Fowler (2011) proposed an evolutionary model based on resource competition scenarios. Numerical calculation results showed that overconfidence will maximize individual adaptability, and when the benefit–cost ratio of competing resources is large enough, the group will tend to overdo it. Confidence, whereas a "rationally" unbiased strategy is stable only under limited conditions. On the other hand, some scholars have questioned the value of overconfidence and believed we should note the difference between cognitive bias and outcome bias (Marshall et al. 2013): the steady state formed by outcome bias is suboptimal, but cognitive bias may be optimal. Li et al. (2016) proposed a co-evolutionary resource competition game model with overconfidence and bluffing based on previous work. Simulation results showed that bluffing is more likely to succeed but is punished more frequently than overconfidence. Liu et al. (2021a) proposed a heuristic model based on coevolution to study the evolutionary dynamics of competitive cognitive biases and environmental feedback. Huang et al. (2018) combined prior heterogeneous cooperation beliefs and imitation dynamics and found through simulation on a square network that heterogeneous cooperation beliefs can enable individuals to overcome the negative feedback mechanism introduced by network reciprocity.

The literature on beliefs and cooperation is rich and covers a wide range of scenarios, most of which investigate changes in individual behavior under repeated games through simulation or laboratory experiments, with attention generally concentrated on the payoff of strategies and the evolution of beliefs. However, the research on the interactions between the evolution of cooperation and belief is not sufficient enough.

2.2 Research on social learning and belief updating

The process by which members of a population continuously adjust their own cognition through direct perception of external signals and the influence of other people's opinions is called social learning. This concept was originally a supplement to the behaviorist learning theory by Bandura, which emphasized the vital role of human sociality in learning (Bandura 1962), that is, people can learn from observation and imitation. In subsequent research, social learning was gradually developed into a theoretical system (Bandura and Walters 1977).

The learning process can be divided into sequential social learning (Banerjee 1992; Conway and Christiansen 2001) and network social learning (DeGroot 1974; Gale and Kariv 2003). The former process emphasizes the observation of late-comers on the previous people, while the latter focuses on the impact of the current belief snapshot on exactly the next time period. In addition, from the conditions on which the learning process depends, it can be divided into Bayesian and non-Bayesian social learning, while the former relies more on thumb rules (Ellison and Fudenberg 1993). Since Bayesian social learning is more rigorous and rationally describes the process of human beings understanding the nature of the objective world state through signals to a certain degree (Porot and Mandelbaum 2021), it has widely been used in the previous study as the driving force for individual belief updating process, and gradually developed into two forms of Bayesian social learning model (Gale and Kariv 2003; Acemoglu et al. 2011; Mueller-Frank 2014). The main applicable scenario of social learning theory is human (or other biological) society. Hence, the purpose of research on its dynamics is often not to find an optimal model, but to find a model that best fits the realistic characteristics of human society. Based on the consideration of human practice scenarios, Jadbabaie et al. (2012) proposed a non-Bayesian social learning model in 2012. Compared with traditional theories that want to explain the dynamics of people's beliefs and behaviors, non-Bayesian social learning models focus more on describing them. Regarding the comparison between Bayesian and non-Bayesian learning, Acemoglu and Ozdaglar (2011) conducted an in-depth discussion on previous works about belief and opinion dynamics in social networks.

Various social learning mechanisms have been proposed to fit different scenarios. Yet, previous studies seldom took the fitness of individuals into account to reflect the impact of interactions’ outcomes on the updating process itself.

3 Model

In this work, we consider a well-mixed population consisting of \(N\) individuals. Individuals are randomly matched with those who belong to this population and form a group with a fixed size \(G\). Thereafter, each individual would participate in a round of TPGG with his \(G - 1\) partners at every time step. Here, the available strategies belong to a discrete binary set \(S \in \left\{ {C,D} \right\}\), that is, individuals can only choose one action from “cooperation” or “defection”. In each round of games, if an individual chooses to cooperate, he will contribute \(c\) units to the public pot in advance; however, if he adopts a defective strategy, his contribution is zero. In the following stage, collective action will decide whether to proceed and generate corresponding benefits based on whether the number of cooperators in the group reaches the minimum level required. If the number of cooperators is lower than the threshold \(T\), none of the individuals in this group could gain any payoff from the interaction. Conversely, when a group reaches the threshold \(T\), each individual could receive the basic benefit \(bc\), in addition to a special reward \(fc\) for each additional cooperator exceeding the threshold. Therefore, the payoff \(\prod_{S}\) not only depends on the individual’s own strategy \(S\) but also on his partner’s in the same group. Presuming that \(j\) is the current number of cooperators in a group, we have:

$$\prod\nolimits_{D} [j] = \left( {bc + fc(j - T)} \right)\Theta [j - T],$$
(1)
$$\prod\nolimits_{C} [j] = \prod\nolimits_{D} [j] - c,$$
(2)

where \(\Theta [x]\) is the Heaviside unit step function, whose value is 0 when \(x < 0\) and 1 when \(x \ge 0\).

In addition, we add an adjustable punishment factor \(\delta\) to the payoff structure, which denotes the negative consequences of violating social norms. The value of \(\delta\) represents the relative quantity between the punishment and the cost paid by cooperators and \(\delta = 0\) means no punishment is imposed on defectors. Hereafter, Eq. (1) can be transformed into:

$$\prod\nolimits_{D} [j] = \left( {bc + fc(j - T)} \right)\Theta [j - T] - \delta c.$$
(3)

We define the cooperation density \(\rho_{c}\) as the proportion of cooperators in the whole population, which can be expressed as:

$$\rho_{c} = \frac{1}{N} \sum\limits_{i = 1}^{N} S_i,$$
(4)

where Si = 1 if individual i cooperates and Si = 0 if individual i defects.

In this model, everyone in the population has his own cognitive bias, which is based on the current average cooperation density of the whole population. Hence, such bias can also be regarded as one’s belief about the willingness of other individuals to cooperate, denoted by \(\sigma_{i}\). Without loss of generality, an individual with cognitive bias can estimate the fraction of cooperators in the population as:

$$\hat{\rho }_{c} = \rho_{c}^{{10^{{ - \sigma_{i} }} }} = \exp \left[ {10^{{ - \sigma_{i} }} \ln [\rho_{c} ]} \right].$$
(5)

If \(\sigma_{i} = 0\), we have \(\hat{\rho }_{c} = \rho_{c}\), individual \(i\) has no cognitive bias at the current time step, and his cognition is consistent with the real situation. When an individual adopting strategy \(S\) interacts in a well-mixed population of fixed size \(N\), he will compare the relative payoff of choosing cooperation \(f_{C} [\hat{\rho }_{c} ]\) with that of choosing defection \(f_{D} [\hat{\rho }_{c} ]\) based on its own cognition on cooperative situation. Since the population is large enough, each individual thinks it is equally possible to interact with others. Hence, the expected payoff of adopting cooperation or defection strategies is:

$$f_{C} [\hat{\rho }_{c} ] = \sum\limits_{k = 0}^{G - 1} {\left( {\begin{array}{*{20}c} {N - 1} \\ {G - 1} \\ \end{array} } \right)}^{ - 1} \left( {\begin{array}{*{20}c} {N\hat{\rho }_{c} - 1} \\ k \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {N(1 - \hat{\rho }_{c} )} \\ {G - 1 - k} \\ \end{array} } \right)\prod\nolimits_{C} [k + 1],$$
(6)
$$f_{D} [\hat{\rho }_{c} ] = \sum\limits_{k = 0}^{G - 1} {\left( {\begin{array}{*{20}c} {N - 1} \\ {G - 1} \\ \end{array} } \right)}^{ - 1} \left( {\begin{array}{*{20}c} {N\hat{\rho }_{c} } \\ k \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {N(1 - \hat{\rho }_{c} ) - 1} \\ {G - 1 - k} \\ \end{array} } \right)\prod\nolimits_{D} [k].$$
(7)

Different from the previous study, we set the individual's cognitive bias to be heterogeneous and dynamic, reflecting the evolution of people's beliefs when they interact over time. We consider using uniform distribution to describe the level of initial cognitive bias and employ a parameter \(\omega\) to control the diverse degree of bias at the initial stage. Combining the factors mentioned above, the initial cognitive biases of individuals are equally spaced on interval \([ - \omega ,\omega ]\). In particular, when \(\omega = 0\), the cognitive bias of all individuals in the population is 0, and the model returns to the original version; when \(\omega\) increases, the distribution range of initial cognitive biases will be more extensive, and the differences of opinions among individuals will be enlarged accordingly.

A synchronous updating rule is employed during the updating process of strategy. At each time step, individuals can decide whether to change their strategies based on the cooperation environment in the past round, together with their own cognitive bias. Therefore, the change in individuals’ expectation of cooperation at this step does not affect others’ judgment. On the one hand, as the difference between the expected payoffs of the two strategies expands, the possibility of individuals adopting the strategy with higher returns will increase steadily. On the other hand, individuals sometimes may be affected by exogenous factors and spontaneously switch from one strategy \(X\) to another \(Y\) with a certain probability. Here, we set the mutation rate as \(\mu\), and the probability of an individual transiting his strategy is obtained by comprehensively considering these two factors (Fudenberg and Levine 1998):

$$\mu + (1 - \mu )\left( {1 + e^{{ - \beta (f_{Y} - f_{X} )}} } \right)^{ - 1} .$$
(8)

In the homogeneous population, the transition probability of the system increasing or decreasing a cooperator can be expressed as (Traulsen et al. 2006):

$$T^{ + } [x] = (1 - x)\left( {\mu + (1 - \mu )\left( {1 + e^{{ - \beta \left(f_{C} \left[ {\rho_{c}^{{10^{{ - \sigma_{d} }} }} + \frac{1}{N}} \right] - f_{D} \left[ {\rho_{c}^{{10^{{ - \sigma_{d} }} }} } \right]\right)}} } \right)^{ - 1} } \right),$$
(9)
$$T^{ - } [x] = x\left( {\mu + (1 - \mu )\left( {1 + e^{{ - \beta \left(f_{D} \left[ {\rho_{c}^{{10^{{ - \sigma_{c} }} }} - \frac{1}{N}} \right] - f_{C} \left[ {\rho_{c}^{{10^{{ - \sigma_{c} }} }} } \right]\right)}} } \right)^{ - 1} } \right),$$
(10)

where \(\sigma_{c}\) and \(\sigma_{d}\) are the common biases of all cooperators and defectors, respectively. However, the situation is different in the heterogeneous population, where their cognition may differ even if they adopt the same strategy. Therefore, we calculate the probability that each individual would change their strategy separately, based on their unique value of bias, and take the average level as the transition probability of the whole population.

To make cognitive bias, as a special kind of belief, have an impact on individuals’ cooperative expectation and, in turn, be influenced by the cooperation results, we reconstructed the updating rule of individual cognitive bias derived from existing social learning models (DeGroot 1974; Del Vicario et al. 2017; Liu et al. 2021b; Alvim et al. 2021). Considering that our model is based on a well-mixed population rather than one on the network, we presume that individual \(i\) randomly selects one member \(h\) from those who have participated in the same TPGG group. Thereafter, individual \(i\) compares his own real payoff with his partner to update his opinion, we have:

$$\sigma_{i}^{t + 1} = \sigma_{i}^{t} + \varepsilon_{i,h}^{t} \nu \left( {\sigma_{h}^{t} - \sigma_{i}^{t} } \right),$$
(11)

where \(\sigma_{i}^{t + 1}\) and \(\sigma_{i}^{t}\) represent the cognitive bias of individual \(i\) at time steps \(t\) and \(t + 1\), respectively. We assume that the cognitive bias value is within \([ - 2,2]\), which means that individuals cannot make their cognitive biases exceed the upper bound 2 through the updating process and vice versa. Besides, the updating rule models the evolving process of individuals' beliefs. \(\varepsilon_{i,h}^{t}\) is the bias factor and is defined as:

$$\varepsilon_{i,h}^{t} = \left( {\tilde{\Pi }_{h}^{t} - \tilde{\Pi }_{i}^{t} } \right)\Theta [\tilde{\Pi }_{h}^{t} - \tilde{\Pi }_{i}^{t} ],$$
(12)

where \(\tilde{\Pi }_{h}^{t}\) and \(\tilde{\Pi }_{i}^{t}\) is the normalized payoff of individual \(h\) and \(i\) at time step \(t\), respectively. The Heaviside function \(\Theta [\tilde{\Pi }_{h}^{t} - \tilde{\Pi }_{i}^{t} ]\) ensures that the belief of individual \(i\) would move toward individual \(h\)’s only when the payoff of individual \(h\) is higher. The parameter \(\nu\) is the learning speed of the focal player or the peer pressure from group members, which adjusts the updating rate in any case. Since individuals become more and more similar over time through this interaction, and eventually lead to hemophilia, the overall cognition of the entire population will converge to a certain level.

4 Results and discussion

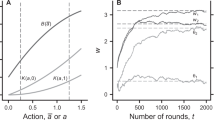
Our works are mainly based on numerical simulations, to help understand the simulation results we are about to analyze, we plot the flow diagram in Fig. 1, which briefly describes the framework of our model as well as individuals’ actions during each time step. The population size \(N = 500\) and PGG group size \(G = 11\) are fixed in the simulation, and selection intensity \(\beta = 10\) and mutation rate \(\mu = 0.01\) also remain unchanged. We set the contribution \(c = 1\), and to reduce the uncertainty caused by random effects, the results of each data point are averaged over 10 independent runs.

Fig. 1
figure 1

Flow diagram of individual \(i\) performing an updating process in a single step

Full size image

To verify the rationality of the model after introducing heterogeneous bias with a belief updating process and explore the impact of the inherent parameters in the original TPGG model on the cooperation density, we plot the comparison curves of cooperation density as a function of \(b\) under different cooperation thresholds \(T\) in Fig. 2. Five different values of \(T\) are considered in this figure, and the remaining parameters are fixed at \(f = 1.5\), \(\omega = 1\) and \(\nu = 0.01\). It can be observed from the figure that under each cooperation threshold \(T\), as the basic income \(b\) increases, the cooperation density of the population maintains an upward trend. When the cooperation threshold \(T = 5\), even if the fixed basic income is 0, the cooperation density still reaches 30%. With the increase of \(T\), the critical \(b\) value required for the emergence and dominance of cooperators also increases. For instance, in the case of \(T = 10\), there is no cooperator until \(b = 7\) except for the mutant factor, which means more incentives are required in a group with a relatively high threshold. Hence, it is easy to draw a conclusion that lowering the threshold for cooperation effectively relaxes the conditions for achieving common goals and reaching cooperation within a group. Hence, more individuals start to find that cooperative behavior is profitable at a lower level of basic income, which promotes the emergence and prosperity of cooperation.

Fig. 2
figure 2

Comparison curves of cooperation density with \(b\) under different cooperation thresholds \(T\)

Full size image

From Fig. 3, in the given parameter space where \(b = 9\), \(\omega = 1\) and \(\nu = 0.01\), the cooperation density \(\rho_{c}\) generally shows an upward trend with the increase of extra reward \(f\). However, the number of cooperators remains stable even if the value of \(f\) changes significantly from 0 to 1.5, which shows that \(f\) does not seem to impact the \(\rho_{c}\) when \(T\) is relatively high. It is worth noting that in the scenarios of \(T = 6\), 7 and 8, it can be clearly observed that when the extra reward is less than 1, which corresponds to the area to the left of the black dotted line in Fig. 3, a higher threshold is more conducive to the cooperation. We speculate that this might be because when the extra reward is less than 1, the extra reward is not enough to cover the cost of those who have paid for adopting a cooperative strategy in a PGG group. Therefore, once the group has reached the threshold for cooperation, group members have no additional motivation to become a cooperator. As a result, the cooperation density decreases when the threshold is lowered. On the contrary, in the case of \(f \ge 1\), because the extra incentive brought by the number of people exceeding the threshold in the PGG group was greater than the contribution of every single cooperator, individuals would find it profitable to cooperate. For populations with the potential to achieve a high level of cooperation, even if the number of cooperators in the group has already reached the threshold, the higher extra benefit can still motivate members to further contribute to the public pool.

Fig. 3
figure 3

Comparison curves of cooperation density as a function of extra reward \(f\) under different cooperation thresholds \(T\)

Full size image

The definition of initial heterogeneity of bias \(\omega\) has been introduced in the previous section. Obviously, the larger \(\omega\) is, the wider the range of the initial distribution becomes, and the differences in cognition among individuals are more significant. Figure 4 displays the cooperation density as a function of \(\omega\) for five different values of \(T\), and the rest of parameters are set as \(b = 10\), \(f = 1.5\), \(\nu = 0.01\). It can be easily seen from Fig. 4 that the cooperation density is polarized when the heterogeneity of bias is not significant. At that time, the population is in a full cooperation state when the threshold is relatively low (\(T \le 8\)), while dominated by defectors when the condition for cooperation is too strict (\(T \ge 9\)). For the curves originally reach full cooperation, with the enhancement of the \(\omega\), the level of cooperation remains unchanged in the early stage (\(\omega \le 0.8\)), then drops rapidly, and the change becomes flatter when \(\omega\) gets bigger. However, for the population with a high threshold, the trend of \(\rho_{c}\) is just the opposite as the value of \(\omega\) increases. Overall, the increase of \(\omega\) makes the curves under different \(T\) move toward the region with a medium level of cooperation. From a microscopic perspective, cognitive bias can affect individuals' estimation of expected return, and the enhancement of \(\omega\) leads to greater differences in the judgment of expected payoff, even among those who adopt the same strategy. Therefore, the response of some individuals may not coordinate with their partners. The macroscopic manifestation of this chaos is that the boundary of the selection gradient becomes more blurred, which leads to the level of cooperation closer to the neutral state when the population reaches the evolutionary steady state. This result also reflects the fact that an excessively wide range of opinions may lead to a significant disagreement on collective action, which is consistent with our observation in real life.

Fig. 4
figure 4

Comparison curves of \(\rho_{c}\) with changing heterogeneity \(\omega\) under different cooperation threshold \(T\)

Full size image

To investigate the combined effect of \(b\), \(f\) and \(\omega\), we draw the heatmap of \(\rho_{c}\) in Fig. 5. In this figure, the X-axis represents for \(\omega\) in both of the subplots, the Y-axis indicates \(b\) and \(f\) respectively, and each color encodes a certain range of cooperators density at the stable state. The other configurations in both subgraphs are set as: \(T = 6\), \(\nu = 0.01\). Figure 5a shows the combined effect of basic benefit \(b\) and initial heterogeneity of bias \(\omega\) on the evolution of cooperation within a certain parameter space. Obviously, no matter what the value of \(\omega\) is, the cooperation density consistently shows a growing trend with the increase of \(b\), which is similar to the results demonstrated in Fig. 2. In the case of \(\omega < 0.5\), the transition region between full cooperation and full defection is quite narrow, and the phase transition process is achieved with only a very slight change of \(b\). However, in the scenario of \(\omega > 0.5\), more areas with a medium level of cooperation density are introduced into the trumpet-shaped transition region, making the phase transition from full cooperation to full defection smoother. For a fixed value of \(b\), when it is small, the cooperation density rises with the increase of \(\omega\); however, when \(b > 2\), the cooperation density will go down when \(\omega\) becomes larger. Figure 5b shows the combined effect of extra reward \(f\) and initial heterogeneity of bias \(\omega\) on the cooperation density \(\rho_{c}\). The population gradually transitions from the bright yellow in the upper left corner to the dark blue area in the lower right corner, which generally shows that the cooperation density and \(f\) are positively correlated, while negatively related with \(\omega\) overall. However, it can be noticed that when the special reward is fixed at \(f = 1.2\), with the increase of \(\omega\), the cooperation density does not show a monotonically decreasing trend. This phenomenon indicates that there is a combination of \(f\) and \(\omega\) which enable the population to achieve a full cooperation state with a minimum value of extra reward. Additionally, it is convincing to derive an inference that the optimal situation can be obtained by adjusting the initial heterogeneity of bias so that the system can achieve a high level of cooperation density with relatively smaller incentives.

Fig. 5
figure 5

Heatmap of the cooperation density \(\rho_{c}\) with various \(b\), \(f\) and \(\omega\). a \(f = 1.5\); b \(b = 10\). Other configurations are set as: \(T = 6\), \(\nu = 0.01\)

Full size image

To further explore the effect of parameters in this model, we plot the comparison curves of \(\rho_{c}\) as a function of basic income \(b\) and extra reward \(f\) under different levels of \(\omega\) and the parameters are fixed in Figs. 6 and 7: \(T = 6\), \(\nu = 0.01\). It can be clearly observed from Fig. 6 that no matter what value the initial heterogeneity of bias \(\omega\) is, the fraction of cooperators in the population grows as \(b\) increases. The curves with smaller values of \(\omega\) (when \(\omega \le 0.7\)) start with a full defection state and then have a dramatic change in the vicinity of \(b = 1.5\). Evidently, the range of \(b\) for the coexistence of cooperators and defectors becomes wider as \(\omega\) increases, which seems to be considered as the countervailing effects of heterogeneity on basic income. Additionally, it is noteworthy that there exists a threshold value of \(b\) around 1.75. In the case of \(b < 1.75\), a bigger value of \(\omega\) is more conducive to the cooperation; however, when \(b > 1.75\), it shows the opposite trend that a small value of is more beneficial to cooperators. We speculate that the reason for this phenomenon is the interference from heterogeneity, for the effect of \(b\) is limited when its value is small. However, cognitive bias influences individuals’ expectations of payoff and misleads some players to adopt a cooperative strategy. According to Fig. 7, it is obvious that the cooperation density rises at all levels of heterogeneity as the extra reward \(f\) increases. In the scenarios of \(\omega \le 0.9\), the four curves both grow at a steady pace; they get closer and closer and eventually coincide with each other when \(f\) has reached a high value. However, in the case of \(\omega = 1.5\), although this curve also shows an upward trend, it remains almost parallel to the curve represented for \(\omega = 0.5\) in the given parameter space. This result reveals that the initial heterogeneity of bias is able to weaken the positive effect of extra reward when \(\omega\) exceeds a critical value, which makes the cooperation density constantly below those with a relatively small \(\omega\). Besides, when \(\omega\) changes in a certain range, the increase of extra reward could eliminate and even offset the negative impact of bias on cooperation.

Fig. 6
figure 6

Comparison curves of cooperation density \(\rho_{c}\) as a function of basic returns \(b\) under different \(\omega\)

Full size image
Fig. 7
figure 7

Relationship between the cooperation density \(\rho_{c}\) and extra reward \(f\) with different \(\omega\)

Full size image

To examine the impact of learning speed \(\nu\) on the density of cooperation when the population reaches a steady state, we plot a set of comparison curves with the changing initial heterogeneity \(\omega\) in a specific parameter space: \(T = 7\), \(b = 6\), \(f = 1.5\). According to Fig. 8, the curves generally show a downward trend with the increase of \(\omega\) at all levels of \(\nu\), and this result is basically consistent with the previous analysis. It is evident that the belief updating rule based on learning the cognition of individuals with higher payoff has largely delayed the declining trend of cooperation density, and the phase transition point of full cooperation gradually moved from \(\omega = 0.7\) to \(\omega = 1.1\) as \(\nu\) increases. However, when the level of initial heterogeneity is high, that is, in the right half of the graph, the curve with a larger learning speed has a lower position, and the order of cooperation density from high to low is exactly the opposite of the previous scenario. We infer that this learning mechanism can play a more vital role when the initial heterogeneity is greater because the differences in beliefs among individuals are more significant. In addition, since the speed of belief updating itself is much faster than the changing rate of cooperation in the system when the learning speed is too high, individual beliefs will quickly converge to a certain level, making it impossible for individuals to effectively improve their strategies through repeated interactions. In this configuration, the cognition of some individuals may converge prematurely to specific intervals in the early stage, which makes the model closer to the version with a homogeneous bias in most of the time steps.

Fig. 8
figure 8

Comparison curves of \(\rho_{c}\) as a function of initial heterogeneity \(\omega\) under different updating speed \(\nu\)

Full size image

We plot the heatmap of \(\rho_{c}\) in the full \(b - f\) plane to further explore the impact of updating speed on the evolution of cooperation in Fig. 9. Different colors represent specific levels of cooperation density \(\rho_{c}\) that the population is at when the system reaches the steady state, among them, the dark blue area means the population is dominated by defectors and the yellow region indicates that the population has reached a high level of cooperation. By comparing the scenarios of \(\nu = 0\) (the original version without the updating process) and \(\nu = 0.03\) (where the updating speed is fast), it is clear that the speed of cognitive updating only has a small effect on the evolution of cooperation when both the basic income \(b\) and the extra income \(f\) are relatively small (the lower left region of the two figures); however, when \(b\) and \(f\) are of high levels (the upper right region of the two figures), the faster updating speed introduces a region with a high level of cooperation. This phenomenon suggests that when the values of income factors are small, their incentive effect on cooperation behavior is quite limited, while inter-individual differences in the payoff are relatively small. At this time, even if there exists a cognitive updating process based on payoff, individuals with lower payoff are unable to adjust their cognition quickly to the cognitive level of individuals with higher payoff through this process. In addition, the system has a certain degree of randomness, while a fast learning speed can amplify this effect. This may cause the cognition of some individuals to converge prematurely to specific intervals, while the evolution of cooperation enters the steady state much earlier, thus coarsening the boundary of the different ranges of cooperation density.

Fig. 9
figure 9

Heatmap of \(\rho_{c}\) as a function of \(b\) and \(f\) under different \(\nu\). a \(\nu = 0\); b \(\nu = 0.3\)

Full size image

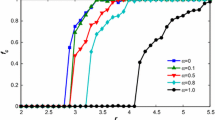
Punishment has been widely employed as a micro mechanism to solve social dilemmas and promote the emergence of cooperation. However, the incentive function of punishment may be affected by cognitive bias in an unexpected way. Here, we modify the rules of interaction to include a penalty for defectors, which amount is \(\delta c(0 \le \delta \le 1)\). The value of \(\delta\) indicates how much the penalty imposed compares to the initial contribution paid by cooperators. When \(\delta = 0\), it indicates that no penalty has been imposed, and \(\delta = 1\) indicates that all advantages of the defectors over the cooperators are eliminated. To comprehensively investigate the impact of \(T\) and \(\nu\) on the efficiency of punishment, we plot the comparison curves of \(\rho_{c}\) with various \(\delta\) in a specific parameter space, and the remaining parameters are fixed at \(b = 6\) and \(f = 1.5\). It can be easily seen from Fig. 10 that the punishment factor \(\delta\) always has a positive effect on cooperation, because it reduces the relative cost of cooperators, thus making the difference in the expected payoff between the two strategies when individuals face the same situation. By comparing the subgraphs on the two rows, we can find that the effect of punishment factors is more significant when the value of \(\omega\) is small and \(T = 10\). However, when the value of \(\omega\) is relatively big and \(T = 7\), different from the previous case, this effect becomes milder. We can infer that the heterogeneity of cognitive bias flattens the upward trend brought by punishment factors. Besides, it’s evident that the trend in subgraphs on the right (when \(\nu = 0.03\)) is more unstable. Compared with the smooth curves on the first column, the curves have more fluctuation when \(\nu\) are high, and this result ties well with what is shown in Fig. 9.

Fig. 10
figure 10

Comparison curves of \(\rho_{c}\) as a function of punishment factor \(\delta\) under different cooperation thresholds \(T\) and updating speed \(\nu\). a \(T = 7,\;\nu = 0\); b \(T = 7,\;\nu = 0.2\); c \(T = 10,\;\nu = 0\); d \(T = 10,\;\nu = 0.2\). Other parameters: \(b = 10\), \(f = 1.5\), and \(\nu = 0.01\)

Full size image

5 Conclusion

Understanding how to maintain cooperation in various social dilemmas is critical to addressing many of the challenges in society today. This effort could benefit from recognizing the influence of cognitive bias in cooperation dynamics and establishing proper incentives that conform to social norms. Motivated by the previous work related to cognitive bias and belief updating in multi-agent systems, we propose a heterogeneous population with a specific distribution of cognitive bias at the initial stage, along with its updating rule during the evolution process of cooperation. We conduct numerical simulations to investigate the impact of evolving bias and its combined effect with the inherent parameters of the original TPGG model. Simulation results reveal that heterogeneous cognitive bias shows the opposite affection in populations with a high and low cooperation threshold. That is, cognitive bias is more conducive to cooperation where the cooperative environment is relatively tough but inhibits cooperation in the population that has originally achieved a high level of cooperation. This opposite effect is further exacerbated as the initial heterogeneity of the bias increases, resulting in similar levels of cooperation for different groups, even if the conditions under which they could achieve common benefits differ significantly. Besides, the findings indicate that the effectiveness of incentive methods is smoothed by cognitive bias with strong heterogeneity, while the updating process of bias brings more uncertainty to the system. In addition, the effect of bias heterogeneity is related to the inherent parameters of the PGG. Thus, it is possible to maximize the outcome of collective actions at a given level of cognitive bias by adjusting the payoff structure of the PGG.

Our study mainly focuses on the evolutionary dynamics when cognitive bias is heterogeneous and affected by the initial distribution and learning mechanism. However, this work is limited in several ways. Firstly, all these simulations conducted above are based on a well-mixed population. In the future, interaction structures between individuals can be introduced to the current framework. Besides, the learning process evidently has an impact on both the evolution of cognitive bias and cooperation. Therefore, considering different social learning mechanisms may contribute to understanding how beliefs and cooperative behavior change in various social circumstances.