Introduction

Foundational quantum photonics devices are rapidly developing towards real-world applications for advanced quantum communication and quantum computation1,2,3. The general scaling-up strategy is to utilize small-size entangled states as seeds that can subsequently be fused by probabilistic linear optics gates to realize a universal resource for quantum-information processing4,5,6,7,8,9,10. Traditionally these entangled seed states have been generated with probabilistic sources; however, a massive overhead of multiplexing is required to make this approach scalable11.

An alternative and resource-efficient strategy has been proposed for the deterministic generation of multi-photon entangled seed states using a single quantum emitter12,13. Recent experimental work on multi-photon entanglement generation has made significant progress both using single atoms14 and quantum dots15,16,17,18; in the former case an impressive 14-photon high-fidelity deterministic entangled source was realized. Yet solid-state alternatives remain attractive due to their high speed and ease of operation, and potential scalability to multiple emitters19. These features are essential when constructing realistic architectures for scaled-up quantum-information processing based on deterministic entanglement sources7.

Previous work on solid-state emitters has been limited to either two-qubit entanglement15,20, or relied on theoretical assumptions to infer multi-particle entanglement16,17,18. Ref. 16 measured two-qubit correlations and used them to determine the full process map of a single entanglement cycle. Repeated application of the process map was then used to reconstruct an n-photon cluster state and infer an entanglement length of ten photons. The validity of this procedure requires that imperfections between different cycles are uncorrelated, i.e., a purely Markovian noise process. Ref. 17 also measured two-qubit correlations and inferred a lower bound on the three-qubit entanglement fidelity based on two hypotheses: 1) the spin initializes in a perfect mixed state at the beginning of the entanglement sequence, and 2) two successive photons emission having the same polarization after spin initialization. While the assumptions of these studies can be reasonable and are, to some extent, justified by additional measurements, they lack a direct measurement of the density matrix of the generated three-qubit state. Moreover, a related demonstration was conducted for a source with limited indistinguishability in ref. 18, but it only demonstrated three-partite entanglement by 1.5 standard deviations and did not implement active spin control as required for scalability.

In this work, we directly verify genuine three-qubit entanglement with a solid-state quantum-dot (QD) source. High-fidelity realization of such states has been proposed as the fundamental building block of quantum computing architectures5. The generated three-qubit Greenberger-Horne-Zeilinger (GHZ) state consists of one electron spin and two photons. Without any theoretical assumptions or background subtraction, we measure a quantum state fidelity of 56(2)% and single photon indistinguishability exceeding 90%. Further data analysis demonstrates genuine three-qubit entanglement through violation of a biseparablity criteria by 10 standard deviations.

Results

We realize a recently proposed time-bin multi-photon entanglement protocol21,22. The protocol proceeds by entangling the QD spin with the emission time of deterministically generated single photons21,22. Previous works require the natural spin precession at a low magnetic field (few mT)16,17,18. For such an approach, scaling up to higher numbers of entangled qubits requires increasing the number of spin precessions within the short spin dephasing time ( ≈2 ns for electron spin), but reducing the precession period is at odds with producing indistinguishable photons from two ground states separated by the precession frequency and this constrains the fidelity. In contrast, we operate in the regime of a strong Voigt magnetic field which enables active spin control and clearly distinguishable optical transitions. The former allows for preserving the spin coherence in a noisy solid-state environment via spin-echo sequences and nuclear spin narrowing. The latter is essential for high photon indistinguishability, enabling fusion operations between different seed states.

In our previous work on deterministic entanglement generation, the entanglement fidelity was primarily limited by the quality of optical spin rotations15. There a hole spin was applied since the inhomogeneous spin dephasing time \({T}_{2}^{*} \, \approx \, \) 20 ns was several times longer than the duration of a π pulse on the spin (Tp = 7 ns), which is the key requirement for the protocol. However, the laser rotation pulses were found to induce incoherent (T1) spin-flip errors of the hole spin, which limited the π-rotation fidelity to Fπ ≈ 88%. This error alone sets an upper bound to the two-qubit entanglement fidelity to 77%.

To resolve this bottleneck, we employ the electron spin since the laser-induced spin-flip rate (κ) has been shown to be an order of magnitude lower23. Conversely, the electron dephasing time is inherently short \({T}_{2}^{*} \, \approx\) 2 ns24 and therefore must be prolonged in order to enable high-fidelity spin rotations. To this end, we implement nuclear spin narrowing by optical coupling25, see Fig. 1, whereby the spin nuclear noise is significantly reduced and \({T}_{2}^{*}\) prolonged. The nuclear spin ensemble couples to the electron spin via the Overhauser field, where the shift of the electron spin resonance (ESR) is proportional to the net polarization of the nuclei Iz. In the presence of material strain, optical rotations on the electron spin mediate the nuclear spin-flip transition. By driving and resetting the electron spin with two optical pulses, Iz converges toward a stable point such that its fluctuations are suppressed.

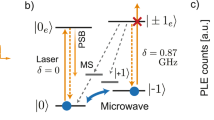
Fig. 1: Deterministic GHZ state generation from a QD embedded in a PCW.
figure 1

A three-qubit GHZ state is realized by entangling the QD (yellow dot) electron spin and two QD-emitted single photons (red wavepackets). We collect the single photons through the PCW and couple them to free space via a grating outcoupler. The QD electron spin (dark green arrow) is subjected to the Overhauser field induced by nearby nuclear spins (purple arrows). To improve \({T}_{2}^{*}\) of the electron spin, we reduce fluctuations of the Overhauser field by employing nuclear spin narrowing. The QD is operated in the Voigt geometry with an in-plane magnetic field of 4 T along the x-axis. The energy level scheme of the QD is presented in the inset. The Raman laser Ωr (blue) is used for coherent spin manipulation of two Zeeman ground states \(\left\vert \uparrow \right\rangle\) and \(\left\vert \downarrow \right\rangle\). To generate single photons, a picosecond pulsed laser Ωp (red) drives photon emissions on the diagonal cycling transition \(\left\vert \downarrow \right\rangle \to \left\vert \uparrow \downarrow \Uparrow \right\rangle\). The same transition is used for the spin readout. Spin initialization is realized through optical pumping on the non-cycling transition \(\left\vert \downarrow \right\rangle \to \left\vert \downarrow \uparrow \Downarrow \right\rangle\).

Full size image

The single-photon emitter is a self-assembled InAs QD embedded in a GaAs photonic-crystal waveguide (PCW) inside a closed cycle cryostat held at 4 K. The QD is grown in a tunable p-i-n diode heterostructure where a bias voltage charges the QD with an electron as the spin qubit. An external magnetic field of Bx = 4 T is applied (Voigt geometry), which Zeeman splits the electron spin ground state into \(\left\vert \uparrow \right\rangle\) and \(\left\vert \downarrow \right\rangle\) by Δg = 22 GHz and excited state into \(\left\vert \uparrow \downarrow \Uparrow \right\rangle\) and \(\left\vert \downarrow \uparrow \Downarrow \right\rangle\) by Δe  = 12 GHz, resulting in four optical transitions.

The PCW offers distinct advantages in the time-bin entanglement protocol. First, the close-to-unity on-chip coupling efficiency (β > 98% experimentally demonstrated26) allows scalable operation towards large photon states, which can be further evanescently coupled to a reconfigurable quantum photonic circuit with a very low loss27,28. Second, the PCW generally Purcell enhances one linear dipole and suppresses the orthogonal dipole, leading to an inherently large optical cyclicity in the Λ-level scheme, where a spin-preserving optical transition and spin rotating Raman transitions can both be implemented29. We find that the decay rate of the inner (outer) optical transition γX (γY) to be enhanced (suppressed) and measured a cyclicity of C = γX/γY = 36(3), which is the highest recorded value for QDs in the Voigt geometry and an essential figure-of-merit for the entanglement protocol30.

The GHZ generation protocol utilizes spin-dependent emission of a single photon, and when combined with coherent spin rotations, it allows entanglement generation between the spin state and the time bin of emitted photons15, see Fig. 2. First, a π/2-rotation pulse prepares the spin in a superposition state \((\left\vert \! \! \uparrow \! \right\rangle -\left\vert \! \! \downarrow \! \right\rangle )/\sqrt{2}\). A picosecond laser pulse then drives the cycling transition \(\left\vert \! \! \downarrow \! \right\rangle \to \left\vert \! \! \uparrow \! \downarrow \Uparrow \right\rangle\), see inset of Fig. 1, resulting in the single-photon emission in the early time bin. A spin π-rotation pulse subsequently swaps the \(\left\vert \! \! \uparrow \! \right\rangle\) and \(\left\vert \! \! \downarrow \! \right\rangle\) population and a second picosecond laser pulse potentially creates a photon in a later time bin. The last π-pulse swaps spin population again, resulting in the Bell state \((\left\vert e\downarrow \right\rangle -\left\vert l\uparrow \right\rangle )/\sqrt{2}\). By iterating this pulse sequence n − 1 times (apart from the first π/2-pulse), a GHZ state of n − 1 photonic qubits and one spin qubit \(\left\vert {\psi }_{{\rm{GHZ}}}\right\rangle=({\left\vert 0\right\rangle }^{\otimes n}-{\left\vert 1\right\rangle }^{\otimes n})/\sqrt{2}\) is generated, where we translate \(\left\vert \downarrow \right\rangle\)(\(\left\vert \uparrow \right\rangle\)) and early(late) emitted photon into the logical qubit \(\left\vert 0\right\rangle\)(\(\left\vert 1\right\rangle\)).

Fig. 2: Schematic diagram of time-bin GHZ state generation.
figure 2

a The experimental sequence consists of nuclear spin narrowing and spin initialization, which is then followed by the GHZ protocol with a series of π/2, π-pulses (blue) and single photon generations (red). The last part of the sequence (enclosed in the box) is repeated n − 1 times to generate an n qubit GHZ state. The duration of the full sequence is 1.8 μs. Nuclear spin narrowing consists of two overlapped 1.1 μs Raman pulse and a 1.2 μs pump pulse. The longer pump pulse optically drives the \(\left\vert \downarrow \right\rangle \to \left\vert \downarrow \uparrow \Downarrow \right\rangle\) transition and initializes the spin state to \(\left\vert \! \! \uparrow \! \right\rangle\) before the GHZ state generation. b Time bin interferometer (TBI) setup: A picosecond pulsed laser (blue) propagates through the long and short arm of TBI to excite a QD emitting a single photon in the early and late time bin, respectively. The single photon is collected through the same TBI but in the opposite direction. Each photonic qubit has three peaks in the output that are separated by 12 ns, which is determined by the path-length difference between the long and short arms of the TBI.

Full size image

Characterization of spin control after nuclear spin narrowing

Prior to running the entanglement protocol, we first characterize the quality of spin control by performing Ramsey spectroscopy and observing Rabi oscillations after nuclear spin narrowing. In the former, we initialize the electron spin in \(\left\vert \uparrow \right\rangle\) by optically pumping \(\left\vert \downarrow \right\rangle \to \left\vert \downarrow \uparrow \Downarrow \right\rangle\) and vary the time delay Td between two π/2-rotation pulses. The pulses are -200 MHz detuned from the spin transitions to reveal oscillations of the Ramsey decay with Td, see Fig. 3a. We model the Ramsey data assuming a Gaussian decay and find \({T}_{2}^{*}=\) 33(3) ns, which is one order of magnitude longer than the spin π-rotation pulse of Tp = 4 ns used in the GHZ generation sequence, thus enabling high rotation fidelity. In Fig. 3b, we drive the spin with a rotation pulse of varying duration Tp to observe Rabi oscillations between \(\left\vert \uparrow \right\rangle\) and \(\left\vert \downarrow \right\rangle\). We extract a spin Rabi frequency of Ωr = 2π ⋅ 123.6 MHz and a quality factor of Q = 34(2), i.e., Q quantifies the number of π-pulses before the oscillation visibility falls to 1/e. We estimate the π-rotation fidelity via \({F}_{\pi }=\frac{1}{2}(1+{e}^{-1/{\rm{Q}}}) \, \approx \, 98.6\%\)23. For comparison, the π-rotation fidelity error due to finite \({T}_{2}^{*}\) is \(2/{({\Omega }_{r}{T}_{2}^{*})}^{2}=0.3\%\)31, and we attribute the remaining fidelity error to laser-induced spin-flip processes15,23: \(\frac{1}{2}(1-{e}^{-\pi \tilde{\kappa }})\). The extracted normalized spin-flip rate is \(\tilde{\kappa }=\kappa /{\Omega }_{r}\approx 3\times 1{0}^{-3}\), which is an order of magnitude lower compared to the case of a hole spin15.

Fig. 3: Electron spin spectroscopy.
figure 3

a and b display Ramsey interference and Rabi oscillation data, respectively. We use the former data to extract a spin coherence time of \({T}_{2}^{*}=\) 33(3) ns, where we model the data by assuming inhomogeneous broadening with a Gaussian distribution. From the Rabi oscillation data, we extract a Q-factor of 34(2). c shows the Hahn-echo visibility as a function of the spacing between the center of π/2-pulses and the middle π-pulse. The solid black line is a model of the data by including the nuclear noise spectrum. The dashed-vertical line indicates the echo-pulse spacing used in the GHZ entanglement generation experiment.

Full size image

To shield the electron spin qubit against nuclear spin noise, the GHZ generation protocol exploits a built-in spin-echo sequence. We now discuss the spin-echo sequence and benchmarks of the spin coherence. The spin echo consists of three equally spaced π/2, π, and π/2-rotation pulses. We measure the spin echo visibility as a function of the spacing between the pulses. The fringe visibility at each spacing is extracted by altering the phase shift of the last π/2-pulse between 0 and π relative to the previous pulses. We observe a rapid decay of the visibility and a subsequent revival at Ts ≈29 ns, see Fig. 3c. The revival peak is located approximately at the inverse of the Larmor frequency of Indium nuclear spins at 4 T32. The optimal pulse delay corresponding to the peak is then adopted in the entanglement protocol. The maximum spin-echo visibility is 76%, which constitutes a 20% improvement over previous work15. This is an essential figure-of-merit contributing to fidelity of the multi-photon entanglement, as discussed later.

We model the data of Fig. 3(c) using the nuclear noise spectral density in InAs QDs as presented by Stockill et al.32. Very good agreement is reached where the observed coherence revival is reproduced. In the model, we consider the linearly coupled Overhauser field components along the quantization axis of the electron and only use the overall amplitude as a free parameter. We fit the data at Ts ≥ 3 ns, where the observed discrepancy between data and model at shorter time delays is attributed to interference between the driving pulses. Details of the theoretical model are presented in Supplementary Section VIII.B. The quantitative understanding of the spin-echo visibility is essential for pinpointing how to improve the spin-photon entanglement fidelity in future experiments.

We also perform an extended experiment with two additional π-pulses at the same spacing, i.e., a pulse sequence of π/2 - π - π - π - π/2, and find a maximum echo visibility of 65%. Compared to the 3-qubit GHZ generation protocol, this measurement is free from excitation errors associated with single-photon generation, the measured visibility therefore poses an upper bound on the three-qubit correlations along the equatorial plane of the Bloch sphere.

GHZ state generation and fidelity analysis

The GHZ state is generated and analyzed with the self-stabilized time-bin interferometer in Fig. 2b15. For the photonic qubit, the output consists of three peaks. The first (last) peak corresponds to early (late) emitted photons going through the short (long) arm and constitutes a measurement in the \(\left\vert 1\right\rangle\) (\(\left\vert 0\right\rangle\)) basis. The middle peak corresponds to the early photon going through the long arm and the late photon going through the short arm, corresponding to the \(\left\vert 0\right\rangle+{e}^{i\theta }\left\vert 1\right\rangle\) basis, where θ is readily controlled via a stack of waveplates and a polarizer15. By changing θ, the photonic qubit is measured on the equatorial basis of the Bloch sphere. Spin readout is performed by optically driving the cycling transition \(\left\vert \downarrow \right\rangle \to \left\vert \uparrow \downarrow \Uparrow \right\rangle\) with a 200 ns pulse. Since only photons are emitted when the spin state is \(\left\vert \downarrow \right\rangle\), an additional π-pulse is applied before the readout to measure \(\left\vert \uparrow \right\rangle\). Similarly, to measure the spin qubit on the equatorial plane, a π/2 pulse is performed instead.

The entanglement fidelity is decomposed as \({{\mathcal{F}}}_{{\rm{GHZ}}}={\rm{Tr}}\{{\rho }_{\exp }| {\psi }_{{\rm{GHZ}}}\rangle \langle {\psi }_{{\rm{GHZ}}}| \}={\rm{Tr}}\{{\rho }_{\exp }({\hat{{\mathcal{P}}}}_{z}+\hat{\chi })/2\}\)33, where \(\left\vert {\psi }_{{\rm{GHZ}}}\right\rangle\) is the ideal GHZ state and \({\rho }_{\exp }\) is the experimentally measured density matrix. \({\hat{{\mathcal{P}}}}_{z}=\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n}+\left\vert 1\right\rangle {\left\langle 1\right\vert }^{\otimes n}\) projects all qubits on the z-basis and \(\hat{\chi }=\left\vert 0\right\rangle {\left\langle 1\right\vert }^{\otimes n}+\left\vert 1\right\rangle {\left\langle 0\right\vert }^{\otimes n}=\frac{1}{n}{\sum }_{k}{(-1)}^{k}{\hat{{\mathcal{M}}}}_{k}\) is composed of \({\hat{{\mathcal{M}}}}_{k}\) operators that are equally spread along the x-y plane of the Bloch sphere, see Fig. 4c. The measurement of each operator proceeds from three-photon coincidences between two photonic qubits and a photon from the spin readout in their respective bases. The normalized three-fold coincidences in each basis are shown in Fig. 4a–b. From here the state fidelity is found to be \({{\mathcal{F}}}_{{\rm{GHZ}}}=56(2)\)%, where \(\langle {\hat{{\mathcal{P}}}}_{z}\rangle\) and \(\langle {\hat{{\mathcal{M}}}}_{1,2,3}\rangle\) are 76(2)% and  −40(5)%, 35(4)%,  −33(4)%, respectively. In the present experiment, the 3-qubit generation rate is estimated to be \({R}_{{\rm{GHZ}}}={\eta }_{p}^{2}{R}_{\exp }\simeq\) 70 kHz, with the experimental repetition rate of \({R}_{\exp }=\) 560 kHz. The photon efficiency ηp includes less-than-π optical excitation (80% due to 0.7π excitation pulse), emission into the zero-phonon line (95%)34, the two-sided waveguide geometry (50%), and waveguide coupling efficiency (β ≈ 90%)35. Additional off-chip loss of the entanglement characterization setup constitutes  ≈ 14 dB (see Sec. XI of Supplementary Material). Immediate optimization opportunities include operating on a single-sided waveguide28 and increasing the operation speed to \({R}_{\exp }=\) 1 MHz with a reduced nuclear spin narrowing duty cycle, whereby RGHZ = 0.5 MHz is immediately reachable. For subsequent applications of the entanglement source, high-efficiency outcoupling strategies from the chip to the optical fiber can be readily implemented28.

Fig. 4: Fidelity measurement of 3-qubit GHZ state and single-photon characterization.
figure 4

a Illustration of the measurement basis on the Bloch sphere. b, c Histogram of fidelity measurement in the z-basis and x, y-basis, respectively. In c, \(\left\vert+\right\rangle\) and \(\left\vert -\right\rangle\) are eigenstates of the operator \({\hat{{\mathcal{M}}}}_{i}\). The acquisition time for each operator is  ~2 h. The shaded bars in (a–c) indicate the ideal cases. d Measurement of HOM visibility and single-photon purity at different excitation powers (normalized to the π-pulse power). Single-photon indistinguishability Vs is extracted from the y-intercept of the linear extrapolation. g(2)(0) is measured in the first and third time bins whereas VHOM is measured in the second time bin, see main text. The error bars represent one standard deviation.

Full size image

As a complementary entanglement characterization, we also measure biseparability of the generated state, whereby violation of the following inequality implies genuine three-qubit entanglement: \(| \chi | \le \sqrt{{\rho }_{001}{\rho }_{110}}+\sqrt{{\rho }_{110}{\rho }_{001}}+\sqrt{{\rho }_{101}{\rho }_{010}}\)36. For our experiment, the left and right hand side of the inequality equates to \(\langle \hat{\chi }\rangle=35.8(2.5)\%\) and 9.6(1.1)%, respectively. The inequality is violated by 10 standard deviations, providing a clear demonstration of genuine 3-particle entanglement.

Fidelity error contribution and future outlook

To unravel experimental imperfections, we have performed detailed Monte-Carlo simulations including all relevant physical errors, see Supplementary Sections VIII and IX for full details. For the 3-qubit GHZ state, we predict \({{\mathcal{F}}}_{{\rm{GHZ}}}^{{\rm{sim}}}=57.1(8)\%\), which is in very good agreement with the recorded experimental value. Table 1 lists the three main sources of fidelity error. The largest contribution originates from optical excitation of the unwanted cycling transition \(\left\vert \uparrow \right\rangle \to \left\vert \downarrow \uparrow \Downarrow \right\rangle\), since the two cycling transitions (the diagonal transitions in Fig. 1) are only frequency split by Δ = 10 GHz, which is similar to the excitation laser bandwidth (12.5 GHz). To minimize off-resonant excitation, we excite via an optical 0.7 π pulse at a frequency 2 GHz red-detuned from the targeted cycling transition \(\left\vert \downarrow \right\rangle \to \left\vert \uparrow \downarrow \Uparrow \right\rangle\). For future experiments, this excitation error could be almost entirely mitigated by orienting the waveguide in the orthogonal direction so that the vertical transitions become cycling.

Table 1 Fidelity error contribution of the three primary simulated errors
Full size table

The second largest error contribution is the high-frequency nuclear spin noise that was responsible for the reduced spin-echo visibility in Fig. 3c, which then manifests as fidelity error in the entanglement protocol. The noise spectrum is strain dispersion dependent and therefore will constitute a fundamental limit for strain-induced grown QDs (Stranski-Krastanov method) such as InAs QDs in GaAs, but droplet-epitaxy GaAs QDs have proven to be significantly less noisy37. Finally, the third main contribution stems from rotation errors due to laser-induced spin flips. A lower rotation error has been observed in a GaAs QD device37 and the lack of a blocking barrier in these devices suggests a similar design to mitigate laser-induced spin flips in InAs QDs.

In future experiments, we can readily eliminate the first and the most dominant error source by rotating the PCW by 90∘, leading to a Purcell-enhanced y-dipole, see Fig. 1 inset. In this configuration, the two transitions with the highest energy difference are cycling transitions with a frequency splitting of  ≈30 GHz. Consequently, this would allow generating 3 and 4-qubit GHZ states with fidelity of 67% and 58%, respectively (See Sec. VIII of Supplementary Material). Improving beyond this would require reducing the two latter errors. To this end, GaAs QDs have proven to be a highly promising platform. From the numerical simulations, we predict 8.8(1)% fidelity error per photon for GaAs QDs, meaning that GHZ strings of 8 qubits should be attainable, where we have used the QD parameters reported in ref. 37. Figure 5 summarizes the experimental and simulated findings of the GHZ state fidelity for the various experimental situations.

Fig. 5: Summary of experimental results and outlook for future experiments.
figure 5

Results of three Monte Carlo simulations (SIM): with the current splitting between cycling transitions Δ = 2π  ⋅ 10 GHz, with the expected modification of a larger Δ = 2π  ⋅ 30 GHz corresponding to properly oriented waveguides relative to the dipole axes, and with GaAs QD where the effect of nuclear spin noise is negligible and we assume Δ = 2π  ⋅ 30 GHz and a π spin rotation fidelity improved by a factor of 237. For all parameters, we run Monte Carlo simulation (104 realizations) from 2 to 4 qubits, while the fidelity of higher qubit numbers is extrapolated with an exponential fit. For GaAs QD, Nmax is the predicted maximum attainable number of entangled qubits from the fit, given that \({{\mathcal{F}}}_{{\rm{GHZ}}}\) is one standard deviation above 50%. The minor deviation between measurement and simulation is likely due to an overestimation of the nuclear spin noise and an underestimation of other experimental errors, e.g., an imperfect excitation laser polarization.

Full size image

Single-photon purity and indistinguishability measurements

Finally, to characterize the quality of emitted photons, we perform Hanbury-Brown-Twiss (HBT) and Hong-Ou-Mandel (HOM) interferometry to measure single-photon purity and indistinguishability, respectively29. Here we use a different experimental sequence where we initialize the spin in \(\left\vert \downarrow \right\rangle\) with a π-rotation pulse, and excite the QD twice with the pulsed laser. The pair of emitted photons propagate through TBI and arrive at two detectors in the early, middle and late time bins, which align to the three peaks in Fig. 2(b). For HBT, we look at two-detector coincidences in the early or late time bin. We extract g(2)(0) from the ratio between coincidence counts occurring in the same experimental cycle and two consecutive cycles. For HOM, we extract the HOM visibility VHOM by recording two-detector coincidence counts in the middle bin, normalized to coincidences between the middle bin in one detector and early or late time bin in the other detector. We measure both VHOM and g(2)(0) for a range of excitation powers, see Fig. 4(d).

Setups

Nmax

Fidelity error per photon

Measurement

3 (\({{\mathcal{F}}}_{{\rm{GHZ}}}\) = 56(2)%)

27(3)%

SIM: Δ = 10 GHz

3 (\({{\mathcal{F}}}_{{\rm{GHZ}}}\) = 57.1(8)%)

17(2)%

SIM: Δ = 30 GHz

4 (\({{\mathcal{F}}}_{{\rm{GHZ}}}\) = 58.0(8)%)

15(1)%

SIM: GaAs QD

8 (\({{\mathcal{F}}}_{{\rm{GHZ}}}\) = 51.6(4)%)

8.8(1)%

The intrinsic single-photon indistinguishability Vs would be measured in HOM interferometry if the multi-photon contribution and laser leakage were negligible, i.e., g(2)(0) = 0. We observe a close to linear relationship between Vs and g(2)(0). Using linear regression, i.e., VHOM = Vs − F ⋅ g(2)(0)38, we obtain F = 2.0(3) and Vs = 97(2)% after averaging over the data acquired at the first and last time bins. While F = 2 has been widely used in the literature39,40, the relationship between g(2)(0) and Vs can be more complicated where F varies between 1 and 3, depending on the origin of the multi-photon contribution41. F ≈ 2 indicates that the recorded VHOM is primarily limited by distinguishable multi-photon component, which could potentially be removed at the cost of lower brightness, e.g., by time gating. To reduce laser leakage, we perform additional frequency filtering using a pair of etalon filters (with a full width at half maximum of 3 GHz) before the TBI. We note the indistinguishability has a lower bound of 92(1)% when F = 1. The high degree of indistinguishable photons means that the demonstrated entanglement source is readily applicable for realizing photon fusion, which is the essential operation enabling photonic quantum computing6.

Discussion

We have presented a direct demonstration of the on-demand generation of a genuine three-qubit entangled state using a QD spin-photon interface. This realizes a foundational building block for scalable photonic quantum-information processing towards photonic quantum computers6 or one-way quantum repeaters42. The full account of entanglement infidelities is laid out, which is essential for further improvements of the approach in future experiments.

The InAs QD platform is predicted to be scalable to strings of 4 entangled qubits (Fig. 5), which suffices for implementing small-scale measurement-based quantum algorithms. Importantly, the high degree of indistinguishability means that such a source can be used to fuse much larger entangled states by de-multiplexing the photons43 and subsequently interfering them in, e.g., an integrated photonic circuit. Interestingly, the current limitation to fidelity can be overcome with a straightforward correction of the device orientation, thanks to a larger splitting between two cycling transitions Δ. We expect the next iteration of the experiment to go to 3 photons and 1 spin, limited by the rotation fidelity error and nuclear spin noise. Longer strings of entangled photons may be realized with strain-free GaAs droplet-epitaxy QDs, where the π-spin rotation error is halved and the high-frequency nuclear noise with a narrower spectrum can be effectively filtered37. Such deterministic entanglement sources relying on spin-photon interfaces may offer fundamentally new opportunities for resource-efficient photonic quantum computing architectures8,9.