Fully nonlinear neuromorphic computing with linear wave scattering

Abstract

The increasing size of neural networks for deep learning applications and their energy consumption create a need for alternative neuromorphic approaches, for example, using optics. Current proposals and implementations rely on physical nonlinearities or optoelectronic conversion to realize the required nonlinear activation function. However, there are considerable challenges with these approaches related to power levels, control, energy efficiency and delays. Here we present a scheme for a neuromorphic system that relies on linear wave scattering and yet achieves nonlinear processing with high expressivity. The key idea is to encode the input in physical parameters that affect the scattering processes. Moreover, we show that gradients needed for training can be directly measured in scattering experiments. We propose an implementation using integrated photonics based on racetrack resonators, which achieves high connectivity with a minimal number of waveguide crossings. Our work introduces an easily implementable approach to neuromorphic computing that can be widely applied in existing state-of-the-art scalable platforms, such as optics, microwave and electrical circuits.

Main

The explosive growth in neural network size has led to an exponential increase in energy consumption and training costs. This has created a need for more efficient alternatives, sparking the rapidly developing field of neuromorphic computing¹, relying on physical artificial neurons.

Neural networks connect neurons through linear maps and nonlinear activation functions. So far, neuromorphic devices have realized linear maps via linear dynamics and employed physical nonlinearities or approaches like optoelectronic conversion for nonlinear activation function. Among the many neuromorphic platforms^2,3,4,5, optical systems^2,3,6 are one of the most promising contenders implementing the linear aspects in a highly parallel and scalable manner at broad bandwidth. Furthermore, linear computations can be performed passively^7,8 with exceedingly small propagation losses, making these devices potentially very energy efficient. Linear optical networks (in free space or integrated photonics) for matrix–vector multiplication have already become the basis of commercial chips⁹.

On the other hand, physical nonlinearities are still hard to implement, incurring substantial hardware overhead, fabrication challenges and other possibly demanding requirements^10,11,12 such as high laser powers when using nonlinear optics. An alternative approach bypasses these challenges by applying nonlinearities optoelectronically^13,14,15,16. However, such devices require more components, are less energy efficient and may suffer from delays.

Moreover, efficient physics-based training in the presence of nonlinearities is an open challenge, although some conceptual progress has been made, especially in the form of equilibrium propagation^17,18,19 and Hamiltonianecho backpropagation²⁰ as general approaches. These complement strategies for specific types of nonlinearity^6,21,22,23 or approaches^13,15 performing physical backpropagation on the linear components. In contrast, feedback-based parameter shifting^9,24 scales unfavourably with network size²⁵. Recent hybrid approaches combine simulation and physical inference²⁶, requiring a suitable model.

Here we propose an approach for a fully nonlinear neuromorphic system that is only based on linear scattering, thereby bypassing all of the challenges associated with realizing and training physical nonlinearities. The key idea lies in encoding the neural network input in the system parameters (Fig. 1a): although there is a linear relation between a probe signal and the response via the scattering matrix, that matrix itself depends nonlinearly on those parameters. Remarkably, this nonlinear dependence enables us to implement a fully functional neural network capable of performing the same tasks as standard artificial neural networks (ANNs) (Supplementary Section XI provides a conceptual comparison versus standard machine learning methods). As a major advantage, gradients needed for updating other, learnable system parameters during training can be directly measured in scattering experiments without the need to have complete knowledge or control of the system. We simulate and train our approach on handwritten digit recognition as well as on the Fashion-MNIST dataset, achieving classification accuracies that clearly surpass the results of a linear classifier and are comparable with the accuracies obtained by standard ANNs.

Fig. 1: Fully nonlinear neuromorphic system with linear wave propagation.

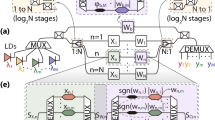
a, Input to the linear, neuromorphic system is encoded in some of the tunable system parameters, whereas the output is determined through the scattering response to a probe signal. Other controllable parameters serve as learnable parameters. b, Example for an implementation using wave propagation through a network of coupled modes (for example, optical resonators). Here detunings Δ_j of some of the optical modes are utilized as input x, whereas other detunings and coupling constants J_j between the modes are learnable parameters θ. The output is a suitable set of scattering matrix elements (equations (3) and (4)), which we obtain by comparing the response to the probe field (equation (2)). c,d, Due to the linearity of these systems, we have access to the gradients with respect to the system parameters required for training. The gradients are given by the products of the scattering matrix elements (equations (7) and (8)). In particular, the derivative with respect to detuning Δ_ℓ involves products S_ℓ,pS_r,ℓ (the scattering responses between probe site p, site ℓ and response site r) (c) and the derivative with respect to couplings J_ℓ,ℓ′ only depends on S_ℓ,pS_r,ℓ′ and S_ℓ′,pS_r,ℓ (for clarity, the latter is not shown) (d).

Our proposal can be readily implemented with existing state-of-the-art scalable platforms, for example, in photonics^7,8,27. Concretely, we propose an implementation with optical racetrack resonators in an architecture allowing for a densely connected network at a minimal number of waveguide crossings.

Our results are very general and are applicable to any type of linear system. For instance, in analogue electrical circuits²⁸, the scattering matrix is replaced by the impedance matrix²⁹, and tunable resistances, capacitors or inductances can serve as the input.

Nonlinear neuromorphic computing with linear scattering

Concept

Waves propagating through a linear system establish a linear relation between the probe signals and response signals via the scattering matrix S(ω, x, θ) at a given frequency ω. This matrix explicitly depends on the system parameters. We choose to subdivide those into x, representing the input vector to the neuromorphic system, and θ, the set of training parameters.

Concretely, the system could consist of a number of coupled modes (for example, optical resonators), which we call neuron modes. The mode-field amplitudes evolve under linear evolution equations^30,31, which, in the frequency domain, read as follows (Methods):

$$-{{{\rm{i}}}}\omega {{{\bf{a}}}}(\omega )=-{{{\rm{i}}}}H({{{\bf{x}}}},\theta ){{{\bf{a}}}}(\omega )-\sqrt{\kappa }\,{{{{\bf{a}}}}}_{{{{\rm{probe}}}}}(\omega ).$$

(1)

Here we collected the field amplitudes of the neuron modes in the vector a(ω) ≡ (a₁(ω)…a_N(ω))^T, and H denotes the dynamical matrix describing the interaction between modes (Methods). For full generality, we also assumed that every mode is coupled to a probe waveguide at rate κ_j and driven by an incoming amplitude a_probe,j(ω), although we later specialize to scenarios in which only some modes will be probed. For brevity, κ collects κ_j in a diagonal matrix.

The neuron-mode fields and probe fields are connected to the outgoing response fields a_j,res(ω) via the input–output relation^30,31 ${a}_{j,{{{\rm{res}}}}}(\omega )={a}_{j,{{{\rm{probe}}}}}(\omega )+\sqrt{{\kappa }_{j}}{a}_{j}(\omega )$. Inserting the solution for a_j(ω) from equation (1) yields the scattering matrix as

$${{{{\bf{a}}}}}_{{{{\rm{res}}}}}(\omega )=S(\omega ,{{{\bf{x}}}},\theta ){{{{\bf{a}}}}}_{{{{\rm{probe}}}}}(\omega )$$

(2)

with

$$\begin{array}{rcl}S(\omega ,{{{\bf{x}}}},\theta )&=&{\mathbb{1}}-{{{\rm{i}}}}\sqrt{\kappa }G(\omega ,{{{\bf{x}}}},\theta )\sqrt{\kappa }\\ &=&{\mathbb{1}}-{{{\rm{i}}}}\sqrt{\kappa }{[\omega {\mathbb{1}}-H({{{\bf{x}}}},\theta )]}^{-1}\sqrt{\kappa }.\end{array}$$

(3)

Here $G(\omega ,{{{\bf{x}}}},\theta )\equiv -{{{\rm{i}}}}{(\omega {\mathbb{1}}-H(\omega ,{{{\bf{x}}}},\theta ))}^{-1}$ is the system’s Green function.

Equation (3) reveals the general idea behind our concept. Although the relation between the probe and response is linear (equation (2)), the scattering matrix S(ω, x, θ) (equation (3)) is a nonlinear function of the system parameters. Hence, we are now able to represent learnable nonlinear functions of the input x. In a wider sense, producing a neuromorphic system by parametrically encoding the input into a linear scattering system can be viewed as one application of what has been recently termed as structural nonlinearity³².

The network’s output is a suitable set of scattering matrix elements S_j,ℓ, which are measured as a ratio between the response and probe signals. Since S_j,ℓ is generally complex, one can consider an arbitrary quadrature as the output:

$${y}_{r}={{{\rm{Re}}}}\,({\rm{e}}^{{{{\rm{i}}}}\phi }{S}_{r,p}),$$

(4)

with a suitable set of p and r and convenient ϕ. Here p refers to a probe site and r refers to a site at which the response is recorded (the term ‘site’ denotes the neuron mode). The number of response sites r equals the output dimension N_out. In practice, the quadrature can be measured through homodyne detection. There are two obvious, convenient choices for p and r. (1) The probe site p is fixed and we consider different sites r for recording the system response. This allows to infer the output vector of the neuromorphic system with a single measurement. (2) We set p = r. This requires N_out measurements to infer the output, but we found that the training converges more reliably.

Input replication for improved nonlinear expressivity

The nonlinearity of the scattering matrix (equation (3)) as a function of x stems from the matrix inverse, representing a specific type of nonlinearity. For instance, considering a scalar input x, any element S_j,ℓ is of the form (ax + b)/(cx + d), where a, b, c and d are some quantities depending on other system parameters. This nonlinearity stems from waves propagating back and forth between the modes and the scattering matrix (equation (3)) is a result of the interference between all the waves. We see this by expressing the matrix inverse of $M=\omega {\mathbb{1}}-H({{{\bf{x}}}},\theta )$ (equation (3)) via the adjugate ${({M}^{-1})}_{j,\ell }={(-1)}^{j+\ell }\frac{\det {M}^{\;(j,\ell )}}{\det M}$, where M^(j, ℓ) denotes the matrix in which the jth row and ℓth column are omitted. Applying the Laplace expansion, it is straightforward to see that both detM^(j,ℓ) and detM linearly depend on any matrix entry M_m,n; therefore, both denominator and numerator in the previous expression depend linearly on x.

Note, however, that the matrix determinant of detM (similarly detM^(j,ℓ)) contains terms such as M_1,1M_2,2M_3,3… and M_1,1M_2,3M_3,2…. This allows us to overcome the seeming limitation in expressivity (as explained above, the nonlinearity provided by the scattering matrix only leads to rational functions with both numerator and denominator linearly depending on x), namely, by letting the input value x explicitly enter in more than one system parameter. In this way, it is possible to show that one can represent general nonlinear functions via the scattering matrix, in which the number of input replications R (that is, R denotes the number of times the input enters) determines how well the target function can be approximated. Letting R→∞, the approximation approaches the target function. We prove this in Supplementary Section I for one-dimensional inputs.

Most applications of machine learning, however, operate on high-dimensional input spaces. In this case, the situation becomes even more favourable: even without replication, correlations between different elements of the input vector appear, that is, the scattering matrix automatically includes terms such as x₁x₂x₃…. Therefore, in practice, it can be sufficient to keep R low. We will show later that for a digit recognition task (Fig. 2), it was sufficient to let the input only enter twice, that is, R = 2.

Fig. 2: Digit recognition using a scattering neuromorphic system with a layered structure.

a, Scattering network used for digit recognition consisting of two or three fully connected layers with N₁ = 128, N₃ = 10 and either without a hidden layer or with N₂ ∈ {20, 30, 60, 80}. We consider equal decay rates κ, set the intrinsic decay to zero (κ′ = 0) at the probe sites and start from J/κ = 2 with an added random disorder. The input consisting of 64 grey-scale pixel values is encoded in the detuning of the first layer to which we initially add a trainable offset. A vector of pixel values serves as the input. We choose to detune the background to x_j = 5κ and make the foreground—the numerals—resonant, that is, x_j = 0. The inset illustrates the nonlinear effect of the first layer, showing the real and imaginary parts of ${[{{{{\mathcal{G}}}}}_{1}(0)]}_{j,\;j}$ (equation (13)). The response to a probe signal at the third layer constitutes the output vector. The index ℓ of maximal y_ℓ = ImS_ℓ,ℓ constitutes the class. b, Evolution of the test accuracy during training for different architectures (left, early times; right, full training): without the hidden layer or with N₂ = {20, 30, 60, 80}. We compare this with a linear classifier, ANN and CNN. During one epoch, each image in the training set is shown to the network once in mini-batches of 200 randomly chosen images; the shown test accuracy is evaluated on the entire test set. Increasing the size of the hidden layer improves both convergence speed and best accuracy. c, Confusion matrix corresponding to the best result with N₂ = 80 after 2,922 epochs. d, Convergence and training progress for selected input pictures. One iteration corresponds to one mini-batch. The scattering matrix element with the largest imaginary part indicates the class. In most cases, the training rapidly converges towards the correct classification results. Digits with a similar appearance, however, are frequently mistaken for the other, such as the digits 4 and 9, and only converge relatively late during training.

Source data

Training

We will now show one particularly useful consequence of working with a steady-state linear scattering system: it is possible to perform gradient descent based on physically measurable gradients, which is rare in neuromorphic systems. Specifically, gradients with respect to θ are directly measurable as products of scattering matrix elements.

The aim of the training is to minimize a cost function ${{{\mathcal{C}}}}$, for example, the square distance between target output y_tar and system output y (equation (4)): ${{{\mathcal{C}}}}=| {{{{\bf{y}}}}}_{{{{\rm{tar}}}}}-{{{\bf{y}}}}{| }^{2}$. Its gradient is

$$\frac{\partial {{{\mathcal{C}}}}}{\partial {\theta }_{j}}={\nabla }_{y}{{{\mathcal{C}}}}\cdot \left(\frac{\partial {{{\bf{y}}}}}{\partial {\theta }_{j}}\right),$$

(5)

where y is linear in S via equation (4) and the error signal ${\nabla }_{y}{{{\mathcal{C}}}}=2({{{\bf{y}}}}-{{{{\bf{y}}}}}_{{{{\rm{tar}}}}})$. Given the mathematical structure of the scattering matrix (equation (3)), we obtain a simple formula for its derivative (Supplementary Section II):

$$\frac{\partial {S}_{r,p}}{\partial {\theta }_{j}}={{{\rm{i}}}}\sqrt{{\kappa }_{p}{\kappa }_{r}}{\left(G\frac{\partial H}{\partial {\theta }_{j}}G\right)}_{r,p},$$

(6)

where $G={\sqrt{\kappa }}^{-1}(S-{\mathbb{1}}){\sqrt{\kappa }}^{-1}$ is the Green’s function (3). Since ∂H/∂θ_j is local, gradients can be obtained from scattering experiments as a combination of scattering matrix elements. Therefore, gradients can be physically extracted, allowing for very efficient training.

Implementation based on coupled modes

To make the previous considerations more concrete, we consider a system of coupled resonant modes, for example, in the microwave or optical regime, or in electrical circuits, but we stress that the concept is general and applicable to a variety of platforms. These modes (Fig. 1b) reside at frequencies ω_j with detunings Δ_j ≡ ω_j − ω₀ from some suitable reference ω₀, and with intrinsic decay at rate ${\kappa }_{j}^{{\prime} }$. The modes can, in full generality, be coupled via any form of bilinear coherent interactions, such as beamsplitter interactions (tunnel coupling of modes), single-mode or two-mode squeezing, or via linear engineered dissipators. For simplicity, we will focus on beamsplitter couplings at strengths J_j,ℓ between resonators j and ℓ (Fig. 1b). Furthermore, a probe a_j,probe is injected via a waveguide coupled to the mode at rate κ_j, inducing additional losses. This implies that the dynamical matrix H(x, θ) has entries H_j,ℓ = J_j,ℓ for j ≠ ℓ and ${H}_{j,\;j}=-{{{\rm{i}}}}\frac{{\kappa }_{j}+{\kappa }_{j}^{{\prime} }}{2}+{\varDelta }_{j}$. The detunings of some of the neuron modes serve as input x, whereas other tunable parameters, such as detunings and coupling strengths, are learnable parameters θ. We obtain the network’s output (equation (4)) by performing a suitable homodyne measurement on the responses a_j,res. Importantly, not all of the system parameters need to be tunable.

Coming back to training, we can now more explicitly present the gradients of the scattering matrix. Recalling that H depends linearly on the detunings Δ_j and the couplings J_j,ℓ, we can compute the derivative of the scattering matrix according to equation (6) (Supplementary Section III). The derivative with respect to detuning at the jth site is given by the scattering path from the probe site r to site j, and from j to the response site r (Fig. 1c):

$$\frac{\partial {S}_{r,p}}{\partial {\varDelta }_{j}}={{{\rm{i}}}}\sqrt{{\kappa }_{p}{\kappa }_{r}}\,{G}_{j,p}{G}_{r,\;j},$$

(7)

where ${G}_{m,n}=({S}_{m,n}-{\delta }_{m,n})/\sqrt{{\kappa }_{m}{\kappa }_{n}}$ is the Green’s function. Similarly, the derivative with respect to the coupling between the jth and ℓth site is (Fig. 1d)

$$\frac{\partial {S}_{r,p}}{\partial {J}_{j,\ell }}={{{\rm{i}}}}\sqrt{{\kappa }_{p}{\kappa }_{r}}({G}_{j,p}{G}_{r,\ell }+{G}_{\ell ,p}{G}_{r,\;j}).$$

(8)

This training procedure works even when arbitrary non-tunable linear components are added to the setup, and these need not be characterized but can be treated as a black box. Gradients can be efficiently measured, requiring only N_out measurements. These measurements record the full scattering response to a probe at any of the sites p, so the network can be evaluated (inference) at the same time as obtaining the gradients. During training, gradients can either be applied directly or be post-processed to average over mini-batches or to perform an adaptive gradient descent.

Although we focus on photonic systems in the following, our results are very general and apply to any type of linear system. For instance, for electrical circuits, the scattering matrix is replaced by the impedance matrix²⁹ obtained from the circuit’s Green’s function and tunable resistances can serve as an input of the network (Supplementary Section X).

Test case: digit recognition

To benchmark our model, we train a network with three layers (Fig. 2a) on a dataset³³ with 8 × 8 images of handwritten digits. The input x is encoded in the first layer; each x_j is replicated into the detunings of pairs of modes (R = 2) and trainable offsets of alternating signs are added (Methods). We found that beyond improving the expressivity as explained above, this also leads to faster convergence during training. The system output is taken to be y_ℓ ≡ ImS_ℓ,ℓ(ω = 0, x, θ) at the last layer. We train both detunings and coupling rates with a categorical cross-entropy cost function and one-hot encoding in the ten output neuron modes. In Methods, we derive a recursive analytic formula for the scattering matrix of a layered system, which reveals a mathematical structure similar to an ANN (Methods and Extended Data Fig. 1) and which we conveniently use in our simulations to facilitate faster training.

Both convergence speed and maximal test accuracy depend on the size N₂ of the second layer (which we call the hidden layer; Fig. 2b). Above N₂ ≥ N_opt, the system possesses the maximal number of independent training parameters at given input dimension D and replication R (Methods and Supplementary Section V). For this dataset, N_opt = 70. We obtained the best accuracy of 97.1% for the system with N₂ = 80 after 2,922 epochs using a straightforward gradient descent (Methods). We show the best-case confusion matrix in Fig. 2c. Adam optimization can sometimes improve the convergence speed (Fig. 2d). The obtained accuracy is clearly beyond the 92.3% test accuracy of a linear classifier with the same number of parameters (obtained with an input layer of 64 neurons, a hidden layer of 150 neurons and an output layer of 10 neurons) and on par with the 97.0% test accuracy achieved by a standard ANN with the same architecture and sigmoid activation functions, as well as the accuracy of 96.7% achieved by a convolutional neural network (CNN) (Methods). The convergence speed of our neuromorphic system is comparable with that of the ANN (Fig. 2b), although this depends on the chosen learning rates.

For the more challenging classification task on Fashion-MNIST, see Methods and Extended Data Fig. 2.

Proposed optical implementation

Racetrack resonator architecture

Any experimental realization of our proposal requires (1) a sufficiently large number of tunable system parameters and (2) high connectivity. A simple geometry could consist of localized resonators connected by waveguides. However, we found an integrated photonics design offering better tunability and connectivity. It is based on racetrack resonators as neuron modes connected either via tunable couplings^34,35 or via additional resonators placed at the intersections (Fig. 3a). In the latter case, the effective coupling strengths can be controlled via the detuning of the coupling resonators (Supplementary Information).

Fig. 3: Implementation with racetrack resonators.

a, Neuron modes are represented by racetrack resonators (light blue); racetrack resonators of different layers in the neural network are crossed, employing techniques to reduce the cross-talk between them. They can either be coupled via tunable couplings, or smaller racetrack resonators with tunable detunings (dark blue)—the coupler modes—which change the effective coupling as the detuning is varied. This is illustrated in the ersatz image (right). b, The advantage of this design is that the system can be scaled up and requires only a minimal number of waveguide crossings; the neuron modes can still be accessed with waveguides from the outside. c, Two possibilities to measure the gradients: following the expression for the gradient in terms of the scattering matrix elements, one can either measure the response at the racetrack resonators and use equation (8) or, if coupling modes are used, directly at the coupling resonators and use equation (7) to update the parameters. As an alternative to coupling waveguides to each resonator, optical grating tap monitors can be utilized that light up according to the output signal at the resonator, which can be recorded by a camera^15,50. Grating tap monitors can be complemented by integrated photodetectors for a faster readout. To be sensitive to a specific quadrature (equation (4)), the light coupled to the grating tap monitor can be combined with light from a local oscillator (not shown) to perform a homodyne measurement. d, Scale of the relevant frequencies in an optical implementation. e, Distribution of neuron-mode detunings and tunable couplings after training.

Source data

To achieve high connectivity, we propose crossing the resonators of different network layers (Fig. 3b) using techniques for cross-talk reduction^36,37. As a special feature of our proposed design, the neuron modes are spatially extended, whereas the coupling is local. The device layout (Fig. 3c) can be seen as a visualization of the coupling matrix between the layers. This layout could also be applied in other optical neuromorphic systems to achieve high connectivity at a minimal number of waveguide crossings.

Following our procedure to measure gradients based on the scattering matrix (equations (7) and (8)), there are two options (Fig. 3c): (1) one only measures at the neuron modes to obtain gradients with respect to their detunings, (equation (7)) and uses equation (8) to infer the gradients for the tunable couplings or coupler modes; (2) if the couplings are tuned via coupler modes, one can infer the gradient with respect to the coupler detunings from the measurements at the neuron modes, or additionally measure at the coupler modes to directly obtain gradients with respect to their detunings. To reduce the number of waveguides, one can couple the grating tap monitors to each resonator, which can be monitored either with a camera¹⁵ or integrated photodetectors for a faster readout. To detect a specific quadrature (4), one can perform a homodyne measurement on the emerging light.

Here we focus on the design with tunable couplings since it allows to work with smaller tuning ranges (Supplementary Information). Figure 3e shows the distribution of neuron-mode detunings Δ and tunable couplings J after training a system with N₂ = 80. The detunings spread over a range of approximately ∣Δ∣/κ ≈ 6 and the couplings over a range of J/κ ≈ 2, which is well within the experimental capabilities^34,35,38 (Fig. 3d).

One advantage of our proposed photonic implementation is that gradients can be locally extracted as described above. In principle, analogous expressions to equation (6) also apply to free-space experiment; however, in practice, measuring the scattering response at the position of the optical element introducing the training parameters may be difficult.

Experimental requirements

The approach proposed here relies on the efficient tunability of a linear system, both for input encoding and for learning. During training (or device calibration), the detuning range needs to be sufficiently large to overcome any fabrication disorder. Figure 3d shows the relevant frequency scales. In optical systems, disorder in the resonance frequencies typically amounts to about 1% of the free spectral range, and this can easily be overcome via electrical thermo-optic tuners that have shown^39,40 tuning by a full free spectral range in resonators of the scale considered here (10–100 μm; Fig. 3e) operating on timescales⁴⁰ of 10 μs. For input encoding, it is desirable to have faster responses, but conversely, the tuning range can be much smaller, on the order of the couplings or decay rates. Electro-optic tuning^41,42 has demonstrated tuning by many linewidths at speeds of tens of megahertz for microtoroids⁴³ and tens of gigahertz for photonic-crystal resonators⁴⁴ and³⁸ racetrack resonators. Designs for racetrack resonators with tuning ranges up to hundreds of gigahertz⁴⁵ were proposed, which would be sufficient to compensate for initial frequency disorder. By omitting coupler modes, tuning the couplings between racetrack resonators³⁵ has been demonstrated at multiples of the linewidth³⁴. One can expect tuning speeds of multiple gigahertz^38,46, which, with further optimization, could reach 100 GHz (ref. ⁴⁷), allowing for fast training and inference. Assuming a 5 GHz modulation frequency, one could complete all the tuning steps of one epoch in 0.8 μs and an entire training run over 5,000 epochs (Fig. 2b) in only 3.8 ms. Supplementary Information discusses further aspects of scalability.

Conclusions

We introduced a concept for neuromorphic computing relying purely on linear wave scattering and not requiring any physical nonlinearities. As an additional advantage, gradients needed for training can be directly measured. Our proposal can be implemented in state-of-the-art integrated photonic circuits in which high tuning speeds enable rapid processing and training.

In future work, we propose to explore different architectures and the possibility of employing Floquet schemes for input replication or the use of multiple modes of the same cavity to reduce the hardware overhead (Supplementary Section VIII). Furthermore, the framework developed here is very general and applies to a range of settings beyond optics, for instance, analogue electronic circuits (Supplementary Section X). Therefore, our work opens up new possibilities for neuromorphic devices with physical backpropagation over a broad range of platforms.

During the completion of our manuscript, two related works appeared as preprints^48,49. In contrast to these works, our approach is based on the steady-state scattering response and it allowed us to formulate a simple technique for physically extracting gradients.

Methods

Further details about coupled mode theory and the scattering matrix

In the main text, we consider systems of coupled neuron modes, such as resonator modes. In general, the evolution equations for the complex field amplitudes a_j(t) of these modes evolving under linear physical processes are of the form^30,31

$${\dot{a}}_{j}(t)=-{{{\rm{i}}}}\mathop{\sum}\limits_{\ell }{H}_{j,\ell }{a}_{\ell }(t)-\sqrt{{\kappa }_{j}}{a}_{j,{{{\rm{probe}}}}}(t).$$

(9)

Here H is the dynamical matrix that encodes the coupling strength between the modes, decay rates and detunings. For instance, its diagonal can encode the decay due to intrinsic losses ${\kappa }_{j}^{{\prime} }$ and the coupling to probe waveguides κ_j as well as detunings ${\varDelta }_{j},{H}_{j,\;j}=-{{{\rm{i}}}}\frac{{\kappa }_{j}+{\kappa }_{j}^{{\prime} }}{2}+{\varDelta }_{j}$, whereas its off-diagonal entries H_j,ℓ correspond to couplings between the modes. Probe waveguides are coupled to all or some of the modes, which allows to inject the probe field a_j,probe(t) to the jth mode. For full generality, in the discussion around equation (1), we assumed that waveguides are attached to all the modes, although this is not a requirement for our scheme to work. In fact, we consider a scenario in which we only probe the system at a few modes in the next section. In this case, we set κ_j = 0 in equations (1) and (9) for any modes that are not coupled to waveguides.

In a typical experiment, one records the system response to the coherent probe field a_j,probe(t) = a_j,probe(ω)e^iωt at a certain frequency ω. Therefore, it is convenient to express equation (9) in the frequency domain by performing a Fourier transform as ${a}_{j}(\omega )=\frac{1}{\sqrt{2\uppi }}\int\nolimits_{-\infty }^{\infty }{{{\rm{d}}}}t\,{\rm{e}}^{{{{\rm{i}}}}\omega t}{a}_{j}(t)$, which leads to the dynamical equation in the frequency domain (equation (1)).

We obtain the expression for the scattering matrix (equation (3)) by solving equation (1) for ${{{\bf{a}}}}(\omega )=-{{{\rm{i}}}}{(\omega {\mathbb{1}}-H({{{\bf{x}}}},\theta ))}^{-1}\sqrt{\kappa }{{{{\bf{a}}}}}_{{{{\rm{probe}}}}}(\omega )$ and inserting this expression into the input–output relations^30,31 as ${a}_{j,{{{\rm{res}}}}}(\omega )$$={a}_{j,{{{\rm{probe}}}}}(\omega )+\sqrt{{\kappa }_{j}}{a}_{j}(\omega )$, which establishes a relation between the mode fields a_j(ω), the external probe fields a_j,probe(ω) and the response fields a_j,res(ω). By convention, both a_j,probe(ω) and a_j,res(ω) are in units of Hz^1/2. Solving for a_res(ω), we obtain

$$\begin{array}{rcl}{{{{\bf{a}}}}}_{{{{\rm{res}}}}}(\omega )&=&[{\mathbb{1}}-{{{\rm{i}}}}\sqrt{\kappa }{(\omega {\mathbb{1}}-H({{{\bf{x}}}},\theta ))}^{-1}\sqrt{\kappa }]{{{{\bf{a}}}}}_{{{{\rm{probe}}}}}(\omega )\\ &\equiv &S(\omega ,{{{\bf{x}}}},\theta ){{{{\bf{a}}}}}_{{{{\rm{probe}}}}}(\omega )\end{array},$$

(10)

which yields the expression for the scattering matrix given in equation (3). Note that this matrix is still well defined in the case when not all the modes are coupled to waveguides since intrinsic losses ${\kappa }_{j}^{{\prime} }$ ensure that H(x, θ) is invertible.

Layered architecture

Recursive solution to the scattering problem

The physical mechanism giving rise to information processing in the neuromorphic platform introduced here is, at first glance, fundamentally different from standard ANNs since waves scatter back and forth in the device rather than propagating unidirectionally. Nevertheless, with this in mind, we can choose an architecture that is inspired by the typical layer-wise structure of ANN (Extended Data Fig. 1a). It allows us to gain an analytic insight into the scattering matrix; in particular, the mathematical structure of the scattering matrix reveals a recursive structure reminiscent of the iterative application of maps in a standard ANN (Extended Data Fig. 1b). The analytic formulas also allow us to derive optimal layer sizes to make efficient use of the number of independent parameters available. This correspondence between the mathematical structure of the scattering matrix and standard neural networks only arises in a layered physical structure and is absent in a completely arbitrary scattering setup (which is, however, also covered by our general framework).

We consider a layered architecture (Fig. 2a) with L layers and N_ℓ neuron modes in the ℓth layer. Neuron modes are only coupled to neuron modes in consecutive layers but not within a layer. Note that although we sketch fully connected layers (Fig. 2a), the network does not, in principle, have to be fully connected. However, fully connected layers have the advantage that there is a priori no ordering relation between the modes based on their proximity within a layer.

This architecture allows us to gain an analytic insight into the mathematical structure of the scattering matrix. For a compact notation, we split the vector a of neuron modes (equation (1)) into vectors ${{{{\bf{a}}}}}_{n}\equiv ({a}_{1}^{(n)},\ldots ,{a}_{{N}_{n}}^{(n)})$ collecting the neuron modes of the nth layer. Correspondingly, we define the detunings of the neuron modes in the nth layer as ${\varDelta }^{(n)}={{{\rm{diag}}}}\,({\varDelta }_{1}^{(n)}\ldots {\varDelta }_{{N}_{n}}^{(n)})$, the extrinsic decay rates to the waveguides ${\kappa }^{\;(n)}={{{\rm{diag}}}}\,({\kappa }_{1}^{(n)},\ldots ,{\kappa }_{{N}_{n}}^{(n)})$, the intrinsic decay rates ${\kappa }^{{\prime} (n)}={{{\rm{diag}}}}\,({\kappa }_{1}^{{\prime} (n)},\ldots ,{\kappa }_{{N}_{n}}^{{\prime} (n)})$, the total decay rate ${{\kappa }_{{{{\rm{tot}}}}}}^{(n)}={\kappa }^{{\prime} (n)}+{\kappa }^{\;(n)}$ and J⁽ⁿ⁾, which is the coupling matrix between layer n and (n + 1) where the element ${J}_{j,\ell }^{\;(n)}$ connects neuron mode j in layer n to neuron mode ℓ in layer (n + 1). Note that this accounts for the possibility of attaching waveguides to all the modes in each layer to physically evaluate gradients according to equations (7) and (8). In the frequency domain, we obtain the equations of motion for the nth layer as

$$\begin{array}{rcl}-{{{\rm{i}}}}\omega {{{{\bf{a}}}}}_{n}&=&\left(-\frac{{\kappa }_{{{{\rm{tot}}}}}^{(n)}}{2}-{{{\rm{i}}}}{\varDelta }^{(n)}\right){{{{\bf{a}}}}}_{n}-{{{\rm{i}}}}{J}^{(n)}{{{{\bf{a}}}}}_{n+1}-{{{\rm{i}}}}{[\;{J}^{\;(n-1)}]}^{{\dagger} }{{{{\bf{a}}}}}_{n-1}\\ &&-\sqrt{{\kappa }^{\;(n)}}{{{{\bf{a}}}}}_{n,{{{\rm{probe}}}}},\end{array}$$

(11)

where we omitted the frequency argument ω for clarity. Equation (11) does not have the typical structure of a feed-forward neural network since neighbouring layers are coupled to the left and right—a consequence of wave propagation through the system.

We are interested in calculating the scattering response at the last layer L (the output layer), which defines the output of the neuromorphic system; therefore, we set a_n,probe = 0 for n ≠ L in equation (11) and only consider the response to the probe fields a_L,probe. The following procedure allows us to calculate the scattering matrix block S_out relating only a_L,probe to a_L,res. A suitable set of matrix elements of S_out then defines the output of the neuromorphic system via equation (4).

Solving for a₁(ω), then a₂(ω) and subsequent layers up to a_L(ω), we obtain a recursive formula for a_n(ω):

$${{{{\bf{a}}}}}_{n}={{{\rm{i}}}}{{{{\mathcal{G}}}}}_{n}\;{J}^{\;(n)}{{{{\bf{a}}}}}_{n+1}$$

(12)

with

$${{{{\mathcal{G}}}}}_{n}(\omega )\equiv {\left[\frac{{\kappa }_{{{{\rm{tot}}}}}^{(n)}}{2}+{{{\rm{i}}}}({\varDelta }^{(n)}-\omega )+{{J}^{\;(n-1)}}^{{\dagger} }{{{{\mathcal{G}}}}}_{n-1}{\;J}^{\;(n-1)}\right]}^{-1}$$

(13)

and ${{{{\mathcal{G}}}}}_{0}=0$; therefore, in the last layer, we have

$${{{{\bf{a}}}}}_{L}={{{{\mathcal{G}}}}}_{L}(\omega ){{{{\bf{a}}}}}_{L,{{{\rm{probe}}}}}.$$

(14)

At the last layer, the matrix ${{{{\mathcal{G}}}}}_{L}(\omega )$ is equal to the system’s Green function as $G(\omega )={{{{\mathcal{G}}}}}_{L}(\omega )$ (equation (3)).

Employing input–output relations^30,31 ${{{{\bf{a}}}}}_{L,{{{\rm{res}}}}}={{{{\bf{a}}}}}_{L,{{{\rm{probe}}}}}+\sqrt{{\kappa }^{(L)}}{{{{\bf{a}}}}}_{L}$, we obtain the scattering matrix for the response at the last layer as

$${S}_{{{{\rm{out}}}}}(\omega ,{{{\bf{x}}}},\theta )={\mathbb{1}}-\sqrt{{\kappa }^{(L)}}{\left[\frac{{\kappa }_{{{{\rm{tot}}}}}^{(L)}}{2}+{{{\rm{i}}}}({\varDelta }^{(L)}-\omega )+{{J}^{\;(L-1)}}^{{\dagger} }{{{{\mathcal{G}}}}}^{(L-1)}{J}^{\;(L-1)}\right]}^{-1}\sqrt{{\kappa }^{\;(L)}}.$$

(15)

The structure of equations (13) and (15) is reminiscent of a generalized continued fraction, with the difference that scalar coefficients are replaced by matrices. We explore this analogy further in Supplementary Information where we also show that for scalar inputs and outputs, the scattering matrix in equation (15) can approximate arbitrary analytic functions. Furthermore, the recursive structure defined by equations (13) and (14) mimics that of a standard ANN in which the weight matrix is replaced by the coupling matrix and the matrix inverse serves as the activation function. However, in contrast to the standard activation function, which is applied element-wise for each neuron, the matrix inversion acts on the entire layer. To gain intuition for the effect of taking the matrix inverse, we plot a diagonal entry of ${[{{{{\mathcal{G}}}}}_{1}(0)]}_{j,\;j}/\kappa ={\left[\frac{1}{2}+{{{\rm{i}}}}{\varDelta }_{j}^{(1)}/{\kappa }_{j}^{(1)}\right]}^{-1}$ (Fig. 2a). The real part follows a Lorentzian, whereas the imaginary part is reminiscent of a tapered sigmoid function.

Our approach bears some resemblance to the variational quantum circuits of the quantum machine learning literature^51,52 in which the subsequent application of discrete unitary operators allows the realization of nonlinear operations. In contrast, here we consider the steady-state scattering response, which allows waves to propagate back and forth, giving rise to yet more complicated nonlinear maps (equation (3)).

Further details on the test case of digit recognition

Training the neuromorphic system

The dataset consists of 3,823 training images (8 × 8 pixels) of handwritten numerals between 0 and 9 as well as 1,797 test images. We choose an architecture in which the input is encoded in the detunings ${\varDelta }_{j}^{(1)}$ of the first layer to which we add a trainable offset ${\varDelta }_{j}^{(0)}$:

$$\begin{array}{rcl}{\varDelta }_{2j}^{(1)}&=&{\varDelta }_{2j}^{(0)}+{x}_{j}\\ {\varDelta }_{2j+1}^{(1)}&=&-{\varDelta }_{2j+1}^{(0)}+{x}_{j}\end{array},$$

(16)

which we initially set to Δ_2j = Δ_2j+1 = 4κ (for simplicity, we consider equal decay rates ${\kappa }_{j}^{(n)}+{\kappa }_{j}^{{(n)}^{{\prime} }}\equiv \kappa$ from now on). In this way, the input enters the second layer in the form of [G₁(0)]_j,j/κ once with a positive sign and once with a negative sign (the plot of [G₁(0)]_j,j/κ is shown in Fig. 2b). This doubling of the input fixes the layer size to N₁ = 2 × 64. The second layer (hidden layer) can be of variable size and we train a system (1) without a hidden layer, (2) with N₂ = 20, (3) with N₂ = 30, (4) with N₂ = 60 and (5) with N₂ = 80. As we discuss in the next section and show in the Supplementary Information, N₂ = 70 is the optimal number of independent parameters for this input size and given value of R; at N₂ < 70, the neuromorphic system does not have enough independent parameters, and at N₂ > 70, there are more parameters than strictly necessary that may help with the training. We use one-hot encoding of the classes, so the output layer is fixed at N₃ = 10. We choose equal decay rates ${\kappa }_{j}^{(n)}+{\kappa }_{j}^{(n){\prime} }\equiv \kappa$ and express all the other parameters in terms of κ. For simplicity, we set the intrinsic decay to zero (κ′ = 0) at the last layer where we probe the system.

We initialize the system by making the neuron modes in the second and third layers resonant and add a small amount of disorder, that is, ${\varDelta }_{j}^{(n)}/\kappa ={w}_{\varDelta }({\xi }_{j}^{\;(n)}-1/2)$ with w_Δ = 0.002 and ξ ∈ [0, 1). Similarly, we set the coupling rates to 2κ and add a small amount of disorder, that is, ${J}_{j,\ell }^{\;(n)}/\kappa =2+{w}_{J}{\xi }_{j,\ell }^{\;(n)}$ with w_J = 0.2. We empirically found that this initialization leads to the fastest convergence of the training. Furthermore, we scale our input images such that the background is off-resonant at Δ/κ = 5 and the numerals are resonant at Δ/κ = 0 (Fig. 2a) since, otherwise, the initial gradients are very small.

As the output of the system, we consider the imaginary part of the diagonal entries of the scattering matrix (equation (15)) at the last layer at ω = 0, that is, y_ℓ ≡ ImS_ℓ,ℓ(ω = 0, x, θ) (Fig. 2a). The goal is to minimize the categorical cross-entropy cost function ${{{\mathcal{C}}}}=-{\sum }_{j}{\;y}_{j}^{{{{\rm{tar}}}}}\log \left(\frac{{e}^{\;\beta {y}_{j}}}{{\sum }_{\ell }{e}^{\beta {y}_{\ell }}}\right)$ with β = 8 in which ${y}_{j}^{{{{\rm{tar}}}}}$ is the jth component of the target output of the system, which is 1 at the index of the correct class and 0 elsewhere. We train the system by performing stochastic gradient descent, that is, for one mini-batch, we select 200 random images, and compute the gradients of the cost function according to which we adjust the system parameters: the detunings ${\varDelta }_{j}^{(n)}$ and the coupling rates ${J}_{j,\ell }^{\;(n)}$.

We show the accuracy evaluated on the test set at different stages during the training for five different architectures (Fig. 2b). Both convergence speed and maximally attainable test accuracy depend on the size of the hidden layer, with the system without the hidden layer performing the worst. This should not surprise us, since an increase in N₂ also increases the number of trainable parameters. Interestingly, we observed that systems with smaller N₂ have a higher tendency to get stuck. Training these systems for a very long time may, in some cases, however, still lead to convergence to a higher accuracy. The confusion matrix of the trained system with N₂ = 80 after 2,922 epochs is shown in Fig. 2c.

We show the evolution of the output scattering matrix elements evaluated for a few specific images (Fig. 2d). For this training run, we used Adam optimization. During training, the scattering matrix quickly converges to the correct classification result. Only for images that look very similar (for example, the image of the numerals 4 and 9 (Fig. 2d)), the training oscillates between the two classes and takes a longer time to converge.

Comparison to conventional classifiers

Comparing neuromorphic architectures against standard ANNs in terms of achievable test accuracy and other measures can be useful, provided that the implications of such a comparison are properly understood. In performing this comparison, we have to keep in mind the main motivations for switching to neuromorphic architectures: exploiting the energy savings afforded by analogue processing based on the basic physical dynamics of the device, getting rid of the inefficiencies stemming from the von Neumann bottleneck (separation of memory and processor) and potential speedup by a high degree of parallelism. Therefore, the use of neuromorphic platforms can be justified even when, for example, a conventional ANN with the same parameter count is able to show higher accuracy. The usefulness of such a comparison rather lies in providing a sense of scale: we want to make sure that the neuromorphic platform can reach good training results in typical tasks, not too far off those of ANNs, with a reasonable amount of physical resources. Furthermore, the classification results attained by either ANNs or neuromorphic systems depend on hyperparameters and initialization. Although ANNs have been optimized over the years, it stands to reason that strategies for achieving higher classification accuracies can also be found for neuromorphic systems (such as our approach) in the future.

We compared our results against a linear classifier (ANN with linear activations) and an ANN with an input layer size of 64 neurons, a hidden layer of size 150 (to obtain the same number of parameters as in the neuromorphic system) and an output layer of size 10. For the ANN, we used sigmoid activation functions and a softmax function at the last layer. In the first case, we used a mean-squared-error cost function (to benchmark the performance of a purely linear classifier); in the latter case, we used a categorical cross-entropy cost function. The linear classifier attained a test accuracy of 92.30%, which is clearly surpassed by our neuromorphic system, whereas the ANN achieved a test accuracy of 97.05%, which is on par with the accuracy attained by our neuromorphic system (97.10%). To allow for a fair comparison of the convergence speed (Fig. 2b), we trained all the networks with the stochastic gradient descent.

We also compare these results with a CNN. The low image resolution of the dataset prevents the use of standard CNNs (such as LeNet-5). Since the small image size only allows for one convolution step, we trained the following CNN: the input layer is followed by one convolutional layer with six channels and a pooling layer, followed by densely connected layers of sizes 120, 84 and 10. We used two different kernels for the convolution: (1) 3 × 3 with stride 2 and (2) 5 × 5 with stride 2; in the former, we obtained a test accuracy of 96.4%, whereas in the latter, the test accuracy amounted to 96.7%. Figure 2b shows the accuracy during training. Although the maximal accuracy of the CNN lies below that of the fully connected neural network, it converges faster. We attribute the slightly worse performance of the CNN to the low resolution of the dataset.

The accuracies obtained by ANNs and CNNs lie below the record accuracy achieved by a CNN on MNIST. However, this should not surprise us since (1) the dataset we study³³ is entirely different from the MNIST dataset, (2) the resolution of the dataset is lower than of the MNIST dataset (8 × 8 instead of 28 × 28).

Case study: Fashion-MNIST

To study the performance of our approach on a more complex dataset, we performed image classification on the Fashion-MNIST dataset⁵³. This dataset consists of 60,000 images of 28 × 28 pixels of ten different types of garment in the training set and 10,000 images in the test set. Fashion-MNIST is considered to be more challenging than MNIST; in fact, most typical classifiers perform considerably worse on Fashion-MNIST than on MNIST.

We consider a transmission setup in which the probe light is injected at the first layer, illuminating all the modes equally, and the response is measured at the other end of the system, Extended Data Fig. 2a (in contrast to the study in the main text for which probe and response were chosen at the last layer) since we (2) wanted to test an architecture even closer to standard layered neural networks and (2) found this to somewhat increase the performance for this dataset. Following an analogous derivation as that for equation (15), we obtain the following expression for the scattering matrix:

$${S}_{{{{\rm{out}}}}}(\omega ,{{{\bf{x}}}},\theta )=-\mathrm{i}\sqrt{{\kappa }^{\;(L)}}\left\{\displaystyle\prod_{n = 2}^{L}{\tilde{\chi }}_{n}{[\;{J}^{\;(n-1)}]}^{{\dagger} }\right\}{\tilde{\chi }}_{1}\sqrt{{\kappa }^{(1)}}{\xi }_{{{{\rm{probe}}}}},$$

(17)

in which, as above, the coupling matrix acting on layer n − 1 is [J^(n–1)]^† and ${\xi }_{j,{{{\rm{probe}}}}}=1/\sqrt{{N}_{1}}$. The recursively defined effective susceptibilities are given by (n = L − 1…1)

$${\tilde{\chi }}_{n}={\left({\chi }_{n}^{\;-1}-{J}^{\;(n)}{\tilde{\chi }}_{n+1}{[\;{J}^{\;(n)}]}^{{\dagger} }\right)}^{-1},$$

(18)

in which χ_n = (ω – Δ⁽ⁿ⁾ + iκ⁽ⁿ⁾/2)^–1 and ${\tilde{\chi }}_{L}={\chi }_{L}$. We note that κ⁽¹⁾ is the diagonal matrix containing the (uniform) decay rates that describe the coupling of an external waveguide to all the neuron modes of layer 1, which, thus, experience a homogeneous probe drive. Furthermore, inputs x are encoded into layer 1 by adding them to the frequencies Δ⁽¹⁾. In the experiments studied below, we did not need any input replication to obtain good results.

Specifically, we study two different architectures of our neuromorphic system: (1) a layer architecture of three fully connected layers; (2) an architecture inspired by a CNN with the aim of reducing the parameter count and directly comparing against convolutional ANNs (Supplementary Section VI). In both cases, we trained the networks on both full resolution images and downsized versions of 14 × 14 pixels obtained by averaging over 2 × 2 patches.

We show the test accuracy during training (Extended Data Fig. 2b) for two different learning rates (10⁻³ and 10⁻⁴) using AMSGrad as the optimizer⁵⁴ (performing slightly better than Adam) and compare them with ANNs and CNNs and a linear neural network with (approximately) the same number of parameters and the same training procedure. A comparison of the best attained accuracies as well as a list of the number of parameters and neuron modes or ANN neurons is provided in Supplementary Table I. We obtained the best test accuracy of 89.8% with the fully connected layer network on both small and large images with a learning rate of 10⁻³ as well as on small images with a learning rate of 10⁻⁴. This clearly exceeds the performance of the linear neural network, which only achieves a peak test accuracy of 86.5%. The comparable digital ANN achieved 89.7% on the small images at a learning rate of 10⁻³, 90.5% on the large images at a learning rate of 10⁻³ and 90.6% on the small images at a learning rate of 10⁻⁴. For the sake of a more systematic comparison, we used a constant learning rate for the results reported here. However, we found that introducing features like learning-rate scheduling can lead to slightly better results with our setup (for example, we reached up to 90.1% accuracy for the fully connected layer neuromorphic setup trained on small images in only 100 epochs using a linearly cycled learning rate peaking at 0.1).

Our best convolutional network achieved 88.2% on the large image data with learning rates of 10⁻³ and 10⁻⁴, whereas the comparable CNNs attained 90.5% and 91.2%, respectively. These architectures contain only a fraction of the number of parameters of the fully connected architecture; therefore, they may be preferable for implementations. Increasing the number of parameters of CNNs close to that of the fully connected ANNs (by increasing the number of channels) can increase the accuracy to 93% (ref. ⁵⁵), but comes at the cost of a large number of parameters. Furthermore, more advanced CNNs with features such as dropout as well as the use of data augmentation or other preprocessing techniques can achieve a test accuracy above 93% (ref. ⁵⁵), but for the sake of comparability, we chose to train ANNs and CNNs with a similar architecture as our neuromorphic system. For comparison, a detailed list of benchmarks with various digital classifiers without preprocessing is provided in another work⁵³, with logistic regression achieving 84.2% and support vector classifiers attaining 89.7%.

Remark on Adam optimization

Using adaptive gradient descent techniques, such as Adam optimization, can help increase the convergence speed. We successfully used adaptive optimizers (such as Adam and AMSGrad) for training optimization on the Fashion-MNIST dataset. However, during the training on the digit recognition dataset (with small images and thus small neuron counts), we observed that Adam optimization causes the cost function and accuracy to strongly fluctuate and the training can, in some cases, get stuck. We attribute this to the fact that in the training on the digit dataset, the gradients get small very quickly (on the order of 10⁻⁶), which is known to make Adam optimization unstable. Stochastic gradient descent does not suffer from the same problem, which was, therefore, more suited for training on the digit dataset. The best accuracy we achieved when using Adam optimization on the digit dataset was 96.0%, which is below the 97.1% value that we achieved with stochastic gradient descent.

Hyperparameters

The architecture we propose has the following hyperparameters, which influence the accuracy and convergence speed: (1) the number of neuron modes per layer N_ℓ; (2) the number of layers L; (3) the number of input replications R; (4) the intrinsic decay rate of the system.

(1) The number of neuron modes in the first layer should match the product of the input dimension D and the number of replications of the input R. The number of neurons in the final layer is given by the output dimension, for example, for classification tasks, the dimension corresponds to the number of classes. The sizes of intermediate layers should be chosen to provide enough training parameters; as shown in Fig. 2b, both convergence speed and best accuracy rely on having a sufficient number of training parameters available, as, for instance, a system with a second layer of only 20 neuron modes performs worse than a system with 60 neuron modes in the second layer. In particular, as we show in the Supplementary Information, independent of the architecture, the maximal number of independent couplings for an input of dimension D, input replication R and output dimension N_out is given by

$${N}_{{{{\rm{opt}}}}}=\frac{(RD+{N}_{{{{\rm{out}}}}})(RD+{N}_{{{{\rm{out}}}}}+1)}{2}.$$

(19)

In addition, there are RD + N_out local detunings that can be independently varied. For the layered structure (Fig. 2a), this translates to an optimal size of the second layer as N_2,opt = ⌈(N₁ + N₃ + 1)/2⌉. For a system with N₁ = 128 and N₃ = 10, the optimal value N_2,opt is given by N_2,opt = 70. Smaller N₂ leads to fewer independent parameters, whereas larger N₂ introduces redundant parameters. In our simulations, the system with N₂ = 60 already achieved a high classification accuracy; therefore, it may not always be necessary to increase the layer size to N_2,opt. Further increasing the number of parameters and introducing redundant parameters can help avoid getting stuck during training. Indeed, we obtained the best classification accuracy for a system with N₂ = 80. Similarly, even though a neuromophic system with all-to-all couplings provides a sufficient number of independent parameters, considering a system with multiple hidden layers can be advantageous for training.

(2) Similar considerations apply to choosing the number of layers of the network. L should be large enough to provide a sufficient number of training parameters. At the same time, L should not be too large to minimize attenuation losses. For deep networks with L ≿ 3, localization effects may become important^56,57, which may hinder the training; therefore, it is advisable to choose an architecture with sufficiently small L.

(3) The choice of R depends on the complexity of the training set. For the digit recognition task, R = 2 was sufficient, but more complicated datasets can require larger R. We explore this question in the Supplementary Information, where we show for scalar functions that R determines the approximation order and utilize our system to fit scalar functions. To fit quickly oscillating functions or functions with other sharp features, we require larger R.

Here we only considered encoding the input in the first layer. However, it could be interesting to explore, in the future, whether spreading the (replicated) input over different layers holds an advantage, since this would allow to make subsequent layers more ‘nonlinear’.

In general, the input replication R can be thought of as the approximation order of the nonlinear output function. Specifically, an input replication R implies that the scattering matrix is not only a function of x_j but also ${x}_{j}^{2}$…${x}_{j}^{R}$. This statement also holds in other possible neuromorphic systems based on linear physics, for example, in a sequential scattering setup.

(4) The intrinsic decay rate determines the sharpest feature that can be resolved, or, equivalently, a larger rate κ smoothens the output function. It is straightforward to see from equation (7) that the derivative of the output with respect to a component of the input scales with κ. In the context of one-dimensional function fitting, this is straightforward to picture, and we provide some examples in the Supplementary Information. However, a larger decay rate can be compensated for by rescaling the range of input according to κ. For instance, for the digit recognition training, we set the image background to Δ/κ = 5 and made the pixels storing the number resonant Δ/κ = 0, which is still possible in lossy systems.

Extended data

Extended Data Fig. 1 Physical architecture vs. data processing.

a While signals scatter back and forth in the physical architecture, b data processing via the scattering matrix for such a layered physical architecture can be cast into a recursive form, Eqs. (12) to (15), which is reminiscent of the sequential processing in artificial neural networks.

Extended Data Fig. 2 Image classification on Fashion-MNIST.

a Modified setup in which we inject the probe signal at the first layer and record the response at the last. The sample image is part of the Fashion-MNIST dataset^53,55. b Test accuracies for fully connected and convolutional setups with learning rate 10⁻³ and c learning rate 10⁻⁴. We trained all of the networks for 1,000 epochs (except for the convolutional network on the large images which already converged during the 538 epochs we trained) and indicate the maximum accuracy achieved in this period. As baseline, we show the best result obtained with a linear neural network with softmax applied to the output (trained on the large images) for each architecture and learning rate. The observed decrease in test accuracy after reaching a maximum is due to over-fitting.

Source data

Source data

Source Data Fig. 2

Data for individual curves in Fig. 2b.

Source Data Fig. 3

Data (trained system parameters) for histograms in Fig. 3e.

Source Data Extended Data Fig. 2

Test accuracies for different models (neuromorphic system and ANNs) trained at different learning rates (10⁻³ versus 10⁻⁴) on either the full 28 × 28 images (‘large’) or downsized 14 × 14 images (‘small’).