Introduction

In recent times, there has been a rising fascination among scientists with Nonlinear Evolution Equations (NLEEs), which have become key focal points in various scientific disciplines. These equations showcase intriguing properties, significantly impacting fields ranging from mathematics and physics to communication systems and optical illusions. The wave phenomena originating from NLEEs find versatile applications in diverse areas, including physics, biology, and the exploration of fluid dynamics and oceans1,2,3,4. In the last few decades, a distinctive method for solving NLEEs has remained underexplored. Consequently, researchers have worked diligently to create a variety of dependable, potent, and straightforward techniques for tackling NLEEs equations, including the modified Kudryashov technique5, the \((\frac{{G}{\prime}}{{G}{\prime}+G+A})\)-expansion approach6, the extended of \(sine\)-Gordon equation expansion technique7, the enhanced \((\frac{{G}{\prime}}{{G}^{2}})\)-expansion approach8, Laplace transform method9, the \((\frac{{G}{\prime}}{G},\frac{1}{G})\)-expansion process10,11, Modified extended auxiliary equation mapping method12, the multiple simplest equation method13, the direct algebraic technique14, the approach of Frobenius Integrable Decomposition15, the modified extended tanh-function approach16,17, the technique of the Simplest Equation18, the unified technique19, Darboux transformation20, the improved \(F\)-expansion approach21, the multiplier homotopy scheme22, the modified Khater approach23, the trigonometric quantic B-Spline approach24, the comprehensive exponential rational function method25, the advanced \(exp(-\varphi (\xi ))\)-expansion method26,27,28,29,30, the adapted direct algebraic process31, the Adomian Decomposition system32, the \(sech-tanh\) method34, the sub-equation procedure34, the transform system of \(q\)-homotopy analysis35, the simplified Hirota method36, the mesh less collocation method37, and so on.

Wilson38 presented the DSW equation, a mathematical model for dispersive water waves. The resulting wave phenomena from this equation have since played a crucial role in the realms of fluid dynamics, ocean engineering, and scientific studies. The coupled DSW equation is expressed in the succeeding mathematical form39

$$\left\{\begin{array}{c}{v}_{t}+a u {u}_{x}=0\\ {u}_{t}+b v {u}_{x}+c{ v}_{x} u+d {u}_{xxx}=0,\end{array}\right.$$
(1)

where \(a, b, c,\) as well \(d\) are constants that are not zero. The exploration of new transiting wave solutions for the DSW equation has been a subject of investigation using various mathematical methods. The behavior of long surface water waves in a two-dimensional ideal fluid is modeled using the fractional coupled DSW equation40. It is a generalization of the well-known KdV equation, and it has been used in research into the stability and solitonic behavior of water waves in a variety of physical systems39. The coupled DSW equation has abundant applications in numerous fields of science. It is an essential tool for simulating long surface water waves in oceanography and fluid dynamics, offering insights into wave behavior in many aquatic environments41. The equation is used by environmental scientists to comprehend how waves affect coastal ecosystems and regions. Environmental scientists use this equation to understand how waves impact coastal regions and ecosystems. The equation permits the study of solitary wave solutions and their effects in many physical systems by generalising the KdV equation to the domain of solitons and nonlinear waves43. In mathematical physics, it is a helpful model to study the mathematical properties of NLEEs. Geophysicists can benefit from studying wave dynamics in geological environments, such as the propagation of tsunamis. The equation serves as a benchmark issue in numerical analysis and simulation, allowing researchers to assess the accuracy and efficiency of methods developed to solve NLEEs. Moreover, wave phenomena research in many other domains depends on the DSW equation41.

Initially, the direct algebra method40 was employed, leading to the discovery of novel solutions. Subsequently, Fan41 utilized the algebraic method, successfully identifying exact solutions for the coupled DSW equation. The application of the generalized Jacobi elliptic function method42 resulted in diverse exact solutions, encompassing bell solutions, N-soliton solutions, kink solutions, singular solutions as well as periodic solutions. Additionally, the adomain decomposition method43 was employed to find approximately doubly periodic wave solutions for the coupled DSW equation. Furthermore, the application of the Darboux transformation44 to the coupled DSW equation proved effective in reducing the problem and identifying exact solutions. Bashar, Md Habibul, et al.39, have uncovered novel wave solutions and investigated the impact of unrestricted parameters on the coupled DSW equation.

In this work, the wave dynamics of the coupled DSW equation is explored using a reliable analytical technique. The projected technique, namely, the \(exp(-\phi (\xi ))\)-expansion method45, is applied to inspect the deliberated coupled DSW equation for the very first time in this study. The gotten wave solutions not only authorize the previously reported wave behavior for DSW equation in the literature but also produce some novel results. A comparison of the presented results with the previous studies obtainable in the literature is carried out to highlight the novel and interesting outcomes of this study. The \(exp(-\phi (\xi ))\)-expansion method is modern and reliable expansion method which have been successfully utilized to build the traveling wave solutions of a large class of NLPDEs arising in mathematical physics in a number of recent studies. The proposed technique is powerful, straight forward, efficient and usually provide a variety of traveling wave solutions, including solitary waves and solitons. The effectiveness of the proposed methodology to study the considered the coupled DSW equation is established through the comparison of the obtained results with the previous literatures39,40,43.

The following is the arrangement of the sections that follow in this paper: Section "Explanation and some topographical features of CD" offers an in-depth exploration of the definition and diverse characteristics of conformable derivatives (CD). In Section "Methodology of the -expansion method", we detail the methodologies utilized in our study. Section "Implementation of the -expansion approach" centers on the practical application of these methodologies to the DSW equation, yielding insightful solutions. Advancing to Section "Outcomes and discussions", we showcase graphical representations of the solutions obtained. Section "Comparison" represents the Comparison. Lastly, the concluding section "Conclusion" consolidates our findings, offering a comprehensive summary and conclusion.

Explanation and some topographical features of CD

Khalil et al.46 mainly recognized the concept of CD alongside the reason of limit.

Definition

If we consider a mapping \(f:(0,\infty ) \to \Re \,,\) then CD of \(f\) order \(\omega\) can be written as \(T_{t}^{\omega } f(t) = \mathop {\lim }\limits_{\varepsilon \to 0} \left( {\frac{{f\,\left( {t + \varepsilon \,t^{1 - \omega } } \right) - f(t)}}{\varepsilon }} \right)\,,\) for all \(t > 0,\;0 < \omega \le 1.\)

Exponential functions rule, the Gronwalls disparity, the chain rule, convinced and indeterminate incorporation by slices, Fourier transformation, Laplace transform, as well Taylor's control series expansions for CD in the advancement of fractional value according to order have all remained reputable in advance by one of the prominent researchers Abdeljawad47. The exertion of the contemporary adapted Riemann Liouville derivative47 classification can be smoothly intimidated by the portrayal of CD. Recently Bashar et al.48 and Mamun et al.8,16 recycled this CD theory to solve some time fractional PDEs.

Theorem 1

Assume \(\omega \in \,\,(0,\,1],\) additionally function \(f = f(t),\,\,{\text{and }}g = g(t){\kern 1pt} ,\) be \(\omega\)-CD at the point \(t > 0,\) then we can state-owned as.

  1. (i)

    \(T_{t}^{\omega } \left( {cf + dg} \right) = cT_{t}^{\omega } f + dT_{t}^{\omega } g,\) for all \(c,\,d \in \Re\)

  2. (ii)

    \(T_{t}^{\omega } \left( {t * \gamma } \right) = \gamma \,t^{\gamma - \omega } ,\;\) for all \(\gamma \in \Re\)

  3. (iii)

    \(T_{t}^{\omega } \left( {f * g} \right) = gT_{t}^{\omega } \left( f \right) + f\;T_{t}^{\omega } \left( g \right)\,,\;\)

  4. (iv)

    \(T_{t}^{\omega } \left( \frac{f}{g} \right) = \frac{{gT_{t}^{\omega } \left( f \right) - f\,T_{t}^{\omega } \left( g \right)}}{{g^{2} }}.\)

Moreover, if this function \(f\) is derivable, then \(T_{t}^{\omega } \left( {f(t)} \right) = \,\,t^{1 - \omega } \frac{df}{{dt}}.\)

Theorem 2

Consider \(f:(0,\omega ) \to R{\kern 1pt} {\kern 1pt} ,\) be a function of real type in such a way as \(f\) is able to differentiate additionally \(\omega\)-CD. Moreover, suppose that \(g\) be a function that is both well-defined and differentiable within designated range of \(f\). In such a scenario, we possess \(T_{t}^{\omega } \left( {fog} \right)\,\left( t \right) = t^{1 - \omega } g(t)^{\omega - 1} \;g^{\prime}(t)\,T_{t}^{\omega } \left( {f(t)} \right)_{t = g(t)} \,,\) whereas prime indicates the simple derivatives with regard to \(\text{the point } t\).

We were considerate in our study when it came to the favored equation and the idea of CD. While numerous functions may not exhibit increasing behavior as demonstrated by Taylor's power order analysis at specific points in basic calculus, their existence can still be accounted for through the application of conformable order derivatives. While complicated plans happen in the logic of important fractional geometry, CD accomplishes well in the product and chain law. Wherever the Riemann derivative of fractional order is not the topic, the CD of a function characterized by a constant type is corresponding to zero. The Mittag Leffler functions play a significant role in fractional order calculus, serving as an alternative elucidation to the exponential type of function. This is evident in the fractional order representation of the exponential type function expressed as f(t) = e \(\frac{{t}^{\alpha }}{\alpha },\) particularly in the context of CD.

Methodology of the \(\mathbf{e}\mathbf{x}\mathbf{p}\left(-\boldsymbol{\varphi }\left({\varvec{\xi}}\right)\right)\)-expansion method

Within this segment, we have discussed our previously stated \(\text{exp}\left(-\varphi \left(\xi \right)\right)\)-expansion approach26,27,28,29,30 detailed stepwise. Consider a NLEE characterized by the provided structure

$$\Theta \left(\psi ,{ \psi }_{x},{D}_{t}^{\theta }\psi ,{ \psi }_{xx},{D}_{tt}^{2\theta }\psi ,{ \psi }_{xxx},\cdots \cdots \cdots \right)=0,$$
(2)

where \(\psi =\psi \left(x,t\right)\) denotes a function of which the specific characteristics are not defined, \(\Theta \) can be represented as a polynomial function in terms of \(\psi \), it involves a dissimilar form of partial derivatives, encompassing both nonlinear terms and the higher-order derivatives in the expression.

Step-01. We will now adopt a variable transformation for the wave with a interpretation to non-dimensionality. We unify all independent variables into a singular variable as

$$U\left(x,t\right)=\psi \left(\xi \right), \xi =x-\delta \frac{{t}^{\gamma }}{\gamma }.$$
(3)

Through the substitution of this variable transformation, we can simplify Eq. (2) into an ODE of the following structure

$$\text{R}\left(\psi ,{\psi }{\prime},{\psi }^{{\prime}{\prime}},\cdots \cdots \cdots \right)=0.$$
(4)

Step-02. Let's contemplate that the solution to the ODE in Eq. (4) can be formulated as

$$\uppsi =\sum_{i=0}^{N}{{\text{A}}_{i}\text{exp}\left(-\varphi \left(\xi \right)\right)}^{i}, {\text{A}}_{N}\ne 0,$$
(5)

where determination of the positive integer \(N\) is achieved by equating the peak order derivatives to the corresponding peak order nonlinear portions found in Eq. (4). Additionally, the ODE is satisfied by the derivative of \(\varphi (\xi )\) and is expressed in the succeeding structure

$${\varphi }{\prime}\left(\xi \right)-\text{ exp}\left(-\varphi \left(\xi \right)\right)-\alpha \text{exp}\left(\varphi \left(\xi \right)\right)-\beta =0,$$
(6)

Consequently, the solutions for the ODE represented by Eq. (6) are:

Case I

A hyperbolic function-based solution (for \({\upbeta }^{2}-4\alpha >0, \alpha \ne 0\)):

$$\varphi \left(\xi \right)=\text{ln}\left(\frac{-\sqrt{{\beta }^{2}-4\alpha }\text{tanh}(\frac{\sqrt{{\beta }^{2}-4\alpha }}{2} (\xi +k))-\beta }{2\alpha }\right)$$
(7)

and

$$\varphi \left(\xi \right)=\text{ln}\left(\frac{-\sqrt{{\beta }^{2}-4\alpha }\text{coth}(\frac{\sqrt{{\beta }^{2}-4\alpha }}{2} (\xi +k))-\beta }{2\alpha }\right).$$
(8)

Case II

A trigonometric function-based solution (for \({\upbeta }^{2}-4\alpha <0, \alpha \ne 0\)):

$$\varphi \left(\xi \right)=\text{ln}\left(\frac{\sqrt{4\alpha -{\beta }^{2}}\text{tan}(\frac{\sqrt{4\alpha -{\beta }^{2}}}{2} (\xi +k))-\beta }{2\alpha }\right)$$
(9)

and

$$\varphi \left(\xi \right)=\text{ln}\left(\frac{\sqrt{4\alpha -{\beta }^{2}}\text{cot}(\frac{\sqrt{4\alpha -{\beta }^{2}}}{2} (\xi +k))-\beta }{2\alpha }\right).$$
(10)

Case III

When \({\upbeta }^{2}-4{\upalpha }>0\) and \({\upalpha }=0,\upbeta \ne 0\)

$$\varphi \left(\xi \right)=-\text{ln}\left(\frac{\beta }{\text{exp}(\beta \left(\xi +k\right))-1}\right).$$
(11)

Case IV

When \({\upbeta }^{2}-4{\upalpha }=0\) and \(\alpha \ne 0,\upbeta \ne 0\)

$$ \varphi \left( \xi \right) = {\text{ln}}\left( { - \frac{{2\left( {\beta \left( {\xi + k} \right) + 2} \right)}}{{\beta^{2} \left( {\xi + k} \right)}}} \right). $$
(12)

Case V:

When \({\upbeta }^{2}-4{\upalpha }=0\) and \(\alpha =0,\upbeta =0\)

$$ \varphi \left( \xi \right) = {\text{ln}}\left( {\xi + k} \right), $$
(13)

where \(k\) is an integrating constant.

Step-3. By plugging Eq. (6) as well Eq. (5) to Eq. (4) and assembling in the identical order of \(\text{exp}\left(-p\varphi \left(\xi \right)\right)\),\(\text{p}=0, \pm 1, \pm 2, \pm 3, \dots \) organized, then we accomplish an expression in polynomials structure of \(\text{exp}\left(-p\varphi \left(\xi \right)\right)\) and by equating individually coefficient of the obtained polynomial equal to zero, a system of algebraic equations (SAE) is derived.

Step-4. The purpose of constants can be achieved through one or more solution sets by evaluating the scientific surroundings established in step 3. Substituting the constant values into the equations derived from Eq. (6) yields new and extensive precise expressions for the traveling wave resolutions of the nonlinear evaluation presented in Eq. (1).

Implementation of the \(\mathbf{e}\mathbf{x}\mathbf{p}\left(-\boldsymbol{\varphi }\left({\varvec{\xi}}\right)\right)\)-expansion approach

Within this part, we relate the stated scheme which well-defined in the Section "Methodology of the -expansion method" to explore new exact solutions for the coupled DSW equation38,39,41. In instruction to explain our described equation, we deliberate wave transformation \(v\left(x,t\right)=V\left(\xi \right),\) \(u\left(x,t\right)=U\left(\xi \right)\) where \(\xi =l(x-\delta \frac{{t}^{\beta }}{\beta })\), \(\delta \ne 0\) and substituting this alteration in Eq. (1), the subsequent equation is derived

$$\left\{\begin{array}{c}-l\delta {V}{\prime}+alUU{\prime}=0\\ -l\delta {U}{\prime}+blV{V}{\prime}+clU{V}{\prime}+d{l}^{3}{U}^{{\prime}{\prime}{\prime}}=0.\end{array}\right.$$
(14)

From 1st equation in Eq. (14), we have

$$V=\frac{a{U}^{2}}{2\delta }.$$
(15)

Using (15) into the 2nd equation in Eq. (14) and by integrating then we acquire under mentioned ODE.

$$-6{\delta }^{2}U+a\left(b+2c\right){U}^{3}+6d\delta {l}^{2}{U}^{{\prime}{\prime}}=0.$$
(16)

By balancing \(U^{\prime\prime}\) and \({U}^{3},\) we get the value of \(N=1.\) From Eq. (5), we have

$$U\left(x,t\right)={A}_{0}+{A}_{1}\text{exp}(-\varphi (\xi )).$$
(17)

where \({A}_{0} and {A}_{1}\) are real parameters which are nonentities and resolute later.

Utilizing Eq. (6) and Eq. (17) in Eq. (16), a polynomial expressed in terms of \(exp(-\varphi (\xi ))\) is derived. Upon paralleling all coefficients of \(exp(-\varphi (\xi ))\) to the value zero, we arrive at a SAE as follows:

$$6d\delta {l}^{2}{A}_{1}\alpha \beta +ab{A}_{0}^{3}+2ac{A}_{0}^{3}-{6\delta }^{2}{A}_{0}=0$$
$$6{\beta }^{2}d\delta {l}^{2}{A}_{1}+12\alpha d\delta {l}^{2}{A}_{1}+3ab{A}_{0}^{2}{A}_{1}+6ac{A}_{0}^{2}{A}_{1}-6{\delta }^{2}{A}_{1}=0$$
$$18\beta d\delta {l}^{2}{A}_{1}+3ab{A}_{0}{A}_{1}^{2}+6ac{A}_{0}{A}_{1}^{2}=0$$
$$ab{A}_{1}^{3}+2ac{A}_{1}^{3}+12d\delta {l}^{2}{A}_{1}=0.$$

Solving these SAE, we get a solution set as follows:

$$ \delta = \frac{1}{2}dl^{2} \left( {4\alpha - \beta^{2} } \right),\,A_{0} = \mp \frac{{3\beta dl^{2} \left( {4\alpha - \beta^{2} } \right)}}{{\sqrt { - 6a\left( {b + 2c} \right)\left( {4\alpha - \beta^{2} } \right)} }},\,{\text{and}}\,A_{1} = \pm \frac{{\sqrt { - 6a\left( {b + 2c} \right)\left( {4\alpha - \beta^{2} } \right)} l^{2} d}}{{a\left( {b + 2c} \right)}}. $$
(18)

Case I (for \({{\varvec{\upbeta}}}^{2}-4\boldsymbol{\alpha }>0,\boldsymbol{ }\boldsymbol{\alpha }\ne 0\))

Family 1

Using the solution of SAE and Eqs. (7) and (8), we get following general travelling wave solutions of Eq. (17):

$$ \begin{aligned} U_{1,2} \left( {x,t} \right) & = \mp \frac{{3\beta d\left( { - \beta^{2} + 4\alpha } \right)l^{2} }}{\rho } \pm \frac{{2\rho l^{2} \alpha d}}{{a\left( {b + 2c} \right)\left( { - \sqrt {\beta^{2} - 4\alpha } \tanh \left( {\frac{1}{2}\sqrt {\beta^{2} - 4\alpha } \left( {\xi + k} \right)} \right) - \beta } \right)}}\,{\text{and}} \\ U_{3,4} \left( {x,t} \right) & = \mp \frac{{3\beta d\left( { - \beta^{2} + 4\alpha } \right)l^{2} }}{\rho } \pm \frac{{2\rho l^{2} \alpha d}}{{a\left( {b + 2c} \right)\left( { - \sqrt {\beta^{2} - 4\alpha } \coth \left( {\frac{1}{2}\sqrt {\beta^{2} - 4\alpha } \left( {\xi + k} \right)} \right) - \beta } \right)}}, \\ \end{aligned} $$

where \(\rho =\sqrt{-6a\left(b+2c\right)\left(-{\beta }^{2}+4\alpha \right)}\).

Case II (for \({{\varvec{\upbeta}}}^{2}-4\boldsymbol{\alpha }<0,\boldsymbol{ }\boldsymbol{\alpha }\ne 0\))

Family 2

Using the solution of SAE and Eq. (9) as well as Eq. (10) into Eq. (17), we arrive at following general travelling wave solutions:

$$ \begin{aligned} U_{5,6} \left( {x,t} \right) & = \mp \frac{{3\beta d\left( { - \beta^{2} + 4\alpha } \right)l^{2} }}{\rho } \pm \frac{{2\rho l^{2} \alpha d}}{{a\left( {b + 2c} \right)\left( { - \sqrt {\beta^{2} - 4\alpha } \cot \left( {\frac{1}{2}\sqrt {\beta^{2} - 4\alpha } \left( {\xi + k} \right)} \right) - \beta } \right)}}\,{\text{and}} \\ U_{7,8} \left( {x,t} \right) & = \mp \frac{{3\beta d\left( { - \beta^{2} + 4\alpha } \right)l^{2} }}{\rho } \pm \frac{{2\rho l^{2} \alpha d}}{{a\left( {b + 2c} \right)\left( {\sqrt { - \beta^{2} + 4\alpha } \tan \left( {\frac{1}{2}\sqrt { - \beta^{2} + 4\alpha } \left( {\xi + k} \right)} \right) - \beta } \right)}}, \\ \end{aligned} $$

where \(\rho =\sqrt{-6a\left(b+2c\right)\left(-{\beta }^{2}+4\alpha \right)}\).

Case III

Family 3: (when \({\upbeta }^{2}-4\alpha >0, \alpha \ne 0,\upbeta \ne 0\))

Using the solution of SAE and Eq. (11) into Eq. (17) we get following general travelling wave solutions:

$$ U_{9,10} \left( {x,t} \right) = \pm \frac{{\sqrt 6 \beta^{2} l^{2} d}}{{2\sqrt {a\left( {b + 2c} \right)} }} \pm \frac{{\sqrt 6 \sqrt {a\left( {b + 2c} \right)} \beta^{2} l^{2} d}}{{a\left( {b + 2c} \right)\left( {\exp \left( {\beta \left( {\xi + k} \right)} \right) - 1} \right)}}, $$

where \(\xi =l\left(x-\delta \frac{{t}^{\gamma }}{\gamma }\right).\)

Rational solution is excluded for its predefined circumstance.

Outcomes and discussions

In the following portion, we delve into the physical interpretation of the precise solutions derived for the couple DSW equation. We illustrate these solutions graphically, discussing their various types. The computational tools Maple-18 and MATLab were instrumental in solving the equations and producing graphical representations correspondingly.

Physical interpretation

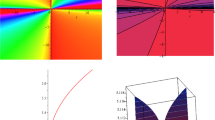
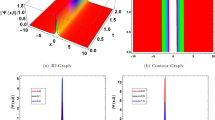
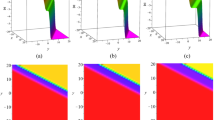
Herein subdivision, we unhurried the physical explanation of the exact outcomes of the projected equations by disbursing the \(\text{exp}\left(-\varphi \left(\xi \right)\right)\)-expansion approach. The derived solutions encompass hyperbolic, trigonometric, as well as rational functions. Figure 1, characterizes the soliton shape rises in hyperbolic function solutions for the function \({U}_{1} (x, t)\) with parameter values \(\alpha =2, \beta =4, a=1, b=-1, c=1, d=-3, l=-.5, k=4\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. Subfigures \((a, b, c)\) showcase 3D plot views, \((d)\) features the contour plot, and subfigures \((e, f, g)\) illustrate 2D line graphs for \(x=0\) corresponding to figures \((a, b, c),\) respectively. The 2D line chart displays the oscillations in frequency and amplitude, distinguishing between higher and lower values across the functional solutions. In Fig. 1, we detected that different solution outlines rise with the intensification of fractional order derivative. The solution changes singular soliton to dark soliton outline at the accumulative of fractional value \(\gamma =0.25\) and \(\gamma =0.50\) to \(\gamma =0.75\). At the increasing of fractional value \(\gamma = 0.25\) and 0.5 to \(\gamma =0.75\) the solution changes singular soliton to multiple soliton shape. The amplitude of the singular soliton is abated with the increase of unrestricted parameters \(a\) and \(b.\) On the contrary, the multiple soliton shape is comparatively slower with the variations of γ but spread faster with the decrease of the free variable of \(a\) as well \(b\). Figure 2, exhibits the multiple soliton shape for the function \({U}_{5} (x, t)\) with parameter values \(\alpha = 2, \beta = 2, a = 1, b = -1, c = 5, d = 1, l = -0.5, k = -4\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. The solution's form remains unchanged with variations in parameters. Figure 3, represents the kink type multiple soliton shape for the function \({U}_{5} (x, t)\) with parameter values \(=2, \beta =2, a=1, b=-1, c=5, d=1, l=-0.60, k=-4\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. Changing parameters does not result in any alterations to the solution's shape. In Fig. 4, the shape of the one-soliton solution is represented for the function \({U}_{8} (x, t)\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = 1, c = 2, d = 1, l = -0.15, k = -8\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. The solution's shape remains constant with parameter changes, showing only subtle fluctuations in amplitude and frequency. Figure 5 depicts the shape of the periodic soliton solution for the function \({U}_{8}(x, t)\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = 1, c = 2, d = 1, l = -0.30, k = -8\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. The modification of parameters leaves the solution shape unchanged. The shape of the periodic soliton solution is showcased in Fig. 6 for the function \({U}_{8}(x, t)\) with parameter values \(\alpha =2, \beta =0, a=1, b=1, c=2, d=1, l=-0.25, k=-8\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. No changes in the solution's shape are observed with parameter adjustments, only frequency and amplitude are slightly varied with the change of parameters. Figure 7, represents the three soliton solution for the function \({U}_{8} (x, t)\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = -1, c = 5, d = 1, l = 0.3, k = -4\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. Figure 8, represents the two soliton solution for the function \({U}_{8}(x, t)\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = 1, c = 2, d = 1, l = -0.20, k = -8\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. The solution's shape remains unaffected by changes in parameters.

Figure 1
figure 1

Capturing the dynamic evolution arising from the solution of \({U}_{1} (x, t)\) with parameter values \(\alpha =2, \beta =4, a=1, b=-1, c=1, d=-3, l=-.5, k=4.\) Subfigures (a),(b), and (c) present 3D perspectives, while subfigure (d) highlights a contour plot. Additionally, subfigures (e),(f), and (g) showcase 2D line graphs along \(x=0\), equivalent to the corresponding 3D plots in (a),(b), and (c).

Full size image
Figure 2
figure 2

Illustrating the dynamic performance emanating from the solution of \(\left|\text{Real }{U}_{5}(x, t)\right|\) with parameter values \(\alpha = 2, \beta = 2, a = 1, b = -1, c = 5, d = 1, l = -0.5, k = -4.\) Subfigures (a),(b), and (c) offer 3D perspectives, while subfigure (d) emphasizes a contour plot. Additionally, subfigures (e),(f), and (g) showcase 2D line graphs along \(x=0\), corresponding to the respective 3D plots in (a) to (c).

Full size image
Figure 3
figure 3

Taking the dynamic comportment developing from the solution of \(\left|\text{Real }{U}_{5}(x, t)\right|\) with parametric values \(\alpha =2, \beta =2, a=1, b=-1, c=5, d=1, l=-0.60, k=-4\). Subfigures \((\mathbf{a},\mathbf{b},\mathbf{c})\) cabinet 3D plot views, \((\mathbf{d})\) topographies the contour plot, and subfigures \((\mathbf{e},\mathbf{f},\mathbf{g})\) illustrate 2D line graphs for \(x=0\) corresponding to figures \((\mathbf{a},\mathbf{b},\mathbf{c}),\) correspondingly.

Full size image
Figure 4
figure 4

Illustrating the dynamic evolution ascending from the solution of \(\left|\text{Real }{U}_{8}(x, t)\right|\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = 1, c = 2, d = 1, l = -0.15, k = -8.\) Subfigures (a),(b), and (c) present 3D plot views, while subfigure (d) cabinets the contour plot. Moreover, subfigures (e),(f), and (g) depict 2D line graphs along \(x=0\), consistent to the corresponding 3D plots in (a) to (c).

Full size image
Figure 5
figure 5

Illustrating the dynamic evolution resulting from the solution of \(\left|\text{Real }{U}_{8}(x, t)\right|\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = 1, c = 2, d = 1, l = -0.30, k = -8.\) Subfigures (a),(b), and (c) offer 3D plot views, offering a comprehensive view of the evolving behavior. Subfigure (d) highlights a contour plot, offering additional insights into the solution. Furthermore, subfigures (e),(f), and (g) depict 2D line graphs along \(x=0,\) providing corresponding to the respective 3D plots in (a) to (c).

Full size image
Figure 6
figure 6

Capturing the dynamic evolution arising from the solution of \(\left|\text{Real }{U}_{8}(x, t)\right|\) with parameter values \(\alpha =2, \beta =0, a,b,c,d=1, l=-0.25, and k=-8.\) The subfigures (a),(b), and (c) present 3D perspectives, while subfigure (d) highlights a contour. Additionally, subfigures (e),(f), and (g) showcase 2D line graphs along \(x=0\), equivalent to the corresponding 3D plots in (a) to (c).

Full size image
Figure 7
figure 7

Illustrating the dynamic performance emanating from the solution of \(\left|\text{Real }{U}_{8}(x, t)\right|\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = -1, c = 5, d = 1, l = 0.3, k = -4.\) Subfigures (a),(b), and (c) offer 3D perspectives, while subfigure (d) emphasizes a contour plot. Furthermore, subfigures (e),(f), and (g) showcase 2D line graphs along \(x=0\), respected to the respective 3D plots in (a) to (c).

Full size image
Figure 8
figure 8

Illustrating the dynamic evolution resulting from the solution of \(\left|\text{Real }{U}_{8}(x, t)\right|\) with parameter values \(\alpha = 2, \beta = 0, a = 1, b = 1, c = 2, d = 1, l = -0.20, k = -8.\) Subfigures (a),(b), and (c) provide 3D plot views, offering a comprehensive view of the evolving behavior. Subfigure (d) highlights a contour plot, offering additional insights into the solution. Additionally, the subfigures (e),(f), and (g) depict 2D line graphs along \(x=0,\) providing equivalent to the corresponding 3D plots in (a) to (c).

Full size image

Graphical representation

In this part of the paper, graphical behavior of the obtained solutions of the couple DSW equation is discussed. In order to illustrate the dynamical behavior of the wave phenomena governed by the couple DSW equation, 3D, 2D and contour graphical simulations are generated. The parametric values are suitably selected in accordance with the proposed methodologies such that well-defined solution expressions are obtained. The 3D surface graph highlights the shape of the traveling wave or soliton whereas the contour graph illustrates the structure of the constructed wave through plots of level curves. The 2D line graphs of the solutions are also plotted for increasing values of time to illustrate the progression of the wave along- \(x\) axis.

All the graphs displayed above depicts the construction of multiple solitons, as well as periodic traveling waves, is a single unit solutions. A localized rise in wave amplitude is characteristic of the bright soliton. Because they may travel great distances, bright solitons are important. Singular solitons are crucial in scientific research because of their capacity to reflect extremely concentrated and localized events, making them useful tools for examining extreme behavior in physical systems. In the field of nonlinear dynamics, the solution serves as standards, making it easier to understand and characterize complex, nonlinear processes that defy linear models. Singular solitons are associated with shock waves and provide valuable information about the interaction and propagation of shock events via various materials. Additionally, contour graphics enhance the quality of studies by providing a visual representation of spatial patterns, facilitating data interpretation, facilitating effective communication, demystifying complex information, and increasing analytical depth. The study's overall robustness is further increased by their ability to highlight anomalies and support predictive modelling.

Comparison

The comparison of the conveyed outcomes with the preceding studies in the literature indicates that the offered results not only authorize some of the previously reported wave behavior for the coupled DSW equation but also provide more detailed insight into the traveling waves designated by the afore-mentioned equation. Bashar et al.39 have found the dynamical actions of the developed solutions in the arrangement of the bell, kink, kinky lump, multi-wave, interaction lump, periodic lump, and kink types have been exemplified but they failed to discuss the dynamical diversity of multiple soliton shape. Yao et al.40,41 used the algebraic method to find the closed-form travelling wave solutions but they did not focus on dynamical analysis of the obtained solutions. A group of scientist42,43,44 also found the traveling wave solutions of DSW equation including bright soliton and periodic wave but no periodic kink type soliton was not reported. These comparisons and observations confirm the novelty and significance of the results presented in the current manuscript.

In this portion, we have compared the achieved solutions with Bashar et al.39 solutions by the modified extended tanh method. Contrast between Bashar et al.39 solutions by the modified extended tanh technique and our solutions.

Bashar et al.39 solutions by modified extended tanh method

Our solutions by \(\text{exp}\left(-\varphi \left(\xi \right)\right)\)-expansion method

Hyperbolic solution because of \(\mathbf{\rm E}<0\)

\({V}_{\text{1,2}}=\mp 2\sqrt{-\frac{6\text{\rm E}}{\alpha \beta +2\alpha s} }{k}^{2}\eta \sqrt{-\text{\rm E}}\text{ tanh}(\sqrt{-\text{\rm E}}\zeta )\)

For the parametric values \(E=-1,\eta =\alpha =s=Z=1,\beta =2,k=0.55, {\Omega }_{0}={\Delta }_{1}=0\), figure demonstrates the bell shape of the solution \({U}_{\text{1,2}}(x,t)\) at the values of the fractional parameters \(\updelta =0.3\text{ to }0.50, { and \delta }=0.75\) to \(\updelta =0.98\) correspondingly

With the changes of fractional parameter \(\updelta \) there is no dynamical changes in the frequency and amplitude of the shape

Hyperbolic solution because of \((\mathbf{f}\mathbf{o}\mathbf{r}\boldsymbol{ }{{\varvec{\upbeta}}}^{2}-4\boldsymbol{\alpha }>0,\boldsymbol{ }\boldsymbol{\alpha }\ne 0)<0\)

\({U}_{\text{1,2}}\left(x,t\right)=\mp \frac{3\beta d\left({-\beta }^{2}+4\alpha \right){l}^{2}}{\rho }\pm \frac{2\rho {l}^{2}\alpha d}{a\left(b+2c\right)\left(-\sqrt{{\beta }^{2}-4\alpha }\text{tanh}\left(\frac{1}{2}\sqrt{{\beta }^{2}-4\alpha }\left(\xi +k\right)\right)-\beta \right)}\)

We have shown the dynamical changes of one soliton to multiple soliton shape rises in hyperbolic function solutions for the function \({U}_{\text{1,2}}, (x, t)\) with parameter values \(\alpha =2, \beta =4, a=1, b=-1, c=1, d=-3, l=-.5, k=4\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. We have clearly shown that with the change of fractional parameter \(\gamma =0.25\) , \(\gamma =0.50\) and \(\gamma =0.75\) the one soliton shape turned into the multiple soliton shape. This types of findings is very new in our study compared to Bashar’s et al.39 solutions

Trigonometric solution because of \(\mathbf{\rm E}>0\)

\({V}_{\text{21,22}}=\mp 2\sqrt{-\frac{6\text{\rm E}}{\alpha \beta +2\alpha s} }{k}^{2}\eta \sqrt{\text{\rm E}}\text{ tan}(\sqrt{\text{\rm E}}\zeta )\)

The periodic wave solution demonstrates from the solutions \({U}_{\text{21,22}}(x,t)\) for putting value of parameters \(E=0.1,\eta =-s=k=z=1,\beta =0.50,\alpha =2,{\Omega }_{0}={\Delta }_{1}=0\) where the values of the fractional parameters \(\updelta =0.30\text{ to}=0.50, { and \delta }=0.75\) to \(\updelta =0.98\) correspondingly. With the changes of fractional parameter \(\updelta \) there is no dynamical changes in the frequency and amplitude of the shape

Trigonometric solution because of \((\text{for }{\upbeta }^{2}-4\alpha <0, \alpha \ne 0)>0\)

\({U}_{\text{5,6}}\left(x,t\right)=\mp \frac{3\beta d\left({-\beta }^{2}+4\alpha \right){l}^{2}}{\rho }\pm \frac{2\rho {l}^{2}\alpha d}{a(b+2c)(\sqrt{{-\beta }^{2}+4\alpha }\text{tan}\left(\frac{1}{2}\sqrt{{-\beta }^{2}+4\alpha }\left(\xi +k\right)\right)-\beta )}\),

Figure 2, exhibits the multiple soliton shape for the function \({U}_{\text{5,6}} (x, t)\) with parameter values \(\alpha = 2, \beta = 2, a = 1, b = -1, c = 5, d = 1, l = -0.5, k = -4\) within the interval − 10 ≤ \(t\),\(x\) ≤ 10. The solution's form remains unchanged with variations in fractional parameters. If we put \({\upbeta }^{2}-4\alpha =E\) and \(\left(\eta ,Z,k\right)=\left(a,b,c\right)=1\) then our solution coincide the solution of Bashar’s et al.39. That is the multiple soliton shape turn into the periodic solution shape

Conclusion

This paper has effectively applied the \(exp(-\phi (\xi ))\)-expansion method to the DSW equation. Through our investigation, we have established novel solutions that depict diverse wave shapes, incorporating various unrestricted parameters. The wave outlines have been visually represented through 3D and 2D plots, along with contour plots, providing a comprehensive understanding of the impact of free parameters on the DSW equation. Notably, variations in the free parameters lead to changes in both wave amplitude and phase components. Our comprehensive study underscores the efficacy of the \(exp(-\phi (\xi ))\)-expansion method as a potent mathematical tool. Its application not only facilitates the discovery of numerous solutions for various types of NLEEs but also proves invaluable in the fields of water wave mechanics, ocean engineering, and scientific research. The results of our analysis showed that the recommended methods were straightforward, trustworthy, and efficient. The versatility of this approach suggested that more nonlinear partial differential equations might be analytically solved using it in the future. This study provided analytical solutions and insightful information by offering a comprehensive exploration of the solitary wave dynamics for the DSW equation through numerical simulations. By contrasting the results with those from earlier research, the significance and originality of the obtained results were determined. Fractional order derivative will be used to study the DSW equation in the future in order to obtain more intriguing and practical findings.