Introduction

During the onset of a large-scale infectious disease (in fact, humanity currently lacks the ability and technology to completely eradicate large-scale infectious diseases like COVID-19), conducting widespread nucleic acid testing and isolating positive cases can effectively prevent and interrupt the spread. However, large-scale nucleic acid testing requires substantial human and material resources, and the efficiency of testing negatively impacts societal operational efficiency.

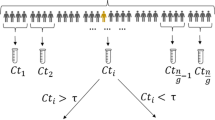
Pooled testing in mass infectious disease surveillance refers to a strategy where samples from multiple individuals are combined, or “pooled,” and tested together as a single unit. This approach is particularly useful when dealing with a large number of samples, such as in the case of mass testing for infectious diseases like COVID-19. Instead of conducting individual tests for each person, samples are grouped into pools. If a pool tests negative, it is assumed that all individuals within that pool are negative. If a pool tests positive, further individual testing needs to be conducted to identify the infected samples.

Pooled testing is a good strategy commonly used in public health efforts, especially during pandemics or large-scale infectious disease surveillance. In the past COVID-191,2,3,4 epidemics, the pooled nucleic acid testing5,6,7 is the most important means to find COVID-19 patients. COVID-19 pooled nucleic acid testing for large populations is usually 10 people per group, that is, the tests from 10 people are placed in the same test tube. The negative result means that there is no infection in this group. Otherwise someone in this group definitely has been infected.

An important question arises: what is the optimal number of samples to pool together for testing? Testing all samples together clearly lacks differentiation, while testing each individual’s sample separately would require a prohibitively large number of tests. On the other hand, in the early stages of an outbreak with low infection rates and a large population, widespread testing can promptly help interrupt the spread of the epidemic. Therefore, the efficiency of pooled testing is crucial for large-scale testing scenarios. It is worthwhile to consider optimizing the number of samples in each pool, i.e., the allocation scheme, to improve efficiency and reduce the total cost of pooled testing8,9,10.

As an emerging field of study, granular computing (GrC)11,12,13,14,15,16,17,18 divides the problem space into many subspaces that form a hierarchical structure before solving the problem. Granularity selection19,20 is a prosperous issue in GrC, which aims to search an appropriate granularity to improve the efficiency of solving problems. Granular computing models are particularly well-suited for optimization challenges like pooled testing. First, GrC models excel in creating hierarchical structures that break down complex problems into more manageable subproblems. In pooled testing, this ability allows for a systematic exploration of different grouping strategies, helping to identify the most cost-effective configuration. Second, GrC models can operate at various levels of detail, or granularity. This flexibility is crucial in pooled testing optimization, where the optimal group size may vary depending on the prevalence of the infectious disease and other factors. By adjusting the granularity, GrC models can dynamically find the best grouping strategy. Third, The use of fuzzy equivalence relations in GrC enables the handling of uncertainties and imprecise information, which are inherent in real-world testing scenarios. This feature is particularly beneficial in optimizing pooled testing, where exact outcomes and costs can be uncertain. As an effective GrC model for uncertain information processing, quotient space theory (HQS)21,22 involves the human ability to perceive the real world at different granularities. The HQS structure provides a more effective means to make inferences based on fuzzy equivalence relations21.

To address this optimization challenge, this paper introduces an efficient multi-granularity search model based on statistical expectations. By analyzing probability variations across different granular levels and integrating quotient space theory, the proposed method effectively identifies low-probability events quickly, offering a new approach for handling such events. This study primarily addresses the issue of testing cost control during the early stages of an outbreak within a large population. By reasonably applying the pooled testing method to the population and designing a rational allocation strategy, the proposed method can identify the optimal testing strategy, significantly reducing the number of tests and ultimately lowering both social and economic costs.

Specifically, this model transforms pooled groups into multilevel structures, decomposing complex problems into several sub-tasks, allowing for more flexible and optimized group allocations. We leverage the extension of fuzzy equivalence relations-hierarchical quotient space (HQS)-to develop a cost-sensitive multi-granularity decision model. This model considers both testing and collection costs, aiming to minimize the total cost through optimal grouping strategies. Through this hierarchical framework, we systematically explore various group allocations and identify the most cost-effective strategy for large-scale infectious disease testing.

The experimental results presented in this paper, based on both simulated and real data, demonstrate the effectiveness of the proposed models in reducing testing costs and enhancing efficiency, particularly in scenarios with fixed numbers of individuals and varying positive probabilities.

The main contributions of this paper are as follows:

  • This paper proposes a novel efficient search model and granularity computation method based on statistical expectations. By integrating HQS theory, it achieves favorable results in quickly identifying individuals with low-probability events within a large scope, providing a new approach for rapidly handling such events.

  • More than single-granularity optimization method, this paper further develops two multi-granularity approaches for pooled testing. These methods are designed to identify the optimal hierarchical grouping, significantly advancing the field of pooled testing by enhancing efficiency.

  • On both simulated datasets and real COVID-19 datasets, the experimental results validate that the proposed methods can effectively reduce testing costs. Furthermore, this paper discusses potential issues related to varying infection rates in practical applications and provides relevant solutions, offering essential guidance on applying these methods in real-world scenarios.

Related works

As an emerging field of study, granular computing (GrC)11,12,13,14,15,16,17,18 is an umbrella term for a category of models inspired by human cognitive processes. Each GrC model has its own method for solving problems. Fundamentally, there are three main GrC models: fuzzy sets23,24,25, quotient space21,22, and rough sets26,27,28. At present, GrC has received much attention20,29,30,31,32,33,34,35,36,37. Pedrycz29,30 proposed the principle of justifiable granularity by combining the construction and optimization method of granularity. Yao31,32,36 studied the two fields of three-way decisions and granular computing, and further proposed three-way GrC based on the idea of cognitive science, which explained the basic concept of GrC based on the philosophy of three-way decisions. Wang33,38 summarized the works on GrC from three aspects: granularity optimization, granularity switching, and multi-granularity computing. Song34 described the ability of granular neural networks to process complex non-numerical data or numerical, by comprehensively reviewing different types of granular neural networks. Qi37 introduced the idea of GrC into the traditional data analysis theory, and combined formal concept analysis with GrC to form a multi-granularity analysis method. Li35 discussed in detail the existing multi-granularity analysis methods from different perspectives.

As a GrC model, hierarchical quotient space abstract and consider only those things that serve a specific interest, and to switch among different granularities. The HQS model is a typical representation for multi-granulation spaces. As a tool for the essential description of fuzzy equivalence relations, the current quotient space theory has been applied to many fields of artificial intelligence39,40,41,42,43, including knowledge graphs39,44, medical science40,45, data processing41,42,46, and applied mathematics43,47. Recently, Zhang48 presented a covering algorithm based on quotient space granularity analysis on spark, which is a scalable approach for accurate web service recommendation in large-scale scenarios. Orthey49 proposed the quotient-space rapidly-exploring random trees, which grows trees on the quotient-spaces both sequentially and simultaneously to guarantee a dense coverage. Lu50 proposed a case retrieval algorithm based on granularity synthesis theory, which introduced quotient space into the similarity calculation based on attribute.

Moreover, progress has been made in soft computing and fuzzy intelligence. For example, Kang et. al51 propose a stratified decision-making strategy by expolit the stratified fuzzy multi-criteria decision making approach. Geetha et. al extend the Stepwise Weight Assessment Ratio Analysis (SWARA) method with hesitant fuzzy (HF) set for calculating the weights of the criteria and ranking the alternatives by using VIKOR method52. The proposed method are demonstrated through numerical examples. Prabu et. al53 propose an Intuitionistic FCM (IFCM) algorithm is for medical image segmentation and obtain better performance than FCM.Narayanamoorthy et al. introduce innovative methodologies integrating fuzzy logic and decision-making techniques to address complex environmental and transportation challenges, aiming to optimize solutions amidst uncertainty and improve decision-making processes54,55,56.

Ethical approval

No humans are involved in our study, and as such, the requirements regarding experiments on humans, institutional approvals, and informed consent are not applicable to our manuscript.

Preliminaries

To facilitate the discussion in this paper, this section reviews the related concepts of granular computing and quotient space. Suppose that U is a finite domain and non-empty set and \({R\subseteq U\times U}\) is an equivalence relation on U.

Definition 1

(Granular structure)33 In granular computing, data with similar relationships form information granules (IG). All IG are obtained by the granulation criterion for a practical problem. And the relationship between IG constitutes a granular layer. The structure, consisting of the granular layer used for representing and interpreting a problem, is called a granular structure.

Figure 1 shows the entire granular structure. The granular layer is an abstract description of the problem space. Herein, \(Layer_k\) represents the finest layer, and each node represents the finest data. Due to the diversification of granulation degree and application requirements, data in the same problem space will produce different granular layers according to the granulation criteria of different requirements.

Suppose that U/R constitutes a partition of U, according to Definition 1, which is called a granular layer or granular space, denoted by \(K_R\) in this paper. Equivalence classes in U/R is referred to information granule. Moreover, let \(K = (U, {\mathfrak {R}})\) be a knowledge base, where \({\mathfrak {R}}\) is a family of equivalence relations. If \(R_1, R_2\in {\mathfrak {R}}\), \(K_{R_1}= \{ p_1, p_2,..., p_l \}\) and \(K_{R_2} = \{q_1, q_2, ..., q_m \}\) are two granular spaces induced by \(R_1\), \(R_2\). \(\forall _{p_i \in K_{R_1}} (\exists _{q_j \in K_{R_2}} (p_i \subseteq q_j))\), then \(K_{R_1}\) is finer than \(K_{R_2}\), denoted by \(K_{R_1} \preceq K_{R_2}\). If \(\forall _{p_i \in K_{R_1}} (\exists _{q_j \in K_{R_2}} (p_i \subset q_j))\), then \(K_{R_1}\) is strictly finer than \(K_{R_2}\), denoted by \(K_{R_1} \prec K_{R_2}\).

Figure 1
figure 1

The diagram of information granule, granularity layer, and granularity structure.

Full size image

Definition 2

(Fuzzy equivalence relation)21 If \({\widetilde{R}}\) satisfies the following conditions:

  1. (1)

    \(\forall x \in U, {\widetilde{R}}(x,x) = 1\).

  2. (2)

    \(\forall x,y \in U, {\widetilde{R}}(x,y) = {\widetilde{R}}(y,x)\).

  3. (3)

    \(\forall x,y,z \in U, {\widetilde{R}}(x,z) \ge {\sup _{y \in X}} \min ({\widetilde{R}}(x,y),{\widetilde{R}}(y,z))\).

Then \({\widetilde{R}}\) is a fuzzy equivalence relation on U.

Definition 3

(\(\lambda\)-cut relation)21 Suppose \({\widetilde{R}}\) is a fuzzy equivalence relation on U, and \({\widetilde{R}}_{\lambda }=\{\langle x, y\rangle \mid {\widetilde{R}}(x, y) \geqslant \lambda \}\) (\(0 \leqslant \lambda \leqslant 1\)). Then \({\widetilde{R}}_{\lambda }\) is called a \(\lambda\)-cut relation of \({\widetilde{R}}\), and its corresponding quotient space is denoted by \(U/{\widetilde{R}}_{\lambda }\).

Definition 4

(Hierarchical quotient space, HQS)21 Suppose \({\widetilde{R}}\) is a fuzzy equivalence relation on U and \(D=\{{\widetilde{R}}(x, y) \mid x \in U \wedge y \in U \wedge {\widetilde{R}}(x, y)>0\}\) is a value domain of \({\widetilde{R}}\), then \(\pi _{{\widetilde{R}}}(U)=\{U / {\widetilde{R}}_{\lambda } \mid \lambda \in D\}\) is called a hierarchical quotient space of \({\widetilde{R}}\).

In a HQS \(\pi _{{\widetilde{R}}}(U)\) corresponding to \({\widetilde{R}}\), if \(0 \leqslant \lambda _{1}<\lambda _{2}<\cdots <\lambda _{t} \leqslant 1\), then \(U / {\widetilde{R}}_{\lambda _{t}} \preceq U / {\widetilde{R}}_{\lambda _{t-1}} \preceq \cdots \preceq U / {\widetilde{R}}_{\lambda _{1}}\)

Example

Suppose \(U=\left\{ x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}\), \({\widetilde{R}}\) is a fuzzy equivalence relation on U and the corresponding fuzzy equivalence relation matrix \(M_{{\widetilde{R}}}\) as follows:

$$\begin{aligned} M_{{\widetilde{R}}}=\left[ \begin{array}{ccccc} 1 &{} 0.2 &{} 0.6 &{} 0.4 &{} 0.4 \\ 0.2 &{} 1 &{} 0.2 &{} 0.2 &{} 0.2 \\ 0.6 &{} 0.2 &{} 1 &{} 0.4 &{} 0.4 \\ 0.4 &{} 0.2 &{} 0.4 &{} 1 &{} 0.8 \\ 0.4 &{} 0.2 &{} 0.4 &{} 0.8 &{} 1 \end{array}\right] . \end{aligned}$$

Then its corresponding HQS \(\pi _{{\widetilde{R}}}(U)\) is:

\(U / {\widetilde{R}}_{\lambda _{1}}=\left\{ \left\{ x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\} \right\}\), where \(0<\lambda _{1} \leqslant 0.2\);

\(U / {\widetilde{R}}_{\lambda _{2}}=\left\{ \left\{ x_{1}, x_{3}, x_{4}, x_{5}\right\} ,\left\{ x_{2}\right\} \right\}\), where \(0.2<\lambda _{2} \leqslant 0.4\);

\(U / {\widetilde{R}}_{\lambda _{3}}=\left\{ \left\{ x_{1}, x_{3}\right\} ,\left\{ x_{4}, x_{5}\right\} ,\left\{ x_{2}\right\} \right\}\), where \(0.4<\lambda _{3} \leqslant 0.6\);

\(U / {\widetilde{R}}_{\lambda _{4}}=\left\{ \left\{ x_{1}\right\} ,\left\{ x_{3}\right\} ,\left\{ x_{4}, x_{5}\right\} ,\left\{ x_{2}\right\} \right\}\), where \(0.6<\lambda _{4} \leqslant 0.8\);

\(U/{\widetilde{R}}_{\lambda _{5}}=\left\{ \left\{ x_{1}\right\} ,\left\{ x_{3}\right\} ,\left\{ x_{4}\right\} ,\left\{ x_{5}\right\} ,\left\{ x_{2}\right\} \right\}\), where \(0.8<\lambda _{5} \leqslant 1\).

Single-granularity model for pooled testing

In the context of pooled testing, consider a sample set with a size denoted as N, and randomly divide it into M groups, i.e. the size of each group is \(k_{1}=N / M\). The probability of being positive for each individual is p, while the probability of being negative for each individual is \(q=1-p\). The cost of pooled testing and one pooled testing collection is denoted by \(t_{1}\) and \(t_{2}\), respectively. The probability distribution corresponding to the number of pooled testings and the collections after testing are shown in Tables 1 and  2, respectively.

Table 1 Probability distribution of the number of pooled testing.
Full size table
Table 2 Probability distribution of the number of collections after pooled testing.
Full size table

The mathematical expectation of \(X_{1}\) can be obtained:

$$\begin{aligned} E\left( X_{1}\right) =q^{k_{1}} \frac{1}{k_{1}}+\left( 1+\frac{1}{k_{1}}\right) \left( 1-q^{k_{1}}\right) . \end{aligned}$$
(1)

Then the average testing \({\text {cost}}\) required by N individuals is:

$$\begin{aligned} T C_{1}=N t_{1}\left( q^{k_{1}} \frac{1}{k_{1}}+\left( 1+\frac{1}{k_{1}}\right) \left( 1-q^{k_{1}}\right) \right) . \end{aligned}$$
(2)
  1. (1)

    Therefore, the average testing cost for N individuals is less than \(N t_{1}\). The average collection cost required for N individuals after pooled testing is:

$$\begin{aligned} TC_{2}=N t_{2}\left( 1-q^{k_{1}}\right) . \end{aligned}$$
(3)
  1. (2)

    Thus, the total cost is:

$$\begin{aligned} TC=TC_{1}+TC_{2}=N t_{1}\left( q^{k_{1}}\frac{1}{k_{1}}+\left( 1+\frac{1}{k_{1}}\right) \left( 1-q^{k_{1}}\right) \right) \ +Nt_{2}\left( 1-q^{k_{1}}\right) . \end{aligned}$$
(4)

Example

Suppose that 10000 people are tested for nucleic acid at \(p=0.0001\) and \(t_{1}=t_{2}=10\). If the current method of allocating tests in groups of 10 people \(\left( k_{1}=10\right)\) is followed, the testing cost is \(T C_{1}=10^{5} t_{1}\left( q^{10} \frac{1}{10}+\left( 1+\frac{1}{10}\right) \left( 1-q^{10}\right) \right)\). If a group is tested to be positive, all the people in this positive group need to be collected again for nucleic acid, then the collection cost is \(TC_{2}=10^{4}t_{2}\left( 1-q^{10}\right)\).

The total cost is:

$$\begin{aligned} TC = 10^{5} \left( 0.9999^{10} \cdot \frac{1}{10} + \left( 1 +\frac{1}{10}\right) \left( 1-0.9999^{10}\right) \right) + 10^{5} \left( 1 - 0.9999^{10}\right) = 102000. \end{aligned}$$

If allocating tests in groups of 20 people \(\left( k_{1}=20\right)\), then the total cost will be:

$$\begin{aligned} TC=10^{5}\left( 0.9999^{20}\cdot \frac{1}{20}+\left( 1+\frac{1}{20}\right) \left( 1-0.9999^{20}\right) \right) +10^{5}\left( 1-0.9999^{20}\right) =54000. \end{aligned}$$

Obviously, the total cost of pooled testing in groups of 20 is nearly half of that in groups of 10. Therefore, the current pooled testing in groups of 10 is not the best solution. From the perspective of cost, this paper proposes a novel single-granularity model for pooled testing (SGrC_NAD). Figure 2 displays a schematic of SGrC_NAD, where the nodes in each layer represent various groups. Herein, red node means that there are positive tests in this group, while white node means that all tests in this group are negative. The detailed process of SGrC_NAD is shown in Algorithm 1.

Figure 2
figure 2

The schematic of SGrC_NAD.

Full size image
Algorithm 1
figure a

Single-granularity model for pooled testing (SGrC_NAD).

Full size image

Theorem 1

\(TC_{2}\) decreases with the increasing number of groups M.

Proof

From Eq. 3, \(TC_{2}=Nt_{2}\left( 1-q^{k_{1}}\right)\).

Because \(k_{1}=N / M\), we have \(T C_{2}=N t_{2}\left( 1-q^{N / M}\right)\).

Therefore, N/M decreases when M increases, then \(q^{N / M}\) increases because \(q<1\), obviously \(1-q^{N / M}\) will decrease.

Finally, it is clear that \(TC_{2}\) decreases with M increases. \(\square\)

Cost-sensitive multi-granularity model for pooled testing

For a complex problem, traditional problem solving models at a single granularity are no longer applicable. In GrC, the complex problem usually needs to be decomposed into multiple subtasks. The “coarse to fine” progressive multi-granularity cognitive model adapts the decision-action decomposition mechanism, i.e., the cognitive behavior is decomposed into different stages, and a corresponding cognitive result can be obtained in each stage. From a multi-granularity perspective, a progressive decomposition of complex problem for solution, that is, solving the problem at joint multi-granularity layers is able to significantly improve the solution efficiency.

In this section, the single-granularity model for pooled testing mentioned above is extended to the case of multiple layers. Then two multi-granularity models for pooled testing are constructed, which can search for the optimal hierarchical group are constructed. The Fig. 3 is the schematic of multi-granularity model for pooled testing. The nodes in each layer represent various groups (test set). Herein, red node denotes that there are positive tests in this group, while white node denotes that all tests in this group are negative. The probability distribution laws corresponding to the number of pooled testing and nucleic acid collections after the tests in \(L_{th}\) layer are shown in Tables 3 and 4, respectively.

Figure 3
figure 3

The schematic of multi-granularity model for pooled testing.

Full size image
Table 3 Probability distribution of the number of pooled testing.
Full size table
Table 4 Probability distribution of the number of collections after pooled testing.
Full size table

Then the average testing cost of \(L_{th}\) layer for N individuals required is:

$$\begin{aligned} \begin{aligned} TC_{1}^{L} = Nt_{1} \left( {q^{{k_{1} }} \frac{1}{{k_{1} }} + \sum \limits _{{i = 2}}^{L} {\left( {\sum \limits _{{j = 1}}^{{\text {i}}} {\frac{1}{{k_{j} }}\left[ {\prod \limits _{{j = 1}}^{{i - 1}} {(1 - q^{{k_{j} }} )} } \right] q^{{k_{i} }} } } \right) } + \left( {1 + \frac{L}{{k_{L} }}} \right) \prod \limits _{{i = 1}}^{L} {(1 - q^{{k_{i} }} )} } \right) .\end{aligned} \end{aligned}$$
(5)

The average collection cost of of \(L_{th}\) layer required for N individuals after pooled testing is:

$$\begin{aligned} TC_{2}^L = N{t_2}(1 - {q^{{k_L}}}). \end{aligned}$$
(6)

Therefore, the total cost is:

$$\begin{aligned} \begin{aligned} TC^{L} = TC_{1}^{L} + TC_{2}^{L} = Nt_{1} \left( {q^{{k_{1} }} \frac{1}{{k_{1} }} + \sum \limits _{{i = 2}}^{L} {\left( {\sum \limits _{{j = 1}}^{{\text {i}}} {\frac{1}{{k_{j} }}\left[ {\prod \limits _{{j = 1}}^{{i - 1}} {(1 - q^{{k_{j} }} )} } \right] q^{{k_{i} }} } } \right) } + \left( {1 + \frac{L}{{k_{L} }}} \right) \prod \limits _{{j = 1}}^{L} {(1 - q^{{k_{i} }} )} } \right) + Nt_{2} (1 - q^{{k_{L} }} ). \end{aligned} \end{aligned}$$
(7)

Where \({k_l} = {N \bigg / {\prod \limits _{i = 1}^L {{M_i}} }}\).

The mathematical expectation of X can be obtained:

$$\begin{aligned} \begin{aligned} E({X_1}) = {q^{{k_1}}}\frac{1}{{{k_1}}} + (1 + \frac{1}{{{k_1}}})(1 - {q^{{k_1}}}). \end{aligned} \end{aligned}$$
(8)
Algorithm 2
figure b

Multi-granularity model for pooled testing (MGrC_NAD).

Full size image

The detailed process of MGrC_NAD is shown in Algorithm 2. Compared to Algorithm 1, Algorithm 2 is able to search for the optimal hierarchical group, which improves the efficiency from the perspective of GrC. However, when N is fixed, Algorithm 2 results in excessive size in each group or too many layers. Moreover, the occurrence of uneven distribution of people number in each group is handled by Algorithm 2 in a rounded manner. This leads to calculation error of expectations, which in turn affects the final stratification results. To solve this problem and further improve the efficiency of Algorithm 2, this paper proposes an improved multi-granularity model for pooled testing (IMGrC_NAD) as shown in Algorithm 3.

Algorithm 3
figure c

Improved multi-granularity model for pooled testing (IMGrC_NAD).

Full size image

Algorithm 3 adpots the averaging method to calculate the expectation. Therefore, compared with Algorithm 2, Algorithm 3 reduces the number of layers and the number of peoples in each group at the cost of a small increase in tests number, which can greatly reduce the running time and is more suitable to the real situation of pooled testing.

Computational complexity analysis

The computational complexity of the Single-granularity Model (SGrC_NAD) is \(O(N)\), primarily determined by the grouping process. The Multi-granularity Model (MGrC_NAD) has a complexity of \(O(N^{\frac{3}{2}})\). The literature computational complexity of the improved Multi-granularity Model (IMGrC_NAD) is \(O(N^{\frac{3}{2}})\). However, in practical applications, the MGrC_NAD model first determines the number of groups and then determines the number of individuals per group. This can lead to uneven group sizes, resulting in errors in expectation calculations and ultimately affecting the grouping results. On the other hand, the IMGrC_NAD algorithm first determines the number of individuals per group and then determines the number of groups. For groups that cannot be evenly divided, the IMGrC_NAD algorithm introduces a method for calculating expectations for uneven groups, further improving the accuracy of the grouping. From practical applications, for each layer, when \(N\) is the same, the time complexity of the MGrC_NAD algorithm is xxx, while the time complexity of the IMGrC_NAD algorithm is \(O(\sqrt{N} \times N/2)\). Compared to MGrC_NAD, this reduces the computational cost. While MGrC_NAD and IMGrC_NAD have higher theoretical complexities, their optimized strategies significantly enhance testing efficiency and reduce costs in practical applications.

Experiments and analysis

The above sections have discussed three cost-sensitive GrC models of pooled testing ( SGrC_NAD, MGrC_NAD, and IMGrC_NAD). In this section, we will validate the models proposed in this paper through relevant experiments. The hardware configuration of the experiments is a desktop computer with Intel i5-10500 CPU, 8G RAM, and Windows 10 64 bit OS, and MATLAB R2022a (https://ww2.mathworks.cn/en/products/new_products/release2022a.html) software is used for simulation.

Figure 4
figure 4

Comparisons of testing cost for three GrC models with different numbers of people.

Full size image

Figure 4 shows the comparisons of testing cost for three GrC models under fixed number of people in the worst case. The testing cost of MGrC_NAD and IMGrC_NAD are much lower than that of SGrC_NAD at different sizes of the number of people. Furthermore, to some extent, the testing cost of IMGrC_NAD is less than that of MGrC_NAD with the positive probability decreases.

Figure 5
figure 5

Comparisons of testing cost for three GrC models with different positive probabilities.

Full size image

Figure 5 shows that the comparisons of testing cost for three GrC models under fixed positive probability in the worst case. When the number of people increases to a certain level, the testing cost of MGrC_NAD and IMGrC_NAD are much lower than that of SGrC_NAD at different positive probabilities. Furthermore, the testing cost of IMGrC_NAD is less than that of MGrC_NAD with the number of people increases.

Table 5 Related results of IMGrC_NAD under different positive probabilities \(N=10^{6}\).
Full size table

Table 5 lists the related results of IMGrC_NAD under different positive probabilities, including the number of people in each group, the optimal layer, and its corresponding expectation. Obviously, the expectation becomes smaller, and \(G{L_{opt}}\) becomes deeper as the probability decreases.

Furthermore, to verify the testing efficiency of MGrC_NAD and IMGrC_NAD compared with SGrC_NAD, two test sets are introduced. For test set 1, \(N_{1} = 10^{4}\), and for test set 2, \(N_{2} = 10^{6}\). Suppose that the number of tests of SGrC_NAD is denoted as \(S_{s}\), and the number of tests of MGrC_NAD or IMGrC_NAD is denoted as \(M_{s}\). Then the testing efficiency increment is defined as follows:

$$\begin{aligned} \Delta Efficient = \frac{{{M_s} - {S_s}}}{{{S_s}}} \times 100\%. \end{aligned}$$
(9)

Figure 6 shows the testing efficiency increment of MGrC_NAD and IMGrC_NAD, respectively. It is clear that whether MGrC_NAD or IMGrC_NAD, they are much more efficient than SGrC_NAD under different positive probabilities. \(\Delta Efficient\) of IMGrC_NAD increases monotonically with decreasing positive probability. Moreover, \(\Delta Efficient\) of IMGrC_NAD is greater than that of MGrC_NAD in most cases.

Figure 6
figure 6

The testing efficiency increment of MGrC_NAD and IMGrC_NAD.

Full size image

Furthermore, to compare the efficiency of IMGrC_NAD and MGrC_NAD, suppose that the running time of MGrC_NAD and IMGrC_NAD is denoted as \(T_{1}\) and \(T_{2}\), respectively. Then we define the parameter \(\Delta OET\) as follows:

$$\begin{aligned} \Delta OET = \frac{{{T_1} - {T_2}}}{{{T_1}}} \times 100\%. \end{aligned}$$
(10)

From Fig. 7, in terms of efficiency, IMGrC_NAD is much higher than MGrC_NAD in different cases. This is because that IMGrC_NAD greatly reduce the number of layers and the number of peoples in each group, which enables a significant reduction in running time.

Figure 7
figure 7

The efficiency increment of IMGrC_NAD over MGrC_NAD in different cases.

Full size image

Figure 8 shows that the comparisons of total cost for three GrC models in different cases, where we suppose that testing cost and collection cost are 50 and 1 for each people, that is \(t_1 = 50\) and \(t_2 = 1\). It is obviously that the total cost of MGrC_NAD and IMGrC_NAD are much lower than that of SGrC_NAD. Especially, as the positive probability decreases, the total cost of MGrC_NAD and IMGrC_NAD is significantly lower than SGrC_NAD. Moreover,the total cost of IMGrC_NAD is always less than the one of MGrC_NAD under different positive probabilities.

Figure 8
figure 8

Comparisons of total cost for three GrC models.

Full size image

In order to better evaluate the application of our algorithm in practical testing scenarios, we utilized data from the COVID-19 resource center at Johns Hopkins University. The specific dataset used is “COVID-19: Daily tests vs. daily new confirmed cases per million,” which can be accessed through this link (https://ourworldindata.org/grapher/covid-19-daily-tests-vs-daily-new-confirmed-cases-per-million?country=BHS BRB BMU DOM SLV GRD HTI JAM MEX PAN PRI KNA LCA VCT TTO USA VIR). We extracted COVID-19 data for five countries from June 22, 2022.

In our experiments, we compared the number of tests required using the single-granularity approach and the multi-granularity approach under worst-case scenarios. This comparison aimed to demonstrate the efficiency and effectiveness of the proposed multi-granularity decision model in real-world applications, specifically in the context of COVID-19 testing. The details data are shown in Table 6. This table lists the actual infection rates for five countries. Considering the potential increase in infection rates during the testing process, we adjusted the actual infection rates upward (please see the column of ’Increased Probability’ in Table 6). Even with this adjustment, the proposed method still maintains a significant advantage in the actual number of tests required. As can be seen from the last two columns of Table 6, the number of tests without using the multi-granularity layered testing method (second-to-last column) is about 2 to 9 times higher than the number of tests required using our method (last column). Bold numbers in Table 6 indicate the number of tests required by the proposed IMGrC_NAD model. These bold reflects the most efficient testing strategy to minimize the number of total tests while maintaining accuracy and coverage in large-scale nucleic acid testing.

Table 6 Comparison of single-granularity and multi-granularity testing in different countries.
Full size table

Discussion and case study

The above experimental results demonstrate the effectiveness of three cost-sensitive GrC models for pooled testing (SGrC_NAD, MGrC_NAD, and IMGrC_NAD). As shown in Fig. 4, the MGrC_NAD and IMGrC_NAD models exhibit significant efficiency improvements over SGrC_NAD when the infection rate exceeds 1‰. Interestingly, this 1‰infection rate appears to be a critical threshold. However, it is important to note that even above the 1‰infection rate, our models still significantly reduce the number of tests compared to the single-granularity model. The experimental results in Fig. 4 indicate that our models achieve more noticeable savings in the number of tests at lower infection rates. Additionally, when comparing different population sizes, such as Fig. 4c versus f, it is evident that the larger the population, the more stable the model performance. The lower bound on the number of tests generated by the multi-granularity model is consistently about \(N \times 0.1\) fewer than that of the single-granularity model. This further illustrates that our method is most suitable for scenarios with low infection rates and large populations.

From a practical application perspective, we compared the number of tests required using the single-granularity method and the multi-granularity method under worst-case scenarios. As seen in Table 6, for a population size of 1 million, the single-granularity method requires about 100k tests, whereas the multi-granularity method reduces the number of tests to approximately 11k to 41k. The main influencing variable here is the size of the positive probability, i.e., the infection rate. The experimental results (Table 6) show that for Lithuania, with a relatively low infection rate, the multi-granularity method achieves a \(\Delta Efficient\) of up to 89%. In contrast, for Israel, the \(\Delta Efficient\) drops to 62.5%. Notably, for Switzerland, to simulate the change in infection rate, we increased the actual infection rate by 6 percentage points, resulting in a \(\Delta Efficient\) of 76.9% for the multi-granularity model. However, for the United States, which has a similar infection rate to Switzerland, we conservatively increased the infection rate by 59.7%, reaching 0.05%. The multi-granularity model achieved a \(\Delta Efficient\) of 74% on the United States data. This indicates that changes in the infection rate do not significantly affect the testing efficiency increment of the multi-granularity model.

To enhance understanding of the ideas and execution steps of our model among a broader audience, we have added a specific case study to demonstrate our approach. This algorithm utilizes an expectation model to construct multi-layered testing, where the number of individuals per group and the number of layers are determined by the total number of individuals to be tested and the probability of disease.

For example, suppose there are \(N = 10,000\) individuals to be tested with a disease probability of \(p = 0.001\), resulting in a maximum of \(M = N \times p = 10\) confirmed cases.

The hierarchical nucleic acid testing algorithm is structured as Table 7:

Table 7 Number of groups and individuals per group in different layers.
Full size table
Figure 9
figure 9

The decision process for 10000 people’s case study.

Full size image

As the Fig. 9 shows, when testing 10,000 people, with 10 infected individuals, assume the worst-case testing scenario where the first layer has 313 groups, each with 32 people. In this scenario, there is 1 infected individual per group, so at most 10 groups will test positive. These 10 groups need to be retested in the second layer.

For the second layer, the positive 10 groups from the first layer are each split into 2 groups of 16 people. At this stage, there will be 1 group testing positive, which needs to be retested.

In the third layer, the positive group from the second layer is split into 2 groups of 8 people. Again, there will be 1 group testing positive, which needs to be retested.

In the fourth layer, the positive group from the third layer is split into 2 groups of 4 people. There will again be 1 group testing positive, which needs to be retested.

In the fifth layer, each individual is tested separately to finally identify the infected individuals.

The total number of tests required is:

$$\begin{aligned} 313 + 10 \times (2 + 2 + 2 + 4) = 413 \end{aligned}$$

Conclusion

GrC is a new concept and computational paradigm in the current artificial intelligence field, which adopts a multi-level decomposition solution model for the structured analysis of complex problems. From the perspective of GrC, selecting the optimal granularity for handling the uncertainty problems is a crucial issue. In this paper, to further reduce the cost and improve the efficiency of pooled testing, drawing on the idea of HQS which is an extension of fuzzy equivalence relation, we propose two cost-sensitive multi-granularity models for pooled testing, which is able to search the optimal hierarchical group. Finally, the experimental simulation results show that the two models proposed are efficient and can largely reduce the total cost of pooled testing. These findings underscore the potential of GrC concepts to revolutionize pooled testing strategies, making them more adaptable and economically viable in the face of future pandemics. Notably, this study primarily focuses on large-scale population wide-spectrum testing with low infection rates, specifically targeting the initial infection distributions where there are no clear transmission chains, and thus assuming independence between observations. However, for scenarios like COVID-19, where transmission paths are not independent, additional considerations such as Markov chains, graph theory, and other related theories may be necessary to supplement our model. In future research, these aspects will be further investigated to improve the applicability of the model to more complex and realistic scenarios. Additionally, predicting increases in the infection rate during the testing process is a subject for future research.