Coexistence and tuning of spin-singlet and triplet transport in spin-filter Josephson junctions

Abstract

The increased capabilities of coupling more and more materials through functional interfaces are paving the way to a series of exciting experiments and extremely advanced devices. Here we focus on the capability of magnetically inhomogeneous superconductor/ferromagnet (S/F) interfaces to generate spin-polarized triplet pairs. We build on previous achievements on spin-filter ferromagnetic Josephson junctions (JJs) and find direct correspondence between neat experimental benchmarks in the temperature behavior of the critical current and theoretical modelling based on microscopic calculations, which allow to determine a posteriori spin-singlet and triplet correlation functions. This kind of combined analysis provides an accurate proof of the coexistence and tunability of singlet and triplet transport. This turns to be a powerful way to model disorder and spin-mixing effects in a JJ to enlarge the space of parameters, which regulate the phenomenology of the Josephson effect and could be applied to a variety of hybrid JJs.

Introduction

The growing complexity of the Josephson junctions (JJs) in terms of layout and materials has significantly increased the “parameters space” for a full understanding and control of their properties^1,2. Ferromagnetic (SFS) JJs are a unique platform to integrate the coherent quantum nature of superconductors and ferromagnets into unconventional mechanisms and smart tunable functionalities. The rich literature has established several key elements, which arise when superconducting pair correlations traverse the exchange field of a ferromagnet^{3,4,5,6,7,8,9}. JJs with multiple F-layer barriers have been theoretically and experimentally studied in connection to unconventional triplet superconductivity with equal-spin Cooper pairs, characterized by total spin momentum S = 1 and spin z-component S_z = ±1 (${\left|11\right\rangle }_{S,{S}_{z}}=\left|\uparrow \uparrow \right\rangle$ and ${\left|1-1\right\rangle }_{S,{S}_{z}}=\left|\downarrow \downarrow \right\rangle$), which can be artificially generated in these structures^{5,6,10,11,12,13,14,15,16,17,18}. Compared to spin-singlet Cooper pairs and opposite-spin triplet Cooper pairs (total spin momentum S = 1 and spin z-component S_z = 0, ${\left|10\right\rangle }_{S,{S}_{z}}=1/\sqrt{2}(\left|\uparrow \downarrow \right\rangle +\left|\downarrow \uparrow \right\rangle )$), the spin-aligned triplet Cooper pairs are immune to the exchange field of the F layer and can carry a non-dissipative spin current. Therefore, spin-triplet Cooper pairs constitute the essential element for the emerging field of superconducting spintronics^{10,11,13,15,17,18}.

It is well established that spin-polarized triplet pairs are generated via spin-mixing and spin-rotation processes at magnetically inhomogeneous S/F interfaces^{6,13,15,17,19,20}. Evidence of equal-spin triplets has been reported in S-F’-F-F”-S JJs, where the F’, F” spin-mixer layers mediate the conversion of singlet to triplet pair correlations^{10,11,12,14,15,16,18,21,22}. Recently, theoretical and experimental studies have been dedicated to an alternative mechanism for triplet pair generation involving spin–orbit coupling (SOC) in combination with a magnetic exchange field^23,24,25. These systems may benefit from the capability to generate controllable spin-polarized supercurrents with a single ferromagnetic layer, compared to magnetically textured JJs.

The strong evidence for the presence of spin-triplet supercurrents in a JJ is the slower decay of the characteristic voltage of the junction with increasing F-layer thickness^{7,10,11,12,13,15,16,17,18,26}, due to the robustness of spin-triplet Cooper pairs to the exchange field. However, it has been suggested that a mechanism of phase compensation can arise in clean S/F heterostructures, which may cancel the destructive interference effect due to the exchange field on conventional spin-singlet pairing^21,27. Therefore, a conclusive evidence for the spin-triplet nature of the supercurrent could be supported by the capability to distinguish singlet and triplet components. The capability of quantifying the amount of spin-polarized supercurrents remains a fundamental benchmark to further prove triplet correlations and a key step toward real applications.

In parallel with the work on diffusive ferromagnets, superconducting tunnel junctions with ferromagnetic insulator (FI) barriers (SFIS), namely spin-filter NbN/GdN/NbN JJs, have revealed unique transport properties, such as spin-polarization phenomena^28,29,30,31, an interfacial exchange field in the superconducting layer^32,33, macroscopic quantum tunneling³⁴ and an unconventional incipient 0–π transition³⁵. They are especially well-suited for the implementation in superconducting circuits in which a very low dissipation is required^{36,37,38,39,40,41,42}. In these systems, evidence of spin-triplet transport has been reported^7,30,35,43.

Here, we build on a previous study of the critical current I_c as a function of the temperature T in NbN–GdN–NbN JJs³⁵, now performed in presence of magnetic field to demonstrate coexistence and tuning of singlet and triplet components. By using a tight-binding Bogolioubov de Gennes (BdG) approach^44,45,46,47, we model the I_c(T) curves in the whole temperature range, along with the corresponding current-phase relation (CPR) as a function of the temperature T. It turns out that measurements of the temperature behavior of the critical current along with microscopic modeling approach provide an alternative accurate method to assess the spin-triplet transport, which can be extended to different types of JJs: the amount of spin-singlet and -triplet correlations can be quantified and parametrized in terms of disorder parameter and spin-mixing mechanisms through a direct fitting of experimental data.

The large variety of materials and configurations employed in diffusive SFS JJs in literature allows to access a wide range of behaviors for the thermal dependence of the I_c^1,5. Particularly relevant to our work, the possibility of generating oscillations in the superconducting order parameter by means of a finite exchange field in the F interlayer results in a π phase-shift in the CPR and a sudden drop of the I_c towards zero at temperatures T_π < T_c, followed by an increase of the I_c for T > T_π^3,5. Therefore, the non-monotonic behavior for the I_c(T) in systems in which a 0-π transition occurs is characterized by a peculiar cusp at the transition point T_π^3,5. In this work, we focus on the peculiar behavior of the I_c(T) in tunnel ferromagnetic spin-filter JJs, in which an unconventional 0–π transition occurs. Above a GdN thickness d_F = 3.0 nm, the I_c is not completely suppressed at T_π, thus suggesting that a 0–π transition broadened in a range of temperatures of the order of some K occurs³⁵. Therefore, in the devices discussed here, the I_c(T) curve shows a region in which the I_c is constant in a wide range of temperatures, i.e., it shows a plateau, or it shows a non-monotonic trend characterized by a non-zero local minimum, i.e., the I_c(T) exhibits an incipient 0–π transition³⁵. Such unconventional I_c(T) behavior turns out to be the benchmark for the coexistence of spin-singlet and spin-triplet superconductivity in SFIS junctions. When the I_c(T) curve shows a plateau over a wide range of temperatures, the competition between the singlet and triplet pairing amplitudes becomes significant, in both s-wave and p-wave symmetries. This behavior sets in due to the combined effects of impurities and spin-mixing mechanisms. When the I_c(T) curve exhibits an incipient 0–π transition, the equal-spin triplet component is gradually suppressed, becoming irrelevant in the limit case of a more standard cusp-like 0–π transition. This last situation corresponds to relatively low values of disorder and spin-mixing effects.

An external magnetic field perpendicular to the Josephson transport direction gradually modifies the experimental I_c(T) curves, i.e., a plateau extended over a wide range of temperatures evolves into a non-monotonic behavior by increasing the magnetic field. Such experimental evidence of an “in situ” tuning of the relative weight between spin-singlet and spin-triplet supercurrents in single-layered SFIS JJs, is explained in terms of a reduced disorder parameter in presence of magnetic field for a multidomain ferromagnet. The ability to describe the combined effect of magnetic inhomogeneities and disorder in complex barriers, with clear benchmarks on the phenomenology of the junctions, can be of reference for a variety of structures.

Results

Spin-filter Josephson junctions and microscopic modeling

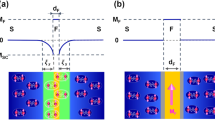
The junctions under study are NbN/GdN/NbN JJs³⁵, with a special focus on devices with thick FI layers. The superconducting electrodes have thicknesses of 100 nm and the analyzed FI thicknesses are d_F = 3.0, 3.5, and 4.0 nm. A sketch of the JJs is reported in the inset of Fig. 1. In this work, we report measurements of the I_c(T) curves performed down to 20 mK and measurements of the I_c(T) curves as a function of an external magnetic field.

Fig. 1: Spin-filter Josephson junction and two-dimensional lattice model scheme.

Picture of the superconductor/insulating ferromagnet/superconductor two-dimensional lattice model. The barrier (highlighted in blue) has a total thickness L along x. The junction width is W along y. The spin-mixing mechanism due to the spin–orbit coupling is depicted by the spin-flipping process highlighted at the interface between the superconducting boundaries (red sites) and the barrier. The impurities, with random strength depicted by the height of the yellow potential peaks, are represented on each site of the lattice. The exchange field h (violet arrow) is parallel to the z axis, while the hopping t between nearest-neighbor sites is here represented by pink arrows. In the inset, sketch of NbN–GdN–NbN Josephson junctions reported in this work. The external magnetic field H is parallel to the z axis.

We model the S/FI/S junctions using a tight-binding BdG Hamiltonian on a two-dimensional (2D) lattice^48,49. A schematization of the 2D-lattice model is reported in Fig. 1, where L is the length of the FI barrier and W is the width of the junction expressed in lattice units.

The Hamiltonian of the junction in the Nambu ⊗ spin space is given by^44,45,46

$$\check{{{{{{{{\mathcal{H}}}}}}}}}=\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} }{{{\Psi }}}^{{{{\dagger}}} }({{{{{{{\bf{r}}}}}}}})\left[\begin{array}{cc}\hat{H}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )&\hat{{{\Delta }}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )\\ -{\hat{{{\Delta }}}}^{* }({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )&-{\hat{H}}^{* }({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )\end{array}\right]{{\Psi }}({{{{{{{\bf{r}}}}}}}}^{\prime} ),$$

(1)

with ${{\Psi }}({{{{{{{\bf{r}}}}}}}})={\left[{\psi }_{\uparrow }({{{{{{{\bf{r}}}}}}}}),{\psi }_{\downarrow }({{{{{{{\bf{r}}}}}}}}),{\psi }_{\uparrow }^{{{{\dagger}}} }({{{{{{{\bf{r}}}}}}}}),{\psi }_{\downarrow }^{{{{\dagger}}} }({{{{{{{\bf{r}}}}}}}})\right]}^{T}$. Here, ${\psi }_{\mu }^{{{{\dagger}}} }({{{{{{{\bf{r}}}}}}}})$ and ψ_μ(r) are the field operators creating/destructing an electron with spin μ at the lattice point r = jx + my, with j = 0, 1, …, L, L + 1 and m = 1, …, W. Here and in the following, the symbols $\hat{.}$ and $\check{.}$ describe the 2 × 2 and 4 × 4 matrices, in spin and Nambu ⊗ spin spaces, respectively.

In Eq. (1), $\hat{H}$ is the normal-state Hamiltonian of the junction, while $\hat{{{\Delta }}}$ describes the superconducting pairing potential. The latter is non-zero only in the S leads, for which conventional s-wave superconductivity is assumed¹. Thus, $\hat{{{\Delta }}}$ is proportional to ${{\Delta }}{{{\mbox{e}}}}^{{{\mbox{i}}}{\phi }_{{{\mbox{L}}}}}$ (${{\Delta }}{{{\mbox{e}}}}^{{{\mbox{i}}}{\phi }_{{{\mbox{R}}}}}$) in the left (right) S lead, where Δ is the order parameter and ϕ_L (ϕ_R) is the superconducting phase in the left (right) S lead. The normal-state Hamiltonian $\hat{H}$ can be written as $\hat{H}={\hat{H}}_{{{\mbox{S}}}}+{\hat{H}}_{{{\mbox{FI}}}}$, with ${\hat{H}}_{{{\mbox{S}}}}$ and ${\hat{H}}_{{{\mbox{FI}}}}$ referring to the S-electrodes and the FI barrier, respectively. Their explicit form is shown in Supplementary Note 1.

In the S leads, $\hat{{H}_{{{\mbox{S}}}}}$ is described by the parameters t_S and μ_S, representing the hopping integral among nearest-neighbor lattice sites and the chemical potential, respectively. Relevant parameters of the Hamiltonian $\hat{{H}_{{{\mbox{FI}}}}}$, instead, are the hopping integral t, the Fermi energy μ_FI and the amplitude of the spin–orbit interaction α, used to introduce a spin-symmetry breaking^48,49. Further, we include on-site random impurity potential with strength v_r uniformly distributed in the range −V_imp/2 ≤ v_r ≤ V_imp/2. Finally, an exchange field is assumed to be slightly disordered, and is modeled as ${h}^{\prime}=h+{\delta }_{h}$. Here, δ_h are small on-site fluctuations given randomly in the range −h/10 ≤ δ_h ≤ h/10 (along the h-direction). The combined effect of SOC and impurities in the FI region efficiently mimics the presence of magnetic inhomogeneities in the barrier, which are more likely to occur in devices with large areas^7,13. The junctions under study, in fact, are characterized by areas of ~50 μm². This approach is meant to include all possible effects occurring in the FI barrier, and it is a powerful platform to describe a large variety of JJs. As shown below, fitting of experimental I_c(T) curves will allow to identify the coexistence of spin-singlet and -triplet transport. When compared with what is available in the literature, the correlation functions are determined a posteriori from the experimental data and allow to quantify the weight between the different transport channels.

The Josephson current J at finite temperature T is derived from the Matsubara Green’s function (GF) of the FI barrier, calculated with the recursive Green’s function (RGF) technique^44,45,46,47. The barrier Green’s function (GF) ${\check{G}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )$ connecting two lattice sites located at r and ${{{{{{{\bf{r}}}}}}}}^{\prime}$ reads

$${\check{G}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )=\left[\begin{array}{cc}{\hat{G}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )&{\hat{F}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )\\ -{\hat{F}}_{{\omega }_{n}}^{* }({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )&-{\hat{G}}_{{\omega }_{n}}^{* }({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}^{\prime} )\end{array}\right],$$

(2)

and solves the following Gor’kov equation^44,45,46:

$$ \left[\,{{\mbox{i}}}\,{\omega }_{n}{\hat{\tau }}_{0}{\hat{\sigma }}_{0}-\mathop{\sum}\limits_{{{{{{{{{\bf{r}}}}}}}}}_{1}}\left(\begin{array}{ll}\hat{H}({{{{{{{\bf{r}}}}}}}},{{{{{{{{\bf{r}}}}}}}}}_{1})&\hat{{{\Delta }}}({{{{{{{\bf{r}}}}}}}},{{{{{{{{\bf{r}}}}}}}}}_{1})\\ -{\hat{{{\Delta }}}}^{* }({{{{{{{\bf{r}}}}}}}},{{{{{{{{\bf{r}}}}}}}}}_{1})&-{\hat{H}}^{* }({{{{{{{\bf{r}}}}}}}},{{{{{{{{\bf{r}}}}}}}}}_{1})\end{array}\right)\right]\times {\check{G}}_{{\omega }_{n}}({{{{{{{{\bf{r}}}}}}}}}_{1},{{{{{{{\bf{r}}}}}}}}^{\prime} )={\hat{\tau }}_{0}{\hat{\sigma }}_{0}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{r}}}}}}}}^{\prime} ),$$

(3)

Here ω_n = (2n + 1)πT is the fermionic Matsubara frequency, T is the temperature and ${\hat{\tau }}_{0}$ and ${\hat{\tau }}_{\nu }$ (ν = 1, 2, 3) are analogous of the identity and Pauli matrices in the Nambu space, respectively. The Josephson current originates from the GFs connecting two adjacent sites along the x direction (namely ${\check{G}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}+{{{{{{{\bf{x}}}}}}}})$ and ${\check{G}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}}+{{{{{{{\bf{x}}}}}}}},{{{{{{{\bf{r}}}}}}}})$), and reads

$$J=-\frac{\,{{\mbox{i e}}}\,}{2}T\mathop{\sum}\limits_{{\omega }_{n}}\mathop{\sum }\limits_{m=1}^{W}Tr\left[{\hat{\tau }}_{3}{\check{T}}_{+}{\check{G}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}+{{{{{{{\bf{x}}}}}}}})-{\hat{\tau }}_{3}{\check{T}}_{-}{\check{G}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}}+{{{{{{{\bf{x}}}}}}}},{{{{{{{\bf{r}}}}}}}})\right]\!.$$

(4)

Here, Tr stands for the trace over the Nambu ⊗ spin space and ${\check{T}}_{\pm }$ matrices describe the hopping and the SOC along the propagation direction (their explicit form is reported in Supplementary Note 1)⁴⁵. In order to consider the contribution of the lattice sites along the y direction, in Eq. (4) we perform a summation $\mathop{\sum }\nolimits_{m = 1}^{W}$. Furthermore, the summation over Matsubara frequencies until convergence is performed. Finally, we calculate the CPR from Eq. (4) at fixed temperature T by varying the phase difference ϕ = ϕ_L − ϕ_R between the S leads from 0 to π. Then, we compute the I_c(T) curves from the maximum of the CPRs at T ranging from 0 to T_c.

The off-diagonal terms of the matrix in the right-hand side of Eq. (2) are the so-called anomalous Green’s functions ${\hat{F}}_{{\omega }_{n}}$. From these latter, taking the elements with ${{{{{{{\bf{r}}}}}}}}^{\prime} ={{{{{{{\bf{r}}}}}}}}=j{{{{{{{\bf{x}}}}}}}}+m{{{{{{{\bf{y}}}}}}}}$, we can derive the four pairing components with s-wave symmetry at each position in the barrier (j = 1, …, L) along the x direction⁴⁵:

$$\frac{1}{W}\mathop{\sum}\limits_{{\omega }_{n}}\mathop{\sum }\limits_{m=1}^{W}{\hat{F}}_{{\omega }_{n}}({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}})=\mathop{\sum }\limits_{\nu =0}^{3}{f}_{\nu }{\hat{\sigma }}_{\nu }\ \,{{\mbox{i}}}\,\ {\hat{\sigma }}_{2},$$

(5)

where f₀ is the spin-singlet component and f_ν, with ν = 1, 2, 3 are the spin-triplet components. In particular, f₃ is the opposite-spin triplet component and the equal-spin triplet components f_↑ ( f_↓) are defined as f_↑ (↓) = if₂ ∓ f₁ (see Supplementary Note 1 for details). Here, similarly to Eq. (4), the summation $\mathop{\sum }\nolimits_{m = 1}^{W}$ is performed to take into account all the lattice sites with the same longitudinal coordinate j and different index m in the transverse direction.

Analogous considerations can be applied to the GFs connecting the sites at the position r with their neighbors in r − x and r + x, from which we can calculate the odd-parity p-wave pairing functions. Thus, the p-wave correlations, at the position j along x inside the barrier (r = jx + my), can be expressed as:

$$\begin{array}{l} \frac{1}{4W}\mathop{\sum}\limits_{{\omega }_{n}}\mathop{\sum }\limits_{m=1}^{W}\left[{\hat{F}}_{{\omega }_{n}}\left({{{{{{{\bf{r}}}}}}}}+{{{{{{{\bf{x}}}}}}}},{{{{{{{\bf{r}}}}}}}}\right)+{\hat{F}}_{{\omega }_{n}}\left({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{x}}}}}}}}\right)-{\hat{F}}_{{\omega }_{n}}\left({{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{r}}}}}}}}+{{{{{{{\bf{x}}}}}}}}\right)-{\hat{F}}_{{\omega }_{n}}\left({{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{x}}}}}}}},{{{{{{{\bf{r}}}}}}}}\right)\right]\\ = \mathop{\sum }\limits_{\nu =0}^{3}{f}_{\nu }{\hat{\sigma }}_{\nu }\ \,{{\mbox{i}}}\,\ {\hat{\sigma }}_{2}.\end{array}$$

(6)

Experimental results and theoretical interpretation

In Fig. 2a–c, we show the comparison between the I_c(T) curves measured down to 20 mK at zero field for the junctions with GdN barriers d_F = 3.0 , 3.5, and 4.0 nm (black points), respectively, and the simulations obtained with the tight-binding BdG lattice model (red straight lines). In the insets, we report the measured I_c(T) values down to dilution temperatures. The experimental data evolve from a plateau over a wide range of temperatures (a few Kelvins) observed for the junctions with GdN thickness d_F = 3.0 and 3.5 nm into a non-monotonic I_c(T) curve for the junction with d_F = 4.0 nm. The agreement between numerical outcomes and experimental data is certified by the capability to reproduce the unconventional plateau (Fig. 2a, b) and the non-monotonic behavior (Fig. 2c).

Fig. 2: Comparison between the experimental temperature dependence of the critical current, tight-binding simulations, and corresponding current-phase relations.

Critical current I_c as a function of the temperature T (black points) for spin-filter junctions with GdN barrier thickness d_F = 3.0 nm (a), d_F = 3.5 nm (b), and d_F = 4.0 nm (c). In the insets of figures (a–c): measured saturation of the I_c(T) down to 20 mK. The error bars on the measured I_c are of the order of 1% and represent the statistical error due to thermally induced critical current fluctuations³⁴. The red lines are the best I_c(T) curves obtained from the maximum of the current-phase relations (CPRs) calculated with the microscopic two-dimensional lattice Bogoliubov–De Gennes Hamiltonian, with simulations parameters reported in Supplementary Note 2. The amplitude of the simulated critical current has been multiplied by the experimental I_c measured at 20 mK. d–f CPRs at selected temperatures near the 0–π transition to highlight the arising of higher-order harmonics, compared with those in the 0 and π state, at 0.05 T_c and 0.7 T_c, respectively, being T_c the critical temperature. The CPRs have been normalized to the maximum value of the current at 0.05 T_c. The color-gradient in (a–c) represents the temperature range for the 0-state (light blue), the π state (light red), and the width of the 0–π transition region (yellow region), obtained from the CPRs in (d–f).

Details on Hamiltonian parameters used in the simulations can be found in Supplementary Note 2. However, we here briefly discuss the spirit of our lattice modeling. All the energy parameters are expressed in dimensionless units where the energy scale is the hopping t in the FI. The strength of the SOC, α, is scaled by ta (with a lattice constant), while the Josephson current is calculated in units of J₀ = eΔ. In our simulations, we fix t = 1, μ_FI = 0, μ_s = 3, Δ = 0.005, h = 0.25. Further, we note that NbN (S leads) and GdN (FI barrier) are characterized by almost equal hopping parameters^50,51,52, which are set equal t_s = t for the sake of simplicity. The choice of assuming different chemical potentials for the S and FI regions is made in order to model the experimental devices as tunnel junctions with a ferromagnetic half-metallic GdN barrier, as experimentally observed⁵³ and predicted by full atomistic simulations^54,55. The estimate for the exchange energy h is chosen in agreement to the exchange field measured in several materials and is kept fixed to that of the bulk GdN^{20,32,51,52,56}. This is consistent with t ≈ 3 eV and the experimental constant lattice of GdN is a_GdN = 4.974 Å^50,51,52.

When modeling the experiments, we use α as a measure of the spin-mixing and it is chosen to be α = 0.04, unless otherwise indicated. Although we choose a small spin–orbit field so that α ≪ h, it breaks the spin symmetry at interfaces and is sufficient to cause the generation of long-range triplet-correlation pairs with total spin projection S_z = ±1.

The numerical simulations in Fig. 2 are performed on lattices characterized by: (a) L = 8, W = 24, (b) L = 8, W = 28, (c) L = 8, W = 32, expressed in units of lattice sites. Tunnel junctions experience an exponential suppression of the critical current when increasing the barrier thickness¹. In our model, this implies dealing with systems of few lattice sites, hence, we choose L = 8 and keep it fixed in all the numerical simulations, in agreement with the short-junction limit. However, the main effect of increasing the experimental sample thickness (and so the magnetic area of the FI) consists in enhancing the magnetic activity of the junction^28,30,31,35. In our model, we manage to mimic this effect by changing the flux of the exchange field Φ(h) = LWh through the JJ (by the means of the width of the barrier W) and by tuning the impurity potential strength V_imp (thus, changing the influence of disorder effects in the system). Therefore, we use these quantities as effective control parameters when modeling the peculiar behavior of the I_c(T) curve in each experimental device. For the I_c(T) simulations in Fig. 2 (as well as for the corresponding correlation functions in Fig. 3), we set V_imp = 0.3 for the simulated curve in (a), V_imp = 0.37 in (b), and V_imp = 0.23 in (c). Here, the presence of random on-site impurities requires the need to perform ensamble averages over several samples (see Supplementary Note 2 for details).

Fig. 3: S- and p-wave spin-singlet and -triplet pair-correlation amplitudes in the ferromagnetic insulator barrier.

a–c The amplitudes of the ensamble average of the s-wave correlation functions 〈∣f∣〉, determined by numerical simulations at temperature T = 0.025 T_c, being T_c the critical temperature, are shown as a function of the lattice position in the barrier along the x direction (with index j) for the junctions with GdN thickness d_F = 3.0, 3.5 and 4.0 nm, respectively. f₀ is the spin-singlet (black line and square symbols), f₃ is the opposite-spin triplet (red line and circles) and f_↑ (f_↓) is the equal-spin triplet with up (down) S_z projection (blue line and up-triangle symbols, and green line and down-triangle symbols, respectively). d–f We show the same correlation functions components for the p-wave symmetry.

We notice that the Hamiltonian parameters, as well as the lattice size, have no microscopic (atomistic) origin and are chosen to describe the main mechanisms that are expected to occur in the experimental devices. Even though the lattice size is scaled down compared to the experimental system, we think that our theoretical model gives qualitatively an accordance with the experimental results as long as the model parameters are adjusted accordingly.

We can relate the plateau in the I_c(T) curve to an overall broadening of a 0–π transition in temperature. The calculated CPRs in Fig. 2d–f indicate that at low temperatures the JJs are in the 0-state (light blue gradient region in Fig. 2a–c), while at temperatures above T = 0.7 T_c the JJs are in the π state (red gradient region). Compared to what has been theoretically and experimentally observed in 0–π SFS and SFIS JJs^{3,36,37,40,57}, when the plateau is measured in the JJs with d_F = 3.0 nm and 3.5 nm in Fig. 2a, b, the CPRs exhibit the presence of higher-order harmonics in the Josephson current J for a wide range of temperatures (yellow gradient region). The transition region is reduced when the I_c(T) curve gradually points towards a non-monotonic behavior, as shown in Fig. 2c. In all the cases reported in Fig. 2, the 0–π transition extends over a few Kelvins in temperature around 4.2 K, in agreement with previous findings³⁰.

In Fig. 3, we show the amplitude of the correlation functions $\langle | f| \rangle$ determined from numerical simulations for the three devices at T = 0.025 T_c (corresponding to 0.3 K) and ϕ = 0, where ϕ is the phase difference across the device. The correlation functions are determined for the spin-singlet (f₀), spin-triplet with opposite spins (f₃) and equal-spin triplet functions (f_↑ and f_↓), both in s-wave (Fig. 3a–c) and p-wave symmetries (Fig. 3d–f), as a function of the position in the lattice along the x direction, with index j = 1, …, L. In order to assure the total antisymmetry of the fermionic wavefunction, triplet superconductivity for even-frequency pairing is conventionally of p-wave type⁵⁸. As shown in the following, for symmetry reasons here the dominant orbital part in the triplet pairing channel happens to be of s-wave type. We use $\langle \rangle$ to indicate the ensemble average, due to the presence of random on-site impurities in the 2D-lattice. Details on the calculation of the spatial profile of the correlation function can be found in Supplementary Note 1. All the cases show a dominant s-wave singlet component f₀ at the superconductor/barrier interface that strongly decays toward the middle of the barrier thickness. This is reasonable because the sides of the FI-layer are attached to the superconducting leads with a usual Bardeen–Cooper–Schrieffer s-wave symmetry⁵⁹ and, due to the proximity effect, the singlet pair wavefunction enters the barrier. In the middle of the barrier (lattice position j = 4), where the spin mixing and the exchange field effects take place, a competition between the s-wave triplet and singlet pair amplitudes arises. On the contrary, for the p-wave case, the singlet component f₀ turns out to be much lower than the corresponding s-wave one. At the same time, we may observe a prevalence of the zero-spin p-wave triplet component f₃ at the superconductor/barrier interface, while in the middle of the barrier thickness the spin-aligned triplet correlations become relevant. These results are justified by symmetry considerations^6,13,17. Indeed, for the s-wave symmetry, the singlet is an even-frequency function, while the triplets are odd-frequency. The vice versa is valid for the p-wave case.

The 3.0 nm-thick barrier junction exhibits s-wave triplet correlations functions larger than the singlet one, with a major contribution provided by the equal-spin triplet component with S_z = +1, f_↑ (Fig. 3a). For what concerns the p-wave spin-correlation functions for this device, f₃ provides the main contribution at the borders, while f_↓ competes with f₃ in the middle of the barrier (lattice position j = 4), as shown in Fig. 3d. Moreover, the opposite- and equal-spin p-wave triplet components are nearly a factor 2 larger than the corresponding s-wave singlet component. By increasing the thickness of the barrier, thus gradually pointing towards an incipient 0–π transition with a non-monotonic behavior in the I_c(T) curve, in the s-wave cases we can observe a progressive suppression of the equal-spin triplet components and a dominant spin-singlet channel. At the same time, in the p-wave case, we observe a slight reduction of the ratio between the equal-spin triplets (f_↑, f_↓) and the major zero-spin component (f₃). Thus, the p-wave opposite spin-triplet components are of the same order of magnitude compared to the corresponding s-wave spin-singlet component, while the equal-spin triplet components are instead reduced.

In order to investigate the peculiar transport properties arising in these systems, we have probed the I_c(T) response to an external magnetic field applied in the plane of the JJs. In Fig. 4, we show the evolution of the normalized critical current I_c(T, H/H₀)/I_c(0.3 K, H/H₀) as a function of a weak magnetic field H/H₀, where H₀ is the amplitude of the first lobe of the Fraunhofer pattern curve, acquired by applying the magnetic field from +2.4 mT to −2.4 mT. H₀ is estimated at each investigated temperature T (from T = 0.3 K to T = 8 K). Details on the measurement procedure can be found in the Methods section “Experimental I_c(T) curves at zero- and finite-field”.

Fig. 4: Tuning of the temperature behavior of the critical current in presence of an external magnetic field.

Normalized critical current I_c(T, H/H₀)/I_c(0.3 K, H/H₀) density plots as a function of the percentage of magnetic field periodicity H/H₀ and the temperature T, for the Josephson junctions with GdN thickness (a) d_F = 3.0 nm and (b) d_F = 3.5 nm. The critical current I_c values at each temperature T are measured by fixing the external magnetic field to H/H₀, where H₀ is the amplitude of the first lobe of the Fraunhofer pattern measured at the same temperature T. More details can be found in the Methods section “Experimental I_c(T) curves at zero- and finite-field”. Blue, red, and green lines refer to the cross-sections reported in (c) and (d): blue squares for H/H₀ = 0%, red circles for H/H₀ = 75% in (c) and H/H₀ = 65% in (d), green triangles for H/H₀ = 85% in (c) and H/H₀ = 75% in (d). Straight lines in plots (c) and (d) are only a guide for the eye. The error bar on each measured point is of the order of few percent and it is due to thermally induced I_c fluctuations³⁴. The white dashed arrows in (a) and (b) are a guide for the eye and highlight the shift of the minimum in the I_c(T, H/H₀)/I_c(0.3 K, H/H₀) by increasing H/H₀.

The results are reported in Fig. 4 in the two density plots Fig. 4a, b for the junctions with d_F = 3.0 nm and 3.5 nm, respectively. Increasing the field H/H₀, the plateau structure at zero field evolves into a non-monotonic behavior with a minimum (dark region around 70–80%H₀ and between 2 and 4 K) and a maximum (bright region around 70–80%H₀ and between 4 and 6 K). The effect is more pronounced for the JJ with d_F = 3.0 nm. The blue, green, and red dashed line cuts are related to the cross-section curves reported in Fig. 4c, d, where the gradual appearance of an enhanced dip and a non-monotonic behavior in the normalized I_c(T) curves can be observed by increasing H/H₀. The dependence of the I_c as a function of the normalized magnetic field H/H₀ is reported in Supplementary Fig. 2 for the JJ with GdN thickness d_F = 3.0 nm at three selected temperatures: 0.3 K, 3 K where a minimum of the I_c(T) curve is measured for H/H₀ = 75%, and 7 K where a maximum of the I_c(T) is observed for the same value of H/H₀. While a standard Fraunhofer-like I_c(H) dependence is recovered at the three selected temperatures, for magnetic fields close to a quantum flux and at high temperature, e.g., 7 K, I_c is larger than the value measured at low temperature, e.g., 0.3 K. In order to stress this point, the IV curves measured at H/H₀ = 75% for the three selected temperatures are shown in Supplementary Fig. 2 as a term of reference.

Such a progressive variation of the I_c(T) curves in presence of an external magnetic field is not observed in junctions with thinner GdN barriers, as shown in Supplementary Fig. 3, in which we report the I_c(T, H/H₀)/I_c(0.3 K, H/H₀) density-plot measured on a NbN–GdN-NbN junction with GdN barrier thickness d_F = 1.5 nm. For this device, a standard Ambegaokar-Baratoff (AB) trend^59,60 for the I_c(T) curve is preserved in presence of the external magnetic field. Compared to devices with thin GdN barriers, the samples analyzed in this work are indeed sensitive to a weak magnetic field^30,34,35. A finite shift of the order of 0.1 mT in the Fraunhofer pattern curves arises when ramping the field from positive to negative values, and vice versa⁶¹. Even if the strength of the external magnetic field is not enough to generate a complete magnetic ordering, slight modifications in the microscopic structure of the barrier arise⁶², which has been already predicted to occur in systems with tunable domain walls⁶³, intrinsic SOC⁶⁴, and magnetic impurities⁶⁵. At zero field, the magnetic disorder is maximum and likely introduces electronic defect states in the barrier⁶⁶. As the field increases, the system undergoes toward a more ordered phase, and hence defect states density reduces. Therefore, the tunability of the I_c(T) shape from the plateau toward a non-monotonic curve by applying an external magnetic field can be related to a reduction of the disorder in the barrier.

This picture is supported by numerical simulations obtained when changing the strength of the impurity potential in the 2D-lattice model while keeping fixed all the other parameters. As a matter of fact, in order to have a good agreement with experimental data, we model the GdN as a ferromagnetic half metal^53,54,55. Hence, local impurity potentials in the FI barrier are assumed to induce small site-dependent fluctuations of the chemical potential. In our approach, the coexistence of spin-mixing mechanisms, promoted by SOC-like interactions, and on-site impurities model the magnetic disorder. In Fig. 5a, in fact, we can notice that the characteristic 0–π behavior is modified by increasing the impurity potential V_imp. The enhancement of the impurity strength produces a shift of the minimum of the curve toward lower temperatures and higher critical current values, with a consequent broadening of the typical 0–π cusp that progressively gives rise to the plateau. Vice versa, decreasing V_imp, one can recover the 0–π transition. Details on the parameters are reported in Supplementary Note 2.

Fig. 5: Simulated temperature behavior of the critical current and calculated pair-correlation amplitudes as a function of the impurity potential.

In (a), normalized critical current I_c vs. temperature T curves simulated with the two-dimensional lattice model at fixed dimensions for three different impurity potential V_imp values: V_imp = 0.05 (green curve), V_imp = 0.23 (red curve), and V_imp = 0.3 (blue curve). Simulation parameters are reported in Supplementary Note 2. The current is normalized to the maximum of the current-phase relation at the lowest investigated temperature T, while T is normalized to the critical temperature T_c. In (b–d), calculated s-wave ensamble average of the pair amplitude 〈∣f∣〉 in arbitrary units for different impurity potential values V_imp in (a). In (e–g), calculated p-wave ensamble average of the pair amplitude 〈∣f∣〉 in arbitrary units for different impurity potential values V_imp in (a). f₀ is the spin-singlet component (black line and square symbols), f₃ is the opposite-spin triplet component (red line and circle symbols), f_↑(↓) is the up (down) equal-spin triplet component (blue lines and up-triangle symbols, and green lines and down-triangle symbols, respectively). Both s- and p-wave data are reported on a log scale.

In Fig. 5, we finally report the s- and p-wave correlation functions corresponding to simulated I_c(T) curves for different impurity potentials V_imp in Fig. 5a: V_imp = 0.3, V_imp = 0.23 and V_imp = 0.05. We here take as a reference the JJ with d_F = 4.0 nm, i. e. the simulations for lattice dimensions L = 8, W = 32. For the s-wave symmetry reported in Fig. 5b–d, the effect of increasing the impurity strength V_imp results in a pronounced enhancement of the equal-spin triplet pairing correlations, f_↑ and f_↓, while the p-wave components appear to be approximately unaffected by disorder (e.g., Fig. 5e–g).

Discussion

The theoretical results in Figs. 2 and 3 show that the characteristic behavior of the I_c(T) is related to the amplitude of the different s-wave spin-correlation functions. In Table 1, we summarize the values of the pair correlations in the middle of the barrier thickness (lattice position j = 4), in units of the majority zero-spin component, i. e. f₀ for the s-wave (Table 1A) and f₃ for the p-wave cases (Table 1B), respectively. Indeed, we observe a general decrease in the relative weight of the s-wave equal-spin triplet components (f_↑ and f_↓) in the junctions that show an increasing non-monotonicity of the I_c(T) curves. Hence, the more I_c(T) exhibits a behavior approaching the 0–π regime, the lower is the weight of the s-wave equal-spin correlations. This is in agreement with the fact that spin-aligned supercurrents are insensitive to the exchange field and, thus, cannot give rise to 0–π transitions.

Table 1 S- and p-wave symmetry spin correlations.

In Fig. 6, we show how the impurities and the SOC affect the I_c(T) shape. Lattice dimensions are L = 8, W = 32, i. e. they refer to the JJ with d_F = 4.0 nm. To accomplish the I_c(T) diagram, we select values for α and V_imp as described in Fig. 6 (a-p). For small values of α and V_imp (bright red- and blue-scales), the simulated I_c(T) curve shows a cusp-like 0−π transition, provided that the exchange field h in the junction is non-zero, as it occurs in SFS JJs tipically reported in literature^{3,36,37,40,57}. By increasing α (dark red-scale), the main effect is to reduce the height of the second maximum in the I_c(T) curve, without recovering the plateau structure observed in SFIS JJs. At very large α (see Fig. 6a), the 0–π transition is washed out and an AB-like shape sets in, stabilizing a “0”-phase. In this case the main contribution is expected from the spin-singlet, though the spin-triplet correlations are increased compared to the cases with smaller α.

Fig. 6: Competition between the spin–orbit coupling and the impurity potential and their effect on the temperature behavior of the critical current.

Normalized critical current I_c vs. temperature T curves simulated with the tight-binding Bogoliubov–De Gennes two-dimensional lattice model as a function of the spin–orbit coupling α and the on-site impurity potential V_imp. In (a) α = 0.2, V_imp = 0.05; (b) α = 0.2, V_imp = 0.23; (c) α = 0.2, V_imp = 0.3; (d) α = 0.2, V_imp = 0.5; (e) α = 0.1, V_imp = 0.05; (f) α = 0.1, V_imp = 0.23; (g) α = 0.1, V_imp = 0.3; (h) α = 0.1, V_imp = 0.5; (i) α = 0.07, V_imp = 0.05; (j) α = 0.07, V_imp = 0.23; (k) α = 0.07, V_imp = 0.3; (l) α = 0.07, V_imp = 0.5; (m) α = 0.04, V_imp = 0.05; (n) α = 0.04, V_imp = 0.23; (o) α = 0.04, V_imp = 0.3; and (p) α = 0.04, V_imp = 0.5. In all the panels, the I_c (y axis) is normalized to its value at the lowest temperature, i. e. T = 300 mK, while the T (x axis) is normalized to the critical temperature of the device T_c. Red-color scale refers to increasing values of α, while blue-color scale refers to increasing V_imp values, with parameters reported in Discussion and in the Supplementary Note 2. The scale on the y axis on each plot ranges from 0 to 1.1, as on the x axis. Minor thicks represent an increment of 0.1. We also highlight in panels (a), (d), (j), and (p) the state of the Josephson junction: 0, 0–π, or π.

At the same time, by keeping the spin–orbit field weak and by increasing V_imp (dark-blue scale), the minimum of the 0–π transition occurs at higher critical current values and it is broadened in temperature, but always showing a non-monotonic trend for the I_c(T). The characteristic plateau structure is observed only when considering a combined effect of SOC and impurities, once fixed the dimensions of the system. As it is shown for the SFIS JJ with d_F = 3.0 nm in Fig. 2a and Fig. 3a, the formation of the plateau goes along with the coexistence of comparable spin-singlet and -triplet superconductivity. In the limit of large V_imp and α (see Fig. 6d), an AB-like behavior is recovered. This latter corresponds to a stable “0”-phase, reflecting the fact that, in the competition between SOC and impurity scattering, the equilibrium state is dominated by α. This also confirms the presence of a threshold value of α (at fixed value of h), above which the JJ is always in the “0”-phase^45,47. In the limit of large V_imp and small α (see Fig. 6p), the 0–π transition is shifted toward very low T values, stabilizing a “π”-phase almost over the whole temperature range. This evidence is given by the sharp decrease of I_c when the temperature drops. In this regime, in agreement with Fig. 5, we predict an enhanced contribution of the s-wave spin-triplet components due to the interplay of spin–orbit and disorder.

A transition between the peculiar plateau-shape of the I_c(T) curve toward an incipient 0–π curve is experimentally observed increasing the strength of an external weak magnetic field (Fig. 4). The position in temperature of the I_c(T) dip is an important benchmark relating the 0–π transition induced by the weak magnetic field to the combined effect of impurities, exchange field fluctuations, and spin–orbit coupling in the simulations. For weak on-site impurity potential, by increasing α, the minimum of the I_c(T) curve occurs at the same temperature. Instead, as shown in Fig. 5, when increasing V_imp, the minimum is shifted in temperature, as it occurs in the experimental I_c(T) curves at a finite external magnetic field. We highlight the evolution of the 0–π transition and the dip shift in the experimental data in Fig. 4a, b by using the dashed white arrow, which is here only a guide for the eye.

In conclusion, in this work, we have investigated on the occurrence of the unconventional I_c(T) behaviors observed in SFIS JJs. The presence of a plateau extended over a wide range of temperatures and the peculiar non-monotonic behavior in the I_c(T) when increasing the thickness of the barrier can be explained in terms of the coexistence of spin-singlet and triplet superconductivity, whose correlation functions have been calculated by using a tight-binding BdG description of the system^44,45,46. This approach highlighted also the role played by the disorder in the barrier. At the same time, the presence of a spin-mixing effect, in this context provided by the spin–orbit interaction, is crucial to reproduce the characteristic plateau in the I_c(T) curves. Furthermore, the obtained results confirm that the reinstatement of an overall ordering in the system by the means of an external magnetic field points toward the recovery of more standard 0–π transition. Within this picture, the application of a weak magnetic field represents a tool for controlling the relative weight of equal-spin triplet transport in SFIS JJs.

Methods

Experimental I _c(T) curves at zero- and finite-field

The I_c(T) measurements at zero field have been performed by using an evaporation cryostat from 0.3 K up to the critical temperature of the devices T_c ~12 K^42,67. Measurements below 0.3 K have been performed by using a wet dilution refrigerator Kelvinox400MX^42,68 and a dry dilution cryostat Triton400. The three refrigerators employed are equipped with customized low-noise filters anchored at different temperature stages^42,67.

The I_c(T) curves at the finite external magnetic field have been measured by using the evaporation cryostat, which is equipped with a NbTi coil able to generate a magnetic field perpendicular to the transport direction^35,67. The protocol followed is based on the measurement of the Fraunhofer pattern curve at a fixed temperature for the spin-filter JJs with d_F = 3.0 nm and 3.5 nm. The I_c(H) curve is acquired ramping the magnetic field from positive to negative values, in a maximum field range of ±2.4 mT. The investigated range of temperatures corresponds to the plateau regime at zero field (from 2 to 8 K). Measurements at 0.3 K have been performed as a term of comparison with the I_c(T) curves at zero field.

At each temperature, we have measured the amplitude of the first lobe of the Fraunhofer pattern H₀. The error on H₀ is 3%. Then, we have estimated the critical current I_c at different percentages of H₀, from 0%H₀ to 85%H₀ for the JJ with d_F = 3.0 nm. The I_c for the JJ with d_F = 3.5 nm at high temperatures is less than some nanoamperes³⁵, hard testing the observation of the Fraunhofer modulation. This limited the maximum magnetic field range investigated to 75%H₀. The step in the field was chosen to be sufficiently small to avoid the interpolation of the I_c from the pattern curve. Thus, the I_c has been measured directly from the I(V) curves at the field corresponding to H/H₀. Moreover, to distinguish a peak structure in temperature, the step in temperature was fixed to 0.5 K.

Given the small range of the field explored, the shift of the maximum in the Fraunhofer pattern due to the hysteretic magnetization of the barrier was of the order of ~0.1 mT^30,35. We have removed the hysteretic shift in post-processing to guarantee that any measured effect is only related to the local magnetic field. The error on I_c ranges from 1 to 5% for currents below the nanoamperes^35,42.