Probing heavy charged Higgs bosons through bottom flavored hadrons in the $H^+\rightarrow \bar{b}t\rightarrow B+X$ channel in 2HDM

Abstract

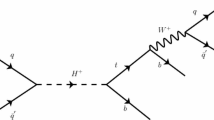
Observing light or heavy charged Higgs bosons $H^\pm$, lighter or heavier than the top quark, would be instant evidence of physics beyond the Standard Model. For this reason, in recent years searches for charged Higgs bosons have been in the center of attention of current colliders such as the CERN Large Hadron Collider (LHC). In spite of all efforts, no signal has been yet observed. Especially, the results of CMS and ATLAS experiments have excluded a large region in the MSSM $m_{H^+}-\tan \beta$ parameter space for $m_{H^+}=80{-}160$ GeV corresponding to the entire range of $\tan \beta$ up to 60. Therefore, it seems that one should concentrate on probing heavy charged Higgs bosons ($m_{H^\pm }>m_t$) so in this context each new probing channel is welcomed. In this work, we intend to present our proposed channel to search for heavy charged Higgses through the study of scaled-energy distribution of bottom-flavored mesons (B) inclusively produced in charged Higgs decay, i.e., $H^+\rightarrow t\bar{b}\rightarrow B+X$. Our study is carried out within the framework of the generic two Higgs doublet model (2HDM) using the massless scheme where the zero mass parton approximation is adopted for bottom quark.

1 Introduction

Despite of all successes of the standard model (SM), this model does not represent a theory of everything since there remain many unsolved open questions such as the origin of dark matter, matter-antimatter asymmetry in the universe, the hierarchy problem, etc. To solve these problems many theories have been proposed which are generally qualified as the theories beyond the SM (BSM). Among the most important ones are those based on the supersymmetry. These extended models often contain an extended Higgs sector. As an overview, the minimal extensions known as two-Higgs-doublet models (2HDMs) [1] include a second complex Higgs doublet which, after spontaneous symmetry breaking, leads to five physical Higgs boson states, i.e., two neutral scalars (h and H, with the assumption $m_h < m_H$), two charged Higgs bosons ($H^\pm$) and one neutral pseudoscalar (A) [2]. Furthermore, after imposing a discrete symmetry that gives natural flavor conservation the 2HDMs can be also classified into four categories; Type I, II, III and IV, according to the couplings of the doublets to the fermions. The minimal supersymmetric standard model (MSSM) [3] is one of the most popular and very well-studied BSM scenarios where one doublet couples to up quarks and the other to down quarks and charged leptons. It should be noted that, the Higgs sector of the MSSM is a Type-II 2HDM which provides elegant solutions to some of the short comings of the SM. It does also predict rich and various phenomenology to be testable in colliders.

Since there is no fundamental charged scalar boson in the SM, then the discovery of a charged scalar boson would clearly represent unambiguous evidence for the presence of new physics beyond the standard model. In this context, searching for the charged Higgs bosons signal is unique and in this work we propose a new channel to search for them at the current and future colliders.

In all classes of 2HDM scenario, the charged Higgs bosons $H^\pm$ can appear lighter or heavier than the top quark, while the lightest CP-even Higgs boson h can align with the properties of the SM. Therefore, looking for charged Higgs bosons $H^\pm$ in various decay channels over a wide range of masses is a top priority program in the current LHC experiments and future colliders.

Experimental searches for light charged Higgs bosons ($m_{H^\pm }< m_t$) have already been started at the Tevatron. For example, the CMS [4] and the ATLAS [5] collaborations have reported their results of proton–proton collision data recorded at $\sqrt{s}=8$ TeV using the $\tau +jets$ channel with a hadronically decaying $\tau$ lepton in the final state, i.e., $t\rightarrow bH^+(\rightarrow \tau ^+\nu _\tau )$. Last results on searching for charged Higgs bosons in the $H^\pm \rightarrow \tau ^\pm \nu _\tau$ decay channel in proton–proton collisions at $\sqrt{s}=13$ TeV is reported by the CMS experiment [6]. According to reported results, the large region in the MSSM $m_{H^+}-\tan \beta$ parameter space is excluded for $m_{H^+}=80{-}160$ GeV corresponding to the entire range of $\tan \beta$ up to 60, except a hole around $m_{H^+}\approx 150{-}160$ GeV for $\tan \beta \approx 10$. Here, $\tan \beta$ is the ratio of the vacuum expectation values of the neutral components of the two Higgs doublets. Therefore, it seems that there is no much chance to find the light charged Higgs bosons and colliders should concentrate on probing the heavy charged Higgs bosons ($m_{H^\pm }>m_t$).

Heavy charged Higgs bosons are mainly produced directly in association with a top quark (and also a bottom quark) [7, 8]. Moreover, charged Higgs bosons can be produced in supersymmetric (SUSY) cascade decays via heavier neutralino and chargino production in squark and gluino decays, see Refs. [9, 10]. On the other hand, in many models a heavy charged Higgs boson is predicted to decay predominantly either to a tau and its associated neutrino, or to a top and a bottom quark ($H^+\rightarrow t\bar{b}$). However, the channel $H^+\rightarrow t\bar{b}$ suffers from large multi-jet background, but it dominates in the heavy mass region, see Refs. [11,12,13,14]. Searches for the signature $H^+\rightarrow t\bar{b}$ have been interpreted by the ATLAS and CMS Collaborations in proton–proton collisions at center-of-mass energies of 8 [12] and 13 TeV [13,14,15] and a small excluded region in the MSSM $m_{H^+}-\tan \beta$ parameter space has been presented. For example, the corresponding searches carried out by ATLAS at $\sqrt{s}=13$ TeV and the integrated luminosity $L = 13.2$ fb$^{-1}$ have excluded $m_{H^+}\approx 300{-}900$ GeV for a very low $\tan \beta (\approx 0.5-1.7)$ region [11], where as for high values of $\tan \beta >44(60)$, $m_{H^+}\approx 300(366)$ GeV have been excluded. Therefore, large regions in the parameter space are still allowed and corresponding searches are in progress.

In the present work, we study the dominant decay mode $H^+\rightarrow t\bar{b}$ followed by $b\rightarrow B+X$, where B is the bottom-flavored hadron and X collectively denotes the unobserved final state particles. Therefore, our proposed channel to search for heavy charged Higgs bosons at colliders is to study the energy distributions of B-hadrons inclusively produced in the decay mode $H^+\rightarrow B+X$. To this aim, our primary purpose is the evaluation of the next-to-leading order (NLO) QCD corrections to the differential partial decay width $d\Gamma (H^+\rightarrow t\bar{b}(+g))/dx_b$, where $x_b$ stands for the scaled-energy of bottom quark. This differential width, which is presented for the first time, is needed to obtain the energy spectrum of B-mesons through heavy charged Higgs decays. Also, the hadronization process $b\rightarrow B$ is described by the nonperturbative fragmentation functions (FFs) which will be introduced in Sect. 3. The differential decay width at the parton level ($d\Gamma /dx_b$), the nonperturbative FFs and the factorization theorem, introduced in Sect. 3, allow us to compute the desired physical quantity; the energy spectrum of B-hadrons. Beforehand, in Ref. [16] we have studied the energy spectrum of B-mesons produced form direct decay of top quarks in the SM, i.e., $t\rightarrow BW^++X$. It would be expected that a comparison between the energy spectrum of B-mesons from charged Higgs decays and those from top decays at SM indicates a signal for new physics beyond the SM.

This paper is organized as follows. In Sect. 2, we express our analytical results of the $\mathcal{O}(\alpha _s)$ QCD corrections to the Born level rate of $H^+\rightarrow t\bar{b}$. We shall apply the massless scheme where the bottom quark mass is ignored but the arbitrary value of charged Higgs mass is retained. In Sect. 3, we give our numerical analysis of inclusive production of B-hadrons from heavy charged Higgs decay considering the factorization theorem and the DGLAP evaluation equations. Sect. 4 is devoted to our summary and conclusions.

2 Parton level results in the general 2HDM

Assuming $m_{H^+}>m_t$, we first study the NLO radiative corrections to the partial decay width

$$\begin{aligned} H^+\rightarrow t\bar{b}, \end{aligned}$$

(1)

in the general 2HDM, where $H_1$ and $H_2$ are the doublets whose vacuum expectation values (VEV’s), i.e., $\mathbf{v} _1$ and $\mathbf{v} _2$, give masses to the down and up type quarks, respectively. The squared sum of VEV’s is fixed by the Fermi constant $G_F$ as $\mathbf{v} _1^2+\mathbf{v} _2^2=(\sqrt{2} G_F)^{-1}=(246~GeV)^2$. However, the ratio of two VEV’s is a free parameter and can be characterized by the angle $\beta$ by introducing $\tan \beta =\mathbf{v} _2/\mathbf{v} _1$. A linear combination of the charged components of doublets $H_1$ and $H_2$ does also give the observable charged Higgs $H^\pm$, i.e., $H^\pm =H_2^\pm \cos \beta -H_1^\pm \sin \beta$.

In a general 2HDM, tree-level flavor-changing neutral currents (FCNC) can be avoided if one does not couple the same Higgs doublet to up- and down-type quarks simultaneously. Therefore, for our purpose we need the specific models which naturally stop these problems by restricting the Higgs coupling. In this context, there are two possibilities (which are also called two models) for the two Higgs doublets to couple to the quarks.

In the first possibility (or model I), the Higgs doublet $H_1$ couples to all bosons and another doublet $H_2$ couples to all quarks in the same manner as in the SM. In this model, the Yukawa couplings between the top- and the bottom-quark and the charged Higgs are given by the following Lagrangian [17]

$$\begin{aligned} L_1= & {} \frac{g_{_W}}{2\sqrt{2}m_W}V_{tb}\cot \beta \bigg \{H^+\bar{t}\big [m_t(1-\gamma _5) \nonumber \\&- m_b(1+\gamma _5)\big ]b\bigg \}+H.c, \end{aligned}$$

(2)

where, $g_W^2=4\sqrt{2} m_W^2 G_F$ and the CKM matrix element is labeled by $V_{tb}$.

In the second possibility (model II), the doublet $H_1$ couples only to the right chiral down-type quarks while the $H_2$ couples only to the right chiral up-type quarks. In this model, the charged Higgs boson couplings to fermions are given by the following Lagrangian

$$\begin{aligned} L_{2}= & {} \frac{g_{_W}}{2\sqrt{2}m_W}V_{tb} \bigg \{H^+\bar{t}\big [m_t\cot \beta (1-\gamma _5) \nonumber \\&+ m_b\tan \beta (1+\gamma _5)\big ] b\bigg \}+H.c . \end{aligned}$$

(3)

These two models are also known as Type-I and Type-II 2HDM scenarios and, as mentioned in the Introduction, the MSSM [18,19,20] is a special case of a Type-II 2HDM.

For the process (1), considering the interaction Lagrangians (2) and (3) the current density is expressed as $J^{\mu }\propto \psi _b(a+b\gamma _5)\bar{\psi }_t$ so that the coupling factors in two models are given by

$$\begin{aligned} \mathbf{model} I :\quad a= & {} \frac{g_{_W}}{2\sqrt{2}m_W}V_{tb}(m_t-m_b)\cot \beta ,\nonumber \\ b= & {} \frac{g_{_W}}{2\sqrt{2}m_W}V_{tb}(m_t+m_b)\cot \beta , \end{aligned}$$

(4)

and

$$\begin{aligned} \mathbf{model} II :\quad a= & {} \frac{g_{_W}}{2\sqrt{2}m_W}V_{tb}(m_t \cot \beta +m_b\tan \beta ),\nonumber \\ b= & {} \frac{g_{_W}}{2\sqrt{2}m_W}V_{tb}(m_t \cot \beta -m_b\tan \beta ). \end{aligned}$$

(5)

In next section, we describe the technical detail of our calculation for the $\mathcal{O}(\alpha _s)$ radiative corrections to the tree-level decay rate of $H^+\rightarrow t\bar{b}$ using dimensional regularization to regularize all divergences.

2.1 Born decay width of $H^+\rightarrow t\bar{b}$

The decay process (1) is analyzed in the rest frame of the charged Higgs boson. It is straightforward to calculate the Born term contribution to the partial decay rate of the process (1) in the 2HDM. According to the given Lagrangian in Eqs. (2) and (3), the coupling of the charged-Higgs to the fermions (top and bottom quark in (1)) can either be expressed as a superposition of scalar and pseudoscalar coupling factors or as a combination of right- and left-chiral coupling factors [17]. Therefore, the lowest order decay amplitude is of the form

$$\begin{aligned} M_0=v_b(a\varvec{1}+b\gamma _5)\bar{u}_t=v_b\left\{ g_t\frac{1+\gamma _5}{2}+g_b\frac{1-\gamma _5}{2}\right\} \bar{u}_t,\nonumber \\ \end{aligned}$$

(6)

where, $g_t=a+b$ and $g_b=a-b$. Therefore, the tree-level decay width reads

$$\begin{aligned} \Gamma _0= & {} \frac{N_c m_H}{8\pi }\lambda ^{\frac{1}{2}}(1,R,y)\bigg [2(a^2+b^2)(S-R)\nonumber \\&-2(a^2-b^2)\sqrt{Ry}\bigg ], \end{aligned}$$

(7)

where $\lambda (x,y,z)=(x-y-z)^2-4y z$ is the Källén function and $N_c=3$ is a color factor. Here, for simplicity, we have defined: $R=(m_b/m_H)^2$, $y=(m_t/m_H)^2$ and $S=(1+R-y)/2$. This result is in complete agreement with the one presented in Ref. [21]. In the limit of vanishing bottom quark mass, the tree-level decay width is of the form

$$\begin{aligned} \Gamma _0=\frac{N_c m_H(1-y)^2}{8\pi }(a^2+b^2), \end{aligned}$$

(8)

where, in both models I and II one has

$$\begin{aligned} a^2+b^2=\sqrt{2}G_F |V_{tb}|^2 m_t^2\cot ^2\beta . \end{aligned}$$

(9)

Since $m_b<<m_t$, finite-$m_b$ corrections are expected to be negligible in the case at hand. This expectation has been actually confirmed in Ref. [16], by a comparative analysis of the partial width of the decay $t\rightarrow bW^+$ in the general-mass variable-flavor-number scheme (GM-VFNS), where bottom-quark mass is preserved, and the zero-mass variable-flavor-number scheme (ZM-VFNS), where bottom is included among the massless quark flavors. Then, throughout this work we apply the ZM-VFNS or massless scheme.

In next section, we compute the $\mathcal{O}(\alpha _s)$ QCD corrections to the Born-level decay rate of $H^+\rightarrow t\bar{b}$ and present, for the first time, the analytical parton-level expressions for $d\Gamma (H^+\rightarrow B+X)/dx_B$ at NLO in the ZM-VFNS. To this aim, we calculate the quantity $d\Gamma _b/dx_b$ where,

$$\begin{aligned} x_b=\frac{E_b}{E_b^{max}}=\frac{2E_b}{m_H(1-y)}, \end{aligned}$$

(10)

is the scaled-energy of b-quark. It ranges as $0\le x_b\le 1$.

2.2 $\mathcal{O}(\alpha _s)$ virtual corrections

The QCD virtual one-loop corrections to the process $H^+\rightarrow t\bar{b}$ contain both infrared (IR) and ultraviolet (UV) divergences where the UV-divergences appear when the integration region of the internal momentum of the virtual gluon goes to infinity and the IR-divergences arise from the soft-gluon singularities. In this work, we adopt the “on-shell” mass renormalization scheme and apply the dimensional regularization scheme to regularize all divergences. Through this scheme, all singularities are regularized in $D =4-2\epsilon$ dimensions to become single poles in $\epsilon$. Considering the two-body phase space for the virtual corrections the contribution of virtual radiations into the differential decay width reads

$$\begin{aligned} \frac{d\Gamma ^\mathbf{vir }_b}{dx_b}=\frac{S}{8\pi m_H} \overline{|M^\mathbf{vir }|^2}\delta (1-x_b), \end{aligned}$$

(11)

where, $\overline{|M^\mathbf{vir }|^2}=\sum _{Spin}(M_0^{\dagger } M_{loop}+M_{loop}^{\dagger } M_0)$. Here, $M_0$ is the Born term amplitude (6) and the renormalized amplitude of the virtual corrections is given by $M_{loop}=v_b(\Lambda _{ct}+\Lambda _l)(a+b\gamma _5)\bar{u}_t$, where $\Lambda _{ct}$ represents the counterterm and $\Lambda _l$ arises from the one-loop vertex correction [22]. Following Refs. [23, 24], the counterterm of the vertex includes the wave-function renormalizations of quarks as well as the top quark mass renormalization

$$\begin{aligned} \Lambda _{ct}=\frac{\delta Z_b}{2}+\frac{\delta Z_t}{2}- \frac{\delta m_t}{m_t}. \end{aligned}$$

(12)

Since, we are working in the ZM-VFN scheme where $m_b=0$ is assumed, then the b-quark mass counterterm is $\delta m_b=0$. The wave function and the mass renormalization constants are given by [25]

$$\begin{aligned} \delta Z_b= & {} -\frac{\alpha _s(\mu _R)}{4\pi }C_F\left[ \frac{1}{\epsilon _{UV}}-\frac{1}{\epsilon _{IR}}\right] ,\nonumber \\ \delta Z_t= & {} -\frac{\alpha _s(\mu _R)}{4\pi }C_F\left[ \frac{1}{\epsilon _{UV}}+\frac{2}{\epsilon _{IR}} -3\gamma _E+3\ln \frac{4\pi \mu _F^2}{m_t^2}+4\right] , \nonumber \\ \frac{\delta m_t}{m_t}= & {} \frac{\alpha _s(\mu _R)}{4\pi }C_F\left[ \frac{3}{\epsilon _{UV}}-3\gamma _E+ 3\ln \frac{4\pi \mu _F^2}{m_t^2}+4\right] , \end{aligned}$$

(13)

where, $\gamma _E=0.5772\cdots$ is the Euler constant, $C_F=(N_c^2-1)/(2N_c)=4/3$ for $N_c=3$ quark colors, and $\mu _F$ is the factorization scale which is arbitrarily set as $\mu _F=m_H$ in our work. Conventionally, $\epsilon _{IR}$ and $\epsilon _{UV}$ represent the infrared and the ultraviolet divergences, respectively.

The real part of the vertex correction is given by

$$\begin{aligned} \Lambda _l= & {} \frac{\alpha _s N_c m_H^2}{\pi }C_F(a^2+b^2)\big [y-1+(1-y)B_0(0,0,0)\nonumber \\&-yB_0(m_H^2,0,m_t^2)+B_0(m_t^2,0,m_t^2) \nonumber \\&-(1-y)^2m_H^2 C_0(0,m_t^2,m_H^2,0,0,m_t^2)\big ], \end{aligned}$$

(14)

where, $B_0$ and $C_0$ are the Passarino–Veltman 2-point and 3-point integrals [26]. By summing all virtual corrections up, the UV-singularities are canceled so that the virtual differential decay rate is ultraviolet finite. But, the IR-divergences are remaining which are now labeled by $\epsilon$. Eventually, the virtual one-loop contributions read

$$\begin{aligned} \frac{d\Gamma ^\mathbf{vir }_b}{dx_b}= & {} \Gamma _0 \frac{\alpha _s(\mu _R)}{2\pi }C_F \delta (1-x_b)\bigg \{2Li_2(y)-\frac{1}{\epsilon ^2}+\frac{F}{\epsilon } \nonumber \\&-\frac{F^2}{2}+(2y-5)\ln \frac{1-y}{y}+\ln ^2y-\frac{3\pi ^2}{4}-\frac{7}{8}\bigg \},\nonumber \\ \end{aligned}$$

(15)

where, $Li_2(y)=-\int _0^y (dt/t) \ln (1-t)$ is the Spence function and

$$\begin{aligned} F=-\ln \frac{4\pi }{y}+2\ln \frac{1-y}{y}+\gamma _E-\frac{5}{2}. \end{aligned}$$

(16)

2.3 Real gluon corrections (Bremsstrahlung)

To obtain the infrared-finite physical results for $d\Gamma _b/dx_b$ one must include the contributions of real gluons emission. Considering two Feynman graphs including the real gluon emissions from the top and bottom quark, the $\mathcal{O}(\alpha _s)$ real gluon emission (tree-graph) amplitude reads

$$\begin{aligned} M^\mathbf{real }= & {} g_s\frac{\lambda ^a}{2} v(p_b, s_b)\left\{ -\frac{2p_t^\mu + {\not \!\!p}_g \gamma ^\mu }{2p_t \cdot p_g}+\frac{p_b^\mu +\gamma ^\mu {\not \!\!p}p_g}{2p_b\cdot p_g}\right\} \nonumber \\&(a\mathbf{1} +b\gamma _5) \bar{u}(p_t, s_t)\epsilon _{\mu }^{\star }(p_g,r), \end{aligned}$$

(17)

where $\epsilon (p_g,r)$ refers to the polarization vector of the emitted real gluon with the spin r. The first and second expressions in the curly brackets are related to the real gluon emissions from the top and bottom quarks, respectively. In order to regulate the IR-divergences which arise from the soft and collinear real-gluon emissions, as before, we apply dimensional regularization scheme. According to this scheme, the real differential decay rate for the process $H^+\rightarrow t\bar{b}g$ is given by

$$\begin{aligned} d\Gamma ^\mathbf{real }=\frac{\mu _F^{2(4-D)}}{2m_H}|M^\mathbf{real }|^2dR_3(p_t, p_b, p_g, p_{_{H^+}}), \end{aligned}$$

(18)

where, $\mu _F$ is an arbitrary reference mass and the phase space element $dR_3$ is defined as

$$\begin{aligned} \frac{d^{D-1}\mathbf {p}_b}{2E_b}\frac{d^{D-1}\mathbf {p}_t}{2E_t}\frac{d^{D-1}\mathbf {p}_g}{2E_g} (2\pi )^{3-2D}\delta ^D\left( p_H-\sum _{g,b,t} p_f\right) .\nonumber \\ \end{aligned}$$

(19)

To evaluate the differential decay rate $d\Gamma ^{real}_b/dx_b$, we fix the momentum of bottom quark in Eq. (18) and integrate over the gluon energy which ranges as

$$\begin{aligned} m_H\frac{(1-y)(1-x_b)}{2}\le E_g \le m_H\frac{(1-y)(1-x_b)}{2(1-x_b(1-y))}. \end{aligned}$$

(20)

Note that, when we integrate over the phase space of the real gluon radiation, terms of the form $(1-x_b)^{-1-2\epsilon }$ appear which are due to the radiation of soft gluon, i.e., $E_g\rightarrow 0 \equiv x_b\rightarrow 1$. Thus, we employ the following prescription introduced in Ref. [27]

$$\begin{aligned} (1-x_b)^{-1-2\epsilon }= & {} -\frac{1}{2\epsilon }\delta (1-x_b)+\bigg (\frac{1}{1-x_b}\bigg )_+\nonumber \\&-2\epsilon \bigg (\frac{\ln (1-x_b)}{1-x_b}\bigg )_+, \end{aligned}$$

(21)

where the plus distributions are defined as

$$\begin{aligned} \int _0^1 (f(x))_{_+}h(x)dx=\int _0^1f(x)[h(x)-h(1)]dx. \end{aligned}$$

(22)

2.4 Analytical results for $d\Gamma /dx_i$ at parton level

The $\mathcal{O}(\alpha _s)$ corrections to the differential decay rate of $H^+\rightarrow t\bar{b}$ is obtained by summing the Born, the virtual and the real gluon contributions. It reads

$$\begin{aligned} \frac{d\Gamma ^\mathbf{nlo }_b}{dx_b}= & {} \Gamma _0\left[ \delta (1-x_b)+ \frac{C_F\alpha _s}{2\pi }\left\{ \left[ -\frac{1}{\epsilon }+\gamma _E-\ln 4\pi \right] \right. \right. \nonumber \\&\times \left. \left. \left[ \frac{3}{2}\delta (1-x_b)+\frac{1+x_b^2}{(1-x_b)_+}\right] +T_1\right\} \right] , \end{aligned}$$

(23)

where, by defining $S=(1-y)/2$ (with $y=m_t^2/m_H^2$) one has

$$\begin{aligned} T_1= & {} \delta (1-x_b)\bigg \{\frac{3}{2}\ln y+4S\ln \frac{y}{1-y}-2Li_2\frac{1}{y}-\frac{\pi ^2}{3}-2\bigg \}\nonumber \\&+2(1+x_b^2)\bigg (\frac{\ln (1-x_b)}{1-x_b}\bigg )_+\nonumber \\&+\frac{1+x_b^2}{(1-x_b)_+}\bigg \{\ln \frac{4S^2x_b^2}{1-2Sx_b}+\frac{1}{(1-2Sx_b)^2}\bigg [-2S^2x_b^2\nonumber \\&+\frac{(1-x_b)^2+2x_b(4Sx_b-1)}{1+x_b^2}\bigg ]\bigg \}. \end{aligned}$$

(24)

Our result of differential decay rate, which is presented for the first time, after integration over $x_b$ ($0\le x_b \le 1$) is in complete agreement with the result presented in [21].

Note that, our main purpose is to evaluate the energy distribution of B-hadrons produced in heavy charged Higgs boson decay: $H^+\rightarrow t\bar{b}(+g)\rightarrow B+X$, where B-hadrons can be produced from the fragmentation of b-quark as well as the emitted real gluons. Therefore, in order to obtain the most accurate energy spectrum of produced B-hadrons we have to consider the contribution of gluon fragmentation as well. It should be noted that, the gluon splitting contribution is important at the low energy of the observed B-hadron so this contribution decreases the size of decay rate at the threshold, see Refs. [28, 29]. With this explanation, we also need to compute the NLO differential decay rate $d\Gamma ^\mathbf{nlo }_g/dx_g$, where $x_g=2E_g/(m_H (1-y))$ is the scaled-energy of emitted real gluon, as in (10). Ignoring the details of calculation, this differential decay rate is given by

$$\begin{aligned}&\frac{d\Gamma ^\mathbf{nlo }_g}{dx_g}\nonumber \\&\quad =\Gamma _0\frac{C_F\alpha _s}{2\pi }\bigg \{\frac{1+(1-x_g)^2}{x_g}\left( -\frac{1}{\epsilon }+\gamma _E-\ln 4\pi \right) +T_2\bigg \}, \end{aligned}$$

(25)

where,

$$\begin{aligned} T_2= & {} \frac{1+(1-x_g)^2}{x_g}\ln \frac{S^2x_g^2(1-x_g)^2(1-2Sx_g)}{y^2}\nonumber \\&+\frac{(x_g+2)^2-8}{x_g}. \end{aligned}$$

(26)

In Eqs. (23) and (25), the terms $T_1$ and $T_2$ are free of all IR-divergences. In order to subtract the singularities remaining in the differential decay widths, we employ the modified minimal-subtraction $(\overline{MS})$ scheme, where the singularities are absorbed into the bare fragmentation functions (FFs). This renormalizes the FFs, endowing them with $\mu _F$ dependence, and creates in the differential decay widths the finite terms of the form $(\alpha _s/\pi )\ln (m_H^2/\mu _F^2)$ which are rendered perturbatively small by choosing $\mu _F=\mathcal{O}(m_H)$. Following the $\overline{MS}$ scheme, in order to have the finite coefficient functions we have to subtract from Eqs. (23) and (25), the $\mathcal{O}(\alpha _s)$ term multiplying the characteristic $\overline{MS}$ constant, i.e., $-1/\epsilon +\gamma _E-\ln 4\pi$ [27].

3 Numerical results

In this work, using the ZM-VFNS we study the decay process

$$\begin{aligned} H^+\rightarrow t\bar{b}(+g), \end{aligned}$$

(27)

followed by $\bar{b}/g\rightarrow B+X$. In this process, top quark dominantly decays as: $t\rightarrow bW^+\rightarrow bl^+\nu _l$. In the narrow-width approximation (NWA), where we set $p_t^2=m_t^2$ and $p_{W^+}^2=m_{W^+}^2$ and ignore small terms of order $\mathcal{O}(\Gamma _i^2/m_i^2)(i=t,W^+)$, the total decay rate reads

$$\begin{aligned}&\Gamma (H^+\rightarrow b\bar{b}l^+\nu _l)\nonumber \\&\quad = \Gamma (H^+\rightarrow t\bar{b})\times B(t\rightarrow bW^+)\times B(W^+\rightarrow l^+\nu _l),\nonumber \\ \end{aligned}$$

(28)

where, for the branching ratios one has $B(t\rightarrow bW^+)=96.2\%$ and $B(W^+\rightarrow l^+\nu _l)=10.86\%$ [30]. More details about the NWA can be found in Ref. [31].

Having the differential decay widths for the process (27), i.e., Eqs. (23) and (25), we are now in a situation to make our phenomenological predictions for the scaled-energy ($x_B$) distribution of B-hadrons inclusively produced in the decay of heavy charged Higgs bosons. To present our results for the $x_B$-distribution, we consider the differential distribution $d\Gamma ^{nlo}/dx_B$ of the partial width of the decay $H^+\rightarrow B+X$, where $x_B=2E_B/(m_H(1-y))$ is the scaled-energy of B-hadrons in the charged Higgs rest frame. The $x_B$-variable is defined as $x_b$ in (10).

Our tool to compute the scaled energy distribution of B-hadrons is the factorization theorem of QCD-improved parton model [32]. According to this theorem [33], the energy distribution of B-hadrons can be expressed as the convolution of the parton-level spectrum $d\Gamma _a/dx_a (a=b, g)$ with the nonperturbative FFs of $a\rightarrow B$, describing the hadronization process of $a\rightarrow B$. The $a\rightarrow B$ FFs are labeled by $D_a^B(z, \mu _F)$, where $\mu _F$ is the factorization scale and $z=E_B/E_a$ is the fragmentation variable which indicates the energy fraction of parent parton carried by the produced hadron. The factorization theorem is expressed as

$$\begin{aligned} \frac{d\Gamma }{dx_B}=\sum _{a=b, g}\int _{x_a^\text {min}}^{x_a^\text {max}} \frac{dx_a}{x_a}\,\frac{d\Gamma _a}{dx_a}(\mu _R, \mu _F) D_a^B\left( \frac{x_B}{x_a}, \mu _F\right) , \end{aligned}$$

(29)

where, $\mu _R$ and $\mu _F$ are the renormalization and factorization scales, respectively. The scale $\mu _R$ is related to the renormalization of the QCD coupling constant. In this paper, we use the convention $\mu _R=\mu _F=m_H$, a choice often made.

Several searches for the signature $H^+\rightarrow t\bar{b}$ in the context of 2HDMs have been done by the ATLAS and CMS Collaborations in proton–proton collisions at center-of-mass energies of 8 and 13 TeV [12,13,14]. For example, in Ref. [13] the presented results are based on proton–proton collision data collected in 2016 at $\sqrt{s}=13$ TeV by the CMS experiment, corresponding to an integrated luminosity of $35.9~ fb^{-1}$. Figure 7 in this reference shows the excluded parameter space in the MSSM scenarios. Based on their results, the maximum $\tan \beta$ value excluded is 0.88 for $0.20< m_{H^\pm }< 0.55$ TeV. The corresponding searches carried out by ATLAS at $\sqrt{s}=13$ TeV and the integrated luminosity $L = 13.2$ fb$^{-1}$ have been excluded $m_{H^+}\approx 300-900$ GeV for a very low $\tan \beta (\approx 0.5-1.7)$ region [11], where as for high values of $\tan \beta >44(60)$, $m_{H^+}\approx 300(366)$ GeV are excluded. Although, a definitive search over the $m_{H^+}-\tan \beta$ plane is a program that still has to be carried out and this belongs to the LHC experiments and future colliders.

In this work, for our numerical analysis we restrict ourselves to the allowed regions of the $m_{H^+}-\tan \beta$ parameter space evaluated by the CMS experiments, see Fig.7 in Ref. [13]. Moreover, from Ref. [34] we adopt other input parameters as $G_F = 1.16637\times 10^{-5}$ GeV$^{-2}$ and $m_t = 172.98$ GeV. We will also evaluate the QCD coupling constant $\alpha _s$ at NLO in the $\overline{\text {MS}}$ scheme through the following relation

$$\begin{aligned} \alpha ^{(n_f)}_s(\mu )=\frac{1}{b_0\ln (\mu ^2/\Lambda ^2)} \left\{ 1-\frac{b_1 \ln \big [\ln (\mu ^2/\Lambda ^2)\big ]}{b_0^2\ln (\mu ^2/\Lambda ^2)}\right\} , \end{aligned}$$

(30)

where, $\Lambda$ is the QCD scale parameter. Also, $b_0$ and $b_1$ are given by

$$\begin{aligned} b_0=\frac{33-2n_f}{12\pi }, \quad b_1=\frac{153-19n_f}{24\pi ^2}, \end{aligned}$$

(31)

where, $n_f$ is the number of active quark flavors. In this work, we adopt $\Lambda _{\overline{\text {MS}}}^{(5)}=231.0$ MeV adjusted such that $\alpha _s^{(5)}(\mu )=0.1184$ for $\mu =m_Z=91.1876$ GeV [34].

First, we present the numerical results for the NLO decay rate $\Gamma (H^+\rightarrow t\bar{b})$ at the ZM-VFN scheme. To do this, we consider $d\Gamma _b/dx_b$ (23) and integrate over $x_b (0\le x_b\le 1)$. Our results for various values of $m_{H^+}$ read

$$\begin{aligned} \Gamma ^{NLO}= & {} \Gamma _0(1-0.01574),\quad \text {for}\ m_{H^+}=200~\text {GeV}\nonumber \\ \Gamma ^{NLO}= & {} \Gamma _0^\prime (1-0.05396),\quad \text {for}\ m_{H^+}=400~\text {GeV}\nonumber \\ \Gamma ^{NLO}= & {} \Gamma _0^{\prime \prime }(1-0.07050),\quad \text {for}\ m_{H^+}=800~\text {GeV}. \end{aligned}$$

(32)

The decay rate at the Born level (8) depends on $m_{H^+}$ and $\tan \beta$. For the tree-level decay rates in the above relations we have $\Gamma _0=0.7493\cot ^2\beta$, $\Gamma _0^\prime =15.6038\cot ^2\beta$ and $\Gamma _0^{\prime \prime }=42.9046\cot ^2\beta$. From Eq. (32), it is seen that the QCD corrections decrease the charged Higgs boson decay width and their amounts depend on the charged Higgs mass. Note that, for the total decay rate of process $H^+\rightarrow \bar{b} t(\rightarrow bW^+(\rightarrow l^+\nu _l))$ the above results should be multiplied by $B(t\rightarrow bW^+)$ and $B(W^+\rightarrow l^+\nu _l)$, see Eq. (28).

Now, we go back to our main aim: the evaluation of energy distribution of B-hadrons in heavy charged Higgs decays. For this purpose, we use the factorization relation (29) where to describe the splitting $(b, g)\rightarrow B$, from Ref. [35] we employ the realistic nonperturbative B-hadron FFs determined at NLO in the ZM-VFN scheme. These FFs have been determined through a global fit to electron-positron annihilation data presented by ALEPH [36] and OPAL [37] at CERN LEP1 and by SLD [38] at SLAC SLC. According to the approach used in [35], the power ansatz $D_b(z,\mu _F^\text {ini})=Nz^\alpha (1-z)^\beta$ is adopted for the $b\rightarrow B$ splitting where the free parameters have been determined at the initial scale $\mu _F^\text {ini}=4.5$ GeV. The fit yielded $N=2575.014$, $\alpha =15.424$, and $\beta =2.394$. The gluon FF is assumed to be zero at the initial scale $\mu _F^\text {ini}$ and generated via the DGLAP evolution equations [39, 40].

Fig. 1

The $x_B$ spectrum in heavy charged Higgs decay in the 2HDM. The NLO result (dashed line) is compared to the LO one (solid line) taking $\tan \beta =2$ and $m_{H^+}=200$ GeV

In Fig. 1, our prediction for the energy spectrum of bottom-flavored hadrons is presented by plotting $d\Gamma /dx_B$ versus $x_B$. For this prediction, we have studied the size of the NLO corrections by comparing the LO (solid line) and NLO (dashed line) distributions. In order to study the importance of NLO corrections at the parton level, we evaluated the LO distribution using the same NLO $b\rightarrow B$ FF. Our results show that the NLO corrections lead to a significant enhancement of the partial decay width in the peak region and above, while these corrections decrease the size of partial decay rate in the lower-$x_B$ range. It should be noted that, the contribution of gluon splitting is appreciable only in the low-$x_B$ region. For higher values of $x_B$, the contribution of b-quark fragmentation dominates, as expected [16].

In Fig. 2, the dependence of $x_B$ spectrum on $\tan \beta$ is studied, taking $m_{H^+}=200$ GeV. As is seen, when the value of $\tan \beta$ increases the decay rate decreases, because the Born rate $\Gamma _0$ (8) is proportional to $\cot ^2\beta$.

In Fig. 3, by fixing $\tan \beta =2$ we have investigated the dependence of $x_B$ spectrum on the charged Higgs mass taking $m_{H^+}=200$ (solid line), $m_{H^+}=400$ GeV (dashed line) and $m_{H^+}=600$ GeV (dot-dashed line). This figure shows that, if $m_{H^+}$ increases the size of partial decay width increases as well. Nevertheless, the peak position of $x_B$-distribution is approximately independent of the charged Higgs mass.

Fig. 2

$d\Gamma (H^+\rightarrow BX)/x_B$ as a function of $x_B$ in the 2HDM considering different values of $\tan \beta =1$, 3 and 6. The mass of heavy charged Higgs is fixed to $m_{H^+}=200$ GeV

Fig. 3

The $x_B$ spectrum in charged Higgs decay for different values of charged Higgs mass: $m_{H^+}=200$ GeV (solid line), $m_{H^+}=400$ GeV (dashed line) and $m_{H^+}=600$ GeV (dot-dashed line)

4 Conclusions

The SM of particle physics predicts one neutral Higgs boson, whereas the Minimal Supersymmetric requires five Higgs particles, three neutral bosons and two charged bosons. The discovery of charged Higgs bosons would be proof of new physics beyond the SM. For this reason, searches for the charged Higgs bosons are strongly motivated so that in recent years it has been a goal of many high energy colliders such as the CERN LHC. Searches for light charged Higgs bosons (particles lighter than the top quark) has been inconclusive and no evidence has been yet found. In this regard, the results reported by the CMS and ATLAS Collaborations show the large excluded region in the MSSM $m_{H^+}-\tan \beta$ parameter space. Therefore, it sounds that most efforts should be concentrated on probing heavy charged Higgs bosons (heavier than the top quark). These scalar bosons are predicted to decay predominantly either to a tau and its associated neutrino ($\tau \bar{\nu }_\tau$), or to a top and a bottom quark ($t\bar{b}$). In spite of the fact that the decay channel $H^+\rightarrow t\bar{b}$ suffers from large multi-jet background, but it dominates in the heavy mass region.

In this work, we studied the dominant decay channel $H^+\rightarrow t\bar{b}(+g)$ followed by the hadronization process $(b,g)\rightarrow B$. At colliders, the bottom-flavored hadrons could be identified by a displaced decay vertex associated whit charged lepton tracks. On other words, B-hadrons decay to the $J/\psi$ followed by the $J/\psi \rightarrow \mu ^+\mu ^-$ decays, see Ref. [41]. Then a muon in jet is associated to the b-flavored hadron. Furthermore, one can also explore an other way to associated the $J/\psi$ with the corresponding isolated lepton- by measuring the jet charge of identified b and not requiring the tagging muon. Therefore, at the LHC and future colliders the decay channel $H^+\rightarrow B+X$ is proposed to search for the heavy charged Higgs bosons and evaluating the distribution in the scaled-energy ($x_B$) of B-mesons would be of particular interest. This distribution is studied by evaluating the quantity $d\Gamma /dx_B$. To present our phenomenological prediction of the $x_B$-distribution, we first calculated an analytic expression for the NLO radiative corrections to the differential decay width $d\Gamma (H^+\rightarrow t\bar{b})/dx_a (a=b, g)$ and then employed the nonperturbative $(b,g)\rightarrow B$ FFs, relying on their universality and scaling violations. Our results have been presented in the ZM-VFN scheme where the b-quark mass is ignored from the beginning. In this scheme, results are the same in both the type-I and II 2HDM scenarios.

Our analysis is expected to make a contribution to the LHC searches for charged Higgs bosons. In fact, a comparison between the energy spectrum of B-mesons produced from charged Higgs decays at 2HDM and those from top decays at SM ($t\rightarrow B+X$) would indicate a signal for new physics beyond the SM.

Our analysis can be also extended to the production of hadron species other than the B-hadron, such as pions, kaons and protons, etc. This would be possible by using the nonperturbative $(b, g)\rightarrow \pi /K/P/D^+$ FFs presented in Refs. [42,43,44,45].