1 Introduction

Modern cosmologists are facing a significant challenge with the late-time expansion of our universe. A wealth of observationally supported data [1,2,3,4,5] suggests that our cosmos is continuously expanding. Interestingly, this expansion is believed to be driven by an unknown form of energy called dark energy (DE), which makes up around two-thirds of the total energy present in the universe. The mysterious nature of DE is thought to accelerate the late-time cosmic expansion, while dark matter, the second leading component in the cosmos distribution, acts as invisible matter and supports the gravitational clustering procedure. The existence of both DE and dark matter is affirmed by their gravitational impact.

Einstein’s general relativity (GR) theory, which outlines the effects of gravity on a local scale, fails to produce accurate results when considering the global concept of universe-accelerated expansion. To investigate this concept, many modified theories of gravity have been proposed. Modified theories of gravity are successful approaches to discussing the gravitational impact and various stages of cosmic history. These theories are obtained by simply changing the curvature part of GR action. A variety of modified gravity theories can be found in the literature, such as f(R) gravity, \(f(R,\tau )\) gravity, f(G) gravity, f(R, G) gravity, and f(T) gravity and some other theories (R is Ricci scalar, T is torsion, G is Gauss-Bonnet term), which all have different approaches to the concept of cosmic expansion. These theories are widely discussed and explored in papers such as [6,7,8,9,10].

One of the notable amended theories of gravity is the f(R) theory [11], which is regarded as a primary extension of GR. Unlike a linear Ricci scalar, the action of this theory involves a function of the Ricci scalar R. Another interesting approach is the formulation of torsion-based theories, with the first such gravitational framework being the “Teleparallel Equivalent to General Relativity” (TEGR). This theory depends on the Weitzenbock connection, making it a curvature-less theory with non-zero torsion [12]. A generalisation of this theory was proposed, with the Lagrangian being a function of the torsion scalar T (similar to the f(R) extension of GR). It is worth noting that f(T) gravity is considered simpler than f(R) gravity because its field equations are of second order, whereas those of f(R) gravity result in fourth-order field equations. However, it has been argued in the literature [13, 14] that the Platini version of f(R) gravity yields a system of second-order field equations. In comparison to GR, it has been observed [15] that f(T) gravity exhibits an additional degree of freedom under Lorentz transformations, thus remaining invariant. Interestingly, since f(T) gravity is invariant under Lorentz transformations, the choice of a good or bad tetrad plays a crucial role in this theory. It has been noticed that every solution for GR is also acceptable for TEGR. A significant amount of research has been conducted in the literature to discuss the accelerated expansion of the universe using the f(T) gravitational framework. To overcome the limitations of f(T) gravity for diagonal tetrads in producing solar systems, it is argued that off-diagonal tetrads (good tetrads) can be utilized [16, 17].

Einstein’s GR theory postulates a minimal coupling between spacetime geometry and matter field, resulting in the conservation law of the energy-momentum tensor (EMT). However, this conservation law only holds true for Minkowski’s flat spacetime or weak gravitational fields, leaving room for modifications to the theory. Rastall [18, 19] proposed an amendment to GR that improves upon the conservation law to account for its violation in curved spacetime. This amendment introduces the Rastall coupling parameter,\(\lambda \), which measures the affinity of spacetime geometry to couple with matter field in a non-minimal way. The limiting value of \(\lambda \), i.e., zero coupling, reverts the modified form back to GR. The revised conservation law is expressed as \(\nabla _{\nu }T^{\nu \mu }=\lambda R^{,\mu }\). The modified field equations derived from this amendment are given as:

$$\begin{aligned} G_{\mu \nu }+\kappa \lambda g_{\mu \nu }R=\kappa T_{\mu \nu }, \end{aligned}$$

where \(\kappa \) denotes the gravitational coupling constant.

It is noteworthy that the modified Rastall theory (RT) shares all vacuum solutions with GR. Nonetheless, when the Rastall parameter \(\lambda \) is considered, the non-vacuum solutions show substantial differences from those in GR. Leading to a growing interest in RT among researchers, they showed their interest by making a variety of comments regarding the novelty and correctness of RT. Although researchers have shown an increasing interest in exploring the fascinating and mysterious features of the RT, Visser [20] recently claimed that the RT is simply equivalent to GR. However, Darabi et al. [21, 22] disagreed, arguing that these theories are distinct and that Visser’s claim was inaccurate. Visser argued that the energy-momentum-tensor (EMT) proposed by Rastall was flawed and that Rastall’s proposal was simply a rearrangement of the matter sector of GR. In contrast, Darabi et al. argued that Rastall’s EMT definition was consistent with the conventional definition of EMT. To reinforce their argument, they offered a compelling example of the f(R) theory of gravity, using the same method as Visser [20], but demonstrating that the f(R) theory is not equivalent to GR. In essence, the RT is a modified form of GR, as we previously noted that for a specific value of \(\lambda \) (i.e., the Rastall parameter), GR can be restored. It is worth noting that the thorough analysis of Darabi et al. [21, 22] was supported by the recent study of Hansraj et al. [23].

Various modifications have been proposed for Rastall gravity since its emergence. For instance, in a study referenced as [24], Rastall’s theory has been generalized by the authors by postulating \(\nabla _\mu T^{\mu \nu }=\nabla _\nu (\lambda ^\prime R)\), where \(\lambda ^\prime \) is a function varying in space-time coordinates. In another reference [25], the authors assume \(\nabla _\mu T^{\mu \nu }=\lambda \nabla ^\nu f(R)\), which leads to the presentation of a solution for an electrically and magnetically neutral regular black hole. Additionally, a modified version of teleparallel gravity based on Rastall’s assumption is introduced in [26, 27].

Researchers are interested in exploring the formation of extremely dense matter in extreme conditions, as a compact star could be the ultimate stage in the life cycle of a regular star. Pulsars and other rotating stars with strong magnetic fields are examples of compact stellar objects that exhibit very high densities and are significant in astrophysics [28]. Originally, it was thought that spherically symmetric matter distribution in a perfect fluid, where the radial and tangential pressures are equivalent, could describe these objects. However, in 1992, Jeans [29] proposed that the unusual conditions inside a stellar body required anisotropy to better explain the displacement of matter. Anisotropy, which measures the deviation from isotropic conditions (\(\Delta =p_t-p_r\)), may arise from several sources such as superfluids, fluid mixtures, solid cores, phase transitions, viscosity, and magnetic fields within the star [29,30,31,32,33,34,35].

In this study, we investigate the creation of dense stars in an anisotropic scenario using the environmental effect of MRT gravity. Our research also includes an analysis of the stability and physical characteristics of anisotropic stellar objects. We examine parameters such as metric functions, energy density, pressure (both radial and transverse), anisotropy, gradients, equations of state, sound speeds using Abreu criteria, and the balance of Tolman–Oppenheimer–Volkoff (TOV) forces. Torsion-dependent theories are typically founded on tetrad formalism, so we have selected the off-diagonal tetrad field for this study. We provide a detailed explanation of the formation of compact stellar bodies based on gravity and assess the suitability of the chosen tetrad form, which can be adjusted to accommodate all forms of gravity modification. It is widely recognised that the conservation of the EMT, which is the cornerstone of GR, governs the behaviour of matter and its interaction with gravity [36]. Nevertheless, this conservation principle is modified by the MRT gravity theory. This enables the EMT not to be conserved, thereby modifying the dynamics of matter and its gravitational interaction [37]. The researchers hope to understand the ramifications of this divergence from energy-momentum conservation by studying compact objects in the context of MRT gravity. In particular, many researchers are interested in how extremely dense and compact systems such as neutron stars and white dwarfs are affected by the effects of this modified conservation principle on the behaviour and properties of matter. This study opens up new perspectives on how matter and gravity interact in unprecedented ways. It allows researchers to examine how the gravitational field, the structure of compact objects, and their observable properties are all affected by the non-conservation of the EMT. In addition, the study of compact objects within the framework of MRT gravity makes it possible to compare the theoretical assumptions of this alternative theory with actual observations. Researchers can test the theory’s validity and correctness in explaining current astrophysical systems by comparing the predictions of MRT gravity with the behaviour and characteristics of observable compact objects. What’s more, the study of MRT gravity in the context of compact objects contributes to the wider endeavour of understanding the fundamental properties of gravity itself. Researchers can use it to assess the effects of relaxing certain assumptions about gravity and study different theoretical frameworks. This advances our knowledge of compact objects and provides important new insights into the underlying principles that govern the universe.

We will now proceed with the next phase of our study, which follows the scheme outlined as: In Sect. 2, we will introduce the fundamentals of MRT gravity, and we will use an off-diagonal tetrad to assess the field equations. In Sect. 3, we will employ the embedding class-I approach to determine the metric functions. Section 4 will detail our assessment of the generalised field equations, which will be based on the hybrid function f(T) and the EoS for the calculation of h(T). In Sect. 5, we will match the interior and exterior geometries to determine the constant parameters utilised in our stellar modeling. Section 6 will focus on the evaluation of generalised field equations based on the hybrid function f(T) and the logarithmic function h(T). We will then present a discussion of our results in Sect. 7, followed by a conclusion in Sect. 8.

2 MRT gravity: basic formulation

The study of stars requires a fundamental understanding of their structure, which is why spherically symmetric spacetime is often used as a model. This type of spacetime is uniform in all directions and can be described mathematically using different models, like the Schwarzschild metric. By analysing spherically symmetric spacetimes, researchers can gain insights into the behaviour and evolution of stars. These insights are essential to various fields of astrophysics.

$$\begin{aligned} ds^{2}=-e^{a(r)}dt^2+e^{b(r)}dt^2+r^2sin^{2}\theta d\phi ^{2}+d\theta ^{2}. \end{aligned}$$
(1)

It is possible to represent the metric tensor \(g_{\mu \nu }\) defined on a manifold using the tetrad fields \(e_\mu ^i\) and the Minkowski metric \(\eta _{i j}={\text {diag}}(-1,1,1,1)\).

$$\begin{aligned} g_{\mu \nu }=\eta _{i j} e_\mu ^i e_\nu ^j, \end{aligned}$$
(2)

where the Greek alphabet \((\mu , \nu , \ldots =0,1,2,3)\) represents space-time indices and the Latin alphabet \((i, j, \ldots =0,1,2,3)\) represents tangent space indices. The Weitzenböck connection in a mathematical concept is defined as:

$$\begin{aligned} \Gamma _{\mu \nu }^\alpha =e_i^\alpha \partial _\nu e_\mu ^i=-e_\mu ^i \partial _\nu e_i^\alpha . \end{aligned}$$
(3)

The teleparallel theory utilises the above-given specific type of connection that possesses non-zero torsion but zero curvature. The connections are responsible for defining the torsion tensor, which can be denoted as follows:

$$\begin{aligned} T_{\mu \nu }^\sigma \equiv \Gamma _{\nu \mu }^\sigma -\Gamma _{\mu \nu }^\sigma =e_i^\sigma \left( \partial _\mu e_\nu ^i-\partial _\nu e_\mu ^i\right) . \end{aligned}$$
(4)

The Weitzenbock connection is linked to the Levi-Civita connection, \({\bar{\Gamma }}_{\mu \nu }^\sigma \), by the following relation

$$\begin{aligned} \Gamma _{\mu v}^\sigma =\Gamma _{\mu \nu }^\sigma -K_{\mu v}^\sigma , \end{aligned}$$
(5)

where \(K{ }_{\mu \nu }\) is the notion of the contorsion tensor, which is given by:

$$\begin{aligned} K_{\mu \nu }^\sigma =\frac{1}{2}\left( T_\mu ^\sigma \sigma _\nu +T_\nu ^\sigma \sigma _\mu -T_{\mu \nu }^\sigma \right) . \end{aligned}$$
(6)

The expression for torsion scalar is read as

$$\begin{aligned} T=S^{\sigma \mu \nu } T_{\sigma \mu \nu }, \end{aligned}$$
(7)

where the expression for super-potential \(S^{\sigma \mu \nu }\) is given by:

$$\begin{aligned} S^{\sigma \mu \nu }=-S^{\sigma \nu \mu }=\frac{1}{2}\left( K^{\mu \nu \sigma }-g^{\sigma \nu } T^{\alpha \mu \mu }+g^{\sigma \mu } T^{a \nu }\right) . \end{aligned}$$
(8)

The action of the modified teleparallel gravity is presented by

$$\begin{aligned} S=S_G+S_m=\frac{1}{4 \kappa } \int e f(T) d^4 x+\int e L_m d^4 x, \end{aligned}$$
(9)

in which the function f(T) depends on the torsion scalar, while the determinant of the tetrad field \(e^a{_F}\) is denoted as e. Additionally, the matter Lagrangian is represented by \(L_m\). By taking the variation of the action with respect to the tetrad field, we can obtain the corresponding field equation.

$$\begin{aligned}{} & {} S_i^{\mu \nu } f_{T T} \partial _\mu T+e^{-1} \partial _\mu \left( e S_i^{\mu \nu }\right) f_T-T^\alpha { }_{\mu i} S_\sigma ^{\nu \mu } f_T \nonumber \\{} & {} \quad -\frac{1}{4} e_i{ }^\nu f=-\kappa \theta _{\mu }^{\nu }, \end{aligned}$$
(10)

where \(\Theta _\mu ^v\) is addressed to the usual EMT of the perfect fluid. It is shown that

$$\begin{aligned}{} & {} \Bigg (S_i^{\mu v} f_{T T} \partial _\mu T+e^{-1} \partial _\mu \left( eS_{i}{ }^{\mu \nu }\right) f_T-T^\sigma { }_{\mu i} S_\sigma ^{\nu \mu } f_T \nonumber \\{} & {} \quad -\frac{1}{4} e_i^v f\Bigg )_{; v}=0, \end{aligned}$$
(11)

where a semicolon is used to denote the covariant derivative that is in teleparallel structure

$$\begin{aligned} V_{; \nu }^\mu =\partial _\nu V^\mu +\left( \Gamma _{\lambda \nu }^\mu -K_{\lambda \nu }^\mu \right) V^\lambda , \end{aligned}$$
(12)

for any space-time vector \(V^{\mu }\). The above-given expression ensures that the covariant derivative of the EMT also vanishes:

$$\begin{aligned} \Theta ^{\nu }{}_{\mu ;\nu } = 0. \end{aligned}$$
(13)

We have the same energy-momentum conservation equation in both Einstein’s theory and our modified teleparallel gravity theory. However, the conservation equation in Einstein’s theory was challenged by Rastall [18], who proposed a new equation \(T^{\mu }_{\nu ;\;\mu }=\lambda R{,\nu }\) that involves an intriguing interaction between matter and geometry. This idea suggests that there is a connection between the two, and it leads to a modified field equation. Building on Rastall’s concept, we apply the same assumption to our modified teleparallel gravity theory. By linking matter and geometry through the scalar torsion of geometry, we establish a connection where the divergence of the EMT \(\Theta ^{\nu }{}_{\mu }\) is proportional to the divergence of the torsion scalar

$$\begin{aligned} \Theta ^{\nu }{}_{\mu ;\nu } = \lambda {h(T)_{,\mu }}, \end{aligned}$$
(14)

where \(\lambda \) is a real constant and h(T) is an analytical function of torsion. Then, the field Eq. (11) can be restated as follows,

$$\begin{aligned}{} & {} S_u^{\mu \nu } f \gamma \tau \partial _\mu T+e^{-1} \partial _\mu \left( S_i^{\mu \nu }\right) f_T-T_\mu ^\sigma S_\sigma ^{\nu \mu } f_T \nonumber \\{} & {} \quad -\frac{1}{4} e_i^\nu f-\delta _\mu ^\nu \kappa \lambda h(T)=-\kappa \Theta _{\mu }^\nu . \end{aligned}$$
(15)

Here, \(\kappa \) is the gravitational constant in RT, which is a comparison with Newtonian gravity and is expressed as

$$\begin{aligned} \kappa =\frac{4 \gamma -1}{6 \gamma -1} \kappa _G, \end{aligned}$$
(16)

where \(\gamma =\lambda \kappa \) leading to

$$\begin{aligned} \lambda =\frac{6 \gamma -1}{ 4 \gamma -1} \frac{\gamma }{\kappa _G}, \end{aligned}$$
(17)

and \(\kappa _G\) notions the Einstein coupling constant \(\kappa _G=4 \pi G\). In the case where \(\lambda = 0\), or equivalently \(\gamma = 0\), the parameter \(\kappa \) takes the value of \(\kappa _G\). In this particular scenario, Einstein’s gravity is recovered, leading to the conservation of the EMT. It should be noted that Rastall’s gravitational coupling constant, i.e., \(\kappa \), diverges when \(\gamma = \frac{1}{6}\), as indicated by (16). Therefore, the case where \(\gamma = \frac{1}{6}\) is not allowable. Moreover, as shown in (17), the parameter \(\lambda \) diverges when \(\gamma = \frac{1}{4}\). Consequently, the case where \(\gamma = \frac{1}{4}\) is not allowable either. Accordingly, the Newtonian limit analysis indicates that both the cases \(\gamma = \frac{1}{6}\) and \(\gamma = \frac{1}{4}\) are not allowable within the theory [38]. The EMT \(\Theta _\mu \) is assumed to describe a non-isotropic fluid given as:

$$\begin{aligned} \Theta _\mu ^v=\left( p+p_t\right) u_\mu u^v-p_t b_\mu ^v+\left( p_r-p_t\right) v_\mu v^v, \end{aligned}$$
(18)

where vector \(u_\mu \) represents the four velocities in the time-like direction, while \(v_\mu \) is a unit space-like vector in the radial direction. The relationship between these vectors is given by \(u_0 u^0=-v_1 v^1=1\).

The tetrad fields, denoted by \(e^i_\mu \), are an important part of the teleparallel technique used in general relativity. These fields represent the coordinates of the manifold through holonomic (Greek indices) and the frame through anholonomic (Latin indices). By combining the frame and coordinate indices, we can use the same idea to describe the tetrad matrix \(e^i_\mu \) and its inverse. We can determine that \(e_i^\mu e^\nu _i = \delta ^\mu _\nu \) and \(e^\mu _i e^\mu _j = \delta _{ij}\). The motivation behind the teleparallel technique is to develop a more generalised manifold that includes torsion in addition to curvature. The Riemannian curvature tensor is supposed to be zero (part without torsion plus some contribution from torsion), which allows us to use either the torsion-free part (geometry) or the torsion part (tetrad) to explain the gravitational field. Therefore, the use of tetrad fields and torsion provides an alternative to the geometric definition of gravity. Tamanini and Böhmer introduced the concept of a “good tetrad” in their work [39], which refers to a tetrad that does not impose any additional constraints on the functional form of f(T). This allows for the study of a broader class of f(T) cosmologies. Böhmer et al. [40] explored the existence of relativistic stars in f(T) modified gravity and constructed various classes of static perfect fluid solutions for both diagonal and off-diagonal tetrad. However, the diagonal tetrad is unsuitable for spherical symmetry as the exact solutions correspond to a constant torsion scalar. The literature suggests using off-diagonal tetrad (good tetrad), and numerous aspects of spherically symmetric spacetime have been presented for review (one can consult some of the available references [15, 41,42,43,44,45] and some others).

In this study, we will develop field equations using the off-diagonal tetrad matrix given in [39, 40, 46].

$$\begin{aligned} e^j{ }_\mu =\left( \begin{array}{cccc} e^{a / 2} &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{b / 2} \sin \theta \cos \phi &{} r \cos \theta \cos \phi &{} -r \sin \theta \sin \phi \\ 0 &{} e^{b / 2} \sin \theta \sin \phi &{} r \cos \theta \sin \phi &{} r \sin \theta \cos \phi \\ 0 &{} e^{b / 2} \cos \theta &{} -r \sin \theta &{} 0 \end{array}\right) \text{. } \end{aligned}$$
(19)

where \(g_{tt}=e^{a(r)}\) and \(g_{rr}=e^{b(r)}\). The determimant of the above tetrad field is given by \(e=det\left( e^j{ }_\mu \right) =r^2 \sin \theta e^{(a+b)/2}\). The torsion scalar obtained from Eqs. (4, 7, 8) is given as:

$$\begin{aligned} T(r)=\frac{2 e^{-b}}{r^2}\left( e^\frac{b}{2}-1\right) \left( e^\frac{b}{2}-1-r a^{\prime }\right) . \end{aligned}$$
(20)

Replacing Eqs. (18, 19, and 20) in the field Eq. (1), the obtained nonzero components of the EMT are read as:

$$\begin{aligned} \kappa \rho (r)=&\frac{e^{-b / 2}}{r}\left( 1-e^{-b / 2}\right) f_T^{\prime }\nonumber \\&-\left( \frac{T}{4}-\frac{1}{2 r^2}\right) f_T +\frac{e^{-b}}{2 r^2}\left( r b^{\prime }-1\right) \nonumber \\&\times f_T+\frac{f}{4}+\gamma h(T), \end{aligned}$$
(21)
$$\begin{aligned} \kappa p_r(r)=&\left[ \frac{T}{4}-\frac{1}{2 r^2}+\frac{e^{-b}}{2 r^2}\left( 1+r a^{\prime }\right) \right] \nonumber \\&\times f_T-\frac{f}{4}-\gamma h(T), \end{aligned}$$
(22)
$$\begin{aligned} \kappa p_t(r)=&\frac{e^{-b}}{2}\left( \frac{a^{\prime }}{2}+\frac{1}{r}-\frac{e^{b / 2}}{r}\right) f_T^{\prime }-\frac{f}{4}-\gamma h(T)+f_T\nonumber \\&\times \left\{ \frac{T}{4}+\frac{e^{-b}}{2 r}\left[ \left( \frac{1}{2}+\frac{r a^{\prime }}{4}\right) \left( a^{\prime }-b^{\prime }\right) +\frac{r a^{\prime \prime }}{2}\right] \right\} . \end{aligned}$$
(23)

The presence of the Rastall term \(\gamma h(T)\) and the coefficient \(\kappa \) in equations has a significant impact on the behaviour and magnitude of the components, potentially altering the energy conditions. To obtain solutions for compact objects, one must consider a range of assumptions for the f(T) functions available.

3 Evaluation of metric functions by Karmarkar condition

Generally, the spherically symmetric metric given in Eq. (1) is actually of second class. If this metric space admits the Karmarkar condition, it would be called a metric space of class one. The curvature tensor \(R_{h i j k}\) components in the case of the spherically symmetric metric are like

$$\begin{aligned} R_{2323}&=\frac{\sin ^2 \theta \left( e^b-1\right) r^2}{e^b},\; R_{1212}=\frac{b^{\prime } r}{2},\; R_{2424}=\frac{e^{(a-b)}}{2},\nonumber \\ R_{1224}&=0, R_{1414}=\frac{e^a}{4}\left[ 2 a^{\prime \prime }+a^{\prime 2}-b^{\prime } a^{\prime }\right] , \nonumber \\ R_{3434}&= \sin ^2 \theta R_{2424}. \end{aligned}$$
(24)

Karmarkar condition Eq. (24) in light of curvature tensor ingredients will result in the given form of differential equation:

$$\begin{aligned} \frac{a^{\prime \prime }}{a^{\prime }}+\frac{a^{\prime }}{2}=\frac{b^{\prime b}}{2\left( e^b-1\right) }. \end{aligned}$$
(25)

The solution of Eq. (25) for gravitational potential a(r) will result as follows:

$$\begin{aligned} a(r)=2 \ln \left[ A+B \int \sqrt{\left( e^{b(r)}-1\right) } d r\right] , \end{aligned}$$
(26)

where the process of integration will generate A and B, the non-vanishing constants. One notable observation is that the solution to the Einstein field equations, given an anisotropic matter distribution, relies on either the a or b metric functions. This is due to the direct relationship between the metric functions established by the Karmarkar condition. To achieve this, we adopt the same approach as Maurya et al. [47] by utilising the ansatz previously used for \(e^{b}\).

$$\begin{aligned} b(r)=\log \left( 1+\frac{r^2 (x-y)}{1+r^2 y}\right) , \end{aligned}$$
(27)

where x and y are both non-zero constants with dimensions of \([length]^{-2}\). Substituting Eq. (27) into Eq. (26), we get

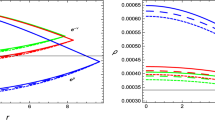
$$\begin{aligned} a(r) = 2 \log \left( A y+B \sqrt{r^2 y+1} \sqrt{x-y}\right) -2 \log (y),\nonumber \\ \end{aligned}$$
(28)

where A and B are constants with dimensions of \([length]^{2}\). To construct a valid physical model, it is essential that the metric functions \(e^{b}\) and \(e^{a}\) exhibit two key properties. Firstly, they must remain finite at the center of the gravitational source. Secondly, these functions must increase monotonically as a function of the radial distance from the center. These conditions are necessary to ensure that the resulting solution accurately represents a physically realistic spacetime, which can provide insight into the behaviour of massive objects under the influence of gravity, as shown in Fig. 1. One can observe from Eqs. (27 and 28)

$$\begin{aligned} e^{b(r)}|_{r=0}=1,\; e^{a(r)}|_{r=0} = \frac{1}{y^{1/2}}\left[ Ay+B\sqrt{(x-y)}\right] ^{2}\nonumber \\ \end{aligned}$$
(29)

which are clearly definite and out of the singularity.

Fig. 1
figure 1

Profiles of metric potentials \(e^{b(r)}\) and \(e^{-a(r)}\) versus radial coordinate, r ([km]), for different values of \(y=0.0.002,\;0.0018,,\;0.0016,\;0.0014,\;0.0012,\;0.0007,\;0.0006,0.0005,\;0.0004,\;0.0003,\;0.0026,\;0.0025,\;0.0024,\;0.0023,0.0022~\textrm{km}^{-2}\)

Full size image

4 Case-I: hybrid form of \(f(T)=\beta e^{m T} T^n\) and application of EoS \(p_r=\xi \rho +\phi , \; 0< \xi < 1\) for evaluation of h(T)

Eos is a well-known component often used in the study of compact objects. It basically develops a relationship between the energy density \(\rho \) and radial pressure \(p_r\). In the study of compact stars, it is evenly used to facilitate the system’s ability to solve for the separation of an involved function if the system has more variables than the number of equations. Several EoSs are used in the literature. Some of our knowledge includes: Nojiri and Odintsov [48] used asymptotic EoS \(p=(1 + \frac{2}{n}) \rho \), while discussing the singularity of spherically-symmetric spacetime in the quintessence/phantom dark energy universe; Sharif and Faisal [49] used the generalised Chaplygin gas EoS \(p = - \frac{C}{\sigma ^{\gamma }}, \;0 <\gamma \le 1\), while studying the stability of Einstein–Power–Maxwell \((2+1)\)-dimensional wormholes. Exotic matter is a topic of great interest in the scientific community, and several models exist to describe it. One such model is the phantom-like EoS for exotic matter, which can be defined as \(p = \omega \rho \) with \(\omega < 0\). This model can represent various types of matter distributions that depend on the value of \(\omega \). The fascinating aspect of this model is that it can lead to different states of energy depending on the value of \(\omega \). If \(\omega < -1\), then the EoS leads to a phantom energy state. On the other hand, if \(\omega \) lies between \(-1\) and \(-1/3\), it results in a quintessence state. Finally, if \(\omega < -1/3\), it leads to a dark energy state. In summary, the phantom-like EoS for exotic matter is a versatile model that can help in understanding various types of matter distributions. Its implications for our understanding of the universe are truly fascinating. For the purpose of simplicity, we in this study used the below-given EoS [50, 51]:

$$\begin{aligned} p_r=\xi \rho +\phi , \;\;\;\;\; 0< \xi < 1. \end{aligned}$$
(30)

For the first case, we presume the hybrid functional form of teleparallel gravity to be [52]:

$$\begin{aligned} f(T)=\beta e^{m T} T^n, \end{aligned}$$
(31)

where \(m \ge 0\) and n are real constants. This hybrid form of f(T) merges an exponential function \(e^{m T}\) with a power-law term \(T^n\). This choice enables exponential and power-law effects to be combined in the modification of teleparallel gravity. The exponential term incorporates a non-linear dependency on the torsional scalar T, whereas the power-law term incorporates a power-law behavior. The parameters \(\beta \), m, and n control the strength, scale, and shape by which the modification occurs, respectively. The physical importance of this hybrid form lies in its capability to encompass a wide range of gravitational behavior. The exponential term can lead to significant deviations from the GR predictions, particularly in regimes where the torsional scalar T is large. The power-law term provides greater flexibility in modification, allowing the further exploration of diverse modifications to gravitational theory. It is interesting to note that:

  • For \( m=0\; \& \;n\ne 0\), Eq. (31) reduces to the power law of MRT gravity \(f(T)=\beta T^{n}\).

  • For \( m\ne 0\; \& \;n=0\), Eq. (31) reduces to the exponential law of MRT gravity: \(f(T)=\beta e^{mT}\).

  • For \( m\ne 0\; \& \;n\ne 0\), Eq. (31) retains the hybrid form of MRT gravity \(f(T)=\beta e^{m T} T^n\).

In our study, we discussed the above three forms of gravity and showed that our stellar structures are stable in the hybrid, exponential, and power-law forms of f(T) gravity.

Here, we apply Eq. (21), Eq. (22), and Eq. (30) and calculate the function h(T) as given below:

$$\begin{aligned} h(T)= & {} \frac{e^{-b(r)} }{4 \gamma (\xi +1) r^2}\Big [2 f_{T} r a'(r)-2 f_{T} \xi r b'(r)\nonumber \\{} & {} -f \xi r^2 e^{b(r)}+f r^2 \left( -e^{b(r)}\right) +f_{T} \xi r^2 T e^{b(r)}\nonumber \\{} & {} +f_{T} r^2 T e^{b(r)} \!-\!2 f_{T} \xi e^{b(r)}\!-\!2 f_{T} e^{b(r)}\!-\!4 f_T^{\prime } \xi r e^{\frac{b(r)}{2}}\nonumber \\{} & {} -4 k r^2 \phi e^{b(r)}+2 f_{T} \xi +2 f_{T}+4 f_T^{\prime } \xi r\Big ]. \end{aligned}$$
(32)

After all, if we use the Eqs. (20), (27), (28), (31), and (32) in Eqs. (21–23), we get the final versions of field equations as given below:

$$\begin{aligned} \rho= & {} \frac{(6 \gamma -1) \left( \beta l_2(r) l_4(r)-\beta l_5(r) l_3(r)+\beta l_3(r) l_6(r)+\frac{r \left( \beta l_7(r) l_2(r)\right) }{l_{10}(r)}-l_8(r) \right) }{8 \pi r l_{9}(r)}, \end{aligned}$$
(33)
$$\begin{aligned} p_r= & {} \frac{(6 \gamma -1) \left( \beta l_2(r) l_4(r) \xi -\beta l_5(r) l_3(r) \xi +\beta l_3(r) l_6(r) \xi +\frac{r \left( \beta l_7(r) l_2(r) \xi \right) }{l_{10}(r)}+l_8 (r)\right) }{8 \pi r l_{9}(r) }, \end{aligned}$$
(34)
$$\begin{aligned} p_t= & {} \frac{(6 \gamma -1)}{32 \pi l_9(r) r^2} \Big [\beta B \left( -l_{20}(r)\right) l_{18}(r) l_{19}(r) 2^n r^2 r y \sqrt{x-y} \left( l_{16}(r)\right) {}^n+\beta l_2(r) l_{12}(r) (\xi -1)+\beta l_2(r) l_{14}(r) (\xi +1)\nonumber \\{} & {} +\beta l_2(r) l_{15}(r) (\xi +1) +\frac{l_{13}(r) }{l_{11}(r)}+l_{17}(r)\Big ], \end{aligned}$$
(35)

where functions \(l_i(r),\, i=1,2,\dots 20\) are given in Appendix (Figs. 2, 3).

Table 1 Values of constants, by using the \(mass=1.97\;M/M_{\bigodot }\) and \(9.949\;\textrm{km}\) of \(PSRJ1614 - 2230\). We fix \(\phi =2.036\times 10^{-35}\textrm{km}^{-2}\), while choosing Hybrid function \( f(T)=\beta e^{m T} T^n\) of MRT gravity, and EoS \(p_r=\xi \rho +\phi \) (where \(0< \xi < 1\)) in the evaluation of function h(T). We also choose different values of \( m\; \& \;n\) to discuss the power law of f(T) and the exponential form of f(T)
Full size table
Table 2 Values of constants, by using the \(mass=1.97\;M/M_{\bigodot }\) and \(9.949\;\textrm{km}\) of \(PSRJ1614 - 2230\). We choose Hybrid function \( f(T)=\beta e^{m T} T^n\) of MRT gravity and \(h(T)=\psi \log \left( \varphi T^{\chi }\right) \). We also choose different values of \( m\; \& \;n\) to discuss the power law of f(T), and the exponential form of f(T). We fix \(\psi =-0.00000002,\;\varphi =-2,\;\;\chi =5,\;\xi =0.3\)
Full size table

5 Matching conditions

The inside border metric is constant regardless of the geometrical structure of the star, whether viewed from the outside or the inside. An emergent scenario requires that the metric components be continuous to the boundary, regardless of the reference frame. While analysing Schwarzschild’s solution related to stellar remnants in general relativity, it is well thought out to be the major priority out of all the available varied matching situation alternatives. It is also a good idea to account for quasi-pressure and energy density when working with modified gravity theories. Numerous researchers have produced excellent work on boundary conditions [53, 54]. Goswami et al. [55] determined the matching boundaries when studying stellar compact structures by combining some unique constraints to stellar compact structures as well as thermodynamically relevant properties. So the exterior spacetime in this study can be the vacuum case, as given below (Figs. 4, 5, 6, 7):

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2 M}{R}\right) dt^2+\left( 1-\frac{2 M}{R}\right) ^{-1}dt^2\nonumber \\{} & {} +r^2sin^{2}\theta d\phi ^{2}+d\theta ^{2}. \end{aligned}$$
(36)

After comparing the inner spacetime Eq. (1) and outer space-time Eq. (36) at the boundary \(r=R\), we arrive at the given system of equations:

$$\begin{aligned}{} & {} \left( \frac{A y+B \sqrt{R^2 y+1} \sqrt{x-y}}{y}\right) ^2=1-\frac{2 M}{R}, \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \frac{R^2 (x-y)}{R^2 y+1}+1=\frac{1}{1-\frac{2 M}{R}}, \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \frac{2 B R \sqrt{x-y} \left( A y+B \sqrt{R^2 y+1} \sqrt{x-y}\right) }{y \sqrt{R^2 y+1}}=\frac{2 M}{R^2}.\nonumber \\ \end{aligned}$$
(39)

The solution of these equations results in the following form of expressions for constants \(A,\;B,\;x\):

$$\begin{aligned} A= & {} -\frac{B \sqrt{2 R^2 y+2} \sqrt{\frac{M \left( R^2 y+1\right) }{R^2 (R-2 M)}}}{y}-\frac{\sqrt{R-2 M}}{\sqrt{R}}, \end{aligned}$$
(40)
$$\begin{aligned} B= & {} -\frac{M \sqrt{R^2 y+1}}{R^{5/2} \sqrt{R-2 M} \sqrt{-\frac{2 M+R^3 y}{R^2 (2 M-R)}-y}}, \end{aligned}$$
(41)
$$\begin{aligned} x= & {} -\frac{2 M+R^3 y}{R^2 (2 M-R)}. \end{aligned}$$
(42)

Specific values of constant parameters are given in Tables 1 and 2 for both cases of our study, respectively.

Fig. 2
figure 2

Energy density \(\rho \) (\([\textrm{km}^{-2}]\)) and pressure \( p_r\; \& \;p_t\) (\([\textrm{km}^{-2}]\)) profiles versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.002~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0018~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0016~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0014~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0012~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0007~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0026~\textrm{km}^{-2}\) (darker red solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0025~\textrm{km}^{-2}\) (darker cyan long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0024~\textrm{km}^{-2}\) (pink dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0023~\textrm{km}^{-2}\) (darker pink small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0022~\textrm{km}^{-2}\) (orange dotted line) for exponent-law case \( m\ne 0\; \& ~n= 0\)}. Other constant parameters are given in Table 1

Full size image

6 Case-II: hybrid-logarithmic MRT gravity: \( f(T)=\beta e^{m T} T^n\) and \(h(T)=\psi \log \left( \varphi T^{\chi }\right) \)

In this section of our case study, we explore the stellar models by taking the hybrid form of the function f(T) [52],

$$\begin{aligned} f(T)= & {} \beta e^{m T} T^n, \end{aligned}$$
(43)

along with the logarithmic form of the function h(T),

$$\begin{aligned} h(T)= & {} \psi \log \left( \varphi T^{\chi }\right) . \end{aligned}$$
(44)

This logarithmic form of h(T) represents the coupling between the modified teleparallel gravity and the matter content of the compact stars. The logarithmic function is chosen to highlight specific physical behaviours or features of the gravitational-matter interaction. The parameters \(\psi \), \(\varphi \), and \(\chi \) characterise the strength and form of this coupling. The logarithmic form enables a non-linear relationship between h(T) and the matter variables, potentially resulting in unique effects in the dynamics of the compact stars. In addition, parametrization provides a framework for exploring how modifications to gravitational theory and gravity-matter coupling can influence the structure, properties, and stability of compact stellar objects. It can easily be observed from Eqs. (43) and (44) that:

  • For \(m\ne 0\) and \(n\ne 0\), it is hybrid-logarithmic MRT gravity.

  • For \(m=0\) and \(n\ne 0\) if is power-law-logarithmic MRT gravity.

  • For \(m\ne 0\) and \(n=0\) if is exponential-logarithmic MRT gravity.

Fig. 3
figure 3

Anisotropy (\([\textrm{km}^{-2}]\)), gradient (\([\textrm{km}^{-2}]\)) and adiabatic index profiles, respectively from left to right, versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.002~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0018~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0016~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0014~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0012~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0007~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.~\textrm{km}^{-2}5,\; y=0.0004~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0026~\textrm{km}^{-2}\) (darker red solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0025~\textrm{km}^{-2}\) (darker cyan long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0024~\textrm{km}^{-2}\) (pink dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0023~\textrm{km}^{-2}\) (darker pink small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0022~\textrm{km}^{-2}\) (orange dotted line) for exponent-law case \( m\ne 0\; \& ~n= 0\)}. Other constant parameters are given in Table 1

Full size image
Fig. 4
figure 4

Energy conditions (\([\textrm{km}^{-2}]\)) versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.002~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0018~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0016~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0014~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0012~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0007~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0026\) (darker red solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0025~\textrm{km}^{-2}\) (darker cyan long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0024~\textrm{km}^{-2}\) (pink dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0023~\textrm{km}^{-2}\) (darker pink small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0022~\textrm{km}^{-2}\) (orange dotted line) for exponent-law case \( m\ne 0\; \& ~n= 0\)}. Other constant parameters are given in Table 1

Full size image
Fig. 5
figure 5

TOV forces (\([\textrm{km}^{-2}]\)), EoS components versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.002~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0018~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0016~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0014~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0012~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0007~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0026~\textrm{km}^{-2}\) (darker red solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0025~\textrm{km}^{-2}\) (darker cyan long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0024~\textrm{km}^{-2}\) (pink dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0023~\textrm{km}^{-2}\) (darker pink small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0022~\textrm{km}^{-2}\) (orange dotted line) for exponent-law case \( m\ne 0\; \& ~n= 0\)}. Other constant parameters are given in Table 1

Full size image
Fig. 6
figure 6

Sound speeds and Abreu condition versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.002~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0018~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0016~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0014~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0012~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0007~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0026~\textrm{km}^{-2}\) (darker red solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0025~\textrm{km}^{-2}\) (darker cyan long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0024~\textrm{km}^{-2}\) (pink dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0023~\textrm{km}^{-2}\) (darker pink small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0022~\textrm{km}^{-2}\) (orange dotted line) for exponent-law case \( m\ne 0\; \& ~n= 0\)}. Other constant parameters are given in Table 1

Full size image
Fig. 7
figure 7

Mass function, compactness and surface redshift profiles versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.002~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0018~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0016~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0014~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0012~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0007~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5,\; y=0.0004~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0026~\textrm{km}^{-2}\) (darker red solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0025~\textrm{km}^{-2}\) (darker cyan long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0024~\textrm{km}^{-2}\) (pink dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0023~\textrm{km}^{-2}\) (darker pink small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0022~\textrm{km}^{-2}\) (orange dotted line) for exponent-law case \( m\ne 0\; \& ~n= 0\)}. Other constant parameters are given in Table 1

Full size image
Fig. 8
figure 8

Energy density \(\rho \) (\([\textrm{km}^{-2}]\)) and pressure \( p_r\; \& \;p_t\) (\([\textrm{km}^{-2}]\)) profiles versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0003~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0001~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.00009~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.00008~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.00007~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.00006~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}. Other constant parameters are given in Table 2

Full size image
Fig. 9
figure 9

Anisotropy (\([\textrm{km}^{-2}]\)), gradient (\([\textrm{km}^{-2}]\)) and adiabatic index profiles, respectively from left to right, versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0003~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0001~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.00009~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.00008~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.00007~\textrm{km}^{-2}\)(green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.00006~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}. Other constant parameters are given in Table 2

Full size image
Fig. 10
figure 10

Energy conditions (\([\textrm{km}^{-2}]\)) versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\)(black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\)(purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\)(magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0003~\textrm{km}^{-2}\)(red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\)(orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0001~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.00009~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.00008~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.00007~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.00006~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}. Other constant parameters are given in Table 2

Full size image
Fig. 11
figure 11

TOV forces (\([\textrm{km}^{-2}]\)), EoS components versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0003~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0001~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.00009~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.00008~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.00007~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.00006~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}. Other constant parameters are given in Table 2

Full size image
Fig. 12
figure 12

Sound speeds and Abreu condition versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0003~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, and {\(\gamma =1.0,\; y=0.0001~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.00009~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.00008~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.00007~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.00006~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}. Other constant parameters are given in Table 2

Full size image
Fig. 13
figure 13

Mass function, compactness, and surface redshift profiles versus radial coordinate, r (\([\textrm{km}]\)). Here we fix {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0006~\textrm{km}^{-2}\) (black solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.0005~\textrm{km}^{-2}\) (purple long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.0004~\textrm{km}^{-2}\) (magenta dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.0003~\textrm{km}^{-2}\) (red small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.0002~\textrm{km}^{-2}\) (orange dotted line) for hybrid case \( m\ne 0\; \& n\ne 0\)}, and {\(\gamma =1.0~\textrm{km}^{-2},\; y=0.0001~\textrm{km}^{-2}\) (dark brown solid line), \(\gamma =1.5~\textrm{km}^{-2},\; y=0.00009~\textrm{km}^{-2}\) (blue long dashed line), \(\gamma =2.0~\textrm{km}^{-2},\; y=0.00008~\textrm{km}^{-2}\) (cyan dashed line), \(\gamma =2.5~\textrm{km}^{-2},\; y=0.00007~\textrm{km}^{-2}\) (green small dashed line), \(\gamma =3.0~\textrm{km}^{-2},\; y=0.00006~\textrm{km}^{-2}\) (dark green dotted line) for power-law case \( m= 0\; \& ~n= 1\)}. Other constant parameters are given in Table 2

Full size image

The final version of Eqs. (21–23), when taking the hybrid-logarithmic form of MRT gravity, is given below:

$$\begin{aligned} \rho= & {} \frac{(6 \gamma -1)}{4 \pi (4 \gamma -1)} \Big [\beta 2^{n-2} e^{2 ml_{21}(r)} \left( l_{21}(r)\right) {}^n\nonumber \\{} & {} + \beta l_{22}(r) l_{24}(r) l_{27}(r) \left( l_{21}(r)\right) {}^{n-1}\nonumber \\{} & {} + \beta l_{22}(r) l_{27}(r)\left( \left( l_{21}(r)\right) {}^{n-1}\right) {}^{l_{26}(r)}+l_{29}(r)\Big ], \end{aligned}$$
(45)
$$\begin{aligned} p_r= & {} \frac{(6 \gamma -1)}{4 \pi (4 \gamma -1)} \Big [\beta \left( -2^{n-2}\right) e^{2 ml_{21}(r)} \left( l_{21}(r)\right) {}^n\nonumber \\{} & {} -\beta l_{27}(r) l_{22}(r)\left( l_{21}(r)\right) {}^{n-1}{l_{23}(r)}\nonumber \\{} & {} - \gamma \psi \log \left( 2^{\chi } \varphi \left( l_{21}(r)\right) {}^{\chi }\right) \Big ], \end{aligned}$$
(46)
$$\begin{aligned} p_t= & {} \frac{(6 \gamma -1)}{4 \pi (4 \gamma -1)} \Big [\frac{\beta l_{22}(r) l_{31}(r) 2^{n-4}e^{2 ml_{21}(r)} \left( l_{21}(r)\right) {}^{n-1}}{r^4 \left( \frac{r^2 (x-y)}{r^2 y+1}+1\right) ^2}\nonumber \\{} & {} -\beta 2^{n-2} e^{2 ml_{21}(r)} \nonumber \\{} & {} \times \left( l_{21}(r)\right) {}^n+l_{30}(r)\Big ]. \end{aligned}$$
(47)

where functions \(l_i(r),\, i=21,22,\dots 31\) are given in the Appendix. The values of constant parameters are given in Table 2. It is worth saying that, according to our observation, the exponential-logarithmic case does not give a stable configuration.

7 Discussion related to the physical properties of compact configurations

In this section, we will examine the behavior exhibited by the compact star solutions and compare it with the standard requirements. Firstly, we will explore the behaviour of our solutions and then analyse how they match up to the standard requirements. Our study indicates that all three forms of MRT gravity–hybrid, power-law, and exponential-law in case I–are stable. However, the exponential-logarithmic form of MRT gravity is found to be unstable. Moving forward, we will discuss the crucial characteristics of compact objects (Figs. 8, 9, 10, 11, 12, 13):

  • To gain a deeper understanding, let’s take a closer look at equations (21–23), which are based on the metric components \(e^{a(r)}\) and \(e^{b(r)}\). To achieve this, we adopt the approach of embedding class-I spacetime components as described in equations (27–28), where positive constants A, B, x, and y are utilized. As we examine these equations, it becomes apparent that as r approaches zero, \(e^{a(r)}>0\) and \(e^{b(r)}=1\), both of which demonstrate smooth evolutionary behaviour, as depicted in Fig. 1.

  • Physical validity is crucial in studying compact stars, and investing energy into a study that lacks physical admissibility is not worthwhile. The density parameter, \(\rho \), serves as a useful tool to ensure the study’s physical affirmation. The left panel of Fig. 2 for case-I and Fig. 8 for case-II illustrate the legitimate propagation of energy parameters. It is evident that the energy density behaves perfectly in accordance with the criteria, with maximum values at the center and smooth, positive declines everywhere within the star’s distribution (\(0<r\le R\)). Therefore, the energy density function confirms the physical plausibility of the celestial body.

  • The pressure components are crucial factors that determine the physical properties of a celestial object, much like the energy density (\(\rho \)). The pressure profiles, denoted as \(p_r\) and \(p_t\) (middle and right panels of Fig. 2 for case-I and Fig. 8 for case-II), also exhibit distinct physical behaviors. The central point, where \(r \rightarrow 0\), indicates the peak value, followed by a smooth decrease as r increases up to the radius R. Furthermore, the pressure component \(p_t\) at the surface (\(r=R\)) is positive, while \(p_r\) is zero. Additionally, \(p_t\) is greater than \(p_r\). However, in case-I, the EoS limits \(p_r\) to approach zero, but it remains positive throughout the object, which is acceptable and aligned with the expected behaviour of a celestial body. This conforms well to the physical requirements of the object.

  • The presence of repulsive forces is crucial to counterbalance the effects of gradient components, which leads to a significant improvement in the equilibrium and stability of stellar models. The enduring benefits of these repulsive forces are confirmed by the positive anisotropy observed. This anisotropy is determined by the criteria that \(\Delta |_{(0<r\le R)}>0\) when \(p_t>p_r\), where \(\Delta =p_t-p_r\), but as \(r\rightarrow 0\), \(\Delta \) tends towards zero. The anisotropy \(\Delta \) depicted in the left panels of Fig. 3 for case-I and Fig. 9 for case-II demonstrate identical behaviors as our computed results.

  • Gradients are accepted to exhibit a negative and decreasing behavior, starting from zero at the center (i.e., \((\frac{d\rho }{dr}=\frac{d p_r}{dr}=\frac{d p_t}{dr})|{(r\rightarrow 0)}=0\)), except for \((\frac{d\rho }{dr},\;\frac{d p_r}{dr},\;\frac{d p_t}{dr})|{(0<r\le R)}<0\) at their graphical representation. The middle panels of Fig. 3 for case-I and Fig. 9 for case-II reveal that the computed results for gradients conform to this range of values.

  • The study of the adiabatic index is necessary to understand the stability and solidity of compact objects. To predict the stability of relativistic and non-relativistic compact objects based on the manifold of spherically symmetric spacetimes, it is essential to study the adiabatic index. The adiabatic index defines the stability factor and solidity of the EoS at a given density, making it a critical component in the study of stellar objects. Chandrasekhar first discussed stability and solidity under the adiabatic index in [56, 57], followed by several authors [58,59,60,61] who adopted this interesting method of stability. Heintzmann and Hillebrandt [62] established a stability limit for the adiabatic index by setting it to be greater than \(\frac{4}{3}\) for \(0 \le r \le R\).

    The mathematical equation for the adiabatic index is given by,

    $$\begin{aligned} \Gamma =\frac{p_r + \rho }{p_r} v^{2}_r. \end{aligned}$$
    (48)

    The right panels of Fig. 3 for case-I and Fig. 9 for case-II demonstrate the stability of our solutions as the behaviour of \(\Gamma \) completely adheres to the criteria established in [62].

  • In the theory of GR, momentum, mass, and stress are defined by the EMT, which describes the distribution of matter fields and gravitation-free fields (GFF) in spacetime. However, the Einstein field equations (EFEs) do not directly relate to the state of matter or allowable GFF in the spacetime manifold. Instead, energy conditions are used to sanction all forms of matter, contradict GFF in GR, and ensure physically valid solutions to the field equations. To ensure a realistic and physically acceptable distribution of matter, the anisotropic conduct of energy must remain positive and obey certain limiting constraints throughout the stellar body. These constraints, studied in the literature [63, 64], are known as the Strong Energy Condition (SEC), Weak Energy Condition (WEC), Null Energy Condition (NEC), and Dominant Energy Condition (DEC) and are expressed in Eqs. (49–52)

    $$\begin{aligned} SEC&:&\rho +p_\gamma \ge 0,\rho +p_r+2p_t\ge 0, \end{aligned}$$
    (49)
    $$\begin{aligned} WEC&:&\rho \ge 0,\rho +p_\gamma \ge 0, \end{aligned}$$
    (50)
    $$\begin{aligned} NEC&:&\rho +p_\gamma \ge 0, \end{aligned}$$
    (51)
    $$\begin{aligned} DEC&:&\rho >|p_\gamma |. \end{aligned}$$
    (52)

    Here (\(\gamma = r, t\)), r and t denote the radial and tangential coordinates. We present the results of our study, which are shown in Fig. 4 for case-I and Fig. 10 for case-II. These results are consistent with the standard criteria used in the study of compact stars.

  • Equilibrium criteria of a stellar system were suggested in the Tolman-Oppenheimer-Volkoff (TOV) equation [65, 66]. The TOV equation in the common version for MRT gravity is given as:

    $$\begin{aligned}{} & {} \frac{d p_r}{dr}+\frac{a^{'}(\rho +p_r)}{2}- \frac{2(p_t-p_r)}{r}\nonumber \\{} & {} \quad -\frac{\gamma }{4\gamma -1} \left( \frac{d \rho }{d r}-\frac{d p_r}{d r}-\frac{d p_t}{d r}\right) =0, \end{aligned}$$
    (53)
    $$\begin{aligned}{} & {} F_g+F_h+F_a+F_r=0, \end{aligned}$$
    (54)

    where

    $$\begin{aligned} F_g= & {} -\frac{a^{'}(\rho +p_r)}{2}, F_h=-\frac{d p_r}{dr}, F_a=\frac{2(p_t-p_r)}{r}, \nonumber \\ F_e= & {} -\frac{\gamma }{4\gamma -1} \left( \frac{d \rho }{d r}-\frac{d p_r}{d r}-\frac{d p_t}{d r}\right) . \end{aligned}$$

    According to the TOV equation, a stellar system is considered to be in equilibrium when the four forces \(F_a\), \(F_g\), \(F_h\), and \(F_r\) balance each other out, resulting in a net effect of zero, as shown in Eq. (53). This balancing mechanism is essential in preventing the stellar system from collapsing into a singular point during its gravitational collapse. As can be seen from the left panels of Fig. 5 for case-I and Fig. 11 for case-II, all the forces in this section of our study are in perfect balance, thereby ensuring the equilibrium of our solutions.

  • The essence of matter, whether it is real matter or dark matter, is of relative importance in studying compact stellar systems. For realistic or byronic matter equations of state (EoS), \(w_r\) and \(w_t\) must lie within the range of \(0 \le w_r < 1\) and \(0< w_t < 1\). If the system follows these EoS limits, it guarantees that the stellar body is composed of normal (real) matter. Otherwise, the system is composed of dark matter or exotic matter. The EoS expressions are given by:

    $$\begin{aligned} w_r = \frac{p_r}{\rho }\;\;\;\;\textrm{and} \;\;\;\;w_t = \frac{p_t}{\rho }. \end{aligned}$$
    (55)

    For case-I, where \(p_r = \xi \rho +\phi \) was used, \(w_r\) is constant and approximately equal to \(\xi \) when a very small \(\phi \) is chosen. The middle and right panels of Fig. 5 for case-I and Fig. 11 for case-II demonstrate that these EoS parameters satisfy the required limiting criteria, ensuring that matter is generally distributed in the system.

  • Now, we discuss the stability of the stellar system by analysing stability parameters, namely sound speeds \(v_r^2\), the speed along the radial direction, and \(v_t^2\), the speed along the tangent direction. In addition to stability, we also need to consider the anisotropic matter distribution, famously known as the Herrera cracking concept. According to the cracking concept [67], stability is ensured if sound speeds satisfy the constraints \(0< v_r^2, v_t^2 < 1\), where \(c=1\) is the speed of light, and both speeds acquire values less than the speed of light c. The expression for sound speeds is as follows:

    $$\begin{aligned} v_r^2 = \frac{dp_r}{d\rho } \;\;\textrm{and}\;\; v_t^2 = \frac{dp_t}{d\rho }. \end{aligned}$$
    (56)

    Similar to \(w_r\), for case-I, where \(p_r = \xi \rho +\phi \) was used, \(v_r\) is constant and approximately equal to \(\xi \) when a very small \(\phi \) is chosen. Abreu et al. [68] propose another criterion for stability in which the region is considered to have potential strength when \(v_r^2 > v_t^2\), as the sign remains unchanged in \(v_r^2 - v_t^2\). Later, Andreasson generalised this criterion [69] to \(0< |v_t^2 - v_r^2| < 1\), i.e., no cracking and a stable region. Figures 6 and 12 for cases I and II, respectively, demonstrate that our results are in good agreement with the Abreu criteria and the Andreasson limit, indicating the stability of our solutions for compact star studies.

  • The ratio \(\frac{m(R)}{R}\) is an important tool for determining the level of compactness of a stellar body. One can obtain the expression for the mass from the formula given below:

    $$\begin{aligned} m(R)=4\pi \int R^2 \rho dr=\frac{r}{2}\left( 1-e^{-b(r)}\right) , \end{aligned}$$
    (57)

    where \(\rho \) is the density. By incorporating the contribution of Eq. (45), one can obtain an expression for the compactness parameter u(r), which is further used to determine the redshift function \(z_s\):

    $$\begin{aligned}{} & {} u=\frac{m(R)}{R}, \end{aligned}$$
    (58)
    $$\begin{aligned}{} & {} z_s=\left( 1-2u\right) ^{-\frac{1}{2}}-1. \end{aligned}$$
    (59)

    The author [70] set a maximum limiting value for the compactness parameter \(u=\frac{m(R)}{R}<\frac{4}{9}\). This criterion was further generalised for the anisotropic case of matter distribution in [68]. Moreover, Buchdhal [32] established a maximum value criteria for the redshift parameter, \(z_s\le 4.77\). Our study yielded a smooth and regular result for the mass function, as shown in the left panel of Figs. 7 and 13 for cases I and II, respectively. The middle and right panels in Figs. 7 and 13 for cases-I and-II, respectively, demonstrate that our results for the compactness and redshift parameters are well-matched with the defined criteria of physical admissibility of the stellar system.

8 Conclusion

This analysis genuinely represents the compatibility of the tetrad field in the study of compact stellar structures with the effects of gravity expressed by MRT theory. The MRT gravity is the most straightforward modification of f(T), and the inclusion of Rastall’s term makes it different from f(T) gravity. We applied the Karmar technique to evaluate the components of the geometry of spherical symmetric spacetime to draw admissible results to support the choice of off-diagonal tetrad fields. We also investigated the effect of Rastall’s parameter on the results. We made an attempt to explore the different forms of MRT gravity by making the choice of the hybrid function \(f(T)=\beta T^n e^{mT}\), by further reducing it into power law (\(m=0,\;n \ne 0\)) and exponential (\(m \ne 0,\;n=0\)), just altering the values of \(m,\;n\). For the first case, we used the EoS of state to evaluate the function h(T), and for the second case, we chose the logarithmic function h(T). For the purpose of variation and to make the results more clear for different values of Rastall’s parameter \(\gamma \), we also used different values for constant y in each case, as indicated in Tables 1 and 2. Here we have a detailed diagnosis of the anisotropic nature of the solutions of compact stellar bodies in both cases. The brief findings of our results are as follows:

  • It is clear from the graphical analysis that the off-diagonal tetrad is well-matched with the hybrid form of MRT gravity. In the case of the h(T) function evaluated by the EoS \(p_r = \xi \rho +\phi \), all three possible forms of MRT gravity are stable, whereas in the case of \(h(T)=\psi \log \left( \varphi T^{\chi }\right) \), the exponential-logarithmic form (\( n=0,\; \& \; m\ne 0\)) of MRT gravity is not stable.

  • The anisotropic behaviour of all the parameters is well-fitted in this analysis. The behaviour of metric potentials is smooth, i.e., \(e^{b}=1\) when \(r\rightarrow 0\) and \(e^{a}>0\), with the embedding class-I spacetime requirements. The expressions for \(\rho \), \(p_r\), and \(p_t\) agree with the required behaviour within the stellar configurations. The anisotropy parameter \(\Delta \) has shown smooth behaviour starting from the center and going to the boundary. The gradients have negative directions from the center towards the boundary. The inequalities in the energy conditions posed positive behaviour throughout the stellar configurations. The EoS, speed of sound, and causality limits also fulfil the required criteria. The TOV forces also ensure the stability of the stellar system. The adiabatic index, mass function, compactification, and redshift functions also show the required behaviour.

In short, our results are physically acceptable within the framework of the Karmarkar condition in the MRT theory of gravity. Ditta and Xia [71] also developed thefield equations by using the environment of MRT gravity (an extended version of Rastall’s gravity) to discuss the stellar structure by using an anisotropic fluid distribution with a spherically symmetric metric. But the current study is in the environment of MRT gravity (an extended version of f(T) gravity).