1 Introduction

In recent years a huge effort has been devoted to the problem of the computation of loop integrals. The reason is the need of accurate theoretical predictions able to cope with the ever-increasing precision of the data collected in particle physics experiments.

Two competing strategies have appeared. On the one hand, analytic methods based on systems of differential equations [2,3,4], whose solution are the wanted loop integrals, have shown their ability to cope with calculations involving a moderate number of physical scales [5,6,7,8,9,10,11,12,13,14,15]. On the other hand, techniques have been developed to deal with the problem in a fully numerical way [16,17,18,19,20,21,22,23,24].

The first obvious hurdle to overcome in both cases is the presence of infrared (IR) or ultraviolet (UV) divergences, that need to be properly regularized. This is usually done by using dimensional regularization [25, 26], even if four-dimensional methods have started to be used as a viable alternative [27,28,29,30,31,32,33,34,35].

Regardless of the approach employed for regularizing infinities, the finite part of the calculation is plagued by the presence of the so-called threshold singularities. These are integrable singularities avoided by the \(+i \epsilon \) propagator prescription. Such structures are not a problem for analytic calculations, but must be properly addressed when using numerical techniques.

In a previous paper [1], a method has been introduced, which permits an accurate fully numerical treatment of threshold singularities that can be easily implemented in Monte Carlo (MC) codes. The advantage of this technique is that, even if a non-zero \(\epsilon \) must be kept, its influence on the result can be lowered close to the machine precision level, e.g. between \(10^{-12}\) and \(10^{-9}\) times the largest physical scale appearing in the problem.

The performance of this procedure has been studied in [1] in the case of finite multi-loop Feynman integrals, or divergent ones regularized via four-dimensional methods. In this paper we extend for the first time this approach to integrals regularized within dimensional regularization, focusing our attention on scalar integrals that provide a complete basis for any one-loop calculation in massless theories [36, 37]. Higher-loop integrals will be studied in detail elsewhere, although we envisage that the experience gathered at the one-loop level can be comfortably adapted to multi-loop environments.

The structure of the paper is as follows. In Sect. 2 we briefly review the method. Section 3 fixes our kinematics and conventions. Sections 4, 5 and 6 are devoted to the study of the massless 2-, 3- and 4-point scalar one-loop integrals, respectively, and in Sect. 7 we present a simple two-loop example.

Finally, it is important to mention that throughout the paper we distinguish between the \(\epsilon \) and \(\varepsilon \) symbols. The latter parameterizes the n-dimensional loop integration, \(n= 4-2 \varepsilon \), while the former denotes the contour deformation around single-pole singularities. All results presented in this paper are produced with \(\epsilon = 10^{-9}\).

2 The method

In this section we briefly recall the method of [1]. Our aim is to flatten the singular behavior of a threshold singularity parameterized as

$$\begin{aligned} I = \int _{-1}^1 dx\, \frac{F(x)}{x+i\epsilon }, \end{aligned}$$
(1)

where the numerator function F(x) is regular in \(x=0\). To achieve this we introduce a complex integration variable \( z= \alpha + i \beta \) related to x by \( x+i\epsilon = e^{i \pi (1-z)}. \) The requirement that x remains real fixes the path in the complex z plane to be

$$\begin{aligned} \pi \beta = \ln \frac{\epsilon }{\sin [\pi (1-\alpha )]}, \end{aligned}$$
(2)

so that

$$\begin{aligned} x= \frac{\epsilon }{\tan [\pi (1-\alpha )]}. \end{aligned}$$
(3)

Using now

$$\begin{aligned} dz= d\alpha \left( 1+i \frac{d \beta }{d \alpha }\right) = d\alpha \left( 1+i \frac{x}{\epsilon }\right) \end{aligned}$$
(4)

gives

$$\begin{aligned} I = -\frac{i \pi }{g_\epsilon } \int _{{\epsilon }/{\pi }}^{1-{\epsilon }/{\pi }}\!\!\!\!d\alpha \left( 1+i\frac{x}{\epsilon } \right) F(x),~~~ g_\epsilon := 1-\frac{2\epsilon }{\pi }. \end{aligned}$$
(5)

Two comments are in order. Firstly, the integrand of (5) is now regular in \(x=0\) for arbitrarily small values of \(\epsilon \). In fact, the \(\epsilon \) dependence is moved to the boundaries of the integration region, \(x=\pm 1\), which are reached exactly only when \(\epsilon \rightarrow 0\). However, \(x = \pm 1\) are far away from the threshold singularity of (1). That explains why the algorithm survives tiny numerical values of \(\epsilon \). Secondly, if F(x) contains branch cuts in the x complex plane, the fact that x always lies on the real axis ensures that the right Riemann sheet is automatically taken when \(-1 \le x \le 1\). Thus, compared to methods based on contour deformation, one does not have to worry about choosing a path that avoids the pole at \(x= -i \epsilon \) without crossing any cut of F(x).

Equation (5) is optimal for integrating over \(\alpha \). To flatten the integral over \(\beta \), the parameterization complementary to (4) is needed, namely

$$\begin{aligned} dz= d\beta \left( \frac{d \alpha }{d \beta }+i\right) . \end{aligned}$$
(6)

However, (2) implies that \(\alpha \) is a two-valued function of \(\beta \). Therefore, it is necessary to divide (5) into two parts

$$\begin{aligned} I= & {} -\frac{i \pi }{g_\epsilon } \int _{{\epsilon }/{\pi }}^{1/2}\!\! d\alpha \nonumber \\{} & {} \times \left[ \left( 1-i\frac{y_\alpha }{\epsilon }\right) F(-y_\alpha ) +\left( 1+i\frac{y_\alpha }{\epsilon }\right) F(y_\alpha ) \right] , \end{aligned}$$
(7)

where \(y_\alpha := {\epsilon }/{\tan (\alpha \pi )}\). Inserting (6) into (7) gives

$$\begin{aligned} I= & {} - \frac{i \pi }{g_\epsilon } \int _{\beta _-}^{\beta _+} d\beta \nonumber \\{} & {} \times \left[ \left( \frac{\epsilon }{-y_\beta } +i\right) F(-y_\beta ) -\left( \frac{\epsilon }{ y_\beta } +i \right) F( y_\beta ) \right] , \end{aligned}$$
(8)

with

$$\begin{aligned} y_\beta := e^{\pi \beta }\sqrt{1-\left( \frac{\epsilon }{e^{\pi \beta }}\right) ^2},\quad \beta _-= \frac{1}{\pi }\ln \frac{\epsilon }{\sin \epsilon },\quad \beta _+= \frac{\ln \epsilon }{\pi }, \end{aligned}$$

that is optimized for the integration over \(\beta \). In practice, equations (7) and (8) can be merged together by means of a multichannel MC approach [38],Footnote 1 so that the complete \(1/(x+i \epsilon )\) behavior of (1) is flattened.

The described algorithm is implemented in the code GLoop [39]. The present version is able to deal with integrals of the type

$$\begin{aligned} \int _{-\infty }^\infty \prod _{j=1}^m \left( \frac{d \sigma _j}{\sigma _j \pm i \epsilon } \right) F(\sigma _1,\sigma _2,\ldots ,\sigma _m), \end{aligned}$$
(9)

with m up to 4. The numerical results presented in this paper require \(m= 3\) at most.

3 Kinematics and loop integration

For the purposes of this work it is sufficient to consider a \(p_1+p_2 \rightarrow p_3+p_4\) massless kinematics given by

$$\begin{aligned}{} & {} \!\!\!p^\alpha _1 = \frac{\sqrt{s}}{2} (1,1,0,0), \quad \!\!\!p^\alpha _2 = \frac{\sqrt{s}}{2} (1,-1,0,0), \nonumber \\{} & {} \!\!\!p^\alpha _3 = \frac{\sqrt{s}}{2} (1,\cos \theta _{13}, \sin \theta _{13},0), \quad \!\!\!\!p^\alpha _4 = p^\alpha _1+p^\alpha _2-p^\alpha _3. \end{aligned}$$
(10)

In (10) \(s=(p_1+p_2)^2\) and \(\theta _{13}\) is the scattering angle defined by the relation

$$\begin{aligned} t= (p_1-p_3)^2= -\frac{s}{2}(1-\cos \theta _{13}). \end{aligned}$$
(11)

The n-dimensional loop momentum is

$$\begin{aligned} q^\alpha= & {} (q_0,|\textbf{q}|c_\theta ,|\textbf{q}|s_\theta c_\phi , \ldots ), \end{aligned}$$
(12)

where \(c_\theta = \cos {\theta }\), \(s_\theta = \sin {\theta }\), \(c_\phi = \cos \phi \), with \(0 \le \theta \le \pi \) and \(0 \le \phi \le 2 \pi \).

Rescaling \(p_{1,2,3}\) and q by \(\sqrt{s}\) produces the following dimensionless vectors

$$\begin{aligned}{} & {} \pi ^\alpha _1 = \frac{1}{2} (1,1,0,0), \quad \pi ^\alpha _2 = \frac{1}{2} (1,-1,0,0), \nonumber \\{} & {} \pi ^\alpha _3 = \frac{1}{2} (1,c_{13},s_{13},0), \quad \omega ^\alpha _{n} = (\tau ,\rho c_\theta ,\rho s_\theta c_\phi , \ldots ), \end{aligned}$$
(13)

in which \(\tau = {q_0}/{\sqrt{s}}\) and \(\rho = {|\textbf{q}|}/{\sqrt{s}}\). Note that \(\pi ^\alpha _{1,2,3}\) span a three-dimensional space, so that in the one-loop integrands one can trade \(\omega ^\alpha _{n}\) for its four-dimensional projection defined as

$$\begin{aligned} \omega ^\alpha = (\tau ,\rho c_\theta ,\rho s_\theta c_\phi ,\rho s_\theta s_\phi ), ~~\textrm{with}~~s_\phi = \sin \phi . \end{aligned}$$
(14)

In fact \(\omega ^2_n= \omega ^2\) and \(\omega _n \cdot \pi _i= \omega \cdot \pi _i~~\forall i=1,2,3\).

Finally, the integration over the rescaled loop momentum can be parameterized as

$$\begin{aligned} \int \!d^n \omega _n = \int _n \int _{-\infty }^{\infty }\! d\tau , \end{aligned}$$
(15)

where \(\int _n\) is the \((n-1)\)-dimensional integration volume. In terms of \(\rho \), \(\theta \) and \(\phi \) it reads

$$\begin{aligned} \int _n= & {} \frac{2 \pi ^{\frac{n-3}{2}}}{\mathrm{\Gamma }\left( \frac{n-3}{2}\right) } \times \int _{-1}^{1} d c_\theta \, (1-c^2_\theta )^{\frac{n-4}{2}} \nonumber \\{} & {} \times \int _{-1}^{1} d c_\phi \, (1-c^2_\phi )^{\frac{n-5}{2}} \int _0^\infty d \rho \, \rho ^{n-2}. \end{aligned}$$
(16)

If the integrand is independent of \(\phi \), the integration over \(c_\phi \) can be carried out analytically by using

$$\begin{aligned} \int _0^{\pi } (\sin \phi )^m\,d\phi = \sqrt{\pi }\, \frac{\mathrm{\Gamma } \left( \frac{m+1}{2}\right) }{\mathrm{\Gamma } \left( \frac{m+2}{2}\right) }, \end{aligned}$$
(17)

that gives

$$\begin{aligned} \int _n = \frac{2 \pi ^{\frac{n-2}{2}}}{\mathrm{\Gamma }\left( \frac{n-2}{2}\right) } \int _{-1}^{1} d c_\theta \, (1-c^2_\theta )^{\frac{n-4}{2}} \int _0^\infty d \rho \, \rho ^{n-2}. \end{aligned}$$
(18)

Likewise, integrating over \(c_\theta \) produces

$$\begin{aligned} \int _n = \frac{2 \pi ^{\frac{n-1}{2}}}{\mathrm{\Gamma }\left( \frac{n-1}{2}\right) } \int _0^\infty d\rho \, \rho ^{n-2}. \end{aligned}$$
(19)

4 The UV divergent one-loop 2-point integral

Fig. 1
figure 1

The scalar 2-point one-loop function of (20)

Full size image

As a first illustration of our procedure we compute by MC the dimensionally regularized one-loop scalar integral of Fig. 1,

$$\begin{aligned} B(s) = \mu ^{4-n} \int d^n q \frac{1}{D_0 D_1}, \end{aligned}$$
(20)

where \(D_0= q^2+i \epsilon \) and \(D_1= (q+p_1+p_2)^2+i \epsilon \). Given that B(s) diverges in four dimensions, our strategy is to split it into a finite part and a UV divergent piece,

$$\begin{aligned} B(s)= {B}_\textrm{F}(s)+{B}_\textrm{UV}, \end{aligned}$$
(21)

in a way that the former can be computed numerically using the four-dimensional algorithm of Sect. 2, while the latter is evaluated analytically.

Rescaling loop and external momenta by \(\sqrt{s}\) gives

$$\begin{aligned} B(s)= \left( \frac{s}{\mu ^2} \right) ^{-\varepsilon }\! \mathcal{B},~~\textrm{where}~~ \mathcal{B}= \int _n \int _{-\infty }^\infty d \tau \, \frac{1}{d_0 d_1}, \end{aligned}$$
(22)

with \(d_0 = \tau ^2-\rho ^2+i \epsilon \) and \(d_1 = (\tau +1)^2-\rho ^2 +i \epsilon \). The integrand of (22) does not depend on \(\theta \) and \(\phi \). Hence, \(\int _n\) can be taken as in (19). We now integrate over \(\tau \) by using the residue theorem. The result is

$$\begin{aligned} \mathcal{B}= \frac{i \pi }{2} \int _n\,\frac{1}{\rho } \frac{1}{\rho ^2-1/4-i \epsilon }. \end{aligned}$$
(23)

To achieve the splitting of (21), we subtract and add back an integrand with the same \(\rho \rightarrow \infty \) behavior of (23). Among the various possibilities we choose \( \frac{1}{\rho (\rho ^2+1/4)}. \) This allows us to recast \( \mathcal{B}= \mathcal{B}_\textrm{F}+\mathcal{B}_\textrm{UV}\), in which the finite piece reads

$$\begin{aligned} \mathcal{B}_\textrm{F}= 2 i \pi ^2 \int _0^\infty d \rho \,\rho \left[ \frac{1}{\rho ^2-1/4-i \epsilon }- \frac{1}{\rho ^2+1/4}\right] , \end{aligned}$$
(24)

while \(\mathcal{B}_\textrm{UV}\) is easily computed analytically,

$$\begin{aligned} \mathcal{B}_\textrm{UV}= \frac{i \pi ^{2-\varepsilon }}{\mathrm{\Gamma }(1 -\varepsilon )} \left( \frac{1}{\varepsilon } + 2\right) + \mathcal{O}(\varepsilon ). \end{aligned}$$
(25)

Introducing the variable \(\sigma = \rho ^2-1/4\) allows one to rewrite (24) in a form suitable to be integrated with GLoop,

$$\begin{aligned} \mathcal{B}_\textrm{F} = \int _{-\infty }^{\infty } \frac{d \sigma }{\sigma -i \epsilon } F(\sigma ),~~ F(\sigma ) = i \pi ^2\,\frac{\mathrm{\Theta }(\sigma +1/4)}{1 + 2 \sigma }, \end{aligned}$$
(26)

where \(\mathrm{\Theta }\) is the Heaviside step function.

Our MC estimate with \(10^{7}\) MC shots gives

$$\begin{aligned} \mathcal{B}_\textrm{F}/(i \pi ^2)= 3(9)\times 10^{-4} +i\,3.1414(7), \end{aligned}$$
(27)

to be compared to the analytic value

$$\begin{aligned} \mathcal{B}_\textrm{F}/(i \pi ^2) |_\textrm{Analytic}= i\,\pi . \end{aligned}$$
(28)

The time to produce the result of (27) on a single 2.2 GHz processor is of about 1.6 s.

Finally, the analytic continuation to \(s < 0\) is achieved by replacing \(s/\mu ^2 \rightarrow s/\mu ^2 +i \epsilon \) in (22) [40]. This produces

$$\begin{aligned} B(s)= & {} \frac{i \pi ^{2-\varepsilon }}{\mathrm{\Gamma }(1-\varepsilon )} \bigg [ \frac{1}{\varepsilon } +2-L-i\pi +\frac{\mathcal{B}_\textrm{F}}{i \pi ^2} \bigg ] + \mathcal{O}(\varepsilon ), \end{aligned}$$
(29)

with \(L= \ln \big (-{s}/{\mu ^2}- i \epsilon \big )\).

Lastly, it is noteworthy to mention that from a numerical standpoint, the treatment of UV divergences is remarkably similar in terms of dimensional regularization and FDR [27,28,29,30,31, 33]. The sole distinction lies in their action towards the subtracted UV divergent part, which is computed analytically and added back in the former approach, whereas it is judiciously discarded in FDR [1].

5 The IR divergent one-loop 3-point integral

Fig. 2
figure 2

The scalar 3-point one-loop function of (30)

Full size image

Here we study the dimensionally regularized triangle function of Fig. 2 with two massless momenta \(p^2_{1,2}=0\) and massless denominators \(D_0=q^2+i\epsilon \), \(D_1=(q+p_1)^2+i\epsilon \) and \(D_2=(q-p_2)^2+i\epsilon \),

$$\begin{aligned} C(s) = \mu ^{4-n} \int d^n q \frac{1}{D_0D_1D_2}. \end{aligned}$$
(30)

As in the previous section, we rescale all dimensionful quantities by \(\sqrt{s}\). This produces

$$\begin{aligned} C(s) = \frac{1}{s}\left( \frac{s}{\mu ^2} \right) ^{-\varepsilon } \mathcal{C}. \end{aligned}$$
(31)

The rescaled integral \(\mathcal{C}\) reads

$$\begin{aligned} \mathcal{C} = \int _n \int _{-\infty }^\infty d \tau \, \frac{1}{d_0d_1d_2}, \end{aligned}$$
(32)

with \(\int _n\) given in (18) and

$$\begin{aligned} d_0= & {} (\tau +\rho -i \epsilon ) (\tau -\rho +i \epsilon ), \nonumber \\ d_1= & {} (\tau +1/2+R-i \epsilon ) (\tau +1/2-R+i \epsilon ), \nonumber \\ d_2= & {} (\tau -1/2+R-i \epsilon ) (\tau -1/2-R+i \epsilon ), \nonumber \\ R= & {} \sqrt{1/4+\rho ^2+\rho c_\theta }. \end{aligned}$$
(33)

\(\mathcal{C}\) is divergent in the soft and collinear limits, namely it develops \(1/{\varepsilon }\) and \(1/{\varepsilon ^2}\) poles under the n-dimensional integration. To be able to perform the loop integration numerically, we first construct an approximation \(\mathcal{C}_\textrm{IR}\) whose integrand subtracts the infrared behavior in a local fashion. Then we reinsert the result of an analytic computation of \(\mathcal{C}_\textrm{IR}\). Schematically, \(\mathcal{C}= \mathcal{C}_\textrm{F}+\mathcal{C}_\textrm{IR}\), where

$$\begin{aligned} \mathcal{C}_\textrm{F}= \lim _{n \rightarrow 4}\left[ \mathcal{C}-\mathcal{C}_\textrm{IR}\right] \end{aligned}$$
(34)

is computed by MC.

Using the residue theorem to integrate over \(\tau \) gives

$$\begin{aligned} \mathcal{C}= & {} - \frac{i \pi }{2} \int _n \frac{1}{\rho ^2 R } \left( \frac{1}{R-1/2-i \epsilon }-\frac{1}{R-1/2+\rho -i \epsilon } \right. \nonumber \\{} & {} \left. -\frac{1}{R+1/2} +\frac{1}{R+1/2+\rho } \right) . \end{aligned}$$
(35)

Only the first two terms of (35) are divergent when \(\rho < 1/2\). An approximation sharing their IR behavior is constructed by expanding R around \(\rho (1+c_\theta )= 0\), that produces

$$\begin{aligned} \mathcal{C}_\textrm{IR} = i \pi \int _n \frac{\mathrm{\Theta }(1-2 \rho )}{\rho ^3} \left( \frac{1}{1+c_\theta }-\frac{1}{c_\theta +2 \rho -i \epsilon } \right) , \end{aligned}$$
(36)

which can be easily evaluated analytically

$$\begin{aligned} \mathcal{C}_\textrm{IR}= \frac{i \pi ^{2-\varepsilon }}{\mathrm{\Gamma }(1-\varepsilon )} \left( \frac{1}{\varepsilon ^2}+ \frac{i \pi }{\varepsilon } -\frac{2 \pi ^2 }{3} +i \pi \ln (4) \right) + \mathcal{O}(\varepsilon ). \end{aligned}$$

The integrand of (36) can now be subtracted to (35) and the resulting integral produces the finite contribution of (34). In four dimensions (18) gives

$$\begin{aligned} \int _4= 4 \pi \int _0^\infty \! d \rho \, \rho \int _{|R_-|}^{R_+}\! dR\, R, \end{aligned}$$
(37)

with \(R_{\pm }= 1/2\pm \rho \), thus

$$\begin{aligned} \mathcal{C}_\textrm{F}= & {} -2 i \pi ^2 \int _0^\infty \! \frac{d \rho }{\rho }\,\int _{|R_-|}^{R_+} dR\, \bigg \{ \frac{1}{R-1/2-i \epsilon } \nonumber \\{} & {} -\frac{{\mathrm{\Theta }(R_-)}}{R-\sqrt{R_+R_-}-i \epsilon } -\frac{\mathrm{\Theta }(-R_-)}{R-R_-}-\frac{1}{R+1/2} \nonumber \\{} & {} +\frac{1}{R+R_+}-\frac{\mathrm{\Theta }(R_-)}{R+\sqrt{R_+R_-}} +\frac{\mathrm{\Theta }(R_-)}{R+R_-} \bigg \}, \end{aligned}$$
(38)

where the \(-i \epsilon \) is kept only in denominators with threshold singularities.

Now we put (38) in a form suitable to be integrated with GLoop. The terms between curly brackets have denominators of the form \(R+r_i\), where the \(r_{1 \div 7}\) are independent of R. We then introduce two integration variables defined as follows

$$\begin{aligned} \sigma _1= \rho ,~\sigma _2= & {} R+r_i~~\forall \, i= 1 \div 7, \end{aligned}$$
(39)

and rewrite

$$\begin{aligned} \mathcal{C}_\textrm{F} = \int _{-\infty }^{\infty } \prod _{j=1}^2 \left( \frac{d \sigma _j}{\sigma _j-i \epsilon }\right) F_\mathcal{C}(\sigma _1,\sigma _2). \end{aligned}$$
(40)

The numerator \(F_\mathcal{C}(\sigma _1,\sigma _2)\) of (40) is fully expressible in terms of Heaviside functions and is given in Appendix A.

With \(4 \times 10^8\) MC points our estimate is

$$\begin{aligned} \mathcal{C}_\textrm{F}/(i \pi ^2) = 1.644(4) -i\,4.356(1), \end{aligned}$$
(41)

to be compared to the analytic result

$$\begin{aligned} \mathcal{C}_\textrm{F}/(i \pi ^2) |_\textrm{Analytic}= & {} \pi ^2/6-i \pi \ln (4) \nonumber \\= & {} 1.6449 -i\,4.3552. \end{aligned}$$
(42)

The time to produce \(10^{6}\) MC shots on a single 2.2 GHz processor is of about 0.32 s.

In our computation we have assumed \(s > 0\). The analytic continuation to \(s < 0\) is again obtained by replacing \(s \rightarrow s+i \epsilon \) in (31). Expanding in \(\varepsilon \) gives

$$\begin{aligned} C(s)= & {} \frac{i \pi ^{2-\varepsilon }}{\mathrm{\Gamma }(1-\varepsilon )}\frac{1}{s} \bigg [ \frac{1}{\varepsilon ^2}-\frac{L}{\varepsilon }+\frac{L^2}{2} -\frac{\pi ^2 }{6} +i \pi \ln (4)\nonumber \\{} & {} + \frac{\mathcal{C}_\textrm{F}}{i \pi ^2} \bigg ] + \mathcal{O}(\varepsilon ), \end{aligned}$$
(43)

where \(L= \ln \big (-{s}/{\mu ^2}- i \epsilon \big )\).

6 The IR divergent one-loop 4-point integral

Fig. 3
figure 3

The scalar 4-point one-loop function of (44)

Full size image

In this section we consider the massless box diagram of Fig. 3,

$$\begin{aligned}{} & {} D(s,t) = \mu ^{4-n} \int d^nq \frac{1}{D_0 D_1 D_2 D_3}, \nonumber \\{} & {} D_0 = q^2+i\epsilon , \quad D_1=(q+p_1)^2+i\epsilon , \nonumber \\{} & {} D_2=(q-p_2)^2+i\epsilon , \quad D_3=(q+p_1-p_3)^2+i\epsilon , \end{aligned}$$
(44)

where \(p^2_{1,2,3,4}= 0\). By rescaling all dimensionful quantities by \(\sqrt{s}\) one arrives at

$$\begin{aligned} D(s,t) =\frac{1}{s^2} \left( \frac{s}{\mu ^2}\right) ^{-\varepsilon } \mathcal{D}(x), \end{aligned}$$
(45)

where we have defined \(x = -{t}/{s}\), so that in the physical region one has \(0 \le x \le 1\). The rescaled 4-point integral reads

$$\begin{aligned} \mathcal{D}(x)= \int _n \int _{-\infty }^{\infty } d\tau \, \frac{1}{d_0d_1d_2d_3}, \end{aligned}$$
(46)

with \(\int _n\) given in (16). The denominators \(d_{0,1,2}\) are as in (33). Furthermore, \( d_3 = (\tau +S-i \epsilon ) (\tau -S +i \epsilon ) \) with \(S = \sqrt{\rho ^2+U-V\, c_\phi }\) and

$$\begin{aligned} U = x (1 +2 \rho c_\theta ),\quad V = 2 \rho \sqrt{x(1-x)} \sqrt{1 -c_\theta ^2}. \end{aligned}$$
(47)

As before, to compute (46) by MC, we first have to subtract a simpler function \(\mathcal{D}_\textrm{IR}(x)\) with the same local IR behavior of \(\mathcal{D}(x)\). We choose

$$\begin{aligned} \mathcal{D}_\textrm{IR}(x)= & {} \int _n \int _{-\infty }^{\infty } d\tau \, \bigg [\frac{1}{d_0d_1d_3}+\frac{1}{d_0d_2d_3} -\frac{1}{x}\,\frac{1}{d_0d_1d_2}\nonumber \\{} & {} -\frac{1}{x}\,\frac{1}{d_1d_2d_3} \bigg ]-\frac{i\pi ^2}{x}\left( \pi ^2-\ln ^2(x)\right) , \end{aligned}$$
(48)

that can be integrated analytically by means of (42) and (43),

$$\begin{aligned} \mathcal{D}_\textrm{IR}(x)= \frac{i \pi ^{2-\varepsilon }}{\mathrm{\Gamma }(1-\varepsilon )} \frac{1}{x} \left( -\frac{4}{\varepsilon ^2}+ \frac{2}{\varepsilon }\left( \ln x -i \pi \right) \right) + \mathcal{O}(\varepsilon ). \end{aligned}$$

The rationale behind (48) is as follows. On the one hand, it is well known that the four 3-point integrals produce the same \(1/\varepsilon \) and \(1/\varepsilon ^2\) poles of \(\mathcal{D}(x)\) [41]. On the other hand, the last term is chosen in such a way that it compensates their finite contribution. In this way

$$\begin{aligned} \mathcal{D}_\textrm{F}(x)= \lim _{n \rightarrow 4}\left[ \mathcal{D}(x)-\mathcal{D}_\textrm{IR}(x) \right] \end{aligned}$$
(49)

gives the finite part of \(\mathcal{D}(x)\) directly.

Table 1 Numerical estimates of \(\mathcal{D}_\textrm{F}(x)/(10 \,i \pi ^2)\) in (53) for several values of \(x = -t/s \). The analytic result is reported in (54). Numbers obtained with \(4 \times 10^9 \) MC shots. MC errors between parentheses
Full size table

Integrating over \(\tau \) the IR finite combination of integrals appearing in (49) gives

$$\begin{aligned}{} & {} \int _4 \int _{-\infty }^{\infty } d\tau \, \bigg ( \frac{1}{d_0d_1d_2d_3} -\frac{1}{d_0d_1d_3}-\frac{1}{d_0d_2d_3} \nonumber \\{} & {} \qquad +\frac{1}{x}\,\frac{1}{d_0d_1d_2}+\frac{1}{x}\,\frac{1}{d_1d_2d_3} \bigg ) \nonumber \\{} & {} \quad =i \pi \int _4 \frac{1}{\rho ^2 R } \bigg \{ \frac{1}{R-1/2-i \epsilon } \bigg ( \textrm{P}\bigg [\frac{1}{S^2-\rho ^2}\bigg ]-\frac{1}{x} \bigg ) \nonumber \\{} & {} \qquad -\frac{1}{R-1/2+\rho -i \epsilon } \bigg ( \big (1-2\rho \big ) \textrm{P}\bigg [\frac{1}{S^2-\rho ^2}\bigg ]-\frac{1}{x} \bigg ) \nonumber \\{} & {} \qquad -\frac{1}{R+1/2} \bigg ( \textrm{P}\bigg [\frac{1}{S^2-\rho ^2}\bigg ]-\frac{1}{x} \bigg ) \nonumber \\{} & {} \qquad +\frac{1}{R+1/2+\rho } \bigg ( \big (1+2\rho \big ) \textrm{P}\bigg [\frac{1}{S^2-\rho ^2}\bigg ]-\frac{1}{x} \bigg ) \bigg \}, \end{aligned}$$
(50)

where \(\textrm{P}\) denotes the Cauchy principal value,

$$\begin{aligned} \textrm{P}\bigg [\frac{1}{S^2-\rho ^2}\bigg ] = \frac{1}{2}\bigg (\frac{1}{S^2-\rho ^2+ i \epsilon } +\frac{1}{S^2-\rho ^2 - i \epsilon }\bigg ). \end{aligned}$$
(51)

To derive (50) we have systematically identified terms related by the interchange \(\rho \leftrightarrow S\). This is possible because \(\int _4\) is invariant under shifts and rotations of the spatial components of the vectors \(\pi ^\alpha _{1,2,3}\) and \(\omega ^\alpha \). The \(\phi \) dependence is entirely contained in \({S^2-\rho ^2}\) and can be integrated out by using

$$\begin{aligned}{} & {} \int _{-1}^{1} d c_\phi \Big (1-c^2_\phi \Big )^{-1/2} {\textrm{P}}\bigg [\frac{1}{S^2-\rho ^2}\bigg ] \nonumber \\{} & {} \quad =\pi \,{\mathrm{sgn(U)}} \frac{\mathrm{\Theta }(U^2-V^2)}{\sqrt{U^2-V^2}}. \end{aligned}$$
(52)

Finally, inserting (52) and (50) into (49) gives

$$\begin{aligned} \mathcal{D}_\textrm{F}(x) = \int _{-\infty }^{\infty } \prod _{j=1}^2 \left( \frac{d \sigma _j}{\sigma _j-i \epsilon }\right) F_\mathcal{D}(\sigma _1,\sigma _2,x), \end{aligned}$$
(53)

with \(F_\mathcal{D}(\sigma _1,\sigma _2,x)\) provided in Appendix B.

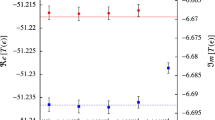
Our MC estimates are presented in Table 1 and compared to the analytic result [40]

$$\begin{aligned} \left. \mathcal{D}_\textrm{F}(x) \right| _\textrm{Analytic}= \frac{i \pi ^2}{x} \left( \pi ^2+2 i \pi \ln (x) \right) . \end{aligned}$$
(54)

The time to generate \(10^{6}\) MC shots on a single 2.2 GHz processor is of about 0.4 s.

7 A two-loop example

In this section we compute the two-loop bubble-box diagram of Fig. 4, which has collinear and soft IR divergences in addition to a UV-divergent sub-diagram,

$$\begin{aligned}{} & {} T= \mu ^{8-2n}\int \frac{d^nq}{i \pi ^{\frac{n}{2}}}\frac{d^nk}{i \pi ^{\frac{n}{2}}} \frac{1}{D_0 D_1 D_2 D_3 D_4}, \nonumber \\{} & {} D_0 = q^2+i\epsilon , \quad D_1=(q-p_1-p_2)^2+i\epsilon , \nonumber \\{} & {} D_2=(q-p_1)^2+i\epsilon , \quad D_3= k^2+i\epsilon , \nonumber \\{} & {} D_4=(k+q-p_3)+i\epsilon , \quad p^2_{1,2,3,4}= 0. \end{aligned}$$
(55)

More precisely, we evaluate its IR and UV subtracted counterpart obtained as described and reported in [42],

$$\begin{aligned} T_\textrm{F}= & {} \int \frac{d^4q}{i \pi ^2}\frac{d^4k}{i \pi ^2} \bigg \{\frac{1}{D_0 D_1 D_2}\bigg (\frac{1}{D_3D_4}- \Big [\frac{1}{D_3D_4}\Big ]_{q= p_1}\bigg ) \nonumber \\{} & {} -\bigg (\frac{1}{D_0D_2}-\frac{1}{(D_0-m^2) (D_2-m^2)}\bigg ) \frac{1}{s(1-x_1)} \nonumber \\{} & {} \times \bigg ( \Big [\frac{1}{D_3D_4} \Big ]_{q= x_1 p_1} -\Big [\frac{1}{D_3D_4} \Big ]_{q= p_1} \bigg ) \nonumber \\{} & {} -\bigg (\frac{1}{D_1D_2}-\frac{1}{(D_1-m^2) (D_2-m^2)}\bigg ) \frac{1}{s(1-x_2)} \nonumber \\{} & {} \times \bigg ( \Big [\frac{1}{D_3D_4} \Big ]_{q= p_1+p_2(1-x_2)} -\Big [\frac{1}{D_3D_4} \Big ]_{q= p_1} \bigg ) \bigg \}. \end{aligned}$$
(56)

The first term of (56) is the original integral, while \(x_1 = \frac{q \cdot p_2}{p_1 \cdot p_2}\) and \(x_2= \frac{(p_1+p_2-q)\cdot p_1}{p_1 \cdot p_2}\) are the fractions of the momenta \(p_1\) and \(p_2\) carried by the internal lines with momenta q and \(p_1+p_2-q\), respectively. Finally, m is an arbitrary mass used to subtract the UV behavior.

Fig. 4
figure 4

The two-loop bubble-box of (55)

Full size image
Table 2 Numerical estimates of \(\mathcal{T}_\textrm{F}(x)\) in (63) for several values of \(x = -t/s\) and \(\mu _0=1\). The analytic result is reported in (64). Numbers obtained with \(8 \times 10^{10} \) MC shots. MC errors between parentheses
Full size table

The best way to apply the algorithm of Sect. 2 to the case at hand is to use the gluing procedure described in [1], which allows one to express (56) in terms of a tree-level part convoluted with the one-loop sub-diagram. To achieve this, we perform analytically the k integration and rescale all dimensionful quantities by \(\sqrt{s}\), which produces

$$\begin{aligned}&\mathcal{T}_F(x)\nonumber \\ {}&\quad \equiv s T_F= -\frac{1}{i \pi ^2} \int d^4 \omega \bigg \{\frac{1}{d_0 d_1 d_2}\,\ln \frac{d_5}{-x+i \epsilon } \nonumber \\&\qquad -\bigg (\frac{1}{d_0 d_2}-\frac{1}{(d_0-\mu _0) (d_2-\mu _0)}\bigg ) \frac{1}{1-x_1} \ln \frac{x_1x-i \epsilon }{x-i\epsilon }\nonumber \\&\qquad -\bigg (\frac{1}{d_1 d_2}-\frac{1}{(d_1-\mu _0) (d_2-\mu _0)}\bigg ) \frac{1}{1-x_2} \ln \frac{x_2x-i \epsilon }{x-i\epsilon } \bigg \},\nonumber \\ \end{aligned}$$
(57)

where \(\mu _0= m^2/s\) and

$$\begin{aligned} d_0= & {} \tau ^2-\rho ^2+i\epsilon \equiv \sigma _0+i \epsilon \nonumber \\ d_1= & {} (\tau -1)^2-\rho ^2+i\epsilon \equiv \sigma _1+i \epsilon \nonumber \\ d_2= & {} \tau ^2-\tau -\rho ^2+\rho c_\theta +i\epsilon \equiv \sigma _2+i \epsilon \nonumber \\ d_5= & {} A+Bc_\phi +i \epsilon . \end{aligned}$$
(58)

In (58) \(d_{0,1,2}= D_{0,1,2}/s\) are rescaled denominators, \(d_5= [(q-p_3)^2+i \epsilon ]/s\) and

$$\begin{aligned} A= & {} \tau ^2-\tau -\rho ^2+\rho c_\theta (1-2x), \nonumber \\ B= & {} 2\rho s_\theta \sqrt{x(1-x)}. \end{aligned}$$
(59)

Next, we trade the integrations over \(\tau \), \(\rho \) and \(c_\theta \) for integrations over \(\sigma _{0,1,2}\) defined in (58). This gives

$$\begin{aligned} \int d^4 \omega = \frac{1}{4} \int d \sigma _0 d \sigma _1 d \sigma _2\, K(\sigma _0,\sigma _1,\sigma _2)\int _0^{2 \pi } d \phi , \end{aligned}$$
(60)

with

$$\begin{aligned} K(\sigma _0,\sigma _1,\sigma _2)= & {} \mathrm{\Theta }[\lambda (1,\sigma _0,\sigma _1)] \nonumber \\{} & {} \!\!\!\!\times \mathrm{\Theta }[\sigma _0+\sigma _1-1-2\sigma _2+\lambda ^{1/2}(1,\sigma _0,\sigma _1)] \nonumber \\{} & {} \!\!\!\!\times \mathrm{\Theta }[2\sigma _2-\sigma _0-\sigma _1+1+\lambda ^{1/2}(1,\sigma _0,\sigma _1)], \nonumber \\ \end{aligned}$$
(61)

where \(\lambda (x,y,z)\) is the Källén function. The integration over the azimuthal angle \(\phi \) can be performed by using

$$\begin{aligned}{} & {} \int _0^{2 \pi }\!d \phi \, \ln (A+B c_\phi + i \epsilon ) \equiv 2 \pi \,G(A,B) \nonumber \\{} & {} \quad =2 \pi \left[ \ln \frac{A+i\epsilon }{2}+\ln \bigg (1+\sqrt{1-\frac{B^2}{(A+i\epsilon )^2}}\bigg ) \right] . \end{aligned}$$
(62)

After that, \(\mathcal{T}_\textrm{F}(x)\) can be written in terms of a triple integral suitable to be evaluated numerically with GLoop,

$$\begin{aligned} \mathcal{T}_\textrm{F}(x) = \int _{-\infty }^{\infty } \prod _{j=0}^2 \left( \frac{d \sigma _j}{\sigma _j+i \epsilon }\right) F_\mathcal{T}(\sigma _0,\sigma _1,\sigma _2,x), \end{aligned}$$
(63)

with \(F_\mathcal{T}(\sigma _0,\sigma _1,\sigma _2,x)\) given in Appendix C. Note that the numerator \(F_\mathcal{T}\) contains branch cuts controlled by the \(i \epsilon \) prescription (see (62)), but because our algorithm maintains \(\sigma _{0,1,2}\) in the real axis, the correct Riemann sheet is automatically taken.

The analytic result in the physical region \(0 \le x \le 1\) reads [42]

$$\begin{aligned} \mathcal{T}_\textrm{F}(x)= & {} -S_{12}(1-x) -3 \zeta _3 -\frac{\pi ^2}{3} \ln \mu _0 + \frac{1}{6} \ln ^3 x \nonumber \\{} & {} +i \pi \left[ \textrm{Li}_2(1-x)-\frac{\pi ^2}{6} +\frac{1}{2} \ln ^2 x \right] , \end{aligned}$$
(64)

where \(S_{12}\) is the Nielsen polylogarithm. Table 2 shows a comparison between our MC estimate based on (63) and (64). The time to produce \(10^{6}\) MC shots on a single 2.2 GHz processor is of about 0.42 s.

8 Conclusion and outlook

Any attempts towards a numerical loop integration requires controlling threshold singularities. A possible approach is contour deformation [43, 44], that calls for analytic knowledge of the cut structure of the integrand [45] or numerical checks establishing whether the deformation stays on the correct side of the singularity. In [1] an alternative has been proposed and shown to be effective in the MC estimate of four-dimensa‘ional multi-loop integrals directly in Minkowski space.

In this paper we have extended this technique to massless scalar one-loop integrals with no more that four external legs, regularized within dimensional regularization. Our strategy is based on a separation of the \(1/\varepsilon \) and \(1/\varepsilon ^2\) poles before integration. The finite part, containing the threshold singularities, can then be integrated numerically in four dimensions. A fully numerical evaluation of one-loop amplitudes with more than four legs is in principle possible if the coefficients of the contributing one-, two-, three- and four-point integrals are also determined in a numerical fashion by using, for instance, the method of [37].

We have presented numerical results obtained with the help of the code GLoop. A MC error of the order of a few per mil can usually be obtained for a modest CPU cost. As with any other numerical method, this level of precision is expected to be sufficient for phenomenological purposes when the gauge cancellations are moderate. If this is not the case, cancellations among diagrams must be enforced to occur before integration. This should be feasible because they are usually controlled by Ward identities operating at the integrand level.

Enlarging the range of applicability of our method beyond one loop requires removing UV and IR divergences by adding appropriate counterterms at the level of the integrand. Ultraviolet counterterms can be constructed by using, for instance, the same procedure that defines FDR integrals [27,28,29,30,31, 33]. As for the infrared behavior, a systematic approach has been developed for two-loop integrals by Anastasiou and Sterman in [42]. In Sect. 7 we have presented a simple two-loop example showing how the subtraction method of [42] can be combined with our algorithm. For all these reasons, we believe that the strategy described in this paper can be extended up to two loops. A deeper exploration of this issue is planned for a future publication.