On the search for the two poles of the $\Xi (1820)$ in the $\psi (3686) \rightarrow \bar{\Xi }^+ \bar{K}^0 \Sigma ^{*-}(\pi ^- \Lambda )$ decay

Abstract

We propose the reaction $\psi (3686) \rightarrow \bar{\Xi }^+ \bar{K}^0 \Sigma ^{*-}$, with the $\Sigma ^{*-}$ decaying to $\pi ^- \Lambda$ in order to show evidence for the existence of two $\Xi (1820)$ states, one around 1824 MeV and narrow, and another one around 1875 MeV and wide. The phase space for $\bar{K}^0 \Sigma ^{*-}$ production reduces the effect of the lower mass resonance, magnifying the effect of the higher mass resonance that shows clearly over the phase space. The estimated rate of the production is bigger than the one of the $\psi (3686) \rightarrow \bar{\Xi }^+ K^- \Lambda$ reaction, where a clear peak for $\Xi (1820)$ was observed by the BESIII collaboration, what makes the Beijing facility ideal to carry out the reaction proposed.

1 Introduction

The recent measurement on the $\psi (3686)\rightarrow K^- \Lambda \bar{\Xi }^+$ decay by the BESIII experiment [1], where the $K^- \Lambda$ spectrum showed a peak around the $\Xi (1820)$ region with an unexpected width of about 73 MeV, spurred theoretical work reclaiming the existence of two $\Xi (1820)$ states. This large width contrasts with the PDG average of $24 \pm 5$ MeV [2], and the large discrepancy reopened the issue of the two $\Xi (1820)$ states predicted in Ref. [3] within the chiral unitary approach. This theoretical framework, applied to the present case, studied the interaction of pseudoscalar mesons with the $J^P = \frac{3}{2}^+$ baryons of the $\Delta$ decuplet and found many resonant states dynamically generated from that interaction, which matched existing states in the N, $\Delta$, $\Lambda$, $\Sigma$, $\Xi$ and $\Omega$ sectors with $J^P = \frac{3}{2}^-$ [3, 4]. One of the predictions of Ref. [3] was an $\Omega$ state originated from the $K^-\Xi (1530)$ and $\eta \Omega$ interaction, which was later identified with the recently found $\Omega (2012)$ state by the Belle collaboration [5]. A discussion followed on the nature of this state (see Ref. [6] for the latest update), which finally led the Belle collaboration to conclude that the experimental information supported the molecular nature of this resonance [7].

Coming back to the $\Xi (1820)$ states, a state at around 1820 MeV was found in Refs. [3, 4], another $\Xi$ state was found around 2100 MeV, and in Ref. [3] a wider pole was found in the complex plane in the 1800–1900 MeV region.

The issue of two poles associated to some known resonances has caught up after the two poles predicted for the $\Lambda (1405)$ [8, 9] were officially admitted in the PDG. Examples of this can be found in Ref. [10] with two states for the $K_1(1270)$, the two poles of the $D^*(2400)$ [11], and the two Y(4260) states of BESIII [12]. Recently a paper [13] shows that the phenomenon of duplication of states is tied to the structure of the Weinberg-Tomozawa interaction. A review on the issue of the two poles of some resonances can be seen in Ref. [14].

From this perspective, the issue of the two $\Xi (1820)$ poles was retaken in the work of Ref. [15], looking at the interaction of the $\Sigma ^* \bar{K}$, $\Xi ^* \pi$, $\Xi ^* \eta$ and $\Omega K$ coupled channels, and by means of it a good description of the BESIII data was obtained, with two poles at $1824-31 i$ MeV and $1875-130 i$ MeV. Work continued in Ref. [16] proposing the $\Omega _c \rightarrow \pi ^+ (\pi ^0, \eta ) \pi \Xi ^*$ reactions, by means of which an interference pattern between the two resonances was found in the $\pi (\eta ) \Xi ^*$ invariant mass distributions that could shed extra information leading to the identification of the two poles. In these reactions the two states interfered in such a way that a dip is seen around 1850 MeV, in a pattern that recalls the interference between the $f_0(500)$ and $f_0(980)$ in $I=0$ S-wave $\pi \pi$ scattering, leading to a dip in the $\pi \pi$ cross section around the $f_0(980)$ region [17].

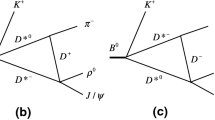
In the present work we propose a reaction, which is a continuation of the BESIII experiment with $\psi (3686)$ decay, but in a different channel. In Ref. [1] the $K^- \Lambda$ mass distribution in $\psi (3686) \rightarrow \bar{\Xi }^+ K^- \Lambda$ was investigated, with the $K^- \Lambda$ mass far below the 1820 MeV region, and mostly the narrow resonance at 1824 MeV showed up, with the wider resonance providing strength in the higher energy region. In the work of Ref. [16] the weight of the resonances is different and gives rise to an interference pattern.

2 Formalism

The reaction we propose is meant to show in a clear way the higher mass resonance. For this we propose to look at the $\bar{K} \Sigma ^*$ final state in the $\psi (3686) \rightarrow \bar{\Xi }^+ \bar{K}^0 \Sigma ^{*-}$ reaction, which has a threshold at about 1880 MeV, although we can attain smaller energies through the tail of the $\Sigma ^*(1385)$ resonance, where the strength of the $\Xi (1820)$ state at 1824 MeV has been drastically reduced, then giving more room to the wide $\Xi (1820)$ state at 1875 MeV. The reaction proposed is thus: $\psi (3686) \rightarrow \bar{\Xi }^+ \bar{K}^0 \Sigma ^{*-} \rightarrow \bar{\Xi }^+ \bar{K}^0 \pi ^- \Lambda$, where the $\bar{K}^0 \pi ^- \Lambda$ mass can go down around 1750 MeV, but the highest strength appears around 1950 MeV.

We recall that the two $\Xi (1820)$ states were obtained as poles of the T matrix from the interaction of the coupled channels, $\bar{K}^0 \Sigma ^{*-}$, $K^- \Sigma ^{*0}$, $\pi ^0 \Xi ^{*-}$, $\eta \Xi ^{*-}$, $\pi ^- \Xi ^{*0}$, $K^0 \Omega ^-$ (for the $\Xi (1820)^-$) [15], via the Bethe-Salpeter equation

$$\begin{aligned} T=[1-VG]^{-1} \, V, \end{aligned}$$

(1)

where

$$\begin{aligned} V_{ij}=-\dfrac{1}{4f^2} C_{ij} (k^0+k^{\prime \,0});\, f=1.28f_{\pi },\, f_{\pi }=93\, \textrm{MeV}, \end{aligned}$$

(2)

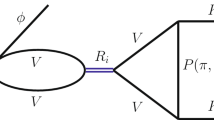
with $k^0$, $k^{\prime \,0}$ the energies of the initial and final pseudoscalar mesons in the meson-baryon rest frame, and $C_{ij}$ the coefficients given in Tables A.4.2 and A.4.3 of Ref. [3]. We reproduce Table A.4.2, suited to our states with total charge $Q=-1$ in Table 1. G in Eq. (1) is the diagonal meson-baryon loop function regularized with a cutoff $q_{\textrm{max}}$, as in Ref. [18]. We take $q_{\textrm{max}}=830 \, \textrm{MeV}$, same as in Ref. [15]. The mechanism for $\bar{K}^0 \Sigma ^{*-}$ production is depicted in Fig. 1.

Analytically, the transition matrix of Fig. 1 corresponds to

$$\begin{aligned} t=C \, \langle B^* \,| \, (\vec {S}^+ \times \vec {p}_{\bar{\Xi }^+}) \cdot \vec {\epsilon } \, | \, \Xi ^- \rangle \, t', \end{aligned}$$

(3)

where C is a global normalization constant, $B^*$ is the baryon of the $\frac{3}{2}^+$ multiplet, $\vec {\epsilon }$ the vector polarization of the $\psi (3686)$ and $\vec {p}_{\bar{\Xi }^+}$ the momentum of the $\bar{\Xi }^+$ in the rest frame of the $\psi (3686)$. The operator $\vec {S}^+$ is the spin transition operator from spin $\frac{1}{2}$ to $\frac{3}{2}$ with the property,

$$\begin{aligned} \sum _M S_i \,|\, M \rangle \,\langle M \,|\, S_j^{\dagger } = \frac{2}{3}\, \delta _{ij} - \frac{i}{3}\, \epsilon _{ijl}\, \sigma _l \, . \end{aligned}$$

(4)

The matrix $t'$ is then given by

$$\begin{aligned} t'=W_{ \bar{K}^0 \Sigma ^{*-}}+\sum _j W_j \, G_j \, t_{j,\bar{K}^0 \Sigma ^{*-} }\,, \end{aligned}$$

(5)

where $t_{j, \bar{K}^0 \Sigma ^{*-}}$ are matrix elements stemming from Eq. (1) ,¹, and $W_j$, with j corresponding to any of the six coupled channels, are the weights for the first step production $\psi (3686) \rightarrow \bar{\Xi }^+ M_j B^*_j$, which are calculated as follows: the $\psi (3686)$, being a $c\bar{c}$ state, is a singlet of SU(3) (for u, d, s quarks). As a consequence, up to a global normalization accounted for by the factor C in Eq. (3), these coefficients are the SU(3) Clebsch-Gordan coefficients of $8 \otimes 10 \rightarrow 8$, choosing for the $8 \otimes 10$ the $MB^*$ states of the coupled channels, and for the final 8 multiplet the state $\Xi ^-$. The coefficients $W_j$ are given in Table 2.

Table 1 The values of $C_{ij}$ coefficients of different channels for $Q=-1$

Fig. 1

Mechanisms for $\bar{K}^0 \Sigma ^{*-}$ production: a tree level; b rescattering of the meson-baryon coupled channels; c decay of $\Sigma ^{*-}$ into the stable $\pi ^- \Lambda$ particles

The coefficients $W_j$ already account for the isospin phase convention $|K^-\rangle =-|\frac{1}{2},-\frac{1}{2}\rangle$, $|\pi ^+\rangle =-|1,1\rangle$, consistent with the convention used in Refs. [3, 15] and the Clebsch–Gordan coefficients of Ref. [19] used here. The intrinsic phase of the SU(3) Clebsch–Gordan coefficients for the mesons can be obtained from $8 \otimes 8 \rightarrow 1$ demanding to get the symmetrical combination $K^+K^- + K^0\bar{K}^0 + \pi ^+\pi ^- + \pi ^0\pi ^0 + \pi ^-\pi ^+ + \eta \eta + K^-K^+$. The phase convention for the decuplet baryons is obtained in a similar way, demanding that $10 \otimes 10 \rightarrow 1$ gives a symmetrical combination of all states and their antiparticles, which results into the isospin multiplets ($\Delta ^{++}$, $\Delta ^{+}$, $\Delta ^{0}$, $\Delta ^{-}$), ($\Sigma ^{*+}$, $\Sigma ^{*0}$, $\Sigma ^{*-}$), ($\Xi ^0$, $\Xi ^-$), as assumed in Ref. [3], but the antiparticles of $\Delta ^{++}$, $\Delta ^{0}$, $\Sigma ^{*0}$, $\Xi ^{*0}$ carry a negative phase.

The mass distribution for the decay $\psi (3686) \rightarrow \bar{\Xi }^+ \bar{K}^0 \Sigma ^{*-}$ is given by

$$\begin{aligned} \frac{d\Gamma }{dM_{\textrm{inv}}(\bar{K}^0 \Sigma ^{*-})} & =\frac{1}{(2\pi )^3} \frac{1}{4M_{\psi }^2} p_{\bar{\Xi }^+} \tilde{p}_{\bar{K}^0}\nonumber \\ & \quad \bar{\sum } \sum |t|^2 2 M_{\bar{\Xi }^+}2 M_{\Sigma ^{*-}} \,, \end{aligned}$$

(6)

where the sum in $|t|^2$ stands for the sums over the spin components of $\Sigma ^{*-}$ and $\bar{\Xi }^+$ and the average for the spins of the $\psi (3686)$. We obtain

$$\begin{aligned} \bar{\sum } \sum |t|^2=\frac{8}{9}C^2 |t'|^2 p_{\bar{\Xi }^+}^2\,, \end{aligned}$$

(7)

Table 2 $W_j$ Clebsch–Gordan coefficients for the different coupled channels

where $\tilde{p}_{\bar{K}^0}$ is the momentum of the $\bar{K}^0$ in the $\bar{K}^0 \Sigma ^{*-}$ rest frame. We can gather some constant factors together and write

$$\begin{aligned} \frac{d\Gamma }{dM_{\textrm{inv}}(\bar{K}^0 \Sigma ^{*-})}= & \frac{1}{(2\pi )^3} \frac{1}{4M_{\psi }^2} p_{\bar{\Xi }^+} \tilde{p}_{\bar{K}^0} |t'|^2 \frac{C'}{M^2_{\psi }} p_{\bar{\Xi }^+}^2 \nonumber \\= & \frac{1}{(2\pi )^3} \frac{C'}{4M_{\psi }^4} p^3_{\bar{\Xi }^+} \tilde{p}_{\bar{K}^0} |t'|^2 , \end{aligned}$$

(8)

with $C'$ a dimensionless constant.

We can go one step forward to consider the mass distribution of the $\Sigma ^{*-}$ and the branching ratio for $\Sigma ^{*-} \rightarrow \pi ^- \Lambda$ decay and write

$$\begin{aligned} & \frac{d\Gamma }{dM_{\textrm{inv}}(\bar{K}^0 \Sigma ^{*-}) dM_{\textrm{inv}}(\Sigma ^{*-})}\nonumber \\ & \quad =-\frac{1}{\pi }\textrm{Im}\frac{\frac{\Gamma _{\pi ^-\Lambda }}{\Gamma _{\Sigma ^{*-}}}}{M_{\textrm{inv}}(\Sigma ^{*-})-M_{\Sigma ^{*-}}+i\frac{\Gamma _{\Sigma ^{*-}}\left( M_{\textrm{inv}}(\Sigma ^{*-})\right) }{2}}\nonumber \\ & \qquad \cdot \frac{1}{(2\pi )^3} \frac{C'}{4M_{\psi }^4} p^3_{\bar{\Xi }^+} \tilde{p}_{\bar{K}^0} |t'|^2, \end{aligned}$$

(9)

with $\tilde{p}_{\bar{K}^0}$ given now by

$$\begin{aligned} \tilde{p}_{\bar{K}^0}=\frac{\lambda ^{1/2}\left( M^2_{\textrm{inv}}(\bar{K}^0 \Sigma ^{*-}), m^2_{\bar{K}^0}, M^2_{\textrm{inv}}(\Sigma ^{*-})\right) }{2M_{\textrm{inv}}(\bar{K}^0 \Sigma ^{*-})} \, . \end{aligned}$$

(10)

In addition, we take the width of the $\Sigma ^{*-}$ energy dependent as

$$\begin{aligned} \Gamma _{\Sigma ^{*-}}\left( M_{\textrm{inv}}(\Sigma ^{*-})\right) =\Gamma _{\textrm{on}} \frac{M_{\Sigma ^{*-}}}{M_{\textrm{inv}}(\Sigma ^{*-})} \left( \frac{\tilde{p}_{\pi }}{\tilde{p}_{\pi ,\textrm{on}}} \right) ^3\,, \end{aligned}$$

(11)

with $\Gamma _{\textrm{on}}$ the width of $\Sigma ^{*-}$, $\tilde{p}_{\pi }$ the $\pi ^-$ momentum in the decay of a $\Sigma ^{*-}$ of invariant mass $M_{\textrm{inv}}(\Sigma ^{*-})$ into $\pi ^- \Lambda$ and $\tilde{p}_{\pi ,on}$ the same momentum for the nominal mass of the $\Sigma ^{*-}$. This formula assumes the energy dependence to be due totally to the $\Sigma ^{*-} \rightarrow \pi ^- \Lambda$ decay, a good approximation when $\Gamma _{\pi ^-\Lambda }/ \Gamma _{\Sigma ^{*-}}=87\%$.

Fig. 2

$d\Gamma /dM_{\textrm{inv}}(\bar{K}^0 \Sigma ^{*-})$ with different options.The thresholds of the different channels are shown by gray vertical lines. The red dashed line: results without the tree level. The green dot-dashed line: results with only the tree level. The blue dotted line: phase space (tree level normalized to the area of the full results). The black continuous line: full results

One explanation is needed here on the explicit consideration of the $\Sigma ^*$ width in the mass distribution. The calculations of the G functions and the t matrices via Eq. (1) are done in Ref. [3] and here assuming the particles stable, this is, ignoring their widths. It is possible to include the widths of the particles and this is done for instance in Ref. [20] (see Eq. (15) of that reference). This is important in cases where the only decay possible is through the decay of these intermediate particles. This is the case in the $T_{cc}$ (or $T_{bb}$ in Ref. [20]), considered as $D^0D^{*+},~D^+D^{*0}$, which only decays through the $DD^*\rightarrow DD\pi$ channel. However, in case of our coupled channels there is decay of the resonances to the $\pi ^0\Xi ^{*-}$ channel, which is about 200 MeV below the $\Xi (1875)$ mass. The width of the $\Xi (1875),~\Xi (1820)$ from the decay to this channel, is not much affected by the mass distribution of the $\Xi ^{*-}$ tied to its width. However, in the production of an explicit $MB^*$ state the consideration of the mass distribution of the $B^*$ states is important, because experimentally the $B^*$ state is reconstructed from its decay channels (in the present state $\Sigma ^*\rightarrow \pi \Lambda$) and to adjust to the experimental measurements one must proceed as we have done here.

In Fig. 2 we show the results that we obtain for $d\Gamma /dM_{\textrm{inv}} (\bar{K}^0 \Sigma ^{*-})$ by integrating Eq. (9) over the mass distribution of the $\Sigma ^{*-}$, $dM_{\textrm{inv}}(\Sigma ^{*-})$. We show there several curves. The upper curve results from ignoring the tree level (term with $W_{\bar{K}^0 \Sigma ^{*-}}$ in $t'$ of Eq. (5)). The vertical lines correspond to the threshold of the channels $K^- \Sigma ^{*0}$, $\bar{K}^0 \Sigma ^{*-}$, $\eta \Xi ^{*-}$, $K^0 \Omega ^-$. We can see that thanks to the mass distribution of the $\Sigma ^{*-}$ we can go below the nominal $K^- \Sigma ^{*0}$ threshold. This allows the contribution of the low mass $\Xi (1820)$, but suppressed by the phase space. This feature is important because then the bulk of the strength of the mass distribution corresponds to the higher mass $\Xi (1820)$ resonance. This is the main purpose of this reaction, which is showing evidence for the higher mass resonance, since in other reactions the lower mass $\Xi (1820)$ plays a dominant role. In Fig. 2 we also show the results obtained with only tree level, which is sizeable, and with the black continuous line we show the full results using all terms in $t'$. It is compared with the tree level normalized to the same area, which is what would correspond to the phase space for the reaction. What we observe is that the actual mass distribution differs appreciably from phase space. We can see that below 1880 MeV there is interference of the tree level and the two resonances, but the excess of strength above 1900 MeV is due to the wide $\Xi (1820)$ resonance of higher energy. In addition we also observe strength in the region of 2100–2200 MeV due to a resonance obtained in this region in Refs. [3, 4], which should also show up in this reaction. Yet, our main concern here is to show that the proposed reaction is particularly suited to show the effect of the second $\Xi (1820)$ resonance predicted theoretically.

3 Conclusions

We have not calculated the absolute value of the strength of the mass distribution. However, since in BESIII the $\psi (3686) \rightarrow \bar{\Xi }^+ K^- \Lambda$ reaction [1] was observed with good statistics, and, as shown in Ref. [15], this reaction involves the same mechanism of $\psi (3686) \rightarrow \bar{\Xi }^+ M B^*$ of Fig. 1, plus the extra step of $M B^* \rightarrow K^- \Lambda$, it looks clear that the strength of the mass distribution of the reaction proposed here should be even bigger than the one observed in the BESIII experiment. With this perspective, we strongly encourage the BESIII collaboration to perform this analysis that should show clear evidence of the existence of the two $\Xi (1820)$ resonances.