SPLHRNMTF: robust orthogonal non-negative matrix tri-factorization with self-paced learning and dual hypergraph regularization for predicting miRNA-disease associations

Abstract

MicroRNAs (miRNAs) have been demonstrated to be closely related to human diseases. Studying the potential associations between miRNAs and diseases contributes to our understanding of disease pathogenic mechanisms. As traditional biological experiments are costly and time-consuming, computational models can be considered as effective complementary tools. In this study, we propose a novel model of robust orthogonal non-negative matrix tri-factorization (NMTF) with self-paced learning and dual hypergraph regularization, named SPLHRNMTF, to predict miRNA-disease associations. More specifically, SPLHRNMTF first uses a non-linear fusion method to obtain miRNA and disease comprehensive similarity. Subsequently, the improved miRNA-disease association matrix is reformulated based on weighted k-nearest neighbor profiles to correct false-negative associations. In addition, we utilize $L_{2,1}$ norm to replace Frobenius norm to calculate residual error, alleviating the impact of noise and outliers on prediction performance. Then, we integrate self-paced learning into NMTF to alleviate the model from falling into bad local optimal solutions by gradually including samples from easy to complex. Finally, hypergraph regularization is introduced to capture high-order complex relations from hypergraphs related to miRNAs and diseases. In 5-fold cross-validation five times experiments, SPLHRNMTF obtains higher average AUC values than other baseline models. Moreover, the case studies on breast neoplasms and lung neoplasms further demonstrate the accuracy of SPLHRNMTF. Meanwhile, the potential associations discovered are of biological significance.

Introduction

MicroRNAs (miRNAs) are a class of non-coding RNA molecules (about 22 nucleotides in length) encoded by endogenous genes [1]. MiRNAs are involved in post-transcriptional gene expression regulation and have been demonstrated to play an important role in many human life processes, including cell proliferation [2], cell growth [3], tumor invasion [4], immune response [5], and so on. In addition, more and more studies have shown that miRNA dysregulation often leads to the occurrence of various human diseases. For example, miR-145 inhibits the cell proliferation of human lung adenocarcinoma by targeting EGFR and NUDT1 [6]. The levels of miR-105 in blood and tumors are related to ZO-1 expression and metastatic progression in breast cancer [7]. The expression of miR-34a is excessive in specific brain regions of Alzheimer’s disease patients as well as in the 3xTg-AD mouse model [8]. Therefore, identifying disease-related miRNAs contributes to revealing the pathogenesis of diseases and discovering potential biomarkers at the miRNA level. Since the identification of miRNA-disease associations using traditional wet experiments is time-consuming and expensive, more and more computational methods have been proposed as efficient complementary tools to infer potential associations between miRNAs and diseases.

Over the past few decades, many computational methods have been proposed based on the assumption that miRNAs with similar functions are associated with phenotypically similar diseases. Chen et al. [9] proposed the RWRMDA method, which predicts potential miRNA-disease associations by performing random walk with restart on the miRNA-miRNA functional similarity network. However, this method is not suitable for miRNAs with no association, which limits its performance improvement. Xuan et al. [10] designed a new prediction method called HDMP, which combines the distribution of disease-related miRNAs in k neighborhoods with miRNA function similarity to predict potential associations between miRNAs and diseases. However, HDMP only considers local network similarity, resulting in suboptimal prediction performance. Xuan et al. [11] further developed a new prediction method to infer miRNA-disease associations based on random walk on miRNA functional similarity network. Chen et al. [12] designed the within and between score for miRNA-disease association prediction (WBSMDA) method to identify disease-related miRNAs by integrating various biological similarity networks. You et al. [13] developed a path-based PBMDA method and used a depth-first search algorithm to predict miRNA-disease associations. Chen et al. [14] presented a bipartite heterogeneous network link prediction method based on co-neighbor to infer the associations between miRNAs and diseases. Li et al. [15] developed the NPRWR method to predict miRNA-disease associations by using dual random walk with restart and network projection technology. Chen et al. [16] presented a deep belief network model called DBNMDA based on Restricted Boltzmann Machines for miRNA-disease association prediction. Ha et al. [17] proposed a novel computational model of metric learning named MLMD for inferring miRNA-disease associations. Based on deep neural networks, Ha et al. [18] further designed a new node2vec-based neural collaborative filtering framework named NCMD to predict the associations between miRNAs and diseases. Based on graph convolutional networks, Li et al. [19] proposed a neural inductive matrix completion method, called NIMCGCN, to infer miRNA-disease associations. Tang et al. [20] also employed graph convolutional networks and multichannel attention mechanism to extract and enhance latent representations of miRNAs and diseases. They predicted potential associations based on the reconstructed miRNA-disease association matrix. Recently, Peng et al. [21] used hypergraph convolutional networks and a variational auto-encoder to develop a MHCLMDA model with contrastive learning for predicting the associations between miRNAs and diseases.

In recent years, many studies have shown that matrix factorization methods with feature extraction and reconstruction capabilities are also considered as promising computational methods. For example, Xiao et al. [22] proposed a non-negative matrix factorization method with graph Laplacian regularization constraint, named GRNMF, to predict potential miRNA-disease associations. Chen et al. [23] designed an IMCMDA method of inductive matrix completion, which constrains integrated miRNA similarity and disease similarity into matrix factorization to predict the associations between miRNAs and diseases. Chen et al. [24] proposed a novel matrix decomposition and heterogeneous graph inference (MDHGI) method for identifying miRNA-disease associations. MDHGI integrates the association probability derived from matrix decomposition through sparse learning method and biological similarity information into a heterogeneous network. Dissez et al. [25] developed a drug repositioning method based on non-negative matrix tri-factorization (NMTF) with graph Laplacian regularization, which utilizes NMTF to simultaneously decompose multiple binary association matrices between indications and drugs, drugs and proteins, proteins and pathways, and drugs and diseases. Jamali et al. [26] presented an NMTF-DTI method of non-negative matrix tri-factorization with multiple kernel fusion for drug-target interaction prediction. This method makes use of graph Laplacian regularization to preserve the local geometric structure of the biological similarity network in low-dimensional space. Zheng et al. [27] proposed the NMFMC method based on non-negative matrix factorization, which decomposes the association matrix into a known part and an unknown part for miRNA-disease association prediction. Ha et al. [28] designed a new method based on probabilistic matrix factorization (PMF), called IMIPMF, to identify miRNA-disease associations. Subsequently, Ha [29] also developed a new computational framework (MDMF) using matrix factorization with disease similarity constraints to identify potential miRNA-disease associations. Through further considering miRNA and disease similarities and integrating them into matrix factorization, Ha [30] designed a simple and effective computational framework, called SMAP, to predict miRNA-disease associations. Recently, Ha [31] also proposed a novel matrix decomposition method named EMFLDA, which applies lncRNA expression profiles to identify the associations between lncRNAs and diseases.

Although the above matrix decomposition-based methods have achieved excellent performance in potential association prediction, most methods still have some limitations. First, it is challenging to reasonably integrate multi-view similarity of miRNAs (or diseases) into a comprehensive similarity network. Most methods employ a linear strategy based on one similarity to integrate the similarity of different views. More specifically, multiple similarities are integrated by using one similarity to fill the missing parts of another similarity or by averaging different types of similarity. However, simple linear fusion can not effectively learn more complex integrated information, thus limiting the improvement of prediction performance. Second, limited by the current level of science and technology, miRNA-disease association data usually have “association, but we don’t know yet” (i.e., false-negative samples) associations in a large number of negative samples, which significantly affects the model prediction performance. Third, most matrix decomposition-based methods utilize Frobenius norm to calculate residual error, which may cause the prediction performance to be affected by noise and outliers. Fourth, because methods based on matrix decomposition usually have non-convexity, these methods can easily obtain a bad local optimal solution. Finally, the pairwise relations within homogeneous graphs are usually considered by most methods while ignoring high-order complex relations present in heterogeneous graphs.

To alleviate the limitations mentioned above, we propose a novel computational model of $\textbf{S}$elf-$\textbf{P}$aced $\textbf{L}$earning and $\textbf{H}$ypergraph regularization into $\textbf{R}$obust orthogonal $\textbf{N}$on-negative $\textbf{M}$atrix $\textbf{T}$ri-$\textbf{F}$actorization (SPLHRNMTF) to identify the associations between miRNAs and diseases, which preserves double orthogonality conditions and dual hypergraph regularization. Compared with simple linear fusion, we first propose a non-linear fusion method to integrate different types of miRNA or disease similarity network into a comprehensive similarity network for miRNAs or diseases. Then, the weighted k-nearest neighbor profiles are used to obtain an improved miRNA-disease association matrix, thereby effectively correcting false-negative samples. Next, we separately introduce $L_{2,1}$ norm and hypergraph regularization into NMTF to effectively alleviate the influence of noise and outliers on prediction performance, and capture the high-order complex relations from hypergraphs related to miRNAs and diseases. Finally, in order to cope with the fact that NMTF with non-convexity easily obtains a bad local solution, we integrate self-paced learning into NMTF to effectively alleviate the problem of falling into such solution by gradually including samples from easy to complex. To solve the optimization problem of SPLHRNMTF, we propose an alternating optimization algorithm, whose convergence is theoretically guaranteed. The 5-fold cross-validation is performed five times to evaluate the proposed SPLHRNMTF model. Specifically, SPLHRNMTF can obtain better prediction performance than other matrix factorization-based models, even superior to some graph and hypergraph convolutional network-based models. Furthermore, the results of ablation experiment indicate that each module in the SPLHRNMTF and preprocessing step are effective. In addition, we conduct case studies on breast neoplasms and lung neoplasms, 48 and 46 of top 50 are confirmed by experimental reports. Moreover, unconfirmed potential associations have biological significance. In summary, SPLHRNMTF model demonstrates efficacy and accuracy in predicting associations between miRNAs and diseases.

Materials

Human miRNA-disease association datasets

The Human MiRNA Disease Database (HMDD) is a database containing experimentally verified human miRNA-disease associations [32, 33]. In this work, HMDD v2.0 and HMDD v3.2 were used as benchmark databases to construct association matrices, where these two databases can be downloaded from http://www.cuilab.cn/hmdd. To more extensively investigate the generalization performance of the model, we also obtained a dataset named MDAv3.2_data1 based on the study of Ning et al. [34]. In addition, we further preprocessed HMDD v2.0 and HMDD v3.2 databases to obtain MDAv2.0_data and MDAv3.2_data2 datasets, respectively. To be more specific, we removed these miRNAs that had no sequence in the miRBase database [35] and were not found in the MISIM 2.0 database [36]. Meanwhile, we deleted these diseases that were not found and whose category was not “C” in Medical Subject Headings (MeSH) tree structure. Finally, the first dataset MDAv2.0_data contains 5896 experimentally verified human miRNA-disease associations between 548 miRNAs and 320 diseases. The second dataset MDAv3.2_data1 involves 853 miRNAs, 591 diseases and 12446 experimentally verified associations. The third dataset MDAv3.2_data2 includes 9676 experimentally confirmed associations between 812 miRNAs and 469 diseases.

Problem formulation

Given a set of miRNAs $\mathcal {M} = \{m_1,m_2,\cdots ,m_{m}\}$ and a set of diseases $\mathcal {D} = \{d_1,d_2,\cdots ,d_{n}\}$, we can construct the miRNA-disease associations into a matrix $X\in \{0,1\}^{m\times n}$, where m and n represent the size of the set of miRNAs and diseases, respectively. Obviously, an entry $x_{ij}$ of the matrix X is set to 1 if a miRNA is associated with a disease. Otherwise, the unknown or unobserved entries are set to 0. In this work, we transformed the identification of miRNA-disease associations into a matrix completion task. However, the matrix X is extremely sparse with a large number of unknown and unobserved entries, which is a challenge to efficiently perform matrix completion. Therefore, miRNA similarity information and disease similarity information were considered as auxiliary information to alleviate the challenge.

Disease semantic similarity

The disease semantic similarity was calculated by using directed acyclic graph (DAG) with disease hierarchical relationships obtained from the MeSH database (https://www.nlm.nih.gov/mesh/). The DAG of a disease $d_i$ can be defined as $DAG(d_i) = (d_i,T(d_i),E(d_i))$, where $T(d_i)$ denotes the set of $d_i$ and its ancestor nodes, $E(d_i)$ represents the set of edges with regard to the direct links between parent nodes and child nodes. Then, the first semantic contribution of diseases $d_k$ to $d_i$ can be defined as follows:

$$\begin{aligned} SC^1(d_i,d_k) = \left\{ \begin{array}{ll} 1, & \text {if } d_k = d_i \\ max\{\Delta \times SC^1\left(d_i,d_k^{'}\right)| \\ d_k^{'}\in children\;of\;d_k\}, & \text {if } d_k \ne d_i. \end{array}\right. \end{aligned}$$

(1)

where $\Delta$ is a semantic contribution decay factor, and we set it to 0.5 according to previous work [37]. Then, the semantic value of disease $d_i$ can be calculated as below:

$$\begin{aligned} SV^1\left(d_i\right) = \sum \limits _{d_k\in T\left(d_i\right)} SC^1\left(d_i,d_k\right) \end{aligned}$$

(2)

On the basis of the assumption that if the intersection of a disease pair in the DAG is larger, their semantic similarity value will be greater. Then, the first disease semantic similarity $SD^1(d_i,d_j)$ between diseases $d_i$ and $d_j$ can be defined as follows:

$$\begin{aligned} SD^1\left(d_i,d_j\right) = \frac{\sum _{d_t\in T\left(d_i\right)\cap T\left(d_j\right)}\left(SC^1\left(d_i,d_t\right)+SC^1\left(d_j,d_t\right)\right)}{SV^1\left(d_i\right)+SV^1\left(d_j\right)} \end{aligned}$$

(3)

However, $SD^1$ fails to consider the significance of semantic contributions of different diseases. It overlooks the fact that diseases appearing in fewer DAG may be more specific, and thus should have higher semantic contribution values. According to previous work [23], the second semantic contribution of disease $d_k$ to $d_i$ can be presented as below:

$$\begin{aligned} SC^2\left(d_i,d_k\right) = -\log \left(\frac{the\; number\; of\; DAGs\; including\; d_k}{the\; number\; of\; disease}\right) \end{aligned}$$

(4)

Similarly, we can define the second semantic value $SV^2(d_i)$ of disease $d_i$ and the second disease semantic similarity $SD^2(d_i,d_j)$ between diseases $d_i$ and $d_j$ as follows:

$$\begin{aligned} SV^2\left(d_i\right) = \sum \limits _{d_k\in T\left(d_i\right)} SC^2\left(d_i,d_k\right) \end{aligned}$$

(5)

$$\begin{aligned} SD^2(d_i,d_j) = \frac{\sum _{d_t\in T(d_i)\cap T(d_j)}(SC^2(d_i,d_t) + SC^2(d_j,d_t))}{SV^2(d_i) + SV^2(d_j)} \end{aligned}$$

(6)

Based on previous study [38], we integrated these two kinds of disease semantic similarity $SD^1(d_i,d_j)$ and $SD^2(d_i, d_j)$ to obtain a more reasonable disease semantic similarity. Finally, the final disease semantic similarity $SD_1(d_i,d_j)$ between diseases $d_i$ and $d_j$ can be presented as below:

$$\begin{aligned} SD_1\left(d_i,d_j\right) = \frac{SD^1\left(d_i,d_j\right) + SD^2\left(d_i,d_j\right)}{2} \end{aligned}$$

(7)

MiRNA functional similarity

On the basis of the assumption that functionally similar miRNAs tend to be associated with phenotypically similar diseases and vice versa, we can calculate miRNA functional similarity scores [37]. In this study, we obtained miRNA functional similarity from the MISIM 2.0 database (http://www.lirmed.com/misim/). Then, we constructed a matrix $SM_1$ by using these data, where $SM_1(m_i,m_j)$ denotes the functional similarity score between miRNA $m_i$ and $m_j$.

MiRNA sequence similarity

According to previous work [39], we obtained the miRNA sequences containing “AUCG” from the miRBase database (https://www.mirbase.org/). Based on the sequence information, we utilized pairwise sequence alignment function “pairwiseAlignment” in R package Biostrings to calculate miRNA sequence similarity score. To be more specific, the gap opening penalty is set to 5, the gap extension penalty is set to 2, the match score is set to 1 and the mismatch score is set to -1 in this function. Finally, the miRNA sequence similarity matrix $SM_2$ can be obtained by min-max normalization as follows:

$$\begin{aligned} SM_2(m_i,m_j) = \frac{Score(m_i,m_j) - Score_{min}}{Score_{max} - Score_{min}} \end{aligned}$$

(8)

where $Score_{min}$ and $Score_{max}$ denote the minimum and maximum similarity score of all miRNA pairs, respectively. $Score(m_i,m_j)$ indicates that sequence similarity score can be calculated by using function “pairwiseAlignment”.

Gaussian interaction profile kernel similarity for miRNAs and diseases

On the basis of assumption that miRNAs with similar functions are more likely to be associated with similar diseases, we can calculate the Gaussian interaction profile kernel similarity through the known miRNA-disease association network [40]. For a given miRNA $m_i$, its interaction profile $IP(m_i)$ was extracted from the known miRNA-disease association matrix. Then, the Gaussian interaction profile kernel similarity for miRNAs $SM_3(m_i,m_j)$ between miRNAs $m_i$ and $m_j$ can be presented as follows:

$$\begin{aligned} SM_3(m_i,m_j) = \exp (-\gamma _m \Vert IP(m_i) - IP(m_j)\Vert ^2) \end{aligned}$$

(9)

where $\gamma _m$ controls the kernel bandwidth, which can be calculated by using the following equation:

$$\begin{aligned} \gamma _m = \frac{\gamma _m^{'}}{\frac{1}{m} \sum _{i=1}^{m} \Vert IP(m_i)\Vert ^2} \end{aligned}$$

(10)

where m represents the number of miRNAs and $\gamma _m^{'}$ is set to 1 based on previous study [40]. Similarly, the Gaussian interaction profile kernel similarity for diseases $SD_2(d_i,d_j)$ between diseases $d_i$ and $d_j$ can be obtained based on the following two equations:

$$\begin{aligned} SD_2(d_i,d_j) = \exp \left(-\gamma _d \Vert IP\left(d_i\right) - IP\left(d_j\right)\Vert ^2\right) \end{aligned}$$

(11)

$$\begin{aligned} \gamma _d = \frac{\gamma _d^{'}}{\frac{1}{n} \sum _{i=1}^{n}\Vert IP\left(d_i\right)\Vert ^2} \end{aligned}$$

(12)

where $IP(d_i)$ is a binary vector extracted from the known miRNA-disease association matrix, n represents the number of diseases and $\gamma _d^{'}$ is also set to 1.

Comprehensive similarity for miRNAs and diseases

Based on previous works [12, 41], integrating different similarity information can not only avoid being too one-sided, but also obtain more accurate and reasonable integrated similarity for miRNAs and diseases. However, the simple linear similarity combination method is challenging to apply for the fusion of multiple biological similarity information. Inspired by previous study [42], we utilized a non-linear fusion method to integrate multiple similarity networks into a single similarity network for miRNAs and diseases, respectively. Next, we took the integration of multiple miRNA similarity information as an example to introduce the construction of comprehensive miRNA similarity.

In the first step, we performed a better normalization to calculate normalized weight matrix $SM_{v}^{'}$ for the v-th type of similarity network as follows:

$$\begin{aligned} SM_{v}^{'}\left(m_i,m_j\right) = \left\{ \begin{array}{ll} \frac{SM_{v}\left(m_i,m_j\right)}{2\sum _{k\ne i}SM_{v}\left(m_i,m_k\right)}, & j\ne i \\ \frac{1}{2}, & j = i \end{array} \right. \end{aligned}$$

(13)

In the second step, we employed k-nearest neighbor (KNN) to measure the local relationship of each similarity network. The detailed calculation process was as below:

$$\begin{aligned} K_{v}\left(m_i,m_j\right) = \left\{ \begin{array}{ll} \frac{SM_{v}\left(m_i,m_j\right)}{\sum _{k\in N_{i}}SM_{v}\left(m_i,m_k\right)}, & j\in N_{i} \\ 0, & otherwise \end{array} \right. \end{aligned}$$

(14)

where $N_i$ is a set of k nearest neighbors for the node $m_i$ of miRNA similarity networks. $K_{v}$ denotes the local affinity kernel of the v-th data type. In this paper, according to previous study [42], we set the neighbor parameter in KNN method approximately as |N|/10, where |N| is the total number of nodes in the similarity network.

In the third step, we iteratively updated the similarity matrix for each type of data using the following procedure:

$$\begin{aligned} SM_{v}^{'\left(t+1\right)} = K_{v}\times \frac{\sum _{k\ne v}SM_{k}^{'\left(t\right)}}{M-1}\times \left(K_{v}\right)^T \end{aligned}$$

(15)

where $v = \{1,2,\cdots ,M\}$ and M denotes the total number of data types. $SM_{v}^{'(t+1)}$ is the status matrix of the v-th data type after t iterations.

In this work, the iteration stops when Eq. (15) reaches a convergence criterion, defined as a relative change $\frac{\Vert SM_{v}^{'(t+1)} - SM_{v}^{'(t)}\Vert }{\Vert SM_{v}^{'(t)}\Vert }$ being less than $10^{-5}$. After iterative update, the ultimate similarity matrix SM could be obtained as follows:

$$\begin{aligned} SM = \frac{SM_{1}^{'\left(t\right)}+SM_{2}^{'\left(t\right)}+\cdots +SM_{M}^{'\left(t\right)}}{M} \end{aligned}$$

(16)

According to the above update rules, the obtained similarity matrix is not a symmetric matrix, so we further calculated $SM = \frac{SM+SM^T}{2}$ as the miRNA comprehensive similarity matrix. Similarly, we can get the disease comprehensive similarity matrix SD based on the same calculation rules of miRNA.

Methods

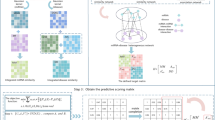
In this paper, we proposed the SPLHRNMTF model that integrates self-paced learning and hypergraph regularization into NMTF using $L_{2,1}$ norm for predicting the associations between miRNAs and diseases. Figure 1 illustrates the whole workflow of SPLHRNMTF.

Fig. 1

The workflow of our proposed SPLHRNMTF model for predicting potential miRNA-disease associations. Note that GIP kernel similarity denotes Gaussian interaction profile kernel similarity

Self-paced learning

In recent years, self-paced learning (SPL) has emerged as a successful approach in mitigating the problem of falling into local optimal solutions, owing to its training strategy of gradually selecting samples from simple to complex [43, 44]. Given a training dataset $\mathcal {D} = \{x_i,y_i\}_{i=1}^{N}$, the objective function of SPL was as follows:

$$\begin{aligned} \min _{\varvec{\theta },\varvec{w}}\sum \limits _{i=1}^{N}w_{i} L \left(f\left(x_i,\varvec{\theta }\right),y_i\right) + g\left(\eta ,\varvec{w}\right) \end{aligned}$$

(17)

where $L (\cdot ,\cdot )$ denotes the training error calculated by the loss function, $\varvec{\theta }$ is the model parameter of the loss function, $\varvec{w} = [w_1,w_2,\cdots ,w_N]^{T}$ represents a weight variable, and $\eta$ is the learning pace parameter.

To better reflect the potential importance of samples and realize the advantages of SPL, a novel SPL regularization term was utilized [45]. The regularization term $g(\eta ,\varvec{w})$ was defined as follows:

$$\begin{aligned} g\left(\eta ,\varvec{w}\right) = - \sum \limits _{i=1}^{N}\zeta \ln \left(w_i + \zeta /\eta \right) \end{aligned}$$

(18)

Based on previous work [45], the optimal $\varvec{w}^{*}$ can be calculated as follows:

$$\begin{aligned} w_i^{*} = \left\{ \begin{array}{ll} 1, & \text {if } l _i\le \zeta \eta /\left(\zeta + \eta \right)\\ 0, & \text {if } l _i \ge \eta \\ \zeta /l _i - \zeta /\eta , & \text {otherwise}. \end{array}\right. \end{aligned}$$

(19)

where $\zeta$ is set to $0.5\times \eta$ for simplicity in our experiments. With the increase of $\eta$, more and more samples will be selected until all samples are chosen.

Hypergraph learning

Recent studies on manifold learning theory and spectral graph theory shows that when original data points were mapped from high-dimensional space to low-dimensional space, k-nearest neighbor graphs can effectively preserve the potential geometric structure of high-dimensional data in low-dimensional space [46]. However, the classic graph structure only considers the pairwise relationships of data points in the neighbor graph, while ignoring high-order relationships. To alleviate this problem, hypergraph, as a generalization of graph, has been proposed for data representation [47, 48]. Figure 2 is an example that shows the difference between classic graph and hypergraph.

Fig. 2

The difference between classic graph and hypergraph. a A classic graph. b A hypergraph and its incidence matrix

Given $G = (V,E,W)$ is a weighted hypergraph, which contains a finite hyperedge set $E = \{e_i|i = 1,2,\cdots ,\overline{m}\}$ and a finite vertex set $V = \{v_j|j = 1,2,\cdots ,\overline{n}\}$. For the construction of hyperedge, we utilized the KNN method to learn hypergraphs for miRNAs and diseases, respectively. For example, we concatenated miRNA-disease associations and miRNA comprehensive similarity as features of node miRNAs. Based on the concatenated features, we calculated the nearest k neighbors of each miRNA based on Euclidean distance, thereby determining a subset (i.e., hyperedge) from the k neighbors. In addition, each hyperedge e is a subset of V. W is a diagonal matrix that indicates the weight of hyperedges. The incidence matrix H of G can be defined as below:

$$\begin{aligned} H(v,e) = \left\{ \begin{array}{ll} 1, & \text {if } v\in e \\ 0, & \text {if } v\notin e. \end{array}\right. \end{aligned}$$

(20)

In this work, we initialized the weight value of each hyperedge in the hypergraph by constructing an affinity matrix. Specifically, the affinity matrix A of hypergraph was calculated as follows:

$$\begin{aligned} A_{ij} = \exp \left(-\frac{\Vert v_i - v_j\Vert ^2}{\sigma ^2}\right) \end{aligned}$$

(21)

where $\sigma$ is standard deviation distance among all vertices. Then, the initial weight of each hyperedge can be defined as follows:

$$\begin{aligned} W_i = \sum \limits _{v_j \in e_i} A_{ij} \end{aligned}$$

(22)

The degree of each vertex $v\in V$ in incidence matrix H was computed as follows:

$$\begin{aligned} d_V(v) = \sum \limits _{e\in E} w(e)H(v,e) \end{aligned}$$

(23)

The degree of each hyperedge $e\in E$ was defined as the number of vertices included in E. Specifically, $d_E(e)$ can be denoted as:

$$\begin{aligned} d_E(e) = \sum \limits _{v\in V} H(v,e) \end{aligned}$$

(24)

Let F denotes the low-dimensional embedding representation of miRNAs (or diseases), we can obtain the following hypergraph structure loss function:

$$\begin{aligned} \Omega & = \frac{1}{2}\sum \limits _{e\in E}\sum \limits _{(v_i,v_j)\in V}\frac{w(e)H\left(v_i,e\right)H\left(v_j,e\right)}{d_E\left(e\right)}\Vert F\left(v_i\right) - F\left(v_j\right)\Vert _F^2 \nonumber \\ & = Tr\left(F^T\left(D_V - HWD_E^{-1}H^T\right)F\right) \nonumber \\ & = Tr\left(F^TL_{hyper}F\right) \end{aligned}$$

(25)

where $D_V$ denotes a diagonal matrix where its elements related to the degree of vertices. $D_E$ can be defined as a diagonal matrix whose elements correspond to the degree of hyperedges. $L_{hyper} = D_V - S$, and $S = HWD_E^{-1}H^T$.

Improved miRNA-disease association

The values of interaction profiles without known association are all zeros, but they could be potential true associations (i.e., false-negative samples). This may result in an unsatisfactory prediction performance. To alleviate the above problems, we performed preprocessing step to calculate new interaction profiles by using weighted k-nearest neighbor (WKNN) profiles.

For each miRNA $m_p$, we conducted a sorting of all other miRNAs in descending order, considering their similarity with $m_p$. Subsequently, the similarity of $m_p$ with its K nearest known miRNAs was computed, ensuring that each of miRNAs has at least one known association. Finally, its similarity information was combined with the corresponding K interaction profiles, resulting in a new interaction profile as follows:

$$\begin{aligned} X_m(m_p) = \frac{1}{E_m}\sum \limits _{i=1}^{K}\theta ^{i-1}\times SM(m_i,m_p)\times X(m_i) \end{aligned}$$

(26)

where $E_m = \sum _{1\le i\le K}SM(m_i,m_p)$ and $\theta \in [0,1]$ are the normalization term and decay term, respectively.

Similar with miRNA, the new interaction profiles for each disease $d_q$ can be calculated as below:

$$\begin{aligned} X_d(d_q) = \frac{1}{E_d}\sum \limits _{j=1}^{K}\theta ^{j-1}\times SD(d_j,d_q)\times X(d_j) \end{aligned}$$

(27)

where $E_d = \sum _{1\le j\le K}SD(d_j,d_q)$.

Finally, we obtained the new interaction profiles of miRNAs and diseases by using the average of $X_m$ and $X_d$. The miRNA-disease adjacency matrix is updated as follows:

$$\begin{aligned} X = \max (X, X_{md}) \end{aligned}$$

(28)

where $X_{md} = (X_m + X_d)/2$.

SPLHRNMTF

Based on previous works [49, 50], two biological entities in the same cluster are more likely to have similar characteristics, so the sparse similarity matrix constructed based on k-nearest neighbors has been effectively applied. The weighted matrix $W^m$ can be calculated according to miRNA comprehensive similarity matrix SM as follows:

$$\begin{aligned} W_{ij}^m = \left\{ \begin{array}{ll} 1, & i\in N_{k}(m_j) \& j\in N_{k}(m_i) \\ 0, & i\notin N_{k}(m_j) \& j\notin N_{k}(m_i) \\ 0.5, & otherwise \end{array} \right. \end{aligned}$$

(29)

where $N_k(m_i)$ and $N_k(m_j)$ denote the sets of k-nearest neighbors of miRNA $m_i$ and miRNA $m_j$, respectively. Then, the graph matrix $SM^{*}$ for miRNAs is presented as follows:

$$\begin{aligned} \forall \ i,j \quad SM_{ij}^{*} = SM_{ij} W_{ij}^{m} \end{aligned}$$

(30)

Similarly, we used the same method to calculate graph matrix $SD^*$ for disease. In this paper, we utilized final miRNA similarity network $SM^*$, disease similarity network $SD^*$ and known miRNA-disease association network to construct a miRNA-disease heterogeneous network. Then, the KNN method was used to learn hypergraphs related to miRNAs and diseases based on the constructed heterogeneous network. Finally, according to learned hypergraphs, we calculated miRNA hypergraph Laplacian matrix $L_{hm}^{*}$ and disease hypergraph Laplacian matrix $L_{hd}^{*}$, respectively.

Non-negative matrix tri-factorization (NMTF) has been widely applied for data representation in various fields [51, 52]. The purpose of NMTF is to obtain three low-dimensional non-negative factor matrices for low-dimensional approximation of the original matrix. However, the bad local optimal solutions are often encountered when solving non-convex optimized NMTF. To effectively alleviate the model from falling into a bad local optimal solution, we combined self-paced learning with NMTF. Moreover, we introduced hypergraph regularization to better preserve the high-order relations of heterogeneous network in low-dimensional space. In addition, $L_{2,1}$ norm was utilized to replace Frobenius norm for calculating residual error, thus reducing the impact of noise and outliers on prediction performance. Finally, the objective function was defined as:

$$\begin{aligned} \underset{U,S,V,\varvec{w}}{\min } & \Vert diag(\varvec{w})(X - USV^T)\Vert _{2,1} + \lambda \Vert S\Vert _F^2 \nonumber \\ & + \alpha Tr(U^TL_{hm}^{*}U)+ \beta Tr(V^TL_{hd}^{*}V) + g(\eta ,\varvec{w}) \nonumber \\ & s.t.\ U\ge 0, S\ge 0, V\ge 0, U^TU=I, V^TV=I \end{aligned}$$

(31)

where $\alpha$ and $\beta$ control the importance of hypergraph Laplacian regularization term. $\odot$ represents the Hadamard product. Meanwhile, we imposed orthogonal constraints on the factor matrices U and V to enhance the uniqueness and stability of the decomposition results. To prevent overfitting, $L_2$ norm was utilized to constrain factor matrix S, and $\lambda$ is regularization coefficient.

For ease of calculation, Eq. (31) can be reformulated by optimizing the following problem:

$$\begin{aligned} \underset{U,S,V,\varvec{w}}{\min } & \sum \limits _{i=1}^{n}d_i\Vert (X - USV^T)_i\Vert _2^2 + \lambda \Vert S\Vert _F^2 \nonumber \\ & + \alpha Tr(U^TL_{hm}^{*}U)+ \beta Tr(V^TL_{hd}^{*}V) + g(\eta ,\varvec{w}) \nonumber \\ & s.t.\ U\ge 0, S\ge 0, V\ge 0, U^TU=I, V^TV=I \end{aligned}$$

(32)

where

$$\begin{aligned} d_i = \frac{w_i}{2\Vert (X - USV^T)_i\Vert _2} \end{aligned}$$

(33)

With simple algebra, Eq. (32) can be written as follows:

$$\begin{aligned} \underset{U,S,V,\varvec{w}}{\min } & Tr((X-USV^T)D(X-USV^T)^T) + \lambda Tr(SS^T) \nonumber \\ & + \alpha Tr(U^TL_{hm}^{*}U)+ \beta Tr(V^TL_{hd}^{*}V) + g(\eta ,\varvec{w}) \nonumber \\ & s.t.\ U\ge 0, S\ge 0, V\ge 0, U^TU=I, V^TV=I \end{aligned}$$

(34)

where D is a diagonal matrix and $D_{ii} = d_i$.

In this work, the alternate iterative updating algorithm was proposed to solve the optimization problem of SPLHRNMTF. More specifically, the objective function alternately optimizes one variable while fixing other variables.

Updating the weight variable $\varvec{w}$

When U, S and V were fixed, optimizing the subproblem involving $\varvec{w}$ was as follows:

$$\begin{aligned} \underset{\varvec{w}}{\min } \sum \limits _{i=1}^{n}w_il _i + g(\eta ,\varvec{w}) \end{aligned}$$

(35)

where $l_i = \Vert (X - USV^T)_i\Vert _2$, which represents the reconstruction error of the i-th sample.

On the basis of previous work [45], a novel soft weighting SPL regularization term was utilized as follows:

$$\begin{aligned} g(\eta ,\varvec{w}) = - \sum \limits _{i=1}^{n}\zeta \ln (w_i + \zeta /\eta ) \end{aligned}$$

(36)

Clearly, the optimal $\varvec{w}^*$ can be easily calculated by

$$\begin{aligned} w_i^{*} = \left\{ \begin{array}{ll} 1, & \text {if } l _i\le \zeta \eta /(\zeta + \eta )\\ 0, & \text {if } l _i \ge \eta \\ \zeta /l _i - \zeta /\eta , & \text {otherwise}. \end{array}\right. \end{aligned}$$

(37)

Updating the factor matrix U

According to the strategy of alternate updating, when the other variables were fixed, the terms in the objective function involving U can be reformulated as follows:

$$\begin{aligned} \underset{U}{\min }\ & Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) +\alpha Tr(U^TL_{hm}^{*}U) \nonumber \\ & s.t. \ U\ge 0, U^TU=I \end{aligned}$$

(38)

Let $\Phi$ and $\Psi$ be the Lagrange multiplier for constraints $U\ge 0$ and $U^TU=I$, respectively. Then, the Lagrange function is

$$\begin{aligned} \mathcal {L}_1 = & Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) +\alpha Tr(U^TL_{hm}^{*}U) \nonumber \\ & + Tr(\Phi U^T) + Tr(\Psi (U^TU - I)^T) \end{aligned}$$

(39)

The partial derivative with respect to the factor matrix U can be obtained as follows:

$$\begin{aligned} \frac{\partial \mathcal {L}_1}{\partial U} = & -2XDVS^T + 2USV^TDVS^T \nonumber \\ & + 2\alpha L_{hm}^{*}U + 2U\Psi + \Phi \end{aligned}$$

(40)

Setting $\frac{\partial \mathcal {L}_1}{\partial U} = 0$, substituting $\Psi = U^TXDVS^T - SV^TDVS^T - \alpha U^TL_{hm}^*U$ and using the Karush-Kuhn-Tucker (KKT) conditions $\Phi _{ij}U_{ij} = 0$, we can obtain the following update rule:

$$\begin{aligned} U_{ij}\longleftarrow U_{ij}\sqrt{\frac{(XDVS^T + \alpha S_{hm}^*U)_{ij}}{(UU^TXDVS^T + \alpha UU^TS_{hm}^*U)_{ij}}} \end{aligned}$$

(41)

Updating the factor matrix S

When $\varvec{w}$, U and V were fixed, the subproblem of optimizing an objective function containing S was as below:

$$\begin{aligned} \underset{S}{\min }\ & Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) + \lambda Tr(SS^T) \nonumber \\ & s.t. \ S\ge 0 \end{aligned}$$

(42)

Let $\Xi$ be the Lagrange multiplier for constraint $S\ge 0$. Then, the Lagrange function is

$$\begin{aligned} \mathcal {L}_2 = & Tr(XDX^T) - 2Tr(USV^TDX^T) + \lambda Tr(SS^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) + Tr(\Xi S^T) \end{aligned}$$

(43)

The partial derivative of the factor matrix S can be calculated as below:

$$\begin{aligned} \frac{\partial \mathcal {L}_2}{\partial S} = -2U^TXDV + 2U^TUSV^TDV + 2\lambda S + \Xi \end{aligned}$$

(44)

Setting $\frac{\partial \mathcal {L}_2}{\partial S} = 0$ and using KKT conditions $\Xi _{ij}S_{ij} = 0$, we obtained the following update rule:

$$\begin{aligned} S_{ij}\longleftarrow S_{ij}\sqrt{\frac{(U^TXDV)_{ij}}{(U^TUSV^TDV + \lambda S)_{ij}}} \end{aligned}$$

(45)

Updating the factor matrix V

When $\varvec{w}$, U and S were fixed, optimizing the subproblem involving V was as follows:

$$\begin{aligned} \underset{V}{\min } & Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) +\beta Tr(V^TL_{hd}^{*}V) \nonumber \\ & s.t. \ V\ge 0, V^TV=I \end{aligned}$$

(46)

Let $\Theta$ and $\Lambda$ be the Lagrange multiplier for constraints $V\ge 0$ and $V^TV=I$, respectively. Then, the Lagrange function is

$$\begin{aligned} \mathcal {L}_3 = & Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) + \beta Tr(V^TL_{hd}^{*}V) \nonumber \\ & + Tr(\Theta V^T) + Tr(\Lambda (V^TV - I)^T) \end{aligned}$$

(47)

The partial derivative with respect to the factor matrix V can be calculated as follows:

$$\begin{aligned} \frac{\partial \mathcal {L}_3}{\partial V} = & -2DX^TUS + 2DVS^TU^TUS \nonumber \\ & + 2\beta L_{hd}^{*}V + 2V\Lambda + \Theta \end{aligned}$$

(48)

Similarly, setting $\frac{\partial \mathcal {L}_3}{\partial V} = 0$, substituting $\Lambda = V^TDX^TUS - V^TDVS^TU^TUS - \beta V^TL_{hd}^*V$ and using KKT conditions $\Theta _{ij}V_{ij} = 0$, we obtained the following update rule:

$$\begin{aligned} V_{ij}\longleftarrow V_{ij}\sqrt{\frac{(DX^TUS + \beta S_{hd}^*V)_{ij}}{(DVV^TX^TUS + \beta VV^TS_{hd}^*V)_{ij}}} \end{aligned}$$

(49)

The detailed optimization of the proposed SPLHRNMTF model was descried step by step in Algorithm 1.

Algorithm 1 The optimization algorithm of SPLHRNMTF

Convergence analysis

In this section, we will study the convergence of the SPLHRNMTF model. To be more specific, we needed to prove that the objective function in Eq. (31) is monotonically decreasing under the updating rules in Eqs. (41), (45) and  (49) and the SPL step in Eq. (37). Based on previous works [43, 53, 54], researchers have demonstrated the effectiveness of SPL in various models. Finally, we only needed to prove that the objective function in Eq. (31) is monotonically decreasing under the updating rules in Eqs. (41), (45) and (49). The following detailed proof process was presented.

Definition 1

$G(x,x^{'})$ is an auxiliary function for F(x) if the conditions

$$\begin{aligned} G(x,x^{'})\ge F(x), G(x,x) = F(x) \end{aligned}$$

are satisfied.

lemma 1

If $G(x,x^{'})$ is an auxiliary function of F(x), then F(x) is non-increasing under the following updating formula:

$$\begin{aligned} x^{t+1} = \arg \min _xG(x,x^{t}) \end{aligned}$$

Proof

$$\begin{aligned} F(x^{t+1})\le G(x^{t+1},x^t)\le G(x^t,x^t) = F(x^t) \end{aligned}$$

Then,

$$\begin{aligned} F(x^{min})\le \cdots \le F(x^{t+1})\le F(x^t) \le \cdots \le F(x^0) \end{aligned}$$

The above mentioned is to introduce the definition of the auxiliary function. Next, in order to demonstrate the convergence of the alternating optimization rules, we needed the following theorems.

Theorem 1

Updating U using Eq. (41) while fixing S and V in each iteration will monotonically decrease the value of the objective function in Eq. (31), hence it converges.

According to Eq. (31), the corresponding objective function when fixed $\varvec{w}$ can be rewritten as below:

$$\begin{aligned} \mathcal {J}(U,S,V) = & \sum \limits _{i=1}^{n}d_i\Vert (X - USV^T)_i\Vert _2^2 + \lambda \Vert S\Vert _F^2 \nonumber \\ & + \alpha Tr(U^TL_{hm}^{*}U) + \beta Tr(V^TL_{hd}^{*}V) \nonumber \\ & s.t.\ U\ge 0, S\ge 0, V\ge 0, U^TU=I, V^TV=I \end{aligned}$$

(50)

Our goal is to prove that the updating rule for U while fixing S and V will result in a monotonically decreasing value of $\mathcal {J}(U,S,V)$. To conduct the corresponding proof, we needed the following lemma.

lemma 2

Updating U using Eq. (41) while fixing S and V, the following inequality holds:

$$\begin{aligned} & \sum \limits _{i=1}^{n}d_i\Vert (X - U^{t+1}SV^T)_i\Vert _2^2 + \alpha Tr(U^{T(t+1)}L_{hm}^{*}U^{(t+1)}) \le \nonumber \\ & \sum \limits _{i=1}^{n}d_i\Vert (X - U^{t}SV^T)_i\Vert _2^2 + \alpha Tr(U^{T(t)}L_{hm}^{*}U^{(t)}) \end{aligned}$$

(51)

where $U^TU = I$.

Proof

To prove the constrained problem in Lemma 2, we needed to prove the following Lagrangian function:

$$\begin{aligned} \mathcal {J}(U) & = Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) +\alpha Tr(U^TL_{hm}^{*}U) \nonumber \\ & + Tr(\Psi (U^TU - I)^T) \end{aligned}$$

(52)

The auxiliary function can be first defined as follows:

$$\begin{aligned} \mathcal {J}(U,U^{'}) & = Tr\left(XDX^T - \Psi \right) \nonumber \\ & + \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \frac{\left(U^{'}SV^TDVS^T + U^{'}\Psi \right)_{ij}U_{ij}^2}{U^{'}_{ij}} \nonumber \\ & -2\sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \left(XDVS^T\right)_{ij}U^{'}_{ij}\left(1 + \log \frac{U_{ij}}{U^{'}_{ij}}\right) \nonumber \\ & + \alpha \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n}\frac{\left(L_{hm}^{*}U^{'}\right)_{ij}U_{ij}^2}{U^{'}_{ij}} \end{aligned}$$

(53)

According to previous work [55], the following inequality holds:

$$\begin{aligned} \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{k}\frac{(AC^{'}B)_{ij}C_{ij}^2}{C_{ij}^{'}}\ge Tr(C^TACB) \end{aligned}$$

(54)

where A, B and C are non-negative matrices, and A and B are symmetric. Furthermore, we knew the inequality, $w\ge 1+\log (w)$ for all $w>0$. Therefore, we had

$$\begin{aligned} & Tr(U^TUSV^TDVS^T) + Tr(\Psi U^TU) \nonumber \\ \le & \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \frac{(U^{'}SV^TDVS^T)_{ij}U_{ij}^2}{U^{'}_{ij}} + \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n}\frac{(U^{'}\Psi )_{ij}U_{ij}^2}{U^{'}_{ij}} \nonumber \\ = & \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \frac{(U^{'}SV^TDVS^T + U^{'}\Psi )_{ij}U_{ij}^2}{U^{'}_{ij}} \end{aligned}$$

(55)

and

$$\begin{aligned} \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n}\frac{(L_{hm}^{*}U^{'})_{ij}U_{ij}^2}{U^{'}_{ij}} \ge Tr(U^TL_{hm}^{*}U) \end{aligned}$$

(56)

It can be seen that Eq. (53) can serve as a valid auxiliary function. Consequently, we can determine the stationary point of $\mathcal {J}(U,U^{'})$. As defined in Eq. (53), taking the derivative of $\mathcal {J}(U,U^{'})$ w.r.t U

$$\begin{aligned} \frac{\partial \mathcal {J}(U,U^{'})}{\partial U_{ij}} = & 2\frac{(U^{'}SV^TDVS^T + \alpha L_{hm}^{*}U^{'} + U^{'}\Psi )_{ij}U_{ij}}{U_{ij}^{'}} \nonumber \\ & -2(XDVS^T)_{ij}\frac{U_{ij}^{'}}{U_{ij}} \end{aligned}$$

(57)

Setting Eq. (57) to zero and substituting $\Psi = U^{'T}XDVS^T - SV^TDVS^T - \alpha U^{'T}L_{hm}^*U^{'}$, we can obtain the following stationary point:

$$\begin{aligned} U_{ij}\longleftarrow U_{ij}^{'}\sqrt{\frac{(XDVS^T + \alpha S_{hm}^*U^{'})_{ij}}{(U^{'}U^{'T}XDVS^T + \alpha U^{'}U^{'T}S_{hm}^*U^{'})_{ij}}} \end{aligned}$$

(58)

To confirm that the stationary point is the minimum of $\mathcal {J}(U,U^{'})$, it is necessary to examine whether the Hessian matrix is a positive semidefinite matrix. To this end, we further took the second derivative w.r.t U

$$\begin{aligned} & \frac{\partial ^{2}\mathcal {J}(U,U^{'})}{\partial V_{ij}\partial V_{kl}} =\left( 2(XDVS^T)_{ij}\frac{U_{ij}^{'}}{U_{ij}}\right) \delta _{ik}\delta _{jl} \nonumber \\ & + \left( 2\frac{(U^{'}SV^TDVS^T + \alpha L_{hm}^{*}U^{'} + U^{'}\Psi )_{ij}U_{ij}}{U_{ij}^{'}}\right) \delta _{ik}\delta _{jl} \end{aligned}$$

(59)

It is clear that the Hessian matrix is a positive semidefinite matrix, thereby indicating $\mathcal {J}(U,U^{'})$ is a convex function. This observation suggests that the stationary point in Eq. (58) represents the unique global minima of $\mathcal {J}(U,U^{'})$. Based on Lemma 1, it becomes evident that Lemma 2 is established. Hence, Theorem 1 has been proven too. It is worth noting that if substituting $U = U^{t+1}$ and $U^{'} = U^{t}$ for Eq. (58), we obtained the updating rule in Eq. (41).

Theorem 2

Updating S using Eq. (45) while fixing U and V in each iteration will monotonically decrease the value of the objective function in Eq. (31), hence it converges.

In the same way, our goal is to prove that the updating rule for S while keeping U and V fixed, results in a monotonically decreasing value of $\mathcal {J}(U,S,V)$. To conduct the corresponding proof, we needed the lemma as follows.

lemma 3

Updating S using Eq. (45) while fixing U and V, the following inequality holds:

$$\begin{aligned} & \sum \limits _{i=1}^{n}d_i\Vert (X - US^{t+1}V^T)_i\Vert _2^2 + \lambda \Vert S^{t+1}\Vert _F^2 \le \nonumber \\ & \sum \limits _{i=1}^{n}d_i\Vert (X - US^{t}V^T)_i\Vert _2^2 + \lambda \Vert S^{t}\Vert _F^2 \end{aligned}$$

(60)

Proof

Similar with Eq. (52), we can get the Lagrangian function for $\mathcal {J}(S)$ as follows:

$$\begin{aligned} \mathcal {J}(S) & = Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) +\lambda Tr(SS^T) \end{aligned}$$

(61)

Also, an appropriate auxiliary function was defined as:

$$\begin{aligned} \mathcal {J}\left(S,S^{'}\right) & = Tr\left(XDX^T\right) \nonumber \\ & + \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \frac{\left(U^TUS^{'}V^TDV\right)_{ij}S_{ij}^2}{S^{'}_{ij}} \nonumber \\ & -2\sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n}\left(U^TXDV\right)_{ij}S_{ij}^{'}\left(1+\log \frac{S_{ij}}{S_{ij}^{'}}\right) \nonumber \\ & + \lambda \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \frac{\left(S^{'}\right)_{ij}S_{ij}^2}{S^{'}_{ij}} \end{aligned}$$

(62)

Similar to prove Lemma 2, Lemma 3 can be proved. The rest proof of Theorem 2 is similar to the proof of Theorem 1.

Theorem 3

Updating V using Eq. (49) while fixing U and S in each iteration will monotonically decrease the value of the objective function in Eq. (31), hence it converges.

Similarly, our goal is to prove that the updating rule for V while keeping U and S fixed, results in a monotonically decreasing value of $\mathcal {J}(U,S,V)$. To conduct the corresponding proof, we needed the lemma as follows.

lemma 4

Updating V using Eq. (49) while fixing U and S, the following inequality holds:

$$\begin{aligned} & \sum \limits _{i=1}^{n}d_i\Vert (X - USV^{T(t+1)})_i\Vert _2^2 + \beta Tr(V^{T(t+1)}L_{hd}^{*}V^{(t+1)}) \le \nonumber \\ & \sum \limits _{i=1}^{n}d_i\Vert (X - USV^{T(t)})_i\Vert _2^2 + \beta Tr(V^{T(t)}L_{hd}^{*}V^{(t)}) \end{aligned}$$

(63)

where $V^TV = I$.

Proof

Similar with Eq. (52), we obtained the Lagrangian function for $\mathcal {J}(V)$ and an appropriate auxiliary function as follows:

$$\begin{aligned} \mathcal {J}(V) & = Tr(XDX^T) - 2Tr(USV^TDX^T) \nonumber \\ & + Tr(USV^TDVS^TU^T) + \beta Tr(V^TL_{hd}^{*}V) \nonumber \\ & + Tr(\Lambda (V^TV - I)^T) \end{aligned}$$

(64)

$$\begin{aligned} \mathcal {J}\left(V,V^{'}\right) & = Tr\left(XDX^T - \Lambda \right) \nonumber \\ & + \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \frac{\left(DV^{'}S^TU^TUS + V^{'}\Lambda \right)_{ij}U_{ij}^2}{U^{'}_{ij}} \nonumber \\ & -2\sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n} \left(DX^TUS\right)_{ij}V^{'}_{ij}\left(1 + \log \frac{V_{ij}}{V^{'}_{ij}}\right) \nonumber \\ & + \beta \sum \limits _{j=1}^{c}\sum \limits _{i=1}^{n}\frac{\left(L_{hd}^{*}V^{'}\right)_{ij}V_{ij}^2}{V^{'}_{ij}} \end{aligned}$$

(65)

Similar to prove Lemma 2, we can prove Lemma 4. The rest proof of Theorem 3 is also similar to the proof of Theorem 1.

In summary, the objective function in Eq. (31) decreases monotonically in the alternative updating rules in Eqs. (41), (45) and (49).

Results

Experimental settings and evaluation metrics

To more comprehensively and systematically show the ability of SPLHRNMTF in predicting potential associations between miRNAs and diseases, we conducted 5-fold cross-validation five times experiments based on known miRNA-disease associations. In 5-fold cross-validation, we randomly split all miRNA-disease pairs into five equal-sized subsets. Note that there is no overlap between five equal-sized subsets. In each fold, one subset as a testing set in turn and the remaining four subsets are considered as a training set. To effectively evaluate the prediction ability of the model, the area under the receiver operating characteristic (AUC) curve, the area under the precision-recall (AUPR) curve, and F1 score were used to evaluate the performance of all models.

Baseline models

To comprehensively evaluate the prediction performance of SPLHRNMTF, we compared several previously proposed computational models. In this paper, we applied the same dataset to train these models for a fairer comparative analysis. The specific information of introduced models was as follows.

NMTF [56]: As an extension of NMF, non-negative matrix tri-factorization (NMTF) can provide more degrees of freedom than NMF.

$L_{2,1}$-NMTF [57]: Kong et al. proposed robust non-negative matrix factorization by using $L_{2,1}$ norm instead of Frobenius norm. Based on the study of Kong et al., we extended NMF to NMTF and named it $L_{2,1}$-NMTF.

GRNMF [22]: This is a method based on graph regularized non-negative matrix factorization for miRNA-disease association prediction.

IMCMDA [23]: Chen et al. developed an inductive matrix completion method based on non-negative constraints to predict the associations between miRNAs and diseases, which combines integrated miRNA and disease similarity matrices into matrix factorization.

MDHGI [24]: The matrix decomposition-based MDHGI combines sparse learning method with heterogeneous graph inference method to infer the associations between miRNAs and diseases.

SPLGRNMF [45]: Huang et al. proposed the SPLNMF model by integrating self-paced learning (SPL) into NMF and using $L_{2,1}$ norm to constrain the objective function. To conduct a more reasonable comparative analysis with the proposed model, we imposed double orthogonal constraints on the latent representations and introduced dual graph Laplacian regularization based on the SPLNMF model. The improved model is called SPLGRNMF.

NMTFDR [25]: Dissez et al. presented a drug repositioning model based on the non-negative matrix tri-factorization with graph Laplacian regularization by using multiple interaction matrices of drugs, proteins, pathways and diseases. For convenience, the drug repositioning model is called NMTFDR.

NMTF-DTI [26]: NMTF-DTI is a model based on nonnegative matrix tri-factorization for drug-target interaction prediction, which constructs a weighted interaction matrix to correct false-negative samples and utilizes graph Laplacian regularization to improve prediction performance.

SPLNMTF [58]: SPLNMTF combines self-paced learning with non-negative matrix tri-factorization to perform drug repositioning, which also considers graph Laplacian regularization to preserve local geometric structures in low-dimensional space.

NMFMC [27]: The method divides non-negative matrix factorization into a known part and an unknown part, and introduces graph regularization to preserve local geometric structures for miRNA-disease association prediction.

NIMCGCN [19]: NIMCGCN makes use of a neural inductive matrix completion method based on graph convolutional networks to identify the associations between miRNAs and diseases.

MMGCN [20]: Tang et al. applied graph convolutional networks and multichannel attention mechanism to extract and enhance latent representations of miRNAs and diseases, predicting potential associations from the reconstructed miRNA-disease matrix.

MHCLMDA [21]: MHCLMDA first captured high-order interactions between similarity network nodes based on hypergraph convolutional networks and hypergraph contrastive learning. Then, a variational auto-encoder was used to extract miRNA and disease features from known miRNA-disease associations. Finally, MHCLMDA integrated different miRNA and disease features to predict miRNA-disease associations.

Parameters analysis

In this study, we analyzed the impact of several hyperparameters on the prediction performance of SPLHRNMTF by utilizing the MDAv2.0_data dataset. To be more specific, we applied grid search to determine hyperparameter combinations under 5-fold cross-validation. Among them, compared with other hyperparameters, $\lambda$ has less influence on model prediction performance. First, we empirically fixed $\lambda = 0.0001$ and searched the optimal values of other hyperparameters. Then, we searched the optimal value of $\alpha$ and $\beta$ from $\{0.00002,0.0002,0.002,0.02,0.2,1,2\}$. As shown in Fig. 3a, when $\alpha = 0.00002$ and $\beta = 0.02$, SPLHRNMTF obtained better prediction performance. Similarly, varying matrix rank r within $\{3,7,\cdots ,23,27\}$ and set $r = 23$ in Fig. 3b. Next, the optimal $k_1$ value in KNN method used by constructing hypergraphs can be searched from $\{2,6,\cdots ,38,42\}$ and set $k_1 = 34$ as shown in Supplementary Figure S1(a). In addition, we searched the optimal decay term $\theta$ from $\{0.1,0.2,0.3,\cdots ,0.9,1\}$ and set $\theta = 0.9$ in Supplementary Figure S1(b). The $k_2$ in WKNN method was also searched from $\{2,4,6,\cdots ,12,14\}$and $k_2$ was set to 10 that the model achieved better prediction performance as shown in Supplementary Figure S1(c). Finally, we trained $k_3$ in KNN method used by sparse similarity matrix from $\{1,2,3,\cdots ,9,10\}$ and set the optimal $k_3$ to 2 as shown in Supplementary Figure S1(d). It is worth noting that hyperparameter selection was required for other experimental datasets as well. The detailed results of hyperparameter adjustments can be found in Supplementary Figures S2 and S3.

Fig. 3

The influence of different hyperparameters on SPLHRNMTF based on the MDAv2.0_data dataset. a The impact of hyperparameters $\alpha$ and $\beta$ on SPLHRNMTF. b The impact of hyperparameter r on SPLHRNMTF

Comparison experiments

All comparison experiments adopt the same datasets and evaluation settings for a fairer comparative analysis. To better show the optimal performance of baseline models, we performed grid search on GRNMF, SPLGRNMF, NMTF-DTI and NMFMC models with hyperparameters controlling the graph Laplacian regularization. The detailed hyperparameter tuning can be found in Supplementary Parameters Analysis. For fairness, we uniformly set the same rank as SPLHRNMTF for all baseline models on different datasets. To conduct more reasonable evaluation experiments, we performed 5-fold cross-validation five times. In addition, we also randomly selected unobserved elements equal to the positive sample size as negative samples 10 times. The reported average results represent the outcome, providing a more reasonable evaluation. Finally, we provided detailed parameter information of each model on three datasets in Supplementary Material.

Table 1 The prediction performance of all models evaluated by 5-fold cross-validation five times on MDAv3.2_data1 and MDAv3.2_data2 datasets

Table 1 shows the comparative analysis of the prediction performance of all models for 5-fold cross-validation five times, from which we can see that SPLHRNMTF outperformed other baseline models, even including graph and hypergraph convolutional network-based models, on MDAv3.2_data1 and MDAv3.2_data2 datasets in terms of AUC and AUPR. To be more specific, the average AUC value of SPLHRNMTF was 0.9304 on the MDAv3.2_data1 dataset, whereas the average AUC values of NMTF, $L_{2,1}$-NMTF, IMCMDA, GRNMF, MDHGI, SPLGRNMF, NMTFDR, NMTF-DTI, SPLNMTF, NMFMC, NIMCGCN, MMGCN and MHCLMDA were 0.9110, 0.9128, 0.7783, 0.9041, 0.8877, 0.7691, 0.9073, 0.9279, 0.8428, 0.9082, 0.8540, 0.9004, 0.9255, respectively. Similarly, SPLHRNMTF obtained the average AUC value of 0.9358, which was also better than other baseline models on the MDAv3.2_data2 dataset. It is worth noting that the standard deviation of the prediction performance of SPLHRNMTF was relatively small. These results indicate that SPLHRNMTF not only has superior prediction performance but also exhibits better robustness and stability. Although the F1 value of SPLHRNMTF is slightly lower than that of MMGCN and MHCLMDA on the MDAv3.2_data2 dataset, the AUC and AUPR values of SPLHRNMTF are better than those of MMGCN and MHCLMDA. This shows that even compared to models based on graph and hypergraph convolutional networks, SPLHRNMTF has a certain competitiveness. From Supplementary Table S1, we observed that the proposed SPLHRNMTF model also obtained good prediction performance on the MDAv2.0_data dataset. More importantly, the prediction performance of $L_{2,1}$-NMTF was superior to NMTF. Specifically, $L_{2,1}$-NMTF obtained certain performance gains over NMTF by 5.98%, 0.20% and 4.06% in terms of AUC on MDAv2.0_data, MDAv3.2_data1 and MDAv3.2_data2 datasets, respectively. This result demonstrates that using $L_{2,1}$ to calculate residual error can effectively alleviate the impact of noise and outliers, thereby improving prediction performance.

Ablation studies

To better validate the effectiveness of non-linear fusion method, preprocessing step using WKNN, self-paced learning and hypergraph regularization, we further constructed SPLHRNMTF$^{-}$, SPLHRNMTF$^{*}$, HRNMTF and SPLGRNMTF as four variants of SPLHRNMTF for comparative analysis. (1) SPLHRNMTF$^{-}$: we utilized linear fusion instead of non-linear fusion to explore whether learning non-linear relationships in similarity networks can improve prediction performance. (2) SPLHRNMTF$^{*}$: we removed the preprocessing step using WKNN to explore whether using the WKNN method can effectively correct false-negative samples and improve model prediction performance. (3) HRNMTF: in order to verify the effectiveness of self-paced learning, we retained other modules except self-paced learning. (4) SPLGRNMTF: we replaced hypergraph Laplacian regularization with graph Laplacian regularization to explore whether the use of hypergraph regularization can effectively capture high-order relations.

Table 2 The prediction performance of ablation experiment evaluated by 5-fold cross-validation five times on the MDAv3.2_data2 dataset

Table 2 shows the comparative analysis of ablation experiments for different variant models on the MDAv3.2_data2 dataset. From Table 2, we can observe that SPLHRNMTF was significantly better than SPLHRNMTF$^{*}$. This result demonstrates that the use of WKNN method can effectively correct false-negative samples, thereby improving model prediction performance. Moreover, after using non-linear fusion method, the prediction performance of SPLHRNMTF outperformed SPLHRNMTF$^{-}$, which suggests that the non-linear fusion method can more reasonably integrate similarity information while improving prediction performance by capturing non-linear relationships. Similarly, after using self-paced learning, SPLHRNMTF can achieve better prediction performance than HRNMTF, which shows that integrating self-paced learning into NMTF can effectively alleviate the model from falling into a bad local optimal solution and improve prediction performance. Finally, compared with SPLGRNMTF, the prediction performance of SPLHRNMTF has been improved to a certain extent, which indicates that the use of hypergraph regularization can capture the high-order relationships of biological similarity networks. Notably, the standard deviation of SPLHRNMTF’s prediction performance in the 5-fold cross-validation five times is relatively small, indicating that adding other modules helps to enhance the model’s robustness and stability.

Case studies

To further validate the predictive accuracy of SPLHRNMTF in identifying associations between miRNAs and specific diseases, we conducted case studies on two significant tumor diseases, namely breast neoplasms and lung neoplasms, using the MDAv2.0_data dataset. For a specific disease, negative miRNA-disease associations and experimentally verified positive miRNA-disease associations on the MDAv2.0_data dataset were used as training samples, and unverified associations with the specific disease on the MDAv2.0_data dataset are considered as candidate samples. Through training the SPLHRNMTF model on training samples, we can rank candidate samples by their predicted association scores and select the top 50 candidate associations with the specific disease. Finally, we verified the top 50 prediction results by finding supporting evidence from the lasted HMDD v4.0 [59] and dbDEMC [60].

Table 3 shows the top 50 prediction results of miRNAs that are closely related to breast neoplasms. From Table 3, we can see that 48 of the top 50 breast neoplasms-related miRNAs were successfully confirmed by HMDD v4.0 and dbDEMC databases. Note that unconfirmed refers to miRNAs that have not been confirmed by relevant evidence. Similarly, Supplementary Table S2 demonstrates that the top 50 predicted lung neoplasms-related results and 46 predictions can be confirmed according to the above two databases. Meanwhile, we also observed that miRNAs showing higher similarity were predicted to be associated with the same specific disease. For example, hsa-mir-138-1 and hsa-mir-138-2 can function by directly targeting the polycomb epigenetic regulator EZH2, and they have been demonstrated to be novel regulators of invasion and epithelial-mesenchymal transition in breast cancer cells [61].

Table 3 Top 50 breast neoplasms-related miRNAs predicted by SPLHRNMTF based on the MDAv2.0_data dataset. Note that the number in evidence means PubMed Unique Identifier (PMID)

To further validate the biological significance of the potential miRNA-disease associations identified by the SPLHRNMTF model, we conducted enrichment analysis on gene sets comprising the target genes of the miRNAs. First, miRTarBase [62] was used to obtain the target genes of each miRNA. Then, we applied Metascape [63] to investigate the biological process and pathway information related to these target gene sets. Figure 4 shows the enrichment analysis of the discovered breast neoplasms-related hsa-mir-19b-2, from which we can see that target gene sets associated with hsa-mir-19b-2 were significantly enriched in several terms closely related to breast cancer, including regulation of hormone secretion, response to steroid hormone, insulin signaling and MAPK6/MAPK4 signaling. To be more specific, breast cancer growth is dependent upon estrogenic hormones and can be inhibited by antiestrogenic antagonists [64]. A lot of evidence also suggests that interactions between steroid hormones and growth factors act as a regulator of endocrine response in breast cancer, while abnormalities in growth factor signaling are common contributors to the endocrine-resistant phenotype [65]. Furthermore, the dysregulation of the expression and function of insulin and its downstream signaling effectors often drives breast cancer initiation and progression in a subtype-dependent manner [66]. In addition, the high expression of MAPK4 defines a large subset or subtype of triple-negative breast cancer (TNBC) that responds to MAPK4 blockade, and targeting MAPK4 both inhibits TNBC growth and sensitizes tumors to PI3K blockade [67]. Finally, we observed that many biological processes and other terms were obtained based on the above enrichment analysis. Through utilizing Metascape, we further captured the relationships between these terms. As shown in Supplementary Figure S8, we selected a subset of enriched terms and presented them as a network graph, where terms with similarity > 0.3 are connected by edges. According to the network graph, we discovered that several terms associated with breast cancer clustered together. In summary, the aforementioned biological analysis suggests a potential association between hsa-mir-19b-2 and the occurrence and progression of breast cancer.

Fig. 4

The enrichment analysis of target gene sets related to hsa-mir-19b-2

Conclusion

Identification of disease-related miRNAs through computational models can contribute to accelerating the understanding of the pathogenic mechanisms of human diseases and the discovery of potential therapeutic targets. In this study, we develop a SPLHRNMTF model of robust orthogonal non-negative matrix tri-factorization with self-paced learning and dual hypergraph regularization for predicting miRNA-disease associations. To be more specific, we first utilize a non-linear fusion method to obtain comprehensive similarity for miRNAs and diseases. Then, weighted k-nearest neighbor profile method is used to replace zero values in the association matrix with likelihood scores for correct false-negative associations. Furthermore, SPLHRNMTF makes use of $L_{2,1}$ norm instead of Frobenius norm to calculate residual error for effectively alleviating the impact of noise and outliers on model prediction performance. Meanwhile, we integrate self-paced learning into NMTF using $L_{2,1}$ norm to alleviate the model from falling into bad local optimal solutions. Finally, hypergraph regularization is introduced to preserve the high-order complex relations of biological similarity networks in the low-dimensional embedding space. The experimental results of 5-fold cross-validation five times and ablation studies show that SPLHRNMTF outperforms other baseline models and has good robustness. Each module in SPLHRNMTF and the preprocessing step are also demonstrated to be effective. Furthermore, the meaningful results of case studies on breast neoplasms and lung neoplasms indicate that 48 and 46 of the top 50 predicted disease-related miRNAs are confirmed, further demonstrating that the SPLHRNMTF model can accurately infer miRNA-disease associations. In addition, unconfirmed miRNA-disease associations have biological significance through enrichment analysis. To sum up, SPLHRNMTF can be used as an effective model to predict the associations between miRNAs and diseases.