Multiple-sets split feasibility problem and split equality fixed point problem for firmly quasi-nonexpansive or nonexpansive mappings

Abstract

In this paper, we propose a new iterative algorithm for solving the multiple-sets split feasibility problem (MSSFP for short) and the split equality fixed point problem (SEFPP for short) with firmly quasi-nonexpansive operators or nonexpansive operators in real Hilbert spaces. Under mild conditions, we prove strong convergence theorems for the algorithm by using the projection method and the properties of projection operators. The result improves and extends the corresponding ones announced by some others in the earlier and recent literature.

1 Introduction and preliminaries

Let $H_{1}$, $H_{2}$, and $H_{3}$ be three real Hilbert spaces with inner product $\langle \cdot,\cdot \rangle$ and induce norm $\|\cdot \|$. We use $\mathrm{Fix}(T)$ to denote the set of fixed points of a mapping T.

The split feasibility problem (SFP) in finite-dimensional Hilbert spaces was first introduced by Censor and Elfving [6] for modeling inverse problems which arise from phase retrievals and in medical image reconstruction [3]. The SFP can be formulated as finding a point $x^{*}$ in $\mathbb{R}^{n}$ with the property

$$\begin{aligned} x^{*} \in C\quad \text{and} \quad Ax^{*} \in Q, \end{aligned}$$

(1.1)

where C and Q are nonempty closed convex subsets of $\mathbb{R}^{n}$ and $\mathbb{R}^{m}$, respectively, and A is an $m \times n$ matrix. SFP (1.1) has recently been studied in a more general space. For example, Xu [21] studied it in an infinite dimensional Hilbert space.

The SFP has been widely studied in recent years. Recently, it has been found that it can also be used to model the intensity-modulated radiation therapy; see, e.g., [7–11]. One of the well-known methods for solving the SFP is Byrne’s CQ algorithm [3, 4], which generated a sequence $\{x_{n}\}$ by the following iterative algorithm:

$$\begin{aligned} x_{n+1}=P_{C} \bigl(x_{n}- \tau _{n}A^{*}(I-P_{Q})Ax_{n} \bigr), \end{aligned}$$

(1.2)

where C and Q are nonempty closed convex subsets of $H_{1}$ and $H_{2}$ and the step size $\tau _{n}$ is located in the interval $(0,2/\|A\|^{2})$, $A^{*}$ is the adjoint of A, $P_{C}$ and $P_{Q}$ are the metric projections onto C and Q.

The multiple-set split feasibility problem (MSSFP), which has functions in the inverse problem of intensity-modulated radiation therapy (see [18]), has recently been presented in [5] and is formulated as follows:

$$\begin{aligned} \text{find a point }x\in C:=\bigcap_{i=1}^{r_{1}}C_{i} \text{ such that }Ax\in Q:= \bigcap_{j=1}^{r_{2}}Q_{j}, \end{aligned}$$

(1.3)

where $r_{1},r_{2}\in N, C_{1},\ldots,C_{r_{1}}$ are closed convex subsets of $H_{1}$, $Q_{1},\ldots,Q_{r_{2}}$ are closed convex subsets of $H_{2}$, and $A:H_{1}\rightarrow H_{2}$ is a bounded linear operator.

Assuming consistency of the MSSFP, Censor et al. [5] introduced the following projection algorithm:

$$\begin{aligned} x_{n+1}=P_{\Omega } \Biggl(x_{n}-\gamma \Biggl(\sum _{i=1}^{r_{1}}\alpha _{i}(x_{n}-P_{C_{i}}x_{n})+ \sum_{j=1}^{r_{2}}\beta _{j}A^{*}(I-P_{Q_{j}})Ax_{n} \Biggr) \Biggr),\quad n\geq 0, \end{aligned}$$

(1.4)

where $0<\gamma <\frac{2}{L}$ with $L=\sum_{i=1}^{r_{1}}\alpha _{i}+\rho (A^{*}A)\sum_{j=1}^{r_{2}} \beta _{j}$ and $\rho (A^{*}A)$ is the spectral radius of $A^{*}A$. They proved convergence of algorithm (1.4) in the case where both $H_{1} and H_{2}$ are finite dimensional.

Moudafi [17] came up with the split equality problem (SEP) as follows:

$$\begin{aligned} \text{find }x\in C, y\in Q,\text{ such that }Ax=By, \end{aligned}$$

(1.5)

where $A:H_{1}\rightarrow H_{3}$, $B:H_{2}\rightarrow H_{3}$ are two bounded linear operators, $C\subset H_{1}$, $Q\subset H_{2}$ are two nonempty closed convex sets. Let $B=I$, it is easy to see that the SFP is the special case of the SEP. The SEP has already been applied in game theory (see [1]) and intensity-modulated radiation therapy [5, 12]. Furthermore, the author considered the following scheme for solving the SEP:

$$\begin{aligned} \textstyle\begin{cases} x_{k+1}=P_{C_{k}}(x_{k}-\gamma A^{*}(Ax_{k}-By_{k})), \\ y_{k+1}=P_{Q_{k}}(y_{k}+\gamma B^{*}(Ax_{k+1}-By_{k})). \end{cases}\displaystyle \end{aligned}$$

(1.6)

He obtained a weak convergence of (1.6) under certain appropriate assumptions on the parameters.

Shi [19] proposed a modification of Moudafi’s ACQA algorithms to solve the SEP and proved its strong convergence:

$$\begin{aligned} w_{n+1}=P_{S} \bigl\{ (1-\alpha _{n}) \bigl[I- \gamma G^{*}G \bigr]w_{n} \bigr\} , \end{aligned}$$

(1.7)

i.e.,

$$\begin{aligned} \textstyle\begin{cases} x_{k+1}=P_{C}\{(1-\alpha _{k})x_{k}-\gamma A^{*}(Ax_{k}-By_{k})\},\quad n \geq 0, \\ y_{k+1}=P_{Q}\{(1-\alpha _{k})y_{k}+\gamma B^{*}(Ax_{k}-By_{k})\},\quad n \geq 0. \end{cases}\displaystyle \end{aligned}$$

(1.8)

Recently, Moudafi [16] introduced the following split equality fixed point problem (SEFPP):

$$\begin{aligned} \text{find }x\in C:=F(U), y\in Q:=F(T)\text{ such that }Ax=By, \end{aligned}$$

(1.9)

where $U:H_{1}\rightarrow H_{1}$ and $T:H_{2}\rightarrow H_{2}$ are two firmly quasi-nonexpansive operators. The SEFPP has been proved very useful in decomposition methods for PDEs as well as in game theory and intensity-modulated radiation therapy. For solving SEFPP (1.9), he proposed the following iterative algorithm:

$$\begin{aligned} \textstyle\begin{cases} x_{k+1}=U(x_{k}-\gamma _{k} A^{*}(Ax_{k}-By_{k})), \\ y_{k+1}=T(y_{k}+\gamma _{k} B^{*}(Ax_{k+1}-By_{k})). \end{cases}\displaystyle \end{aligned}$$

(1.10)

Further, he proved a weak convergence theorem for SEFPP (1.9) under some mild restrictions on the parameters.

In this paper, we introduce a multiple-sets split feasibility problem (MSSFP) and a split equality fixed point problem (SEFPP), the MSSFP is to find a pair $(x,y)$ such that

$$\begin{aligned} (x,y)\in C\times Q:=\bigcap_{i=1}^{t_{1}}C_{i} \times \bigcap_{j=1}^{r_{1}}Q_{j} \quad\text{and}\quad (A_{1}x,B_{1}y)\in D\times \Theta:= \bigcap_{i=1}^{t_{2}}D_{i} \times \bigcap_{j=1}^{r_{2}}\Theta _{j}. \end{aligned}$$

(1.11)

The SEFPP is to find a pair $(x,y)$ such that

$$\begin{aligned} x\in F(T_{1}),\qquad y\in F(T_{2})\quad \text{and} \quad A_{2}x=B_{2}y, \end{aligned}$$

(1.12)

where $T_{1}, T_{2}$ are two firmly quasi-nonexpansive operators or nonexpansive operators, and $A_{1}:H_{1}\rightarrow H_{3}, A_{2}:H_{1}\rightarrow H_{3}, B_{1}:H_{2} \rightarrow H_{3}, B_{2}:H_{2}\rightarrow H_{3}$ are four bounded linear operators. $C_{i}\in H_{1},i=1,2,\ldots,t_{1}; Q_{j}\in H_{2},j=1,2,\ldots,r_{1}; D_{i}\in H_{3},i=1,2,\ldots,t_{2}; \Theta _{j}\in H_{3},j=1,2 ,\ldots,r_{2}$, are nonempty closed convex subsets.

Guan [15] proposed a new iterative scheme to solve the above problems:

$$\begin{aligned} \begin{aligned}[b] x_{k+1} ={}&T_{1} \Biggl[x_{k}-\lambda _{k}\sum_{i=1}^{t_{1}} \alpha _{i}(x_{k}-P_{C_{i,k}}x_{k})- \xi _{k}\sum_{i=1}^{t_{2}}\beta _{i}A_{1}^{*}(A_{1}x_{k}-P_{D_{i,k}}A_{1}x_{n}) \\ & {}-\tau A_{2}^{*}(A_{2}x_{k}-B_{2}y_{k}) \Biggr] \end{aligned} \end{aligned}$$

(1.13)

and

$$\begin{aligned} \begin{aligned}[b] y_{k+1} ={}&T_{2} \Biggl[y_{k}-\sigma _{k}\sum_{j=1}^{r_{1}} \gamma _{j}(y_{k}-P_{Q_{j,k}}y_{k})- \zeta _{k}\sum_{j=1}^{r_{2}}\delta _{j}B_{1}^{*}(B_{1}y_{k}-P_{ \Theta _{j,k}}B_{1}y_{k}) \\ &{} -\tau B_{2}^{*}(B_{2}y_{n}-A_{2}x_{k+1}) \Biggr]. \end{aligned} \end{aligned}$$

(1.14)

Further, he proved a weak convergence theorem under some mild restrictions on the parameters.

Inspired by the results, we propose the following questions.

Question 1.1

Can we modify iterative scheme (1.8) to a more general iterative scheme for solving a multiple-sets split feasibility problem and a split equality fixed point problem instead of solving the split equality problem?

Question 1.2

Can we obtain a strong convergence by the iterative scheme for MSSFP and SEFPP?

The purpose of this paper is to construct a new algorithm for MSSFP and SEFPP so that strong convergence is guaranteed. The paper is organized as follows. In Sect. 2, we denote the concept of minimal norm solution of MSSFP and SEFPP. Using Tychonov regularization, we obtain a net of solutions for some minimization problem approximating such minimal norm solutions (see Theorem 2.5). In Sect. 3, we introduce an algorithm and prove the strong convergence of the algorithm, more importantly, its limit is the minimum-norm solution of MSSFP and SEFPP (see Theorem 3.2).

Throughout the rest of this paper, let I denote the identity operator on a Hilbert space H, and let ▽f denote the gradient of the function $f:H\rightarrow R$.

Definition 1.3

([21])

An operator T on a Hilbert space H is nonexpansive if, for each x and y in H,

$$\begin{aligned} \Vert Tx-Ty \Vert \leq \Vert x-y \Vert . \end{aligned}$$

T is said to be strictly nonexpansive if, for each x and y in H,

$$\begin{aligned} \Vert Tx-Ty \Vert < \Vert x-y \Vert . \end{aligned}$$

An operator T on a Hilbert space H is firmly nonexpansive if, for each x and y in H,

$$\begin{aligned} \langle x-y,Tx-Ty\rangle \geq \Vert Tx-Ty \Vert ^{2}. \end{aligned}$$

T is firmly nonexpansive if $2T-I$ is nonexpansive, Equivalently, $T=(I+S)/2$, where $S: H\rightarrow H$ is nonexpansive.

T is said to be averaged if there exist $0<\alpha <1$ and a nonexpansive operator N such that

$$\begin{aligned} T=(1-\alpha )I+\alpha N. \end{aligned}$$

T is said to be quasi-nonexpansive if $F(T)\neq \emptyset$ for each x in H, q in $F(T)$,

$$\begin{aligned} \Vert Tx-q \Vert \leq \Vert x-q \Vert . \end{aligned}$$

T is said to be strictly quasi-nonexpansive if $F(T)\neq \emptyset$ for each x in H, q in $F(T)$,

$$\begin{aligned} \Vert Tx-q \Vert < \Vert x-q \Vert . \end{aligned}$$

T is said to be firmly quasi-nonexpansive if $F(T)\neq \emptyset$ for each x in H, q in $F(T)$,

$$\begin{aligned} \Vert Tx-q \Vert ^{2}\leq \Vert x-q \Vert ^{2}- \Vert x-Tx \Vert ^{2}. \end{aligned}$$

Let $P_{S}$ denote the projection from H onto a nonempty closed convex subset S of H; that is,

$$\begin{aligned} P_{S}(w)= \Bigl\{ x\in S,\min_{x\in S} \Vert x-w \Vert \Bigr\} . \end{aligned}$$

It is well known that $P_{S}(w)$ is characterized by the inequality

$$\begin{aligned} \bigl\langle w-P_{S}(w),x-P_{S}(w) \bigr\rangle \leq 0, \quad \forall x\in S, \end{aligned}$$

$P_{S} and (I-P_{S})$ are nonexpansive, averaged, and firmly nonexpansive.

Next we should collect some elementary facts which will be used in the proofs of our main results.

Lemma 1.4

([13, 14])

Let X be a Banach space, C be a closed convex subset of X, and $T: C\rightarrow C$ be a nonexpansive mapping with $\mathrm{Fix}(T)\neq \emptyset$. If $\{x_{n}\}$ is a sequence in C weakly converging to x and if $\{(I-T)x_{n}\}$ converges strongly to y, then $(I-T)x=y$.

Lemma 1.5

([2])

Let $\{s_{n}\}$ be a sequence of nonnegative real numbers, $\{\alpha _{n}\}$ be a sequence of real numbers in [0,1] with $\sum_{n=1}^{\infty }\alpha _{n}=\infty$, $\{u_{n}\}$ be a sequence of nonnegative real numbers with $\sum_{n=1}^{\infty }u_{n}<\infty$, and $\{t_{n}\}$ be a sequence of real numbers with $\limsup_{n}t_{n}\leq 0$. Suppose that

$$\begin{aligned} s_{n+1}=(1-\alpha _{n})s_{n}+\alpha _{n}t_{n}+u_{n},\quad \forall n \in N. \end{aligned}$$

Then $\lim_{n\rightarrow \infty }s_{n}=0$.

Lemma 1.6

([20])

Let $\{w_{n}\}, \{z_{n}\}$ be bounded sequences in a Banach space, and let $\{\beta _{n}\}$ be a sequence in [0,1] which satisfies the following condition:

$$\begin{aligned} 0< \liminf_{n\rightarrow \infty }\beta _{n}\leq \limsup _{n\rightarrow \infty }\beta _{n}< 1. \end{aligned}$$

Suppose that $w_{n+1}=(1-\beta _{n})w_{n}+\beta _{n}z_{n}$ and $\limsup_{n\rightarrow \infty }\|z_{n+1}-z_{n}\|-\|w_{n+1}-w_{n}\|\leq 0$, then $\lim_{n\rightarrow \infty }\|z_{n}-w_{n}\|=0$.

Lemma 1.7

([4])

Let f be a convex and differentiable function, and let C be a closed convex subset of H. Then $x\in C$ is a solution of the problem

$$\begin{aligned} \min_{x\in C}f(x) \end{aligned}$$

if and only if $x\in C$ satisfies the following optimality condition:

$$\begin{aligned} \bigl\langle \bigtriangledown f(x),v-x \bigr\rangle \geq 0,\quad \forall v\in C. \end{aligned}$$

Moreover, if f is, in addition, strictly convex and coercive, then the minimization problem has a unique solution.

Lemma 1.8

([4])

Let $A,B$ be averaged operators and suppose that $\mathrm{Fix}(A)\cap \mathrm{Fix}(B)$ is nonempty. Then $\mathrm{Fix}(A)\cap \mathrm{Fix}(B)=\mathrm{Fix}(AB)=\mathrm{Fix}(BA)$.

2 Minimum-norm solution of SEFPP and MSSFP

In this section, we define the concept of the minimal norm solution of MSSFP (1.11) and SEFPP (1.12). Using Tychonov regularization, we obtain a net of solutions for some minimization problems approximating such minimal norm solutions.

We use Γ to denote the solution set of SEFPP and MSSFP, i.e.,

$$\begin{aligned} \begin{aligned}[b] \Gamma = {}& \Biggl\{ (x,y) \in H_{1} \times H_{2},x \in \bigcap_{i=1}^{t_{1}}C_{i} ,y \in \bigcap_{j=1}^{r_{1}}Q_{j},A_{1}x \in \bigcap_{i=1}^{t_{2}}D_{i} ,B_{1} y \in \bigcap_{j=1}^{r_{2}} \Theta _{j},A_{2} x=B_{2} y, \\ &x \in F(T_{1}),y \in F(T_{2}) \Biggr\} \end{aligned} \end{aligned}$$

and assume the consistency of SEFPP and MSSFP, so that Γ is closed, convex, and nonempty.

We aim to propose a new iterative algorithm for solving MSSFP (1.11) and SEFPP (1.12). Let the sets $C_{i}, Q_{i}, D_{i}, \Theta _{i}$ be defined as

$$\begin{aligned} C_{i}= \bigl\{ x\in H_{1}:c_{i}(x)\leq 0 \bigr\} ,\qquad Q_{j}= \bigl\{ y\in H_{2}:q_{j}(y) \leq 0 \bigr\} \end{aligned}$$

(2.1)

and

$$\begin{aligned} D_{i}= \bigl\{ u\in H_{1}:d_{i}(u)\leq 0 \bigr\} ,\qquad \Theta _{j}= \bigl\{ v\in H_{2}:\phi _{j}(v) \leq 0 \bigr\} , \end{aligned}$$

(2.2)

where $c_{i}:H_{1}\rightarrow \mathbb{R},i=1,2,\ldots,t_{1};q_{i}:H_{2} \rightarrow \mathbb{R},j=1,2,\ldots,r_{1};d_{i}:H_{3}\rightarrow \mathbb{R},i=1,2,\ldots,t_{2}$; and $\phi _{i}:H_{3}\rightarrow \mathbb{R},j=1,2,\ldots,r_{2}$, are convex functions.

In order to solve MSSFP (1.11) and SEFPP (1.12), we consider the following minimization problem:

$$\begin{aligned} \min_{(x,y) \in \mathrm{Fix}(T_{1})\times \mathrm{Fix}(T_{2})}h(x,y), \end{aligned}$$

(2.3)

where

$$\begin{aligned} &h(x,y)=f(x)+g(y)+\frac{1}{2} \Vert A_{2}x-B_{2}y \Vert ^{2}, \\ &f(x)=\frac{1}{2}\sum_{i=1}^{t_{1}} \alpha _{i} \bigl\Vert (I-P_{C_{i}})x \bigr\Vert ^{2}+ \frac{1}{2}\sum_{i=1}^{t_{2}} \beta _{i} \bigl\Vert (I-P_{D_{i}})A_{1}x \bigr\Vert ^{2}, \\ &g(y)=\frac{1}{2}\sum_{j=1}^{r_{1}} \gamma _{j} \bigl\Vert (I-P_{Q_{j}})y \bigr\Vert ^{2}+ \frac{1}{2}\sum_{j=1}^{r_{2}} \delta _{j} \bigl\Vert (I-P_{\Theta _{j}})B_{1}y \bigr\Vert ^{2}, \end{aligned}$$

here $\sum_{i=1}^{t_{1}}\alpha _{i}=\sum_{i=1}^{t_{2}}\beta _{i}= \sum_{j=1}^{r_{1}}\gamma _{j}=\sum_{j=1}^{r_{2}}\delta _{j}=1$. The minimization problem is in general ill-posed. A classical way to deal with such a possibly ill-posed problem is the well-known Tychonov regularization, which approximates a solution of problem (2.3) by the unique minimizer of the regularized problem

$$\begin{aligned} \min_{(x,y) \in \mathrm{Fix}(T_{1})\times \mathrm{Fix}(T_{2})}h_{\alpha }(x,y)=f(x)+g(y)+ \frac{1}{2} \Vert A_{2}x-B_{2}y \Vert ^{2}+ \frac{1}{2}\alpha \bigl( \Vert x \Vert ^{2}+ \Vert y \Vert ^{2} \bigr), \end{aligned}$$

(2.4)

where $\alpha >0$ is the regularization parameter. Denote by $w_{\alpha }=(x_{\alpha },y_{\alpha })$ the unique solution of (2.4).

Lemma 2.1

For the sake of convenience, let $H=H_{1}\times H_{2}$, define:

$$\begin{aligned} &M:= \begin{pmatrix} \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}}) & 0 \\ 0 & \sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}}) \end{pmatrix} , \\ &N:= \begin{pmatrix} \sum_{i=1}^{t_{2}}\beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1} & 0 \\ 0 & \sum_{j=1}^{r_{2}}\delta _{j}B_{1}^{*}(I-P_{\Theta _{j}})B_{1} \end{pmatrix} , \end{aligned}$$

and

$$\begin{aligned} G:=(A_{2},-B_{2}), G^{*}G:= \begin{pmatrix} A_{2}^{*}A_{2}&-A_{2}^{*}B_{2} \\ -B_{2}^{*}A_{2}&B_{2}^{*}B_{2}\end{pmatrix} , \end{aligned}$$

where $G:H\rightarrow H_{3}$ and $G^{*}G:H\rightarrow H$, then $M, \lambda _{1}N$ and $\lambda _{2}G^{*}G$ are firmly nonexpansive operators, where $0<\lambda _{1}<1/(\max \{\rho (A_{1}^{*}A_{1}),\rho (B_{1}^{*}B_{1})\})$ and $0<\lambda _{2}<1/\rho (G^{*}G)$.

Proof

By $(I-P_{S})$ and $P_{S}$ are firmly nonexpansive operators, $x=(x_{1},x_{2})\in H_{1}\times H_{2}, y=(y_{1},y_{2})\in H_{1} \times H_{2}. \|Mx-My\|^{2}=\|\sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x_{1}- \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})y_{1}\|^{2}+\|\sum_{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}})x_{2}-\sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}})y_{2} \|^{2}\leq \langle x_{1}-y_{1}, \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x_{1}- \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})y_{1}\rangle +\langle x_{2}-y_{2}, \sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}})x_{2}-\sum_{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}})y_{2}\rangle =\langle x-y,Mx-My\rangle$, so M is a firmly nonexpansive operator. Similarly, we can prove that $\lambda _{1}N$ and $\lambda _{2}G^{*}G$ are firmly nonexpansive operators. □

Proposition 2.2

Let $T=T_{1}\times T_{2}$, which is mentioned in (1.12), $w=(x,y)$. For any $\alpha >0$, the solution $w_{\alpha }=(x_{\alpha },y_{\alpha })$ of (2.4) is uniquely defined. Then $w_{\alpha }=(x_{\alpha },y_{\alpha })$ is characterized by the inequality

$$\begin{aligned} \bigl\langle \bigtriangledown h(w_{\alpha })+\alpha w_{\alpha },w-w_{\alpha } \bigr\rangle \geq 0, \quad\forall w\in \mathrm{Fix}(T), \end{aligned}$$

i.e.,

$$\begin{aligned} & \Biggl\langle \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x_{\alpha }+ \sum _{i=1}^{t_{2}}\beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}x_{\alpha }+A_{2}^{*}(A_{2}x_{\alpha }-B_{2}y_{\alpha })+ \alpha x_{\alpha },x-x_{\alpha } \Biggr\rangle \geq 0, \\ &\quad \forall x \in \mathrm{Fix}(T_{1}); \end{aligned}$$

and

$$\begin{aligned} & \Biggl\langle \sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}})y_{\alpha }+ \sum _{j=1}^{r_{2}}\delta _{j}B_{1}^{*}(I-P_{\Theta _{j}})B_{1}y_{\alpha }-B_{2}^{*}(A_{2}x_{\alpha }-B_{2}y_{\alpha })+ \alpha y_{\alpha },y-y_{\alpha } \Biggr\rangle \geq 0, \\ &\quad \forall x \in \mathrm{Fix}(T_{2}). \end{aligned}$$

Proof

It is well known that $h(x,y)=\frac{1}{2}\sum_{i=1}^{t_{1}}\alpha _{i}\|(I-P_{C_{i}})x\|^{2}+ \frac{1}{2}\sum_{i=1}^{t_{2}}\beta _{i}\|(I-P_{D_{i}})A_{1}x\|^{2}+ \frac{1}{2}\sum_{j=1}^{r_{1}}\gamma _{j}\|(I-P_{Q_{j}})y\|^{2}+ \frac{1}{2}\sum_{j=1}^{r_{2}}\delta _{j}\|(I-P_{\Theta _{j}})B_{1}y \|^{2}+\frac{1}{2}\|A_{2}x-B_{2}y\|^{2}$ is convex and differentiable with gradient $\bigtriangledown h(w)=Mw+Nw+G^{*}Gw, h_{\alpha }(w)=h(w)+\frac{1}{2} \alpha \|w\|^{2}$. We can get that $h_{\alpha }$ is strictly convex, coercive, and differentiable with gradient

$$\begin{aligned} \begin{aligned}[b] \bigtriangledown h_{\alpha }(w)=Mw+Nw+G^{*}Gw+ \alpha w. \end{aligned} \end{aligned}$$

It follows from Lemma 1.7 that $w_{\alpha }$ is characterized by the inequality

$$\begin{aligned} & \bigl\langle \bigtriangledown h(w_{\alpha })+\alpha w_{\alpha },w-w_{\alpha } \bigr\rangle \geq 0,\quad \forall w\in \mathrm{Fix}(T). \end{aligned}$$

(2.5)

We can get that

$$\begin{aligned} & \Biggl\langle \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x+ \sum_{i=1}^{t_{2}} \beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}x+A_{2}^{*}(Ax_{\alpha }-By_{\alpha })+ \alpha x_{\alpha },x-x_{\alpha } \Biggr\rangle \geq 0, \\ &\quad \forall x \in \mathrm{Fix}(T_{1}); \end{aligned}$$

and

$$\begin{aligned} & \Biggl\langle \sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}})y+ \sum_{j=1}^{r_{2}} \delta _{j}B_{1}^{*}(I-P_{\Theta _{j}})B_{1}y-B_{2}^{*}(Ax_{\alpha }-By_{\alpha })+ \alpha y_{\alpha },y-y_{\alpha } \Biggr\rangle \geq 0, \\ &\quad \forall x \in \mathrm{Fix}(T_{2}). \end{aligned}$$

 □

Definition 2.3

An element $\bar{w}=(\bar{x},\bar{y})\in \Gamma$ is said to be the $minimal norm solution$ of MSSFP (1.11) and SEFPP (1.12) if $\|\bar{w}\|=\inf_{w\in \Gamma } \|w\|$.

The next result collects some useful properties of $\{w_{\alpha }\}$, the unique solution of (2.4).

Proposition 2.4

Let $w_{\alpha }$ be given as the unique solution of (2.4) for any sequence $\{\alpha _{n}\}$ such that $\lim_{n}\alpha _{n}=0$, let $w_{\alpha _{n}}$ be abbreviated as $w_{n}$. Then the following assertions hold:

• (i) $\|w_{\alpha }\|$ is decreasing for $\alpha \in (0,\infty )$;

• (ii) $\alpha \mapsto w_{\alpha }$ defines a continuous curve from $(0,\infty )$ to H.

Proof

Let $\alpha >\beta >0$; since $w_{\alpha }$ and $w_{\beta }$ are the unique minimizers of $h_{\alpha }$ and $h_{\beta }$, $w_{\alpha }=(x_{\alpha },y_{\alpha }), w_{\beta }=(x_{\beta },y_{\beta })$, respectively, we can get that

$$\begin{aligned} h_{\alpha }(w_{\alpha })=h(w_{\alpha })+\frac{1}{2}\alpha \Vert w_{\alpha } \Vert ^{2} \leq h(w_{\beta })+ \frac{1}{2}\alpha \Vert w_{\beta } \Vert ^{2}=h_{\alpha }(w_{\beta }) \end{aligned}$$

and

$$\begin{aligned} h_{\beta }(w_{\beta })=h(w_{\beta })+\frac{1}{2}\beta \Vert w_{\beta } \Vert ^{2}\leq h(w_{\alpha })+ \frac{1}{2}\beta \Vert w_{\alpha } \Vert ^{2}=h_{\beta }(w_{\alpha }). \end{aligned}$$

Hence we can obtain that $\|w_{\alpha }\|\leq \|w_{\beta }\|$. That is to say, $\|w_{\alpha }\|$ is decreasing for $\alpha \in (0,\infty )$.

By Proposition 2.2, we have

$$\begin{aligned} \bigl\langle \bigtriangledown h(w_{\alpha })+\alpha w_{\alpha },w_{\beta }-w_{\alpha } \bigr\rangle \geq 0 \end{aligned}$$

and

$$\begin{aligned} \bigl\langle \bigtriangledown h(w_{\beta })+\beta w_{\beta },w_{\alpha }-w_{\beta } \bigr\rangle \geq 0. \end{aligned}$$

It follows that

$$\begin{aligned} \langle w_{\alpha }-w_{\beta },\alpha w_{\alpha }-\beta w_{\beta }\rangle \leq \bigl\langle w_{\alpha }-w_{\beta }, \bigtriangledown h(w_{\beta })- \bigtriangledown h(w_{\alpha }) \bigr\rangle . \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned}[b] & \bigl\langle w_{\alpha }-w_{\beta }, \bigtriangledown h(w_{\beta })- \bigtriangledown h(w_{\alpha }) \bigr\rangle \\ &\quad=\langle w_{\alpha }-w_{\beta },Mw_{\beta }+Nw_{\beta }-Mw_{\alpha }-Nw_{\alpha } \rangle \\ &\qquad{} + \bigl\langle w_{\alpha }-w_{\beta },G^{*}G(w_{\beta }-w_{\alpha }) \bigr\rangle \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \bigl\langle w_{\alpha }-w_{\beta },G^{*}G(w_{\beta }-w_{\alpha }) \bigr\rangle \leq 0. \end{aligned}$$

(2.6)

Then

$$\begin{aligned} &\begin{aligned}[b] & \Biggl\langle x_{\alpha }-x_{\beta }, \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x_{\beta }- \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x_{\alpha } \Biggr\rangle \\ &\quad\leq -\sum_{i=1}^{t_{1}}\alpha _{i} \bigl\Vert (I-P_{C_{i}})x_{\alpha }-(I-P_{C_{i}})x_{\beta } \bigr\Vert ^{2}\leq 0 ,\end{aligned} \end{aligned}$$

(2.7)

$$\begin{aligned} &\begin{aligned}[b] & \Biggl\langle x_{\alpha }-x_{\beta }, \sum_{i=1}^{t_{2}}\beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}x_{\beta }- \sum_{i=1}^{t_{2}}\beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}x_{\alpha } \Biggr\rangle \\ &\quad=\sum_{i=1}^{t_{2}}\beta _{i} \bigl\langle A_{1}x_{\alpha }-A_{1}x_{\beta },(I-P_{D_{i}})A_{1}x_{\beta }-(I-P_{D_{i}})A_{1}x_{\alpha } \bigr\rangle \\ &\quad\leq -\sum_{i=1}^{t_{2}}\beta _{i} \bigl\Vert (I-P_{D_{i}})A_{1}x_{\alpha }-(I-P_{D_{i}})A_{1}x_{\beta } \bigr\Vert ^{2}\leq 0, \end{aligned} \end{aligned}$$

(2.8)

$$\begin{aligned} &\begin{aligned}[b]& \Biggl\langle y_{\alpha }-y_{\beta }, \sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}})y_{\beta }- \sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}})y_{\alpha } \Biggr\rangle \\ &\quad\leq -\sum_{j=1}^{r_{1}}\gamma _{j} \bigl\Vert (I-P_{Q_{j}})y_{\alpha }-(I-P_{Q_{j}})y_{\beta } \bigr\Vert ^{2}\leq 0 ,\end{aligned} \end{aligned}$$

(2.9)

$$\begin{aligned} &\begin{aligned}[b]& \Biggl\langle y_{\alpha }-y_{\beta }, \sum_{j=1}^{r_{2}}\delta _{j}B_{1}^{*}(I-P_{ \Theta _{j}})B_{1}y_{\beta }- \sum_{j=1}^{r_{2}}\delta _{j}B_{1}^{*}(I-P_{ \Theta _{j}})B_{1}y_{\alpha } \Biggr\rangle \\ &\quad=\sum_{j=1}^{r_{2}}\delta _{j} \bigl\langle B_{1}y_{\alpha }-B_{1}y_{\beta },(I-P_{\Theta _{j}})B_{1}y_{\beta }-(I-P_{\Theta _{j}})B_{1}y_{\alpha } \bigr\rangle \\ &\quad\leq -\sum_{j=1}^{r_{2}}\delta _{j} \bigl\Vert (I-P_{\Theta _{j}})B_{1}y_{\alpha }-(I-P_{\Theta _{j}})B_{1}y_{\beta } \bigr\Vert ^{2}\leq 0. \end{aligned} \end{aligned}$$

(2.10)

By (2.6)–(2.10), we can get

$$\begin{aligned} \bigl\langle w_{\alpha }-w_{\beta },\bigtriangledown h(w_{\beta })- \bigtriangledown h(w_{\alpha }) \bigr\rangle \leq 0. \end{aligned}$$

Hence

$$\begin{aligned} &\langle w_{\alpha }-w_{\beta },\alpha w_{\alpha }-\beta w_{\beta }\rangle \leq 0 \\ &\alpha \Vert w_{\alpha }-w_{\beta } \Vert ^{2}\leq \bigl\langle w_{\alpha }-w_{\beta },( \beta -\alpha )w_{\beta } \bigr\rangle . \end{aligned}$$

It turns out that

$$\begin{aligned} \Vert w_{\alpha }-w_{\beta } \Vert \leq \vert \alpha -\beta \vert /\alpha \Vert w_{\beta } \Vert . \end{aligned}$$

Thus $\alpha \mapsto w_{\alpha }$ defines a continuous curve from $(0,\infty )$ to H. □

Theorem 2.5

Let $w_{\alpha }$ be given as the unique solution of (2.4). Then $w_{\alpha }$ converges strongly as $\alpha \rightarrow 0$ to the minimum-norm solution of MSSFP (1.11) and SEFPP (1.12).

Proof

For any $0<\alpha <\infty, w_{\alpha }$ is given as (2.4), it follows that

$$\begin{aligned} h_{\alpha }(w_{\alpha })=h(w_{\alpha })+\frac{1}{2}\alpha \Vert w_{\alpha } \Vert ^{2} \leq h(\bar{w})+\frac{1}{2} \alpha \Vert \bar{w} \Vert ^{2}=h_{\alpha }(\bar{w}). \end{aligned}$$

Since $\bar{w}\in \Gamma$ is a solution for MSSFP and SEFPP, we get

$$\begin{aligned} h(w_{\alpha })+\frac{1}{2}\alpha \Vert w_{\alpha } \Vert ^{2}\leq \frac{1}{2} \alpha \Vert \bar{w} \Vert ^{2}. \end{aligned}$$

Hence, $\|w_{\alpha }\|\leq \|\bar{w}\|$ for all $\alpha >0$. That is to say, $\{w_{\alpha }\}$ is a bounded net in $H=H_{1}\times H_{2}$.

For any sequence $\{\alpha _{n}\}$ such that $\lim_{n}\alpha _{n}=0$, let $w_{\alpha _{n}}$ be abbreviated as $w_{n}$. All we need to prove is that $\{w_{n}\}$ contains a subsequence converging strongly to w̄.

Indeed $\{w_{n}\}$ is bounded and $\mathrm{Fix}(T)$ is bounded convex. By passing to a subsequence if necessary, we may assume that $\{w_{n}\}$ converges weakly to a point $\hat{w} \in \mathrm{Fix}(T)$. By Proposition 2.2, we get that

$$\begin{aligned} \bigl\langle \bigtriangledown h(w_{n})+\alpha _{n} w_{n},\bar{w}-w_{n} \bigr\rangle \geq 0 \end{aligned}$$

and

$$\begin{aligned} \bigl\langle \bigtriangledown h(w_{n})+\alpha _{n} w_{n},\hat{w}-w_{n} \bigr\rangle \geq 0. \end{aligned}$$

(2.11)

It follows that

$$\begin{aligned} \bigl\langle \bigtriangledown h(w_{n}),\bar{w}-w_{n} \bigr\rangle \geq \alpha _{n} \langle w_{n},w_{n}-\bar{w} \rangle, \end{aligned}$$

i.e.,

$$\begin{aligned} \Biggl\langle \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x_{n}+ \sum _{i=1}^{t_{2}} \beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}x_{n}+A_{2}^{*}(Ax_{n}-By_{n}), \bar{x}-x_{n} \Biggr\rangle \geq \alpha _{n}\langle x_{n},x_{n}-\bar{x} \rangle, \end{aligned}$$

and

$$\begin{aligned} \Biggl\langle \sum_{j=1}^{r_{1}}\gamma _{j}(I-P_{Q_{j}})y_{n}+ \sum _{j=1}^{r_{2}} \delta _{j}B_{1}^{*}(I-P_{\Theta _{j}})B_{1}y_{n}-B_{2}^{*}(Ax_{n}-By_{n}), \bar{y}-y_{n} \Biggr\rangle \geq \alpha _{n}\langle y_{n},y_{n}-\bar{y} \rangle \end{aligned}$$

i.e.,

$$\begin{aligned} \begin{aligned}[b] & \bigl\langle Mw_{n}+Nw_{n}+G^{*}Gw_{n}, \bar{w}-w_{n} \bigr\rangle \geq \alpha _{n} \langle w_{n},w_{n}-\bar{w}\rangle. \end{aligned} \end{aligned}$$

By $\bar{w}\in \Gamma$,

$$\begin{aligned} \begin{aligned}[b] &\alpha _{n} \langle w_{n},w_{n}- \bar{w}\rangle \\ &\quad\leq \langle Mw_{n}-M\bar{w},\bar{w}-w_{n}\rangle + \bigl\langle G^{*}G(w_{n}- \bar{w}),\bar{w}-w_{n} \bigr\rangle +\langle Nw_{n}-N\bar{w},\bar{w}-w_{n} \rangle \\ &\quad\leq - \Biggl\Vert \sum_{i=1}^{t_{1}} \alpha _{i}(I-P_{C_{i}})x_{n}-\sum _{i=1}^{t_{1}} \alpha _{i}(I-P_{C_{i}}) \bar{x} \Biggr\Vert ^{2} \\ &\qquad{} - \Biggl\Vert \sum_{i=1}^{t_{2}} \beta _{i}(I-P_{D_{i}})A_{1}x_{n}- \sum _{i=1}^{t_{2}}\beta _{i}(I-P_{D_{i}})A_{1} \bar{x} \Biggr\Vert ^{2} \\ &\qquad{} - \Biggl\Vert \sum_{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}})y_{n}- \sum _{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}}) \bar{y} \Biggr\Vert ^{2} \\ &\qquad{} - \Biggl\Vert \sum_{j=1}^{r_{2}} \delta _{j}(I-P_{\Theta _{j}})B_{1}y_{n}- \sum _{j=1}^{r_{2}}\delta _{j}(I-P_{\Theta _{j}})B_{1} \bar{y} \Biggr\Vert ^{2} \\ &\qquad{} - \Vert Gw_{n} \Vert ^{2}, \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} & \Biggl\Vert \sum_{i=1}^{t_{1}} \alpha _{i}(I-P_{C_{i}})x_{n}-\sum _{i=1}^{t_{1}} \alpha _{i}(I-P_{C_{i}}) \bar{x} \Biggr\Vert ^{2} \\ &\qquad{} + \Biggl\Vert \sum_{i=1}^{t_{2}} \beta _{i}(I-P_{D_{i}})A_{1}x_{n}- \sum _{i=1}^{t_{2}}\beta _{i}(I-P_{D_{i}})A_{1} \bar{x} \Biggr\Vert ^{2} \\ &\qquad{} + \Biggl\Vert \sum_{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}})y_{n}- \sum _{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}}) \bar{y} \Biggr\Vert ^{2} \\ &\qquad{} + \Biggl\Vert \sum_{j=1}^{r_{2}} \delta _{j}(I-P_{\Theta _{j}})B_{1}y_{n}- \sum _{j=1}^{r_{2}}\delta _{j}(I-P_{\Theta _{j}})B_{1} \bar{y} \Biggr\Vert ^{2} \\ & \qquad{}+ \Vert Gw_{n} \Vert ^{2} \\ &\quad\leq \alpha _{n} \langle w_{n},w_{n}-\bar{w} \rangle \leq \alpha _{n} \Vert w_{n} \Vert \Vert w_{n}-\bar{w} \Vert \leq 2\alpha _{n} \Vert \bar{w} \Vert ^{2}\rightarrow 0. \end{aligned}$$

Furthermore, note that $\{w_{n}\}$ converges weakly to a point $\hat{w}\in \mathrm{Fix}(T)$, then $\{h(w_{n})\}$ converges weakly to $h(\hat{w})$. It follows that $h(\hat{w})=0$, i.e., $\hat{w}\in \Gamma$.

By (2.11),

$$\begin{aligned} \bigl\langle \bigtriangledown h(w_{n})+\alpha _{n} w_{n},\hat{w}-w_{n} \bigr\rangle \geq 0, \end{aligned}$$

i.e.,

$$\begin{aligned} & \bigl\langle Mw_{n}+Nw_{n}+G^{*}Gw_{n}+ \alpha _{n}w_{n},\hat{w}-w_{n} \bigr\rangle \geq 0, \\ &\begin{aligned}[b] & \bigl\langle Mw_{n}+Nw_{n}+G^{*}Gw_{n}+ \alpha _{n}w_{n},\hat{w}-w_{n} \bigr\rangle \\ &\quad=\langle Mw_{n}-M\hat{w},\hat{w}-w_{n}\rangle +\langle Nw_{n}-N\hat{w}, \hat{w}-w_{n}\rangle + \bigl\langle G^{*}G(w_{n}-\hat{w}),\hat{w}-w_{n} \bigr\rangle \\ &\qquad{} +\langle \alpha _{n}w_{n}-\alpha _{n} \hat{w}, \hat{w}-w_{n} \rangle +\langle \alpha _{n}\hat{w}, \hat{w}-w_{n}\rangle \\ &\quad\leq - \Vert Mw_{n}-M\hat{w} \Vert ^{2}- \Vert Nw_{n}-N\hat{w} \Vert ^{2}- \bigl\Vert G(w_{n}- \hat{w}) \bigr\Vert ^{2} \\ &\qquad{}+\langle \alpha _{n}\hat{w}, \hat{w}-w_{n}\rangle - \alpha _{n} \Vert w_{n}- \hat{w} \Vert ^{2} \\ &\quad\geq 0. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \Vert Mw_{n}-M\hat{w} \Vert ^{2}+ \Vert Nw_{n}-N\hat{w} \Vert ^{2}+ \bigl\Vert G(w_{n}- \hat{w}) \bigr\Vert ^{2}+ \alpha _{n} \Vert w_{n}-\hat{w} \Vert ^{2}\leq \langle \alpha _{n} \hat{w},\hat{w}-w_{n} \rangle, \end{aligned}$$

we have

$$\begin{aligned} \Vert w_{n}-\hat{w} \Vert ^{2}\leq \langle \hat{w}, \hat{w}-w_{n}\rangle. \end{aligned}$$

Consequently, that $\{w_{n}\}$ converges weakly to ŵ actually implies that $\{w_{n}\}$ converges strongly to ŵ. At last, we prove that $\hat{w}=\bar{w}$, and this finishes the proof.

Since $\{w_{n}\}$ converges weakly to ŵ and $\|w_{n}\|\leq \|\bar{w}\|$, we can get that

$$\begin{aligned} \Vert \hat{w} \Vert \leq \liminf_{n} \Vert w_{n} \Vert \leq \Vert \bar{w} \Vert = \min \bigl\{ \Vert w \Vert :w\in \Gamma \bigr\} . \end{aligned}$$

This shows that ŵ is also a point in Γ which assumes a minimum norm. Due to the uniqueness of a minimum-norm element, we obtain $\hat{w}=\bar{w}$. □

Finally, we introduce another method to get the minimum-norm solution of MSSFP and SEFPP.

Lemma 2.6

Let $S=I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G$, where $0<\lambda _{1}<1/(\max \{\rho (A_{1}^{*}A_{1}), \rho (B_{1}^{*}B_{1})\}), 0<\lambda _{2}<1/\rho (G^{*}G), \sigma _{i}>0, i=1, 2, 3$. $\sigma _{1}+\sigma _{2}+\sigma _{3}\leq 1$ with $\rho (A_{1}^{*}A_{1}), \rho ( B_{1}^{*}B_{1}), \rho (G^{*}G)$ being the spectral radius of the self-adjoint operator $A_{1}^{*}A_{1}, B_{1}^{*}B_{1}, G^{*}G$ on H, then we have the following:

(1) $\|S\|\leq 1$ (i.e., S is nonexpansive) and averaged;

(2) $\mathrm{Fix}(S)=\{(x,y)\in H_{1}\times H_{2}, x \in \bigcap_{i=1}^{t_{1}}C_{i}, y \in \bigcap_{j=1}^{r_{1}}Q_{j}, A_{1}x \in \bigcap_{i=1}^{t_{2}}D_{i} , B_{1} y \in \bigcap_{j=1}^{r_{2}}\Theta _{j},A_{2}x=B_{2}y\}, \mathrm{Fix}(P_{\mathrm{Fix}(T)}S)=\mathrm{Fix}(P_{\mathrm{Fix}(T)}) \cap \mathrm{Fix}(S)=\Gamma$;

(3) $w\in \mathrm{Fix}(P_{\mathrm{Fix}(T)}S)$ if and only if w is a solution of the variational inequality $\langle \bigtriangledown h(x,y), v-w\rangle, \forall v\in \mathrm{Fix}(T)$.

Proof

(1)

$$\begin{aligned} & \Vert Mx-My \Vert ^{2} \\ &\quad= \Biggl\Vert \sum_{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})x_{1}- \sum _{i=1}^{t_{1}}\alpha _{i}(I-P_{C_{i}})y_{1} \Biggr\Vert ^{2} \\ & \qquad{} + \Biggl\Vert \sum_{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}})x_{2}-\sum _{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}})y_{2} \Biggr\Vert ^{2} \\ &\quad\leq \Vert x-y \Vert ^{2}, \\ & \Vert \lambda _{1}Nx-\lambda _{1}Ny \Vert ^{2} \\ &\quad=\lambda _{1}^{2} \Biggl\Vert \sum _{i=1}^{t_{2}} \beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}x_{1}- \sum_{i=1}^{t_{2}}\beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}y_{1} \Biggr\Vert ^{2} \\ &\qquad{} +\lambda _{1}^{2} \Biggl\Vert \sum _{j=1}^{r_{2}}\delta _{j}B_{1}^{*}(I-P_{\Theta _{j}})B_{1}x_{2}- \sum_{j=1}^{r_{2}}\delta _{j}B_{1}^{*}(I-P_{\Theta _{j}})B_{1}y_{2} \Biggr\Vert ^{2} \\ &\quad\leq \lambda _{1} \Biggl\Vert \sum _{i=1}^{t_{2}} \beta _{i}(I-P_{D_{i}})A_{1}x_{1}- \sum_{i=1}^{t_{2}}\beta _{i}(I-P_{D_{i}})A_{1}y_{1} \Biggr\Vert ^{2} \\ &\qquad{} +\lambda _{1} \Biggl\Vert \sum _{j=1}^{r_{2}} \delta _{j}(I-P_{\Theta _{j}})B_{1}x_{2}- \sum_{j=1}^{r_{2}}\delta _{j}(I-P_{\Theta _{j}})B_{1}y_{2} \Biggr\Vert ^{2} \\ &\quad\leq \lambda _{1} \Vert A_{1}x_{1}-A_{1}y_{1} \Vert ^{2}+\lambda _{1} \Vert B_{1}x_{2}-B_{1}y_{2} \Vert ^{2} \\ &\quad\leq \Vert x_{1}-y_{1} \Vert ^{2}+ \Vert x_{2}-y_{2} \Vert ^{2}= \Vert x-y \Vert ^{2}. \end{aligned}$$

$\lambda _{2}\|G^{*}G(x-y)\|\leq \|x-y\|$.

Let $S_{1}=\sigma _{1}M+\sigma _{2}\lambda _{1}N+\sigma _{3}\lambda _{2}G^{*}G$, we have

$$\begin{aligned} & \Vert S_{1}x-S_{2}y \Vert \\ &\quad= \bigl\Vert \sigma _{1}Mx-\sigma _{1}My +\sigma _{2}\lambda _{1}Nx-\sigma _{2} \lambda _{1}Ny+\sigma _{3}\lambda _{2}G^{*}Gx- \sigma _{3}\lambda _{2}G^{*}Gy \bigr\Vert \\ &\quad\leq \sigma _{1} \Vert Mx-My \Vert +\sigma _{2} \Vert \lambda _{1}Nx-\lambda _{1}Ny \Vert +\sigma _{3} \bigl\Vert \lambda _{2}G^{*}Gx-\lambda _{2}G^{*}Gy \bigr\Vert \\ &\quad\leq (\sigma _{1}+\sigma _{2}+\sigma _{3}) \Vert x-y \Vert \leq \Vert x-y \Vert . \end{aligned}$$

We can get that $S_{1}$ is a nonexpansive operator.

$$\begin{aligned} &\Vert Sx-Sy \Vert ^{2} \\ &\quad= \bigl\Vert x-y-(S_{1}x-S_{1}y) \bigr\Vert ^{2} \\ &\quad= \Vert x-y \Vert ^{2}+ \Vert S_{1}x-S_{2}y \Vert ^{2}-2\langle x-y,S_{1}x-S_{1}y \rangle \\ &\quad\leq \Vert x-y \Vert ^{2}+2 \Vert \sigma _{1}Mx- \sigma _{1}My \Vert ^{2}+2 \Vert \sigma _{2} \lambda _{1}Nx-\sigma _{2}\lambda _{1}Ny \Vert ^{2} \\ &\qquad{} +2 \bigl\Vert \sigma _{3}\lambda _{2}G^{*}Gx- \sigma _{3}\lambda _{2}G^{*}Gy \bigr\Vert ^{2}-2\langle x-y,S_{1}x-S_{1}y\rangle \\ &\quad\leq \Vert x-y \Vert ^{2}+2\sigma _{1}\langle x-y, \sigma _{1}Mx-\sigma _{1}My \rangle +2\sigma _{2} \langle x-y,\sigma _{2}\lambda _{1}Nx-\sigma _{2} \lambda _{1}Ny\rangle \\ & \qquad{}+2\sigma _{3} \bigl\langle x-y,\sigma _{3} \lambda _{2}G^{*}Gx- \sigma _{3}\lambda _{2}G^{*}Gy \bigr\rangle -2\langle x-y,S_{1}x-S_{1}y \rangle \\ &\quad\leq \Vert x-y \Vert ^{2}+2 \bigl\langle x-y,\sigma _{1}Mx-\sigma _{1}My+\sigma _{2} \lambda _{1}Nx-\sigma _{2}\lambda _{1}Ny+\sigma _{3}\lambda _{2}G^{*}G(x-y) \bigr\rangle \\ &\qquad{} -2\langle x-y,S_{1}x-S_{1}y\rangle \\ &\quad\leq \Vert x-y \Vert ^{2} \end{aligned}$$

so $\|S\|\leq 1$, i.e., S is nonexpansive.

Indeed, let $\eta \in (0,1)$ such that $(\sigma _{1}+\sigma _{2}+\sigma _{3})/(1-\eta )\in (0,1]$, then $S=I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G= \eta I+(1-\eta )V$, where $V=I-\frac{1}{1-\eta }(\sigma _{1}M+\sigma _{2}\lambda _{1}N+\sigma _{3} \lambda _{2}G^{*}G)$ is a nonexpansive mapping. That is to say, S is averaged.

(2) If $w\in \{(x,y)\in H_{1}\times H_{2},x \in \bigcap_{i=1}^{t_{1}}C_{i},y \in \bigcap_{j=1}^{r_{1}}Q_{j},A_{1}x \in \bigcap_{i=1}^{t_{2}}D_{i} ,B_{1} y \in \bigcap_{j=1}^{r_{2}}\Theta _{j},A_{2}x=B_{2}y\}$, it is obvious that $w\in \mathrm{Fix}(S)$. Conversely, assuming that $w\in \mathrm{Fix}(S)$, we have $w=w-\sigma _{1}Mw-\sigma _{2}\lambda _{1}Nw-\sigma _{3}\lambda _{2}G^{*}Gw$, hence $\sigma _{1}Mw+\sigma _{2}\lambda _{1}Nw+\sigma _{3}\lambda _{2}G^{*}Gw=0, \forall \breve{w}\in \Gamma$,

$$\begin{aligned} \begin{aligned}[b] & \bigl\langle \sigma _{1}Mw+\sigma _{2}\lambda _{1}Nw+\sigma _{3}\lambda _{2}G^{*}Gw,w- \breve{w} \bigr\rangle \\ &\quad=\langle \sigma _{1}Mw,w-\breve{w}\rangle +\langle \sigma _{2} \lambda _{1}Nw,w-\breve{w}\rangle + \bigl\langle \sigma _{3}\lambda _{2}G^{*}Gw,w- \breve{w} \bigr\rangle \\ &\quad=\langle \sigma _{1}Mw-\sigma _{1}M\breve{w},w- \breve{w} \rangle + \langle \sigma _{2}\lambda _{1}Nw-\sigma _{2}\lambda _{1}N\breve{w},w- \breve{w}\rangle \\ &\qquad{} + \bigl\langle \sigma _{3}\lambda _{2}G^{*}G(w- \breve{w}),w-\breve{w} \bigr\rangle \\ &\quad\geq \sigma _{1} \Vert Mw \Vert ^{2}+\sigma _{2} \Vert \lambda _{1}Nw \Vert ^{2}+\sigma _{3} \bigl\Vert \lambda _{2}G^{*}Gw \bigr\Vert ^{2} \\ &\quad\geq \Vert \sigma _{1}Mw \Vert ^{2}+ \Vert \sigma _{2}\lambda _{1}Nw \Vert ^{2}+ \bigl\Vert \sigma _{3}\lambda _{2}G^{*}Gw \bigr\Vert ^{2}. \end{aligned} \end{aligned}$$

This leads to $w\in \{(x,y)\in H_{1} \times H_{2},x \in \bigcap_{i=1}^{t_{1}}C_{i},y \in \bigcap_{j=1}^{r_{1}}Q_{j},A_{1}x \in \bigcap_{i=1}^{t_{2}}D_{i} ,B_{1} y \in \bigcap_{j=1}^{r_{2}}\Theta _{j}, A_{2}x=B_{2}y\}$, it is obvious that $w\in \mathrm{Fix}(S)$.

(3)

$$\begin{aligned} \begin{aligned}[b]& \bigl\langle \bigtriangledown h(x,y),v-w \bigr\rangle \geq 0,\quad \forall v\in \mathrm{Fix}(T) \\ &\Leftrightarrow\quad \bigl\langle w-(w-S_{1}w),v-w \bigr\rangle \geq 0,\quad \forall v \in \mathrm{Fix}(T) \\ &\Leftrightarrow\quad w= P_{\mathrm{Fix}(T)}(w-S_{1}w) \\ &\Leftrightarrow\quad w\in \mathrm{Fix}(P_{\mathrm{Fix}(T)}S). \end{aligned} \end{aligned}$$

 □

Remark 2.7

Take constants $\lambda _{1} and \lambda _{2}$, where $0<\lambda _{1}<1/(\max \{\rho (A_{1}^{*}A_{1}), \rho (B_{1}^{*}B_{1}) \} ), 0<\lambda _{2}<1/\rho (G^{*}G)$, with $\rho (A_{1}^{*}A_{1}), \rho (B_{1}^{*}B_{1}), \rho (G^{*}G)$ being the spectral radius of the self-adjoint operator $A_{1}^{*}A_{1}, B_{1}^{*}B_{1}, G^{*}G$. For $\tau _{1}\in (0,(1-\lambda _{1}(\max \{\|A_{1}^{*}A_{1}\|, \|B_{1}^{*}B_{1} \|\}))/\sigma _{2} \lambda _{1}), \tau _{2}\in (0,(1-\lambda _{2}\|G^{*}G \|)/{\sigma _{3}\lambda _{2}}), \tau =\min \{\tau _{1},\tau _{2}\}, (\sigma _{1}+\sigma _{2}+\sigma _{3})/(1-\sigma _{2}\lambda _{1}\tau - \sigma _{3}\lambda _{2}\tau )\in (0,1)$, we define a mapping

$$\begin{aligned} W_{\alpha }(w):=P_{\mathrm{Fix}(T)} \bigl[(1-\sigma _{2}\lambda _{1}\tau -\sigma _{3} \lambda _{2}\tau )I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3} \lambda _{2}G^{*}G \bigr]w. \end{aligned}$$

It is easy to check that $W_{\alpha }$ is contractive. So, $W_{\alpha }$ has a unique fixed point denoted by $w_{\alpha }$, that is,

$$\begin{aligned} w_{\alpha }=P_{\mathrm{Fix}(T)} \bigl[(1-\sigma _{2}\lambda _{1}\tau -\sigma _{3} \lambda _{2}\tau )I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3} \lambda _{2}G^{*}G \bigr]w_{\alpha }. \end{aligned}$$

(2.12)

Theorem 2.8

Let $w_{\alpha }$ be given as (2.12). Then $w_{\alpha }$ converges strongly as $\alpha \rightarrow 0$ to the minimum-norm solution w̄ of MSSFP and SEFPP.

Proof

Let w̆ be a point in Γ. $I-\sigma _{1}/(1-\sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2} \tau )M-\sigma _{2}\lambda _{1}/(1-\sigma _{2}\lambda _{1}\tau - \sigma _{3}\lambda _{2}\tau )N-\sigma _{3}\lambda _{2}/(1-\sigma _{2} \lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau )G^{*}G$ is nonexpansive. It follows that

$$\begin{aligned} \begin{aligned}[b] &\Vert w_{\alpha }-\breve{w} \Vert \\ &\quad= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2} \tau )I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G \bigr]w_{\alpha } \\ &\qquad{} -P_{\mathrm{Fix}(T)} \bigl[I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3} \lambda _{2}G^{*}G \bigr]\breve{w} \bigr\Vert \\ &\quad\leq \bigl\Vert \bigl[(1-\sigma _{2}\lambda _{1} \tau - \sigma _{3}\lambda _{2}\tau )I- \sigma _{1}M- \sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G \bigr]w_{\alpha } \\ &\qquad{} - \bigl[I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G \bigr] \breve{w} \bigr\Vert \\ &\quad\leq (1-\sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau ) \bigl\Vert \bigl(w_{\alpha }- \sigma _{1}/(1-\sigma _{2}\lambda _{1}\tau -\sigma _{3} \lambda _{2}\tau )Mw_{\alpha } \\ &\qquad{} -\sigma _{2}\lambda _{1}/(1-\sigma _{2} \lambda _{1}\tau - \sigma _{3}\lambda _{2}\tau )Nw_{\alpha }-\sigma _{3}\lambda _{2}(1- \sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau )G^{*}Gw_{\alpha } \bigr) \\ & \qquad{}- \bigl(\breve{w}-\sigma _{1}/(1-\sigma _{2} \lambda _{1}\tau -\sigma _{3} \lambda _{2}\tau )M \breve{w} \\ &\qquad{} -\sigma _{2}\lambda _{1}/(1-\sigma _{2} \lambda _{1}\tau - \sigma _{3}\lambda _{2}\tau )N \breve{w}-\sigma _{3}\lambda _{2}/(1- \sigma _{2} \lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau )G^{*}G \breve{w} \bigr) \bigr\Vert \\ &\qquad{} +\tau (\sigma _{2}\lambda _{1}+\sigma _{3} \lambda _{2}) \Vert \breve{w} \Vert \\ &\quad\leq (1-\sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau ) \Vert w_{\alpha }-\breve{w} \Vert +\tau (\sigma _{2}\lambda _{1}+\sigma _{3} \lambda _{2}) \Vert \breve{w} \Vert . \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \Vert w_{\alpha }-\breve{w} \Vert \leq \Vert \breve{w} \Vert . \end{aligned}$$

Then $\{w_{\alpha }\}$ is bounded.

From (2.12), we have

$$\begin{aligned} \bigl\Vert w_{\alpha }-P_{\mathrm{Fix}(T)} \bigl[I-\sigma _{1}M- \sigma _{2}\lambda _{1}N- \sigma _{3}\lambda _{2}G^{*}G \bigr]w_{\alpha } \bigr\Vert \leq \tau \bigl\Vert (\sigma _{2} \lambda _{1}+\sigma _{3} \lambda _{2})w_{\alpha } \bigr\Vert \rightarrow 0. \end{aligned}$$

Next we show that $w_{\alpha }$ is relatively norm compact as $\alpha \rightarrow 0^{+}$. In fact, assuming that $\{\tau _{n}\} \subseteq (0,\min \{(1-\lambda _{1}(\max \{\|A_{1}^{*}A_{1} \|, \|B_{1}^{*}B_{1}\|\}))/\sigma _{2}\lambda _{1}, (1-\lambda _{2} \|G^{*}G\|)/{\sigma _{3}\lambda _{2}}\})$ is such that $\tau _{n}\rightarrow 0^{+}$ as $n\rightarrow \infty$. Put $w_{n}:=w_{\alpha _{n}}$, we have the following:

$$\begin{aligned} \bigl\Vert w_{n}-P_{\mathrm{Fix}(T)} \bigl[I-\sigma _{1}M- \sigma _{2}\lambda _{1}N-\sigma _{3} \lambda _{2}G^{*}G \bigr]w_{n} \bigr\Vert \leq \tau \bigl\Vert (\sigma _{2}\lambda _{1}+ \sigma _{3} \lambda _{2})w_{n} \bigr\Vert \rightarrow 0. \end{aligned}$$

We deduce that

$$\begin{aligned} \begin{aligned}[b] &\Vert w_{\alpha }-\breve{w} \Vert ^{2} \\ &\quad= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2} \tau )I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G \bigr]w_{\alpha } \\ &\qquad{} -P_{\mathrm{Fix}(T)} \bigl[I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3} \lambda _{2}G^{*}G \bigr]\breve{w} \bigr\Vert ^{2} \\ &\quad\leq \bigl\langle \bigl[(1-\sigma _{2}\lambda _{1} \tau - \sigma _{3}\lambda _{2} \tau )I-\sigma _{1}M- \sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G \bigr]w_{\alpha } \\ &\qquad{} - \bigl[I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G \bigr] \breve{w},w_{\alpha }-\breve{w} \bigr\rangle \\ &\quad\leq (1-\sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau ) \bigl\langle \bigl(w_{\alpha }- \sigma _{1}/(1-\sigma _{2}\lambda _{1}\tau - \sigma _{3}\lambda _{2}\tau )Mw_{\alpha } \\ &\qquad{} -\sigma _{2}\lambda _{1}/(1-\sigma _{2} \lambda _{1}\tau - \sigma _{3}\lambda _{2}\tau )Nw_{\alpha }-\sigma _{3}\lambda _{2}(1- \sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau )G^{*}Gw_{\alpha } \bigr) \\ & \qquad{}- \bigl(\breve{w}-\sigma _{1}/(1-\sigma _{2} \lambda _{1}\tau -\sigma _{3} \lambda _{2}\tau )M \breve{w}-\sigma _{2}\lambda _{1}/(1-\sigma _{2} \lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau )N \breve{w} \\ & \qquad{}-\sigma _{3}\lambda _{2}/(1-\sigma _{2} \lambda _{1}\tau - \sigma _{3}\lambda _{2}\tau )G^{*}G\breve{w} \bigr),w_{\alpha }-\breve{w} \bigr\rangle -\tau ( \sigma _{2}\lambda _{1}+\sigma _{3}\lambda _{2}) \langle \breve{w},w_{\alpha }-\breve{w}\rangle \\ &\quad\leq (1-\sigma _{2}\lambda _{1}\tau -\sigma _{3}\lambda _{2}\tau ) \Vert w_{\alpha }-\breve{w} \Vert ^{2}-\tau (\sigma _{2}\lambda _{1}+\sigma _{3} \lambda _{2})\langle \breve{w},w_{\alpha }- \breve{w}\rangle. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert w_{\alpha }-\breve{w} \Vert ^{2}\leq \langle - \breve{w},w_{\alpha }-\breve{w} \rangle. \end{aligned}$$

In particular,

$$\begin{aligned} \Vert w_{n}-\breve{w} \Vert ^{2}\leq \langle - \breve{w},w_{n}-\breve{w}\rangle, \quad\forall \breve{w}\in \Gamma. \end{aligned}$$

Since $\{w_{n}\}$ is bounded, there exists a subsequence of $\{w_{n}\}$ which converges weakly to a point w̄. Without loss of generality, we may assume that $\{w_{n}\}$ converges weakly to w̄. Notice that

$$\begin{aligned} \bigl\Vert w_{n}-P_{\mathrm{Fix}(T)} \bigl[I-\sigma _{1}M- \sigma _{2}\lambda _{1}N-\sigma _{3} \lambda _{2}G^{*}G \bigr]w_{n} \bigr\Vert \leq \tau \bigl\Vert (\sigma _{2}\lambda _{1}+ \sigma _{3} \lambda _{2})w_{n} \bigr\Vert \rightarrow 0, \end{aligned}$$

and by Lemma 1.4, we can get $\bar{w}\in \mathrm{Fix}(TS)=\Gamma$.

By

$$\begin{aligned} \Vert w_{n}-\breve{w} \Vert ^{2}\leq \langle - \breve{w},w_{n}-\breve{w}\rangle, \quad\forall \breve{w}\in \Gamma, \end{aligned}$$

we have

$$\begin{aligned} \Vert w_{n}-\bar{w} \Vert ^{2}\leq \langle - \bar{w},w_{n}-\bar{w}\rangle. \end{aligned}$$

Consequently, that $\{w_{n}\}$ converges weakly to w̄ actually implies that $\{w_{n}\}$ converges strongly to w̄. That is to say, $\{w_{\alpha }\}$ is relatively norm compact as $\alpha \rightarrow 0^{+}$.

On the other hand, by

$$\begin{aligned} \Vert w_{n}-\breve{w} \Vert ^{2}\leq \langle - \breve{w},w_{n}-\breve{w}\rangle, \quad\forall \breve{w}\in \Gamma, \end{aligned}$$

let $n\rightarrow \infty$, we have

$$\begin{aligned} \Vert \bar{w}-\breve{w} \Vert ^{2}\leq \langle -\breve{w},\bar{w}- \breve{w}\rangle, \quad\forall \breve{w}\in \Gamma. \end{aligned}$$

This implies that

$$\begin{aligned} \langle -\breve{w},\breve{w}-\bar{w}\rangle \leq 0,\quad\forall \breve{w}\in \Gamma, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \langle -\bar{w},\breve{w}-\bar{w}\rangle \leq 0,\quad\forall \breve{w}\in \Gamma. \end{aligned}$$

It follows that $\bar{w}\in P_{\mathrm{Fix}(T)}(0)$. Therefore, each cluster point of $w_{\alpha }$ equals w̄. So $w_{\alpha }\rightarrow \bar{w}(\alpha \rightarrow 0)$ is the minimum-norm solution of SFP and SEFPP. □

3 Main results

In this section, we introduce the following algorithm to solve MSSFP and SEFFP. The purpose for such a modification lies in the hope of strong convergence.

Algorithm 3.1

For an arbitrary point $w_{0}=(x_{0},y_{0})\in H=H_{1}\times H_{2}$, the sequence $\{w_{n}\}=\{(x_{n},y_{n})\}$ is generated by the iterative algorithm

$$\begin{aligned} w_{n+1}=P_{\mathrm{Fix}(T)} \bigl\{ (1-\tau _{n}) \bigl[I-\sigma _{1}M-\sigma _{2}\lambda _{1}N- \sigma _{3}\lambda _{2}G^{*}G \bigr]w_{n} \bigr\} , \end{aligned}$$

(3.1)

i.e.,

$$\begin{aligned} \begin{aligned}[b] x_{n+1} ={}&P_{\mathrm{Fix}(T_{1})} \Biggl\{ (1- \tau _{n}) \Biggl[x_{n}-\sigma _{1}\sum _{i=1}^{t_{1}} \alpha _{i}(I-P_{C_{i}})x_{n}- \sigma _{2}\lambda _{1}\sum_{i=1}^{t_{2}} \beta _{i}A_{1}^{*}(I-P_{D_{i}})A_{1}x_{n} \\ & {}-\sigma _{3}\lambda _{2}A_{2}^{*}(A_{2}x_{n}-B_{2}y_{n}) \Biggr] \Biggr\} ,\quad n \geq 0 \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}[b] y_{n+1} ={}&P_{\mathrm{Fix}(T_{2})} \Biggl\{ (1- \tau _{n}) \Biggl[y_{n}-\sigma _{1}\sum _{j=1}^{r_{1}} \gamma _{j}(I-P_{Q_{j}})y_{n}- \sigma _{2}\lambda _{1}\sum_{j=1}^{r_{2}} \delta _{j}B_{1}^{*}(I-P_{\Theta _{j}})B_{1}y_{n} \\ & {}+\sigma _{3}\lambda _{2}B_{2}^{*}(A_{2}x_{n}-B_{2}y_{n}) \Biggr] \Biggr\} ,\quad n \geq 0, \end{aligned} \end{aligned}$$

where $\tau _{n}>0$ is a sequence in (0,1) such that

• (i) $\lim_{n}\tau _{n}=0$;

• (ii) $\sum_{n=0}^{\infty }\tau _{n}=\infty$;

• (iii) $\sum_{n=0}^{\infty }|\tau _{n+1}-\tau _{n}|<\infty$ or $\lim_{n}|\tau _{n+1}-\tau _{n}|/\tau _{n}=0$.

Now, we prove the strong convergence of the iterative algorithm.

Theorem 3.2

The sequence $\{w_{n}\}$ generated by Algorithm 3.1converges strongly to the minimum-norm solution w̄ of MSSFP and SEFPP.

Proof

Let $R_{n}$ and R be defined by

$$\begin{aligned} \begin{aligned}[b] &R_{n}w:=P_{\mathrm{Fix}(T)} \bigl\{ (1-\tau _{n}) \bigl[I-\sigma _{1}M-\sigma _{2}\lambda _{1}N- \sigma _{3}\lambda _{2}G^{*}G \bigr] \bigr\} w=P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})Sw \bigr], \\ &Rw:=P_{\mathrm{Fix}(T)} \bigl(I-\sigma _{1}M-\sigma _{2} \lambda _{1}N-\sigma _{3} \lambda _{2}G^{*}G \bigr)w=P_{\mathrm{Fix}(T)}(Sw), \end{aligned} \end{aligned}$$

where $S=I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G$. By Lemma 2.6 it is easy to see that $R_{n}$ is a contraction with contractive constant $(1-\tau _{n})$; and Algorithm 3.1 can be written as $w_{n+1}=R_{n}w_{n}$.

For any $\breve{w}\in \Gamma$, we have

$$\begin{aligned} \begin{aligned}[b] \Vert R_{n}\breve{w}-\breve{w} \Vert &= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})S\breve{w} \bigr]- \breve{w} \bigr\Vert \\ &= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})S\breve{w} \bigr]-P_{\mathrm{Fix}(T)}(S\breve{w}) \bigr\Vert \\ &\leq \bigl\Vert (1-\tau _{n})S\breve{w}-S\breve{w} \bigr\Vert \\ &=\tau _{n} \Vert S\breve{w} \Vert =\tau _{n} \Vert \breve{w} \Vert . \end{aligned} \end{aligned}$$

Hence

$$\begin{aligned} &\begin{aligned}[b] \Vert w_{n+1}-\breve{w} \Vert &= \Vert R_{n}w_{n}-\breve{w} \Vert \leq \Vert R_{n}w_{n}-R_{n} \breve{w} \Vert + \Vert R_{n}\breve{w}-\breve{w} \Vert \\ &\leq \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})Sw_{n} \bigr]-P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})S \breve{w} \bigr] \bigr\Vert + \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})S\breve{w} \bigr]- \breve{w} \bigr\Vert \\ &\leq (1-\tau _{n}) \Vert w_{n}-\breve{w} \Vert +\tau _{n} \Vert \breve{w} \Vert \\ &\leq \max \bigl\{ \Vert w_{n}-\breve{w} \Vert ,|\breve{w} \Vert \bigr\} , \end{aligned} \\ &\Vert Sw_{n+1}-\breve{w} \Vert \leq \Vert w_{n+1}- \breve{w} \Vert . \end{aligned}$$

It follows that $\|w_{n}-\breve{w}\|\leq \max \{\|w_{0}-\breve{w}\|,|\breve{w}\|\}$. So $\{w_{n}\}$ and $\{Sw_{n}\}$ are bounded.

Next we prove that $\lim_{n}\|w_{n+1}-w_{n}\|=0$.

Indeed,

$$\begin{aligned} \begin{aligned}[b] \Vert w_{n+1}-w_{n} \Vert &= \Vert R_{n}w_{n}-R_{n-1}w_{n-1} \Vert \\ &\leq \Vert R_{n}w_{n}-R_{n}w_{n-1} \Vert + \Vert R_{n}w_{n-1}-R_{n-1}w_{n-1} \Vert \\ &\leq (1-\tau _{n}) \Vert w_{n}-w_{n-1} \Vert + \Vert R_{n}w_{n-1}-R_{n-1}w_{n-1} \Vert . \end{aligned} \end{aligned}$$

Notice that

$$\begin{aligned} \begin{aligned}[b] \Vert R_{n}w_{n-1}-R_{n-1}w_{n-1} \Vert &= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})Sw_{n-1} \bigr]-P_{\mathrm{Fix}(T)} \bigl[(1- \tau _{n-1})Sw_{n-1} \bigr] \bigr\Vert \\ &\leq \bigl\Vert (1-\tau _{n})Sw_{n-1}-(1-\tau _{n-1})Sw_{n-1} \bigr\Vert \\ &= \vert \tau _{n}-\tau _{n-1} \vert \Vert Sw_{n-1} \Vert . \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \Vert w_{n+1}-w_{n} \Vert \leq (1-\tau _{n}) \Vert w_{n}-w_{n-1} \Vert + \vert \tau _{n}- \tau _{n-1} \vert \Vert Sw_{n-1} \Vert . \end{aligned}$$

By virtue of assumptions (i)–(iii) and Lemma 1.5, we have

$$\begin{aligned} \lim_{n} \Vert w_{n+1}-w_{n} \Vert =0. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned}[b] \Vert w_{n}-Rw_{n} \Vert & \leq \Vert w_{n+1}-w_{n} \Vert + \Vert R_{n}w_{n}-Rw_{n} \Vert \\ &\leq \Vert w_{n+1}-w_{n} \Vert + \bigl\Vert (1-\tau _{n})Sw_{n}-Sw_{n} \bigr\Vert \\ &\leq \Vert w_{n+1}-w_{n} \Vert +\tau _{n} \Vert Sw_{n} \Vert \rightarrow 0. \end{aligned} \end{aligned}$$

The demiclosedness principle ensures that each weak limit point of $\{w_{n}\}$ is a fixed point of the nonexpansive mapping $R=TS$, that is, a point of the solution set Γ of MSSFP and SEFPP.

At last, we will prove that $\lim_{n}\|w_{n+1}-\bar{w}\|=0$.

Choose $0<\delta <1$ such that $(\sigma _{1}+\sigma _{2}+\sigma _{3})/(1-\delta )\in (0,1)$, then $S=I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G= \delta I+(1-\delta )V$, where $V=I-\sigma _{1}/(1-\delta )M-\sigma _{2}\lambda _{1}/(1-\delta )N- \sigma _{3}\lambda _{2}/(1-\delta )G^{*}G$ is a nonexpansive mapping. Taking $z\in \Gamma$, we deduce that

$$\begin{aligned} \begin{aligned}[b] \Vert w_{n+1}-z \Vert ^{2} &= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})Sw_{n} \bigr]-z \bigr\Vert ^{2} \\ &\leq \bigl\| [(1-\tau _{n})Sw_{n}-z\bigr\| ^{2} \\ &\leq (1-\tau _{n}) \Vert Sw_{n}-z \Vert ^{2}+ \tau _{n} \Vert z \Vert ^{2} \\ &\leq \bigl\Vert \delta (w_{n}-z)+(1-\delta ) (Vw_{n}-z) \bigr\Vert ^{2}+\tau _{n} \Vert z \Vert ^{2} \\ &\leq \delta \bigl\Vert (w_{n}-z) \bigr\Vert ^{2}+(1- \delta ) \bigl\Vert (Vw_{n}-z) \bigr\Vert ^{2}-\delta (1- \delta ) \Vert w_{n}-Vw_{n} \Vert ^{2}+\tau _{n} \Vert z \Vert ^{2} \\ &\leq \bigl\Vert (w_{n}-z) \bigr\Vert ^{2}-\delta (1- \delta ) \Vert w_{n}-Vw_{n} \Vert ^{2}+\tau _{n} \Vert z \Vert ^{2}. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned}[b] \delta (1-\delta ) \Vert w_{n}-Vw_{n} \Vert ^{2} &\leq \bigl\Vert (w_{n}-z) \bigr\Vert ^{2}- \Vert w_{n+1}-z \Vert ^{2}+\tau _{n} \Vert z \Vert ^{2} \\ &= \bigl( \bigl\Vert (w_{n}-z) \bigr\Vert + \Vert w_{n+1}-z \Vert \bigr) \bigl( \bigl\Vert (w_{n}-z) \bigr\Vert - \Vert w_{n+1}-z \Vert \bigr)+\tau _{n} \Vert z \Vert ^{2} \\ &\leq \bigl( \bigl\Vert (w_{n}-z) \bigr\Vert + \Vert w_{n+1}-z \Vert \bigr) \bigl( \Vert w_{n}-w_{n+1} \Vert \bigr)+\tau _{n} \Vert z \Vert ^{2} \rightarrow 0. \end{aligned} \end{aligned}$$

Note that $S=I-\sigma _{1}M-\sigma _{2}\lambda _{1}N-\sigma _{3}\lambda _{2}G^{*}G= \delta I+(1-\delta )V$, it follows that $\lim_{n}\|Sw_{n}-w_{n}\|=0$.

Take a subsequence $\{w_{n_{k}}\}$ of $\{w_{n}\}$ such that $\limsup_{n}\langle w_{n}-\bar{w},-\bar{w}\rangle =\lim_{k}\langle w_{n_{k}}- \bar{w},-\bar{w}\rangle$.

By virtue of the boundedness of $\{w_{n}\}$, we may further assume, with no loss of generality, that $w_{n_{k}}$ converges weakly to a point w̆. Since $\|Rw_{n}-w_{n}\|\rightarrow 0$, using the demiclosedness principle, we know that $\breve{w}\in \mathrm{Fix}(R)=\mathrm{Fix}(P_{\mathrm{Fix}(T)}S)=\Gamma$. Noticing that w̄ is the projection of the origin onto Γ, we get that

$$\begin{aligned} \limsup_{n}\langle w_{n}-\bar{w},-\bar{w}\rangle = \lim_{k}\langle w_{n_{k}}- \bar{w},-\bar{w}\rangle = \langle \breve{w}-\bar{w},-\bar{w}\rangle \leq 0. \end{aligned}$$

Finally, we compute

$$\begin{aligned} \Vert w_{n+1}-\bar{w} \Vert ^{2} &= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})Sw_{n} \bigr]-\bar{w} \bigr\Vert ^{2} \\ &= \bigl\Vert P_{\mathrm{Fix}(T)} \bigl[(1-\tau _{n})Sw_{n} \bigr]-TS\bar{w} \bigr\Vert ^{2} \\ &\leq \bigl\Vert (1-\tau _{n})Sw_{n}-S\bar{w} \bigr\Vert ^{2} \\ &\leq \bigl\Vert (1-\tau _{n})Sw_{n}-\bar{w} \bigr\Vert ^{2} \\ &= \bigl\Vert (1-\tau _{n}) (Sw_{n}-\bar{w})+\tau _{n}(-\bar{w}) \bigr\Vert ^{2} \\ &=(1-\tau _{n})^{2} \bigl\Vert (Sw_{n}-\bar{w}) \bigr\Vert ^{2}+\tau _{n}^{2} \Vert \bar{w} \Vert ^{2}+2 \tau _{n}(1-\tau _{n})\langle Sw_{n}-\bar{w},-\bar{w}\rangle \\ &=(1-\tau _{n})^{2} \bigl\Vert (Sw_{n}-\bar{w}) \bigr\Vert ^{2}+\tau _{n} \bigl[\tau _{n} \Vert \bar{w} \Vert ^{2}+2(1-\tau _{n})\langle Sw_{n}- \bar{w},-\bar{w}\rangle \bigr]. \end{aligned}$$

Since $\limsup_{n}\langle w_{n}-\bar{w},-\bar{w}\rangle \leq 0, \|Sw_{n}-w_{n} \|\rightarrow 0$, we know that $\limsup_{n}(\tau _{n}\|\bar{w}\|^{2}+2(1-\tau _{n})\langle Sw_{n}- \bar{w},-\bar{w}\rangle )\leq 0$. By Lemma 1.5, we conclude that $\lim_{n}\|w_{n+1}-\bar{w}\|=0$. This completes the proof. □

4 Numerical experiments

We provide a numerical example to illustrate the effectiveness of our algorithm. The program was written in Mathematica. All results are carried out on a personal DELL computer with Intel(R) Core(TM)i5-5200 CPU @ 2.20 GHz and RAM 4.00 GB.

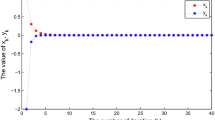
In this algorithm, we take $\mathrm{error} = 10^{-5}, 10^{-7}, 10^{-10}, 10^{-12}, 10^{-15}$, respectively. We consider the split feasibility problem (1.1) with $H_{1}=\mathbb{R}, H_{2}=\mathbb{R}$, $C=(-\infty,0]$, $Q=(-\infty,0]$, $D=(-\infty,0]$, $\Theta =(-\infty,0]$. $T_{1}x=x, T_{2}y=y$, $A_{1}=B_{1}=A_{2}=1, B_{2}=-1$, $\sigma _{1}=\sigma _{2}=\sigma _{3}=\frac{1}{3}$, $\lambda _{1}=\frac{1}{\|A_{1}\|^{2}}, \lambda _{2}=1$. Take $\tau _{n}=\frac{2}{3}$, an initial point $x_{1} = -20, y_{1} = -10$. Obviously, $x^{*}= 0, y^{*} = 0$ is a solution of this problem. In consideration of Algorithm 3.1, we have

$$\begin{aligned} \textstyle\begin{cases} x_{n+1}=P_{\mathrm{Fix}(T_{1})}[\frac{1}{3}(x_{n}-\frac{1}{3}(x_{n}+y_{n}))];\quad n \geq 0; \\ y_{n+1}=P_{\mathrm{Fix}(T_{2})}[\frac{1}{3}(y_{n}-\frac{1}{3}(x_{n}+y_{n}))];\quad n \geq 0. \end{cases}\displaystyle \end{aligned}$$

As for iterative method (1.13) and (1.14), we take $H_{1}=\mathbb{R}, H_{2}=\mathbb{R}$, $C=(-\infty,0]$, $Q=(-\infty,0]$, $D=(-\infty,0]$, $\Theta =(-\infty,0]$. $T_{1}x=x, T_{2}y=y$, $A_{1}=B_{1}=A_{2}=1, B_{2}=-1$, $\lambda =\xi =\sigma =\zeta =\frac{1}{3}$. Take $\tau =\frac{1}{8}$, an initial point $x_{1} = -20, y_{1} = -10$.

In consideration of algorithms (1.13) and (1.14), we have

$$\begin{aligned} \textstyle\begin{cases} x_{n+1}=T_{1}(x_{n}-\frac{1}{8}(x_{n}+y_{n}));\quad n\geq 0; \\ y_{n+1}=T_{2}(y_{n}-\frac{1}{8}(x_{n+1}+y_{n}))];\quad n\geq 0. \end{cases}\displaystyle \end{aligned}$$

From Table 1, it is easy to see that our iterative method converges faster in less time.

Table 1 Effectiveness of Iterative method

5 Conclusions

The paper proposed a new iterative method to solve the split equality fixed point problem of firmly quasi-nonexpansive or nonexpansive operators and multiple-sets split feasibility problem and obtained a strong convergence result without any semi-compact assumption imposed on operators. The results improved and unified many recent results.