1 Introduction

Von Neumann [17] was the one who first started researching fixed points for multivalued (set-valued) mappings. Nadler started the process of developing geometric fixed point theory for multi-valued mapping [16]. To develop the multi-valued contraction principle, also known as Nadler’s contraction mapping principle, he merged the concepts of multi-valued mapping, Lipschitz mapping, and the Hausdorff metric. The generalization of Nadler’s contraction mapping theory has been the subject of numerous studies [1, 23].

In both pure and applied mathematics, fixed point theory is essential. Usually, fixed point techniques have been used in various disciplines, covering biological sciences, the field of economics, technology, the theory of games, nonlinear computer programming, mathematical modeling of differential equations, etc. (see [6, 7]). Later, numerous other writers (see [2–4, 18–20]) expanded this finding and investigated the existence of fixed points and common fixed points of fuzzy mappings meeting a contractive type condition. Numerous researchers have utilized fuzzy theory to the well-known outcomes in numerous disciplines, including quantum physics, nonlinear dynamical systems, population dynamics, computer programming, fuzzy stability issues, statistical convergence, functional equations, approximation theory, nonlinear equations, and many others.

As one of the uncertain ways to build mathematical models compatible with real-world problems in engineering, life science, economics, medicine, language theory, and other fields, Zadeh [25] introduced the concept of fuzzy set in 1965. He introduced the idea of a fuzzy set (FS), which builds on the notion of a crisp set by assigning membership values to each element in the range \([0,1]\). The descriptions of the levels of possession of a certain property are vague because it successfully addresses control issues.

FS theory offers the capacity to deal with issues that crisp set theory finds problematic. Fuzzy sets are used to govern systems that are hazy, complex, and nonlinear in nature. Since it clarifies and condenses the idea of fuzziness and faults, FS theory has made it easier to settle real-world problems. It is currently a widely accepted hypothesis. Many scholars changed fuzzy ideas in many other domains of science, such as [8], due to the theory’s adaptability in solving real-world problems. The fundamental concepts of the fuzzy set have been expanded in many ways (see [9, 26, 27] and references therein).

More specifically, in 1981, Heilpern [10] introduced the idea of fixed point results for fuzzy set-valued mappings and fuzzy contractions by proving a fixed point theorem analogous to the Banach fixed point theorem in the context of fuzzy sets. The existence of fixed points and common fixed points of fuzzy mappings satisfying a contraction kind of requirements was further broadened and examined by a number of authors (see [11–15, 21, 22, 24]).

The aim of this paper is to obtain a common α-fuzzy fixed point of fuzzy mappings under generalized fuzzy contractive conditions in connection with the Hausdorff metric space. This investigation is conducted within the framework of complete metric spaces. To demonstrate how this strategy can be applied, fascinating examples are also provided. We have obtained sufficient conditions for the existence of a common alpha-fuzzy fixed point with three or four fuzzy mappings. The relevant literature’s corollaries are presented as additional prior observations. In our study, we go into greater detail about some consequences that are obvious in this mode and are widely discussed in literature.

2 Preliminaries

In this section, we will go over several key ideas that are necessary for the presentation of our main results, and we will do so in preparation for that presentation.

Definition 2.1

[5] Any self-mapping ϕ defined on a complete metric space \((\aleph ,\xi )\) satisfying

$$ \xi (\phi x_{1}, \phi x_{2}) \leq \beta \xi (x_{1},x_{2})\quad \forall x_{1}, x_{2} \in \aleph , $$

for \(0< \beta <1 \) has a unique fixed point.

Note

Throughout the article, the collection of all non-empty compact subsets of a space ℵ is denoted \(C ( \aleph )\), and the collection of all non-empty closed and bounded subsets of a space ℵ is denoted \(\operatorname{CB}(\aleph )\)

Definition 2.2

[16] Let \((\aleph , \xi )\) be a metric space. The real-valued function Hm defined on \(\operatorname{CB}(\aleph ) \times \operatorname{CB}(\aleph )\) by

$$ Hm(C,D) = \max\Bigl\{ \sup_{a\in C}\xi (a,D), \sup _{b\in D}\xi (C,b)\Bigr\} , $$

where

$$ \xi (x,C) = \inf_{y\in C}\xi (x,y). $$

Definition 2.3

[16] Let \((\aleph , \xi )\) be a metric space. For \(C, D \subseteq \aleph \), the distance \(D^{*}\) between C and D is defined as:

$$ D^{*}(C, D) = \inf_{x\in C, y\in D} \xi (x, y). $$

Definition 2.4

[2] Let ℵ be any non-empty set. A function \(A^{*}\) with domain ℵ and values in \([0, 1]\) is known as fuzzy set in ℵ. If \(A^{*}\) is a fuzzy set and \(x\in \aleph \), then the function value \(A^{*}(x)\) is called the grade of membership of \(x \in A^{*}\). \(\digamma (\aleph )\) stands for the collection of all fuzzy sets in ℵ unless and until stated otherwise.

Example 2.5

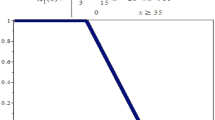
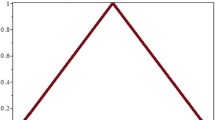
Consider A denotes for the old and B denotes for the young and \(\aleph = [0, 100]\). Then A and B both are fuzzy sets that are defined by

$$\begin{aligned}& A(x)=\textstyle\begin{cases} [1+ (\frac{x-50}{5} )^{-2} ]^{-1}, & \text{if } 50 < x \leq 100, \end{cases}\displaystyle \\& A(x)= 0, \quad \text{otherwise}, \\& B(x)= \textstyle\begin{cases} [1+ (\frac{x-25}{5} )^{2} ]^{-1}, & \text{if } 25 < x \leq 100, \end{cases}\displaystyle \\& B(x)= 0, \quad \text{otherwise}. \end{aligned}$$

Fuzzy sets A and B can be seen graphically in Fig. 1 and Fig. 2, respectively.

Figure 1
figure 1

Graph of fuzzy set A

Full size image
Figure 2
figure 2

Graph of fuzzy set B

Full size image

Definition 2.6

[2] The α-level set o fuzzy set \(A^{*}\) is denoted by \([A^{*}]_{\alpha} \) and is defined as:

$$\begin{aligned}& \bigl[A^{*}\bigr]_{\alpha} = \bigl\{ x: A^{*}(\aleph ) \geq \alpha \bigr\} \quad \text{where } \alpha \in (0,1],\\& \bigl[ A^{*} \bigr] _{0}=\overline{\bigl\{ x:A^{*}(x)>0\bigr\} },\\& \widehat{A^{*}}=\Bigl\{ x:A^{*}(x)=\max_{y\in \aleph}A^{*} ( y ) \Bigr\} . \end{aligned}$$

For crisp subset \(A^{*}\) of ℵ, we denote the characteristic function of \(A^{*}\) by \(\chi _{A^{*}}\). A fuzzy set \(A^{*}\) in a metric linear space V is said to be an approximate quantity if and only if \([ A^{*} ] _{\alpha }\) is compact and convex in V for each \(\alpha \in {}[ 0,1]\) and \(\sup_{x\in V}A^{*}(x)=1\).

Define some sub-collections of \(\digamma (\aleph )\) and \(\digamma (V)\) as follows:

$$\begin{aligned}& \mathcal{W}(V)= \bigl\{ A^{*}\in \digamma (V):A^{*} \text{ is an approximate quantity in }V \bigr\} ,\\& K ( \aleph ) = \bigl\{ A^{*}\in \digamma (\aleph ): \widehat{A^{*}}\in C ( \aleph ) \bigr\} ,\\& \mathfrak{C} ( \aleph ) = \bigl\{ A^{*}\in \digamma ( \aleph ): \bigl[ A^{*} \bigr] _{\alpha }\in C ( \aleph ) , \text{for each } \alpha \in {}[ 0,1] \bigr\} . \end{aligned}$$

For \(A^{*},B^{*}\in \digamma (\aleph )\), \(A^{*}\subset B^{*}\) means \(A^{*}(x)\leqslant B^{*}(x)\) for each \(x\in \aleph \). If there exists an \(\alpha \in {}[ 0,1]\) such that \([ A^{*} ] _{\alpha }, [ B^{*} ] _{\alpha }\in C ( \aleph ) \), then define

$$\begin{aligned}& p_{\alpha }\bigl(A^{*},B^{*}\bigr) = \inf _{x\in [ A^{*} ] _{\alpha },y\in [ B^{*} ] _{\alpha }}\xi (x,y), \\& D_{\alpha }\bigl(A^{*},B^{*}\bigr) = Hm\bigl( \bigl[ A^{*} \bigr] _{\alpha }, \bigl[ B^{*} \bigr] _{\alpha }\bigr). \end{aligned}$$

If \([ A^{*} ] _{\alpha }, [ B^{*} ] _{ \alpha }\in C ( \aleph ) \) for each \(\alpha \in {}[ 0,1]\), then define \(p(A^{*},B^{*}),\xi _{\infty }(A^{*},B^{*}):\mathfrak{C} ( \aleph ) \times \mathfrak{C} ( \aleph ) \rightarrow \mathbb{R} \) (induced by the Hausdorff metric Hm) as follows:

$$\begin{aligned}& p\bigl(A^{*},B^{*}\bigr) = \sup_{\alpha }p_{\alpha } \bigl(A^{*},B^{*}\bigr), \\& \xi _{\infty }\bigl(A^{*},B^{*}\bigr) = \sup _{\alpha }D_{\alpha }\bigl(A^{*},B^{*} \bigr). \end{aligned}$$

For \(x \in \aleph \), we denote the fuzzy set \(\chi _{\{x\}}\) by \(\{x\}\) unless and until it is stated, where \(\chi _{A^{*}}\) is the characteristic function of the crisp set \(A^{*}\).

Definition 2.7

[2] Let ℵ be any non-empty set and Y be a metric space. A mapping T is called a fuzzy mapping if T is a mapping from ℵ into \(\digamma (\aleph )\). A fuzzy mapping T is a fuzzy subset on \(\aleph \times Y \) with membership function \(T(x)(y)\). The function \(T(x)(y)\) is a grade of membership of y in \(T(x)\). For convenience, we denote the α-level set of \(T(x)\) by \([Tx]_{\alpha}\) instead of \([T(x)]_{\alpha}\).

Example 2.8

Let \(\aleph = [-3,3]\). Define \(T:\aleph \longrightarrow \digamma (\aleph )\) by

$$ T(x) (y)= \frac{\sin ^{2} x\cos ^{2} y}{3}. $$

Then T is a fuzzy mapping. Notice that \(T(x)(y)\in [0,1]\), for all \(x, y\in \aleph \). The graphical representation \(v=T(x)(y)\) showing the possible membership values of y in \(T(x)\) is shown in Fig. 3.

Figure 3
figure 3

Graph of fuzzy mapping T

Full size image

Definition 2.9

[2] Let \(T:\aleph \longrightarrow \digamma (\aleph ) \) be a fuzzy mapping. An element \(u \in \aleph \) is called fuzzy fixed point of T if \(u \in [Tu]_{\alpha} \).

Definition 2.10

[2] Let \(S,T: \aleph \rightarrow \digamma (\aleph ) \) be two fuzzy mappings. If for \(x \in \aleph \), there exists \(\alpha _{S(x)}, \alpha _{T(x)} \in (0,1]\) such that \(x \in [Sx]_{\alpha _{Sx}} \cap [Tx]_{\alpha _{Tx}}\), then x is said to b an α-fuzzy common fixed point of S and T.

For the sake of convenience, we first state some known results for subsequent use in the next section.

Lemma 2.11

[16] Let \((V,d) \) be a metric space and \(E,F \in \operatorname{CB}(V) \) with \(Hm(E,F) < \epsilon \). Then for each \(e \in E \), there exists an element \(f \in F \) such that

$$ \xi (e,f) < \epsilon. $$

Lemma 2.12

[16] Let \((V,\xi ) \) be a metric space and \(E,F \in \operatorname{CB}(V) \) with \(Hm(E,F) < \epsilon \). Then for each \(e \in E \),

$$ \xi (e,F) \leq Hm(E,F). $$

3 Main results

Theorem 3.1

Consider a metric space \((V,\xi )\) and \(\operatorname{CB}(V)\) to be the class of all bounded and closed subsets of V. Let \(S, T, F, G : V \rightarrow \digamma (V)\) be fuzzy mappings. Suppose for each \(u \in V\), there exists \(\alpha _{S}(u), \alpha _{T}(u), \alpha _{G}(u), \alpha _{F}(u) \in (0, 1]\) such that \([Su]_{\alpha _{S}(u)}, [Tu]_{\alpha _{T}(u)}, [Fu]_{\alpha _{F}(u)}, [Gu]_{\alpha _{G}(u)}\in \operatorname{CB}(V)\) and

$$ \bigcup_{u \in V} [Su]_{\alpha _{S}(u)} \subseteq \bigcup_{u \in V}[Gu]_{ \alpha _{G}(u)} \quad \textit{and}\quad \bigcup_{u \in V}[Tu]_{\alpha _{T}(u)} \subseteq \bigcup_{u \in V}[Fu]_{\alpha _{F}(u)}. $$
(3.1)

Also suppose that

$$ \bigcup_{u \in V}[Su]_{\alpha _{S}(u)}\quad \textit{or}\quad \bigcup _{u \in V} [Gu]_{ \alpha _{G}(u)} \quad \textit{and} \quad \bigcup_{u \in V} [Tu]_{\alpha _{T}(u)} \quad \textit{or}\quad \bigcup _{u \in V} [Fu]_{\alpha _{F} (u)} $$

are complete. If there exists \(\varpi \in [0,1)\) such that

$$ Hm\bigl([Sj]_{\alpha _{S}(j)},[Tk]_{\alpha _{T}(k)}\bigr) \leq \varpi D\bigl([Fj]_{ \alpha _{F}(j)},[Gk]_{\alpha _{G}(k)}\bigr) \quad \forall j,k \in V $$
(3.2)

then there exists \(u, u' \in V\) such that

$$ [Tu]_{\alpha _{T}(u)}\cap [Gu]_{\alpha _{G}(u)} \neq \emptyset $$

and

$$ \bigl[Su'\bigr]_{\alpha _{S}(u')}\cap \bigl[Fu' \bigr]_{\alpha _{F}(u')}\neq \emptyset . $$

Proof

Let \(j_{0} \in V\) be arbitrary point of V. Choose \(j_{1} \in V\), ∃ \(\alpha \in (0,1]\) such that \(k_{1}\in [Sj_{0}]_{\alpha _{S}(j_{0})}\) and \(k_{2}\in [Tj_{1}]_{\alpha _{T}(j_{1})}\), where \([Sj_{0}]_{\alpha _{S}(j_{0})}\) and \([Tj_{1}]_{\alpha _{T}(j_{1})}\) are closed and bounded subsets of V. Since

$$ \bigcup_{u\in V}[Su]_{\alpha _{S}(u)}\subseteq \bigcup _{u\in V}[Gu]_{ \alpha _{G}(u)} \quad \text{and} \quad \bigcup_{ u\in V}[Tu]_{\alpha _{T}(u)} \subseteq \bigcup _{u\in V}[Fu]_{\alpha _{F}(u)} $$

we can choose \(j_{2}\in V\) such that \(k_{1}\in [Gj_{1}]_{\alpha _{G}(j_{1})}\) and \(k_{2}\in [Fj_{2}]_{\alpha _{F} (j_{2})} \),

$$ \Rightarrow [Sj_{0}]_{\alpha _{S}(j_{0})} \cap [Gj_{1}]_{\alpha _{G}(j_{1})} \neq \emptyset \quad \text{and} \quad [Tj_{1}]_{\alpha _{T}(j_{1})} \cap [Fj_{2}]_{ \alpha _{F}(j_{2})} \neq \emptyset . $$
(3.3)

If \(\varpi = 0\) then by inequality (3.6),

$$\begin{aligned}& Hm\bigl([Sj_{0}]_{\alpha _{S}(j_{0})},[Tj_{1}]_{\alpha _{T}(j_{1})} \bigr) \leq 0 \\& \quad \Rightarrow \quad [Sj_{0}]_{\alpha _{S}(j_{0})}= [Tj_{1}]_{\alpha _{T}(j_{1})} \\& \quad \Rightarrow\quad k_{1} \in [Tj_{1}]_{\alpha _{T}(j_{1})} \cap [Gj_{1}]_{ \alpha _{G}(j_{1})}. \end{aligned}$$

Also,

$$\begin{aligned}& Hm\bigl([Sj_{2}]_{\alpha _{S}(j_{2})} ,[Tj_{1}]_{\alpha _{T}(j_{1}} \bigr)) \leq 0\\& \quad \Rightarrow \quad [Sj_{2}]_{\alpha _{S}(j_{2})} = [Tj_{1}]_{\alpha _{T}(j_{1})}\\& \quad \Rightarrow\quad k_{2} \in [Fj_{2}]_{\alpha _{F}(j_{2})}\cap [Sj_{2}]_{ \alpha _{S}(j_{2})} \end{aligned}$$

\(\Rightarrow j_{1}\) and \(j_{2}\) are coincidence points.

Now if

$$ D\bigl([ Fj_{0}]_{\alpha _{F}(j_{0})},[Gj_{1}]_{ \alpha _{G}(j_{1})} \bigr) = 0 \quad \text{and} \quad D\bigl([Gj_{1}]_{\alpha _{G}(j_{1})}, [Fj_{2}]_{\alpha _{F}(j_{2})}\bigr) =0 . $$

Then the same arguments follow.

If \(D([Fj_{0}]_{\alpha _{F}(j_{0})} ,[Gj_{1}]_{\alpha _{G}(j_{1})}) \neq 0 \), then by inequality (3.6), we have

$$\begin{aligned}& Hm\bigl([Sj_{0}]_{\alpha _{S}(j_{0})},[Tj_{1}]_{\alpha _{T}(j_{1})} \bigr) \leq \varpi D\bigl([Fj_{0}]_{\alpha _{F}(j_{0})} ,[Gj_{1}]_{\alpha _{G}(j_{1})} \bigr), \\& Hm\bigl([Sj_{0}]_{\alpha _{S}(j_{0})},[Tj_{1}]_{\alpha _{T}(j_{1})} \bigr) < \sqrt{\varpi} D\bigl([Fj_{0}]_{\alpha _{F}(j_{0})} ,[Gj_{1}]_{\alpha _{G}(j_{1})}\bigr). \end{aligned}$$

By Lemma 2.11, we can choose \(k_{2} \in [Tj_{1}]_{\alpha _{T}(j_{1})} \) such that

$$ \xi (k_{1},k_{2}) < \sqrt{\varpi} D \bigl([Fj_{0}]_{\alpha _{F}(j_{0})},[Gj_{0}]_{ \alpha _{G}(j_{0})}\bigr). $$
(3.4)

For this \(k_{2}\in [Tj_{1}]_{\alpha _{T}(j_{1})}\),we may use the fact that \(\bigcup_{u \in V}[Tu]_{\alpha _{T}(u)} \subseteq \bigcup_{u\in V}[Fu]_{ \alpha _{F}(u)}\) to obtain \(j_{2}\in V \) such that \(k_{2}\in [Fj_{2}]_{\alpha _{F}(j_{2})}\).

If \(D([Gj_{1}]_{\alpha _{G}(j_{1})} , [Fj_{2}]_{\alpha _{F}(j_{2})} ) \neq 0 \), then by Lemma (2.11) \(k_{3}\in [Sj_{2}]_{\alpha _{S}(j_{2})}\) such that

$$\begin{aligned} Hm\bigl( [Sj_{2}]_{\alpha _{S}(j_{2})},[Tj_{1}]_{\alpha _{T}(j_{1})} \bigr) & \leq \varpi D\bigl([Fj_{2}]_{\alpha _{F}(j_{2})},[Gj_{1}]_{\alpha _{G}(j_{1})} \bigr) \\ &< \sqrt{\varpi} D\bigl([Fj_{2}]_{\alpha _{F}(j_{2})},[Gj_{1}]_{\alpha _{G}(j_{1})} \bigr). \end{aligned}$$

This implies

$$\begin{aligned} \xi ( k_{2},k_{3}) &< \sqrt{\varpi} D\bigl( [Fj_{2}]_{\alpha _{F}(j_{2})},[Gj_{1}]_{ \alpha _{G}(j_{1})}\bigr) \\ &< \sqrt{\varpi} \xi (k_{2},k_{1}) \quad \text{by def (2.3)} \\ &< \varpi D\bigl([Fj_{0}]_{\alpha _{F}(j_{0})},[Gj_{0}]_{\alpha _{G}(j_{0})} \bigr) \quad \text{by inequality (3.4)}. \end{aligned}$$

Continuing this process, we obtain

$$\begin{aligned} \xi (k_{n},k_{n+1})&< \sqrt{\varpi} D\bigl([Fj_{n}]_{\alpha _{F}(j_{n})},[Gj_{n-1}]_{ \alpha _{G}(j_{n-1})} \bigr) \\ &< \sqrt{\varpi} \xi (k_{n},k_{n-1} ) \\ &< \varpi \xi (k_{n-1},k_{n-2} ) \\ &\vdots \\ & < \varpi ^{\frac{n}{2}} \xi ( k_{0},k_{1}) \end{aligned}$$

\(\Rightarrow \{k_{n}\}\) is a Cauchy sequence in \(\bigcup_{u \in V}[Gu]_{\alpha Gu}\). By completeness of \(\bigcup_{u \in V} [Gu]_{\alpha Gu}\), there exists \(z \in \bigcup_{u \in V}[Gu]_{\alpha _{G}(u)}\) such that \(k_{n}\rightarrow z\). (This also holds if \(\bigcup_{u \in V}[Tu]_{\alpha _{T}(u)} \) is complete). It further implies that \(z\in [Gu]_{\alpha _{G}(u)}\) for some \(u\in V \). Now,

$$\begin{aligned} \xi \bigl( z,[Tu]_{\alpha _{T}(u)}\bigr) &\leq \xi (z,k_{n}) + \xi \bigl(k_{n},[Tu]_{ \alpha _{T}(u)}\bigr) \\ &\leq \xi ( z,k_{n})+ Hm\bigl([Sj_{n-1}]_{\alpha _{S}(j_{n-1})}, [Tu]_{ \alpha _{T}(u)}\bigr) \quad \text{by Lemma 2.12} \\ &\leq \xi (z,k_{n})+ \varpi D\bigl([Fj_{n-1}]_{\alpha _{F}(j_{n-1})},[Gu]_{ \alpha _{G}(u)} \bigr) \\ &< \xi (z,k_{n})+ \varpi \xi (k_{n-1},z) \quad \text{by def (2.3)}. \end{aligned}$$

Letting \(n\rightarrow \infty \), we have \(\xi (z,[Tu]_{\alpha _{T}(u)}) \rightarrow 0\), and this implies that

$$ z\in [Tu]_{\alpha _{T}(u)}. $$

Hence

$$ z \in [Tu]_{\alpha _{T}(u)} \cap [Gu]_{\alpha _{G}(u)}. $$

⇒u is a coincidence point of T and G.

Now, since \(\{k_{n}\} \) is a Cauchy sequence in \(\bigcup_{u\in V}[Fu]_{\alpha _{F}(u)}\), so by completeness property \(z\in \bigcup_{u \in V}[Fu]_{\alpha _{F}(u)} \). (This also holds if \(\bigcup_{u \in V}[Su]_{\alpha _{S}(u)} \) is complete). This implies that there exists \(u' \in V \) such that \(z \in [Fu']_{\alpha _{F}(u')}\). Now

$$\begin{aligned} \xi \bigl(z,\bigl[Su'\bigr]_{\alpha _{S}(u')}\bigr) &\leq \xi (z,k_{n})+\xi \bigl(k_{n},\bigl[Su' \bigr]_{ \alpha _{S}(u')}\bigr) \\ & \leq \xi (z,k_{n})+ Hm \bigl([Tj_{n-1}]_{\alpha _{T}(j_{n-1})}, \bigl[Su'\bigr]_{ \alpha _{S}(u')}\bigr) \\ & \leq \xi (z,k_{n})+ \varpi D\bigl([Gj_{n-1}]_{\alpha _{G}(j_{n-1})}, \bigl[Fu'\bigr]_{ \alpha _{F}(u')}\bigr) \\ & \leq \xi (z,k_{n})+ \varpi \xi (j_{n-1},z) \quad \text{by def (2.3)}. \end{aligned}$$

Letting \(n\rightarrow \infty \)

$$\begin{aligned}& \xi \bigl(z,\bigl[Su'\bigr]_{\alpha _{S}(u')}\bigr) = 0\\& \quad \Rightarrow\quad z\in \bigl[Su'\bigr]_{\alpha _{S}(u')}\\& \quad \Rightarrow\quad z\in \bigl[Fu'\bigr]_{\alpha _{F}(u')} \cap \bigl[Su'\bigr]_{\alpha _{S}(u')}. \end{aligned}$$

Hence, \(u'\) is a coincidence point of F and S. Since

$$ z \in \bigl( [Tu]_{\alpha _{T}(u)} \cap [Gu]_{\alpha _{G}(u)}\bigr) $$

and

$$ z \in \bigl(\bigl[Fu'\bigr]_{\alpha _{F}(u')} \cap \bigl[Su'\bigr]_{\alpha _{S}(u')}\bigr). $$

So,

$$\begin{aligned}& \bigl([Tu]_{\alpha _{T}(u)} \cap [Gu]_{\alpha _{G}(u)}\bigr) \neq \emptyset,\\& \bigl(\bigl[Fu'\bigr]_{\alpha _{F}(u')} \cap \bigl[Su' \bigr]_{\alpha _{S}(u')}\bigr) \neq \emptyset . \end{aligned}$$

 □

Example 3.2

Let \(V=[0,\infty )\), \(\xi (j,k)= |j-k|\), whenever \(j,k \in V\) and \(\phi , \psi , \mu , \nu \in (0,1]\). Define mappings \(K,L,M,N : [0,\infty ) \rightarrow \digamma (V) \) as follows:

$$\begin{aligned}& K(j) (t) = \textstyle\begin{cases} \phi , & \text{if } 0\leq t \leq 4j, \\ \frac{\phi}{4}, & \text{if } 4j < t \leq 6j, \\ \frac{\phi}{6}, & \text{if }6j < t \leq 8j, \\ 0, & \text{if }8j < t < \infty , \end{cases}\displaystyle \\& L(j) (t) = \textstyle\begin{cases} \psi , & \text{if }0\leq t \leq 6j, \\ \frac{\psi}{5}, & \text{if }6j < t \leq 8j, \\ \frac{\psi}{7}, & \text{if } 8j < t \leq 10j, \\ 0, & \text{if }10j < t < \infty , \end{cases}\displaystyle \\& M(j) (t) = \textstyle\begin{cases} \mu , & \text{if } t = 6j, \\ \frac{\mu}{4}, & \text{if }t = 8j, \\ \frac{\mu}{8}, & \text{if } t= 10j, \\ 0, & \text{otherwise}, \end{cases}\displaystyle \\& N(j) (t) = \textstyle\begin{cases} \nu , & \text{if } t = 8j, \\ \frac{\nu}{5}, & \text{if }t = 10j, \\ \frac{\nu}{7}, & \text{if } t= 12j, \\ 0, & \text{otherwise}. \end{cases}\displaystyle \end{aligned}$$

Now define \(S, T, F, G : V \rightarrow \digamma (V) \) as follows:

$$\begin{aligned}& S(j) = \textstyle\begin{cases} \chi _{\{0\}} , & \text{if }j=0, \\ K(j), & \text{if }j>0, \end{cases}\displaystyle \\& T(j) = \textstyle\begin{cases} \chi _{\{0\}} , & \text{if }j=0, \\ L(j), & \text{if }j>0, \end{cases}\displaystyle \\& F(j) = \textstyle\begin{cases} \chi _{\{0\}} , & \text{if }j=0, \\ M(j), & \text{if }j>0, \end{cases}\displaystyle \end{aligned}$$

and

$$ G(j) = \textstyle\begin{cases} \chi _{\{0\}} , & \text{if }j=0, \\ N(j), & \text{if }j >0. \end{cases} $$

If \(\alpha _{S}(j) = \phi \), \(\alpha _{T}(j) =\psi \), \(\alpha _{F}(j) = \mu \), \(\alpha _{G}(j) = \nu \) then,

$$\begin{aligned}& \bigl[S(j)\bigr]_{\alpha _{S}(j)} = \textstyle\begin{cases} \{0\} , & \text{if }j=0, \\ {[}0,4j] , & \text{if } j > 0 , \end{cases}\displaystyle \\& \bigl[T(j)\bigr]_{\alpha _{T}(j)} = \textstyle\begin{cases} \{0\} , & \text{if }j=0, \\ {[}0, 6j] , & \text{if }j > 0, \end{cases}\displaystyle \\& \bigl[F(j)\bigr]_{\alpha _{F}(j)} = \textstyle\begin{cases} \{0\} , & \text{if }j=0, \\ \{6j\} , & \text{if } j > 0 , \end{cases}\displaystyle \end{aligned}$$

and

$$ \bigl[G(j)\bigr]_{\alpha _{G}(j)} = \textstyle\begin{cases} \{0\} , & \text{if }j=0, \\ \{ 8j\} , & \text{if } j > 0 , \end{cases} $$

and

$$ \bigcup_{j \in V} [Sj]_{\alpha _{S}(j)} = [0,\infty ) = \bigcup_{j \in V} [Gj]_{\alpha _{G}(j)} $$

and

$$ \bigcup_{j \in V} [Tj]_{\alpha _{T}(j)} = [0,\infty ) = \bigcup_{j \in V} [Fj]_{\alpha _{F}(j)}. $$

If \(j,k =0 \) then,

$$ Hm\bigl([Sj]_{\alpha _{S}(j)},[Tk]_{\alpha _{T}(k)}\bigr) = \varpi D \bigl([Fj]_{ \alpha _{F}(j)},[Gk]_{\alpha _{G}(k)}\bigr) \quad \forall j,k \in V. $$

If \(j,k \neq 0\) then,

$$ Hm\bigl([Sj]_{\alpha _{S}(j)},[Tk]_{\alpha _{T}(k)}\bigr) = 4 \vert j-k \vert . $$

Thus, for \(\varpi = \frac{2}{3} \), all the assumptions of Theorem 3.1 are satisfied to obtain

$$ [T0]_{\alpha _{T}(0)}\cap [G0]_{\alpha _{G}(0)} \neq \emptyset $$

and

$$ [S0]_{\alpha _{S}(0)}\cap [F0]_{\alpha _{F}(0)}\neq \emptyset . $$

Corollary 3.3

Consider a metric space \((V,\xi )\) and \(\operatorname{CB}(V)\) to be the class of all bounded and closed subsets of V. Let \(S, F : V \rightarrow \digamma (V)\) be two fuzzy mappings. Suppose for each \(u \in V\), there exists \(\alpha _{S}(u), \alpha _{F}(u) \in (0, 1]\) such that \([Su]_{ \alpha _{S}(u)}, [Fu]_{\alpha _{F}(u)}\in \operatorname{CB}(V)\) and

$$ \bigcup_{u \in V} [Su]_{\alpha _{S}(u)} \subseteq \bigcup_{u \in V}[Fu]_{ \alpha _{F}(u)}. $$
(3.5)

Also suppose that

$$ \bigcup_{u \in V}[Su]_{\alpha _{S}(u)} \quad \textit{or} \quad \bigcup_{u \in V} [Fu]_{ \alpha _{F}(u)} $$

is complete. If there exists \(\varpi \in [0,1)\) such that

$$ Hm\bigl([Sj]_{\alpha _{S}(j)},[Sk]_{\alpha _{S}(k)}\bigr) \leq \varpi D\bigl([Fj]_{ \alpha _{F}(j)},[Fk]_{\alpha _{F}(k)}\bigr) \quad \forall j,k \in V $$
(3.6)

then there exists \(u' \in V\) such that

$$ \bigl[Su'\bigr]_{\alpha _{S}(u')}\cap \bigl[Fu' \bigr]_{\alpha _{F}(u')}\neq \emptyset . $$

Proof

By setting \(S=T\) and \(F=G\) in Theorem 3.1, we get the required result. □

Theorem 3.4

Consider a metric space \((V,\xi ) \) and \(S,T,F,G : V \rightarrow \digamma (V) \) to be fuzzy mappings. Suppose that \([Fv]_{\alpha _{F}(v)}\) and \([Gv]_{\alpha _{G}(v)}\) are singletons for \(\alpha \in (0,1]\).

$$ \bigcup_{v \in V}[Sv]_{\alpha _{S}(v)} \subseteq \bigcup _{v \in V}[Gv]_{ \alpha _{G}(v)} \quad \textit{and}\quad \bigcup_{v \in V}[Tv]_{\alpha _{T}(v)} \subseteq \bigcup _{v \in V}[Fv]_{\alpha _{F}(v)}, $$

and also one of \(\bigcup_{v \in V}[Sv]_{\alpha _{S}(v)}\) or \(\bigcup_{v \in V}[Gv]_{ \alpha _{G}(v)} \) and \(\bigcup_{v \in V}[Tv]_{\alpha _{T} (v)}\) or \(\bigcup_{v \in V}[Fv] \) are complete, also \([Sv]_{\alpha _{S}(v)}\) and \([Tv]_{\alpha _{T}(v)} \) are closed and bounded subsets of V. If there exists \(\varpi \in [0,1) \) such that

$$ Hm\bigl([Sj]_{\alpha _{S}(j)}, [Tk]_{\alpha _{T}(k)}\bigr) \leq \varpi D\bigl([Fj]_{\alpha _{F}(j)},[Gk]_{\alpha _{G}(k)}\bigr) \quad \forall j,k \in V. $$
(3.7)

Then there exists points \(u, u'\in V \), such that

$$ [Gu]_{\alpha _{G}(u)} \in [Tu]_{\alpha _{T}(u)} \quad \textit{and} \quad \bigl[Fu'\bigr]_{ \alpha _{F}(u')} \in \bigl[Su' \bigr]_{\alpha _{S}(u')}. $$

Proof

By taking \([Fv]_{\alpha _{F}(v)}\) and \([Gv]_{\alpha _{G}(v)}\) singleton in Theorem 3.1, we have the required results. □

Corollary 3.5

Consider a metric space \((V,\xi ) \) and \(S,T, : V \rightarrow \digamma (V) \) to be fuzzy mappings. Suppose that f and g are single valued maps and \(\alpha \in (0,1] \).

$$ \bigcup_{v \in V}[Sv]_{\alpha _{S}(v)} \subseteq gV \quad \textit{and}\quad \bigcup_{v \in V}[Tv]_{\alpha _{T}(v)} \subseteq fV, $$

and also one of \(\bigcup_{v \in V}[Sv]_{\alpha _{S}(v)}\) or gV and \(\bigcup_{v \in V}[Tv]_{\alpha _{T}(v)}\) or fV are complete, also \([Sv]_{\alpha _{S}(v)}\) and \([Tv]_{ \alpha _{T}(v)} \) are closed and bounded subsets of V. If there exists \(\varpi \in [0,1) \) such that

$$ Hm\bigl([Sj]_{\alpha _{S}(j)}, [Tk]_{\alpha _{T}(k)}\bigr) \leq \varpi D(fj,gk) \quad \forall j,k \in V. $$
(3.8)

Then there exists points \(u, u'\in V \), such that

$$ gu \in [Tu]_{\alpha _{T}(u)} \quad \textit{and} \quad fu' \in \bigl[Su'\bigr]_{\alpha _{S}(u')}. $$

Theorem 3.6

Consider a metric space \((V,\xi ) \). Let \(S, T , F : V \rightarrow \digamma (V)\) be fuzzy mappings. Suppose that for \(\alpha \in (0,1] \) \([Sv]_{\alpha _{S}(v)}, [Tv]_{\alpha _{T}(v)}, [Fv]_{\alpha _{F}(v)} \in \operatorname{CB}(V)\) and

$$ \bigcup_{v \in V}[Sv]_{\alpha _{S}(v)} \cup \bigcup_{v \in V}[Tv]_{ \alpha _{T}(v)} \subseteq \bigcup _{v \in V}[Fv]_{\alpha _{F}(v)}, $$
(3.9)

also either \(\bigcup_{v \in V}[Sv]_{\alpha _{S}(v) } \cup \bigcup_{v \in V}[Tv]_{ \alpha _{T}(v)}\) or \(\bigcup_{v \in V}[Fv]_{\alpha _{F}(v)} \) are complete. If there exists \(\varpi \in [0,1) \) such that

$$ Hm\bigl([Sj]_{\alpha _{S}(j)},[Tk]_{\alpha _{T}(k)}\bigr) \leq \varpi D\bigl([Fj]_{ \alpha _{F}(j)},[Fk]_{\alpha _{F}(k)}\bigr), \quad \forall j,k \in V. $$
(3.10)

then there exists \(u \in V \) such that

$$ [Su]_{\alpha _{S}(u)} \cap [Tu]_{\alpha _{T}(u)} \cap [Fu]_{\alpha _{F}(u)} \neq \emptyset . $$

Proof

Let \(j_{0} \) be the arbitrary fixed element of V. Since \([Sj_{0}]_{\alpha _{S}(j_{0})} \neq \emptyset \), so let \(k_{1} \in [Sj_{0}]_{\alpha _{S}(j_{0})} \), then there exists some \(j_{1} \in V \) such that \(k_{1} \in [Fj_{1}]_{\alpha _{F}(j_{1})} \). Thus, \(k_{1} \in [Sj_{0}]_{\alpha _{S}(j_{0})} \cap [Fj_{1}]_{\alpha _{F}(j_{1})} \). Now

$$\begin{aligned} Hm\bigl([Sj_{0}]_{\alpha _{S}(j_{0}) },[Tj_{1}]_{\alpha _{T}(j_{1})} \bigr) & \leq \varpi D\bigl([Fj_{0}]_{\alpha _{F}(j_{0})},[Fj_{1}]_{\alpha _{F}(j_{1})} \bigr) \\ & < \sqrt{\varpi} D\bigl([Fj_{0}]_{\alpha _{F}(j_{0})},[Fj_{1}]_{\alpha _{F}(j_{1})} \bigr) \end{aligned}$$

By Lemma 2.11, we choose \(k_{2} \in [Tj_{1}]_{\alpha _{T}(j_{1})} \) such that

$$ \xi (k_{1},k_{2}) < \sqrt{\varpi} D\bigl([Fj_{0}]_{\alpha _{F}(j_{0})},[Fj_{1}]_{ \alpha _{F}(j_{1})} \bigr) $$

For this \(k_{2} \in [Tj_{1}]_{\alpha _{T}(j_{1})} \), we may use inequality (3.9) to obtain \(j_{2} \in V \) such that \(k_{2} \in [Fj_{2}]_{\alpha _{F}(j_{2})} \), and so

$$\begin{aligned}& k_{2} \in [Tj_{1}]_{\alpha _{T}(j_{1})} \cap [Fj_{2}]_{\alpha _{F}(j_{2})}, \\& Hm\bigl([Sj_{2}]_{\alpha _{S}(j_{2})},[Tj_{1}]_{\alpha _{T}(j_{1})} \bigr) \leq \varpi D\bigl([Fj_{1}]_{\alpha _{F}(j_{1})},[Fj_{2}]_{\alpha _{F}(j_{2})} \bigr) \\& \hphantom{Hm([Sj_{2}]_{\alpha _{S}(j_{2})},[Tj_{1}]_{\alpha _{T}(j_{1})})} < \sqrt{\varpi} D\bigl([Fj_{1}]_{\alpha _{F}(j_{1})},[Fj_{2}]_{\alpha _{F}(j_{2})} \bigr). \end{aligned}$$

By Lemma 2.11, we choose \(k_{3} \in [Sj_{2}]_{\alpha _{S}(j_{2})} \) such that

$$\begin{aligned} \xi (k_{2},k_{3}) &< \sqrt{\varpi} D\bigl([Fj_{1}]_{\alpha _{F}(j_{1})},[Fj_{2}]_{ \alpha _{F}(j_{2})} \bigr) \\ &< \sqrt{\varpi} \xi (k_{1},k_{2}) \quad \text{by def (2.3)} \\ &< \sqrt{\varpi} D\bigl([Fj_{0}]_{\alpha _{F}(j_{0})},[Fj_{1}]_{\alpha _{F}(j_{1})} \bigr) \end{aligned}$$

by continuing this process,

$$\begin{aligned} \xi (k_{n},k_{n+1}) & < \sqrt{\varpi} D\bigl([Fj_{n-1}]_{\alpha _{F}(j_{n-1})},[Fj_{n}]_{ \alpha _{F}(j_{n})} \bigr) \\ & < \sqrt{\varpi} \xi (k_{n-1},k_{n}) \quad \text{by def (2.3)} \\ & < \varpi \xi (k_{n-1},k_{n-2}) \\ & < \cdots \\ & < \varpi ^{\frac{n}{2}} \xi (k_{0},k_{1}). \end{aligned}$$

This implies that \(\{k_{n}\} \) is a Cauchy sequence in \(\bigcup_{v \in V}[Fv]_{\alpha _{F}(v)} \). By completeness there exists an element \(z \in \bigcup_{v \in V}[Fv]_{\alpha _{F}(v)} \), such that \(k_{n} \rightarrow z\). (This also holds if \((\bigcup_{v \in V}[Sv]_{\alpha _{S}(v)}) \cup (\bigcup_{v \in V}[Tv]_{\alpha _{T}(v)}) = \bigcup_{v \in V} ([Sj]_{\alpha _{S}(j)} \cup [Tj]_{\alpha _{T}(j)})\) is complete with \(z \in \bigcup_{v \in V} ( [Sj]_{\alpha _{S}(j)} \cup [Tj]_{ \alpha _{S}(j)} \subseteq \bigcup_{v \in V}[Fv]_{\alpha _{F}(v)} )\). It further implies that

$$ z \in [Fu]_{\alpha _{F}(u)} \quad \text{for some } u \in V. $$

Now

$$\begin{aligned} \xi \bigl(z,[Tu]_{\alpha _{T}(u)}\bigr) & \leq \xi (z,k_{n})+\xi \bigl(k_{n},[Tu]_{ \alpha _{T}(u)}\bigr) \\ & \leq \xi (z,k_{n})+Hm\bigl([Sj_{n-1}]_{\alpha _{S}(j_{n-1})},[Tu]_{ \alpha _{T}(u)} \bigr) \quad \text{by Lemma 2.12} \\ & \leq \xi (z,k_{n})+ \varpi D\bigl([Fj_{n-1}]_{\alpha _{F}(j_{n-1})},[Fu]_{ \alpha _{F}(u)} \bigr) \quad \text{by inequality (3.10)} \\ & < \xi (z,k_{n})+ \sqrt{\varpi} \xi ( k_{n-1},z) . \end{aligned}$$

Letting \(n\rightarrow \infty \),

$$\begin{aligned}& \xi \bigl(z,[Tu]_{\alpha _{T}(u)}\bigr) = 0\\& \quad \Rightarrow\quad z \in [Tu]_{\alpha _{T}(u)}. \end{aligned}$$

Hence \(z \in [Tu]_{\alpha Tu} \cap [Fu]_{\alpha _{F}(u)}\). Now

$$\begin{aligned} \xi \bigl(z,[Su]_{\alpha _{S}(u)}\bigr) & \leq \xi (z,k_{n}) + \xi \bigl(k_{n},[Su]_{ \alpha _{S}(u)}\bigr) \\ & \leq \xi (z,k_{n})+Hm\bigl([Tj_{n-1}]_{\alpha _{T}(j_{n-1})},[Su]_{ \alpha _{S}(u)} \bigr) \quad \text{by Lemma 2.12} \\ & \leq \xi (z,k_{n})+ \varpi D\bigl([Fj_{n-1}]_{\alpha _{F}(j_{n-1})},[Fu]_{ \alpha _{F}(u)} \bigr) \quad \text{by inequality (3.10)} \\ & < \xi (z,k_{n})+ \varpi \xi ( k_{n-1},z) \quad \text{by def (2.3)}. \end{aligned}$$

Letting \(n\rightarrow \infty \),

$$\begin{aligned}& \xi \bigl(z,[Su]_{\alpha _{S}(u)}\bigr) = 0\\& \quad \Rightarrow\quad z \in [Su]_{\alpha _{S}(u)}. \end{aligned}$$

Hence \(z \in ([Fu]_{\alpha _{F}(u)} \cap [Tu]_{\alpha _{T}(u)} \cap [Su]_{ \alpha _{S}(u)}) \), thus \(([Fu]_{\alpha _{F}(u)} \cap [Tu]_{\alpha _{T}(u)} \cap [Su]_{\alpha _{S}(u)}) \neq \emptyset \), and u is a common coincidence fuzzy fixed point of S, T and F. □

Example 3.7

Let \(V=[0,\infty )\), \(\xi (v,w)= |v-w|\), whenever \(v, w \in V\) and \(\delta _{1}, \delta _{2}, \delta _{3} \in (0,1]\). Define mappings \(P, Q, R : [0,\infty ) \rightarrow \digamma (V) \) as follows:

$$\begin{aligned}& P(v) (t) = \textstyle\begin{cases} \delta _{1}, & \text{if } 0\leq t \leq 2v; \\ \frac{\delta _{1}}{2}, & \text{if } 2v < t\leq 3v ; \\ 0, & \text{otherwise,} \end{cases}\displaystyle \\& Q(v) (t) = \textstyle\begin{cases} \delta _{2}, & \text{if } 0\leq t \leq 4v; \\ \frac{\delta _{2}}{3}, & \text{if } 4v < t \leq 6v ; \\ 0, & \text{otherwise,} \end{cases}\displaystyle \\& R(v) (t) = \textstyle\begin{cases} \delta _{3}, & \text{if } t = 6v; \\ \frac{\delta _{3}}{3}, & \text{if } t= 8v ; \\ 0, & \text{otherwise.} \end{cases}\displaystyle \end{aligned}$$

Define \(S, T, F: V\rightarrow \digamma (V)\) as follows

$$\begin{aligned}& S(v) = \textstyle\begin{cases} \chi _{\{0\}}, & \text{if }v= 0 ; \\ P(v) , & \text{if }v>0, \end{cases}\displaystyle \\& T(v) = \textstyle\begin{cases} \chi _{\{0\}}, & \text{if }v= 0 ; \\ Q(v) , & \text{if }v>0, \end{cases}\displaystyle \\& F(v) = \textstyle\begin{cases} \chi _{\{0\}}, & \text{if }v= 0 ; \\ R(v) , & \text{if }v>0. \end{cases}\displaystyle \end{aligned}$$

If \(\alpha _{S}(v) = \delta _{1}\), \(\alpha _{T}(v) = \delta _{2}\), \(\alpha _{F}(v) = \delta _{3} \), then

$$\begin{aligned}& \bigl[S(v)\bigr]_{\alpha _{S}(v)} = \textstyle\begin{cases} \{0\} , & \text{if }v=0, \\ {[}0,2v] , & \text{if } v > 0 , \end{cases}\displaystyle \\& \bigl[T(v)\bigr]_{\alpha _{T}(v)} = \textstyle\begin{cases} \{0\} , & \text{if }v=0, \\ {[}0,4v] , & \text{if } v > 0, \end{cases}\displaystyle \\& \bigl[F(v)\bigr]_{\alpha _{F}(v)} = \textstyle\begin{cases} \{0\} , & \text{if }v=0, \\ \{6v\} , & \text{if } v > 0 , \end{cases}\displaystyle \\& \bigcup_{v \in V} [Sv]_{\alpha _{S}(v)} \cup \bigcup _{v \in V} [Tv]_{ \alpha _{T}(v)} = [0,\infty ) = \bigcup _{v \in V} [Fv]_{\alpha _{F}(v)}. \end{aligned}$$

Then for \(\varpi = \frac{2}{5}\), all the axioms of Theorem 3.6 are satisfied to obtain

$$ [S0]_{\alpha _{S}(0)}\cap [T0]_{\alpha _{T}(0)} \cap [F0]_{\alpha _{F}(0)} \neq \emptyset . $$

Corollary 3.8

Consider a metric space \((V,\xi ) \) and \(S,F : V \rightarrow (V) \) to be fuzzy mappings such that \([Sv]_{\alpha _{S}(v)}, [Fv]_{\alpha _{F}(v)} \in \operatorname{CB}(V)\). Suppose that

$$ \bigcup_{v \in V}[Sv]_{\alpha _{S}(v)} \subseteq \bigcup_{v \in V}[Fv]_{ \alpha _{F}(v)}. $$
(3.11)

Also either \(\bigcup_{v \in V}[Sv]_{\alpha _{S}(v)}\) or \(\bigcup_{v \in V}[Fv]_{ \alpha _{F}(v)}\) are complete. If there exists \(\varpi \in [0,1) \) such that

$$ Hm\bigl([Sj]_{\alpha _{S}(j)}, [Sk]_{\alpha _{S}(k)}\bigr) \leq \varpi D\bigl([Fj]_{ \alpha _{F}(j)},[Fk]_{\alpha _{F}(k)}\bigr)\quad \forall j,k \in V. $$
(3.12)

Then there exists a point \(u \in V \) such that \([Su]_{\alpha _{S}(u)} \cap [Fu]_{\alpha _{F}(u)} \neq \emptyset \).

4 Application

Theorem 4.1

Let \((\aleph ,\xi )\) be a metric space and \(S,T,F,G:\aleph \rightarrow CB(\aleph )\) be multi-valued mappings. Suppose that

$$ S\aleph \subseteq G\aleph \quad \textit{and} \quad T\aleph \subseteq F\aleph , $$

also one of Sℵ or Gℵ and Tℵ or Fℵ are complete. If there exists \(\varpi \in [0,1)\) such that

$$ Hm(Sx, Ty) \leq \varpi D(Fx, Gy),\quad \forall x, y \in \aleph . $$
(4.1)

Then there exist points \(u, u^{\prime}\in \aleph \) such that \(Tu\cap Gu\neq \emptyset \) and \(Su^{\prime}\cap Fu\prime \neq \emptyset \).

Proof

Consider four fuzzy mapping \(A, B, C, D: \aleph \rightarrow \digamma (\aleph )\) defined by

$$ A(x)=\chi _{Tx}, \qquad B(x)=\chi _{Fx}, \qquad C(x)=\chi _{Sx}, \qquad D(x)= \chi _{Gx}, $$

then for

$$\begin{aligned}& \alpha _{A (x )}, \alpha _{B (x )}, \alpha _{C (x )}, \alpha _{D (x )} \in (0, 1], \\& \bigl[A(x) \bigr]_{\alpha _{A (x )}}= \bigl\{ t: A(x) (t) \geq \alpha _{A (x )} \bigr\} \\& \hphantom{ [A(x) ]_{\alpha _{A (x )}}}= \bigl\{ t: \chi _{Tx}(t) \geq \alpha _{A (x )} \bigr\} \\& \hphantom{ [A(x) ]_{\alpha _{A (x )}}}= \bigl\{ t: \chi _{Tx}(t)=1 \bigr\} \\& \hphantom{ [A(x) ]_{\alpha _{A (x )}}}= \{t: t \in Tx \} \\& \hphantom{ [A(x) ]_{\alpha _{A (x )}}}=Tx. \end{aligned}$$

Similarly

$$ \bigl[B(x) \bigr]_{\alpha _{B (x )}}=Fx,\qquad \bigl[C(x) \bigr]_{\alpha _{C (x )}}=Sx, \qquad \bigl[D(x) \bigr]_{ \alpha _{D (x )}}=Gx. $$

Now

$$ \bigcup_{x \in \aleph} \bigl[A(x)\bigr]_{\alpha _{A(x)}}= \bigcup_{x \in \aleph} \bigl\{ t: A(x) (t) \geq \alpha _{A (x )} \bigr\} = \bigcup_{x \in \aleph}Tx=T\aleph \subseteq F\aleph =\bigcup_{x \in \aleph} \bigl[B(x) \bigr]_{\alpha _{B(x)}}. $$

Also

$$ \bigcup_{x \in \aleph} \bigl[C(x)\bigr]_{\alpha _{C(x)}}= \bigcup_{x \in \aleph} \bigl\{ t: C(x) (t) \geq \alpha _{C (x )} \bigr\} = \bigcup_{x \in \aleph}Sx=S\aleph \subseteq G\aleph =\bigcup_{x \in \aleph} [Dx]_{\alpha _{D(x)}}. $$

Since \(Hm ([C(x)]_{\alpha _{C(x)}}, [A(y) ]_{\alpha _{A (y )}} )= Hm(Sx, Ty)\) and \(D ([B(x)]_{\alpha _{B(x)}}, [D(y) ]_{\alpha _{D (y )}} )= D(Fx, Gy)\), Theorem 3.1 can be applied to obtain \(u, u^{\prime} \in \aleph \) such that \(Tu\cap Gu\neq \emptyset \) and \(Su^{\prime}\cap Fu\prime \neq \emptyset \). □

Theorem 4.2

Let \((\aleph ,\xi )\) be a metric space and \(S,T,F:\aleph \rightarrow \operatorname{CB}(\aleph )\) be multi-valued mappings. Suppose that

$$ S\aleph \cup T\aleph \subseteq F\aleph , $$
(4.2)

also either \(S\aleph \cup T\aleph \) or Fℵ is complete. If there exists \(\varpi \in (0,1)\) such that

$$ Hm(Sx, Ty) \leq \varpi D(Fx, Fy), \quad \forall x, y \in \aleph . $$
(4.3)

Then there exist a point \(u \in \aleph \) such that \(Su\cap Tu \cap Fu \neq \emptyset \).

Proof

By setting \(G=F\) in above theorem, the required result can be obtained. □

5 Conclusion

Integral inequalities and integral inclusions arise in several problems in mathematical physics, control theory, critical point theory for non-smooth energy functional, differentials, variational inequalities, fuzzy set arithmetic, traffic theory, etc. These can be solved by fixed point methods. In this study, coupled common coincidence points for two fuzzy mappings that fulfill a rational inequality and common coincidence points for three fuzzy mappings that meet a rational inequality are constructed within the framework of complete metric spaces. Examples are provided to highlight the superiority and rationality of the discovered results. The concept under consideration here unifies and generalizes a number of well-known coincidence point and fixed point theories in the associated literature. Moreover, our work will motivate researchers to go ahead and help them in finding the solutions of various types of equations and inequalities.

We conclude this paper by indicating, in the form of open questions, some directions for further investigation and work.

1. Exploring common coincidence points for mappings having contractive type conditions in rectangular metric, F-metric and fuzzy metric spaces, and so on in the future.

2. Can the conditions of inclusion in all theorems be relaxed?

3. If the answer to 2 is yes, then what hypotheses are needed to guarantee the existence of coincidence points?

4. Whether the concept of coincidence point for these contractions can be extended to more than four mappings?