Abstract
In this paper, the fractional-order Chelyshkov functions (FCHFs) and Riemann-Liouville fractional integrals are utilized to find numerical solutions to fractional delay differential equations, by transforming the problem into a system of algebraic equations with unknown FCHFs coefficients. An error bound of FCHFs approximation is estimated and its convergence is also demonstrated. The effectiveness and accuracy of the presented method are established through several examples. The resulting solution is accurate and agrees with the exact solution, even if the exact solution is not a polynomial. Moreover, comparisons between the obtained numerical results and those recently reported in the literature are shown.
Similar content being viewed by others
1 Introduction
Mathematical models of natural phenomena can be formulated more accurately by utilizing fractional differential equations. Fractional differential equations have many applications in various fields of science, such as physics [7, 11, 17], chemistry [37], biology [49], medicine [18], fluid mechanics [26], continuum mechanics [12], signal processing [40] and propagation of spherical flames [28]. Consequently, much attention has been devoted to find solutions to fractional differential equations. Numerous authors have studied the existence and uniqueness of solutions for fractional differential equations [25, 39]. In recent years, many numerical methods have been presented in the literature to solve these kinds of equations, such as Galerkin method [6], homotopy analysis method [35], differential transformation method [2], collocation method [3, 5], cubic B-spline collocation method [29], hybrid Taylor and block-pulse operational matrix method [45], Euler functions method [30], Chebyshev polynomials method [23, 24], and Chelyshkov functions method [4].
A delay differential equation is a type of differential equation where the derivative of the unknown function at the current time depends not only on the solution at the current time, but also on the solution at previous times. Fractional delay differential equations can be considered as a generalization of delay differential equations of integer orders. They have been used for modeling in different fields of science, such as control [20], biology [9], optics [41] and electrical networks [16]. Many researchers have examined the existence and uniqueness of solutions to fractional delay differential equations [1, 27].
Generally, It is a challenge to find exact solutions for most fractional delay differential equations, hence numerical or approximate methods should be developed to solve these equations. Various techniques have been presented to address this type of problem in recent decades. In [31], a numerical method based on finite differences has been presented to approximate solutions of fractional delay differential equations. The development of a predictor-corrector method with error analysis has been introduced in [14]. The Bernoulli wavelet operational matrix of fractional integration together with the collocation method has been employed in [42] to provide an approximate solution of fractional delay differential equations. In [21], the collocation method, optimization techniques and generalized Laguerre polynomials are applied to approximate a solution of delay fractional differential equations. A numerical technique based on hybrid functions of block-pulse and fractional-order Fibonacci polynomials has been given in [43]. They used Riemann–Liouville fractional integral operational matrix and delay operational matrix of the hybrid functions together with the collocation method to reduce the problem to a system of algebraic equations.
In [15], a computational technique based on the combination of fractional Bessel functions with block-pulse functions to produce a sparse operational matrix to reduce the problem to a system of algebraic equations. A spectral operational matrices-based algorithm has been presented in [48]. These matrices have been generated by using shifted Gegenbauer polynomials. Instead of using the operational matrix of fractional integration, which requires some approximation, a numerical method based on the explicit formula of Riemann–Liouville fractional integral of Legendre wavelets functions has been given in [50]. A numerical method based on applying the exact formula for the Riemann–Liouville fractional integral of Taylor wavelet functions together with the collocation method has been proposed in [47]. Recently, Avci [10] has introduced a numerical spectral technique depending on the operational matrix of fractional integration for fractional-order Taylor basis.
Approximation by orthogonal functions has grown significantly as a useful tool for solving fractional differential equations. They convert the fractional problem into a set of algebraic problems. Some popular orthogonal families are Chebyshev polynomials, Legendre polynomials, Laguerre polynomials, Taylor polynomials, Chelyshkov polynomials and block–pulse functions. Chelyshkov polynomials were presented in [13] and have been used successfully for solving different kinds of fractional differential equations. Solving fractional differential equations with basis functions of integer-order may lead to some issues when the solutions contain terms with fractional powers [19]. The major weaknesses are that the rate of convergence is weak and a large number of basis functions are required to provide accurate results. These drawbacks can be avoided by approximating the solutions using orthogonal functions of fractional order.
Based on the above considerations, the motivation of this paper is to extend the application of FCHFs to present a new numerical method for solving fractional delay differential equations. In order to accomplish this goal, the operational matrix of fractional integral for FCHFs is derived and used together with the collection method to convert the fractional delay problem into a set of algebraic equations. To the best of our knowledge, this is the first time that the operational matrix of fractional integration for FCHFs is applied to solve fractional delay differential equations
The main advantages of the presented technique are:
-
FCHFs are fractional-order orthogonal functions. This feature leads to a good rate of convergence and reduces the number of basis functions required to get satisfactory results.
-
The solution procedure is simple since the fractional delay problem is reduced to a set of algebraic equations.
-
The computational errors are less than in the conventional methods where the obtained numerical results in some cases are the exact solutions and in others are in good agreement with the exact solutions.
The structure of the paper is as follows. Section 2 presents some fundamental concepts of fractional calculus that will be used in our subsequent development. In Sect. 3, the FCHFs are described, and the operational matrix of fractional integration is also constructed. The convergence of FCHFs is demonstrated in Sect. 4. Section 5 describes our new numerical method for solving fractional delay differential equations. Section 6 considers some numerical examples and reports our numerical results as well as some comparisons with other methods. The paper is finally summarized in Sect. 7.
2 Preliminaries on fractional calculus
Here, we review some definitions and properties of fractional integration and differentiation that will be used in the next sections [36, 39].
Definition 2.1
The Riemann–Liouville fractional integration of order \(\nu \geq 0 \) of a function \(g(t)\) is defined as
where \(t^{\nu -1}\ast g(t)\) is the convolution of \(t^{\nu -1}\) and \(g(t)\).
Definition 2.2
The Caputo fractional derivative of order \(\nu >0\) of a function \(g(t)\) is defined as
where \(\lceil \nu \rceil \) denotes the smallest integer greater than or equal to ν.
The following properties are satisfied for Riemann–Liouville fractional integral and Caputo fractional derivative:
where \(\lfloor \nu \rfloor \) denotes the largest integer less than or equal to ν, \(N_{0}=\{0,1,2,\ldots \} \), \(N=\{1,2,3,\ldots \} \) and \(\alpha _{1}\), \(\alpha _{2}\) are constants.
Definition 2.3
(Generalized Taylor’s formula). Suppose that \(D^{l\beta}g(t)\in C(0,1] \) for \(l= 0, 1, \ldots , m+1 \) and \(0<\beta \leq 1\), then [36]
where \(D^{r\beta}=\underbrace{D^{\beta}D^{\beta}\ldots D^{\beta}}_{r~times}\).
If \(\beta =1 \), then the generalized Taylor’s formula converts to the classical Taylor’s formula.
3 Fractional-order Chelyshkov functions properties
3.1 Fractional-order Chelyshkov functions
The fractional-order Chelyshkov functions (FCHFs) can be defined by using Chelyshkov polynomials in the following form [5]:
The set \(\{\varphi^{\beta} _{mr}\}_{r=0}^{m}\) of FCHFs is a family of orthogonal functions over the interval \(\rho =[0,1]\) with respect to the weight function \(w_{\beta}(t) =t^{\beta -1}\). The orthogonality property for these functions is
It is clear from Equation (3.1) that every member of the set \(\{\varphi^{\beta} _{mr}\}_{r=0}^{m}\) is of degree βm. This is the key distinction between the Chelyshkov polynomials and the other sets of orthogonal polynomials. Figures 1 and 2 provide graphs of FCHFs for different values of r and β, respectively. Let the weighted space \(L^{2}_{w_{\beta}}(\rho )\) be the set of all real-valued measurable functions \(u(t)\) on ρ that satisfy
with inner product and norm given by
Suppose that \(\left \{\varphi ^{\beta}_{m0}(t),\varphi ^{\beta}_{m1}(t),\ldots , \varphi ^{\beta}_{mm}(t)\right \}\) is a set of FCHFs and \(\mathbb{A}_{m}=\text{span} \{\varphi ^{\beta}_{m0}(t),\varphi ^{ \beta}_{m1}(t), \ldots ,\varphi ^{\beta}_{mm}(t) \}\). Also, assume that \(g(t)\) is an arbitrary function in \(L^{2}_{w_{\beta}}(\rho ) \). Since \(\mathbb{A}_{m}\) is a closed finite-dimensional subspace of \(L^{2}_{w_{\beta}}(\rho )\), then for any function \(g(t)\) there exists a unique best approximation \(g_{m}(t) \in \mathbb{A}_{m}\) that minimizing the distance to \(g(t)\), that is
Since \(g_{m}(t) \in \mathbb{A}_{m}\), then there are unique coefficients \(\ell _{0},\ell _{1},\ldots ,\ell _{m}\) such that
where L and \(\Phi _{\beta}(t)\) are given by
and
3.2 The operational matrix of fractional integration
This subsection is devoted to construct the fractional integration operational matrix of the FCHFs, which will be used to reduce the fractional delay differential equations into a set of algebraic equations.
Theorem 3.1
Let \(\Phi _{\beta}(t)\) be a \((m+1) \times 1\) vector of FCHFs. The Riemann–Liouville fractional integral of order \(\nu >0\) of the vector \(\Phi _{\beta}(t)\) can be given by
where \(\Lambda ^{(\nu )}=\left (\lambda _{rk}\right )_{r,k=0}^{m}\) is the \((m+1)\times (m+1)\) operational matrix of fractional integral of order ν for FCHFs and its elements can be obtained by
Proof
Using Equation (2.1) to integrate Equation (3.1), yields
By taking the Laplace transform of Equation (3.11), we get
Since
and
Then Equation (3.12) becomes
Now, by utilizing the inverse Laplace transform of Equation (3.15), we obtain
Approximating \(t^{j\beta +\nu} \) in terms of FCHFs, we get
where \(\ell _{jk}\) can be determined from Equations (3.1) and (3.7) as follows
From Equations (3.16), (3.17) and (3.18), we can write
which leads to the desired result. □
4 Convergence analysis
In this section, we discuss the convergence of the best approximation and show that by increasing the number of the FCHFs, the error in calculating the operational matrix of fractional integration tends to zero.
Theorem 4.1
Let \(g(t) \in L^{2}_{w_{\beta}}(\rho )\) such that \(D^{l\beta}g(t)\in C(0,1] \) for \(l= 0, 1, \ldots , m+1 \). Suppose that \(L^{T}\Phi _{\beta}(t)\) is the best estimation of \(g(t)\) in \(\mathbb{A}_{m}\), then
Proof
Assume the generalized Taylor’s formula of \(g(t)\) is denoted by \(\psi (t)\), then from Definition 2.3 the error bound is
where
Since \(L^{T}\Phi _{\beta}(t)\) is the best estimation of \(g(t)\) in \(\mathbb{A}_{m}\) and \(\psi (t)\in \mathbb{A}_{m}\) then by using Equation (4.2), we get
The right-hand side of inequality (4.3) depends on both m and β, so for a fixed β, we have
therefore
□
Theorem 4.2
Let the error vector \(E_{\nu}\) of the operational matrix of fractional integration \(\Lambda ^{(\nu )}\) be given by
Then
Proof
Suppose that \(E_{\nu}= \begin{pmatrix} \epsilon _{0},\epsilon _{1},\ldots ,\epsilon _{m}\end{pmatrix} ^{T}\), then by using Equations (3.10), (3.16) and (3.18), we get
But \(\sum \limits _{k=0}^{m}\ell _{jk}\varphi ^{\beta}_{mk}(t)\) is the approximation of \(t^{j\beta +\nu}\), so from Equation (4.3) we can write
Hence, Equation (4.8) becomes
Therefore
□
5 Numerical method
The aim of this section is to present a new numerical method for solving fractional delay differential equations by using FCHFs and their operational matrix of fractional integration.
Consider the following two problems:
where f and ρ are known analytical functions, τ is delay, \(\eta _{i},\; i=0,1,\ldots,\lceil \nu \rceil -1\) are real constants, y is the unknown function and \(D^{\nu}\) is the Caputo fractional derivative of order ν. To find approximate solutions of Problems (5.1) and (5.2), we approximate \(D^{\nu}y(t) \) by FCHFs as
By applying the Riemann–Liouville integration to Equation (5.3) and using Equations (2.8) and (3.9), we get
where P is the fractional-order Chelyshkov coefficient vector of the polynomial \(\sum \limits _{i=0}^{\lceil \nu \rceil -1}\dfrac{\eta _{i}}{i!}t^{i}\) and is given by
Then for Problems (5.1) and (5.2), \(y(t)\) take the form
Making use of Equations (5.6) and (5.7), we get
By substituting Equations (5.3), (5.6)–(5.9) in Problems (5.1) and (5.2), we obtain the following algebraic equations
Now, by collocate Equations (5.10) and (5.11) at the points \(t_{s}=\cfrac{s}{m}\), \(s= 0, 1, \dots , m\), we obtain the following two systems of \(m+1\) algebraic equations,
These systems can be solved to find \(m+1\) unknown constants \(\ell _{0},\ell _{1},\ldots\ell _{m}\) and hence, an approximate solutions of Problems (5.1) and (5.2) can be determined from Equations (5.6) and (5.7) respectively.
Based on the above, we present an algorithm for solving Problems (5.1) and (5.2) as follows
Algorithm 5.1
- Input::
-
The numbers ν, \(\eta _{i}, i=0,1,\ldots,\lceil \nu \rceil -1 \) and the functions f, ρ
- Step 1::
-
Choose \(m\in N\), \(\beta >0\) and construct the fractional-order Chelyshkov vector \(\Phi _{\beta}(t)\) using Equations (3.1) and (3.8).
- Step 2::
-
Compute the operational matrix \(\Lambda ^{(\nu )}\) and the vector P using Equations (3.10) and (5.5).
- Step 3::
-
Define the unknown vector \(L= \begin{pmatrix} \ell _{0},\ell _{1},\ldots ,\ell _{m}\end{pmatrix} ^{T}\).
- Step 4::
- Step 5::
-
Construct the nonlinear system of algebraic equations (5.12) or (5.13) by using the points \(t_{s}=\cfrac{s}{m}\), \(s= 0, 1, \dots , m\).
- Step 6::
-
Find the unknowns of the algebraic system obtained in Step 5.
- Output::
6 Numerical results
To demonstrate the applicability and effectiveness of the introduced method, we use it to solve some examples, and we compare the numerical results it generates with those reported in the literature. All numerical results have been obtained using Mathematica 11 software and a laptop with Intel(R) Core(TM) i7-4600M 2.90 GHz CPU and 8.0 GB RAM.
Example 1
Consider the following fractional delay differential equation [10, 47, 50]:
The exact solution to this problem is \(y(t)=t^{2}-t\). By using the technique described in Sect. 5, we get
where \(L= \begin{pmatrix} \ell _{0},\ell _{1},\ldots ,\ell _{m}\end{pmatrix} ^{T}\) is the vector of unknown constants that we must identify and P can be calculated from Equation (5.5). By substituting Equations (6.2) into the fractional delay differential equation (6.1), we get the following matrix equations
By considering \(\nu =1\), we take \(m =2\), \(\beta = 1 \) and hence
In case \(\tau \in \left (0,0.5\right ]\), making use of Equation (6.4) and collocate Equations (6.3) at the points 0, \(\frac{1}{2}\), 1, we obtain the following system
Solving system (6.5) for the unknowns \(\ell _{0}\), \(\ell _{1}\), \(\ell _{2}\) gives the solution
thus
which is the exact solution. For \(\tau \in \left (0.5,1\right ]\), we use Equation (6.4) and collocate Equations (6.3) at the points 0, \(\frac{1}{2}\), 1, then we get the following system
Solving system (6.8) for the unknowns \(\ell _{0}\), \(\ell _{1}\), \(\ell _{2}\) gives the same solution
which leads to the exact solution. Further, the total CPU time required to find the solution using the proposed method for the two cases of τ in this example is 0.0156 seconds. Thus, the proposed method is accurate and time-efficient.
For \(\nu =\dfrac{1}{2}\), we take \(m=4 \), \(\beta =\dfrac{1}{2} \), and again we can obtain the exact solution, where
Similarly, by using Equation (6.10), subdivide the interval \((0,1]\) into four subintervals and consider the following cases of τ
then collocate Equations (6.3) at the points \(t_{s}=\dfrac{s}{4}\), \(s=0,1,\ldots ,4\), for each case of τ and solving the resulting systems for the unknowns \(\ell _{0}\), \(\ell _{1}\), \(\ell _{2}\), \(\ell _{3}\), \(\ell _{4}\), we get the same solution
for all cases of τ, thus
which is the exact solution. Additionally, the total CPU time needed to find this solution using the proposed method for the four cases of τ in Equation (6.11) is 24.0608 seconds. Problem (6.1) has been solved in [10, 47, 50]. By comparing the obtained solution with those in [10, 47, 50], it can be observed that the introduced method is more accurate because we get the exact solution for \(\nu =1 \) and for any value of τ with three terms of FCHFs, whereas they used four terms of Legendre wavelets, six terms of Taylor wavelets and eight terms of fractional-order Taylor functions in [47, 50] and [10] respectively to obtain only approximate solutions.
Example 2
Consider the following fractional delay differential equation [8, 10]:
The exact solution is given by \(y(t)=t^{2} \). By applying the method proposed in Sect. 5, we obtain
Equations (6.15) transform Equation (6.14) to
By considering \(m=4\) and \(\beta =\dfrac{1}{2}\) and collocating Equation (6.16) at the nodes \(t_{s}=\dfrac{s}{4}\), \(s=0,1,\ldots ,4\), and solving the resulting system, we obtain the solution
which leads to the exact solution. Also, the total CPU time required to find the solution using the presented method in this example is 0.2969 seconds. This problem has been solved by using the fractional-order Taylor method [10], the Haar wavelet collocation technique [8] and the fractional backward difference method [32]. Their solutions were approximate solutions. By comparing with these methods, it is clear that the proposed method is more effective, more accurate and less time-consuming than these methods.
Example 3
Consider the following fractional delay differential equation [50]:
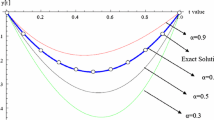
The exact solution to this problem is \(y(t)=t^{2}-t-1 \). Figure 3 displays the approximate solution obtained for various values of β at \(m=10\) with the exact solution, while Fig. 4 plots the absolute error function at \(\beta =0.2\) and \(m=10\). It can be observed that our numerical solutions agree with the exact solution for all choices of β and high-accuracy numerical solutions can be obtained with some terms of FCHFs. Table 1 shows a comparison between the results obtained by the present method and those reported in [50] in terms of absolute errors, where M denotes the number of basis functions used in [50] for solving the problem. From Table 1, it can be seen that the absolute errors achieved by the introduced method are less than those in [50] for all corresponding cases which shows the advantage of using basis functions of fractional-order. In addition, we have used only eleven basis functions, while they used more than a hundred basis functions in [50]. This demonstrates that the introduced method is in more agreement with the exact solution than [50] for this problem and can identify high-precision solutions at reasonable computational costs.
The graph of the approximate solution for various choices of β at \(m=10 \) and the exact solution for Example 3
The graph of the absolute error function at \(m=10 \) and \(\beta =0.2 \) for Example 3
Example 4
Consider the following fractional delay differential equation [15, 50]:
This problem has the exact solution \(y(t)=e^{-t}\) when \(\nu =3 \). Figures 5 and 6 present graphically the obtained results for the approximate solution for various values of ν with the exact solution for \(\nu =3\) and the absolute error at \(\nu =3 \), respectively. From Fig. 5, it can be seen that as ν approaches 3, the approximate solution converges to the exact solution for \(\nu =3\) and from Fig. 6, we can see that the absolute error is at most of order 10−14, which means that the present method has good accuracy using a reasonable number of basis functions. Table 2 compares the results obtained by the present method with the collected results in [15] in terms of absolute errors. It can be observed that the results obtained by the present method are less than those in [15, 22, 38, 46] for most of the listed values in that table by using a fewer number of basis functions for each case. Also, Problem (6.19) has been solved using the Legendre wavelet method [50] by selecting \(M=14\). The maximum absolute error achieved by this method is approximately \(8.78 \times 10^{-12}\) while our maximum absolute error is approximately \(1.74 \times 10^{-15}\) at \(m=10\). This means that the introduced method outperforms the method in [50] with respect to accuracy. These comparisons show that the presented method is more accurate, efficient, and coincidental with the exact solution than [15, 22, 38, 46, 50].
The graph of the approximate solution for various values of ν at \(m=10\), \(\beta =1 \) and the exact solution for Example 4
The graph of the absolute error function at \(m=10\), \(\beta =1 \) and \(\nu =3\) for Example 4
Example 5
Consider the following fractional delay differential equation [21]:
We have \(y(t)=t^{q} \) as the exact solution for this problem. By using the technique described in Sect. 5, we get
The fractional delay differential equation (6.20) can be written after using Equations (6.21) in the form
Consider \(\nu =2\) and \(q=2 \) with the exact solution \(y(x)=t^{2} \). In order to solve this case, we take \(m=2\), and \(\beta =1\), hence
By using Equation (6.23) and collocate Equation (6.22) at the points 0, \(\frac{1}{2}\), 1, we get the following system
Solving Equations (6.24) gives the solution
hence
which is the exact solution. Moreover, the total CPU time required to find this solution using the introduced method in this example is 0.0156 seconds. Therefore, the presented method is accurate and time-efficient. Additionally, in case \(\nu =\dfrac{3}{2}\) and \(q=\dfrac{3}{2} \), we can again obtain the exact solution \(y(x)=t^{\frac{3}{2}}\). By employing \(m=2\) and \(\beta =\dfrac{3}{4} \), computing \(\Lambda ^{(\frac{3}{2})}\), collocate Equation (6.22) at the nodes 0, \(\frac{1}{2}\), 1, and solving the generated system, we obtain the solution
which leads to the exact solution for this case. Also, the total CPU time needed to find the solution using the proposed method for this case is 0.0937 seconds. The collocation Laguerre operational matrix technique [21] has been used to solve Problem (6.20). By comparing with our solution, it is clear that our method is more efficient than [21], because we utilized three terms of FCHFs to get the exact solution for \(\nu =2\), while they used six terms of the generalized Laguerre polynomials to obtain only approximate solution.
Example 6
Consider the following fractional delay differential equation [33, 42]:
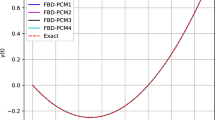
The exact solution to this problem at \(\nu =1 \) is \(y(t)=e^{-t} \). Figures 7 and 8 display the approximate solution obtained for several values of ν and τ together with the exact solution for \(\nu =1\), respectively. Figure 7 shows that as ν approaches 1, the approximate solution converges to that of the integer-order delay differential equation. From Fig. 8, it can be seen that the approximate solution obtained by our method coincides with the exact solution for all the used values of the delay τ. The absolute error of the presented method is plotted in Fig. 9. This figure shows that the proposed method is accurate because the error is at most of order 10−13. Table 3 presents the absolute errors for different values of m. It is obvious that the absolute errors decrease when the value of m increases, which demonstrates the convergence of the introduced method to the exact solution. Table 4 compares the absolute errors obtained by the introduced method with the collected results in [42]. From Table 4, we can note that the presented technique is more accurate and efficient in comparison to the methods [33, 42].
The graph of the approximate solution for different values of ν at \(m=10\), \(\beta =\nu \), \(\tau =0.2\) and the exact solution for Example 6
The graph of the approximate solution for various values of τ at \(m=10 \), \(\beta =\nu =1 \) and the exact solution for Example 6
The graph of the absolute error function at \(m=10\), \(\beta =\nu =1 \) and \(\tau =0.2 \) for Example 6
Example 7
Consider the following fractional delay differential equation [34, 42, 50]:
The exact solution for this problem is \(y(t)=\sin (t) \) when \(\nu =1 \). The approximate solution obtained for different values of ν together with the known exact solution at \(\nu =1\) is plotted in Fig. 10. It can be noted that as ν tends to 1, the approximate solution converges to the exact solution for \(\nu =1\). The absolute error function for \(\nu =1 \) is presented in Fig. 11. This figure shows that even if the exact solution is not a polynomial, an accurate approximation can be achieved using a sufficient number of FCHFs. In Table 5, we compare the absolute errors of the present method with those collected in [50] for the Bernoulli wavelet method [42], the spectral method based on a modification of hat functions [34] and the Legendre wavelet method [50]. These results show that the proposed method is superior to the methods in [34, 42, 50] for most of the listed values of absolute errors by using a smaller number of basis functions than they have been used in [34, 42, 50]. This example shows that the present method provides high efficiency regardless of the type of the exact solution for the problem.
The graph of the approximate solution for several choices of ν at \(m=10\), \(\beta =\nu \) and the exact solution for Example 7
The graph of the absolute error function at \(m=10\) and \(\beta =\nu =1 \) for Example 7
Example 8
Consider the following fractional delay differential equation [42]:
The exact solution for this problem is \(y(t)=\cos (t) \) when \(\nu =2 \). Figure 12 shows the obtained approximate solution for various choices of ν with the exact solution for \(\nu =2\). It can be seen that as ν converges to 2, the approximate solution approaches the exact solution for \(\nu =2\). Figure 13 displays the absolute error function for \(\nu =2\). This graph shows that the presented method has a good convergence rate and its solutions are accurate. Table 6 presents a comparison between the obtained results and those reported in [42] in terms of absolute errors. It can be noted that our method outperforms the method in [42] since the absolute errors achieved by the introduced method are less than those in [42] for all corresponding cases by using a fewer number of basis functions for each case. This demonstrates the agreement of our method with the exact solution with reasonable computational costs.
The graph of the approximate solution for various values of ν at \(m=10\), \(\beta =1 \) and the exact solution for Example 8
The graph of the absolute error function at \(m=10\), \(\beta =1 \) and \(\nu =2\) for Example 8
Example 9
Consider the following fractional delay differential equation [44]:
This problem has the exact solution \(y(t)=e^{t} \) when \(\nu =1 \). The approximate solution for different values of ν is plotted in Fig. 14 along with the exact solution for \(\nu =1\). The absolute error of the presented method is drawn in Fig. 15. These graphs demonstrate the convergence of the obtained approximate solutions to the exact solution. Table 7 compares the results obtained by the present method with the those in [44]. It can be seen that our results are in agreement with the results in [44] for \(m=8\) and slightly better for \(m=9\). This means that the presented method is compatible with the method in [44] for this problem.
The graph of the approximate solution for various values of ν at \(m=9\), \(\beta =\nu \) and the exact solution for Example 9
The graph of the absolute error function at \(m=9 \) and \(\beta =\nu =1\) for Example 9
For all tested examples, the presented method has found the solutions with high accuracy within acceptable computation costs. We can observe that using fractional values of β leads to a good rate of convergence and a low number of basis functions is required to obtain satisfactory results when the solutions of fractional delay differential equations contain terms with fractional powers or when the fractional derivative ν is a proper fraction.
7 Conclusion
This paper has used FCHFs and their properties to provide an accurate numerical method for solving fractional delay differential equations. The fractional derivative was considered in the Caputo sense. The problem of finding a solution to a fractional delay differential equation was transformed into the problem of solving a system of algebraic equations. The convergence of the presented approximation has been discussed. The introduced method has been applied to solve many problems and the obtained results were compared with exact solutions and some other published numerical methods. It can be observed that the presented method has high accuracy by using a smaller number of basis functions than other methods used in the comparisons. This reveals that the presented method is efficient, accurate and its performance is quite satisfactory, which establishes the significance of the present method for solving fractional delay differential equations.
Data Availability
No datasets were generated or analysed during the current study.
References
Abdo, M., Panchal, S.: Existence and uniqueness results for fractional differential equations with infinite delay. Dyn. Contin. Discrete Impuls. Syst., Ser. A Math. Anal. 26, 205–216 (2019)
Ahmad, M.Z., Alsarayreh, D., Alsarayreh, A., Qaralleh, I.: Differential transformation method (DTM) for solving SIS and SI epidemic models. Sains Malays. 46, 2007–2017 (2017)
Ahmed, A.I., Al-Ahmary, T.A.: Fractional-order Chelyshkov collocation method for solving systems of fractional differential equations. Math. Probl. Eng. 2022, 4862650 (2022)
Ahmed, A.I., Al-Sharif, M.S., Salim, M.S., Al-Ahmary, T.A.: Numerical solution of fractional variational and optimal control problems via fractional-order Chelyshkov functions. AIMS Math. 7(9), 17418–17443 (2022)
Al-Sharif, M.S., Ahmed, A.I., Salim, M.S.: An integral operational matrix of fractional-order Chelyshkov functions and its applications. Symmetry 12(11), 1755 (2020)
Alsuyuti, M.M., Doha, E.H., Ezz-Eldien, S.S., Bayoumi, B.I., Baleanu, D.: Modified Galerkin algorithm for solving multitype fractional differential equations. Math. Methods Appl. Sci. 42, 1389–1412 (2019)
Ambrosio, V.: Concentration phenomena for a fractional relativistic Schrödinger equation with critical growth. Adv. Nonlinear Anal. 13, 20230123 (2024)
Amin, R., Shah, K., Asif, M., Khan, I.: A computational algorithm for the numerical solution of fractional order delay differential equations. Appl. Math. Comput. 402, 125863 (2021)
an der Heiden, U.: Delays in physiological systems. J. Math. Biol. 8, 345–364 (1979)
Avci, I.: Numerical simulation of fractional delay differential equations using the operational matrix of fractional integration for fractional-order Taylor basis. Fractal Fract. 6, 10 (2022)
Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus: Models and Numerical Methods. World Scientific, Singapore (2016)
Carpinteri, A., Mainardi, F.: Fractals and Fractional Calculus in Continuum Mechanics. Springer, Wien, New York (1997)
Chelyshkov, V.S.: Alternative orthogonal polynomials and quadratures. Electron. Trans. Numer. Anal. 25(7), 17–26 (2006)
Daftardar-Gejji, V., Sukale, Y., Bhalekar, S.: Solving fractional delay differential equations: a new approach. Fract. Calc. Appl. Anal. 18, 400–418 (2015)
Dehestani, H., Ordokhani, Y., Razzaghi, M.: Numerical technique for solving fractional generalized pantograph-delay differential equations by using fractional-order hybrid Bessel functions. Int. J. Appl. Comput. Math. 6, 9 (2020)
Dehghan, M., Shakeri, F.: The use of the decomposition procedure of Adomian for solving a delay differential equation arising in electrodynamics. Phys. Scr. 78(6), 065004 (2008)
Feng, S., Chen, J., Huang, X.: Critical fractional Schrödinger-Poisson systems with lower perturbations: the existence and concentration behavior of ground state solutions. Adv. Nonlinear Anal. 13, 20240006 (2024)
Hall, M.G., Barrick, T.R.: From diffusion-weighted MRI to anomalous diffusion imaging. Magn. Reson. Med. 59(3), 447–455 (2008)
Hassani, H., Machado, J.T., Naraghirad, E.: Generalized shifted Chebyshev polynomials for fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 75, 50–61 (2019)
Huang, C., Guo, Z., Yang, Z., Chen, Y., Wen, F.: Dynamics of delay differential equations with its applications 2014. Abstr. Appl. Anal. 2015, 359043 (2015)
Hussien, H.S.: Efficient collocation operational matrix method for delay differential equations of fractional order. Iran. J. Sci. Technol. Trans. A, Sci. 43, 1841–1850 (2019)
Iqbal, M.A., Saeed, U., Mohyud-Din, S.T.: Modified Laguerre wavelets method for delay differential equations of fractional-order. Egypt. J. Basic Appl. Sci. 2(1), 50–54 (2015)
Kheybari, S.: Numerical algorithm to Caputo type time-space fractional partial differential equations with variable coefficients. Math. Comput. Simul. 182, 66–85 (2021)
Kheybari, S., Darvishi, M.T., Hashemi, M.S.: Numerical simulation for the space-fractional diffusion equations. Appl. Math. Comput. 348, 57–69 (2019)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, San Diego (2006)
Kulish, V.V., Lage, J.L.: Application of fractional calculus to fluid mechanics. J. Fluids Eng. 124(3), 803–806 (2002)
Maleki, M., Davari, A.: Fractional retarded differential equations and their numerical solution via a multistep collocation method. Appl. Numer. Math. 143, 203–222 (2019)
Meral, F.C., Royston, T.J., Magin, R.: Fractional calculus in viscoelasticity: an experimental study. Commun. Nonlinear Sci. Numer. Simul. 15, 939–945 (2010)
Mirzaee, F., Alipour, S.: Cubic B-spline approximation for linear stochastic integro-differential equation of fractional order. J. Comput. Appl. Math. 366, 112440 (2020)
Mirzaee, F., Bimesl, S., Tohidi, E.: Solving nonlinear fractional integro-differential equations of Volterra type using novel mathematical matrices. J. Comput. Nonlinear Dyn. 10, 061016 (2015)
Moghaddam, B.P., Mostaghim, Z.S.: Numerical method based on finite difference for solving fractional delay differential equations. J. Taibah Univ. Sci. 7, 120–127 (2013)
Morgado, M.L., Ford, N.J., Lima, P.M.: Analysis and numerical methods for fractional differential equations with delay. J. Comput. Appl. Math. 252, 159–168 (2013)
Muroya, Y., Ishiwata, E., Brunner, H.: On the attainable order of collocation methods for pantograph integro-differential equations. J. Comput. Appl. Math. 152(1–2), 347–366 (2003)
Nemati, S., Lima, P., Sedaghat, S.: An effective numerical method for solving fractional pantograph differential equations using modification of hat functions. Appl. Numer. Math. 131, 174–189 (2018)
Odibat, Z.: On the optimal selection of the linear operator and the initial approximation in the application of the homotopy analysis method to nonlinear fractional differential equations. Appl. Numer. Math. 137, 203–212 (2019)
Odibat, Z.M., Shawagfeh, N.T.: Generalized Taylor’s formula. Appl. Math. Comput. 186(1), 286–293 (2007)
Oldham, K.B.: Fractional differential equations in electrochemistry. Adv. Eng. Softw. 41, 9–12 (2010)
Ozturk, Y., Gulsu, M.: Approximate solution of linear generalized pantograph equations with variable coefficients on Chebyshev-Gauss grid. J. Adv. Res. Sci. Comput. 4(1), 36–51 (2012)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Povstenko, V.: Signaling problem for time-fractional diffusion-wave equation in a half-space in the case of angular symmetry. Nonlinear Dyn. 59(4), 593–605 (2010)
Radziunas, M.: New multi-mode delay differential equation model for lasers with optical feedback. Opt. Quantum Electron. 48, 1–9 (2016)
Rahimkhani, P., Ordokhani, Y., Babolian, E.: A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer. Algorithms 74, 223–245 (2017)
Sabermahani, S., Ordokhani, Y., Yousefi, S.-A.: Fractional-order Fibonacci-hybrid functions approach for solving fractional delay differential equations. Eng. Comput. 36, 795–806 (2020)
Saeed, U., ur Rehman, M.: Hermite wavelet method for fractional delay differential equations. J. Differ. Equ. 2014, 359093 (2014)
Samadyar, N., Ordokhani, Y., Mirzaeeb, F.: Hybrid Taylor and block-pulse functions operational matrix algorithm and its application to obtain the approximate solution of stochastic evolution equation driven by fractional Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 90, 105346 (2020)
Sezer, M., Akyuz–Daşcıoǧ lu, A.: A Taylor method for numerical solution of generalized pantograph equations with linear function alargument. J. Comput. Appl. Math. 200, 217–225 (2007)
Toan, P.T., Vo, T.N., Razzaghi, M.: Taylor wavelet method for fractional delay differential equations. Eng. Comput. 37, 231–240 (2021)
Usman, M., Hamid, M., Zubair, T., Haq, R.U., Wang, W., Liu, M.B.: Novel operational matrices-based method for solving fractional-order delay differential equations via shifted Gegenbauer polynomials. Appl. Math. Comput. 372, 124985 (2020)
Yu, Y., Perdikaris, P., Karniadakis, G.E.: Fractional modeling of viscoelasticity in 3D cerebral arteries and aneurysms. J. Comput. Phys. 323, 219–242 (2016)
Yuttanan, B., Razzaghi, M., Vo, T.N.: Legendre wavelet method for fractional delay differential equations. Appl. Numer. Math. 168, 127–142 (2021)
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Contributions
The contributions of all authors are equal.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ahmed, A.I., Al-Sharif, M.S. An effective numerical method for solving fractional delay differential equations using fractional-order Chelyshkov functions. Bound Value Probl 2024, 107 (2024). https://doi.org/10.1186/s13661-024-01913-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-024-01913-8