1 Introduction

Many physical and mathematical models can be described by the partial differential equations (PDEs) in many work and technical problems, and the basic equations of many natural science problems are also PDEs, which play a very important role in these fields [1]. The parabolic equation, as a kind of PDE, is often used to study diffusion and heat conduction problems. Due to the complexity of practical problems, many solutions of the PDEs are numerical. Currently, there are many numerical methods for heat transfer problems [2, 3], such as the finite-difference method (FDM), the finite element method (FEM), the finite volume method (FVM) and the spectrum method. Li [4] presented the useful Crank–Nicolson Galerkin FEM for the nonlinear parabolic problem. The traditional FDM shows great limitations in computational accuracy. An important measure to improve the accuracy of the traditional FDM is to refine the mesh, which in turn will increase the amount of storage and calculation, especially in high-dimensional cases. Therefore, it is of great theoretical significance and practical value to construct a high accuracy and good stability scheme in time and space.

The compact finite-difference scheme (CFDS) is one of the most studied FDM at present. When using CFDS to study complex problems, its high accuracy and stability have also attracted much attention from many scholars. Experience shows that the compact scheme is much more accurate than the corresponding explicit scheme of the same order [5]. Over the past three decades, the methods for developing high-order CFDS have made great progress. Dennis et al. proposed the fourth-order CFDS for convection–diffusion problems [6]; this scheme can get more accurate results with a thicker grid. Lele [7] developed CFDS with pseudo spectral resolution on the basis of summarizing the previous work and proposed a linear sixth-order central CFDS, which can achieve the accuracy of the spectral method. Adams [8] gave a compact ENO scheme. Gaitonde [9] constructed a finite volume scheme based on a compact difference scheme, which had played a certain role in promoting the development of high-precision compact difference schemes. Subsequently, many scholars constructed different schemes of CFDS and solved many types of partial differential equations [10–13], such as integro-differential equations, three-dimensional Poisson equations, the shallow water equations, and the Helmholtz equations, they all achieved better numerical results. Sengupta et al. developed a class of upwind compact difference schemes, and such schemes could be applied to different fields [14]. In the same year, Kumar [15] discussed a high-order compact difference scheme for singularly perturbed reaction–diffusion problems on a new Shishkin mesh. Shukla et al. [16, 17] proposed to use polynomial interpolations also to derive arbitrary high-order compact finite-difference methods of first and second derivatives on non-uniform meshes. However, these compact finite-difference schemes are not asymptotically stable on uniform grids. The fourth-order exact compact difference scheme for mixed derivative parabolic problems with variable coefficients discussed by Sen [18, 19] provides a viable scheme for this paper. Gordin [20] applied the Richardson extrapolation method to improve a fourth-order CFDS to sixth order in 1D parabolic equations and Schrödinger-type equations.

CFDS is a widely used method for spatial discretization of parabolic equations to obtain the ordinary differential equations (ODEs), and then other methods of time discretization are used for discretizing the ODEs, such as the Euler method, multistep methods, and the Runge–Kutta method. Bhatt et al. [21] proposed two fourth-order exponential time difference Runge–Kutta (ETDRK) schemes combined with the spatial fourth-order CFDS to solve Burgers’ equation. In their research, the calculation of the exponential matrices is involved. How to accurately calculate the exponential matrices is an important problem in solving PDEs. Moler et al. [22] summarized 19 schemes for calculating the exponential matrices, including Padé approximations of different orders. These 19 schemes are aimed at different practical problems, and their numerical solutions also have corresponding advantages and disadvantages. In 1994, Zhong [23] proposed the precise integration method (PIM) of exponential matrices to solve the initial value problem of linear ODEs. PIM is an approximation method to calculate the exponential matrices, which contains the Taylor approximation and the Padé approximation. PIM avoided the computer error caused by fine division and improved the numerical solution of exponential matrices by the accuracy of the computation. In the paper, we focus on applying PIM to obtain numerical solutions of high accuracy.

The Alternating Direction Implicit (ADI) method is an empirical method for solving multi-dimensional parabolic equations. ADI, such as the Peacemen–Rachford scheme, the Dyakonov scheme, and the Douglas scheme, are only second-order accuracy schemes [24–26]. ADI often fails to meet the accuracy requirements of practical problems. Li et al. [27] proposed a novel compact ADI scheme for solving two-dimensional nonlinear reaction–diffusion equations. The Strang splitting method (SSM) is a numerical method for solving differential equations that are decomposable into a sum of differential operators, which is to solve multi-dimensional PDEs by reducing them to a sum of one-dimensional problems [28]. This is a scheme of operator splitting method. If the differential operators of the SSM commute, then it will lead to no loss of accuracy. To the best of our knowledge, no high accuracy numerical schemes of CFDS combined with PIM has been developed so far. Hence, the main goal of this paper is to develop high-order PIM schemes in combination with a global sixth-order CFDS for simulating the parabolic equations without using any transformations or linearization techniques. Meanwhile, the proposed schemes extend to multi-dimensional parabolic problems with SSM.

The remainder of the paper is organized as follows. Two high-order exponential time differencing PIMs in combination with a spatially global sixth-order CFDS for solving parabolic equations are presented in Sect. 2. The stability of the proposed schemes is discussed in Sect. 3. In Sect. 4, the Strang splitting method is described, and the proposed schemes are extended to multi-dimensional problems. In Sect. 5, numerical examples are carried out to test the accuracy and adaptability of the proposed schemes. The conclusions are drawn in Sect. 6.

2 One-dimensional case

For the one-dimensional parabolic problem, we consider the following initial and boundary value problem:

$$ \frac{\partial u}{\partial t}-\mu\frac{\partial^{2} u}{\partial x^{2}}=0,\quad x\in[a,b],t\in [0,T] $$
(1)

with the initial condition

$$ u(x,0)=g_{0}(x),\quad x\in[0,T] $$
(2)

and the boundary condition

$$\begin{aligned}& u(0,t)=h_{1}(t),\quad t\in[0,T_{l}], \end{aligned}$$
(3)
$$\begin{aligned}& u(l,t)=h_{2}(t),\quad t\in[0,T_{l}], \end{aligned}$$
(4)

where μ is a real positive constant, \(g_{0}(x)\), \(h_{1}(t)\) and \(h_{2}(t)\) are given enough smooth functions. There is an additional assumption: the analytical solution of Eq. (1) is a function smooth enough.

2.1 Sixth-order compact finite-difference scheme formulas

High-order finite-difference scheme can be classified into two main categories: explicit schemes and Padé-type or compact schemes. Explicit schemes compute the numerical derivatives directly at each grid by using large stencils, while compact schemes obtain all the numerical derivatives along a grid line using smaller stencils and solving a linear system of equations. Next, we will give a sixth-order compact finite-difference scheme for second derivatives.

We firstly apply a sixth-order finite-difference scheme to the discretization in spatial dimension. For simplicity, we only consider the uniform one-dimensional mesh with mesh size \(h=x_{i+1}-x_{i}\), in which \(x_{i}=ih\), \(i=1,2,\ldots,N\), where h is spatial step size.

There are many methods used to generate compact finite-difference formulas to approximate the second-order spatial derivatives. The reader is referred to Refs. [5, 7] for more details on how to generate compact finite-difference formulas. In this study, the spatial derivatives are approximated with the formulas introduced by Li in Ref. [5]. Below the formulas in Ref. [5] are stated without change.

2.1.1 Sixth-order CFDS for interior nodes

At interior points \(x_{i}\), \(3\leq i \leq N-2\), the second-order derivative \(u_{xx}\) (\(u''\) for simplicity) in Eq. (1) is approximated by a sixth-order implicit compact difference scheme

$$ \alpha{u''_{i - 1}} + {u''_{i}} + \alpha{u''_{i + 1}} = {{b \over {4{h^{2}}}}}({u_{i + 2}} - {u_{i}} + {u_{i - 2}}) + {{a \over {{h^{2}}}}}({u_{i + 1}} - 2{u_{i}} + {u_{i - 1}}), $$
(5)

where α, a and b are constants to be determined by matching the Taylor expansion. When \(\alpha=\frac{2}{11}\), \(a=\frac{12}{11}\) and \(b=\frac{3}{11}\), Eq. (5) becomes a sixth-order compact scheme.

2.1.2 Sixth-order CFDS for boundary nodes of Dirichlet boundary conditions

To make those near-boundary points have the same order accuracy as interior points \(x_{i}\), \(3\leq i \leq N-2\), they should be obtained by matching Taylor series expansions to the order of \(O(h^{6})\) at boundary points \(x_{1}\), \(x_{2}\), \(x_{N-1}\) and \(x_{N}\).

At boundary point \(x_{1}\), the sixth-order compact formula is

$$ \begin{aligned}[b] &{u''_{1}} + { {{126} \over {11}}} {u''_{2}}\\&\quad = \frac{1}{{{h^{2}}}} \biggl( {{{{2077} \over {157}}} {u_{1}} - { {{2943} \over {110}}} {u_{2}} + {{{573} \over {44}}} {u_{3}} + {{{167} \over {99}}} {u_{4}} - { {{18} \over {11}}} {u_{5}} + {{{57} \over {110}}} {u_{6}} - {{{131} \over {1980}}} {u_{7}}} \biggr) .\end{aligned} $$
(6)

At boundary point \(x_{2}\), the sixth-order compact formula is

$$ \begin{aligned}[b] &{{{11} \over {128}}} {u''_{1}} + {u''_{2}} + {{{11} \over {128}}} {u''_{3}} \\ & \quad= \frac{1}{{{h^{2}}}} \biggl( {{{{585} \over {512}}} {u_{1}} - {{{141} \over {64}}} {u_{2}} + { {{459} \over {512}}} {u_{3}} + {{9 \over {32}}} {u_{4}} - {{{81} \over {512}}} {u_{5}} + { {3 \over {64}}} {u_{6}} - {{3 \over {512}}} {u_{7}}} \biggr). \end{aligned} $$
(7)

At boundary points \(x_{N-1}\) and \(x_{N}\), their formulas are symmetrical with those of \(x_{1}\) and \(x_{2}\). The CFDS can be written in matrix form,

$$ {\boldsymbol{AU}''} = {\boldsymbol{BU}} $$
(8)

where

$$\begin{aligned}& {\boldsymbol{A}} = {\left [ { \textstyle\begin{array}{ccccccc} 1&{{{{126} \over {11}}}}&{}&{}&{}&{}&{}\\ {{{{11} \over {128}}}}&1&{{{{11} \over {128}}}}&{}&{}&{}&{}\\ {}&{{{2 \over {11}}}}&1&{{{2 \over {11}}}}&{}&{}&{}\\ {}&{}& \ddots& \ddots& \ddots&{}&{}\\ {}&{}&{}&{{{2 \over {11}}}}&1&{{{2 \over {11}}}}&{}\\ {}&{}&{}&{}&{{{{11} \over {128}}}}&1&{{{{11} \over {128}}}}\\ {}&{}&{}&{}&{}&{{{{126} \over {11}}}}&1 \end{array}\displaystyle } \right ]_{N \times N}} , \end{aligned}$$
(9)
$$\begin{aligned}& {\boldsymbol{B}} = \frac {1}{{{h^{2}}}}{\left [ { \textstyle\begin{array}{cccccccc} {{{{2077} \over {157}}}}&{{{{- 2943} \over {110}}}}&{{{{574} \over {44}}}}&{{{{167} \over {99}}}}&{{{{- 18} \over {11}}}}&{{{{57} \over {110}}}}&{{{{- 131} \over {1980}}}}&{}\\ {{{{585} \over {512}}}}&{{{{- 141} \over {64}}}}&{{{{459} \over {512}}}}&{{{9 \over {32}}}}&{{{{- 81} \over {512}}}}&{{{3 \over {64}}}}&{{{{- 3} \over {512}}}}&{}\\ {{{3 \over {44}}}}&{{{{12} \over {11}}}}&{{{{- 51} \over {22}}}}&{{{{12} \over {11}}}}&{{{3 \over {44}}}}&{}&{}&{}\\ {}& \ddots& \ddots& \ddots& \ddots& \ddots&{}&{}\\ {}&{}&{{{3 \over {44}}}}&{{{{12} \over {11}}}}&{{{{- 51} \over {22}}}}&{{{{12} \over {11}}}}&{{{3 \over {44}}}}&{}\\ {}&{{{{- 3} \over {512}}}}&{{{3 \over {64}}}}&{{{{- 81} \over {512}}}}&{{{9 \over {32}}}}&{{{{459} \over {512}}}}&{{{{- 141} \over {64}}}}&{{{{585} \over {512}}}}\\ {}&{{{{- 131} \over {1980}}}}&{{{{57} \over {110}}}}&{{{{- 18} \over {11}}}}&{{{{167} \over {99}}}}&{{{{574} \over {44}}}}&{{{{- 2943} \over {110}}}}&{{{{2077} \over {157}}}} \end{array}\displaystyle } \right ]_{N \times N}} , \end{aligned}$$
(10)
$$\begin{aligned}& {\boldsymbol{U}} = { ( {{u_{1}},{u_{2}}, \ldots ,{u_{N - 1}},{u_{N}}} )^{T}} . \end{aligned}$$
(11)

Hence the sixth-order compact finite-difference approximation of second derivatives \({\boldsymbol{U}''}\) is given by

$$ {\boldsymbol{U}''}={\boldsymbol{A}^{-1}\boldsymbol{BU}}={ \boldsymbol{HU}} . $$
(12)

Note: the matrix A is not invertible at arbitrary N. When \(N>7\), the matrix A is invertible.

2.2 Precise integration method

After the spatial discretization, the governing PDEs become the following ODEs:

$$ \frac{{\mathrm{d}}{\boldsymbol{U}}}{{\mathrm {d}}t}={\boldsymbol{HU}} . $$
(13)

Given \(\tau= {t_{k + 1}} - {t_{k}}\) as the temporal step size, then integrating Eq. (13) directly, the following recurrence formula is obtained:

$$ {{\boldsymbol{U}}^{k + 1}} = {e^{{\boldsymbol {H}}\tau}} {{ \boldsymbol{U}}^{k}}= {\boldsymbol{T}} ( \tau){{\boldsymbol{U}}^{k}}, $$
(14)

where \({\boldsymbol{T}} ( \tau) = {e^{{\boldsymbol{H}}\tau}}\) is an exponential matrix.

The present work will focus on how to compute the exponential matrix T very precisely. Moler et al. [22] had discussed 19 dubious ways to compute the exponential matrix. Besides, they pointed out that the calculation of the exponential matrix had not been fully solved. In this paper, we apply the PIM to calculate the exponential matrix, which was proposed by Zhong et al. [23]. PIM is a high-precision algorithm of an exponential computing matrix, which avoids the computer truncation error caused by the fine division and improves the numerical solution of the exponential matrix by the accuracy of the computer. In a word, PIM is a series of matrix or vector multiplication calculations. Therefore, the main problem is how to calculate the exponential matrix \({e^{{\boldsymbol{H}}\tau}}\). The precise computation of the exponential matrix has two key points [29]:

  1. (1)

    The additional theorem of exponential function is used, whose execution needs the \(2^{n}\) algorithm.

  2. (2)

    Keeping track of the incremental part of the exponential matrix, rather than the total value.

Using the exponential additional theorem, the exponential matrix can be rewritten as follows:

$$ {e^{{\boldsymbol{H}}\tau}} = { \bigl( {{e^{{\boldsymbol{H}}\Delta t}}} \bigr)^{m}}, $$
(15)

where m is an arbitrary integer. Usually, in order to ensure computational accuracy, Ref. [23] suggested

$$ m = {2^{n}},\quad n = 20, m = 1{,}048{,}576, $$
(16)

where \(\Delta t = \frac{\tau}{m}\) is much smaller than τ, and n is defined as a bisection order. Thus, the calculation of \({e^{{\boldsymbol{H}}\tau}}\) becomes m times multiplication of \({e^{{\boldsymbol{H}}\Delta t}}\). Thus, we select two approximation methods for the exponential matrix \({e^{{\boldsymbol{H}}\Delta t}}\), that is, the Taylor approximation and the Padé approximation.

2.2.1 Taylor approximation

The Taylor expansion formula of the exponential matrix \({e^{{\boldsymbol{H}}\Delta t}}\) is

$$ {e^{{\boldsymbol{H}}\Delta t}}= \sum_{j = 0}^{\infty}{\frac{{{{({\boldsymbol{H}}\Delta t)}^{j}}}}{{j!}}}, $$
(17)

where \(\Delta t = \frac{\tau}{m}\) is an extremely small-time interval because τ is usually small. Thus, the fourth-order Taylor expansion can obtain high precision. Hence

$$ {\boldsymbol{T}} ( {\Delta t} ) = {e^{{\boldsymbol {H}}\Delta t}} \cong\sum _{j = 0}^{4} {\frac{{{{({\boldsymbol{H}}\Delta t)}^{j}}}}{{j!}} = {\boldsymbol{I}} + {\boldsymbol{H}} \Delta t + \frac{{{{({\boldsymbol{H}}\Delta t)}^{2}}}}{{2!}} + \frac {{{{({\boldsymbol{H}}\Delta t)}^{3}}}}{{3!}} + \frac{{{{({\boldsymbol {H}}\Delta t)}^{4}}}}{{4!}}} . $$
(18)

Because τ is very small, the series expansion of the first five terms should be enough. The exponential matrix \({\boldsymbol{T}} ( {\Delta t} )\) departs from the unit matrix I to a very small extent. Hence it should be distinguished as

$$ {e^{{\boldsymbol{H}}\Delta t}} \cong{\boldsymbol {I}} + {{\boldsymbol{T}}_{o}} = { \boldsymbol{I}} + {\boldsymbol{H}}\Delta t + \frac {{{{({\boldsymbol{H}}\Delta t)}^{2}}}}{{2!}} + \frac{{{{({\boldsymbol {H}}\Delta t)}^{3}}}}{{3!}} + \frac{{{{({\boldsymbol{H}}\Delta t)}^{4}}}}{{4!}}, $$
(19)

where \(T_{o}\) is the incremental matrix, \(T_{o}= {\boldsymbol{H}}\Delta t + \frac{{{{({\boldsymbol{H}}\Delta t)}^{2}}}}{{2!}} + \frac {{{{({\boldsymbol{H}}\Delta t)}^{3}}}}{{3!}} + \frac{{{{({\boldsymbol {H}}\Delta t)}^{4}}}}{{4!}}\). And o is the variable of the bisection order n, \(o\in[1,n]\).

2.3 Padé approximation

Based on the PIM of Padé approximation, we have the same idea as PIM of the Taylor approximation. The difference is the series expansion of the exponential matrix \({\boldsymbol{T}} ( {\Delta t} )\). At the same time, their approaches depend on the additional theorem of exponents. The \(( {r + s} )\)th-order rational Padé approximation [30, 31] for \({e^{{\boldsymbol{H}}\Delta t}}\) is defined as

$$ {e^{{\boldsymbol{H}}\Delta t}} = \frac {{{{\boldsymbol{N}}_{r}}( {{\boldsymbol{H}}\Delta t} )}}{{{{\boldsymbol{D}}_{s}}( {{\boldsymbol{H}}\Delta t})}}, $$
(20)

where

$$\begin{aligned}& {{\boldsymbol{N}}_{r}} ( {{\boldsymbol{H}}\Delta t} ) = \sum _{j = 0}^{r} {\frac{{ ( {2r - j} )!r!}}{{ ( {2r} )!j!(r - j)!}}} {({\boldsymbol{H}}\Delta t)^{j}} , \end{aligned}$$
(21)
$$\begin{aligned}& {{\boldsymbol{D}}_{s}} ( {{\boldsymbol{H}}\Delta t} ) = \sum _{j = 0}^{s} {\frac{{ ( {2s - j} )!s!}}{{ ( {2s} )!j!(s - j)!}}} {( - {\boldsymbol{H}}\Delta t)^{j}}. \end{aligned}$$
(22)

Equations (21)–(22) were described by Perron [32]. Similar to the Taylor approximation, we also rewrite the Padé approximation as follows:

$$ {e^{{\boldsymbol{H}}\Delta t}} = \frac {{{{\boldsymbol{N}}_{r}}( {{\boldsymbol{H}}\Delta t})}}{{{{\boldsymbol{D}}_{s}}( {{\boldsymbol{H}}\Delta t})}} = \frac {{{\boldsymbol{I}} + {{\bar{\boldsymbol{N}}}_{r}}}}{{{\boldsymbol {I}} + {{\bar{\boldsymbol{D}}}_{s}}}} = { \boldsymbol{I}} + \frac{{{{\bar{\boldsymbol{N}}}_{s}} - {{\bar {\boldsymbol{D}}}_{r}}}}{{\boldsymbol{{I}} + {{\bar{\boldsymbol {D}}}_{r}}}} = {\boldsymbol{I}} + {{\boldsymbol{T}}_{o}}, $$
(23)

where

$$ {\bar{\boldsymbol{N}}_{r}} = \sum_{j = 1}^{r} {\frac{{ ( {2r - j} )!r!}}{{ ( {2r} )!j!(r - j)!}}} {({\boldsymbol {H}}\Delta t)^{j}} , \qquad{\bar{ \boldsymbol{D}}_{s}} = \sum_{j = 1}^{s} { \frac{{ ( {2s - j} )!s!}}{{ ( {2s} )!j!(s - j)!}}} {( - {\boldsymbol {H}}\Delta t)^{j}} . $$
(24)

In this paper, we select the \((4, 4)\)-Padé approximation for \({{\boldsymbol{N}}_{4}}( {{\boldsymbol{H}}\Delta t})\) and \({{\boldsymbol{D}}_{4}}({{\boldsymbol{H}}\Delta t})\),

$$\begin{aligned}& {{\boldsymbol{N}}_{4}}( {{\boldsymbol{H}}\Delta t} ) = {\boldsymbol{I}} + {\bar{ \boldsymbol{N}}_{4}} ,\qquad {\bar{\boldsymbol{N}}_{4}} = \frac {{{\boldsymbol{H}}\Delta t}}{2} + \frac{{3{{({\boldsymbol{H}}\Delta t)}^{2}}}}{{28}} + \frac {{{{({\boldsymbol{H}}\Delta t)}^{3}}}}{{84}} + \frac{{{{({\boldsymbol {H}}\Delta t)}^{4}}}}{{1680}} , \end{aligned}$$
(25)
$$\begin{aligned}& {{\boldsymbol{D}}_{4}}( {{\boldsymbol{H}}\Delta t} ) = {\boldsymbol{I}} + {\bar{ \boldsymbol{D}}_{4}} , \qquad\bar{{\boldsymbol{D}}_{4}} = - \frac {{{\boldsymbol{H}}\Delta t}}{2} + \frac{{3{{({\boldsymbol{H}}\Delta t)}^{2}}}}{{28}} - \frac {{{{({\boldsymbol{H}}\Delta t)}^{3}}}}{{84}} + \frac{{{{({\boldsymbol {H}}\Delta t)}^{4}}}}{{1680}} . \end{aligned}$$
(26)

Substituting Eqs. (25) and (26) into Eq. (23), we obtain

$$ {e^{{\boldsymbol{{H}}}\Delta t}} \cong{\boldsymbol {I}} + {{\boldsymbol{T}}_{o}} = { \boldsymbol{I}} + \frac{{{{\bar{\boldsymbol{{N}}}}_{4}} - {{\bar {\boldsymbol{D}}}_{4}}}}{{{\boldsymbol{I}} + {{\bar{\boldsymbol {D}}}_{4}}}} . $$
(27)

So far, we have introduced two approximation methods of the exponential matrix \({\boldsymbol{T}}( {\Delta t} )\). In order to obtain the exponential matrix \({\boldsymbol{T}}( \tau)\), we need to use a \(2^{n}\) algorithm for the matrix \({\boldsymbol{T}}( {\Delta t} )\).

2.4 \(2^{n}\) algorithm of the exponential matrix

Whether we have the Taylor approximation or the Padé approximation, they all have the problem of complete loss of precision in the exponential additional theorem [33]. In Eqs. (19) and (27), the identity matrix I cannot be directly added to the incremental matrix \({\boldsymbol{T}_{o}}\). \({\boldsymbol{T}_{o}}\) is a tiny matrix (this is a matrix whose elements all approach zero). When they add up directly, \({\boldsymbol {T}_{o}}\) become the mantissa of \({\boldsymbol{I}+\boldsymbol{T}_{o}}\). Thus, \({\boldsymbol{T}_{o}}\) will become an appended part and its precision will be seriously dropped in the round-off operation in computer arithmetic. As a matter of fact, \({\boldsymbol{T}_{o}}\) is an incremental part, which is the second key point mentioned above. If we want to get high-precision solutions, we must separately calculate and store the incremental matrix \({\boldsymbol{T}_{o}}\). Therefore, we will apply a \(2^{n}\) algorithm to calculate \({\boldsymbol{T}_{o}}\). A \(2^{n}\) algorithm is a kind of calculation method and is based on the addition theorem of the exponential matrix. Next, we will show how a \(2^{n}\) algorithm is calculated on the computer.

For computing the matrix \({\boldsymbol{T}}( \tau) = {e^{{\boldsymbol{H}}\tau}}\), Eq. (17) should be factored as

$$ {\boldsymbol{T}}( \tau) = {({\boldsymbol{I}} + {{\boldsymbol{T}}_{o}})^{{2^{n}}}} = {( {{\boldsymbol{I}} + {{\boldsymbol{T}}_{o}}} )^{{2^{n - 1}}}} \times{( {{\boldsymbol{I}} + {{\boldsymbol{T}}_{o}}} )^{{2^{n - 1}}}} . $$
(28)

Such a factorization should be iterated n times. Next, for the arbitrary matrices \({\boldsymbol{T}_{b}}\) and \({\boldsymbol{T}_{c}}\), the identity

$$ ( {{\boldsymbol{I}} + {{\boldsymbol{T}}_{b}}} ) \times ( {{\boldsymbol{I}} + {{ \boldsymbol{T}}_{c}}} ) = {\boldsymbol{I}} + ( {{{\boldsymbol {T}}_{b}} + {{ \boldsymbol{T}}_{c}} + {{\boldsymbol{T}}_{b}} \times{{\boldsymbol{T}}_{c}}} ) $$
(29)

holds if \({\boldsymbol{T}_{b}}\) and \({\boldsymbol{T}_{c}}\) are very small, the multiplication should not be executed after the addition of the unit matrix I as given on the left-hand side. Treating the matrices \({\boldsymbol{T}_{b}}\) and \({\boldsymbol{T}_{c}}\) as \({\boldsymbol{T}_{o}}\), thus \({{\boldsymbol{T}}_{o}} \Rightarrow 2{{\boldsymbol{T}}_{o}} + {{\boldsymbol{T}}_{o}} \times{{\boldsymbol {T}}_{o}}\) is replaced by in each factorization of Eq. (28). Then, \({\boldsymbol{T}_{o}}\) no longer has a small value after such an iteration circulated times according to the following computer cycle language:

$$ \text{for }(o = 1:n)\quad {{\boldsymbol{T}}_{o}} = 2{{\boldsymbol{T}}_{o}} + {{\boldsymbol{T}}_{o}} \times{{\boldsymbol{T}}_{o}} . $$
(30)

At the end of the n cycles, the computer stores \({\boldsymbol {T}_{o}}\). Eq. (30) is the code of \(2^{n}\) algorithm. At this point, \({\boldsymbol{T}_{o}}\) can be directly added to identity matrix I to obtain the exponential matrix \({\boldsymbol {T}}( \tau)\),

$$ {\boldsymbol{T}}(\tau) = {\boldsymbol{I}} + {{\boldsymbol{T}}_{o}} = {e^{{\boldsymbol{H}}\tau}} . $$
(31)

Therefore, both of the Taylor approximation and the Padé approximation can be, respectively, combined with a \(2^{n}\) algorithm to calculate the exponential matrix to obtain a high-precision numerical solution.

According to the equations above, the computing procedure for the exponential matrix \({\boldsymbol{T}}( \tau)\) can be summarized and listed in Table 1.

Table 1 Algorithm: How to calculate exponential matrix with PIM
Full size table

3 Stability analysis

3.1 Stability for periodic boundary condition

In this section the linear stability of the scheme CFDS-PIM of Taylor and Padé approximation is investigated by utilizing an approach suggested and discussed in [34, 35] for the parabolic equations. Although the boundary condition of Dirichlet is adopted in our scheme, we only can prove the stability under the periodic boundary condition for simplicity.

In Eq. (16), if \({\lambda_{i}}\) (\(i = 1,2,\ldots,N-1\)) is the eigenvalue of matrix \({\boldsymbol{H}_{*}}\), then \({e^{{\lambda_{i}}\tau }}\) is the eigenvalue of exponential matrix \({e^{{\boldsymbol {H}_{*}}\tau}}\) with the same corresponding eigenvector \(\boldsymbol {x} = {({x_{1}},{x_{2}}, \ldots,{x_{N-1}})}\). In order to show that CFDS-PIM is unconditionally stable, we need to prove that the spectral radius of matrix \({e^{{\boldsymbol{H}_{*}}\tau}}\) is less than 1. To this end, the following two lemmas are needed.

Lemma 1

If \({\lambda_{i}}\)is an eigenvalue of matrix \({\boldsymbol{H}_{*}} = {{\boldsymbol{A}_{*}}^{- 1}}{\boldsymbol{B}_{*}}\)with its corresponding eigenvectorx, then the eigenvalue \({\lambda_{i}}\)is a real number and \({\lambda_{i}}\leq0\).

Proof

By the definitions of eigenvalue and eigenvector, we may write [34]

$$ {{\boldsymbol{x}}^{T}} {\boldsymbol{B}_{*}\boldsymbol{x}} = {\lambda_{i}} {{\boldsymbol{x}}^{T}} {\boldsymbol{A}_{*}\boldsymbol{x}} . $$
(32)

Here, the matrices \({\boldsymbol{A}_{*}}\) and \({\boldsymbol{B}_{*}}\) of the periodic boundary condition are as follows:

$$\begin{aligned}& {\boldsymbol{A}_{*}} =\left [ { \textstyle\begin{array}{ccccc} 1&{\frac{2}{{11}}}&{}&{}&{\frac{2}{{11}}}\\ {\frac{2}{{11}}}&1&{\frac{2}{{11}}}&{}&{}\\ {}& \ddots& \ddots& \ddots&{}\\ {}&{}&{\frac{2}{{11}}}&1&{\frac{2}{{11}}}\\ {\frac{2}{{11}}}&{}&{}&{\frac{2}{{11}}}&1 \end{array}\displaystyle } \right ] , \end{aligned}$$
(33)
$$\begin{aligned}& {\boldsymbol{B}_{*}} = \frac {1}{{{h^{2}}}}\left [ { \textstyle\begin{array}{ccccccc} {\frac{{- 51}}{{22}}}&{\frac{{12}}{{11}}}&{\frac {3}{{44}}}&{}&{}&{\frac{3}{{44}}}&{\frac{{12}}{{11}}}\\ {\frac{{12}}{{11}}}&{\frac{{- 51}}{{22}}}&{\frac{{12}}{{11}}}&{\frac {3}{{44}}}&{}&{}&{\frac{3}{{44}}}\\ {\frac{3}{{44}}}&{\frac{{12}}{{11}}}&{\frac{{- 51}}{{22}}}&{\frac {{12}}{{11}}}&{\frac{3}{{44}}}&{}&{}\\ {}& \ddots& \ddots& \ddots& \ddots& \ddots&{}\\ {}&{}&{\frac{3}{{44}}}&{\frac{{12}}{{11}}}&{\frac{{- 51}}{{22}}}&{\frac{{12}}{{11}}}&{\frac{3}{{44}}}\\ {\frac{3}{{44}}}&{}&{}&{\frac{3}{{44}}}&{\frac{{12}}{{11}}}&{\frac {{- 51}}{{22}}}&{\frac{{12}}{{11}}}\\ {\frac{{12}}{{11}}}&{\frac{3}{{44}}}&{}&{}&{\frac{3}{{44}}}&{\frac {{12}}{{11}}}&{\frac{{- 51}}{{22}}} \end{array}\displaystyle } \right ] . \end{aligned}$$
(34)

Note: H, A, B are the matrices of the Dirichlet boundary condition; \(\boldsymbol{H}_{*}\), \(\boldsymbol{A}_{*}\), \(\boldsymbol{B}_{*}\) are the matrices of the periodic boundary condition.

Obviously, the matrix, \({\boldsymbol{A}_{*}}\) and \({\boldsymbol {B}_{*}}\) are really symmetrical, so the eigenvalue \({\lambda_{i}}\) is a real number. Meanwhile, for arbitrary \({\boldsymbol{x}} \ne {\boldsymbol{0}}\), the right-hand side of Eq. (32) is

$$ \begin{aligned}[b] {{\boldsymbol{x}}^{T}} {\boldsymbol{A}_{*}\boldsymbol{x}} &= x_{1}^{2} + \frac{4}{{11}}{x_{1}} {x_{2}} + \frac{4}{{11}}{x_{1}} {x_{N - 1}} + x_{2}^{2} + \frac{4}{{11}}{x_{2}} {x_{3}} + \cdots \\ &\quad+ \frac{4}{{11}}{x_{N - 1}} {x_{N - 2}} + x_{N - 1}^{2} + \frac{4}{{11}}{x_{N - 1}} {x_{1}}. \end{aligned} $$
(35)

Using the inequality \(2xy < {x^{2}} + {y^{2}}\), we obtain

$$ \begin{aligned}[b] {{\boldsymbol{x}}^{T}} {\boldsymbol{A}_{*}\boldsymbol{x}} &> x_{1}^{2} - {{2 \over {11}}}\bigl(x_{1}^{2} + x_{2}^{2}\bigr)- {{2 \over {11}}} \bigl(x_{1}^{2} + x_{N - 1}^{2}\bigr) + x_{2}^{2} - {{2 \over {11}}}\bigl(x_{2}^{2} + x_{3}^{2}\bigr) + \cdots \\ &\quad- {{2 \over {11}}}\bigl(x_{N - 2}^{2} + x_{N - 1}^{2}\bigr) + x_{N - 1}^{2}- { {2 \over {11}}}\bigl(x_{N - 1}^{2} +x_{1}^{2} \bigr) \\ & > {{5 \over {11}}}x_{1}^{2} + { {7 \over {11}}}\sum_{i = 2}^{N - 2} {x_{i}^{2}} + {{5 \over {11}}}x_{N - 1}^{2} > 0, \end{aligned} $$
(36)

and the left-hand side of Eq. (32) is

$$ \begin{aligned}[b] {{\boldsymbol{x}}^{T}} {\boldsymbol{B}_{*}\boldsymbol{x}} ={}&+ \frac{3}{{44}}{x_{1}} {x_{N - 2}} + \frac{{12}}{{11}}{x_{1}} {x_{N - 1}} - \frac{{51}}{{22}}x_{1}^{2} + \frac{{12}}{{11}}{x_{1}} {x_{2}} + \frac{3}{{44}}{x_{1}} {x_{3}} \\ &+\frac{3}{{44}}{x_{2}} {x_{N - 1}} + \frac{{12}}{{11}}{x_{2}} {x_{1}} - \frac{{51}}{{22}}x_{2}^{2} + \frac{{12}}{{11}}{x_{2}} {x_{3}} + \frac{3}{{44}}{x_{{2}}} {x_{4}} \\ &+\frac{3}{{44}}{x_{3}} {x_{1}} + \frac{{12}}{{11}}{x_{3}} {x_{2}} - \frac{{51}}{{22}}x_{3}^{2} + \frac{{12}}{{11}}{x_{3}} {x_{4}} + \frac{3}{{44}}{x_{4}} {x_{5}} + \cdots \\ &+\frac{3}{{44}}{x_{N - 3}} {x_{N - 1}} + \frac{{12}}{{11}}{x_{N - 3}} {x_{N - 2}} - \frac{{51}}{{22}}x_{N - 3}^{2} + \frac{{12}}{{11}}{x_{N - 3}} {x_{N - 4}} + \frac{3}{{44}}{x_{N - 3}} {x_{N - 5}} \\ & + \frac{3}{{44}}{x_{N - 2}} {x_{1}} + \frac{{12}}{{11}}{x_{N - 2}} {x_{N - 1}} - \frac{{51}}{{22}}x_{N - 2}^{2} + \frac{{12}}{{11}}{x_{N - 2}} {x_{N - 3}} + \frac{3}{{44}}{x_{N - 2}} {x_{N - 4}} \\ &+\frac{3}{{44}}{x_{N - 1}} {x_{2}} + \frac{{12}}{{11}}{x_{N - 1}} {x_{1}} - \frac{{51}}{{22}}x_{N - 1}^{2} + \frac{{12}}{{11}}{x_{N - 1}} {x_{N - 2}} + \frac{3}{{44}}{x_{N - 1}} {x_{N - 3}}. \end{aligned} $$
(37)

Similarly, using the inequality \(2xy < {x^{2}} + {y^{2}}\), we obtain

$$ \begin{aligned}[b] {{\boldsymbol{x}}^{T}} {\boldsymbol{B}_{*}\boldsymbol{x}} &< - \frac{{12}}{{11}} \bigl( {x_{1}^{2} + x_{N - 1}^{2}} \bigr) - \frac{3}{{44}} \bigl( {x_{1}^{2} + x_{2}^{2} + x_{N - 2}^{2} + x_{N - 1}^{2}} \bigr) \\ &\quad+ \frac{6}{{44}}{x_{1}} {x_{N - 2}} + \frac{2}{{44}}{x_{2}} {x_{N - 1}} + \frac{{24}}{{11}}{x_{N - 1}} {x_{1}}\\& < 0. \end{aligned} $$
(38)

From Eqs. (36) and (38), we can see that the right-hand side of Eq. (32) is \({{\boldsymbol {x}}^{T}}{\boldsymbol{A}_{*}\boldsymbol{x}} > 0\) and the left-hand side of Eq. (32) is \({{\boldsymbol{x}}^{T}}{\boldsymbol{B}_{*}\boldsymbol{x}} < 0\). Thus, \({\lambda_{i}} < 0\). □

Lemma 2

LetWbe an arbitrary square matrix. Then, for any operator matrix norm \(\Vert \cdot \Vert \), we obtain \({{\lambda _{\rho}}}(\boldsymbol{W}) \le \Vert \boldsymbol{W} \Vert \), where \({{\lambda_{\rho}}}(\boldsymbol{W})\)is the spectral radius of matrixW (\({{\lambda_{\rho}} } = \max\vert {{\lambda_{i}}} \vert\), \(1 \le i \le N - 1\)).

Theorem 1

The Taylor approximation of CFDS-PIM is unconditionally stable.

Proof

The Taylor series approximation of \({e^{{{-\lambda_{\rho}}}\tau}}\) is defined as

$$ {{e^{{{-\lambda_{\rho}}}\tau}} =\sum_{j = 0}^{\infty}{\frac{{{{({{-\lambda_{\rho}}}\tau)}^{j}}}}{{j!}}}} . $$
(39)

Using Lemma 1, we obtain \({{-\lambda_{\rho}}}\tau< 0\), thus \({e^{{{-\lambda_{\rho}}}\tau}} < 1\). For the fourth-order Taylor series approximation of the PIM, \({e^{{{-\lambda_{\rho}}}\tau}} < 1\). We use Lemma 2 to see that the spectral radius of matrix \({e^{{\boldsymbol{H}}\tau}}\) is less than 1 in a fourth-order Taylor approximation of the PIM. Thus, the Taylor approximation of CFDS-PIM is unconditionally stable. □

Theorem 2

The Padé approximation of the CFDS-PIM is unconditionally stable.

Proof

The \((4, 4)\)-Padé approximation to \({e^{{{-\lambda_{\rho}}}\tau}}\) is defined as

$$ {e^{{{-\lambda_{\rho}}}\tau}} = \frac{{1680 + 840{({-\lambda_{\rho}})}\tau+ 180{{({-\lambda_{\rho}}\tau)}^{2}} + 30{{({{-\lambda_{\rho}}}\tau)}^{3}} + {{({{-\lambda_{\rho}}}\tau )}^{4}}}}{{1680 - 840{({-\lambda_{\rho}})}\tau+ 180{{({{-\lambda_{\rho}}}\tau)}^{2}} - 30{{({{-\lambda_{\rho}}}\tau)}^{3}} + {{({{-\lambda_{\rho}}}\tau)}^{4}}}} . $$
(40)

Using Lemma 1, \({{-\lambda_{\rho}}} \le0\) and \(\tau> 0\), we see that the numerator of Eq. (41) is smaller than the denominator, thus \({e^{{{-\lambda_{\rho}}}\tau}} < 1\) and the spectral radius of matrix \({e^{{\boldsymbol{H}}\tau}}\) is less than 1. According to Lemma 2, \(\Vert {{e^{{\boldsymbol{H}}\tau}}} \Vert \le1\) in the \((4, 4)\)-Padé approximation of the PIM. Thus, the Padé approximation of the CFDS-PIM is unconditionally stable. □

3.2 Amplification symbol

Definition 1

The rational approximation \(R_{r,s}(z)\) to the exponential \(e^{-z}\) is called A-acceptable when \(\vert{{R_{r,s}}( - z)} \vert< 1\) holds for all −z with negative real part. The approximation is called L-acceptable when it is A-acceptable and it also satisfies \(\vert {{R_{r,s}}( - z)} \vert\to0\) as \(\Re( - z) \to- \infty\).

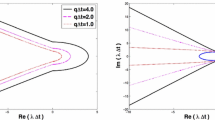
In Fig. 1, we compare the behavior of \(e^{-z}\) and two approximations (Taylor approximation (17) and Padé approximation (20)). It can be observed from the traces that the two approximations are A-acceptable. It can also be seen from Fig. 1 that A-acceptable real number field of a Padé approximation is wider than that of a Taylor approximation.

Figure 1
figure 1

The behavior of the Taylor approximation with the real number field \(z \in[0,2.5]\) and Padé approximation with the real number field \(z \in[0,100]\)

Full size image

Figs. 2 and 3 illustrate the traces of \(e^{-z}\) and two approximations for the different complex planes. Since the results of the functions are complex, we plot their real parts. It can be seen from the plots that the Padé approximation better conforms to A-acceptability Definition 1.

Figure 2
figure 2

The behavior of the Taylor approximation with the complex plane \(z=x+iy\in[0,2.5]\times[-1,1]\)

Full size image
Figure 3
figure 3

The behavior of Padé approximation with the complex plane \(z=x+iy\in[0,100]\times[-50,50]\)

Full size image

3.3 Stability regions

The stability of the CFDS-PIM can be observed from the plots of their stability regions [21, 36]. The linear ordinary differential equation (13) can be rewritten as

$$ {\boldsymbol{u}}_{t}=c{\boldsymbol{u}}. $$
(41)

We assume that a fixed point \(u_{0}\) satisfying \(cu_{0}= 0\) exists, and u is the perturbation of \(u_{0}\). If \(\operatorname{Re}(c)< 0\), then we can say the fixed point \(u_{0}\) is stable. We denote \(x = c\tau\), with τ being a single time step, and then apply two approximations (the Taylor approximation (17) and the Padé approximation (20)) to Eq. (41). The amplification factors \(r(x)\) of the two approximations can be calculated in the following way:

  1. (1)

    Taylor approximation of precise integration method

    $$ \frac{u_{n+1}}{u_{n}}=r(x,y)=1+x+\frac{1}{2}x^{2}+ \frac{1}{6}x^{3}+\frac{1}{24}x^{4} . $$
    (42)
  2. (2)

    Padé approximation of precise integration method

    $$ \frac{u_{n+1}}{u_{n}}=r(x,y)=\frac{{1 + {{1 \over 2}}x + {{3 \over {28}}}{x^{2}} + {{1 \over {84}}}{x^{3}} + {{1 \over {1680}}}{x^{4}}}}{{1 - {{1 \over 2}}x + {{3 \over {28}}}{x^{2}} - {{1 \over {84}}}{x^{3}} + {{1 \over {1680}}}{x^{4}}}} . $$
    (43)

Notice that we assumed \(r(x) < 1\) to obtain the stability regions. Suppose that x is complex. As can be seen in Fig. 4, the stability regions of the two schemes are plotted. The axes of the plots are real and imaginary parts of x. It can be observed from Fig. 4 that the stability regions of the two approximations are the same in shape, but the Padé approximation is more in line with the stability boundary of exponential approximation.

Figure 4
figure 4

The stability regions of the Taylor approximation and Padé approximation

Full size image

4 Multi-dimensional case

The section introduces sixth-order CFDS based on PIM coupled with SMM (CFDS-PIM-SSM), and applies it to solving multi-dimensional parabolic problems.

4.1 Extensions to two-dimensional case

SSM is a numerical method for solving differential equations that are decomposed multi-dimensional problems into a sum of differential operators. This method is named after Gilbert Strang. It is used to speed up the calculation for problems involving operators on very different time scales, and to solve the multi-dimensional PDEs by reducing them to a sum of one-dimensional problems. For simplicity, the following two-dimensional parabolic equation is given:

$$ \frac{{\partial u}}{{\partial t}} =\frac{{{\partial ^{2}}u}}{{\partial{x^{2}}}} + \frac{{{\partial^{2}}u}}{{\partial{y^{2}}}} ,\quad (x,y,t) \in\varOmega\times[0,T]. $$
(44)

As a precursor to Strang splitting, we rewrite Eq. (44) as follows:

$$ \frac{{\mathrm{d}}{\boldsymbol{U}}}{{\mathrm{d}}t} = {\boldsymbol{H}_{x}\boldsymbol{U}} + { \boldsymbol{H}_{y}\boldsymbol{U}} $$
(45)

where \({\boldsymbol{H}_{x}}\) and \({\boldsymbol{H}_{y}}\) are difference operators in the x-direction and the y-direction. The right side of Eq. (45) is already split, in a natural way, into a sum \(a+b\) of relatively simple expressions. Due to one of the properties of difference operator is the distributive law of multiplication, we obtain the following equations:

$$ \frac{{\mathrm{d}}{\boldsymbol{U}}}{{\mathrm{d}}t} = {(\boldsymbol{H}_{x}+\boldsymbol{H}_{y})\boldsymbol{U}.} $$
(46)

For Eq. (45), the exact solution to the associated initial value problem would be

$$ {{\boldsymbol{U}}^{k + 1}}(t) = {e^{ (\boldsymbol{H}_{x}+\boldsymbol{H}_{y})t}} {{ \boldsymbol{U}}^{k}} . $$
(47)

This section focuses on how to calculate the exponential matrix \(e^{(\boldsymbol{{H}}_{x}+\boldsymbol{{H}}_{y})t}\), and the calculation of \(e^{(\boldsymbol{{H}}_{x}+\boldsymbol{{H}}_{y})t}\) is too complicated. Thus, we convert it into calculating the product of \(e^{\boldsymbol{{H_{x}}}t}\) and \(e^{\boldsymbol{{H}}_{y}t}\), but \(e^{\boldsymbol{{H}}_{x}t}\) and \(e^{\boldsymbol{{H}}_{y}t}\) must satisfy the commutativity of the addition theorem

$$ e^{{(\boldsymbol{H}_{x}+\boldsymbol{H}_{y})}t} =e^{\boldsymbol {{H}}_{x}t}e^{\boldsymbol{{H}}_{y}t} \quad\Leftrightarrow\quad {\boldsymbol{{H}}_{x} \boldsymbol{{H}}_{y}} = {\boldsymbol{{H}}_{y} \boldsymbol{{H}}_{x}} . $$
(48)

Nevertheless, the exponentials of \({\boldsymbol{H}_{x}}\) and \({\boldsymbol{H}_{y}}\) are related to that of \({\boldsymbol {H}_{x}+\boldsymbol{H}_{y}}\) by the Trotter product formula

$$ {e^{\boldsymbol{H}_{x}+\boldsymbol{H}_{y}}} = \lim_{m \to\infty} \bigl( {{e^{{{\boldsymbol{H}_{x}} / } m}}} {e^{{{\boldsymbol{H}_{y}} / m}}} \bigr)^{m} . $$
(49)

Gottleib et al. [22] suggested that the Trotter result can be used to approximate \(e^{\boldsymbol{H}}\) by splitting H into \(\boldsymbol{H}_{x}+\boldsymbol{H}_{y}\), because \(m=2^{20}\) in Eq. (16) is already very large. Thus, we use the following approximation:

$$ {e^{\boldsymbol{H}}} = { \bigl( {{e^{{{\boldsymbol {H}_{x}} / m}}} {e^{{{\boldsymbol{H}_{y}} / m}}}} \bigr)^{m}}. $$
(50)

This approach to calculating \({e^{\boldsymbol{H}}}\) is of potential interest when the exponentials of \({\boldsymbol{H}_{x}}\) and \({\boldsymbol{H}_{y}}\) can be accurately and efficiently computed. If \({\boldsymbol{H}_{x}}\) and \({\boldsymbol{H}_{y}}\) commute, we rewrite Eq. (45) as follows:

$$ {{\boldsymbol{U}}^{k + 1}}(t) = {e^{{\boldsymbol {H}}t}} {{ \boldsymbol{U}}^{k}} = {e^{{{\boldsymbol{H}}_{x}}t}} {e^{{{\boldsymbol {H}}_{y}}t}} {{ \boldsymbol{U}}^{k}} . $$
(51)

Thus, the two-dimensional problem becomes two one-dimensional problems. For each one-dimensional problem, it can be solved by the PIM, which was introduced in Sect. 2.

4.2 Extensions to three-dimensional case

For the three-dimensional parabolic equation, we can also use SSM to decompose it into the sum of differential operators of three one-dimensional problems. The CFDS-PIM scheme can be extended to the following three-dimensional case:

$$ \frac{{\partial u}}{{\partial t}} =\frac{{{\partial ^{2}}u}}{{\partial{x^{2}}}} + \frac{{{\partial^{2}}u}}{{\partial{y^{2}}}} + \frac{{{\partial^{2}}u}}{{\partial{z^{2}}}} ,\quad (x,y,z,t) \in\varGamma \times[0,T] . $$
(52)

As a precursor to Strang splitting, we rewrite Eq. (52) as follows:

$$ \frac{{\mathrm{d}}{\boldsymbol{U}}}{{\mathrm{d}}t} = {{\boldsymbol{H}}_{x}} {\boldsymbol{U}} + {{ \boldsymbol{H}}_{y}} {\boldsymbol{U}} + {{\boldsymbol{H}}_{z}} {\boldsymbol{U}}, $$
(53)

where \({\boldsymbol{H}_{x}}\), \({\boldsymbol{H}_{y}}\) and \({\boldsymbol {H}_{z}}\) are difference operators in the x-direction, y-direction, and z-direction, respectively. The right side of Eq. (53) is already split, which becomes a sum \(a+b+c\) of relatively simple expressions. We obtain the following equations:

$$ \frac{{\mathrm{d}}{\boldsymbol{U}}}{{\mathrm{d}}t} = ( {\boldsymbol{H}_{x} + \boldsymbol{H}_{y} + \boldsymbol{H}_{z}} )\boldsymbol{U} . $$
(54)

If \({\boldsymbol{H}_{x}}\), \({\boldsymbol{H}_{y}}\) and \({\boldsymbol {H}_{z}}\) commute for Eq. (54), the exact solution to the associated initial value problem would be

$$ {{\boldsymbol{U}}^{k + 1}}(t) = {e^{{\boldsymbol {H}}t}} {{ \boldsymbol{U}}^{k}} = {e^{\boldsymbol{H}_{x}t}} {e^{\boldsymbol {H}_{y}t}} {e^{\boldsymbol{H}_{z}t}} {{\boldsymbol{U}}^{k}} . $$
(55)

Because we apply SSM to the three-dimensional case, we obtain a sum of difference operators of three one-dimensional parabolic problems, and the scheme has the same accuracy as the one-dimensional cases.

5 Numerical examples and discussion

In this section, we give the five numerical examples to validate the adaptability of the proposed schemes and compare their accuracy with those which are already available in the literature for solving parabolic equations. The accuracy of the schemes is measured in terms of the absolute errors, computing time and the order of convergence of the scheme. In our tables, the error is the maximum error between the exact solutions and CFDS-PIM, and CPU(s) is the computing time. The order of the spatial convergence of the schemes is defined as

$$ {\log_{2}}({{{E_{2h}}} / {{E_{h}}}}), $$
(56)

where \({E_{h}} = \vert{{u_{h}} - u} \vert\) and \({E_{2h}} = \vert {{u_{2h}} - u} \vert\) are discrete maximum absolute errors at 2h and h. All the numerical experiments are conducted on MATLAB R2016a platforms based on an Intel Core i5-6300HQ 2.30 GHz processor.

Example 1

Consider a one-dimensional parabolic problem with constant coefficients,

$$ \begin{gathered} {\frac{{\partial u}}{{\partial t}} = \frac{{{\partial^{2}}u}}{{\partial{x^{2}}}},\quad x \in[0,1],t \ge{{0,}}} \\ {u(x,0) = \gamma( {\sin\alpha x + \sin\beta x} ),\quad x \in[0,1],} \\ {u(0,t) = u(1,t) = 0,\quad t \ge0.} \end{gathered} $$
(57)

The exact solution is \(u(x,t) = {e^{- {\alpha^{2}}t}}\sin\alpha x + {e^{- {\beta^{2}}t}}\sin\beta x\). Two sets of different parameters are set up for the parabolic problem in this example.

Case 1. In the first case, we consider the sample test with \(\alpha= \pi\), \(\beta= 0\), \(\gamma= {10^{8}}\).

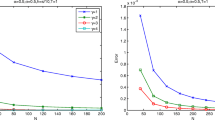
In this case, we choose a spatial step size \(h = 2.5 \times{10^{- 2}}\) and a time step size \(\tau= 4 \times{10^{- 5}}\). Figure 5 presents numerical results of the Taylor and Padé approximation methods of the CFDS-PIM scheme at \(t = 1.8,1.85,1.9,1.95, 2\), respectively. It is obvious that numerical solutions of two schemes are seemingly alike. In order to further compare the Taylor approximation with the Padé approximation, the errors between the exact solutions and two schemes are presented in Fig. 6. It can be seen that the Padé approximation has slightly better accuracy than the Taylor approximation. Moreover, we compare the two approximation methods of CFDS-PIM with the empirical Crank–Nicolson (C-N) scheme in terms of the computational accuracy in Table 2. The number of grid points of CFDS-PIM is much smaller than that of the C-N scheme, but its accuracy is far higher than that of the C-N scheme.

Figure 5
figure 5

The numerical solutions of the Taylor approximation and Padé approximation of CFDS-PIM for case 1 of Example 1

Full size image
Figure 6
figure 6

The errors between the exact solutions and CFDS-PIM approximated solutions of the Taylor approximation (on left-hand side figure) and the errors between the exact solutions and CFDS-PIM approximated solutions of Padé approximation (on right-hand side figure) at \(t=2\) for case 1 of Example 1

Full size image
Table 2 The error comparison between CFDS-PIM and the other method at \(t=2\). N is the number of points of the one-dimensional mesh in case 1 of Example 1
Full size table

Case 2. For the second case we consider the test with \(\alpha= \pi\), \(\beta = 3\pi\), \(\gamma= 1\) to illustrate the difference of the two approximation methods of sixth-order CFDS based on fourth-order PIM and sixth-order CFDS based on the Runge–Kutta fourth-order (RK4) method.

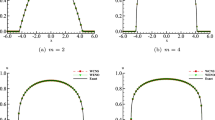
The solutions and the errors between two approximation methods of CFDS-PIM and the exact solutions, which are presented in Fig. 7 with time step size \(\tau= 5 \times{10^{- 5}}\). In the left-hand side figure of Fig. 3, it is obvious that the numerical solutions of the Taylor and Padé approximation method of the CFDS-PIM are in very good agreement with those of the exact solutions. Furthermore, the accuracy of the Taylor approximation is significantly higher than that of the Padé approximation in Fig. 7 (right-hand side figure). Table 3 presents the comparison of the errors and computational time between three approximation methods at \(t = 0.1\) with the different spatial step size. The three numerical methods have the same high-order precision. Moreover, it is clearly noted that the sixth-order CFDS based on fourth-order PIM is able to have excellent computational efficiency.

Figure 7
figure 7

The exact solutions and two numerical solutions (on left-hand side figure) and the errors between Taylor approximation and Padé approximation (on right-hand side figure) with \(N=81\) for case 2 of Example 1

Full size image
Table 3 Numerical results of one-dimensional parabolic problem at \(t=0.1\) for case 2 of Example 1
Full size table

Case 3. For the third case we consider the test with \(\alpha= \pi\), \(\beta = 0\), \(\gamma= 1\) to compare the difference between sixth-order CFDS-PIM and the eighth-order CFDS.

The solutions and the errors between two approximation methods of CFDS-PIM and the exact solutions, which are presented in Fig. 8 with time step size \(\tau= 1\times{10^{- 4}}\). In the left-hand side figure of Fig. 4, it is obviously noted that the numerical solutions of the Taylor and Padé approximation method of the CFDS-PIM are in very good agreement with those of the exact solutions. Furthermore, the accuracy of the Taylor approximation is significantly higher than that of the Padé approximation in Fig. 8 (right-hand side figure). Table 4 presents the comparison of the errors and computational time between sixth-order CFDS-PIM and the eighth-order CFDS at \(t = 1\) with the different spatial step size. It is clearly noted that the sixth-order CFDS-PIM is able to maintain high-order accuracy and excellent computational efficiency.

Figure 8
figure 8

The exact solutions and two numerical solutions (on left-hand side figure) and the errors between Taylor approximation and Padé approximation (on right-hand side figure) with \(N=21\) for case 3 of Example 1

Full size image
Table 4 Numerical results of CFDS-PIM (\(\tau=1\times10^{-4}\)) and Ref. [34] (\(\tau=1\times10^{-6}\)) at \(t=1\) for case 3 of Example 1
Full size table

Example 2

In order to test the applicability of CFDS-PIM. Consider the following parabolic equation with variable coefficients:

$$ \begin{gathered} {\frac{{\partial u}}{{\partial t}} = a ( x ) \frac{{{\partial^{2}}u}}{{\partial{x^{2}}}} + b ( x )u,\quad x \in [0,\pi],t \in[0,1],} \\ {u(x,t) = \sin x,\quad x \in[0,1],} \\ u(0,t) = u(1,t) = 0,\quad t \in[0,1], \end{gathered} $$
(58)

where \(a ( x ) = x + 1\), \(b ( x ) = x\). The exact solution is \(u = {e^{- t}}\sin x\).

Numerical results of the two approximation methods are presented in Fig. 9 with time step size \(\tau=5\times10^{-6}\). In the left-hand side figure of Fig. 9, it is noted that the numerical solutions of the two approximation method are in excellent agreement with the exact solutions. For parabolic equations with variable coefficients, the accuracy of the Padé approximation is significantly higher than that of the Taylor approximation in Fig. 9 right-hand side figure. Table 5 presents the comparison of the errors and computational time between Taylor approximation and Padé approximation at \(t = 0.1\) with the different spatial step size. It is clearly noted that the Padé approximation is able to maintain high-order accuracy.

Figure 9
figure 9

Two numerical solutions (on left-hand side figure) and the errors between Taylor approximation and Padé approximation (on right-hand side figure) with \(N=81\) for Example 2

Full size image
Table 5 Numerical results of one-dimensional parabolic problem with variable coefficients at \(t=0.1\) for Example 2
Full size table

Example 3

In order to extend CFDS-PIM to nonlinear systems with variable coefficients, consider the following nonlinear Shrödinger’s equation(NLSE) with variable coefficients:

$$ i\frac{{\partial u }}{{\partial t}} + a(t)\frac {{{\partial^{2}}u }}{{\partial{x^{2}}}} + b(t) \vert u \vert^{2}u = 0,\quad x \in[ - 10\pi,10\pi],t \ge0, $$
(59)

where \(a(t)=\frac{1}{2}\cos t\) and \(b(t)=\frac{{\cos t}}{{\sin t + 3}}\).

The exact solution is \({u}(x,t) = \frac{1}{{{{(\sin t + 3)}^{1/2}}}}\operatorname{sech} ( {\frac{x}{{\sin t + 3}}} )\exp( {\frac{{i ( {{x^{2}} - 1} )}}{{2(\sin t + 3)}}} )\). We can extract periodic-initial value conditions from the exact solution: \(u(x,0) = \frac{1}{{\sqrt{3} }}\operatorname{sech} ( {\frac{x}{3}} )\exp( {\frac{{i ( {{x^{2}} - 1} )}}{6}} )\). Equation (59) is not only a nonlinear equation but also a parabolic equation with variable coefficients. Since the proposed CFDS-PIM is aimed at a linear parabolic problem, the main step in solving NLSE is to convert the nonlinear Schrödinger’s equation into a linear equation. It is obvious that the periodic-initial value conditions abide by the mass conservation law [37]:

$$ {Q(t): = \int_{\varOmega}{\bigl|u ( {x,0} )\bigr|^{2} \,{\mathrm{d}}x = \int_{\varOmega}{\bigl|u ( {x,0} )\bigr|^{2}} }\, {\mathrm{d}}x = Q(0).} $$
(60)

In this nonlinear problem, we utilize a simplified linearization technique for the nonlinear term of NLSE with the help of the mass conservation law. This linearization technique is to convert the nonlinear term into a linear operator: \(|u ( {x,t} ){|^{2}} = |u ( {x,0} ){|^{2}} = {\boldsymbol{M}}\). Because the linear operators M and H can perform addition, the numerical solution can be written as \(u = {u_{0}}{e^{i(a(t){\boldsymbol {H}} + b(t){\boldsymbol{M}})t}}\) [38]. The solutions of the Taylor approximation and the errors are shown in Fig. 10. The spatiotemporal evolution of the numerical solution is presented in Fig. 11. In Fig. 10, it is obvious that the numerical solutions of the Taylor approximation method of the CFDS-PIM are in very good agreement with the exact solutions. The physical behavior of the numerical solutions described in Fig. 6 is coincident with that given in [39, 40]. It can be seen that the Taylor approximation method of the CFDS-PIM has high accuracy. Thus, the effectiveness of CFDS-PIM, which can extend to nonlinear systems with variable coefficients, is verified by numerical results.

Figure 10
figure 10

The exact solutions and numerical solutions (on left-hand side figure) and the errors between Taylor approximation and exact solutions (on right-hand side figure) with \(N = 21\) and time step size \(\tau= 0.01\) at \(t=20\pi\) for Example 3

Full size image
Figure 11
figure 11

Evolution profile of numerical solutions of the Taylor approximation at time \(t=[0,20\pi]\) with \({N = 41}\), time step size \(\tau= 0.01\) for Example 3

Full size image

Example 4

Consider two-dimensional parabolic problem with constant coefficients

$$ \begin{gathered} {\frac{{\partial u}}{{\partial t}} = \frac{{{\partial^{2}}u}}{{\partial{x^{2}}}} + \frac{{{\partial ^{2}}u}}{{\partial{y^{2}}}},\quad(x,y) \in\varOmega= [0,1] \times [0,1],t \ge0,} \\ {u(x,0) = \gamma\sin\alpha x\sin\beta x,\quad(x,y) \in\varOmega= [0,1] \times[0,1],} \\ {u(x,y,t) = 0,\quad(x,y) \in\partial\varOmega,t > 0,} \end{gathered} $$
(61)

where ∂Ω denotes the boundary of the region \(\varOmega= [0,1] \times[0,1] \). The exact solution is \(u(x,t) = \gamma{e^{- {(\alpha^{2}+\beta^{2})}t}}\sin\alpha x \sin\beta y\). Two sets of different parameters are set up for the two-dimensional parabolic problem in this example.

Case 1. For the first case, we consider the sample test with \(\alpha= \pi\), \(\beta= \pi\), \(\gamma= {10^{17}}\). The solutions of the Taylor and the Padé approximations of CFDS-PIM-SMM are depicted in Fig. 12. It is obvious that numerical solutions of the two schemes look very similar. In order to compare the accuracy of the two approximation methods, the errors between the two schemes and the exact solutions are presented in Fig. 13. It is evident that the numerical results of the Taylor approximation are comparable to the numerical results that obtained by the Padé approximation. In addition, Table 6 presents the errors comparison between CFDS-PIM-SSM and D’Yakonov ADI (DADI) schemes [1] in different positions. Even though CFDS-PIM-SSM has much fewer grid points than the DADI scheme, the numerical results of our schemes are more accurate than the numerical results of the DADI scheme. Besides, the numerical solutions of the sixth-order CFDS of RK4 method coupled SSM are given in Table 6. All three numerical methods, the Taylor approximation, the Padé approximation, and the RK4 method, have the same high-order precision. Moreover, it is clearly noted that the sixth-order CFDS based on fourth-order PIM is able to have excellent computational efficiency.

Figure 12
figure 12

The CFDS-PIM solutions of the Taylor approximation (on left-hand side figure) and Padé approximation (on right-hand side figure) for two-dimensional problem with \(N=41\times41\) at \(t=2\) for case 1 of Example 4

Full size image
Figure 13
figure 13

The errors between the exact solutions and CFDS-PIM solutions of the Taylor approximation (on left-hand side figure) and the error between the exact solutions and the CFDS-PIM solutions of Padé approximation (on right-hand side figure) for two-dimensional problem with \(N=41\times41\) at \(t=2\) for case 1 of Example 4

Full size image
Table 6 The error comparison between CFDS-PIM and other method with spatial step sizes \({h_{x}} = {h_{y}} = 2.5\times10^{-2}\) and time step size \(\tau= 2 \times{10^{- 5}}\) at \(t=2\) for case 1 of Example 4
Full size table

Case 2. For illustrating the difference of the Taylor and Padé approximation methods of the CFDS-PIM-SSM, we consider Eq. (61) with \(\alpha= \pi\), \(\beta= \pi\), \(\gamma= 1\).

Figure 14 presents numerical results of the Taylor and Padé approximated solutions of the CFDS-PIM-SSM, which are seemingly alike. The errors of the two approximation methods of the CFDS-PIM-SSM are depicted in Fig. 15. It is evident that the numerical results of the Taylor approximation are more accurate than that obtained in the Padé approximation with \(N= 81 \times81\). When the spatial step repeatedly doubled, the numerical results of the two schemes are presented in Table 7. It can be seen that the Padé approximation is not able to maintain a high order of convergence with \(N= 81 \times 81\). This example shows that excellent accuracy and efficiency is got by applying the two approximation methods of CFDS-PIM-SSM, but the Taylor approximation is more accurate than the Padé approximation.

Figure 14
figure 14

The numerical solutions of the CFDS-PIM of the Taylor approximation (on left-hand side figure) and the numerical solutions of the CFDS-PIM of Padé approximation (on right-hand side figure) for two-dimensional problem at \(t=0.1\) with \(N=81\times81\) for case 2 of Example 4

Full size image
Figure 15
figure 15

The errors between the exact solutions and CFDS-PIM approximated solutions of the Taylor approximation (on left-hand side figure) and the errors between the exact solutions and CFDS-PIM approximated solutions of Padé approximation (on right-hand side figure) for two-dimensional problem at \(t=0.1\) with \(N=81\times81\) for case 2 of Example 4

Full size image
Table 7 Numerical results of two-dimensional parabolic problem with time step size \(\tau= 5 \times{10^{- 5}}\) at \(t=0.1\) for case 2 of Example 4
Full size table

Example 5

In order to test the applicability of CFDS-PIM. we consider the following parabolic equation with variable coefficients:

$$ \begin{gathered} {\frac{{\partial u}}{{\partial t}} = a ( {x,y} ) \biggl( {\frac{{{\partial^{2}}u}}{{\partial{x^{2}}}} + \frac {{{\partial^{2}}u}}{{\partial{y^{2}}}}} \biggr) + b ( {x,y} )u, \quad(x,y) \in\varOmega= [0,\pi] \times[0,\pi],t \ge0,} \\ {u(x,y,0) = \sin x\sin y,\quad(x,y) \in\varOmega}, \\ {u(x,y,t) = 0,\quad(x,y) \in\partial\varOmega,t \ge0}, \end{gathered} $$
(62)

where \(a ( x ,y ) = xy\), \(b ( x ,y ) = xy\) and time step size \(\tau =5\times10^{-6}\). The exact solution is \(u = {e^{-2 t}}\sin x \sin y\).

Figure 16 presents numerical results of the Taylor and Padé approximated solutions of the CFDS-PIM-SSM which are seemingly alike. The errors of the two approximation methods of the CFDS-PIM-SSM are depicted in Fig. 17. It is evident that the numerical results of the Taylor approximation are more accurate than that obtained in the Padé approximation with \(N= 81 \times81\). The spatial step is repeatedly doubled, and the numerical results of the two schemes are presented in Table 8. It can be seen that the Padé approximation is not able to maintain a high order of convergence with \(N= 81 \times 81\). This example shows that excellent accuracy and efficiency are realized by applying the two approximation methods of CFDS-PIM-SSM, but the Taylor approximation is more accurate than the Padé approximation.

Figure 16
figure 16

The numerical solutions of the CFDS-PIM of the Taylor approximation (on left-hand side figure) and the numerical solutions of the CFDS-PIM of the Taylor approximation and the Padé approximation (on right-hand side figure) for two-dimensional problem at \(t=1\) with \(N=81\times81\) for Example 5

Full size image
Figure 17
figure 17

The errors between the exact solutions and CFDS-PIM approximated solutions of the Taylor approximation (on left-hand side figure) and the errors between the exact solutions and CFDS-PIM approximated solutions of Padé approximation (on right-hand side figure) for two-dimensional problem at \(t=1\) with \(N=81\times81\) for Example 5

Full size image
Table 8 Numerical results of two-dimensional parabolic problem and the spatial step at \(t=1\) for Example 5
Full size table

Example 6

Consider the three-dimensional parabolic problem

$$\begin{gathered} \frac{{\partial u}}{{\partial t}} = \frac{{{\partial ^{2}}u}}{{\partial{x^{2}}}} + \frac{{{\partial^{2}}u}}{{\partial{y^{2}}}} + \frac{{{\partial^{2}}u}}{{\partial{z^{2}}}} , \quad(x, y,z) \in \varGamma= [0,1] \times[0,1] \times [0,1] , t > 0, \\ u(x,y,0) = \sin\pi x\sin\pi y\sin\pi z , \quad(x, y,z) \in \varGamma, \\ u(x,y,z,t) = 0 , \quad(x,y,z) \in\partial\varGamma, t > 0, \end{gathered} $$

where ∂Γ denotes the boundary of the square space \(\varGamma= [0,1] \times[0,1] \times[0,1]\). The exact solution is \(u(x,y,z,t) = {e^{- 3{\pi^{2}}t}}\sin\pi x\sin\pi y\sin\pi z\).

The slice figures of the four-dimensional images are used for observing a three-dimensional parabolic problem, and the slice figures are depicted in Figs. 18, 19, 20, 21. Figure 22 presents the errors of the two approximation methods of the CFDS-PIM-SSM at \(t=0.1\) with \(x=0.5\) and \(y=0.5\). The results of this example show that Strang splitting method is a numerical method with high precision and high efficiency for solving multi-dimensional problems. The comparison is done with solutions obtained by two approximation methods of the CFDS-PIM-SSM for the three-dimensional parabolic equation, which is presented in Table 9. All numerical figures of this example show that the CFDS-PIM-SSM has excellent accuracy and efficiency, but the Taylor approximation is more accurate than the Padé approximation. There is the phenomenon in Table 9 that the convergence order will decrease with the increase of nodes. Zhai et al. [41] gave an explanation for this phenomenon. The convergence order is formally defined when the mesh size approaches zero; therefore, when the mesh size is relatively large, the discretization schemes may not achieve the formal convergence order. Besides, because the mesh size is extremely small, the Padé approximation scheme cannot achieve its formal convergence order.

Figure 18
figure 18

The slices of the four-dimensional figure of the solutions of the three-dimensional problem for the CDF-PIM-SSM with spatial step size \({{h_{x}} = {h_{y}} = {h_{z}} = 0.05}\) and time step size \(\tau= 5 \times{10^{- 5}}\) at \(t=0.1\) for Example 5

Full size image
Figure 19
figure 19

The slices of four-dimensional figures of the solution of the three-dimensional problem for \(x=0.2\) (on left-hand side figure) and \(x=0.4\) (on right-hand side figure) for Example 6

Full size image
Figure 20
figure 20

The slices of the four-dimensional figures of the solution of the three-dimensional problem for \(x=0.5\) (on left-hand side figure) and \(y=0.5\) (on right-hand side figure) for Example 6

Full size image
Figure 21
figure 21

The slices of the four-dimensional figures of the solution of the three-dimensional problem for \(z=0.5\) (on left-hand side figure), and a three-dimensional figures of the solution of the three-dimensional problem at \(t=0.1\) with \(z=0.5\) (on right-hand side figure) for Example 6

Full size image
Figure 22
figure 22

The errors between the exact solutions and CFDS-PIM-SSM approximated solutions of the Taylor approximation (on left-hand side figure), and the errors between the exact solutions and CFDS-PIM-SSM approximated solutions of Padé approximation (on right-hand side figure) for three-dimensional problem at \(t=0.1\) with \(z=0.5\) for Example 6

Full size image
Table 9 Numerical results of three-dimensional parabolic problem at \(t=0.1\) with \(x=0.5\) and \(y=0.5\) for Example 6
Full size table

6 Conclusion

This paper presents two high-order exponential time differencing precise integration method schemes in combination with a spatially global sixth-order compact finite-difference scheme, which have been developed for the numerical solutions of one-dimensional and multi-dimensional parabolic equations. A sixth-order CFDS is used for converting the parabolic equations into the ODEs, and then the Taylor approximation and the Padé approximation of the PIM is used for solving the resulting system of ODEs. For multi-dimensional problems, the Strang splitting method reduces them to a sum of one-dimensional problems. The five examples considered have been studied to confirm the accuracy and utility of the proposed scheme. The findings can be summarized as follows.

  1. (1)

    It is found that the proposed results are in good agreement with the exact solutions. The two schemes of CFDS-PIM have very high excellence in computational accuracy and efficiency.

  2. (2)

    In the one-dimensional example, the computational accuracy of CFDS-PIM is much higher than that of the empirical C-N scheme.

  3. (3)

    In the two-dimensional example, the computational accuracy of CFDS-PIM is much higher than that of the empirical DADI scheme. Taylor approximation has better accuracy than Padé approximation. Besides, Taylor approximation is well combined with Strang splitting method.

  4. (4)

    The Strang splitting method shows the advantage of no precision loss in multi-dimensional calculation. SSM is far superior to DADI schemes in accuracy and efficiency.

  5. (5)

    Compared with the compact schemes of the same type, CFDS-PIM-SMM has better computational efficiency;

  6. (6)

    CFDS-PIM-SMM can easily extend to nonlinear multi-dimensional parabolic systems with variable coefficients.