Keywords

1 Introduction

The gravity gradiometer, that is an analogue of the model developed by Bell Aerospace Laboratory (USA) and currently produced by Lockheed Martin (USA), is considered (Dransfield et al. 2010; Murphy 2010; Hammond and Murphy 2003).

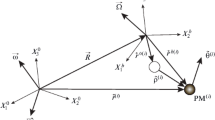
The instrument design is based on the slowly rotating disk with diameter equals 0.2 m and angular rate 0.25 Hz. The parallel pairs of accelerometers are set on the diametrically opposite sides of the mentioned rotating disk and at the same distance from the center of the disk. The accelerometer sensitivity axes are tangent-oriented (Fig. 1). Further, for certainty, we assume that disk has the vertical axis of rotation. This construction of a gradiometer is called GGI (gravity gradiometer instrument).

Fig. 1
figure 1

GGI model

Full size image

Gradiometer designed for airborne gravimetry. Gradiometer should be installed on a gyro stabilized platform.

The linear combination of accelerometer readings generates the GGI output signal. The rotation of the disk induces forced harmonic oscillations, and as a result the output signal becomes modulated at a frequency equal to twice angular rate:

$$\displaystyle \begin{aligned} W&=(f_1+f_2)-(f_3+f_4) = \\ &=l[(\varGamma_{22}-\varGamma_{11}+\omega_2^2 -\omega_1^2)\sin 2\varOmega t +\\ &+ (\varGamma_{12}+\omega_1\omega_2)\cos 2\varOmega t]. \end{aligned} $$
(1)

Here

  • W is the GGI output;

  • f i, i = 1, …, 4 are the components of a specific force measured by accelerometers 1, 2, 3, 4;

  • Γ 11, Γ 22, Γ 12 are the components of the gravity gradient tensor Γ = grad g, where g is the vector of the specific gravity;

  • Ω is the angular rate vector of the disk, and Ω ≫ u, where u is the absolute velocity of earth’s rotation;

  • ω is the absolute angular rate vector of a gyro platform (GGI body frame).

The problem of estimation of Γ tensor component using W measurements solved in post-processing. In this case one have to use current navigation parameters of high accuracy, in particular ω.

The basic method used for increasing the accuracy of the GGI operation is the compensation of its instrument errors. The most stable parameters of these errors can be estimated during calibration that proposes the usage of a specialized test bench. There were discussed several options of the mentioned calibration procedure in recent publications. The first variant proposes the usage of a centrifuge (Yu abd Cai 2018). The second variant is based on the special motion of the disturbing mass (Deng et al. 2018).

The pre-start calibration mode of GGI is also possible, that consists of the regular operation at a fixed point for a short time.

It should be noted that the gradiometer error model includes the combinations of the instrumental errors of the paired accelerometers. So, it is important to do estimation of these combinations exclusively, and not to do estimation of errors of single accelerometers. This is why the calibration procedure should be performed for the assembled GGI.

2 Model of Instrumental Errors of the Gradiometer

The accepted model of instrumental errors is as follows. Let f be the measured value, f′ be the result of the measurement, then f′ = f + Δf, where Δf is the instrumental error. We will use the following designations (Golovan et al. 2018):

  • δ = (δ 1, δ 2, δ 3)T is the small rotation vector that characterizes the installation errors of a GGI on a gyro platform;

  • Δl i = (l i − l)∕2 is the inaccuracy in the distance from the center of the proof mass of the i-th accelerometer with respect to the center of the rotating disk (the true distance equals to l i∕2),

  • χ i is the misalignment error of sensitivity axis of the i-th accelerometer;

  • Δf i0 is the bias of the i-th accelerometer measurement;

  • k i is the scale factor error of i-th accelerometer measurement;

  • Δf is is the noise component of accelerometer measurement.

The error model of the i-th accelerometer is as follows

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_i^{\prime} = (1+k_i) f_i + \varDelta f_{i0} + \varDelta f_{is} + \chi_i f_{i \perp} \end{array} \end{aligned} $$
(2)

where the component χ i f i⊥ reflects the cross-coupling effect of the specific force acting on the proof mass of the accelerometer orthogonally to its longitudinal axis due to a skew in the disk’s plane.

Let \(W' = (f^{\prime }_1+f^{\prime }_2)-(f^{\prime }_3+f^{\prime }_4)\) be the measurement of the W (1). Measurement error ΔW = W′− W contains the frequency components Δ 0, Δ 1, Δ 2:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varDelta W=\varDelta_0 + \varDelta_1 +\varDelta_2. \end{array} \end{aligned} $$
(3)

Taking into account the mentioned definitions, the error model of the gradiometer output takes the form (Golovan et al. 2018):

$$\displaystyle \begin{aligned} \varDelta_0&= (\varDelta f_{10}+\varDelta f_{20}-\varDelta f_{30} - \varDelta f_{40}) + \\ &+(\varDelta f_{1s}+ \varDelta f_{2s}- \varDelta f_{3s} - \varDelta f_{4s}) - \\ &-\frac 12 \dot{\omega}_3 \Big[ k_1 + k_2-k_3- k_4+\chi_1+\chi_2-\chi_3-\chi_4 + \\ &\quad + 2\frac{\varDelta l_1+\varDelta l_2-\varDelta l_3-\varDelta l_4}l \Big] , \end{aligned} $$
(4)
$$\displaystyle \begin{aligned}\begin{array}{rcl} \begin{aligned} \varDelta_1& = \big[ (k_1 - k_2+\chi_3-\chi_4)w_2 + \\ & \quad + (k_3-k_4-\chi_1 +\chi_2)w_1 \big] \cos \varOmega t - \\ & - \big[ (k_1 - k_2 + \chi_3- \chi_4)w_1 - \\ & \quad - (k_3- k_4+\chi_1-\chi_2)w_2 \big] \sin \varOmega t, \end{aligned} \end{array} \end{aligned} $$
(5)

where w 1,w 2 are the horizontal components of a gyro platform’s specific force, \(\dot {\omega }_3\) is the vertical component of the angular acceleration,

$$\displaystyle \begin{aligned} \varDelta_2&= 2l \big[ \delta_1 (\varGamma_{23}+ \omega_2 \omega_3)+ \delta_2 (\varGamma_{13}+ \omega_1 \omega_3) -\\ &\quad -2\delta_3 (\varGamma_{12}+ \omega_1 \omega_2) \big] \sin 2\varOmega t + \\ &+2l \big[2 \delta_3 (\varGamma_{22}-\varGamma_{11}+ \omega_2^2-\omega_1^2)+\delta_1(\varGamma_{13}+\omega_1 \omega_3)-\\ &\quad - \delta_2 (\varGamma_{23}+ \omega_2 \omega_3) \big] \cos 2\varOmega t + \\ &+\Big( k_1+k_2-k_3- k_4+ \chi_1+\chi_2-\chi_3-\chi_4 + \\ & \quad +2\frac{\varDelta l_1+\varDelta l_2 - \varDelta l_3-\varDelta l_4}l \Big) \times \\ & \quad \times \Big[ \frac l4(\varGamma_{22}-\varGamma_{11}+\omega_2^2-\omega_1^2)\sin 2\varOmega t + \\ &\qquad +\frac l2 (\varGamma_{12}+\omega_1\omega_2)\cos 2\varOmega t\Big]. \end{aligned} $$
(6)

3 Calibration Algorithm

The following combinations of the GGI instrument error are of interest:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} {} & \gamma_1=\delta_1, \qquad \gamma_2=\delta_2, \qquad \gamma_3=\delta_3, \\ & \gamma_4 = \varDelta f_{10} +\varDelta f_{20}-\varDelta f_{30}- \varDelta f_{40}, \\ & \gamma_5 = k_1+k_2-k_3 -k_4+\chi_1+\chi_2-\chi_3-\chi_4 + \\ & \qquad +2\frac{\varDelta l_1+\varDelta l_2-\varDelta l_3-\varDelta l_4}l. \end{aligned} \end{array} \end{aligned} $$
(7)

It is obvious that the constructive instrument errors – χ i (that are the mutual misalignments of the sensitive axes of accelerometers) and Δl i (that is the inaccuracy of disk’s radius value) remain unchanged in GGI operation, so it is necessary to include them in the relevant calibration problem. At the same time δ i (that is the GGI installation error), Δf i0 and k i (that are the biases and scale factor errors) may vary from run to run. So these parameters should be estimated during GGI operation.

3.1 Case of Fixed Point

The following reference information is used for calibration of the gradiometer at a fixed point:

  • the vector of earth rotation with respect to the geographical reference frame

    $$\displaystyle \begin{aligned} \begin{array}{rcl} \omega_1 & =&\displaystyle 0 \\ \omega_2 & =&\displaystyle u \cos \varphi \\ \omega_3 & =&\displaystyle u \sin \varphi \end{array} \end{aligned} $$
    (8)

  • the vertical component of angular acceleration equals zero: \(\dot {\omega }_3=0\);

  • the linear accelerations equal zero w 1 = 0, w 2 = 0;

  • the reference values for the gravity tensor components Γ ij.

Then the model for output error of the gradiometer takes the form

$$\displaystyle \begin{aligned} &\quad z= W' -W = \varDelta W = \varDelta [ (f_1 + f_2)-(f_3 + f_4) ]= \\ &= \gamma_4 + (\varDelta f_{1s} + \varDelta f_{2s}- \varDelta f_{3s} - \varDelta f_{4s}) - \\ &+2l \Big[ \gamma_1 (\varGamma_{23}+u^2 \sin \varphi \cos \varphi)+\gamma_2\varGamma_{13}-2\gamma_3\varGamma_{12}+ \\ &+ \frac l4 \gamma_5 (\varGamma_{22}-\varGamma_{11} + u^2 \cos^2 \varphi) \Big] \sin 2\varOmega t + \\ &+2l \Big[ 2\gamma_3 (\varGamma_{22}-\varGamma_{11} +u^2 \cos^2 \varphi)+ \gamma_1 \varGamma_{13} - \\ & -\gamma_2 (\varGamma_{23}+u^2 \sin \varphi \cos \varphi)+ \frac l2 \gamma_5 \varGamma_{12} \Big] \cos 2\varOmega t. \end{aligned} $$
(9)

Denote by x 1, x 2, x 3 the amplitudes of the harmonics in the z measurement:

$$\displaystyle \begin{aligned} x_1 =\gamma_4\end{aligned} $$
(10)
$$\displaystyle \begin{aligned} x_2 &= 2l \Big[ \gamma_1 (\varGamma_{23}+u^2 \sin \varphi \cos \varphi) +\gamma_2\varGamma_{13}-2\gamma_3\varGamma_{12}\Big]+ \\ +& \frac l4 \gamma_5 (\varGamma_{22}-\varGamma_{11} +u^2 \cos^2 \varphi)\end{aligned} $$
(11)
$$\displaystyle \begin{aligned} x_3 &= 2l \Big[ 2\gamma_3 (\varGamma_{22}-\varGamma_{11} +u^2 \cos^2 \varphi) + \gamma_1 \varGamma_{13} -\\ -&\gamma_2 (\varGamma_{23}+u^2 \sin \varphi \cos \varphi) \Big] + \frac l2 \gamma_5 \varGamma_{12}. \end{aligned} $$
(12)

Let assume that instrumental errors are constant during the experiment:

$$\displaystyle \begin{aligned} \varDelta \dot{f}_{i0} & = 0,\ i=1, \ldots, 4 \\ \dot{\delta}_i& = 0,\ i=1, \ldots, 3 \\ \dot{k}_i &= 0, \ i=1, \ldots, 4 \\ \dot{\chi}_i &= 0, \ i=1, \ldots, 4 \\ \varDelta \dot{l}_i& = 0,\ i=1, \ldots, 4. \end{aligned} $$
(13)

Then the estimation problem for the state vector x = (x 1, x 2, x 3)T of linear dynamic system can be set as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \dot{x} & =&\displaystyle 0, \\ z & =&\displaystyle x_1+x_2 \sin 2\varOmega t + x_3 \cos 2\varOmega t +r, \end{array} \end{aligned} $$
(14)

where r is the white noise of a given intensity that is composed by the linear combination of noises of single accelerometers

$$\displaystyle \begin{aligned} r = \varDelta f_{1s}+\varDelta f_{2s}-\varDelta f_{3s}-\varDelta f_{4s} \end{aligned} $$
(15)

The problem posed can be solved by application of the relevant Kalman filter.

Since the set of functions \(1, \sin 2\varOmega t, \cos 2\varOmega t \) are linearly independent, the constant factors in these functions (14) become observable.

So, the estimates of combinations (7) can be obtained and above algorithm can be used in as a pre-start calibration algorithm.

3.2 The Usage of a Stand of Linear Movement

The estimates for combinations k 1 + k 2 − k 3 − k 4 + χ 1 + χ 2 − χ 3 − χ 4 can be derived using test bench of linear movement. Calibration procedure proposes that the gradiometer moves in the horizontal plane with known linear accelerations along a given direction. The algorithm does not require reference values of the gravitational gradient tensor components in this case.

One can form measurements in the following way

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} z_1& =f^{\prime}_1-f^{\prime}_2= \varDelta f_{10}-\varDelta f_{20}+\varDelta f_{1s}-\varDelta f_{2s} - \\ & - [(k_1+k_2) w_1 + (\chi_1+\chi_2) w_2] \sin \varOmega t + \\ & + [(k_1+k_2) w_2 + (\chi_1+\chi_2) w_1 ]\cos \varOmega t \end{aligned} \end{array} \end{aligned} $$
(16)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} z_2& =f^{\prime}_3-f^{\prime}_4= \varDelta f_{30}-\varDelta f_{40}+\varDelta f_{3s}-\varDelta f_{4s} - \\ & - [(k_3+k_4) w_2 - (\chi_3+\chi_4) w_1] \sin \varOmega t - \\ & - [(k_3+k_4) w_1 + (\chi_3+\chi_4) w_2 ]\cos \varOmega t. \end{aligned} \end{array} \end{aligned} $$
(17)

When one selects the orientation of the stands rail in the North-South direction (the linear acceleration component w 1 = 0), then the measurements z 1, z 2 take the form:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} z_1& = \varDelta f_{10} - \varDelta f_{20}+\varDelta f_{1s}-\varDelta f_{2s} - \\ & - (\chi_1+\chi_2) w_2 \sin \varOmega t + (k_1+k_2) w_2 \cos \varOmega t,\\ z_2& =\varDelta f_{30}- \varDelta f_{40}+\varDelta f_{3s}-\varDelta f_{4s} - \\ & - (k_3+k_4) w_2 \sin \varOmega t - (\chi_3+\chi_4) w_2 \cos \varOmega t. \end{aligned} \end{array} \end{aligned} $$
(18)

Let introduce:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \qquad \begin{array}{l} x_1= \varDelta f_{10}-\varDelta f_{20} \\ x_2= k_1 + k_2 \\ x_3= \chi_1 + \chi_2 \\ \end{array} \qquad \begin{array}{l} x_3= \varDelta f_{30}-\varDelta f_{40} \\ x_4= k_3 + k_4 \\ x_5= \chi_3 + \chi_4. \\ \end{array} \end{array} \end{aligned} $$
(19)

Then

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} z_1 & = x_1+x_2 w_2 \cos \varOmega t - x_3 w_2\sin \varOmega t +r_1 \\ z_2 & = x_4 - x_5 w_2 \sin \varOmega t - x_6 w_2 \cos \varOmega t +r_2. \end{aligned} \end{array} \end{aligned} $$
(20)

Thus, the problem is reduced to two independent estimation problems

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} \qquad \begin{array}{l} \dot{x}_1=0 \\ \dot{x}_2=0 \\ \dot{x}_3=0 \\ \end{array} \qquad \mathrm{and} \qquad \begin{array}{l} \dot{x}_4=0 \\ \dot{x}_5=0 \\ \dot{x}_6=0 \\ \end{array} \end{aligned} \end{array} \end{aligned} $$
(21)

with the help of aiding measurement z 1, z 2.

Since the functions \(1, \sin \varOmega t, \cos \varOmega t\) are linearly independent, then the constant factors in these functions are observed. Therefore, the following combination k 1 + k 2, k 3 + k 4, χ 1 + χ 2, χ 3 + χ 4 can be estimated, e.g. applying Kalman Filter.

The similar algorithm can be implemented for the estimation of k 1 + k 2 and k 3 + k 4 combinations in GGI regular operation mode (O’Keefe et al. 1997).

The γ 1, γ 2, γ 3, γ 4, γ 5 components (7) in the GGI error model (4, 6) can be compensated on the basis of corresponding estimates derived by Kalman filters.

4 Conclusion

The algorithms were elaborated for the estimation of instrument errors of GGI. The implementation of these algorithms is fairly easy, they can be included into calibration procedure.