Keywords

15.1 Teacher Noticing, Decision-Making, and Teacher Values

In designing effective teaching environments, classroom culture may be listed alongside the components of teaching dynamics like curriculum, lesson plan, teacher, and student. Among the variables of classroom culture that are important for effective learning are the importance of student thinking, student engagement, coordinating the classroom environment, and the classroom setting, all of which have been emphasized in the literature (Husband 1947; Muijs and Reynolds 2010, pp. 2–3). When it comes to mathematics teaching/learning, The National Council of Teachers of Mathematics [NCTM] (2000) expects teachers to not only teach mathematical knowledge, but have a good understanding of what students know and what kind of support for their studying they need, in order for them to learn better. Weissglass (2002, p. 35) recommended an even wider perspective that includes a school’s culture and role, as well as mathematical knowledge, learning, and instruction.

When considering such frameworks as these, various roles are clearly expected of teachers for effective teaching, such as managing “the blooming, buzzing confusion of sensory data” (Sherin and Star 2011, p. 69) that they encounter while teaching. Within this ‘confusion’ teachers need to determine which elements to register as important and which to ignore, depending on the learning environment. Therefore, which types of circumstances teachers pay attention to, how they interpret these circumstances, and their processes for implementing these interpretations through teaching activities are significant. The combination of these processes can be defined as teacher noticing (Sherin et al. 2011; van Es and Sherin 2002).

Specifically, ‘noticing’ by the teacher in the classroom can be described as seeing and understanding particular aspects of classroom instruction. While this concept is static in some professions, it is active for teachers as it depends on the interplay between the classroom culture and environment, the curriculum and content, and the students and teacher. The structure of noticing concentrates on the elements that teachers pay attention to; that is, noticing is related to what they choose to respond to or ignore, as well as how they interpret these elements within the intricacy of the classroom.

Various studies exist in the literature on conceptualizing teacher noticing (see, Sherin et al. 2011). In the current study, teacher noticing is situated within a framework of teachers attending to the features of classroom interaction that occur during instruction (such as students’ misconceptions, confusion, concurrent requests to speak, and so on), their reasoning and interpreting of what they did attend to, and how the teachers used these reasons and interpretations to decide why and how to respond in the ongoing teaching processes (Jacobs et al. 2010; van Es and Sherin 2002). It is the last component of this sequence, deciding how to respond (Jacobs et al. 2010), which became an important element in this study. This element is observable in the teachers’ active instructional processes, whereas the first two elements cannot be readily observed in the ongoing teaching/learning process.

Teachers have to make decisions within each of the three components of the above process. Such decisions will take into account the sum of physical and cognitive efforts related to selecting and preferring various conditions (Taşçı 2011). In particular decision-making regarding why to respond and then what to do in responding (the second and third components of the above process), is the teacher making such decisions all ‘made in the moment’ when teaching mathematics. But teacher noticing, the first component of the above process, is also influenced by teachers’ decision-making processes since they are ‘deciding’ what to attend to and what to ignore.

Teacher noticing and related decision making have been examined in the past. It has been suggested that teachers’ decisions are impacted by school culture, the teacher’s mathematical knowledge and their knowledge of mathematics teaching, the teaching situation, goals, learning outcomes, teacher’s experience, and their beliefs and values (Bishop and Whitfield 1972; Jacobs et al. 2010). Investigations have also related decision-making processes in terms of teachers’ internal knowledge, beliefs, attitudes, and practices (Bartlett 1932; Fisher et al. 2014; Vondrová and Žalská 2012). Dede (2013) inferred decision-making to be basically influenced by values.

The purpose of this chapter is to explicitly examine teachers’ values related to the decision making process in the moment of teachers’ noticing in mathematics lessons. It is a contention of this chapter that teacher values are principal factors in the moments when teachers make their choices and decisions (Aktaş and Argün 2018; Dede 2013).

15.2 Method and Procedure

15.2.1 The Study Design

The study has been designed as a qualitative case study involving five elementary mathematics teachers in Turkey. The seventh-grade teachers, working in three different elementary schools, were selected through convenience sampling. Each participant is taken as a single case; hence, this study was designed as a multiple case study (Yin 1994). The cases are named T1, T2, T3, T4, and T5. T1 and T4 are females. Teachers’ teaching experience is 1, 13, 14, 23, and 41 years, respectively. The three schools are located in the same geographical and socio-economic district. T1 works at a small school with only one seventh-grade class. The school has a small number of students and focuses on student learning apart from exams. T2, T3 and T5 work at the same school, which has 20 groups of seventh graders. Because this school considers the high school entrance examination to be important, examination preparation tests frequently take place. Although these three participants work at the same institution, their focus in their lessons varies greatly. While T2 stays self-focused during a lesson, T3 is far more focused on student achievement. T2 utilizes a different resource book to T1 and T5 and presents diverse questions. T3 in contrast designs her lessons by simultaneously considering conceptual and operational comprehension. T5 pays attention to the use of mathematical language and student achievement in her teacher-centered classes. T4’s school has four classes of seventh graders, with differences in culture in the different classrooms. The school follows the curriculum strictly. T4 designs her classes by relying on the relevant resource textbook.

Teachers’ values (Bishop 2008a, pp. 191–203) and teachers’ noticing (Vondrová and Žalská 2012) depend, at least to some extent, on the lesson content. In this study, the notion of regular polygons was the focus for all class groups. In general geometry, questions are often visual questions that demand both careful reading and spatial abilities that include drawing skills, as well as algebraic expressions later on. Therefore, the questions can give rise to critical issues for mathematical communication, which applies no less to the specific field of polygons. Thus, this whole field can provide rich data for extending the knowledge about teacher noticing.

15.2.2 Procedure

The data were collected using video-recordings from the classrooms followed by semi-structured interviews with the teachers. Four of each teacher’s classes, each lasting 45 min, were recorded while the participants taught the concept of polygons. Next, the researchers identified the key points in the recordings when a teacher attended and responded to, or ignored, specific situations. For example, such a situation occurred when a teacher was asking a question, he recognized that a student had raised their hand, and the teacher responded to that student’s action. But such a situation could be when a teacher failed to recognize those sitting in the back row were not paying attention, or when a student was thinking differently to the way the teacher had expected.

Following the teaching sessions, each teacher was individually interviewed twice, which yielded ten interviews in total. Each interview lasted between 2–3 hours. During the interviews, participants were first asked to note the key points that they had attended to in their lessons. Secondly, the researchers asked them whether they had paid attention to the key points that the researchers had identified in the video-recordings. In both phases, teachers were asked to clarify how and why they had decided to respond or not respond to the various key points for some of the cases where the researchers’ had pre-identified key points of the lesson. In this way not only were the participants’ confirmation obtained regarding their noticing, but data were also gathered in terms of the values underlying their decision-making.

From this analysis it became clear that the teachers had developed strategies for dealing with decision making at key points of the lessons, as well as being able to assess the effectiveness of those decisions. We were able to identify circumstances where a teacher used the same strategy at least three times at key points. This then allowed us to reflect on what values, if any, were in play during these similar situations.

In summary then, this study sort to reveal the values underlying the reasons for the five teachers’ first noticing and then responding at key points in lessons that were designed to teach the mathematics of polygons. In this chapter ‘key point’ refers to both routine and non-routine situations, those that might have been expected by the teacher and those that were unexpected (see Bishop 2008b; Rowland et al. 2015). Content analysis was adopted as the data analysis procedure for the study (Merriam 2009). We interpreted how the teacher responded to these occurrences by interviewing the teacher as we both watched video recordings of each lesson. We then made a determination as to what values lay underneath her/his decision while responding or not responding. An example of the data analysis is summarized in Fig. 15.1.

Fig. 15.1
figure 1

Analysis process from attending to value

Full size image

After repeated analyses by the researchers a consensus emerged as to various categories to which the teachers’ values could be assigned. An 84.7% consensus rate among the researchers was obtained for this process (Miles and Huberman 1994). The following section outlines in more detail the results that were obtained from this process.

15.3 Teacher Values

This section discusses the underlying values that were influencing teachers’ noticing and their decision making at the key points of lesson, and identifies the categories that subsequently emerged from this analysis. Some sample situations are presented.

T5: How do we express the situation herein? (The sum of two inner angles is equal to the outer non-adjacent angle)

Student: The sum of the two inner angles equals the outer angle that has the non-shared edge.

T5: Which angle?

Student: The angle not included in the calculations, separate from what’s been given.

In this situation, the teacher T5 probes the student’s understanding of angles associated with polygons. This key point was examined with T5 in an interview with the video recording available. The point of the interview was to try and understand how he had interpreted the situation and the implicit values underlying this process. The teacher commented:

T5: […] I want to know all students’ opinions whether correct or incorrect. I want to offer the students that opportunity. Additionally, I want to let them express themselves accurately. The student said “edge” and “length” [at an earlier point] but not “vertice.” Angles do not have length. Having them try to find the true answer is necessary for all students, even if it is inaccurate in the moment. This will stay in their mind. In other words, to ensure most of the students participate… They express things one by one, one mentions angle while another says edge, whereas they must be expressed as a whole, clearly and accurately.

T5 was trying to create a classroom atmosphere where students could express themselves in an open-minded fashion, which is a way to create a democratic classroom setting, the first of the values categories we noted (see Fig. 15.2 later). Within this democratic setting, various values can be found. One is freedom of expression and another is equality, which in this context relates to all students having the same opportunities and rights to contribute to the ongoing class discussion or in other words a sense of fairness in the students’ in-class opportunities.

Another point in T5’s expressions is that of using mathematical language. Using mathematical language can be considered a prerequisite for improving mathematical communication skills, including the types of oral and written communication between students with their teachers, as well as among each other. Bishop (1991, pp. 69–72) noted the importance of mathematical language with all its variety: the use of mathematical symbols and not just words; how to express results in an appropriate manner at the conclusion of a problem solving process; and how students should be encouraged to create and utilize models and diagrams. In this study the use of mathematical language based on the characteristics of the concept of polygons was important.

T5’s statement also draws attention to the valuing of rigorous. In this instance the teacher was valuing rigorous in verbal expressions, an aspect of the more general notion of mathematical language. Mathematical communication skills, both verbal and written, necessitate individuals to be able to express themselves openly and to use mathematical language accurately and effectively (NCTM 2000). Based on this necessity, students’ skills at being able to make mathematical definitions with clear, open, and accurate expressions, at explaining operations or solutions, and at expressing their opinions all give an indication of rigor.

Retention stands out as a value underlying teacher decision making in the classroom, and is at times linked to a teacher’s focus on achievement. Simpson and Weiner (1989) define retention as the ability to remember things. In this chapter, the definition has been adopted. When the T5 says in the above excerpt, “This will stay in their mind” is a clear indicator of T5’s emphasizing knowledge retention.

By keeping in mind that mathematical knowledge is cumulative, others have noted that generalizations are the most visible components of mathematical thinking being reflected in classroom practices (Bishop 1991, pp. 72–75). Various formulas in the concept and application of polygons have an important role in terms of the number of learning outcomes in the Turkish national mathematics curriculum. T5 is clearly dealing with generalizations when the comment is made that “Angles do not have length”.

Although not demonstrated by the written text, the manner in which T5 taught in the classroom and his fervor, which was evident in the interview, also showed an important relationship between conviction, conceptual understanding, and mathematical communication. Investigating the accuracy of mathematical knowledge and being convincing are both important in the mathematics learning process. In addition, teachers have to be convinced of students’ answers and solutions. Moreover, students’ beliefs in a mathematical expression, representation, or modeling are also necessary for learning. Therefore, teachers utilize mathematical process skills and technology to convince students. Teachers’ focus on convincing students of the validity and accuracy of a generalization based on rational argumentation, is shown in another excerpt from T5:

T5: […] So I did it, but why did I do it? Student should be able to answer its reason. So I want to protect from them rote memorization. There is no selfishness here. No dictation for what I say! Everything is for the students.

The emphasis here is on persuading, or a convincing value, which stems from the nature of mathematics. This situation is an important finding since T5 was teaching in a multiple-choice exam-oriented school culture.

Another salient values category that emerged in our analysis was esoteric. At one identified key point during a lesson, T4 was saying:

T4: I will give formulas based on \( n \)-numbered polygons for the number of a regular \( n \)-edge polygon and the measurements of its interior edges. The formula will give us a direct answer.

In discussing this with the researchers during the interview phase, T4 offered the following explanation:

T4: It is hard for students to comprehend [the formula]. Proving it is difficult for them at this age. According to the students’ levels, this will be more challenging. It is not easy to make proofs and provide reasons. It is longitudinal and full of various symbols, which is why it is challenging. Student cannot comprehend it.

Esoteric can be defined as something understood or addressed by a particular group. In this instance the group who understands the knowledge of formulae is the teacher. T4 chooses to just give the formula in this instance since her decision is the students will not comprehend how it is derived. Others may wonder as to whether this decision was a ‘good’ decision by T4, but the key point was observed during the lesson, and later the explanation of why that decision was made was given by T4 in the interview. It seems that esoteric is an appropriate term to use for this value.

Teachers need to take students’ pre-knowledge into consideration when deciding to give feedback to students’ stimuli, when using repetition in their practices, and when choosing problems and exercises, or in short, when designing the course. Moreover, teachers have been found to take into consideration the relevance of concepts in knowledge construction. This situation, a natural outcome from the nature of mathematics, has been found effective in teachers’ decision making as a result of the teacher’s focus on achievement. The following excerpt from T1 is an example of this:

T1: After parallelogram concept, equilateral quadrangle comes next and I wanted to show the differences between them by drawing side by side. For the rest square rectangle, parallelogram and equilateral quadrangle are confused with each other. […] Their readiness level might not be suitable for it. It will be acquired in time, they have just learnt it […].

Teachers’ problem-solving strategies, such as accuracy and consistency in solving problems, and adhering faithfully to the lesson processes embedded in the plan designed by the teacher, includes controlling the class. In this process, one can say that teachers are focused on the concept, the lesson plan, and time, or in short the product and result. The following dialogue can be given as an example of considering control in another dimension:

T1 draws various polygons.

Student A: What is the number of diagonals for a twenty-sided polygon?

Student B: Number of diagonals drawn from one edge is 9.

T1: (Silent. No response: Without feedback or confirmation, the teacher goes on drawing).

This interaction shows how the teacher used their silence to help students focus on the key conceptual point; the underlying reason was revealed after the interview. In this case, the fact that the teacher has emphasized freedom of expression alongside control is worth noting. Why control and freedom of expression were analyzed under different categories in our study will be discussed in the next section of this chapter.

The value of judgment, which emphasizes the teacher’s class authority, is similar to control, but there are also differences. Judgment includes a teacher questioning students’ solutions, answers, opinions, and reasoning, as well as a teacher evaluating their accuracy. While these processes may be desirable for effective learning, what is implied here is that teachers prioritize their own ideas and solution strategies and exercises a judicial provision for which students’ provide feedback. T5’s general opinions about the in-class role of the teacher showed that he exercised judgment. T5’s statement is an example of this meaning:

T5: […] The teacher is the leading actor with an active position, and the students are like the audience, but, I believe they can be more successful if we can save students from the role of audience, include them in the play, and give them a role in it.

This has been interpreted as the teacher strongly wanting to do something such as deciding to teach a concept, or solving a problem, but not by being the sole player in the drama and the students relegated to just listening. In other words, the teacher perceived that their decisive focus on doing something quite different and bringing the students into the drama as players, albeit with different roles to his as the teacher, shows the exercising of judgment and of power to some extent. Dede (2013) placed authority in two categories: absolutist and semi-absolutist. What emerged from this study was the teacher’s presence as an authority resembling semi-absolutism, situations where students are included in the mathematical process and interestingly direct the teacher’s behavior to a certain extent. T5 is the participant who frequently reflected on this value and clearly expressed having adopted this value in the interviews.

During the interview with T1, she noted “Ezgi (student) knows this but because she made a calculation mistake, she reached the wrong conclusion. We must tell the students that they need to be very careful.” This suggests that for T1, motivation and self-confidence are important in the cognitive dimension. But T1 also did not neglect the affective dimension. During a lesson T1 encouraged a student with “You can do it Mustafa (student)!”. Motivation plays an essential role for students’ academic achievement in terms of the choice of activities made by the teacher, but also the level of effort, persistence, and emotional reactions displayed by the students. The latter are clearly privileged by the teacher with words of encouragement. Motivation is defined in the literature as “an intrinsic energy or mental power” (Sternberg and Williams 2002, p. 345). Before introducing self-efficacy as a key factor in social cognitive theory, Bandura (1997) had dealt with human motivation regarding outcome expectations. As a value, motivation impacts on teachers’ decisions to privilege freedom of expression and equality, and is expressed by using supportive gestures, and giving verbal feedback to students regarding their ideas or thoughts.

Self-confidence is the judgment where an individual feels one’s self to be valuable (Bandura 1997, p. 11). Stipek et al. (1998) stated that, while the teacher’s objective is for students to understand and learn concepts using motivation, motivation inspires in a way that will raise students’ willingness to solve a problem and increase positive ambitions through self-confidence.

Mathematical reasoning plays a key role as a means in individuals’ communication and connection processes for mathematical learning and to be able to use what they learn in daily life. Teachers’ lesson designs that aim to develop students’ skills of reasoning, expressing and defending their opinions, interpret data obtained from experience, and attempts at making predictions, are all outcomes of reasoning. The situations that have been mentioned, which Bishop (1991) categorized as rationalism, have been addressed as mathematical reasoning in this study’s findings.

An individual’s value system plays a crucial role in one’s preferences or choices of which value to privilege in the moment of decision in the classroom (Bishop et al. 2003, pp. 721–725). This notion of choosing between values can be described as a teacher’s flexibility. Flexibility is defined as the ability to change to suit new conditions or situations (Simpson and Weiner 1989). It also indicates someone who can change their decisions or thoughts easily according to a situation. Teachers do make changes to their lesson plans during the flow of a lesson by taking student expectations, efficiency, or technological variables into consideration. Often they are able to change course easily when meeting unexpected situations by keeping alternative course plans in mind.

Efficiency, an indicator of flexibility, is defined in the dictionary as “a good use of time and energy” (Simpson and Weiner 1989). In this context efficiency emphasizes the designing of activities for a lesson, preparing whole lesson plans, and preparing for situations where more goals are reached in a shorter time by keeping possible alternative instructional variables in mind. Flexibility also has an element of trying to foresee and considering a variety of students’ expectations. This then covers both changes during unexpected situations in classroom practice, as well as pre-planning lessons by considering students’ affective, cognitive, and psychomotor statuses. So a teacher showing flexibility would be thinking about student expectations and wishes, considering a range of materials to use and carefully making the problem selection including connecting a concept to daily life, and finding out about students’ pre-knowledge of the concepts.

15.4 Discussion, Implications and Conclusion

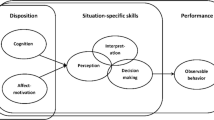
Based on this study’s findings, we may state that teacher noticing can be added as a new variable to Bishop and Whitfield’s (1972, p. 6) decision-making framework. The values underlying teacher noticing, and discussed in the previous section, are given in Fig. 15.2.

Fig. 15.2
figure 2

Teacher values underlying teacher noticing

Full size image

The teacher values that underlie noticing have been grouped under three categories: advanced mathematical process, democracy, and achievement. These values are of course influenced by the education and examination system in Turkey and reflect the classroom and school culture. Although we only studied with elementary mathematics teachers, this model can possibly shed light on future studies in order to provide a framework for noticing, values, and the relationship between them, at all levels of school education.

As stated in the mathematics school curriculum and various mathematics education institutions/organizations in various countries (see NCTM 2000; OECD 2013; Taiwan Ministry of Education 2013; Turkish Ministry of National Education [MEB] 2017), mathematical communication is a mathematical process skill that makes mathematical thinking visible in the processes of mathematical comprehension. Utilizing mathematical symbols, terms, and mathematical opinions accurately and effectively and interpreting their accuracy and meaning can be mentioned is an important aspect of the development of mathematical communication skills.

The indicators of the valuing of rigorous, mathematical language, and convince value lead to the mathematical communication’s sub-category of advanced mathematical processes. When considering the skills of making connections and communication, the interactions between these becomes important. Taking advantage of reasoning skills is necessary for being able to make mathematical connections, as well as for connecting pre-knowledge to mathematical reasoning. A similar situation also occurs for mathematical communication. While designing a setting for discussion occurs as a communication value in the literature (Seah et al. 2014), this study considers it as an advanced mathematical process as this situation creates a setting for reasoning skills. Generalization is also another sub-category fitting under advanced mathematical thinking because in this study it has a dimension that focuses on concepts.

This study has given emphasis to the role of equality in doing/learning mathematics (Seah et al. 2001). Little difference exists between democracy and openness. Openness provides students with a democratic way of expressing their ideas in class (Bishop 1991, pp. 75–77). We have interpreted democracy as a value that emphasizes the equality of opportunities in education. Thus democracy was demonstrated in this study when teachers attempted to reach all students in their classroom. A sub-category of esoteric was included under this theme. In this study, when the teachers seemed to be following aims that allowed students freedom to express themselves openly, it seemed they were giving each student a right within a democratic environment. Freedom of expression has been taken as an indicator of flexibility in the literature (Dede 2013). Within this study teachers were observed to pay attention to students’ needs and academic achievement. As such, flexibility is the reflection of achievement in practice. In short, freedom of expression is a sub-category of democracy while flexibility is a sub-category of achievement. Similarly, efficiency focuses on achievement, which categorically differs from studies in the literature.

Flexibility and authority are quite similar to Dede’s (2013) categories. The national transition system of the secondary education examination in Turkey has an impact for this pair of values in this study. School culture noticeably impacted on teachers’ noticing in some schools. For example, teacher T4 who worked in an examination-focused school paid attention to this aspect of the school culture when to implementing some of her decisions. But T1, who worked in a student-focused school, reflected far more flexibility in the way she taught in her classroom by being able to give more attention importantly to student feedback, and the level of their engagement. The full impact of the school culture is an issue that should be examined in future studies.

Teachers were found to adopt the values of retention and readiness because they give importance to student achievement. The indicators of student-focused readiness have been categorized as pre-knowledge, relevance to concepts, and attracting student interest. In addition, motivation and self-confidence have been found as other interesting sub-categories. Even though value categorizations could be obtained in the affective dimension, the data has indicated that teachers focus on process and achievement in the cognitive dimension.