Keywords

1 Introduction

In this short study, we retrieve and discuss an analytical solution for the electric field response generated by a nonconducting ellipsoid (prolate spheroid) in a homogeneous conducting fluid subject to an external primary electric field. We assume that the primary field can have any angle of incidence with respect to the longer axis of the ellipsoid. We assume that the ellipsoid has a zero (a nonconducting cell membrane) conductivity.

In the main text, we will utilize the well-known analogy between the electrostatics of dielectrics and DC conduction [1,2,3]. This analogy means that the basic equations and the corresponding solutions become identical when the ratio(s) of dielectric constants will coincide with the ratio(s) of conductivities. Since the solution of the present problem for dielectric materials does exist [1], its conversion to the conducting case is rather straightforward, but it requires extra steps for computing the induced charge density at the interface.

Here we also note that such an analogy is not the only one: one might consider a relevant fluid dynamics analogy as well. For example, the solution for a potential flow of an ideal incompressible fluid around a sphere with radius R [4] yields the expression for the hydrodynamic potential in the following form (the flow direction is along the x-axis):

$$ {\varphi}_v=-{v}_{0x}r\cos \theta +\frac{B\cos \theta }{r^2} $$
(1)

An unknown coefficient B is found from the condition\( \frac{\partial {\varphi}_v}{\partial r}=0 \), which allows us to write the following expression for the potential:

$$ {\varphi}_v=-{v}_{0x}r\cos \theta -\frac{v_{0x}{R}^3\cos \theta }{2{r}^2} $$
(2)

Simultaneously, the tangential velocity at the sphere surface is given by

$$ {v}_{\tau }=\frac{1}{r}\operatorname{}\frac{\partial {\varphi}_v}{\partial \theta }{\left|{}_{r=R}={v}_{0x}\sin \theta +\operatorname{}\frac{v_{0x}{R}^3\sin \theta }{2{r}^3}\right|}_{r=R}=\frac{3{v}_{0x}\sin \theta }{2} $$
(3)

This solution is equivalent to the steady electric current solution for a nonconducting sphere in a conducting fluid. In particular, the electric field inside the sphere is given by (cf. [3]):

$$ {\overrightarrow{E}}_i=\frac{3}{2}{\overrightarrow{E}}_0 $$
(4)

where \( {\overrightarrow{E}}_0 \) is the primary electric field. On the other hand, for a dielectric sphere with permittivity ε in a dielectric medium with permittivity ε, the corresponding solution for the field inside has the following form [1,2,3]:

$$ {\overrightarrow{E}}_i=\frac{3{\varepsilon}^{(e)}}{2{\varepsilon}^{(e)}+{\varepsilon}^{(i)}}{\overrightarrow{E}}_0 $$
(5)

Two solutions (4) and (5) indeed coincide when

$$ \raisebox{1ex}{${\varepsilon}^{(i)}$}\!\left/ \!\raisebox{-1ex}{${\varepsilon}^{(e)}$}\right.=0 $$
(6)

2 Materials and Methods

In Ref. [1], the problem is solved for the electric field of an ellipsoid with half axes a, b, c, with permittivity ε(i) in a dielectric medium with permittivity ε(e) when a primary or external field \( {\overrightarrow{E}}_0 \) is applied. This solution will be repeated here; the final result implies that the permittivities should be replaced by conductivities.

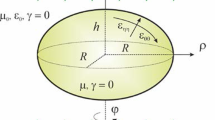
We consider an ellipsoid in the form of a prolate spheroid (a > b = c). The coordinate system (see Fig. 1) is chosen as follows: the z-axis is directed along a so that the angle between the z-axis and the vector \( {\overrightarrow{E}}_0 \) is less than 90 degrees. The x-axis is located in a plane defined by the z-axis and vector \( {\overrightarrow{E}}_0 \). The y-axis is then chosen to construct the right-handed Cartesian system.

Fig. 1
figure 1

Ellipsoid along with the coordinate system used

Full size image

In this coordinate system, the depolarization tensor [1] becomes diagonal with the following components:

$$ {\displaystyle \begin{array}{c}{n}_{zz}=\frac{abc}{2}\underset{0}{\overset{\infty }{\int }}\frac{ds}{\left(s+{a}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}},\\ {}{n}_{yy}=\frac{abc}{2}\underset{0}{\overset{\infty }{\int }}\frac{ds}{\left(s+{b}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}},\\ {}{n}_{xx}=\frac{abc}{2}\underset{0}{\overset{\infty }{\int }}\frac{ds}{\left(s+{c}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}}\end{array}} $$
(7)

For the prolate spheroid, simplifications are made in the following form [1]:

$$ {\displaystyle \begin{array}{c}{n}_{zz}=\frac{1-{e}^2}{e^3}\left(\mathrm{Arth}e-e\right),\\ {}{n}_{yy}={n}_{xx}=\frac{1}{2}\left(1-{n}_{zz}\right)\end{array}} $$
(8)

where\( e=\sqrt{1-\raisebox{1ex}{${b}^2$}\!\left/ \!\raisebox{-1ex}{${a}^2$}\right.} \) is the ellipsoid eccentricity.

3 Results for the Potential and the Electric Field

Accordingly, the electric potential everywhere in space and the electric field inside the ellipsoid have the following form [1] (the ratio of dielectric permittivities in the equations given below must be set to zero to obtain the result for the nonconducting ellipsoid in the conducting fluid):

$$ {\displaystyle \begin{array}{c}{\varphi}^{(i)}=-\left\{\frac{E_{0x}x}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{xx}}+\frac{E_{0y}y}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{yy}}+\frac{E_{0z}z}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{zz}}\right\}\\ {}{\varphi}^{(e)}=\frac{-{E}_{0x}x\left(1+\frac{abc}{2}\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right)\underset{0}{\overset{\xi }{\int }}\frac{ds}{\left(s+{c}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}}\right)}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{xx}}+\\ {}+\frac{-{E}_{0y}y\left(1+\frac{abc}{2}\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right)\underset{0}{\overset{\xi }{\int }}\frac{ds}{\left(s+{b}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}}\right)}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{yy}}+\\ {}+\frac{-{E}_{0z}z\left(1+\frac{abc}{2}\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right)\underset{0}{\overset{\xi }{\int }}\frac{ds}{\left(s+{a}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}}\right)}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{zz}}\\ {}{E}_x=\frac{E_{0x}}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{xx}},{E}_y=\frac{E_{0y}}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{yy}},{E}_z=\frac{E_{0z}}{1+\left(\frac{\varepsilon^{(i)}}{\varepsilon^{(e)}}-1\right){n}_{zz}}\end{array}} $$
(9)

Here, ξ is the ellipsoidal coordinate that is a constant for all ellipsoids being confocal with the given one. For the prolate spheroid, one has \( \xi =\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$\sqrt{a^2-{b}^2}$}\right. \).

Now, we express the electric field in the following form (ϑ is the elevation angle):

$$ {\displaystyle \begin{array}{c}{E}_{0z}={E}_0\cos \vartheta, \\ {}{E}_{0x}={E}_0\sin \vartheta, \\ {}{E}_{0y}=0\end{array}} $$
(10)

After substitution of Eq. (10) into Eq. (9) and using Eq. (6), we obtain

$$ {\displaystyle \begin{array}{c}{\varphi}^{(i)}=-\left\{\frac{E_0x\sin \vartheta }{1-{n}_{xx}}+\frac{E_0z\cos \vartheta }{1-{n}_{zz}}\right\}\\ {}{\varphi}^{(e)}=\frac{-{E}_0x\sin \vartheta \left(1-\frac{abc}{2}\underset{0}{\overset{\xi }{\int }}\frac{ds}{\left(s+{c}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}}\right)}{1-{n}_{xx}}+\\ {}+\frac{-{E}_0z\cos \vartheta \left(1-\frac{abc}{2}\underset{0}{\overset{\xi }{\int }}\frac{ds}{\left(s+{a}^2\right)\sqrt{\left(s+{a}^2\right)\left(s+{b}^2\right)\left(s+{c}^2\right)}}\right)}{1-{n}_{zz}}\\ {}{E}_z=\frac{E_0\cos \vartheta }{1-{n}_{xx}},{E}_x=\frac{E_0\sin \vartheta }{1-{n}_{yy}},{E}_y=0\end{array}} $$
(11)

It follows from Eqs. (8) and (11) that the electric field within the ellipsoid is not parallel to the external primary electric field.

4 Results for the Surface Charge Density

For the prolate spheroid, the ellipsoidal coordinates are reduced to the prolate spheroidal coordinates ξ, η, and ψ. They are converted to Cartesian coordinates using the following expressions [5]:

$$ {\displaystyle \begin{array}{c}x=\frac{d}{2}\sqrt{\left({\xi}^2-1\right)\left(1-{\eta}^2\right)}\cos \psi \\ {}y=\frac{d}{2}\sqrt{\left({\xi}^2-1\right)\left(1-{\eta}^2\right)}\sin \psi \\ {}z=\frac{d}{2}\xi \eta \end{array}} $$
(12)

where d is the spacing between two focal points of the ellipsoid, which is equal to \( 2\sqrt{a^2-{b}^2} \).

In order to find the surface charge distribution, one needs to find the normal derivative of the electric potential at the surface. Since the outer normal derivative of the potential is equal to zero, only the inner derivative is needed.

It is convenient to compute the inner derivative using coordinates ξ, η, and ψ. Then,

$$ {\left.\frac{d\varphi}{d n}\right|}_{surf}=-\frac{1}{H_{\xi }}{\left.\frac{\partial {\varphi}^{(i)}}{\partial \xi}\right|}_{surf} $$
(13)

where Hξ is the corresponding Lamé coefficient. We find this coefficient in the following form:

$$ {\displaystyle \begin{array}{c}{H}_{\xi }=\sqrt{{\left(\frac{\partial x}{\partial \xi}\right)}^2+{\left(\frac{\partial y}{\partial \xi}\right)}^2+{\left(\frac{\partial z}{\partial \xi}\right)}^2}=\\ {}=\frac{d}{2}\sqrt{\frac{1-{\eta}^2}{\xi^2-1}{\xi}^2+{\eta}^2}=\\ {}=\frac{d}{2}\sqrt{\frac{\xi^2-{\eta}^2}{\xi^2-1}}\end{array}} $$
(14)

Here,  ξ0 is the value of ξ on the ellipsoid surface. Following the definition of the prolate spheroid, one obtains \( \xi =\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$\sqrt{a^2-{b}^2}$}\right. \) and\( \eta =\raisebox{1ex}{$z$}\!\left/ \!\raisebox{-1ex}{$a$}\right. \). Then,

$$ {\displaystyle \begin{array}{c}\frac{-1}{H_{\xi }}\operatorname{}\frac{\partial {\varphi}^{(i)}}{\partial \xi }{\left|{}_{\xi ={\xi}_0}=\operatorname{}\left(\frac{E_{0x}}{1-{n}_{xx}}\frac{1}{H_{\xi }}\frac{\partial x}{\partial \xi }+\frac{E_{0z}}{1-{n}_{zz}}\frac{1}{H_{\xi }}\frac{\partial z}{\partial \xi}\right)\right|}_{\xi ={\xi}_0}=\\ {}{\left.=\operatorname{}\left(\frac{E_{0x}}{1-{n}_{xx}}\frac{\xi \sqrt{1-{\eta}^2}}{\sqrt{\xi^2-{\eta}^2}}+\frac{E_{0z}}{1-{n}_{zz}}\frac{\eta \sqrt{\xi^2-1}}{\sqrt{\xi^2-{\eta}^2}}\right)\right|}_{\xi ={\xi}_0}=\\ {}=\frac{E_0\sin \vartheta }{1-{n}_{xx}}\frac{a\sqrt{a^2-{z}^2}}{\sqrt{a^4+{z}^2{b}^2-{z}^2{a}^2}}+\\ {}+\frac{E_0\cos \vartheta }{1-{n}_{zz}}\frac{bz\sqrt{a^2-{b}^2}}{a\sqrt{a^4+{z}^2{b}^2-{z}^2{a}^2}}\end{array}} $$
(15)

It follows from here that the surface charge density as a function of z and ϑ (the elevation angle) is obtained in the following form:

$$ \sigma ={\varepsilon}_0\left(\frac{E_0\sin \vartheta }{1-{n}_{xx}}\frac{a\sqrt{a^2-{z}^2}}{\sqrt{a^4+{z}^2{b}^2-{z}^2{a}^2}}+\frac{E_0\cos \vartheta }{1-{n}_{zz}}\frac{bz\sqrt{a^2-{b}^2}}{a\sqrt{a^4+{z}^2{b}^2-{z}^2{a}^2}}\right) $$
(16)

which completes the solution. This is the surface charge density residing on the surface of the nonconducting ellipsoid in the conducting fluid.

Consider the primary external field that has only one component parallel to the z-axis, and consider b that tends to zero in Eq. (16). Then, the surface charge density is only different from zero at the tips of the ellipsoid, that is, at z → a or z →  − a. This is a physically meaningful result, which is observed for a thin cylinder in a coaxial external field. Here, the opposite charges are concentrated close to the cylinder tips only.