Abstract
In this chapter, we classify orders over a Dedekind domain in terms of ternary quadratic forms; this is the integral analogue to what we did over fields in Chapter.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we classify orders over a Dedekind domain in terms of ternary quadratic forms; this is the integral analogue to what we did over fields in Chapter 5.
1 \(\triangleright \) Quaternion orders and ternary quadratic forms
We begin our project by returning to the classification over fields: in Chapters 5 and 6 (see Main Theorem 5.2.5 and Theorem 6.4.7), we saw that quaternion algebras over a field F are classified by similarity classes of nondegenerate ternary quadratic forms over F. We will soon see that, suitably interpreted, quaternion orders are classified by similarity classes of integral ternary quadratic forms.
Let R be a PID with field of fractions \(F :={{\,\mathrm{Frac}\,}}R\). We recall that the similarity class of a ternary quadratic form \(Q:R^3 \rightarrow R\) is determined by the natural change of variable by \({{\,\mathrm{GL}\,}}_3(R)\) on the domain and by rescaling by \(R^\times \) on the codomain, and that Q is nondegenerate if and only if \({{\,\mathrm{disc}\,}}(Q) \ne 0\).
MainTheorem 22.1.1
Let R be a PID. Then there is a (reduced) discriminant-preserving bijection

One beautiful feature of the bijection in Main Theorem 22.1.1 is that it can be given explicitly. Let \(Q:R^3 \rightarrow R\) be a ternary quadratic form with nonzero discriminant, and let \(e_1,e_2,e_3\) be the standard basis for \(R^3\). Then the extension to F given by \(Q_F :F^3 \rightarrow F\) is a ternary quadratic space whose even Clifford algebra (section 5.3) is a quaternion algebra B. Moreover, the R-lattice \(\mathcal {O}\) with basis
is closed under multiplication and so defines an R-order in B. Explicitly, if the quadratic form Q is given by
with (half-)discriminant
then we associate the quaternion R-order \(\mathcal {O} \subseteq B\) with basis 1, i, j, k and multiplication laws
The other multiplication rules are determined by the skew commutativity relations (4.2.16) coming from the standard involution; one beautiful consequence is the equality
The R-order \(\mathcal {O}\) defined by (22.1.2) is called the even Clifford algebra \({{\,\mathrm{Clf}\,}}^0(Q)\) of Q—its algebra structure is obtained by restriction from the even Clifford algebra of \(Q_F\)—and the reduced discriminant of \(\mathcal {O}\) is \({{\,\mathrm{discrd}\,}}(\mathcal {O})=(N)\). At least one of the minors
of the Gram matrix of Q in the standard basis is nonzero since Q is nondegenerate, so for example if \(w^2-4ab \ne 0\) and \({{\,\mathrm{char}\,}}F \ne 2\), completing the square we find
It is straightforward to show that the isomorphism class of \(\mathcal {O}\) is determined by the similarity class of Q (using the even Clifford algebra construction). Therefore, the proof of Main Theorem 22.1.1 amounts to verifying that every quaternion order arises this way up to isomorphism, and that isomorphic quaternion algebras yield similar ternary quadratic forms.
To this end, we define an inverse to the even Clifford algebra construction. Let \(\mathcal {O} \subset B\) be a quaternion order over R with reduced discriminant \({{\,\mathrm{discrd}\,}}(\mathcal {O})\) generated by \(N \in R\) nonzero. Recalling 15.6, let
be the trace zero elements in the dual of \(\mathcal {O}\) with respect to the reduced trace pairing. Then we associate the ternary quadratic form
explicitly, we have
where 1, i, j, k is an R-basis of \(\mathcal {O}\), so
It is then a bit of beautiful algebra to verify that \(N{{\,\mathrm{nrd}\,}}^\sharp \) has discriminant N and that (22.1.3) furnishes an inverse to the even Clifford map.
Just as in the case of fields, the translation from quaternion orders to ternary quadratic forms makes the classification problem easier: we replace the potentially complicated notion of finding a lattice closed under multiplication in a quaternion algebra with the simpler notion of choosing coefficients of a quadratic form.
To conclude this introduction, we state a more general bijective result stated in terms of lattices. Let R be a Dedekind domain with \(F={{\,\mathrm{Frac}\,}}R\), let \(Q_F :V \rightarrow F\) be a nondegenerate ternary quadratic form. If \(M \subseteq V\) is an R-lattice, and \(\mathfrak l \subseteq F\) is a fractional ideal of R such that \(Q(M) \subseteq \mathfrak l \), then we have an induced quadratic form \(Q:M \rightarrow \mathfrak l \); we call such a form a quadratic module in V. Given a fractional ideal \(\mathfrak a \subseteq F\), the twist by \(\mathfrak a \) of the quadratic module \(Q :M \rightarrow \mathfrak l \) in V is the quadratic module \(\mathfrak a M \rightarrow \mathfrak a ^2\mathfrak l \). A twisted similarity between quadratic modules \(Q,Q'\) in V is a similarity between Q and a twist of \(Q'\). From these notions in hand, we have the following theorem (a special case of Main Theorem 22.5.7).
Theorem 22.1.5
Let R be a Dedekind domain, and let \(Q_F :V \rightarrow F\) be a nondegenerate ternary quadratic form. Let \(B :={{\,\mathrm{Clf}\,}}^0 V\). Then the even Clifford map yields a discriminant-preserving bijection

that is functorial with respect to R.
By functorial with respect to R, we mean the same thing as in Corollary 5.2.6, but with respect to any homomorphism \(R \rightarrow S\) of Dedekind domains. In particular, the bijection in Theorem 22.1.5 is compatible with the bijections obtained over localizations of R, including the bijection over F between quaternion algebras and nondegenerate ternary quadratic forms previously obtained. In the language of quadratic forms (Definition 9.7.13), after some additional work (nailing down the difference between similarity and isometry), we conclude: if the ternary quadratic module Q corresponds to the quaternion order \(\mathcal {O}\), then there is a bijection
i.e. the type number of a quaternion order is the same as the class number of the corresponding ternary quadratic form.
Remark 22.1.7. If we restrict the correspondence to primitive modules \(Q:M \rightarrow \mathfrak l \) (i.e., \(Q(M)=\mathfrak l \)), then we need only remember the underlying lattice M, and on the right-hand side we obtain precisely the Gorenstein orders; these orders will be introduced in 24.1.1 and this correspondence is proven in section 24.2.
2 Even Clifford algebras
In this section, we construct the even Clifford algebra associated to a quadratic module: see Remark 22.2.14 below for further references. The reader who wants to skip over technicalities at first is encouraged to skip this section and accept 22.3.2 as a definition.
Let R be a noetherian domain with \(F={{\,\mathrm{Frac}\,}}R\). Let \(Q:M \rightarrow L\) be a quadratic module over R (see section 9.7), so that M is a projective R-module of finite rank and L is an invertible R-module (rank 1). Write  and \(M^{\otimes 0}=R\). (For further reference on tensor algebra, see Matsumura [Mat89, Appendix C] or Curtis–Reiner [CR81, §12].)
and \(M^{\otimes 0}=R\). (For further reference on tensor algebra, see Matsumura [Mat89, Appendix C] or Curtis–Reiner [CR81, §12].)
22.2.1
Let

Now \({{\,\mathrm{Ten}\,}}^0(M;L)\) has a natural tensor multiplication law (rearranging tensors), so \({{\,\mathrm{Ten}\,}}^0(M;L)\) is a graded R-algebra. Let \(I^0(Q)\) be the two-sided ideal of \({{\,\mathrm{Ten}\,}}^0(M;L)\) defined by

note that \(Q(x) \in L\) so \(g(Q(x)) \in R\). We define the even Clifford algebra of Q to be the quotient
Remark 22.2.4. We might try to define

unfortunately, \({{\,\mathrm{Ten}\,}}(M;L)\) does not have a natural tensor multiplication law, because there is no natural map  . But see 22.2.16 below for the odd part.
. But see 22.2.16 below for the odd part.
Example 22.2.5
Under the inclusion \(R \hookrightarrow F\), we have a natural identification
We conclude that the R-lattice in \({{\,\mathrm{Clf}\,}}^0(Q_F)\) defined by the image of \(R^3\) is closed under multiplication—something that may also be verified directly—and so \({{\,\mathrm{Clf}\,}}^0(Q)\) is an R-order in \({{\,\mathrm{Clf}\,}}^0(Q_F)\).
22.2.7
As in 5.3.7, for all \(x,y \in M\) and  , the calculation
, the calculation
holds in \({{\,\mathrm{Clf}\,}}^0(Q)\), where \(T(x,y)=Q(x+y)-Q(x)-Q(y) \in L\).
22.2.9
If \(M \simeq R^n\) is free with basis \(e_1,\dots ,e_n\) and \(L=Rg\) is free, then \({{\,\mathrm{Clf}\,}}^0(Q)\) is a free R-module with basis
as a consequence of 22.2.8, just as in the case over fields 5.3.9. In particular, by localizing, if M has rank n as an R-module, then \({{\,\mathrm{Clf}\,}}^0(Q)\) is projective of rank \(2^{n-1}\) as an R-module. We write elements of \({{\,\mathrm{Clf}\,}}^0(Q)\) without tensors, for brevity.
22.2.10
The reversal map defined on simple tensors
for \(x_i \in M\) and  , and extended R-linearly, is an R-linear involution.
, and extended R-linearly, is an R-linear involution.
Theorem 22.2.11
The association \(Q \mapsto {{\,\mathrm{Clf}\,}}^0(Q)\) is a functor from the category of quadratic R-modules under similarities to the category of projective R-algebras with involution under isomorphism. Moreover, this association is functorial with respect to R.
We call the association \(Q \mapsto {{\,\mathrm{Clf}\,}}^0(Q)\) in Theorem 22.2.11 the even Clifford functor.
22.2.12
The statement “functorial with respect to R” means the following: given a ring homomorphism \(R \rightarrow S\), there is a natural transformation between the even Clifford functors over R and S. Explicitly, given a ring homomorphism \(R \rightarrow S\) and a quadratic module \(Q:M \rightarrow L\), we have a quadratic module \(Q_S :M \otimes _R S \rightarrow L \otimes _R S\), and \({{\,\mathrm{Clf}\,}}^0(Q) \otimes _R S \cong {{\,\mathrm{Clf}\,}}^0(Q_S)\) in a way compatible with morphisms in each category. In particular, this recovers the identification in Example 22.2.5 arising from \(R \hookrightarrow F\).
Remark 22.2.13. The association \(Q \mapsto {{\,\mathrm{Clf}\,}}(Q)\) of the full Clifford algebra is a functor from the category of quadratic R-modules under isometries to the category of R-algebras with involution under isomorphism that is also functorial with respect to R. See Bischel–Knus [BK94].
Proof of Theorem 22.2.11
The construction in 22.2.1 yields an R-algebra that is projective as an R-module; we need to define an association on the level of morphisms. Let \(Q' :M' \rightarrow L'\) be a quadratic module and (f, h) be a similarity with  and
and  satisfying \(Q'(f(x))=h(Q(x))\). We mimic the proof of Lemma 5.3.21. We define a map via
satisfying \(Q'(f(x))=h(Q(x))\). We mimic the proof of Lemma 5.3.21. We define a map via
for \(x,y \in M\) and  and extending multiplicatively, where
and extending multiplicatively, where
is the pullback under \(h^{-1}\). Then
and since
we conclude that \(I^0(Q)\) is mapped to \(I^0(Q')\). Repeating with the inverse similarity \((f^{-1},h^{-1})\), and composing to get the identity, we conclude that the induced map \({{\,\mathrm{Clf}\,}}^0(Q) \rightarrow {{\,\mathrm{Clf}\,}}^0(Q')\) is an R-algebra isomorphism.
Functoriality in the sense of 22.2.12 then follows directly. \(\square \)
Remark 22.2.14. In his thesis, Bichsel [Bic85] constructed an even Clifford algebra of a line bundle-valued quadratic form on an affine scheme using faithfully flat descent. A related and more general construction was given by Bischel–Knus [BK94]. Several other constructions are available: see Auel [Auel2011, §1.8] and the references therein.
The direct tensorial construction given above is given for ternary quadratic modules by Voight [Voi2011a, (1.10)] and in general by Auel [Auel2011, §1.8] and with further detail in Auel [Auel2015, §1.2]; for a comparison of this direct construction with others, see Auel–Bernardara–Bolognesi [ABB2014, §1.5, Appendix A].
Remark 22.2.15. Allowing the quadratic forms to take values in a invertible module is essential for what follows and for many other purposes: for an overview, see the introduction to Auel [Auel2011].
22.2.16
Let

Then \({{\,\mathrm{Ten}\,}}^1(M;L)\) is a graded \({{\,\mathrm{Ten}\,}}^0(M;L)\)-bimodule under the natural tensor multiplication. Let \(I^1(Q)\) be the R-submodule of \({{\,\mathrm{Ten}\,}}^1(M;L)\) generated by the image of multiplication of \(I^0(Q)\) by M on the left and right: then \(I^1(Q)\) is the \({{\,\mathrm{Ten}\,}}^0(M;L)\)-bisubmodule generated by the set of elements of the form
with \(x,y \in M\) and  .
.
We define the odd Clifford bimodule as
Visibly, \({{\,\mathrm{Clf}\,}}^1(Q)\) is a bimodule for the even Clifford algebra \({{\,\mathrm{Clf}\,}}^0(Q)\).
22.2.17
When \(L=R\), we can combine the construction of the even Clifford algebra and its odd Clifford bimodule to construct a full Clifford algebra, just as in section 5.3 over a field: see Exercise 22.7. This direct tensorial construction does not extend in an obvious way when \(L \ne R\), as we would need to define a multiplication map  .
.
22.2.18
We will employ exterior calculus in what follows: this is a convenient method for keeping track of our module maps in a general setting. Let M be an R-module and let \(r \ge 1\). The r th exterior power of M (over R) is
where \(E_r\) is the R-module
We let \(\smash {{\textstyle {\bigwedge }}}^0 M=R\) (and \(\smash {{\textstyle {\bigwedge }}}^1 M = M\)). The image of \(x_1 \otimes \dots \otimes x_r \in M^{\otimes r}\) in \(\smash {{\textstyle {\bigwedge }}}^r M\) is written \(x_1 \wedge \dots \wedge x_r\). If M is projective of rank n over R, then \(\smash {{\textstyle {\bigwedge }}}^r M\) is projective of rank \(\left( {\begin{array}{c}n\\ r\end{array}}\right) \).
3 Even Clifford algebra of a ternary quadratic module
Now suppose that \(Q:M \rightarrow L\) is a ternary quadratic module, which is to say M has rank 3; in this section, we examine its even Clifford algebra \({{\,\mathrm{Clf}\,}}^0(Q)\). Recall that an R-order is projective if it is projective as an R-module. The main result of this section is as follows.
Theorem 22.3.1
Let R be a noetherian domain. Then the association \(Q \mapsto {{\,\mathrm{Clf}\,}}^0(Q)\) gives a functor from the category of
to the category of
In the previous section, we defined the even Clifford functor, whose codomain was the category of projective R-algebras; in this section, we show that the restriction to nondegenerate ternary quadratic modules lands in projective quaternion orders.
We begin with some explicit descriptions.
22.3.2
By 22.2.9, the even Clifford algebra \({{\,\mathrm{Clf}\,}}^0(Q)\) is an R-algebra that is projective of rank 4 as an R-module. Explicitly, as an R-module we have

where \(I^0(Q)\) is the R-submodule generated by elements of the form
for \(x \in M\) and  .
.
We now explicitly give the even Clifford algebra of a ternary quadratic module in the free case; this could also be taken as the definition when R is a PID and \(M=R^3\).
22.3.4
Let \(M=R^3\) with standard basis \(e_1,e_2,e_3\) be equipped with the quadratic form \(Q:M \rightarrow R\) defined by
with \(a,b,c,u,v,w \in R\). Then
By 22.2.9, we have
where
The reversal involution acts by
and similarly \(\overline{j}=v-j\) and \(\overline{k}=w-k\) by (22.2.8).
We then compute directly the multiplication table:
For example,
and
The remaining multiplication laws can be computed in the same way, or by using the reversal involution and (22.3.7): we compute
so \(kj=-vw+ai+wj+vk\). By symmetry, we find:
We note also the formulas
Example 22.3.10
It is clarifying to work out the diagonal case. Let \(B=({a,b} \mid {F})\) with \(a,b \in R\), and let
be the R-order generated by the standard generators, and let \(k=ij\). Then:
Example 22.3.12
Consider
so \((a,b,c,u,v,w)=(0,0,-1,0,0,1)\); then \({{\,\mathrm{disc}\,}}(Q)=-cw^2=1\). Then the even Clifford algebra \({{\,\mathrm{Clf}\,}}^0(Q)=R+Ri+Rj+Rk\) has multiplication table
We find an isomorphism of R-algebras

22.3.15
Returning to the free quadratic form 22.3.4, the group \({{\,\mathrm{GL}\,}}_3(R)\) acts naturally on M by change of basis, and this induces an action on \({{\,\mathrm{Clf}\,}}^0(Q)\) by R-algebra automorphism by functoriality. Explicitly, for \(\rho \in {{\,\mathrm{GL}\,}}_3(R)\), the action on the basis i, j, k is by the adjugate \({{\,\mathrm{adj}\,}}(\rho )\) of \(\rho \), the \(3 \times 3\) matrix whose entries are the \(2 \times 2\) minors of \(\rho \). The verification is requested in Exercise 22.2.
22.3.16
Let \(F={{\,\mathrm{Frac}\,}}R\). By base extension, we have a quadratic form \(Q_F :V \rightarrow F\) where \(V=M \otimes _R F\), and by functoriality 22.2.12 with respect to the inclusion \(R \hookrightarrow F\), we have an inclusion \({{\,\mathrm{Clf}\,}}^0(Q) \hookrightarrow {{\,\mathrm{Clf}\,}}^0(Q_F)\) realizing \({{\,\mathrm{Clf}\,}}^0(Q)\) as an R-order in the F-algebra \({{\,\mathrm{Clf}\,}}^0(Q_F)\).
Lemma 22.3.17
The reversal involution is a standard involution on \({{\,\mathrm{Clf}\,}}^0(Q_F)\).
Proof. To check that the involution is standard, we could appeal to Exercise 3.19, but we find it more illustrative to exhibit the involution on a universal element, yielding a rather beautiful formula. We choose a basis for V and work with the presentation for \({{\,\mathrm{Clf}\,}}^0(Q_F)\) as in 22.3.4.
Let \(\alpha =t+xi+yj+zij\) with \(t,x,y,z \in F\). Then \(\overline{\alpha }=2t+ux+vy+wz - \alpha \), and we find that
where
so that the reversal map \(\alpha \mapsto \tau (\alpha )-\alpha \) defines a standard involution.
Lemma 22.3.19
We have
Proof. The construction of the even Clifford algebra is functorial with respect to localization, and the statement itself is local, so we may suppose that \(M=R^3,L=R\) are free with the presentation for \(\mathcal {O}={{\,\mathrm{Clf}\,}}^0(Q)\) as in 22.3.4.
We refer to section 15.4 and Lemma 15.4.7: we compute
and \({{\,\mathrm{discrd}\,}}(\mathcal {O})=m(i,j,k)R\) as claimed.
Alternatively, we compute directly that
so \({{\,\mathrm{disc}\,}}(\mathcal {O}) = {{\,\mathrm{disc}\,}}(Q)^2 R\), and the result follows by taking square roots (as ideals).
Corollary 22.3.22
If Q is nondegenerate, then \({{\,\mathrm{Clf}\,}}^0(Q)\) is an R-order in the quaternion algebra \(B={{\,\mathrm{Clf}\,}}^0(Q_F)\).
Proof. The standard involution has discriminant \({{\,\mathrm{disc}\,}}({{\,\mathrm{nrd}\,}})={{\,\mathrm{disc}\,}}(\mathcal {O})^2={{\,\mathrm{disc}\,}}(Q_F) \ne 0\); the result then follows from the characterization of algebras with nondegenerate standard involution (Main Theorem 4.4.1 and Theorem 6.4.1).
Remark 22.3.23. Corollary 22.3.22 gives a characteristic independent proof of the fact that the even Clifford algebra of a nondegenerate ternary quadratic form over F is a quaternion algebra over F: we proved this in 5.3.23 and Exercise 6.10 (when \({{\,\mathrm{char}\,}}F=2\)).
Intermediate between the general abstract definition and the explicit description in the free case is the situation where the modules are completely decomposable, and we can work with a pseudobasis.
Example 22.3.24
Let R be a Dedekind domain. Then we can write
for fractional ideals \(\mathfrak a ,\mathfrak b ,\mathfrak c ,\mathfrak l \). Let \(V = M \otimes _R F \simeq F^3\) with basis \(e_1,e_2,e_3\), so then \(M \hookrightarrow V\) is a ternary R-lattice. Then we may take \(Q_F :V \rightarrow F\) to have the form 22.3.5, and \({{\,\mathrm{Clf}\,}}^0(Q_F)=B\) is a quaternion algebra with \(\mathcal {O} :={{\,\mathrm{Clf}\,}}^0(Q) \subseteq B\) an R-order.
Extending the description in 22.3.4, we find that
where i, j, k satisfy the multiplication table (22.3.7). We can verify directly that \(\mathcal {O}\) is closed under multiplication: for example, if \(\alpha \in \mathfrak b \mathfrak c \mathfrak l ^{-1}\) so \(\alpha i \in \mathcal {O}\), then
since \(Q(\mathfrak b e_2)=\mathfrak b ^2 Q(e_2) \subseteq \mathfrak l \) so \(b=Q(e_2) \in \mathfrak l \mathfrak b ^{-2}\) and therefore
Example 22.3.26
Let \(F=\mathbb Q (\sqrt{10})\) and \(R=\mathbb Z _F=\mathbb Q [\sqrt{10}]\) be the ring of integers. Then \(\mathfrak p =(3,4+\sqrt{10})\) is a prime ideal over 3 that is not principal.
Let \(Q:M=R^3 \rightarrow \mathfrak p \) be the quadratic module
We have \(\mathfrak p =Q(R^3)\). The even Clifford algebra is then
with the multiplication law
We have
and in particular \(\mathfrak p \not \mid {{\,\mathrm{discrd}\,}}(\mathcal {O})\), and
with \({{\,\mathrm{disc}\,}}B=(2+w)R\), so \({{\,\mathrm{Ram}\,}}B = \{(2,\sqrt{10}), \mathfrak p , \infty _1,\infty _2\}\) where \(\infty _1,\infty _2\) are the two real places of F.
4 Over a PID
In the previous two sections, we observed that the construction of the even Clifford algebra gives a functorial association from nondegenerate ternary quadratic modules to quaternion orders. In this section, we show that this functor gives a bijection on classes over a PID, following Gross–Lucianovic [GrLu2009, §4].
MainTheorem 22.4.1
Suppose that R is a PID. Then the association \(Q \mapsto {{\,\mathrm{Clf}\,}}^0(Q)\) induces a discriminant-preserving bijection

that is functorial with respect to R.
Remark 22.4.3. The bijection can also be rephrased in terms of the orbits of a group (following Gross–Lucianovic [GrLu2009]). The group \({{\,\mathrm{GL}\,}}_3(R)\) has a natural twisted action on quadratic forms by \((g Q)(x,y,z)=(\det g)(Q(g^{-1}(x,y,z)^{\textsf {t} }))\), i.e., the usual action with an extra scaling factor of \(\det g \in R^\times \). This is the natural action on the R-module  , or equivalently on the set of quadratic modules \(Q:R^3 \rightarrow \smash {{\textstyle {\bigwedge }}}^3 R^3\). Main Theorem 22.1.1 states that the nondegenerate orbits of this action are in functorial bijection with the set of isomorphism classes of quaternion orders over R.
, or equivalently on the set of quadratic modules \(Q:R^3 \rightarrow \smash {{\textstyle {\bigwedge }}}^3 R^3\). Main Theorem 22.1.1 states that the nondegenerate orbits of this action are in functorial bijection with the set of isomorphism classes of quaternion orders over R.
We prove this theorem in a few steps. Throughout this section, let R be a PID.
First, we prove that the map (22.4.2) is surjective, or equivalently that the even Clifford functor is essentially surjective from the category of nondegenerate ternary quadratic forms to the category of quaternion orders.
Proposition 22.4.4
Every quaternion R-order is isomorphic to the even Clifford algebra of a nondegenerate ternary quadratic form.
Proof. We work explicitly with the multiplication table, hoping to make it look like (22.3.7).
Let \(\mathcal {O}\) be a quaternion R-order. Since R is a PID, \(\mathcal {O}\) is free as an R-module. We need a slight upgrade from this, a technical result supplied by Exercise 22.1: in fact, \(\mathcal {O}\) has an R-basis containing 1.
So let 1, i, j, k be an R-basis for \(\mathcal {O}\). Since every element of \(\mathcal {O}\) is integral over R, satisfying its reduced characteristic polynomial of degree 2 over R, we have
for some \(l,m,n,u,v,w \in R\). The product \(jk=r-ai+qj+\alpha k\) can be written as an R-linear combination of 1, i, j, k, with \(q,r,a,\alpha \in R\). Letting \(k':=k-q\), we have
So changing the basis, we may suppose jk is an R-linear combination of 1, i, k (no j term). By symmetry, in the product ki we may suppose that the coefficient of k is zero and in ij the coefficient of i is zero. Therefore:
As before, the other products can be calculated using the standard involution: for example, we have
so
But now from these multiplication laws, we compute that the trace of left multiplication i is \({{\,\mathrm{Tr}\,}}(i)=0+u+\gamma +u=2u+\gamma \). But in a quaternion algebra, we have \({{\,\mathrm{Tr}\,}}(i)=2{{\,\mathrm{trd}\,}}(i)=2u\), so we must have \(\gamma =0\). By symmetry, we find that \(\alpha =\beta =0\). Finally, associativity implies relations on the structure constants in the multiplication table: we have
using (22.4.5) with \(\beta =0\); so equality of coefficients of j, k implies \(r=au\) and \(n=-ab\). By symmetry, we find \(s=bv,t=cw\) and \(m=-ac,n=-ab\), so we have the following multiplication table:
This matches precisely the multiplication table (22.3.7) for the even Clifford algebra of the quadratic form \(Q(x,y,z)=ax^2+by^2+cz^2+uyz+vxz+wxy\).
22.4.7
More generally, if R is a domain and \(\mathcal {O}\) is a quaternion R-order such that \(\mathcal {O}\) is free as an R-module with basis 1, i, j, k, then the proof of Proposition 22.4.4 shows \(\mathcal {O}\) has a basis 1, i, j, k satisfying the multiplication laws (22.3.7) of an even Clifford algebra; we call such a basis a good basis for \(\mathcal {O}\). Moreover, we have seen that given a basis 1, i, j, k, there exist unique \(\eta (i),\eta (j),\eta (k) \in R\) (in fact, certain coefficients of the multiplication table) such that
is a good basis.
To conclude, we need to show that if two quaternion R-orders are isomorphic, then they correspond to similar ternary quadratic forms. To this end, we define an inverse.
22.4.8
Let \(\mathcal {O} \subseteq B\) be a quaternion R-order with R-basis 1, i, j, k. Let \(N \in R\) be such that \((N)={{\,\mathrm{discrd}\,}}(\mathcal {O})\); then \(N \ne 0\) and is well-defined up to multiplication by \(R^\times \). Let \(1^\sharp ,i^\sharp ,j^\sharp ,k^\sharp \) be the dual basis (see 15.6.3); then \({{\,\mathrm{trd}\,}}(i^\sharp )={{\,\mathrm{trd}\,}}(1\cdot i^\sharp )=0\) and similarly for \(j^\sharp ,k^\sharp \), so
We define a candidate quadratic form
well-defined up to similarity (along the way, we chose a basis and a generator for \({{\,\mathrm{discrd}\,}}(\mathcal {O})\)).
Example 22.4.10
We return to Example 22.3.10. The R-order \(\mathcal {O}\) has reduced discriminant \(N=4ab\). The (rescaled) dual basis is
and \(i^\sharp ,j^\sharp ,k^\sharp \) is a basis for \((\mathcal {O}^\sharp )^0\); thus
Example 22.4.11
We return to Example 22.3.12. We have
and \(N=1\) so
Proposition 22.4.12
If \(Q:R^3 \rightarrow R\) is a nondegenerate ternary quadratic form with \({{\,\mathrm{disc}\,}}Q=N\), then \(N{{\,\mathrm{nrd}\,}}^\sharp ({{\,\mathrm{Clf}\,}}^0(Q))\) is similar to Q. If \(\mathcal {O}\) is a quaternion R-order with \({{\,\mathrm{discrd}\,}}(\mathcal {O})=(N)\), then \(N{{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O}) :R^3 \rightarrow R\) has \({{\,\mathrm{Clf}\,}}^0(N{{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O})) \simeq \mathcal {O}\).
Proof. Proposition 22.4.4 shows that the even Clifford functor induces a surjective map from similarity classes of nondegenerate ternary quadratic forms over R to isomorphism classes of quaternion R-orders. If we prove the first statement, then the second follows from set theory (and can be verified in a similar way).
We start with the quadratic form (22.3.5) with \(\mathcal {O}\) satisfying the multiplication laws (22.3.7). Let \(N :={{\,\mathrm{disc}\,}}(Q)\). We claim that
We see that \({{\,\mathrm{trd}\,}}(Ni^\sharp )=0\) and the same with \(j^\sharp ,k^\sharp \). We recall the alternating trilinear form m (defined in 15.4.2). By (22.3.20) we have
and
and similarly \({{\,\mathrm{trd}\,}}(k(Ni^\sharp ))=0\). The other equalities follow similarly, and this verifies the dual basis (22.4.13). In particular, we have \({{\,\mathrm{trd}\,}}(Ni^\sharp )={{\,\mathrm{trd}\,}}(Nj^\sharp )={{\,\mathrm{trd}\,}}(Nk^\sharp )=0\).
We then compute the quadratic form on this basis and claim that
Indeed,
since only the term \({{\,\mathrm{trd}\,}}(Ni^\sharp i)=N\) is nonzero; and
The other equalities follow by symmetry. Then the claim (22.4.14) implies that \(N{{\,\mathrm{nrd}\,}}(xi^\sharp +yj^\sharp +zk^\sharp )=Q(x,y,z)\), as desired.
Corollary 22.4.15
Let \(\mathcal {O}\) be a quaternion R-order. Then
Proof. If we take the identifications in the proof of Proposition 22.4.12 working within \(B \supseteq \mathcal {O}\), we see that \({{\,\mathrm{Clf}\,}}^0(N{{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O}))\) is spanned over R by the elements
where \({{\,\mathrm{discrd}\,}}(\mathcal {O})=(N)\). In order to see that the other factors belong to this ring, we compute
and
If we want to throw in the factors with \(1^\sharp \) as well, then we check:
satisfies
and
The result follows.
Finally, we officially combine our work to prove the main theorem of this section.
Proof of Main Theorem 22.4.1
Combine Propositions 22.4.4 and 22.4.12. \(\square \)
Remark 22.4.19. Just as in section 5.5, we may ask about embeddings of a quadratic ring in an order. However, moving from the rational to the integral is a bit tricky, and the issue of embeddings is a theme that will return with gusto in Chapter 30. In that context, it will be more natural to look at a different ternary quadratic form to measure embeddings; just as in the case of trace zero, it is related to but not the same as the one obtained in the above bijection.
5 Twisting and final bijection
In this final section, we conclude with the final bijection. We must keep track of the extra data of an ideal class, and along the way allow coefficient ideals. Throughout, let R be a Dedekind domain.
We first need the following slightly revised notion of similarity (one that ‘glues together’ local similarities) allowing scaling by fractional ideals.
Definition 22.5.1
Let \(Q :M \rightarrow \mathfrak l \) be a quadratic module with \(\mathfrak l \) a fractional R-ideal. The twist of Q by a fractional R-ideal \(\mathfrak u \) is the quadratic form \(\mathfrak u \otimes Q :\mathfrak u \otimes M \rightarrow \mathfrak u ^2\mathfrak l \) defined by \((\mathfrak u \otimes Q)(u \otimes x) = u^2Q(x)\).
A twisted similarity between quadratic modules Q and \(Q'\) is a similarity between Q and a twist \(\mathfrak u \otimes Q'\) for some fractional R-ideal \(\mathfrak u \).
Example 22.5.2
If \(\mathfrak u =uR\) is a principal fractional ideal, then twisted similarities between Q and \(\mathfrak a Q'=uQ'\) are precisely those obtained from a similarity between Q and \(Q'\), multiplied by u. In particular, if R is a PID, then the notions of similarity and twisted similarity coincide.
Example 22.5.3
Two quadratic modules \(Q,Q' :M,M' \rightarrow \mathfrak l \) with the same codomain are twisted similar if and only if they are similar. Indeed, if \(\mathfrak u ^2\mathfrak l = \mathfrak l \), then \(\mathfrak u =R\).
22.5.4
Second, we extend the definition of the inverse in 22.4.8 using the reduced norm to the noetherian domain R as follows. Let \(\mathcal {O} \subseteq B\) be a quaternion R-order. Since R is a Dedekind domain, the reduced discriminant \({{\,\mathrm{discrd}\,}}(\mathcal {O}) \subseteq R\) of \(\mathcal {O}\) is an invertible R-ideal. Define the map
Lemma 22.5.6
For a quaternion order \(\mathcal {O}\), the map \({{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O})\) defines a ternary quadratic module with values in \({{\,\mathrm{discrd}\,}}(\mathcal {O})^{-1}\).
Proof. The reduced norm defines a quadratic map, so we only need to verify that the codomain is valid. To this end, we may check locally since reduced norm and reduced discriminant commute with localization. Reducing to the local case, suppose R is now a local Dedekind domain hence a PID. Choosing a basis, we verified in (22.4.14) that \(N{{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O}) \subseteq R\), where \({{\,\mathrm{discrd}\,}}(\mathcal {O})=(N)\); the result follows.
MainTheorem 22.5.7
Let R be a Dedekind domain. Then the associations

are mutually inverse, discriminant-preserving bijections that are also functorial with respect to R.
Proof. We proved a version of this statement when R is a PID in Theorem 22.4.1. More generally, we work now with a pseudobasis instead of a basis, explaining the presence of the twisted similarity.
The surjectivity of the even Clifford map follows by generalizing the argument in Proposition 22.4.4 and 22.4.7 to show that \(\mathcal {O}\) has a good pseudobasis: see Exercise 22.5.
Let \(Q:M \rightarrow \mathfrak l \) be a quadratic module with \(\mathcal {O} :={{\,\mathrm{Clf}\,}}^0(Q)\). Returning to Example 22.3.24, we may write
for fractional ideals \(\mathfrak a ,\mathfrak b ,\mathfrak c \), and with \(Q_F(x,y,z) :=Q(xe_1+ye_2+ze_3)\) in the usual form provided by (22.3.5). Let \(N :={{\,\mathrm{disc}\,}}(Q_F)\). Then
Consider now \({{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O}) :(\mathcal {O}^\sharp )^0 \rightarrow {{\,\mathrm{discrd}\,}}(\mathcal {O})^{-1}\): as in 22.4.8 we have
To prepare our twisted similarity, let

Then
We claim that the reduced norm on \(\mathfrak d (\mathcal {O}^\sharp )^0\) has values in \(N^{-1}\mathfrak l \) and is similar to Q. The claim follows from the same calculation in the proof of Proposition 22.4.12, namely that \({{\,\mathrm{nrd}\,}}(xi^\sharp +yj^\sharp + zk^\sharp )=N^{-1}Q_F(x,y,z)\)! We conclude that \({{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O})\) is twisted similar to Q.
We conclude with the following application to quadratic forms.
Corollary 22.5.12
Let \(Q:M \rightarrow \mathfrak l \) be a ternary quadratic module and \(\mathcal {O} :={{\,\mathrm{Clf}\,}}^0(Q)\). Then the even Clifford map induces a bijection \({{\,\mathrm{Cl}\,}}Q \leftrightarrow {{\,\mathrm{Typ}\,}}\mathcal {O}\).
Proof. We first claim that the even Clifford map induces an injection \({{\,\mathrm{Gen}\,}}Q \rightarrow {{\,\mathrm{Gen}\,}}\mathcal {O}\), giving an injection \({{\,\mathrm{Cl}\,}}Q \rightarrow {{\,\mathrm{Typ}\,}}\mathcal {O}\). Indeed, let \(Q' \in {{\,\mathrm{Gen}\,}}Q\), so \(Q' :M' \rightarrow \mathfrak l '\) is locally isometric to Q. Let \(\mathcal {O}' :={{\,\mathrm{Clf}\,}}^0(Q')\). Since \(Q',Q\) are locally isometric, they are locally similar, so \(\mathcal {O}',\mathcal {O}\) are locally isomorphic by Main Theorem 22.4.1, so \(\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}\). And if \(Q' \simeq Q\) are isometric, again they are (twisted) similar, so by Main Theorem 22.5.7 we have \(\mathcal {O}' \simeq \mathcal {O}\).
To finish, we need to show that the even Clifford map is surjective. We pass from similarity classes to isometry classes in the same way as in the proof of Corollary 5.2.6. To this end, let \(\mathcal {O}' \in {{\,\mathrm{Gen}\,}}(\mathcal {O})\). Let \(Q' :=\mathfrak d {{\,\mathrm{nrd}\,}}^\sharp (\mathcal {O}')\) as in (22.5.11). By the same rescaling argument given in Corollary 5.2.6, applying a similarity to \(Q'\) we may further suppose that \({{\,\mathrm{disc}\,}}Q'_F = {{\,\mathrm{disc}\,}}Q_F \in F^{\times }/F^{\times 2}\). By surjectivity in Main Theorem 22.5.7, for every prime \(\mathfrak p \) of R, there exists a twisted similarity from \(Q'_{(\mathfrak p )}\) to \(Q_{(\mathfrak p )}\) over \(R_{(\mathfrak p )}\)—and since each \(R_{(\mathfrak p )}\) is a PID, by Example 22.5.2, these are in fact similarities. Taking such a similarity and considering it as a similarity over F, again repeating the same argument as at the end of Corollary 5.2.6, we conclude that \(Q'\) and Q are locally isometric, so \(Q' \in {{\,\mathrm{Gen}\,}}Q\). Finally, if \(\mathcal {O}' \simeq \mathcal {O}\), repeating these arguments one more time over R (first to go from twisted similar to similar, then to note the similarity gives rise to an isometry) we conclude that \(Q' \simeq Q\).
Remark 22.5.13. The correspondence between ternary quadratic forms and quaternion orders has a particularly rich history. Perhaps the earliest prototype is due to Hermite [Herm1854], who examined the product of automorphs of ternary quadratic forms. Early versions of the correspondence were given by Latimer [Lat37, Theorem 3], Pall [Pall46, Theorems 4–5], and Brandt [Bra43, §3ff] over \(\mathbb Z \) by use of explicit formulas.
Various attempts were made to generalize the correspondence to Dedekind domains, with the thorny issue being how to deal with a nontrivial class group. Eichler [Eic53, §14, p. 96] gave such an extension. Peters [Pet69, §4] noted that Eichler’s correspondence was not onto due to class group issues, and he gave a rescaled version that gives a bijection for Gorenstein orders. Eichler’s correspondence was further tweaked by Nipp [Nip74, §3], who opted for a different scaling factor that is not restricted to a class of orders, but his correspondence fails to be onto [Nip74, p.536].
These correspondences were developed further by Brzezinski [Brz80, §3], [Brz85, §3], where he connected the structure of orders to relatively minimal models of the corresponding integral conic; see also Remark 24.3.11. He revisited the correspondence again in the context of Gorenstein orders [Brz82, §3] and Bass orders [Brz83b, §2]. Lemurell [Lem2011, Theorem 4.3] gives a concise account of the correspondence of Brzezinski over a PID (the guts of which are contained in [Brz82, (3.2)]).
More recently, Gross–Lucianovic [GrLu2009, §4] revisited the correspondence over a PID or local ring, and they extended it to include quadratic forms of nonzero discriminant and without restricting to Gorenstein orders; this extension is important for automorphic reasons, connected to Fourier coefficients of modular forms on \({{\,\mathrm{PGSp}\,}}(6)\), as developed by Lucianovic in his thesis [Luc2003]. Balaji [Bal2007, Theorem 3.1] studied degenerations of ternary quadratic modules in the context of orthogonal groups and Witt invariants and showed that the even Clifford functor is bijective over a general scheme. Finally, Voight [Voi2011a, Theorem B] gave a general and functorial correspondence without any of the above restrictive hypotheses, including the functorial inverse to the even Clifford functor provided above.
Remark 22.5.14. In the most general formulation of the correspondence, allowing arbitrary ternary quadratic modules discriminant over all sorts of rings, Voight [Voi2011a, Theorem A] characterizes the image of the even Clifford functor, as follows. Let B be an R-algebra that is (faithfully) projective of rank 4 as an R-module. Then B is a quaternion ring if \(B \simeq {{\,\mathrm{Clf}\,}}^0(Q)\) for a ternary quadratic module Q. Then B is a quaternion ring if and only if B has a standard involution and for all \(x \in B\), the trace of left (or right) multiplication by x on B is equal to \(2{{\,\mathrm{trd}\,}}(x)\).
For example, if we take the quadratic form \(Q:R^3 \rightarrow R\) defined by \(Q(x,y,z)=0\) identically, the multiplication table on \({{\,\mathrm{Clf}\,}}^0(Q)\) gives the commutative ring
One can see this as a kind of deformation of a quaternion algebra (in an algebro-geometric sense), letting \(a,b \rightarrow 0\).
Exercises
- \(\triangleright \) 1.:
-
Let R be a PID or local noetherian domain. Let A be an R-algebra that is free of finite rank as an R-module. Show that A has an R-basis including 1. [Hint: show that the quotient A/R is torsion-free, hence free; since free modules are projective, the sequence \(0 \rightarrow R \rightarrow A \rightarrow A/R \rightarrow 0\) splits, giving \(A \simeq R \oplus A/R\).]
- \(\triangleright \) 2.:
-
For a free quadratic ternary form (as in 22.3.4), show that a change of basis \(\rho \in {{\,\mathrm{GL}\,}}_3(R)\) acts on \(i,j,k \in {{\,\mathrm{Clf}\,}}^0(Q)\) by the adjugate matrix \({{\,\mathrm{adj}\,}}(\rho ) \in {{\,\mathrm{GL}\,}}_3(R)\) (where the entries of \({{\,\mathrm{adj}\,}}(\rho )\) are the \(2 \times 2\)-cofactors of \(\rho \) and \(\rho {{\,\mathrm{adj}\,}}(\rho )=\det (\rho )\)).
- 3.:
-
Let R be a domain and let \({{\,\mathrm{Pic}\,}}R\) be the group of isomorphism classes of invertible R-modules (equivalently, classes of fractional R-ideals in F). Show that up to twisted similarity, the target of a quadratic module only depends on its class in \({{\,\mathrm{Pic}\,}}R/2{{\,\mathrm{Pic}\,}}R\). [See Example 9.7.5.]
- 4.:
-
Finish the direct verification in Example 22.3.24 that \(\mathcal {O}\) is closed under multiplication.
- \(\triangleright \) 5.:
-
Let R be a Dedekind domain, and let \(\mathcal {O}\) be a quaternion R-order. Show that there exist \(i,j,k \in \mathcal {O}\) and \(\mathfrak a ,\mathfrak b ,\mathfrak c \subset F\) fractional R-ideals such that \(\mathcal {O}=R+\mathfrak a i + \mathfrak b j + \mathfrak c k\) and such that 1, i, j, k satisfy the multiplication rules (22.3.7) for some \(a,b,c,u,v,w \in F\)—called a good pseudobasis for \(\mathcal {O}\). [Hint: revisit what goes into 22.4.7; a simple observation will suffice!]
- 6.:
-
Let \(Q :R^3 \rightarrow R\) be a ternary quadratic form and let \(\mathcal {O} :={{\,\mathrm{Clf}\,}}^0(Q)\). Show that
$$\begin{aligned} {{\,\mathrm{disc}\,}}{{\,\mathrm{nrd}\,}}|_{\mathcal {O}} = ({{\,\mathrm{disc}\,}}Q)^2. \end{aligned}$$[Hint: see (22.3.18).]
- 7.:
-
Let \(Q :M \rightarrow R\) be a quadratic form over R. Construct a Clifford algebra with a universal property analogous to Proposition 5.3.1, and recover the even Clifford algebra and odd Clifford bimodule.
- 8.:
-
Let \(Q:M \rightarrow R\) be a quadratic form such that there exists \(x \in M\) such that \(Q(x) \in R^\times \).
- (a):
-
Show that the odd Clifford bimodule \({{\,\mathrm{Clf}\,}}^1(Q)\) is free of rank 1 as a \({{\,\mathrm{Clf}\,}}^0(Q)\).
- (b):
-
Generalize this result to case where \(Q:M \rightarrow L\) is a quadratic module.
- 9.:
-
Let \(Q:M \rightarrow R\) be a quadratic form over R with M of odd rank as an R-module and let \(F={{\,\mathrm{Frac}\,}}R\). Let \(S :=Z({{\,\mathrm{Clf}\,}}Q) \hookrightarrow K :=Z({{\,\mathrm{Clf}\,}}Q_F)\) be the center of the Clifford algebra of Q. Show that S is an R-order in K.
- \(\triangleright \) 10.:
-
Show that \({{\,\mathrm{nrd}\,}}(\mathcal {O}^\sharp )={{\,\mathrm{nrd}\,}}((\mathcal {O}^\sharp )^0)\). [Hint: use (22.4.18).]
- 11.:
-
Let R be a Dedekind domain with \(F={{\,\mathrm{Frac}\,}}R\), let B be a quaternion algebra over F, and let \(\mathcal {O} \subseteq B\) be an R-order. Let \(S \subseteq \mathcal {O}\) be an R-order.
- (a):
-
Suppose \(S \subseteq \mathcal {O}\) is integrally closed. Prove that \(\mathcal {O}\) is projective of rank 2 as a left S-module.
- (b):
-
If S is not integrally closed, then show that (a) need not hold by the following example. Let \(R=\mathbb Z \) and \(F=\mathbb Q \), let \(B=({-1,-1} \mid \mathbb{Q })\), let
$$\begin{aligned} \mathcal {O}=\mathbb Z + \mathbb Z pi + \mathbb Z j + \mathbb Z ij \end{aligned}$$for an odd prime p (that is pi, not \(\pi \)!). Let \(S=\mathbb Z [pi] \subseteq \mathcal {O}\). Show that \(\mathcal {O}\) is not projective as a left S-module.
- (c):
-
Show that the property that \(\mathcal {O}\) is projective as an S-module is a local property (over primes of R).
- (d):
-
In light of (c), suppose that R is a PID, and write \(\mathcal {O}\) in a good basis (22.3.7). Suppose that \(S=R[i]\) with \(i^2=ui-bc\). Show that \(\mathcal {O}\) is projective as an S-module if and only if the quadratic form \(bx^2 + uxy + cy^2\) represents a unit.
- (e):
-
Using (d), conclude in general that if S has conductor coprime to \({{\,\mathrm{discrd}\,}}\mathcal {O}\), show that \(\mathcal {O}\) is projective as an S-module.
- 12.:
-
Let R be a global ring with \(F :={{\,\mathrm{Frac}\,}}R\), let \(B,B'\) be quaternion algebras over F, and let \(\mathcal {O} \subseteq B\) and \(\mathcal {O}' \subseteq B'\) be R-orders. Consider the quaternary quadratic forms \(Q :={{\,\mathrm{nrd}\,}}|_\mathcal {O} :\mathcal {O} \rightarrow R\) and similarly \(Q'\) on \(\mathcal {O}'\).
- (a):
-
Show that Q is isometric to \(Q'\), then there is an isomorphism of F-algebras
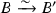 .
. - (b):
-
In light of (a), suppose \(\mathcal {O},\mathcal {O}' \subseteq B=B'\). Show that \(\mathcal {O},\mathcal {O}'\) are isomorphic as R-orders if and only if \(Q,Q'\) are isometric as (quaternary) quadratic modules. [Hint: if Q is isometric to \(Q'\), then show that there is a similarity on the trace zero elements of the duals, thereby giving an isomorphism
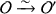 ].
].
- 13.:
-
Let \(Q:M \rightarrow L\) be a quadratic module. Show that the even Clifford algebra \({{\,\mathrm{Clf}\,}}^0(Q)\) with its map
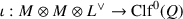 has the following universal property: if A is an R-algebra and \(\iota _A:M \otimes M \otimes L \rightarrow A\) is an R-module homomorphism such that
has the following universal property: if A is an R-algebra and \(\iota _A:M \otimes M \otimes L \rightarrow A\) is an R-module homomorphism such that - (i):
-
\(\iota _A(x \otimes x \otimes f)=f(Q(x))\) for all \(x \in M\) and
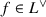 , and
, and - (ii):
-
\(\iota _A(x \otimes y \otimes f)\iota _A(y \otimes z \otimes g)=f(Q(y))\iota _A(x \otimes z \otimes g)\) for all \(x,y,z \in M\) and
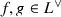 ,
,
then there exists a unique R-algebra homomorphism \(\phi :{{\,\mathrm{Clf}\,}}^0(Q) \rightarrow A\) such that the diagram
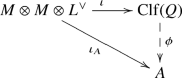
commutes. Conclude that the pair \(({{\,\mathrm{Clf}\,}}^0(Q),\iota )\) is unique up to unique isomorphism.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Quaternion orders and ternary quadratic forms. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_22
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


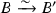 .
.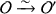 ].
].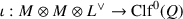 has the following universal property: if A is an R-algebra and
has the following universal property: if A is an R-algebra and 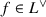 , and
, and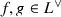 ,
,