Effective Semantics for the Modal Logics K and KT via Non-deterministic Matrices

Abstract

A four-valued semantics for the modal logic K is introduced. Possible worlds are replaced by a hierarchy of four-valued valuations, where the valuations of the first level correspond to valuations that are legal w.r.t. a basic non-deterministic matrix, and each level further restricts its set of valuations. The semantics is proven to be effective, and to precisely capture derivations in a sequent calculus for K of a certain form. Similar results are then obtained for the modal logic KT, by simply deleting one of the truth values.

We thank the anonymous reviewers for their useful feedback. This research was supported by NSF-BSF (grant number 2020704), ISF (grant numbers 619/21 and 1566/18), and the Alon Young Faculty Fellowship.

1 Introduction

Propositional modal logics extend classical logic with modalities, intuitively interpreted as necessity, knowledge, or temporal operators. Such extensions have several applications in computer science and artificial intelligence (see, e.g., [7, 9, 13]).

The most common and successful semantic framework for modal logics is the so called possible worlds semantics, in which each world is equipped with a two-valued valuation, and the semantic constraints regarding the modal operators consider the valuations in accessible worlds. While this has been the gold standard for modal logic semantics for many years, alternative semantic frameworks have been proposed. One of these approaches, initiated by Kearns [10], is based on an infinite sequence of sets of valuations in a non-deterministic many-valued semantics. Since then, several non-deterministic many-valued semantics, without possible worlds, were developed for modal logics (see, e.g., [4, 8, 12, 14]). The current paper is a part of that body of work. Having an alternative semantic framework for modal logics, different than the common possible worlds semantics, has the potential of exposing new intuitions and understandings of modal logics, and also to form the basis to new decision procedures.

Our main contribution is a four-valued semantics for the modal logic ${\texttt {K}}$. The key characteristic of the semantics that we present is effectiveness: when checking for the entailment of a formula $\varphi$ from a set $\varGamma$ of formulas in ${\texttt {K}}$, it suffices to only consider partial models, defined over the subformulas of $\varGamma$ and $\varphi$. To the best of our knowledge, this is the first effective Nmatrices-based semantics for ${\texttt {K}}$. Such a semantics has the potential of being subject to reductions to classical satisfiability [3], as it is based on finite-valued truth tables, and thus improving the performance of solvers for modal logic by utilizing off-the-shelf SAT solvers. Another advantage of this semantics is that it precisely captures derivations in a sequent calculus for ${\texttt {K}}$ that admit a certain property. Following Kearns, models of this semantics are based on the concept of levels—valuations of level 0 are the ordinary valuations of Nmatrices, while each level $m>0$ introduces more constraints. We show that valuations of level m correspond to derivations in the calculus whose largest number of applications of the rule that correspond to the axiom ${\textsc {(K)}}$ in any branch of the derivation is at most m. Our restrictions between the levels are more complex than the original restrictions in Kearns’ work, in order to obtain effectiveness. Another precise correspondence between the semantics and the proof system that we prove, is between the domains of valuations and the formulas allowed to be used in derivations.

Finally, we observe that by deleting one of the truth values, a three-valued semantics for the modal logic ${\texttt {KT}}$ is obtained, which is similar to the one presented in [8]. Like the case of ${\texttt {K}}$, the resulting semantics is effective, and tightly correspond to derivations in a sequent calculus for ${\texttt {KT}}$.

Outline. The paper is organized as follows: Sect. 2 reviews standard notions in non-deterministic matrices. In Sect. 3, we present our semantics for the modal logic ${\texttt {K}}$, as well as the sequent calculus our investigation will be based on, which is coupled with the notion of ${\textsc {(K)}}$-depth of derivations. In Sect. 4, we prove soundness and completeness theorems between the sequent calculus and the semantics. In Sect. 5, we prove that the semantics that we provide is effective, not only for deciding entailment, but also for producing countermodels when an entailment does not hold. In Sect. 6 we establish similar results for the modal logic ${\texttt {KT}}$. We conclude with §7, where directions for future research are outlined.

Related Work. In [10], Kearns initiated the study of modal semantics without possible worlds. This work was recently revisited by Skurt and Omori [14], who generalized Kearns’ work and reframed his framework within the framework of logical Non-deterministic matrices. As indicated in [14], it was not clear how to make this semantics effective, as it requires checking truth values of infinitely many formulas when considering the validity of a given formula (see, e.g., Remark 42 of [14]). In [4], Coniglio et al. develop a similar framework for modal logics, and some bound over the formulas that need to be considered was achieved. However, in [5], the authors clarified that it is unclear how to effectively use the resulting semantics. A semantics based on Nmatrices for the modal logics ${\texttt {KT}}$ and ${\texttt {S4}}$ was presented in [8] by Grätz, that includes a method to extend a partial model in that semantics into a total one, which results in an effective semantics. We chose here to focus on ${\texttt {K}}$, which is a weaker logic, forming a common basis to all other normal modal logics. By deleting one out of four truth values, we obtain corresponding results for ${\texttt {KT}}$ as well. The semantics that we present here is similar in nature to the one presented in [8], however: (i) the truth tables are different, as we intentionally enforced the many-valued tables of the classical connectives to be obtained by a straightforward duplication of truth values from the original two-valued truth tables; and (ii) the semantic condition for levels of valuations that we define here is inductive, where each level relies on lower levels (thus refraining from a definition of a more cyclic nature as the one in [8], that is better understood operationally). A variant of the semantics from [14] was also introduced and studied in [12], but without considering the ability to perform effective automated reasoning but instead focusing on infinite valuations rather than on partial ones. A complete proof theoretic characterization in terms of sequent calculi to the various levels of valuations was not given in any of the above works. Also, an effective semantics for ${\texttt {K}}$, which is the most basic modal logic, was not given in any of the above works.

Non-deterministic matrices were introduced in [2], and have since became a useful tool for investigating non-classical logics and proof systems (see [1] for a survey). They generalize (deterministic) matrices [15] by allowing a non-deterministic choice of truth values in the truth tables. Like matrices, Nmatrices enjoy the semantic analyticity property, which allows one to extend a partial valuation into a full one. Our semantic framework can be viewed as a further refinement of non-deterministic matrices, namely restricted non-deterministic matrices, introduced in [6].

2 Preliminaries

In this section we provide the necessary definitions about Nmatrices following [1]. We assume a propositional language ${\mathcal {L}}$ with countably infinitely many atomic variables $p_1,p_2,\ldots$. When there is no room for confusion, we identify ${\mathcal {L}}$ with its set of well-formed formulas (e.g., when writing $\varphi \in {\mathcal {L}}$). We write $sub (\varphi )$ for the set of subformulas of a formula $\varphi$. This notation is extended to sets of formulas in the natural way.

Valuations. In the context of a set ${\mathcal {V}}$ of “truth values”, a valuation is a function v from some domain ${\mathsf {Dom(}v ) }\subseteq {\mathcal {L}}$ to ${\mathcal {V}}$. For a set ${\mathcal {F}}\subseteq {\mathcal {L}}$, an ${\mathcal {F}}$-valuation is a valuation with domain ${\mathcal {F}}$. (In particular, an ${\mathcal {L}}$-valuation is defined on all formulas.) For $X\subseteq {\mathcal {V}}$, we write ${v^{-1}[{X}]}$ for the set $\left\{ \varphi {\ |\ }v(\varphi )\in X\right\}$. For $x\in {\mathcal {V}}$, we also write ${v^{-1}[{x}]}$ for the set $\left\{ \varphi {\ |\ }v(\varphi )= x\right\}$.

Definition 1

Let $\mathcal {D}\subseteq {\mathcal {V}}$ be a set of “designated truth values”. A valuation v $\mathcal {D}$-satisfies a formula $\varphi$, denoted by $v\models _{\mathcal {D}}\varphi$, if $v(\varphi )\in \mathcal {D}$. For a set $\varSigma$ of formulas, we write $v\models _{\mathcal {D}}\varSigma$ if $v\models _{\mathcal {D}}\varphi$ for every $\varphi \in \varSigma$.

Notation 2

Let $\mathcal {D}\subseteq {\mathcal {V}}$ be a set of designated truth values and $\mathbb {V}$ be a set of valuations. For sets L, R of formulas, we write $L\vdash _{{\mathcal {D}}}^{{\mathbb {V}}} R$ if for every $v\in \mathbb {V}$, $v\models _{\mathcal {D}} L$ implies that $v\models _{\mathcal {D}}\varphi$ for some $\varphi \in R$. We omit L or R in this notation when they are empty (e.g., when writing $\vdash _{{\mathcal {D}}}^{{\mathbb {V}}} R$), and set parentheses for singletons (e.g., when writing $L \vdash _{{\mathcal {D}}}^{{\mathbb {V}}} \varphi$).

Nmatrices. An Nmatrix $M$ for ${\mathcal {L}}$ is a triple of the form ${\langle {\mathcal {V}},\mathcal {D},{\mathcal {O}} \rangle }$, where ${\mathcal {V}}$ is a set of truth values, $\mathcal {D}\subseteq {\mathcal {V}}$ is a set of designated truth values, and ${\mathcal {O}}$ is a function assigning a truth table ${\mathcal {V}}^{n} \rightarrow P({\mathcal {V}}) {\setminus } \left\{ \emptyset \right\}$ to every n-ary connective $\diamond$ of ${\mathcal {L}}$ (which assigns a set of possible values to each tuple of values). In the context of an Nmatrix $M={\langle {\mathcal {V}},\mathcal {D},{\mathcal {O}} \rangle }$, we often denote ${\mathcal {O}}(\diamond )$ by $\tilde{\diamond }$.

An ${\mathcal {F}}$-valuation v is $M$-legal if $v(\varphi )\in \mathsf {pos\text {-}val}({\varphi },{M},{v})$ for every formula $\varphi \in {\mathcal {F}}$ whose immediate subformulas are contained in ${\mathcal {F}}$, where $\mathsf {pos\text {-}val}({\varphi },{M},{v})$ is defined by:

• 1. $\mathsf {pos\text {-}val}({p},{M},{v})={\mathcal {V}}$ for every atomic formula p.

• 2. $\mathsf {pos\text {-}val}({\diamond (\psi _1,\dots ,\psi _n)},{M},{v})=\tilde{\diamond }(v(\psi _1),\dots ,v(\psi _n))$ for every non-atomic formula $\diamond (\psi _1,\dots ,\psi _n)$.

In other words, there is no restriction regarding the values assigned to atomic formulas, whereas the values of compound formulas should respect the truth tables.

Lemma 1

([1]). Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ be a set closed under subformulas and $M$ an Nmatrix for ${\mathcal {L}}$. Then every $M$-legal ${\mathcal {F}}$-valuation v can be extended to an $M$-legal ${\mathcal {L}}$-valuation.

3 The Modal Logic ${\texttt {K}}$

In this section we introduce a novel effective semantics for the model logic ${\texttt {K}}$. We first present a known proof system for this logic (Sect. 3.1), and then our semantics (Sect. 3.2). From here on, we assume that the language ${\mathcal {L}}$ consists of the connectives $\supset$, $\wedge$, $\vee$, $\lnot$ and $\Box$ with their usual arities. The standard $\Diamond$ operator can be defined as a macro . Obviously, using De-Morgan rules, fewer connectives can be used. However, we chose this set of connectives in order to have a primitive language rich enough for the examples that we include along the paper.

3.1 Proof System

Figure 1 presents a Gentzen-style calculus, denoted by $\mathsf {{{G}_{{\texttt {K}}}}}$, for the modal logic ${\texttt {K}}$ that was proven to be equivalent to the original formulation of the logic as a Hilbert system (see, e.g., [16]). We take sequents to be pairs ${\langle \varGamma ,\varDelta \rangle }$ of finite sets of formulas. For readability, we write $\varGamma \Rightarrow \varDelta$ instead of ${\langle \varGamma ,\varDelta \rangle }$ and use standard notations such as $\varGamma ,\varphi \Rightarrow \psi$ instead of $(\varGamma \cup \left\{ \varphi \right\} ) \Rightarrow \left\{ \psi \right\}$.

The ${\textsc {(cut)}}$ rule is included in $\mathsf {{{G}_{{\texttt {K}}}}}$ for convenience, but applications of ${\textsc {(cut)}}$ can be eliminated from derivations (see, e.g., [11]). Since the focus of this paper is semantics rather than cut-elimination, we allow ourselves to use cut freely and do not distinguish derivations that use it from derivations that do not. We write $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}\varGamma \Rightarrow \varDelta$ if there is a derivation of a sequent $\varGamma \Rightarrow \varDelta$ in the calculus $\mathsf {{{G}_{{\texttt {K}}}}}$.

Fig. 1.

The sequent calculus $\mathsf {{{G}_{{\texttt {K}}}}}$

In the sequel, we provide a semantic characterization of $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}$. It is based on a more refined notion of derivability that takes into account: (i) the set ${\mathcal {F}}$ of formulas used in the derivation; and (ii) the ${\textsc {(K)}}$-depth of the derivation, as defined next.

Definition 3

A derivation of a sequent $\varGamma \Rightarrow \varDelta$ in $\mathsf {{\mathsf {{{G}_{{\texttt {K}}}}}}}$ is a tree in which the nodes are labeled with sequents, the root is labeled with $\varGamma \Rightarrow \varDelta$, and every node is the result of an application of some rule of $\mathsf {{{G}_{{\texttt {K}}}}}$ where the premises are the labels of its children in the tree. A derivation is called an ${\mathcal {F}}$-derivation if it employs only sequents composed of formulas from ${\mathcal {F}}$. The ${\textsc {(K)}}$-depth of a derivation is the maximal number of applications of rule ${\textsc {(K)}}$ in any of the branches of the derivation.

Notation 4

We write $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varDelta$ if there is a derivation of $\varGamma \Rightarrow \varDelta$ in $\mathsf {{{G}_{{\texttt {K}}}}}$ in which only ${\mathcal {F}}$-sequents occur and that has ${\textsc {(K)}}$-depth at most m. We drop ${\mathcal {F}}$ from this notation when ${\mathcal {F}}={\mathcal {L}}$; and drop m to dismiss the restriction regarding the ${\textsc {(K)}}$-depth.

Example 1

Let and ${\mathcal {F}}= sub (\varphi )$. The following is a derivation of $\Rightarrow \varphi$ in $\mathsf {{{G}_{{\texttt {K}}}}}$ that only uses ${\mathcal {F}}$-formulas and has ${\textsc {(K)}}$-depth of 1 (though the number of applications of ${\textsc {(K)}}$ in the derivation is 2):

$$ \dfrac{\dfrac{\dfrac{\dfrac{\dfrac{}{p_1,p_2\Rightarrow p_1}{\textsc {(id)}}}{p_1\wedge p_2\Rightarrow p_1}(\wedge \Rightarrow )}{\Box (p_1\wedge p_2)\Rightarrow \Box p_1}{\textsc {(K)}}~~~~~\dfrac{\dfrac{\dfrac{}{p_1,p_2\Rightarrow p_2}{\textsc {(id)}}}{p_1\wedge p_2\Rightarrow p_2}(\wedge \Rightarrow )}{\Box (p_1\wedge p_2)\Rightarrow \Box p_2}{\textsc {(K)}}}{\Box (p_1\wedge p_2)\Rightarrow \Box p_1\wedge \Box p_2}(\Rightarrow \wedge )}{\Rightarrow \Box (p_1\wedge p_2)\supset \Box p_1\wedge \Box p_2}(\Rightarrow \supset ) $$

3.2 Semantics

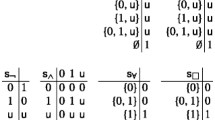
The semantics is based on a four-valued Nmatrix stratified with “levels”, where for every m, legal valuations of level $m+1$ are a subset of legal valuations of level m. The underlying Nmatrix, denoted by $\mathsf {M}_{{\texttt {K}}}$, is obtained by duplicating the classical truth values. Thus, the sets of truth values and of designated truth values are given by:

The truth tables are as follows (we have ):

We employ the following notations for subsets of truth values:

For the classical connectives, the truth tables of $\mathsf {M}_{{\texttt {K}}}$ treat just like , and just like , and are essentially two-valued—the result is either $\mathcal {D}$ or $\overline{\mathcal {D}}$, and it depends solely on whether the inputs are elements of $\mathcal {D}$ or $\overline{\mathcal {D}}$. Thus, for the language without $\Box$, this Nmatrix provides a (non-economic) four-valued semantics for classical logic.

While the output for $\Box$ is also always $\mathcal {D}$ or $\overline{\mathcal {D}}$, it differentiates between (that results in $\mathcal {D}$) and (that results in $\overline{\mathcal {D}}$), and similarly between and . In fact, this table is captured by the condition: $\tilde{\Box }(x)\in \mathcal {D}$ iff .

Example 2

Let ${\mathcal {F}}= sub (\varphi )$ where $\varphi$ is the formula from Example 1. The following valuation v is an ${\mathcal {F}}$-valuation that is $\mathsf {M}_{{\texttt {K}}}$-legal:

To show that it is $\mathsf {M}_{{\texttt {K}}}$-legal, one needs to verify that $v(\psi )\in \mathsf {pos\text {-}val}({\psi },{\mathsf {M}_{{\texttt {K}}}},{v})$ for each $\psi \in {\mathcal {F}}$. For example, . As another example, since , we have that , and hence . Notice that v does not satisfy $\varphi$.

The truth table for $\Box$ can be understood via “possible worlds” intuition. Our four truth values are intuitively captured as follows, assuming a given formula $\psi$ and a world w:

• : $\psi$ holds in w and in every world accessible from w;

• : $\psi$ holds in w but it does not hold in some world accessible from w;

• : $\psi$ does not hold in w but does hold in every world accessible from w; and

• : $\psi$ does not hold in w and it does not hold in some world accessible from w.

In the possible worlds semantics, $\Box \psi$ holds in some world w iff $\psi$ holds in every world that is accessible from w, which intuitively explains the table for $\Box$. Note that non-determinism is inherent here. For example, if $\psi$ holds in w and in every world accessible from w (i.e., $\psi$ has value ), we know that $\Box \psi$ holds in w, but we do not know whether $\Box \psi$ holds in every world accessible from w (thus $\Box \psi$ has value or ).

Now, the Nmatrix $\mathsf {M}_{{\texttt {K}}}$ by itself is not adequate for the modal logic ${\texttt {K}}$ (as Examples 1 and 2 demonstrate). What is missing is the relation between the choices we make to resolve non-determinism for different formulas. Continuing with the possible worlds intuition, we observe that if a formula $\varphi$ follows from a set of formulas $\varSigma$ that hold in all accessible worlds (i.e., $\varphi$ follows from formulas whose truth value is or ), then $\varphi$ itself should hold in all accessible worlds (i.e., $\varphi$’s truth value should be or ). Directly encoding this condition requires us to consider a set $\mathbb {V}$ of $\mathsf {M}_{{\texttt {K}}}$-legal ${\mathcal {F}}$-valuations for which the following holds (recall Notation 2 from Sect. 2):

In turn, to obtain completeness we take a maximal set $\mathbb {V}$ that satisfies the necessitation condition. While it is possible to define this set of valuations as the greatest fixpoint of necessitation, following previous work, we find it convenient to reach this set using “levels”:

Definition 5

The set $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ is inductively defined as follows:

• $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0}$ is the set of $\mathsf {M}_{{\texttt {K}}}$-legal ${\mathcal {F}}$-valuations.

• 

We also define:

Similarly to the idea originated by Kearns in [10], valuations are partitioned into levels, which are inductively defined. The first level, $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0}$, consists solely of the $\mathsf {M}_{{\texttt {K}}}$-legal valuations with domain ${\mathcal {F}}$. For each $m>0$, the m’th level is defined as a subset of the $(m-1)$’th level, with an additional constraint: a valuation v from level $m-1$ remains in level m, only if every formula $\varphi \in {\mathcal {F}}$ entailed (at the $m-1$ level) from the set of formulas that were assigned a value from by v, is itself assigned a value from by v. As we show below, in the “end” of this process, by taking $\bigcap _{m\ge 0}\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$, one obtains the greatest set $\mathbb {V}$ satisfying the necessitation condition

Remark 1

The necessitation condition is similar to the one provided in [8] to the modal logics ${\texttt {KT}}$ and ${\texttt {S4}}$. In contrast, the condition from [4, 10, 14] is simpler and does not involve at all, but also does not give rise to decision procedures.

Example 3

Following Example 2, while the formula $\varphi$ is not satisfied by all valuations in $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0}$, it is satisfied by all valuations in $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ for every $m>0$. In particular, the valuation v from Example 2 is not in $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},1}$: we have $p_1\wedge p_2\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0}}} p_1$ and (so ), but .

For each set ${\mathcal {F}}\subseteq {\mathcal {L}}$ and $m\ge 0$, we obtain a consequence relation $\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}$ between sets of ${\mathcal {F}}$-formulas. Disregarding m, we also obtain the relation $\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}}$ (for every ${\mathcal {F}}$), which we will show to be sound and complete for ${\texttt {K}}$. We note that all these relations are compact. The proof of the following theorem relies on the completeness theorems that we prove in Sect. 4.

Theorem 1 (Compactness)

• 1. For every $m\ge 0$, if $L\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}R$, then $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}\varDelta$ for some finite $\varGamma \subseteq L$ and $\varDelta \subseteq R$.

• 2. If $L\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}}R$, then $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}}\varDelta$ for some finite $\varGamma \subseteq L$ and $\varDelta \subseteq R$.

Now, to show that $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$ is indeed the largest set $\mathbb {V}$ of $\mathsf {M}_{{\texttt {K}}}$-legal ${\mathcal {F}}$-valuations that satisfies necessitation, we use the following two lemmas. The first is a general construction that relies only on the use of finite-valued valuation functions.

Lemma 2

Let $v_0,v_1,v_2,\ldots$ be an infinite sequence of valuations over a common domain ${\mathcal {F}}$. Then, there exists some v such that for every finite set ${\mathcal {F}}'\subseteq {\mathcal {F}}$ of formulas and $m\ge 0$, we have $v|_{{\mathcal {F}}'} = v_k|_{{\mathcal {F}}'}$ for some $k\ge m$.

Proof (Outline)

First, if ${\mathcal {F}}$ is finite, then there is only a finite number of ${\mathcal {F}}$-valuations, and there must exists some ${\mathcal {F}}$-valuation $v_m$ that occurs infinitely often in the sequence $v_0,v_1,\ldots$. We take $v = v_m$, and the required property trivially holds. Now, assume that ${\mathcal {F}}$ is infinite, and let $\varphi _0,\varphi _1,\ldots$ be an enumeration of the formulas in ${\mathcal {F}}$. For every $i\ge 0$, let ${\mathcal {F}}_i=\left\{ \varphi _0 ,\dots ,\varphi _i\right\}$. We construct a sequence of infinite sets $A_0,A_1,\ldots \subseteq \mathbb {N}$ such that:

• For every $i\ge 0$, $A_{i+1}\subseteq A_i$.

• For every $0\le j\le i$, $a\in A_j$, and $b\in A_i$, $v_a(\varphi _j)=v_b(\varphi _j)$.

To do so, take some infinite set $A_0\subseteq \mathbb {N}$ such that $v_a(\varphi _0)=v_b(\varphi _0)$ for every $a,b\in A_0$ (such set must exist since we have a finite number of truth values). Then, given $A_i$, we let $A_{i+1}$ be some infinite subset of $A_i$ such that $v_a(\varphi _{i+1})=v_b(\varphi _{i+1})$ for every $a,b\in A_{i+1}$. The valuation v is defined by $v(\varphi _i)=v_a(\varphi _i)$ for some $a\in A_i$. The properties of the $A_i$’s ensure that v is well defined, and it can be shown that it also satisfies the required property.    $\square$

Using Lemma 2 and the compactness property, we can show the following:

Lemma 3

Let $v_0,v_1,\ldots$ be a sequence of valuations over a common domain ${\mathcal {F}}$ such that $v_m \in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ for every $m\ge 0$. Then, there exists some $v \in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$ such that for every $\varphi \in {\mathcal {F}}$, $v(\varphi )=v_m(\varphi )$ for some $m\ge 0$.

Proof (Outline)

By Lemma 2, there exists some v such that for every finite set ${\mathcal {F}}'$ of formulas, $v|_{{\mathcal {F}}'} = v_m|_{{\mathcal {F}}'}$ for some $m\ge 0$. It is easy to verify that v satisfies the required properties. In particular, one shows that $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ for every $m\ge 0$ by induction on m. In that proof we use Theorem 1 to obtain a finite such that $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m-1}}}\varphi$ from the assumption that . Then, the above property of v is applied with ${\mathcal {F}}'=\varGamma \cup \left\{ \varphi \right\}$.    $\square$

Now, our characterization theorem easily follows:

Theorem 2

The set $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$ is the largest set $\mathbb {V}$ of $\mathsf {M}_{{\texttt {K}}}$-legal ${\mathcal {F}}$-valuations that satisfies necessitation.

Proof (Outline)

To prove that $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$ satisfies necessitation, one needs to prove that if , then also for some $m\ge 0$. This is done using Lemma 3. For maximality, given a set $\mathbb {V}$, we assume by contradiction that there is some m such that $\mathbb {V}\not \subseteq \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$, take a minimal such m, and show that it cannot be 0. Then, from $\mathbb {V}\subseteq \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}{m-1}$, it follows that actually $\mathbb {V}\subseteq \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$, and thus we obtain a contradiction.    $\square$

Finite Domain. By definition we have $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0} \supseteq \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},1} \supseteq \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},2} \supseteq \ldots$ (and so, $\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0}}} \subseteq {} \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},1}}} {}\subseteq {} \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},2}}} \subseteq \ldots$). Next, we show that when ${\mathcal {F}}$ is finite, then this sequence must converge.

Lemma 4

Suppose that $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}=\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m+1}$ for some $m\ge 0$. Then, $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}=\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$.

Lemma 5

For a finite set ${\mathcal {F}}$ of formulas, $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}} = \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},4^{\vert {\mathcal {F}} \vert }}$.

Proof

The left-to-right inclusion follows from our definitions. For the right-to-left inclusion, note that by Lemma 4, $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}=\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m+1}$ implies that $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}=\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},k}$ for every $k\ge m$. Thus, it suffices to show that $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}=\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m+1}$ for some $0\le m\le 4^{{\vert {\mathcal {F}} \vert }}+1$. Indeed, otherwise we have $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0} \supset \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},1} \supset \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},2} \supset \ldots \supset \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},4^{{\vert {\mathcal {F}} \vert }}+1}$, but this is impossible since there are only $4^{\vert {\mathcal {F}} \vert }$ functions from ${\mathcal {F}}$ to ${\mathcal {V}}_{4}$.    $\square$

Optimized Tables. Starting from level 1, the condition on valuations allows us to refine the truth tables of $\mathsf {M}_{{\texttt {K}}}$, and reduce the search space for countermodels. For instance, since $\psi \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},0}}} \varphi \supset \psi$ (for every ${\mathcal {F}}$ with $\left\{ \psi ,\varphi , \varphi \supset \psi \right\} \subseteq {\mathcal {F}}$), at level 1 we have that if , then . This allows us to remove and from the first and third columns (when ) in the table presenting $\tilde{\supset }$. The following entailments (at level 0), all with a single occurrence of some connective, lead to similar refinements, resulting in the optimized tables below for $\supset$, $\wedge$ and $\vee$:

We note that level 1 valuations are not fully captured by these tables. For example, they must assign to every formula of the form $\varphi \supset \varphi$, while the table above allows also when . A decision procedure for ${\texttt {K}}$ can benefit from relying on these optimized tables instead of the original ones, starting from level 1.

4 Soundness and Completeness

In this section we establish the soundness and completeness of the proposed semantics. For that matter, we first extend the notion of satisfaction to sequents:

Definition 6

An ${\mathcal {F}}$-valuation v $\mathcal {D}$-satisfies an ${\mathcal {F}}$-sequent $\varGamma \Rightarrow \varDelta$, denoted by $v\models _{\mathcal {D}}\varGamma \Rightarrow \varDelta$, if $v\not \models _{\mathcal {D}}\varphi$ for some $\varphi \in \varGamma$ or $v\models _{\mathcal {D}}\varphi$ for some $\varphi \in \varDelta$.

To prove soundness, we first note that except for ${\textsc {(K)}}$, the soundness of each derivation rule easily follows from the Nmatrix semantics:

Lemma 6 (Local Soundness)

Consider an application of a rule of $\mathsf {{{G}_{{\texttt {K}}}}}$ other than ${\textsc {(K)}}$ deriving a sequent $\varGamma \Rightarrow \varDelta$ from sequents $\varGamma _1\Rightarrow \varDelta _1 ,\dots ,\varGamma _n\Rightarrow \varDelta _n$, such that $\varGamma \cup \varGamma _1 \cup \ldots \cup \varGamma _n \cup \varDelta \cup \varDelta _1 \cup \ldots \cup \varDelta _n \subseteq {\mathcal {F}}$. Let $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ for some $m\ge 0$. If $v\models _{\mathcal {D}}\varGamma _i\Rightarrow \varDelta _i$ for every $1 \le i \le n$, then $v\models _{\mathcal {D}}\varGamma \Rightarrow \varDelta$.

For ${\textsc {(K)}}$, we make use of the level requirement, and prove the following lemma.

Lemma 7 (Soundness of (K))

Suppose that $\varGamma \cup \Box \varGamma \cup \left\{ \varphi , \Box \varphi \right\} \subseteq {\mathcal {F}}$, and $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m-1}}}\varphi$. Then, $\Box \varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}\Box \varphi$.

Proof

Let $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ such that $v\models _{\mathcal {D}} \Box \varGamma$. We prove that $v\models _{\mathcal {D}}\Box \varphi$. By the truth table of $\Box$, we have that for every $\psi \in \varGamma$, and we need to show that . Since for every $\psi \in \varGamma$, we have . Since $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m-1}}} \varphi$, we have . Since $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$, it follows that .    $\square$

The above two lemmas together establish soundness, and from soundness for each level, we easily derive soundness for arbitrary ${\textsc {(K)}}$-depth.

Theorem 3

(Soundness for m). If $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varDelta$, then $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}} \varDelta$.

Theorem 4

(Soundness without m). If $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}}}\varGamma \Rightarrow \varDelta$, then $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}} \varDelta$.

By taking ${\mathcal {F}}={\mathcal {L}}$ in Theorem 4 we get that if $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}\varGamma \Rightarrow \varDelta$, then $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}} \varDelta$.

Next, we prove the following two completeness theorems:

Theorem 5

(Completeness for m). Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ closed under subformulas and $\varGamma \Rightarrow \varDelta$ an ${\mathcal {F}}$-sequent. If $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}\varDelta$, then $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varDelta$.

Theorem 6

(Completeness without m). Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ closed under subformulas and $\varGamma \Rightarrow \varDelta$ an ${\mathcal {F}}$-sequent. If $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}}\varDelta$, then $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}}}\varGamma \Rightarrow \varDelta$.

In fact, since ${\mathcal {F}}$ may be infinite, we need to prove stronger theorems than Theorems 5 and 6, that incorporate infinite sequents.

Definition 7

An $\omega$-sequent is a pair ${\langle L,R \rangle }$, denoted by ${L}\Rightarrow {R}$, such that L and R are (possibly infinite) sets of formulas. We write $\Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}{L}\Rightarrow {R}$ if $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varDelta$ for some finite $\varGamma \subseteq L$ and $\varDelta \subseteq R$.

Other notions for sequents (e.g., being an ${\mathcal {F}}$-sequent) are extended to $\omega$-sequents in the obvious way. In particular, $v\models _{\mathcal {D}}{L}\Rightarrow {R}$ if $v(\psi )\notin \mathcal {D}$ for some $\psi \in L$ or $v(\psi )\in \mathcal {D}$ for some $\psi \in R$.

Theorem 7

($\omega$-Completeness for m). Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ closed under subformulas and ${L}\Rightarrow {R}$ an $\omega$-${\mathcal {F}}$-sequent. If $L\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}R$, then $\Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}{L}\Rightarrow {R}$.

Theorem 8

($\omega$-Completeness without m). Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ closed under subformulas and ${L}\Rightarrow {R}$ an $\omega$-${\mathcal {F}}$-sequent. If $L\vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}}R$, then $\Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}}}{L}\Rightarrow {R}$.

Theorem 5 is a consequence of Theorem 7. Indeed, by Theorem 7, $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}\varDelta$ implies that $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}\varGamma '\Rightarrow \varDelta '$ for some (finite) $\varGamma '\subseteq \varGamma$ and $\varDelta '\subseteq \varDelta$. Using ${\textsc {(weak)}}$, we obtain that $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varDelta$. Similarly, Theorem 6 is a consequence of Theorem 8. Also, using Lemma 3, we obtain Theorem 8 from Theorem 7. Hence in the remainder of this section we focus on the proof of Theorem 7.

Proof of Theorem 7. We start by defining maximal and consistent $\omega$-sequents, and proving their existence.

Definition 8

(Maximal and consistent $\omega$-sequent). Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ and $m\ge 0$. An ${\mathcal {F}}$-$\omega$-sequent ${L}\Rightarrow {R}$ is called:

• 1. ${\mathcal {F}}$-maximal if ${\mathcal {F}}\subseteq L\cup R$.

• 2. ${\langle \mathsf {{{G}_{{\texttt {K}}}}},{\mathcal {F}},m \rangle }$-consistent if $\not \Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}{L}\Rightarrow {R}$.

• 3. ${\langle \mathsf {{{G}_{{\texttt {K}}}}},{\mathcal {F}},m \rangle }$-maximal-consistent (in short, ${\langle \mathsf {{{G}_{{\texttt {K}}}}},{\mathcal {F}},m \rangle }$-max-con) if it is ${\mathcal {F}}$-maximal and ${\langle \mathsf {{{G}_{{\texttt {K}}}}},{\mathcal {F}},m \rangle }$-consistent.

Lemma 8

Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ and ${L}\Rightarrow {R}$ an ${\mathcal {F}}$-$\omega$-sequent. Suppose that $\not \Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}{L}\Rightarrow {R}$. Then, there exist sets $L_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{m},{{L}\Rightarrow {R}})}$ and $R_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{m},{{L}\Rightarrow {R}})}$ such that the following hold:

• $L\subseteq L_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{m},{{L}\Rightarrow {R}})}$ and $R\subseteq R_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{m},{{L}\Rightarrow {R}})}$.

• $L_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{m},{{L}\Rightarrow {R}})} \cup R_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{m},{{L}\Rightarrow {R}})} \subseteq {\mathcal {F}}$.

• ${L_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{ m},{{L}\Rightarrow {R}})}}\Rightarrow {R_{MC({\mathsf {{{G}_{{\texttt {K}}}}}},{{\mathcal {F}}},{ m},{{L}\Rightarrow {R}})}}$ is ${\langle \mathsf {{{G}_{{\texttt {K}}}}},{\mathcal {F}},m \rangle }$-max-con.

Thus, given an underivable $\omega$-sequent, we can extend it to a ${\langle \mathsf {{{G}_{{\texttt {K}}}}},{\mathcal {F}},m \rangle }$-max-con $\omega$-sequent. This $\omega$-sequent induces the canonical countermodel, as defined next.

Notation 9

We denote the set $\left\{ \psi \in {\mathcal {F}}{\ |\ }\Box \psi \in X\right\}$ by ${{\mathbb {B}}_{{\mathcal {F}}}^{X}}$.

Definition 10

Suppose that $L \uplus R = {\mathcal {F}}$. The canonical model w.r.t.  ${L}\Rightarrow {R}$, ${\mathcal {F}}$, and m, denoted by $v({{\mathcal {F}}},{{L}\Rightarrow {R}},{m})$, is the ${\mathcal {F}}$-valuation defined as follows (in $\lambda$ notation):

Clearly, $v({{\mathcal {F}}},{{L}\Rightarrow {R}},{m}) \not \models _{\mathcal {D}} {L}\Rightarrow {R}$. The proof of Theorem 7 is done by induction on m, and then carries on by showing that if ${L}\Rightarrow {R}$ is ${\langle \mathsf {{{G}_{{\texttt {K}}}}},{\mathcal {F}},m \rangle }$-max-con, then $v({{\mathcal {F}}},{{L}\Rightarrow {R}},{m})$ belongs to $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ for every m.

Concretely, let . We show that $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},k}$ for every $k\le m$ by induction on k. The base case $k=0$ is straightforward. For $k>0$, we have $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},k-1}$ by the induction hypothesis. Let $\varphi \in {{\mathcal {F}}}$, and suppose that . To show that , we prove that $\Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m-1}{{{\mathbb {B}}_{{\mathcal {F}}}^{L}}}\Rightarrow {\varphi }$. By the outer induction hypothesis (regarding the completeness theorem itself), implies that , which implies that . Hence, there is a finite set such that $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m-1}\left\{ \varphi _1,\dots ,\varphi _n\right\} \Rightarrow \varphi$. For every $1\le i\le n$, since , we have that $\Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m-1}{{{\mathbb {B}}_{{\mathcal {F}}}^{L}}}\Rightarrow {\varphi _i}$ and hence $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m-1}{\varGamma _i}\Rightarrow {\varphi _i}$ for some $\varGamma _i\subseteq {{\mathbb {B}}_{{\mathcal {F}}}^{L}}$. Using n applications of ${\textsc {(cut)}}$ on these sequents and $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m-1}\left\{ \varphi _1,\dots ,\varphi _n\right\} \Rightarrow \varphi$, we obtain that $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m-1}\varGamma _1,\dots ,\varGamma _n\Rightarrow \varphi$, and so $\Vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m-1}{{\mathbb {B}}_{{\mathcal {F}}}^{L}}\Rightarrow \varphi$.

5 Effectiveness of the Semantics

In this section we study the effectiveness of the semantics introduced in Definition 5 for deciding $\vdash _{{\mathsf {M}_{{\texttt {K}}}}}^{{}}{}$. Roughly speaking, a semantic framework is said to be effective if it induces a decision procedure that decides its underlying logic.

Consider Algorithm 1. Given a finite set $\varGamma$ of formulas and a formula $\varphi$, it checks whether any valuations in $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ is a countermodel. The correctness of this algorithm relies on the analyticity of $\mathsf {{{G}_{{\texttt {K}}}}}$, namely:

Lemma 9

([11]). If $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}\varGamma \Rightarrow \varDelta$, then $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{ sub (\varGamma \cup \left\{ \varphi \right\} )}\varGamma \Rightarrow \varDelta$.

Using Lemma 9, we show that the algorithm is correct.

Lemma 10

Algorithm 1 always terminates, and returns “YES” iff $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}}\varphi$.

Proof

Termination follows from the fact that $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ is finite. Suppose that the result is “YES” and assume for contradiction that $\varGamma \not \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}}\varphi$. Hence, there exists some $u\in \mathbb {V}_{{\texttt {K}}}$ such that $u\models _{\mathcal {D}}\varGamma$ and $u\not \models _{\mathcal {D}}\varphi$. Consider . Then, $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}\subseteq \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$, which contradicts the fact that the algorithm returns “YES”. Now, suppose that the result is “NO”. Then, there exists some $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ such that $v\models _{\mathcal {D}}\varGamma$ and $v\not \models _{\mathcal {D}}\varphi$. By Lemma 5, $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$. Hence, $\varGamma \not \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}}\varphi$. By Theorem 3, we have $\not \vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}}}\varGamma \Rightarrow \varphi$. By Lemma 9, we have $\not \vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}\varGamma \Rightarrow \varphi$. By Theorem 6, we have $\varGamma \not \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}}\varphi$.    $\square$

Lemma 10 shows that Algorithm 1 is a decision procedure for $\vdash _{{\mathsf {M}_{{\texttt {K}}}}}^{{}}{}$, when ignoring the additional output provided in Line 5. However, it is typical in applications that a “YES” or “NO” answer is not enough, and often it is expected that a “NO” result is accompanied with a countermodel. Algorithm 1 returns a valuation v in case the answer is “NO”, but Lemma 10 does not ensure that v is indeed a countermodel for $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}}\varphi$. The issue is that the valuation v from the proof of Lemma 10 witnesses the fact that $\not \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}}$ only in a non-constructive way. Indeed, using the soundness and completeness theorems, we are able to deduce that $v'\models _{\mathcal {D}}\varGamma$ and $v'\not \models _{\mathcal {D}}\varphi$ for some $v'\in \mathbb {V}_{{\texttt {K}}}$, but the relation between v and $v'$ is unclear. Most importantly, it is not clear whether v and $v'$ agree on ${\mathcal {F}}$-formulas. In the remainder of this section we prove that $v'$ extends v, and so the returned countermodel of Line 5 can be trusted.

We say that a valuation $v'$ extends a valuation v if ${\mathsf {Dom(}v ) }\subseteq {\mathsf {Dom(}v' ) }$ and $v'(\varphi )=v(\varphi )$ for every $\varphi \in {\mathsf {Dom(}v ) }$ (identifying functions with sets of pairs, this means $v \subseteq v'$). Clearly, for a ${\mathsf {Dom(}v ) }$-formula $\psi$ we have that $v'\models _{\mathcal {D}}\psi$ iff $v\models _{\mathcal {D}}\psi$. We first show how to extend a given valuation $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ by a single formula $\psi$ such that $sub (\psi ){\setminus }\left\{ \psi \right\} \subseteq {\mathcal {F}}$, obtaining a valuation $v'\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}\cup \left\{ \psi \right\} ,m}$ that agrees with v on all formulas in ${\mathcal {F}}$.

Lemma 11

Let $m\ge 0$, ${\mathcal {F}}\subseteq {\mathcal {L}}$, and $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$. Let $\psi \in {\mathcal {L}}{\setminus }{\mathcal {F}}$ such that $sub (\psi ){\setminus }\left\{ \psi \right\} \subseteq {\mathcal {F}}$. Then, v can be extended to some $v'\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}\cup \left\{ \psi \right\} ,m}$.

We sketch the proof of Lemma 11.

When $m=0$, $v'$ exists from Lemma 1. For $m>0$, we define $v'$ as follows:¹

The proof of Lemma 11 then carries on by showing that $v'\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}\cup \left\{ \psi \right\} ,m}$.

Next, Lemma 11 is used in order to extend partial valuations into total ones.

Lemma 12

Let $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ for some ${\mathcal {F}}$ closed under subformulas. Then, v can be extended to some $v'\in \mathbb {V}_{{\texttt {K}}}^{m}$.

Finally, Lemmas 3 and 12 can be used in order to extend any partial valuation in $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$ into a total one.

Lemma 13

Let $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$ for some set ${\mathcal {F}}$ closed under subformulas. Then, v can be extended to some $v'\in \mathbb {V}_{{\texttt {K}}}$.

We conclude by showing that when Algorithm 1 returns (“NO”, v), then v is a finite representation of a true countermodel for $\varGamma \vdash _{{\mathsf {M}_{{\texttt {K}}}}}^{{}}{}\varphi$.

Corollary 1

If $\varGamma \not \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}}\varphi$. Then Algorithm 1 returns (“NO”, v) for some v for which there exists $v'\in \mathbb {V}_{{\texttt {K}}}$ such that $v=v'|_{ sub (\varGamma \cup \left\{ \varphi \right\} )}$, $v'\models _{\mathcal {D}}\varGamma$, and $v'\not \models _{\mathcal {D}}\varphi$.

Proof

Suppose that $\varGamma \not \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}}}\varphi$. Then by Lemma 10, Algorithm 1 does not return “YES”. Therefore, it returns (“NO”, v) for some $v\in \mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}$ such that $v\models _{\mathcal {D}}\varGamma$ and $v\not \models _{\mathcal {D}}\varphi$, where ${\mathcal {F}}= sub (\varGamma \cup \left\{ \varphi \right\} )$ and $m = 4^{{\vert {\mathcal {F}} \vert }}$. By Lemma 5, $v\in \mathbb {V}_{{\texttt {K}}}{{\mathcal {F}}}$. By Lemma 13, v can be extended to some $v'\in \mathbb {V}_{{\texttt {K}}}$. Therefore, $v=v'|_{ sub (\varGamma \cup \left\{ \varphi \right\} )}$, $v'\models _{\mathcal {D}}\varGamma$, and $v'\not \models _{\mathcal {D}}\varphi$.    $\square$

Remark 2

Notice that in scenarios where model generation is not important, m can be set to a much smaller number in Line 2 of Algorithm 1, namely, the “modal depth” of the input.² The reason for that is that for such m, it can be shown that $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varphi$ iff $\vdash _{\mathsf {{{G}_{{\texttt {K}}}}}}^{{\mathcal {F}}}\varGamma \Rightarrow \varphi$, by reasoning about the applications of rule ${\textsc {(K)}}$. Using the soundness and completeness theorems, we can get $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}}}\varphi$ iff $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}}}\varphi$, and so limiting to such m is enough. Notice however, that we do not necessarily get $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}},m}=\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$ for such m, and so the valuation returned in Line 5 might not be an element of $\mathbb {V}_{{\texttt {K}}}^{{\mathcal {F}}}$.

6 The Modal Logic ${\texttt {KT}}$

In this section we obtain similar results for the modal logic ${\texttt {KT}}$. First, the calculus $\mathsf {{{G}_{{\texttt {KT}}}}}$ is obtained from $\mathsf {{{G}_{{\texttt {K}}}}}$ by adding the following rule (see, e.g., [16]):

Derivations are defined as before. (In particular, the ${\textsc {(K)}}$-depth of a derivation still depends on applications of rule ${\textsc {(K)}}$, not of rule (T).) We write $\vdash _{\mathsf {{{G}_{{\texttt {KT}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varDelta$ if there is a derivation of $\varGamma \Rightarrow \varDelta$ in $\mathsf {{{G}_{{\texttt {KT}}}}}$ in which only ${\mathcal {F}}$-sequents occur and that has ${\textsc {(K)}}$-depth at most m.

Next, we consider the semantics. For a valuation $v\in \mathbb {V}_{{\texttt {K}}}$ to respect rule (T), we must have that if $v\models _{\mathcal {D}}\varGamma ,\varphi \Rightarrow \varDelta$, then $v\models _{\mathcal {D}}\varGamma ,\Box \varphi \Rightarrow \varDelta$. In particular, when $v\not \models _{\mathcal {D}}\varGamma \Rightarrow \varDelta$, we get that if $v(\varphi )\notin \mathcal {D}$, then $v(\Box \varphi )\notin \mathcal {D}$. Now, if , then $v(\Box \varphi )\in \mathcal {D}$ according to the truth table of $\Box$ in $\mathsf {M}_{{\texttt {K}}}$. But, we must have $v(\Box \varphi )\notin \mathcal {D}$. This leads us to remove from $\mathsf {M}_{{\texttt {K}}}$.

We thus obtain the following Nmatrix $\mathsf {M}_{{\texttt {KT}}}$: The sets of truth values and of designated truth values are given by³

and the truth tables are as follows:

Again, one may gain intuition from the possible worlds semantics. There, the logic ${\texttt {KT}}$ is characterized by frames with reflexive accessibility relation. Thus, for instance, if $\psi$ holds in w but not in some world accessible from w (i.e., $\psi$ has value ), we know that $\Box \psi$ does not hold in w, and the reflexivity of the accessibility relation implies that $\Box \psi$ does not hold in some world accessible from w (thus $\Box \psi$ has value ).

Example 4

Let and . The sequent $\Rightarrow \varphi$ has a derivation in $\mathsf {{{G}_{{\texttt {KT}}}}}$ using only ${\mathcal {F}}$ formulas of ${\textsc {(K)}}$-depth of 1. However, it is not satisfied by all $\mathsf {M}_{{\texttt {KT}}}$-legal ${\mathcal {F}}$-valuations. For example, the following valuation is an $\mathsf {M}_{{\texttt {KT}}}$-legal valuation that does not satisfy $\varphi$:

Next, we define the levels of valuations for $\mathsf {M}_{{\texttt {KT}}}$. These are obtained from Definition 5 by removing the value :

Definition 11

The set $\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}},m}$ is recursively defined as follows:

• $\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}},0}$ is the set of $\mathsf {M}_{{\texttt {KT}}}$-legal ${\mathcal {F}}$-valuations.

• 

We also define:

Example 5

Following Example 4, we note that for every $v\in \mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}},m}$ with $m>0$, we have $v\models _{\mathcal {D}}\varphi$. In particular, the valuation v from Example 4 does not belong to $\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}},m}$: , $\Box (p_1\wedge p_2) \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}},0}}}p_1$, but .

Similarly to Theorem 2, the levels of valuations converge to a maximal set that satisfies the following condition:

Theorem 9

The set $\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}}}$ is the largest set $\mathbb {V}$ of $\mathsf {M}_{{\texttt {KT}}}$-legal ${\mathcal {F}}$-valuations that satisfies ${ necessitation}_{{\texttt {KT}}}$.

The proof of Theorem 9 is analogous to that of Theorem 2.

Remark 3

The ${ necessitation}_{{\texttt {KT}}}$ condition is equivalent to the one given in [8], except that the underlying truth table is different. Theorem 9 proves that our gradual way of defining $\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}}}$ via levels coincides with the semantic condition from [8].

As we demonstrated for ${\texttt {K}}$, starting from level 1, the condition on valuations allows us to refine the truth tables of $\mathsf {M}_{{\texttt {KT}}}$, and reduce the search space. Simple entailments (at level 0) lead to the optimized tables below for $\supset$, $\wedge$ and $\vee$:

Soundness and completeness for $\mathsf {{{G}_{{\texttt {KT}}}}}$ are obtained analogously to $\mathsf {{{G}_{{\texttt {K}}}}}$, keeping in mind that $\mathsf {M}_{{\texttt {KT}}}$ is obtained from $\mathsf {M}_{{\texttt {K}}}$ by deleting the value . For soundness, this is captured by the rule (T). For completeness, the same construction of a countermodel is performed , while rule (T) ensures that it is three-valued.

Theorem 10 (Soundness and Completeness)

Let ${\mathcal {F}}\subseteq {\mathcal {L}}$ closed under subformulas and $\varGamma \Rightarrow \varDelta$ an ${\mathcal {F}}$-sequent.

• 1. For every $m\ge 0$, $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}},m}}}\varDelta$ iff $\vdash _{\mathsf {{{G}_{{\texttt {KT}}}}}}^{{\mathcal {F}},m}\varGamma \Rightarrow \varDelta$.

• 2. $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}}}}}\varDelta$ iff $\vdash _{\mathsf {{{G}_{{\texttt {KT}}}}}}^{{\mathcal {F}}}\varGamma \Rightarrow \varDelta$.

Effectiveness is also shown similarly to ${\texttt {K}}$. For that matter, we use the following main lemma, whose proof is similar to Lemma 13. The only component that is added to that proof is making sure that the constructed model is three-valued.

Lemma 14

Let $v\in \mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}}}$ for some set ${\mathcal {F}}$ closed under subformulas. Then, v can be extended to some $v'\in \mathbb {V}_{{\texttt {KT}}}$.

Let Algorithm 2 be obtained from Algorithm 1 by setting m to $3^{{\vert {\mathcal {F}} \vert }}$ in Line 2, and taking $v\in \mathbb {V}_{{\texttt {KT}}}^{{\mathcal {F}},m}$ in Line 3. Similarly to Lemma 10 and Corollary 1, we get that Algorithm 2 is a model-producing decision procedure for $\vdash _{{\mathsf {M}_{{\texttt {KT}}}}}^{{}}{}$.

Lemma 15

Algorithm 2 always terminates, and returns “YES” iff $\varGamma \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {KT}}}}}\varphi$. Further, if $\varGamma \not \vdash _{{\mathcal {D}}}^{{\mathbb {V}_{{\texttt {KT}}}}}\varphi$, then it returns (“NO”, v) for some v for which there exists $v'\in \mathbb {V}_{{\texttt {KT}}}$ such that $v=v'|_{ sub (\varGamma \cup \left\{ \varphi \right\} )}$, $v'\models _{\mathcal {D}}\varGamma$, and $v'\not \models _{\mathcal {D}}\varphi$.

7 Future Work

We have introduced a new semantics for the modal logic ${\texttt {K}}$, based on levels of valuations in many-valued non-deterministic matrices. Our semantics is effective, and was shown to tightly correspond to derivations in a sequent calculus for ${\texttt {K}}$. We also adapted these results for the modal logic ${\texttt {KT}}$.

There are two main directions for future work. The first is to establish similar semantics for other normal modal logics, such as ${\texttt {KD}}$, ${\texttt {K4}}$, ${\texttt {S4}}$ and ${\texttt {S5}}$, and to investigate $\Diamond$ as an independent modality. The second is to analyze the complexity, implement and experiment with decision procedures for ${\texttt {K}}$ and ${\texttt {KT}}$ based on the proposed semantics. In particular, we plan to consider SAT-based decision procedures that would encode this semantics in SAT, directly or iteratively.