1 Introduction

The operation of supply chains is a major cost driver for all manufacturing companies. It is imperative to keep this cost at a minimum and the service level at a maximum to enable companies to redirect investment to their core goals, such as the development of new drugs in the healthcare industry. The field that deals with this task is called inventory management and has served as an intensely studied research area for many decades. In practice, companies often rely on parameterized reorder policies for the operation of inventory management (e.g., De Kok et al. 2018). These consist, for example, of a periodic reorder timing (T) and a reorder quantity (Q) that depends on the difference of the current inventory on hand (IOH) and the target IOH. The conceptual designs of such parameterized reorder policies are usually hand-crafted and based on historical experiences, sales forecast information, and safety stock considerations. Parameterized reorder policies are intuitive and easily applicable—on the other hand, they tend to be an oversimplified solution for a complex challenge due to the stochastic characteristics of the problem: E.g., demand anomalies require a situational T and Q, which highlights the importance of so-called dynamic reorder policies.

Finding an optimized, dynamic reorder policy for a given network of inventory systems is a challenging task. With recent advances in the field of Artificial Intelligence (AI), the question naturally arises: Can AI help to make better decisions, and thus, reduce the cost for the operation of supply chains? This question is justified, especially when one considers that the best chess player in the world is not a human being anymore (Silver et al. 2017). Just like chess, inventory management is a challenge in which the optimal sequence of decisions is sought. If with chess, we are looking for the optimal sequence of decisions that maximize the chances of winning, in the case of inventory management we are looking for the optimal sequence of decisions that minimize the cost.

Reinforcement Learning (RL) is the paradigm in the field of machine learning dedicated to learning an optimized policy in sequential decision-making challenges. At a high level, an agent takes situational decisions and receives feedback on the quality of the agent’s decision in return. As a consequence, the agent takes the feedback into account to improve the policy. In the latest research publications, policies are based on deep neural networks, in which case the methodology is referred to as Deep Reinforcement Learning (DRL). DRL has recently attracted considerable attention: An RL agent beats professional players in the classic board game Go, which is considered to be the most challenging board game use-case for AI due to its high number of possible combinations (Silver et al. 2016). DRL enables autonomous driving (Kiran et al. 2020) and can potentially be leveraged for precision dosing in the healthcare sector (Ribba et al. 2020). In this chapter we review the applicability of DRL for Multi-Echelon Inventory Optimization (MEIO).

This chapter aims to provide an introduction to the domain of MEIO with RL and is structured into eight sections: Sect. 2 introduces the term MEIO and explains the multiple challenges that are connected to it from an optimization perspective. Section 3 provides a brief overview of research streams in the field MEIO. Section 4 connects the topics MEIO and RL before Sect. 5 provides a detailed introduction to the concept of RL. Section 6 showcases an experiment to evaluate the applicability of RL in MEIO challenges. In Sect. 7 the results are discussed. Section 8 provides an outlook of potential future research streams. Section 9 showcases conclusions and provides an outlook of future research efforts.

2 Challenges of Multi-Echelon Inventory Management from an Optimization Perspective

The goal of inventory management optimization is to optimize the reorder policy in a way so that the cost related to the operation of inventory systems are minimized. This section introduces five layers of complexity explaining why inventory management is a highly challenging optimization task:

The major operational cost of inventory systems can be structured into holding-, shortage-, and reordering costs. This aspect introduces the first layer of complexity with regards to the optimization challenge: Minimizing holding cost through lowering the inventory level increases the likelihood of a stock-out and the associated shortage costs. To prevent stock-out, the ordering frequency can be increased, whereby this impacts the reordering cost on the other hand. This observation suggests that each cost category is interrelated leading to a complex, non-linear cost function.

The second layer of complexity is due to the stochastic characteristics of an inventory system: Each day, the IOH is reduced by the number of outgoing items (e.g., because of sales). This value depends on customer behavior, which can be estimated but is always associated with uncertainties, which is why this challenge falls under the category of stochastic optimization. Next to the demand, the lead time, which is defined as the time duration between order placement and supply delivery is another stochastic parameter. As a consequence, the decision-making must be optimal under the consideration of uncertainty.

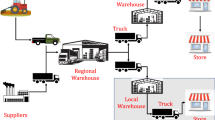
The third layer is due to the interconnected characteristic of reordering policies within a supply chain distribution network. This can be briefly illustrated by an example: A large reorder from one warehouse can use up the entire reserves of the parent warehouse, with all further reorders from other warehouses subsequently no longer being able to be serviced. This example makes clear why the optimization must be carried out holistically and not in a warehouse-by-warehouse manner. Optimization approaches addressing this holistic problem characteristic are referred to as MEIO.

The fourth layer results from the third layer: Given the fact that the optimal ordering policy of an individual inventory system can only be found if the reorder policy of the entire inventory system network is optimal, this leads to a high number of parameters that have to be optimized. Many algorithms that still meet the requirements related to a highly complex cost function, stochastic system dynamics, and holistic optimization fail to scale to real-world supply chain dimensions. The holistic view of the problem leads to a dilemma: Either one resorts to high-performance algorithms, which outperform the rule-based approaches by far, or one wants to perform a holistic optimization, in which case the high-performance algorithms are not applicable anymore. This is probably also the reason why many companies still use comparably simple methods such as rule-based control.

The fifth layer is the variability of model and optimization goal assumptions: Multi-Echelon Inventory Systems (MEIS) can be divergent, convergent, sequential, or mixed (Clark and Scarf 1960). The policy to be optimized can either be periodic (all reorders at fixed time intervals) or dynamic (De Kok et al. 2018). The same applies to the reorder quantity: This can be flexible for certain applications—in other cases, the lot sizes are fixed and the optimization goal is to select the best available option. It can be seen that optimization algorithms must be adapted to the specific situation and that the underlying model assumptions are highly variable. In the next section, it will be shown that many traditional optimization approaches have to be tailored exactly to the problem—and general applicability is not given.

In the remainder of this section, we want to emphasize a potential solution to this dilemma—before that we want to have a deeper look at existing research efforts in the MEIO domain.

3 Literature Review of Inventory Management

Due to the immense relevance and high complexity of multi-echelon inventory management, many research paths have developed in the area with the first major research papers dating back to the 1960s. De Kok et al. (2018) composed a comprehensive literature overview on stochastic multi-echelon inventory models. In fact, most of the research efforts from the early days focused on the development of exact models: In Clark and Scarf (1960) a mathematical proof was presented that the reorder policy of an individual warehouse can only be optimal if the reorder policy is optimal for the entire network. However, due to the complexity of the problem, these models are based on highly-simplified assumptions limiting the applicability to real-world supply chains (Gijsbrechts et al. 2021). De Kok et al. (2018) state that developing optimal policy structures has turned out to be intractable. This fact, combined with the technological development in the semiconductor field and the associated increase in computational capacities, has led the research focus shifting to other methodologies such as parameterized, simulation-based, and approximative policy optimization. These are by no means completely separate fields of research—many seminal papers proposed a combination of the aforementioned algorithm categories. In order to provide the reader with an easy-to-understand intuition, the three areas are discussed separately below.

Parameterized policy optimization experienced its rise in the 1990s (De Kok et al. 2018). One prominent representative of parameterized policies is the base-stock policy, also known as (s, S) inventory control policy. Each time when the inventory level drops below the reorder point s, a reorder is triggered to fill up the inventory level to a target inventory level S. Now, the entire inventory system behavior can be described in two parameters (s, S). The task of optimally configuring these parameters has been tackled via meta-heuristic or simulation-based approaches.

Heuristic methods aim at solving optimization problems under the constraint of limited prior knowledge and limited time. Examples of heuristic methods are, e.g., genetic algorithms (Grahl et al. 2016).

Unfortunately, there are some disadvantages associated with heuristic methods: (1) they do not provide optimality guarantees, and (2) they lack general applicability. If there are changes in the supply chain network structure or in the model assumption, the method needs to be revised—whereby finding the right parameters can become a huge effort.

Simulation-based policy optimization is a frequently used approach with numerous variations (Chu et al. 2015). The main ingredients are: (1) A model simulates the inventory system network taking policy parameters as an input and outputs the corresponding performance measures. Three model categories are particularly well suited: The MEIS can be interpreted as a classic coupled tank system in control engineering turning the problem into a set of complicated differential equations which is challenging to be solved. Another option is an agent-based model as performed in (Chu et al. 2015). Each individual inventory system is modeled by the interaction of four different agents: A facility agent, an order agent, a shipment agent, and a customer agent. The characteristic of such an agent-based system can be categorized as a black-box function. The third option is a hybrid model allowing to access specific model structures while other components remain black-box functions. (2) A Monte-Carlo method estimating the expected value of the performance measure for a given set of policy parameters over multiple simulation time steps. (3) An optimization algorithm evaluating how to update the policy parameters to iteratively optimize the performance. Two drawbacks are related to this approach. Similar to the heuristic methods, the Monte-Carlo estimation performed in step (2) is computationally intense leading to poor scaling properties. Secondly, the optimization algorithm converges to a minimum, but this may be a bad local minimum.

Approximative policy optimization interprets the inventory system as a Markov Decision Process (MDP) which is covered in more detail in Sect. 4.1 (Powell 2007). MDPs are typically solved with dynamic programming (DP) approaches. However, due to the complexity of the system, these methodologies do not have the required scaling properties to be a suitable solution to a MEIO challenge. Thus, approximate dynamic programming approaches have been developed to simplify the underlying dynamic program. According to Gijsbrechts et al. (2021), these can be structured into three distinct research branches: The first branch exploits the problem structure by simplifying assumptions such as very short lead times. Another branch aggregates multiple states to a single state based on hand-crafted features. The third branch approximates the value or the policy function of the MDPs. Two famous representatives using function approximation are linear programming-approximate dynamic programming Approximate Dynamic Programming (LP-ADP) and RL with the remainder of this chapter focusing on the latter method.

4 Reinforcement Learning for Inventory Management

4.1 Markov (Decision) Processes

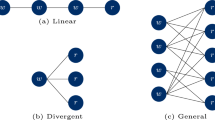
The operation of inventory systems is related to multiple stochastic processes (e.g., the demand and lead times) and can be modeled as a Markov Process (MP) (e.g.,  Broyles et al. 2010). The relevant components and quantities describing a Markov chain are states, transition probabilities, and, optionally, performance metrics describing the quality of a state. Figure 1a showcases a Markov chain modeling a highly-simplified inventory system for explanatory purposes. The state space consists of two states representing a low IOH-level (LIOH) and a high IOH-level (HIOH). Each time step, the IOH transitions from one state to another state if the IOH exceeds (e.g., through backordering) or falls below (e.g., through customer demand) a certain threshold—otherwise the system remains in the same state. The set of all transition probabilities is referred to as system dynamics and regulates the probabilities via which the state of the system changes to another state and remains constant over the full period of time to fulfill the so-called Markov property. The system dynamics result from processes impacting the state of the inventory systems such as the demand and reordering activities. In this use-case, we consider one performance metric describing the overall cost associated with the operation of the inventory system. To create an intuition, we can associate the state HIOH with low cost and the state LIOH with high cost. This example is arbitrary and for explanatory purposes only, but could be justified with a higher likelihood of the event of a stock-out in case of a LIOH and with shortage cost outweighing the cost for holding a high number of inventory. The expected cost over multiple time steps depends on the number of time steps and the equilibrium distribution describing how often the system is in state LIOH or HIOH respectively. The equilibrium distribution solely depends on the system dynamics and can be calculated analytically or in case of complex Markov chains estimated with a Markov Chain Monte Carlo (MCMC) simulation.

Fig. 1
figure 1

(a) Describes the stochastic behavior of the inventory systems IOH in a highly-simplified way. In each time step the system can either remain in the same state or transition to the other state. Processes such as the demand may cause the IOH to decrease. Processes such as reordering may increase the IOH. The behavior of the system is described with the system dynamics displayed in (b). (d) Displays a MDP with a policy responsible for the reorder decision summarized as \(\pi \text {(the policy)}\) and non-controllable processes such as the demand. In each time step, an agent takes a decision (reorder or no reorder) according to the policy. The overall system behavior can thus be defined as a combination of the policy \(\pi \) and the system dynamics P as illustrated in (e)

Full size image

The Markov model is a suitable framework for describing stochastic systems—however, to use it as a basis for finding an optimal control strategy some extensions need to be applied: Firstly, we need to differentiate processes, which influence the system dynamics, into controllable and non-controllable processes. With regards to an inventory system, e.g., the reorder decision is a controllable process, whereby there are limited options to control the customers demand. The non-controllable processes remain referred to as system dynamics, whereby controllable processes are denoted as the policy. Modelwise, this means that each system state (LIOH/HIOH) is followed by a decision (e.g., reorder (R)/not-reorder (NR)) taken by an agent in accordance with the policy, which by itself is followed by the successor state with a dependency on the selected action and the corresponding system dynamics. With the possibility of actively intervening into the system through the policy, we have introduced the concept of an MDP (Puterman 1990). Figure 1c highlights the difference between an MP and an MDP. The policy is referred to as an optimal policy in case it minimizes the expected overall cost in a way that no other policy can be associated with a lower expected overall cost.

As mentioned, however, this is a greatly simplified model and the reality is far more complex. On the one hand, an order does not immediately lead to an increase in the inventory level. Instead, it often takes a few days for the delivery. A policy should be aware of open orders to avoid multiple reorders in a low inventory level state. In fact, this is one aspect explaining why the state space is of much higher complexity than displayed in Fig. 1: There must be a specific state for each IOH and open order combination, whereby the open-order situation can be quantified with two additional dimensions: the order timing and the order quantity. Furthermore, the inventory level should be structured in a much more fine-granular way: We need one state for each possible inventory level—instead of grouping it into low and high IOH-levels. Moreover, the action choices need to be revised: In Fig. 1 it is distinguished between reordering and not-reordering. In reality, inventory systems can select one of the multiple order quantities. These examples should provide the reader an intuition, why the real state and action space is much more complex and high-dimensional compared to the simplified variant illustrated in Fig. 1.

5 Introduction to Reinforcement Learning

RL is a promising approach to tackle inventory optimization challenges because of the following reasons:

  • The policy can be represented by a deep neural network with all its related advantages: The representative capacity of neural networks is high, allowing to properly identify n-order dependencies of the input variables. In addition, deep neural networks are capable of generalization: It is not necessary to simulate every situation in a training stage (which would be computationally impossible)—it is enough to have encountered a limited set of situations and apply an action that performed well according to generalized experiences. Furthermore, the input values can be relatively unstructured and may include information that is redundant to identify the optimal control.

  • RL is generally applicable to every inventory system setups—with only little expert knowledge or intense model tuning required. Intuitively speaking, the algorithm finds its own way to the optimal policy. This is the aspect that distinguishes RL from other methods that are often used in inventory optimization challenges—especially from heuristic approaches.

  • Thanks to the expected reward properties which are discussed in the following section, RL is optimizing decisions considering the long-term outcomes instead of optimizing the short-term consequences. This is a very important feature of many decision-making processes.

5.1 Value-Based Methods

We already introduced five essential components in RL. The current state of a system is captured in a state vector. In an inventory system context, this state vector may include the current inventory level on hand and the open-order situation. The agent then applies a policy taking the state vector as an input and mapping it onto an action vector. This action vector may include information such as whether to reorder and how much to reorder. The action is subsequently applied to the environment causing effects regarding the systems state: The system transitions from one state to another state. Next to the state, the environment returns another signal that enables the policy to learn an optimal policy: The reward. The reward provides the agent with the information, whether the action taken in the last state was actually a good choice or not. In the case of a supply chain cost optimization use-case, this reward may represent the overall cost. However, optimizing the immediate reward can be myopic: In the short term, total cost can be reduced by not ordering and avoiding transportation cost. In the long term, this causes shortage cost due to stock-out. This example showcases the need to consider the long-term consequences of an action. A mathematical basis for integrating these long-term consequences is provided by the Bellman equation: The quality of a state is defined as the expected sum of rewards collected in the next time step and all future time steps. This value can be assigned to every state (state value v), and to every state-action pair (action value q) (Sutton and Barto 2018a).

Fig. 2
figure 2

An agent applies a policy \(\pi (a_t|s_t)\) by mapping a state vector \(s_t\) onto an action vector \(a_t\). The action is then applied to a system that is denoted as environment. The systems state is changed due to the agents action with the new state \(s_{t+1}\) and the reward signal \(r_{t+1}\) passed to the agent

Full size image

The state value is defined as the expected reward \(G_t\) at time step t conditioned on the state \(S_t\) at time step t following a policy \(\pi \).

$$\begin{aligned} V(s) = {\mathbb {E}}_{\pi }[G_t|S_t=s]\end{aligned}$$
(1)

The expected reward \(G_t\) can be expressed as the sum of rewards collected at the next time step and all future time steps k. Since the uncertainty increases with increasing k, each reward can be considered with a discount factor \(\gamma ^{t+k+1}\), with \(\gamma \in [0,1]\). If \(\gamma = 1\), each future reward is weighted equally, independent of the moment of occurrence. In contrast to this, a \(\gamma \) close to zero focuses on nearby rewards through masking out distant future rewards. From this it follows that

$$\begin{aligned} V(s) = {\mathbb {E}}_{\pi }\left[ \sum _{k=0}^{\infty } \gamma ^k R_{t+k+1}| S_t=s\right] \end{aligned}$$
(2)

The summand related to \(k = 0\) need to be extracted from the sum, to prepare the following steps introduced in Eq. 3–5.

$$\begin{aligned} V(s) = {\mathbb {E}}_{\pi }[R_{t+1}+\gamma \sum _{k=0}^{\infty } \gamma ^k R_{t+k+2}| S_t=s] \end{aligned}$$
(3)

The expected reward depends on the policy \(\pi (a|s)\) and the system dynamics \(p(s',r|s,a)\). Taking these equations as deterministic equations helps to move them out of the expected value:

$$\begin{aligned} V(s) = \sum _{a} \pi (a|s) \sum _{s'} \sum _{r} p(s',r|s,a)[r+\gamma {\mathbb {E}}_{\pi }[\sum _{k=0}^{\infty }\gamma ^k R_{t+k+2}| S_{t+1=s'}] \end{aligned}$$
(4)

A close look suffices to replace the remaining term in the expected value with a deterministic expression. The term within the expected value is similar to the expression in Eq. 2. The only difference is that Eq. 2 formulates the state value for state s, where the expected value in Eq. 4 refers to the expected value of the successor state \(s'\). Therefore Eq. 4 can be rewritten as

$$\begin{aligned} V(s) = \sum _{a} \pi (a|s) \sum _{s'} \sum _{r} p(s',r|s,a)[r+\gamma v_{\pi }(s')] \end{aligned}$$
(5)

Equations 1–5 and more details are summarized by Sutton and Barto (2018b). The expected reward of a state or a state-action combination depends on the policy \(\pi \), system dynamics p, the reward of the current time step r, the discount factor \(\gamma \), and the quality of the next state \(v_\pi (s')\). While the policy-dependency seems to be intuitive (the better the decision-making, the better the expected outcome), one challenging factor must be considered: Both, the system dynamics p and the state-values may be unknown. One way to deal with this is to try to estimate the value function V(s) and to further improve the estimation with every additional interaction.

Two common value function estimation methodologies exist: The Monte-Carlo (MC) method and Temporal Difference (TD) learning (Sutton and Barto 2018a). Both are based on the Bellman equation. The MC method learns in an episode-by-episode sense by accumulating the reward encountered after taking action \(a_t\) in state \(s_t\) in time step t. On the other hand, the TD method allows updating the state value in every time step.

The TD method is based on the definition of the expected reward:

$$\begin{aligned} G_t = R_{t+1} + \gamma R_{t+2} + \gamma ^2R_{t+3} + \gamma ^3R_{t+4} + ... \end{aligned}$$
(6)

The \(\gamma \) for the second summand and all following summands can be factored out.

$$\begin{aligned} G_t = R_{t+1} + \gamma \cdot (R_{t+2} + \gamma ^1R_{t+3} + \gamma ^2R_{t+4} + ...) \end{aligned}$$
(7)

As a consequence, the expected reward of the current time step t can be formulated as a sum of the reward and the expected reward of the next time step \(t+1\):

$$\begin{aligned} G_t = R_{t+1} + \gamma G_{t+1} \end{aligned}$$
(8)

The characteristics illustrated in Eq. 8 can be leveraged as a basis for learning: The expected rewards \(G_t\) and \(G_{t+1}\) are estimates and may originate from a model output. On the other hand, the right side of the equation incorporates a \(R_{t+1}\) which has been encountered by interacting with the environment. Thus, it can be assumed that the right side of the equation is generally more accurate and can serve as the TD target. The left-hand side can be seen as a TD prediction. The difference between TD target and TD prediction can be understood as the TD error. This underlines the analogy to supervised learning methods. A model can now be trained according to the prediction and the target, wherein RL the target is only a better estimate and in supervised learning ground truth. From another perspective, while the goal of supervised learning is to minimize the difference between the prediction and the target, RL faces an additional challenge as the target is a moving target being updated in every learning step. The procedure of updating an estimate with another estimate is called bootstrapping and explains why RL is typically more computationally intensive compared to supervised learning. Next to the learning aspect, RL is also more computationally intensive from a sampling process perspective. In supervised learning, the labeled dataset is usually static and already given at the beginning of the learning process. In the case of RL, the data is collected during the learning process through interacting with an environment.

The value function \(V(S_t)\) can be updated with the temporal difference using the following update rule:

$$\begin{aligned} V(S_t) = V(S_t) + \alpha [R_{t+1} + \gamma V(S_{t+1}) - V(S_t)], \end{aligned}$$
(9)

with \(\alpha \) representing the update step length. An analogous contemplation can also be carried out for action values.

So far, it was discussed how to estimate and update a value for each specific state. Each state must be visited multiple times until the value function can estimate the corresponding value accurately. This is possible if the state of the environment can be described with a discrete vector and a limited amount of distinct states. However, if the state space becomes more numerous or even continuous, this approach becomes infeasible due to computational complexity—the computation time to develop an appropriate value estimate for each state would grow toward infinity. For this reason, we need to look at models that can approximate without much loss of performance. Is it possible to draw conclusions from an experience in one state for similar states?

This question leads inevitably to the topic of neural networks. The idea of leveraging Multi-layer Perceptrons (MLPs) as non-linear function approximators in RL was considered to be unstable until Mnih et al. (2013) proposed Deep Q-Networks (DQN). Two contributions are responsible for this breakthrough:

Firstly, the concept of an experience replay buffer was introduced: Instead of learning from experiences as they occur, they are stored in a table named replay buffer. The information stored consists of the state-action pair \(s_t, a_t\), the corresponding reward \(r_t+1\) and the successor state \(s_t+1\). Subsequently, the experience-making and the learning process can be seen as decoupled processes as the learning takes place on the basis of randomly selected samples from the replay buffer. This procedure removes the temporal correlation between the samples and stabilizes the convergence properties.

Secondly, the concept of target networks was introduced: Two function approximators are used instead of one: (1) A target network and (2) a behavior network. The target network represents a copy of the behavior network and is used to calculate the Bellman update. The Bellman update is used to update the parameters of the behavior network. The parameters of the target network are periodically updated according to the behavior network. This concept keeps the target more stable compared to updating the target in every time step and has a stabilizing effect on the training process. Many extensions of DQN have been published such as Double Deep Q-Networks (Double DQN) (van Hasselt et al. 2015), Prioritized Experience Replay (Schaul et al. 2015), or Dueling Deep Q Networks (Dueling DQN) (Wang et al. 2016).

Despite all advantages, value-based methods cannot handle continuous action spaces without leveraging an additional optimization technique. According to (Lillicrap et al. 2015), the idea to simply discretizing a continuous action space into a fine-granular discrete action space often fails: Even small systems with little degrees of freedom are related to a sprawling action space leading to a too high sample complexity. One method to enable the control of continuous action spaces is introduced in the subsequent section.

5.2 Policy-Based Methods

This section introduces the fundamental concepts of policy-gradient algorithms. The underlying idea is to represent the policy by a parametric probability distribution \(\pi _\theta (s) = P(a|s,\theta )\), where \(\theta \) represents the parameters of the function approximator. In contrast to value-based methods, the output represents a probability density function that assigns a probability to each possible action. Typically, policy-gradient algorithms try to adapt the model parameter \(\theta \) by estimating the gradient of the expected return G (Sutton et al. 1999). Intuitively, this can be interpreted to mean that actions that have led to a positive outcome are more likely to be selected in the future in the same or similar states:

$$\begin{aligned} \nabla _\theta {\mathbb {E}}_{a \sim \pi _\theta (s)}[G(a)] \end{aligned}$$
(10)

The gradient of the expected value cannot be calculated analytically due to the infinite set of state-action combinations. Alternatively, two common methods for estimating the gradient exist REINFORCE (Sutton et al. 1999) and the reparameterization trick (Kingma and Welling 2013). In the following, REINFORCE is described in three steps. Firstly, an episodes trajectory \(\tau \) of length T including state, action, and reward information is collected:

$$\begin{aligned} \tau = (s_0, a_0, r_1, s_1, a_1, r_2, s_2, ..., a_T, r_{T+1}, s_{T+1}), \end{aligned}$$
(11)

with \(s_t\), \(a_t\), \(r_t\) representing the state, the action and the reward at time step t.

In a second step, the expected reward of each visited state is estimated: The reward \(r_k\) of each time step within the trajectory multiplied with its corresponding discount factor \(\gamma \) is accumulated:

$$\begin{aligned} G_t \leftarrow \sum _{k=t+1}^{T+1} \gamma ^{t-k-1} R_{k} \end{aligned}$$
(12)

where k denotes the number of time steps ahead of t.

Finally, the model parameters are updated according to the following equation:

$$\begin{aligned} \theta _{t+1} = \theta _t + \alpha G_t\frac{\nabla _{\theta }\pi (A_t|S_t,\theta _t)}{\pi (A_t|S_t,\theta _t)} \end{aligned}$$
(13)

The process of estimating the expected reward is similar to the Monte-Carlo method, which is related to some advantages and disadvantages: On the one hand, the estimate is unbiased as it is based on a real trajectory. On the other hand, only a small change in the policies’ parameters may change to another decision within the trajectory leading to a completely different outcome. This is why the estimation is related to a high-variance-affected credit assignment. Furthermore, the weakness of REINFORCE can be seen from another perspective: Imagine an agent taking a bad decision in time step t and good decisions in all successor time steps. REINFORCE rewards the bad action for its long-term positive outcome. This explains, why policy-based methods are considered to be less sample efficient. An alternative approach to reduce variance in the update steps can be found in the reparameterization trick. The policy \(\pi (a|s,\theta )\) is reformulated by a probability distribution \(g_\theta \) depending on an expected value \(\mu _\theta \), standard deviation \(\sigma _\theta \) and a stochastic value \(\epsilon \).

$$\begin{aligned} g_\theta (\epsilon )=\mu _\theta +\epsilon \sigma _\theta \end{aligned}$$
(14)

This transformation decouples the expectation of the policy parameter \(\theta \) and has a simplifying effect on the calculation of the gradient. Research papers demonstrate that the reparameterization trick has a variance-reducing effect (Xu et al. 2018).

5.3 Actor-Critic Methods

Actor-critic methods consist of a policy-gradient-based actor and a value-function-based critic. The actor maps the state vector onto an action vector and its corresponding update step works in the same way compared to the policy-gradient techniques introduced in Sect. 5.2. The critic takes the state vector and the action vector chosen by the actor as input and maps it on a scalar critic value. The critic value serves as a reward signal for the actor. In contrary to policy-based methods, the expected return is not estimated according to the Monte-Carlo method as denoted in Eq. 12. Instead, the expected reward is estimated according to the critic network. Two fundamental representatives are presented in Eq. 15 and in Eq. 16.

$$\begin{aligned} \nabla _\theta J(\theta ) = {\mathbb {E}}{\sum _{t=0}^{T-1}\nabla _\theta log \pi _\theta (a_t|s_t)Q(s,a)} \end{aligned}$$
(15)

and the Advantage Actor-Critic as denoted in Eq. 16,

$$\begin{aligned} \nabla _\theta J(\theta ) = {\mathbb {E}}{\sum _{t=0}^{T-1}\nabla _\theta log \pi _\theta (a_t|s_t)A(s,a)}, \end{aligned}$$
(16)

whereas the advantage is defined as \(A(s,a) = Q(s,a)-V(s)\). Substituting the Monte-Carlo-based expected reward estimate with a value-function-based expected reward estimate counteracts the high-variance issue related to pure policy-gradient-based methods.

The field of actor-critic methods has evolved rapidly in recent years and numerous extensions have been developed. One measure to stabilize the training process is to parallelize the learning process (Mnih et al. 2016). Asynchronous Actor-Critic (A3C) uses multiple agents with identical model architecture interacting with their own copy of the environment and collecting their own experiences. Two novel update strategies are to be considered: Firstly, the decentralized agents perform an asynchronous update step of the centralized agent using their own network gradients. These gradients contain information on how to update the network parameters based on the individual agent’s experiences accumulated over multiple timesteps. Furthermore, the decentralized network parameters are substituted with the parameters of the global network. This parallelization has a stabilizing effect since the learning process is based on decoupled learning experiences similar to the experience replay buffer proposed in Sect. 5.1. In addition to the parallelization, the authors pointed out another important property: Adding the policy entropy \(\mathscr {H}(\pi (\cdot |s_t))\) as a regularizer to the objective function reduces the risk of converging to a bad local optimum.

6 Evaluation

In the previous sections, many theoretical points have been discussed. Now, we are interested in how well RL works in practice. Thus, a small experiment is conducted:

The environment: A divergent 2-layer MEIS is considered. One middle warehouse orders supply from a factory and distribute supply to two leaf warehouses. The following assumptions are applied: The factory-level inventory system always has enough supplies to serve orders from a middle warehouse. The middle warehouse and the leaf warehouses can be affected by stock-out. The demand at the leaf warehouses is triggered by local wholesalers and hospitals and is modeled with a normal distribution. The demand at the middle warehouse corresponds to the orders of the two leaf warehouses (Fig. 3).

Fig. 3
figure 3

The environment setup consists of four inventory systems, whereby three of them are to be controlled by the RL agent. The material flow is from top to bottom while the information flow (the orders) is from bottom to top

Full size image

The cost. The delivery of an order is accomplished after a stochastic lead time, provided that sufficient supplies are available on the upstream level. Unserved orders due to stock-out are backlogged. The longer the waiting time for unserved demand gets, the higher is the likelihood of a buyer withdrawing the order leading to shortage cost at leaf warehouse level. Stock-out may occur at the middle warehouse level as well, however, this does not directly lead to lost sales since the middle warehouse is not directly connected to the market and therefore the shortage cost at middle warehouse level are assumed to be zero. In addition to shortage cost, there are holding cost and reordering cost. The overall cost in each time step is denoted in Eq. 17:

$$\begin{aligned} c_{total}(t) = \sum _{i \epsilon M} c_{i, shortage}(t) + c_{i, reordering}(t) + c_{i, holding}(t), \end{aligned}$$
(17)

while each cost type is defined as

$$\begin{aligned} c_{shortage}(t)&= k_{shortage} \cdot min(0, ioh_{i}(t)) \cdot ppp_{i} \end{aligned}$$
(18)
$$\begin{aligned} c_{reordering}(t)&= {\left\{ \begin{array}{ll} 0,&{} \text {if no reorder}\\ min(c_{min. reorder cost}, k_{reorder} * q_{i reorder}), &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
(19)
$$\begin{aligned} c_{holding}(t)&= k_{holding} \cdot max(0, ioh_{i}(t)) \cdot ppp_{i}, \end{aligned}$$
(20)

whereby \(c_{shortage}(t)\), \(c_{reordering}(t)\), \(c_{holding}(t)\) denote the shortage, reordering, and holding cost at time step t. \(k_{shortage}\) and \(k_{reorder}\) denote cost specific constants and \(ppp_i\), \(ioh_i(t)\) represent the price per product and the IOH at inventory system i and time step t. To transform the cost minimization challenge to a maximization task, we define \(reward = -c_{total}\).

Table 1 Specifications
Full size table

The state. The state vector consists of four elements per warehouse: (1) the current IOH, (2) the order quantity of the oldest open order, (3) the number of dates since the oldest open order was placed, and (4) the reorder quantity of all open orders. The respective state vectors for each warehouse are concatenated into a global state vector. The resulting state dimension is 12, if we consider three warehouses with four corresponding state dimensions.

The action. The output space is 13-dimensional as the agent has the choice to choose one out of 13 options. The first option is that no warehouse orders—all remaining options represent the situation that only one warehouse can reorder at the same time step while the reorder quantity can be small, medium, large or extra large.

The agent. The optimal policy is developed with the A3C approach. The model consists of two Fully-Connected Multi-layer Perceptrons (FCMLPs)—one for the actor and one for the critic. Further model and training hyperparameters are listed in Table 1.

Fig. 4
figure 4

Visualization of the RL model training performance. The blue line reflects the smoothed scores, i.e., smoothed means of negative cost achieved during training. The blue shaded area denotes standard deviations of these score values. The orange line denotes the overall best result obtained so far during training

Full size image

Figure 4 illustrates the training performance progress. It can be observed that the cost converges to an annual cost of below 10M CHF. However, the cost fluctuation remains on a high level. This issue is further discussed in Sect. 8.

7 Discussion of Results

Section 6 describes an experiment on MEIO with the A3C approach. The RL agent is capable of learning a reorder policy with minimized overall cost for a small, divergent multi-echelon network. It remains a research question to be answered, how good the performance is compared to other optimization methods. Gijsbrechts et al. (2021) performed a similar experiment by comparing two different kinds of base-stock policies: One base-stock policy is associated with constant base-stock values, while the other is state-dependent, whereby the corresponding base-stock values are selected by an A3C agent. The experiment shows, that the A3C-based approach outperformed the other approach by 9–12% less overall cost. On the other hand, the experiment performed in Sect. 6 shows, that the training converges to a minimized cost—on the other hand, the variance of the performance remains comparably high and no performance guarantees are given. In summary, RL shows promising results for inventory management tasks and many other sequential decision-making use-cases, however, a number of research challenges complicate the applicability to real-world systems. Some of them are introduced in Sect. 8.

8 Outlook

The most important open research challenge in the field of MEIO with RL is to make DRL-agents reliable and trustworthy. The experiment presented in Sect. 6 demonstrated, that A3C learns an optimized policy. Numerous very good runs alternate with a few very bad runs. With a deep neural network as a function approximator, the policy remains a black-box function with limited interpretability and thus no performance guarantees can be given. It still needs to be clarified how the trustworthiness of DRL can be increased and guaranteed. One research branch targeting this is analysed by Garcýa and Fernández (2015). Another aspect targets the environment: This is based on simplifying assumptions that often do not match the properties of real supply chains. One example is perishability and associated write-off cost in case of product expiry. Other examples are physical constraints (e.g., constraint workloads regarding the number of processible orders) or legal constraints (e.g., fixed safety stock regulations). Furthermore, the demand, which is sampled from a normal distribution in Sect. 6 may oversimplify the real demand characteristics and make the simulation-based learned policy not suitable for the application in real-world settings. Special events (e.g., a pandemic leading to demand artifacts) or low demands in the rare disease area facing high uncertainty may lead to poor results in reality if they are not considered in the simulation. In future research efforts, this characteristic could be captured with temporal point processes (e.g., Reinhart 2018).

9 Conclusions

DRL is a rapidly evolving research field. Experiments show two-fold results: On the one hand, DRL learns an optimized reorder policy with a low overall cost. On the other hand, the performance variance is relatively high with many good episodes alternating with some poor episode results. This makes DRL a promising approach to optimizing inventory management in the future—however, with the current lack of performance stability, DRL inventory management requirements and state of the art are too remote to be considered as a serious alternative for application to real-world supply chains.