Measure and Dimension of the Free Boundary

Abstract

This chapter is dedicated to the measure theoretic structure of the free boundary ∂ Ω_u. The results presented here are mainly a consequence of the Lipschitz continuity and the non-degeneracy of the minimizer u (Theorem 3.1 and Proposition 4.1).

This chapter is dedicated to the measure theoretic structure of the free boundary ∂ Ω_u. The results presented here are mainly a consequence of the Lipschitz continuity and the non-degeneracy of the minimizer u (Theorem 3.1 and Proposition 4.1). The chapter is organized as follows:

• Section 5.1 . Density estimates for the domain Ω_u.

  This section is dedicated to the density estimate of Ω_u at the boundary ∂ Ω_u. The argument presented here is precisely the one from the original work of Alt and Caffarelli [3].

• Section 5.2 . The positivity set Ω_u has finite perimeter.

  In this section we prove that the set Ω_u has (locally) finite perimeter in the sense of De Giorgi. We will use this result, together with the density estimate of the previous section in order to prove that the singular part of the free boundary has zero $\mathcal {H}^{d-1}$ Hausdorff measure. The proof that we give here is the local counterpart of an argument proposed by Bucur in [8] for estimating the perimeter of the optimal sets for the higher eigenvalues of the Dirichlet Laplacian.

• Section 5.3 . Hausdorff measure of the free boundary.

  In this section, we prove that the $\mathcal {H}^{d-1}$ measure of ∂ Ω_u is (locally) finite.¹ Our argument is very general and essentially uses the Lipschitz continuity and non-degeneracy of u and the fact that the optimality condition (4.1) implies that Ω_u has a finite inner Minkowski content in a sense that will be specified below.

5.1 Density Estimates for the Domain Ω_u

In this section, we prove that if u minimizes $\mathcal F_\Lambda$ in a set $D\subset \mathbb {R}^d$, then the set Ω_u = {u > 0} satisfies lower and upper (Lebesgue) density estimates at the boundary ∂ Ω_u. The result and the proof are due to Alt and Caffarelli [3].

Lemma 5.1 (Density Estimate)

Let $D\subset \mathbb {R}^d$ be a bounded open set. Let $u:D\to \mathbb {R}$ be a non-negative function such that:

• (a) u is Lipschitz continuous and $L:=\|\nabla u\|{ }_{L^\infty (D)}$;

• (b) u is non-degenerate, that is, there is a constant κ ₀ > 0 such that

  

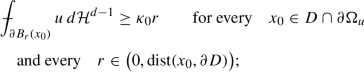
• (c) u is subharmonic in D;

• (d) there is Λ > 0 such that u satisfies the optimality condition (3.3) , that is,

  $$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,D)\le \mathcal F_\Lambda(v,D)\qquad \mathit{\text{for every}}\quad v\in H^1(D)\quad \mathit{\text{such that}}\quad v\ge u. \end{aligned}$$

There is a constant δ ₀ ∈ (0, 1), depending on the dimension d, the Lipschitz constant L and the non-degeneracy constant κ ₀ , such that

$$\displaystyle \begin{aligned} \delta_0|B_r|\le \big|\Omega_u\cap B_r(x_0)\big|\le (1-\delta_0)|B_r|, \end{aligned} $$

(5.1)

for every x ₀ ∈ D ∩ ∂ Ω _u and every r ∈(0, dist (x ₀, ∂D)). In particular, (5.1) holds for every local minimizer of $\mathcal F_\Lambda$ in D.

Remark 5.2

Notice that the conditions (b) and (c) are fulfilled by any function satisfying the suboptimality condition (4.1). All the conditions (a), (b), (c) and (d) are satisfied for functions that minimize $\mathcal F_\Lambda$ in an open set $\mathcal U$ containing the compact set $\overline D$.

Proof of Lemma 5.1

Without loss of generality we can suppose that x ₀ = 0.

We first prove the estimate by below in (5.1). Indeed, since 0 ∈ ∂ Ω_u, the non-degeneracy condition (b) implies that $\|u\|{ }_{L^\infty (B_{\frac {r}2})}\ge \kappa _0\frac {r}2$. Thus, there is a point y ∈ B _r∕2 such that $u(y)\ge \kappa _0\frac {r}2$. Now, the Lipschitz continuity of u implies that u > 0 on the ball B _ρ(y), where $\displaystyle \rho =\frac {r}2\min \left \{1,\frac {\kappa _0}{L}\right \}$, and so, we get the first estimate in (5.1).

For the upper bound on the density, we consider the harmonic replacement h of u in the ball B _r. Since u is subharmonic, we get that u ≤ h in B _r. Now, the optimality condition (3.1), implies that

$$\displaystyle \begin{aligned} \Lambda\big|\{u=0\}\cap B_r\big|\ge \int_{B_r}|\nabla u|{}^2\,dx-\int_{B_r}|\nabla h|{}^2\,dx=\int_{B_r}|\nabla(u-h)|{}^2\,dx. \end{aligned}$$

By the Poincaré inequality on the ball B _r we have that

$$\displaystyle \begin{aligned} \int_{B_r}|\nabla (h-u)|{}^2\,dx\ge \frac{C_d}{r^2}\int_{B_r}|h-u|{}^2\,dx\ge \frac{C_d}{|B_r|}\left(\frac{1}{r}\int_{B_r}(h-u)\,dx\right)^2. \end{aligned}$$

The non-degeneracy of u now implies

By the Harnack inequality applied to h, there is a dimensional constant c _d > 0 such that

$$\displaystyle \begin{aligned} h\ge c_d\, \kappa_0\, r\quad \text{in the ball}\quad B_{\frac{r}2}\ , \end{aligned}$$

On the other hand, the Lipschitz continuity of u and the fact that u(0) = 0 give that

$$\displaystyle \begin{aligned} u\le L{\varepsilon} r\qquad \text{in the ball}\qquad B_{{\varepsilon} r}. \end{aligned}$$

Choosing ε > 0 small enough such that c _d κ ₀ ≥ 2εL, we get

$$\displaystyle \begin{aligned} \int_{B_r}(h-u)\,dx\ge \int_{B_{{\varepsilon} r}}(h-u)\,dx\ge \frac 12c_d\,\kappa_0\,r\,|B_{{\varepsilon} r}|, \end{aligned}$$

which concludes the proof. □

5.2 The Positivity set Ω_u Has Finite Perimeter

In this section we prove that the (generalized) perimeter of Ω_u is locally finite in D. In particular, this means that Ω_u has locally finite perimeter. The proof that we give here was already generalized in two different contexts: for the vectorial Bernoulli problem (see [42]) and for a shape optimization problem with drift (see [46]). In fact, our proof is inspired by the global argument of Bucur (see [8]) used in the context of a shape optimization problem in $\mathbb {R}^d$. The main result of this subsection is the following:

Proposition 5.3 (Inwards-Minimizing Sets Have Locally Finite Perimeter)

Suppose that D is a bounded open set in $\mathbb {R}^d$ and that u ∈ H ¹(D) is non-negative and satisfies the following minimality condition:

$$\displaystyle \begin{aligned} & \mathcal F_\Lambda(u,D)\le \mathcal F_\Lambda(v,D)\quad \mathit{\text{for every}}\ \ v\in H^1(D))\ \ \mathit{\text{such that}}\ \ v\le u\ \mathit{\text{in}}\ D\ \\ & \quad \mathit{\text{and}}\ u-v\in H^1_0(D). \end{aligned} $$

Then Ω _u has locally finite perimeter in D.

As a direct consequence, we obtain that the support Ω_u of a minimizer u of $\mathcal F_\Lambda$ has locally finite perimeter.

Corollary 5.4 (Minimizers have Locally Finite Perimeter)

Suppose that D is a bounded open set in $\mathbb {R}^d$ and that the non-negative function u ∈ H ¹(D) is a minimizer of $\mathcal F_\Lambda$ in D. Then Ω _u has locally finite perimeter in D.

We divide the proof of Proposition 5.3 in two main steps: Lemmas 5.5 and 5.6. Lemma 5.5 is a sufficient condition for the local finiteness of the perimeter of a super-level set of a Sobolev function, while in Lemma 5.6, we will show that the subsolutions satisfy this condition. The conclusion of the proof of Proposition 5.3 is given at the end of the subsection.

Lemma 5.5

Suppose that $D\subset \mathbb {R}^d$ is an open set and that ϕ : D → [0, +∞] is a function in H ¹(D) for which there exist $\overline {\varepsilon }>0$ and C > 0 such that

$$\displaystyle \begin{aligned} \int_{\{0< \phi\le {\varepsilon}\}\cap D}|\nabla \phi|{}^2\,dx+\Lambda\big|\{0< \phi\leq {\varepsilon}\}\cap D\big|\le C {\varepsilon}\,,\quad \mathit{\text{for every}}\quad 0<{\varepsilon}\le \overline{\varepsilon}. \end{aligned} $$

(5.2)

Then, $Per\big (\{\phi >0\};D\big )\le C\sqrt {\Lambda }.$

Proof

By the co-area formula, the Cauchy-Schwarz inequality and (5.2), we have that, for every ${\varepsilon }\le \overline {\varepsilon }$,

$$\displaystyle \begin{aligned} \int_0^{\varepsilon} \mathcal H^{d-1}\big(\{\phi=t\}\cap D\big)\,dt & =\int_{\{0< \phi\leq {\varepsilon}\}\cap D}|\nabla \phi|\,dx\\ & \leq\big|\{0< \phi\leq {\varepsilon}\}\cap D\big|{}^{{1}/{2}}\, \Big(\int_{\{0< \phi\leq {\varepsilon}\}\cap D}|\nabla\phi|{}^2\,dx\Big)^{{1}/{2}}\leq {\varepsilon}\, C\sqrt{\Lambda}. \end{aligned} $$

Taking ε = 1∕n, we get that there is δ _n ∈ [0, 1∕n] such that

$$\displaystyle \begin{aligned} \mathcal H^{d-1}\big(\partial^*\{\phi>\delta_n\}\cap D\big)\le n\int_0^{\frac1n} \mathcal H^{d-1}\big(\{\phi=t\}\cap D\big)\,dt\le C\sqrt{\Lambda}. \end{aligned}$$

Passing to the limit as n →∞, we obtain

$$\displaystyle \begin{aligned} \mathcal H^{d-1}\big(\partial^*\{\phi>0\}\cap D\big)\leq C\sqrt{\Lambda}, \end{aligned}$$

which concludes the proof of the lemma. □

Lemma 5.6

Suppose that u ∈ H ¹(B _2r(x ₀)) is non-negative and satisfies the following minimality condition in the ball $B_{2r}(x_0)\subset \mathbb {R}^d$:

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u)\le \mathcal F_\Lambda(v)\quad \mathit{\text{for every}}\quad v\in H^1(B_{2r}(x_0))\quad \mathit{\text{such that}}\quad \begin{cases} v\le u\quad \mathit{\text{in}}\quad B_{2r}(x_0),\\ u=v\quad \mathit{\text{on}}\quad \partial B_{2r}(x_0). \end{cases}\end{aligned}$$

Then, there exists a constant C > 0 such that

$$\displaystyle \begin{aligned} & \int_{\{0< u\le {\varepsilon}\}\cap B_{r}(x_0)}|\nabla u|{}^2\,dx+\Lambda\big|\{0< u\leq {\varepsilon}\}\cap B_{r}(x_0)\big|\le C {\varepsilon}\\ & \quad \mathit{\text{for every}}\qquad 0<{\varepsilon}\leq 1. \end{aligned} $$

(5.3)

Precisely, one can take

$$\displaystyle \begin{aligned} \displaystyle C=C_d\left(r^{-1}\|\nabla u\|{}_{L^2(B_{2r}(x_0))}+r^{-2}\right), \end{aligned}$$

where C _d is a dimensional constant.

Proof

We fix a function $\phi \in C^\infty (\mathbb {R}^d)$ such that

For a fixed ε > 0 we consider the functions

$$\displaystyle \begin{aligned} u_{\varepsilon}=(u-{\varepsilon})_+\qquad \text{and}\qquad \tilde u_{\varepsilon}=\phi u+(1-\phi)u_{\varepsilon}. \end{aligned}$$

We now calculate $|\nabla \tilde u_{\varepsilon }|{ }^2$ in the ball B _2r.

Now setting

$$\displaystyle \begin{aligned} \displaystyle C=2\|\nabla u\|{}_{L^2(B_{2r})}\|\nabla\phi\|{}_{L^2(B_{2r})}+\|\nabla\phi\|{}_{L^2(B_{2r})}^2, \end{aligned}$$

and using the optimality of u, we get

$$\displaystyle \begin{aligned} 0& \ge \int_{B_{2r}} |\nabla u|{}^2\,dx-\int_{B_{2r}} |\nabla \tilde u_{{\varepsilon}}|{}^2\,dx+\big|\{u>0\}\cap B_{2r}\big|-\big|\{u_{\varepsilon}>0\}\cap B_{2r}\big|\\ & = \int_{B_{2r}} |\nabla u|{}^2\,dx-\int_{B_{2r}} |\nabla \tilde u_{{\varepsilon}}|{}^2\,dx+\big|\{0<u\le {\varepsilon}\}\cap B_r\big|\\ & \ge \int_{\{0<u\le {\varepsilon}\}\cap B_{2r}} (1-\phi^2)|\nabla u|{}^2\,dx+\big|\{0<u\le {\varepsilon}\}\cap B_r\big|-C{\varepsilon}\\ & \ge \int_{\{0<u\le {\varepsilon}\}\cap B_{r}} |\nabla u|{}^2\,dx+\big|\{0<u\le {\varepsilon}\}\cap B_r\big|-C{\varepsilon}, \end{aligned} $$

which concludes the proof. □

Proof of Proposition 5.3

Lemma 5.6 implies that (5.3) does hold. By Lemma 5.5, we obtain that the perimeter is locally bounded. Precisely,

Per( Ω_u;B _r∕2(x ₀)) ≤ C for every B _r(x ₀) ⊂ D,

where C depends on r, Λ and d. □

5.3 Hausdorff Measure of the Free Boundary

In this section we prove that the (d − 1)—dimensional Hausdorff measure of ∂ Ω_u is locally finite in D. In particular, this means that Ω_u has locally finite perimeter and so, we recover Proposition 5.3. We will use the Lipschitz continuity and the non-degeneracy of the solution, as well as, the inner Hausdorff content estimate (5.4), which is a consequence of Lemma 5.6. This is a very general result, which may find application to different free boundary problems (see for instance [42]).

Proposition 5.7

Let $D\subset \mathbb {R}^d$ be a bounded open set and $u:D\to \mathbb {R}$ a Lipschitz continuous function such that:

• (a) u is non-degenerate, that is, there is a constants c > 0 such that

  $$\displaystyle \begin{aligned} \sup_{B_r(x_0)}u\ge cr\quad \mathit{\text{for every}}\quad x_0\in\partial\Omega_u\cap D\quad \mathit{\text{and every}}\quad 0<r<\mathit{\text{dist}}(x_0,\partial D). \end{aligned}$$

• (b) u satisfies the following (sub-)minimality condition:

  $$\displaystyle \begin{aligned} & \mathcal F_\Lambda(u,D)\le \mathcal F_\Lambda(v,D)\quad \mathit{\text{for every}}\ \ v\in H^1(D)\ \ \mathit{\text{such that}}\ \ v\le u\ \mathit{\text{in}}\ D\\ & \quad \mathit{\text{and}}\ u-v\in H^1_0(D). \end{aligned} $$

Then, for every compact set K ⊂ Ω, we have $\mathcal {H}^{d-1}(K\cap \partial \Omega _u)<\infty$.

As an immediate corollary, we obtain:

Corollary 5.8 (Hausdorff Measure of the Free Boundary)

Let D be a bounded open set in $\mathbb {R}^d$ and the non-negative function u ∈ H ¹(D) be a minimizer of $\mathcal F_\Lambda$ in D. Then, for every compact set K ⊂ D, we have $\mathcal {H}^{d-1}(K\cap \partial \Omega _u)<\infty$.

The proof of Proposition 5.7 is a consequence of Lemma 5.6 and the following lemma.

Lemma 5.9

Let $D\subset \mathbb {R}^d$ be an open set and $u:D\to \mathbb {R}$ a Lipschitz continuous function such that:

• (a) u is non-degenerate, that is, there is a constants c > 0 such that

  $$\displaystyle \begin{aligned} \sup_{B_r(x_0)}u\ge cr\quad \mathit{\text{for every}}\quad x_0\in\partial\Omega_u\cap D\quad \mathit{\text{and every}}\quad 0<r<\mathit{\text{dist}}(x_0,\partial D). \end{aligned}$$

• (b) there is a constant C > 0 such that u satisfies the estimate

  $$\displaystyle \begin{aligned} \big|\{0<u\le{\varepsilon}\}\cap D\big|\le C{\varepsilon}\quad \mathit{\text{for every}}\quad {\varepsilon}>0.\end{aligned} $$

  (5.4)

Then, for every compact set K ⊂ Ω, we have $\mathcal {H}^{d-1}(K\cap \partial \Omega _u)<\infty$.

Proof

Let us first recall that, for every δ > 0 and every $A\subset \mathbb {R}^d$,

$$\displaystyle \begin{aligned} \mathcal{H}^{d-1}_{2\delta}(A)\le\omega_{d-1}\,\inf\Big\{\sum_{j=1}^\infty r_j^{d-1}\ :\ \text{for every }\ B_{r_j}(x_j)\ \text{such that}\ \bigcup_{j=1}^\infty B_{r_j}(x_j)\supset A\ \text{and}\ r_j\le \delta\Big\}.\end{aligned}$$

and

$$\displaystyle \begin{aligned} \mathcal H^{d-1}(A)=\lim_{\delta\to0}\mathcal{H}^{d-1}_\delta(A). \end{aligned}$$

Let δ > 0 be fixed and let $\{B_\delta (x_j)\}_{j=1}^N$ be a covering of K ∩ ∂ Ω_u such that x _j ∈ ∂ Ω_u for every j = 1, …, n and the balls B _δ∕5(x _j) are disjoint. The non-degeneracy of u implies that, in every ball B _δ∕10(x _j) there is a point y _j such that u(y _j) ≥ cδ∕10. The Lipschitz continuity of u implies that B _cδ∕10L(y _j) ⊂ Ω_u, where $L=\max \{1,\|\nabla u\|{ }_{L^\infty }\}$. On the other hand, since u(x _j) = 0, we have that

$$\displaystyle \begin{aligned} u<L\left(\frac{c\delta}{10L}+\frac{c\delta}{10}\right)=(L+1)\frac{c\delta}{10}\qquad \text{on}\qquad B_{c\delta/10L}(y_j). \end{aligned}$$

This implies that the balls B _cδ∕10L(y _j), j = 1, …, N, are disjoint and contained in the set $\big \{0<u<(L+1)\frac {c\delta }{10}\big \}$. Now, the estimate from point (b) implies that

$$\displaystyle \begin{aligned} C(L+1)\frac{c\delta}{10}\ge \sum_{j=1}^N|B_{{c\delta}/{10L}}(y_j)|\ge N\omega_d\frac{c^d\delta^d}{L^d10^d}, \end{aligned}$$

which implies that

$$\displaystyle \begin{aligned} N\,d\omega_d\delta^{d-1}\le dC\frac{10^{d-1}}{c^{d-1}}L^d(L+1). \end{aligned}$$

Since, the right-hand side does not depend on δ, we get that

$$\displaystyle \begin{aligned} \mathcal{H}^{d-1}(K\cap\partial\Omega_u)\le dC\frac{10^{d-1}}{c^{d-1}}L^d(L+1). \end{aligned}$$

□