Keywords

1 Introduction

The transition in the automotive industry towards electric vehicles - amplified by governmental policies - poses a great challenge, both in product development and in production [1]. This transformation further accelerates the trend in recent years towards a greater product diversity [2]. Linear assembly lines, which are currently well-established in the automotive industry, cannot meet the new requirements in a satisfactory manner [2]. Therefore, more flexible production systems are necessary [2].

Traditionally, the manual final assembly accommodates the largest product diversity [3, pp. 1–4]. However, the escalated demand for electric and hybrid vehicles causes a notable increase in diversity of vehicle bodies too [4]. As a result, not only the final assembly but also the highly automated body-in-white (BIW) production needs to become more flexible to meet the market demands [5].

Modular production addresses these issues [6]. In this production paradigm, the logistics is decoupled from the actual production by breaking up the assembly line into individual, modular production units and automated guided vehicles (AGVs) which transport the parts between the workstations [6]. This radically improves the flexibility of the production system [6].

The scheduling of modular production systems is intimately connected with the job-shop scheduling problem (JSP). The JSP refers to the NP-hard problem of scheduling n jobs of different processing times on m different workstations (WS) of varying processing power, the objective being to minimize the makespan [7]. The traditional JSP only considers the scheduling of the operations on the workstations, but in modular production, the dynamic transportation durations between the workstations have to be considered as well [8].

Mixed-Integer programming (MIP) modelling is a widely used approach for scheduling tasks [9]. For instance, in 2014, 14 out of the 40 papers published in the Journal of Scheduling used different MIP approaches, more than any other technology [9]. Due to its comprehensive modelling capabilities, its potential to find global optima and its prevalence in the literature, the authors have chosen a MIP approach to schedule the modular BIW production. The main novelty of this MIP formulation lies in including precedence graphs for modelling the joining steps of the BIW production and allowing for different workstation capabilities in the production system.

2 State of the Art

Consistently with the chosen approach, the literature review is limited to MIP approaches that encompass both the scheduling of the workstations and the AGVs. Bilge et al. [10] presented the first MIP model for the joint production and transportation scheduling for flexible production systems. However, it could not be solved due to its size and non-linearity. Instead, the authors developed an iterative procedure to determine a feasible workstation schedule. Using this schedule, a time window is calculated during which job delivery is possible. A heuristic schedules the AGVs to deliver a job within this time schedule.

Fontes et al. [8] proposed a MIP model which takes into consideration the dynamic transportation durations between the workstations, thus making it interesting for flexible production systems in general. They use precedence variables to sequence both the production operations and the AGV transportation tasks. Their modelling approach uses one set of chained decision variables for the workstations and another for the AGVs. These sets are interconnected through the completion time constraints both for the workstations and the AGVs. Since all AGVs are considered identical, the model does not explicitly consider the AGVs. This way, the use of an additional index can be avoided, thus heavily reducing the number of decision variables and constraints.

Homayouni et al. [11] enhanced the model of Fontes et al. [8] by adding more detail to the modelling of the workstations. Due to the NP-hard nature of the problem, the calculation time exponentially escalates with an increasing problem size. Therefore, they proposed a local search-based heuristic to find solutions to the problem.

This paper extends the work of Fontes et al. [8] and Homayouni et al. [11] by including the following features, necessary for the BIW production:

  • The operations of one BIW are not serial, but are formed as a precedence graph [12], exemplified in Fig. 1. For instance, the order of the side walls is indifferent, but both side walls need to be added before the roof can be assembled.

  • In the BIW production, many different joining technologies are used [13, pp. 36–39]. Since not all workstations can be assumed to be able to perform all technologies, each workstation can have its own capabilities. For example, one workstation can weld, another can glue, a third can weld and clinch etc.

  • The parts are considered as an input. This is implemented as a stepping stone for future work, in which logistical bottlenecks might lead to parts shortages.

Fig. 1.
figure 1

Examples of precedence graphs.

Full size image

3 Proposed Mixed-Integer Programming Model

3.1 Notations

Table 1 summarizes all the notations used in the model in Sect. 3.2.

Additionally, a directed precedence graph of operations is considered instead of a linear job. To this effect, a topological order \(\succeq \) is introduced. For two nodes u and v, this order describes the following relations:

  • u precedes v if a chain of directed edges from u to v exists: \(u \prec v\)

  • u succeeds v if a chain of directed edges from v to u exists: \(u \succ v \)

  • u is indifferent to v if no such chains exist:

    • \(u \succeq v \implies u\) succeeds or is indifferent to v

    • \(u \preceq v \implies u\) precedes or is indifferent to v

This partial order introduces the notion of predecessors and successors for each operation. For any given operation, each predecessor creates a required part whereas each successor requires a created part.

Table 1. Notations used for the model formulation.
Full size table

3.2 Model

The main novelties of this model are taking into account a graph of operations for each job, rather than a linear succession of operations, considering that different workstations can have different capabilities and using parts as input. We consider that each operation can have several predecessors, but only one direct successor.

The input of the model consists of the needed parts, the workstations of the production system and their capabilities, the number of AGVs in the production system and the jobs that are to be produced and their precedence graphs. The objective of the model is to minimize the total production makespan (Eq. 1), defined as the latest completion time of every operation (Eq. 2), that is the time at which every job has been completed and unloaded.

Each operation is carried out on one workstation and has an immediate predecessor (Eq. 3) and an immediate successor (Eq. 4) on the workstation in question. The topological order, as explained in Sect. 3.1, ensures that the predecessors and successors follow the logic of the precedence graph. The dummy jobs f and t ensure the coherence of these constraints for the first and last operations executed on the workstations as boundary conditions.

The AGVs assure the movement of jobs between the workstations. The number of AGVs mobilized is limited by the number of AGVs available (Eq. 5). In addition, we ensure that the same number of AGVs finish the day as start the day (Eq. 6). Concerning the parts, primary parts for the operations are initially stored at the factory entrance, or loading dock. These parts must be transported (Eq. 7), either as the first operation of an AGV, or after another operation. Other transported operations must also have a predecessor on the AGV, or be the first transported (Eq. 8). Symmetrically, the last operation of a job must be transported (Eq. 9) as it represents the unloading of the job, and transported operations are either the last operations transported by their AGV, or have a successor (Eq. 10). To ensure the fluidity of these transports, a flow constraint (Eq. 11) is also present. In addition, not all of the operations are to be transported: an operation either follows its predecessor on the same workstation or retrieves the part created by this predecessor via an AGV (Eq. 12).

The model then ensures that the workstations are properly attributed to each job, in particular assigning the same workstation to two consecutive operations (Eq. 13) and a single workstation to each operation (Eq. 14), as well as assigning each operation to a workstation of the correct category (Eq. 15). Furthermore, dummy jobs are assigned to a single workstation (Eq. 16), and the unloading dock is only assigned to the dummy exit variable of each job (Eq. 17).

In order to define the schedule, one must define the completion and arrival times for each operation. The completion of an operation depends on the arrival time of all of the required parts and on the processing time on the assigned workstation (Eq. 18). Since a workstation can only process one operation at a time, the completion of the previous operation on the same workstation is a necessity. The operation can only be declared complete after this previous operation and its own processing on that workstation (Eq. 19). After the completion of the predecessor operations, the required parts are transported towards the workstation of the current operation, which defines the arrival time. (Eq. 20). If an operation contains primary parts, those parts must be fetched from the loading area and brought to the designated workstation (Eq. 21).

In order to drop off parts for an operation, the AGV carrying them has to have dropped off the previous load and picked up the required parts of the current operation at the workstation at which they were created (Eq. 22). Finally, should an operation be transported after another and require primary parts, the designated AGV must pick up the parts at the loading area after having dropped off the previous operation (Eq. 23).

$$\begin{aligned}&\min c_{max}{} & {} \end{aligned}$$
(1)
$$\begin{aligned}&\text {subject to }{} & {} \nonumber \\&c_{max} \ge c_{ie_i},{} & {} \forall i \in J \end{aligned}$$
(2)
$$\begin{aligned}&{\sum _{a\in W\setminus {\{U\}}}\left[ \sum _{j \preceq l \in J_k} w_{kj}^{kl,a} + \sum _{\begin{array}{c} i \in J_k\setminus {\{k\}} \\ j \in J_i \end{array}} w_{ij}^{kl,a} + \sum _{j \in J_f} w_{fj}^{kl,a}\right] = 1,}{} & {} \forall k \in J \cup \{t\}, l \in J_k \setminus {\{e_k\}} \end{aligned}$$
(3)
$$\begin{aligned}&{\sum _{a\in W\setminus {\{U\}}}\left[ \sum _{j \succeq l \in J_k} w_{kl}^{kj,a} + \sum _{\begin{array}{c} i \in J_k\setminus {\{k\}} \\ j \in J_i \end{array}} w_{kl}^{ij,a} + \sum _{j \in J_t} w_{kl}^{tj,a} \right] = 1,}{} & {} \forall k \in J \cup \{f\}, l \in J_k \setminus {\{e_k\}} \end{aligned}$$
(4)
$$\begin{aligned}&\sum _{k \in J, l\in J_k, p \in P(l)} u_{kl}^p \le v{} & {} \end{aligned}$$
(5)
$$\begin{aligned}&\sum _{k \in J, l\in J_k, p \in P_k(l)} u_{kl}^p = \sum _{k \in J, l\in J_k, p \in P_k(l)} z_{kl}^p{} & {} \end{aligned}$$
(6)
$$\begin{aligned}&u_{kl}^p + \sum _{\begin{array}{c} j\preceq l \in J_k \\ q \in P_k(j) \end{array}} x_{kj,q}^{kl,p} + \sum _{\begin{array}{c} i \in J \\ i \ne k \end{array}} \sum _{\begin{array}{c} j\in J_i \\ q \in P_i(j) \end{array}} x_{ij,q}^{kl,p} = 1,{} & {} \forall k \in J, \forall l \in J_k, \forall p \in P_k(l)\cap B_k \end{aligned}$$
(7)
$$\begin{aligned}&u_{kl}^p + \sum _{\begin{array}{c} j\preceq l \in J_k \\ q \in P_k(j) \end{array}} x_{kj,q}^{kl,p} + \sum _{\begin{array}{c} i \in J \\ i \ne k \end{array}} \sum _{\begin{array}{c} j\in J_i \\ q \in P_k(j) \end{array}} x_{ij,q}^{kl,p} \le 1,{} & {} \forall k \in J, \forall l \in J_k, \forall p \in P_k(l) \end{aligned}$$
(8)
$$\begin{aligned}&z_{ke_k}^p + \sum _{\begin{array}{c} i \in J \\ i \ne k \end{array}} \sum _{\begin{array}{c} j\in J_i \\ q \in P_i(j) \end{array}} x_{ke_k,p}^{ij,q} = 1,{} & {} \forall k \in J, \forall p \in P_k(e_k) \end{aligned}$$
(9)
$$\begin{aligned}&z_{kl}^p + \sum _{\begin{array}{c} j\succeq l \in J_k \\ q \in P_k(j) \end{array}} x_{kl,p}^{kj,q} + \sum _{\begin{array}{c} i \in J \\ i \ne k \end{array}} \sum _{\begin{array}{c} j\in J_i \\ q \in P_i(j) \end{array}} x_{kl,p}^{ij,q} \le 1,{} & {} \forall k \in J, \forall l \in J_k, \forall p \in P_k(l) \end{aligned}$$
(10)
$$\begin{aligned}&{u_{kl}^p + \sum _{\begin{array}{c} j\preceq l \in J_k \\ q \in P_k(j) \end{array}} x_{kj,q}^{kl,p} + \sum _{\begin{array}{c} i \in J \\ i \ne k \end{array}} \sum _{\begin{array}{c} j\in J_i \\ q \in P_i(j) \end{array}} x_{ij,q}^{kl,p} - \sum _{\begin{array}{c} j\succeq l \in J_k \\ q \in P_k(j) \end{array}} x_{kl,p}^{kj,q} - \sum _{\begin{array}{c} i \in J \\ i \ne k \end{array}} \sum _{\begin{array}{c} j\in J_i \\ q \in P_i(j) \end{array}} x_{kl,p}^{ij,q} - z_{kl}^p = 0,}{} & {} \forall k \in J, l \in J_k, \forall p \in P_k(l) \end{aligned}$$
(11)
$$\begin{aligned}&\sum _{a\in W} w_{kl'}^{kl,a} + \sum _{\begin{array}{c} j\preceq l \in J_k \\ q \in P_k(j) \end{array}} x_{kj,q}^{kl,p} + \sum _{\begin{array}{c} i \in J \\ i \ne k \end{array}} \sum _{\begin{array}{c} j\in J_i \\ q \in P_i(j) \end{array}} x_{ij,q}^{kl,p} = 1,{} & {} \forall k \in J, l \in J_k, \forall l' \in Pred_k(l), \nonumber \\{} & {} {}&\forall p \in P_k(l)\cap C_k(l') \end{aligned}$$
(12)
$$\begin{aligned}&m_{ij}^a + m_{kl}^a \ge M(w_{ij}^{kl,a} - 1) + 2,{} & {} \forall i,k \in J, j \in J_i, l \in J_k, \nonumber \\{} & {} {}&a \in W \setminus {\{U\}} \end{aligned}$$
(13)
$$\begin{aligned}&\sum _{a\in W} m_{ij}^a = 1,{} & {} \forall i \in J, j \in J_i \end{aligned}$$
(14)
$$\begin{aligned}&m_{ij}^a \le \mathbbm {1}_{cat(ij) \in cat(a)}{} & {} \forall i \in J, j\in J_i, a\in W \end{aligned}$$
(15)
$$\begin{aligned}&\sum _{j \in f} m_{fj}^a \le 1, \sum _{j \in t} m_{tj}^a \le 1,{} & {} \forall a \in W \end{aligned}$$
(16)
$$\begin{aligned}&m_{ke_k}^U = 1, \; m_{kl}^U = 0,{} & {} \forall k \in J, l\in J_k\setminus {\{e_k\}} \end{aligned}$$
(17)
$$\begin{aligned}&c_{ij} - v_{ij}^{p} - \sum _{a\in W} m_{ij}^a P_{ij}^a \ge 0,{} & {} \forall i \in J, j \in J_i, p \in P_i(j) \end{aligned}$$
(18)
$$\begin{aligned}&c_{kl} - c_{ij} - P_{kl}^a \ge M(w_{ij}^{kl,a} - 1),{} & {} \forall i,k \in J, j \in J_i, l \in J_k, a\in W\setminus {\{U\}} \nonumber \\{} & {} {}&(\text {if } i = k: l \succeq j) \end{aligned}$$
(19)
$$\begin{aligned}&v_{kl}^{p} - c_{kl'} - T_{a}^{b} \ge M(m_{kl'}^a + m_{kl}^b - 2),{} & {} \forall k \in J, l \in J, l' \in Pred_k(l), \nonumber \\{} & {} {}&\forall p \in P_k(l)\cap C_k(l'), \ a,b\in W \end{aligned}$$
(20)
$$\begin{aligned}&v_{kl}^p - \sum _{a \in W} m_{kl}^a T_{L}^{a} \ge 0,{} & {} \forall k \in J, \forall l\in J_k, \forall p \in P_k(l)\cap B_k \end{aligned}$$
(21)
$$\begin{aligned}&{ v_{kl}^{p} - v_{ij}^{q} - \sum _{a\in W} m_{ij}^a T_{a}^{b} - \sum _{a \in W} m_{kl}^a T_{b}^{a} \ge M(x_{ij,q}^{kl,p} + m_{kl'}^b -2 ),}{} & {} \forall i,k \in J, j \in J_i, l \in J_k, b \in W, \nonumber \\{} & {} {}&l' \in Pred_k(l), p \in P_k(l)\cap C_k(l'), \nonumber \\{} & {} {}&q\in P_i(j) \end{aligned}$$
(22)
$$\begin{aligned}&{v_{kl}^p - v_{ij}^{q} - \sum _{a \in W} m_{ij}^a T_{a}^{L} - \sum _{b\in W} m_{kl}^b T_{L}^{b} \ge M(x_{ij,q}^{kl,p} - 1),}{} & {} \forall i,k \in J, i \ne k, j \in J_i, l\in J_k, \nonumber \\{} & {} {}&p \in P_k(l)\cap B_k, q \in P_i(j) \end{aligned}$$
(23)

4 Results and Discussion

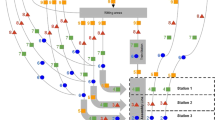
The model reliably calculates the minimal makespan for examples up to five jobs and 22 operations in total. Figure 2 shows an example with three workstations, two AGVs and five jobs with precedence graphs as shown in Fig. 1 (job 1 has the precedence graph on the left, jobs 2, 3, 4 and 5 the one on the right). The production system is a small-scale version of a real modular production system where each workstation has different capabilities. WS1 can glue and clinch, WS2 can weld and WS3 can clinch. Each coloured block means that the workstation or the AGV is currently active during this time interval: a workstation is processing an operation and an AGV is bringing a part to a workstation. The colour of the block corresponds to the job, to which the operation or part belongs. The light blue “empty drive” boxes mean that the AGV is on its way to pick up a part but is currently not carrying anything. As all jobs need a gluing operating (cf. Fig. 1) and WS1 is the only workstation which can glue, the makespan cannot be shorter than the combined execution time of the gluing operations on WS1. Since WS1 is uninterruptedly executing the gluing operations of the jobs, it is evident that the makespan is minimal in this example.

Fig. 2.
figure 2

An example producing five jobs, using three workstations and two AGVs.

Full size image

This small example shows the major novelties of this model. The joining steps of the jobs are modelled as precedence graphs. This represents the flexibility of modular production much more adequately than serial operations. Also, the workstations have different capabilities and the parts are considered as an input.

The model deterministically calculates the minimal makespan for small examples but due to the NP-hard nature of the problem, it struggles with larger, more realistic use cases. The example from Fig. 2 is solved in less than a minute on a regular laptop with an Intel i5 processor (2.8 GHz) with 8 GB RAM. However, if the size of the problem (number of operations, jobs, AGVs and workstations) reaches a real-life BIW production magnitude, no deterministic exact solution is found within reasonable time. Therefore, in further work, the quality of the solutions which can be attained in acceptable time and an adequate definition of acceptable time will be researched. In addition, the authors will look into the possibility of adding further constraints posed by the production which might mitigate the calculation time increase for growing problem sizes.

Each AGV can only carry one part at a time. Since many operations require several parts, either several AGVs are necessary or the AGVs need to do multiple laps. This is obviously not ideal and will be looked into in future work.

Figure 3 shows the makespan and the AGV utilization rate for the example in Fig. 2 as a function of the number of AGVs. The makespan is significantly better with two AGVs in comparison to one single AGV. However, more than two AGVs do not improve the makespan at all. Therefore, two AGVs are deployed. To further shorten the makespan, a different production system is necessary.

Fig. 3.
figure 3

Makespan (blue) and average AGV utilization rate (red) as a function of the number of AGV in the example from Fig. 2.

Full size image

5 Conclusion

In this paper, the authors present a MIP model for the the modular BIW production. The model is inspired by the models by Fontes et al. [8] and Homayouni et al. [11] but adapted to meet the requirements posed by the BIW production. In particular, the model considers that the BIW production operations are not serial, but arranged as a precedence graph. In addition, the whereabouts of the parts as well as the different capabilities of the workstations are included.

The proposed approach is applied to an exemplary production scenario with five jobs and 22 operations which highlights the strengths of the model but also indicates its current limitations, arising from the NP-hard nature of the problem. In future work, the authors will further analyze the performance of the model, assess the quality of its solutions and explore possibilities to reduce the numerical complexity of the model in order to facilitate the scheduling of larger scenarios.