Proof-Theoretic Semantics for Intuitionistic Multiplicative Linear Logic

Abstract

This work is the first exploration of proof-theoretic semantics for a substructural logic. It focuses on the base-extension semantics (B-eS) for intuitionistic multiplicative linear logic ($\mathrm IMLL$). The starting point is a review of Sandqvist’s B-eS for intuitionistic propositional logic (IPL), for which we propose an alternative treatment of conjunction that takes the form of the generalized elimination rule for the connective. The resulting semantics is shown to be sound and complete. This motivates our main contribution, a B-eS for $\mathrm IMLL$, in which the definitions of the logical constants all take the form of their elimination rule and for which soundness and completeness are established.

1 Introduction

In model-theoretic semantics (M-tS), logical consequence is defined in terms of models; that is, abstract mathematical structures in which propositions are interpreted and their truth is judged. As Schroeder-Heister [33] explains, in the standard reading given by Tarski [38, 39], a propositional formula $\varphi$ follows model-theoretically from a context $\mathrm {\Gamma }$ iff every model of $\mathrm {\Gamma }$ is a model of $\varphi$; that is,

$$ \begin{array}{rcl} \mathrm {\Gamma }\models \varphi&\text{ iff }&\text{ for } \text{ all } \text{ models } \mathcal {M}\text{, } \text{ if } \mathcal {M} \models \psi \text{ for } \text{ all } \psi \in \mathrm {\Gamma }\text{, } \text{ then } \mathcal {M} \models \varphi \end{array} $$

Therefore, consequence is understood as the transmission of truth. Importantly, on this plan, meaning and validity are characterized is terms of truth.

Proof-theoretic semantics (P-tS) is an alternative approach to meaning and validity in which they are characterized in terms of proofs—understood as objects denoting collections of acceptable inferences from accepted premisses. This is subtle. It is not that one desires a proof system that precisely characterizes the consequences of the logic of interest, but rather that one desires to express the meaning of the logical constants in terms of proofs and provability. Indeed, as Schroeder-Heister [33] observes, since no formal system is fixed (only notions of inference) the relationship between semantics and provability remains the same as it has always been—in particular, soundness and completeness are desirable features of formal systems. Essentially, what differs is that proofs serve the role of truth in model-theoretic semantics. The semantic paradigm supporting P-tS is inferentialism—the view that meaning (or validity) arises from rules of inference (see Brandom [5]).

To illustrate the paradigmatic shift from M-tS to P-tS, consider the proposition ‘Tammy is a vixen’. What does it mean? Intuitively, it means, somehow, ‘Tammy is female’ and ‘Tammy is a fox’. On inferentialism, its meaning is given by the rules,

These merit comparison with the laws governing $\wedge$ in IPL, which justify the sense in which the above proposition is a conjunction:

There are two major branches of P-tS: proof-theoretic validity (P-tV) in the Dummett-Prawitz tradition (see, for example, Schroeder-Heister [32]) and base-extension semantics (B-eS) in the sense of, for example, Sandqvist [28,29,30]. The former is a semantics of arguments, and the latter is a semantics of a logic, but both are proof-theoretic semantics. This paper is concerned with the latter as explained below.

Tennant [40] provides a general motivation for P-tV: reading a consequence judgement $\mathrm {\Gamma }\vdash _{\!\!} \varphi$ proof-theoretically—that is, that $\varphi$ follows by some reasoning from $\mathrm {\Gamma }$—demands a notion of valid argument that encapsulates what the forms of valid reasoning are. That is, we require explicating the semantic conditions required for an argument that witnesses

$$ \psi _1 , \ldots , \psi _n\text{; } \text{ therefore, } \varphi $$

to be valid. A particular motivation comes from the following programmatic remarks by Gentzen [37]:

The introductions represent, as it were, the ‘definitions’ of the symbols concerned, and the eliminations are no more, in the final analysis, than the consequences of these definitions. This fact may be expressed as follows: In eliminating a symbol, we may use the formula with whose terminal symbol we are dealing only ‘in the sense afforded it by the introduction of that symbol’.

Dummett [9] developed a philosophical understanding of the normalization results of Prawitz [25], which give a kind of priority to the introduction rules, that yields a notion of valid arguments. The result is P-tV—see Schroeder-Heister [32] for a succinct explanation.

More generally, P-tV is about defining a notion of validity of objects witnessing that a formula $\varphi$ follows by some reasoning from a collection of formulae $\mathrm {\Gamma }$. This is quite different from simply giving an interpretation of proofs from some formal system; for example, while the version of P-tV discussed above is closely related to the BHK interpretation of IPL, it is important to distinguish the semantic and computational aspects—see, for example, Schroeder-Heister [32].

Meanwhile, B-eS proceeds via a judgement called support defined inductively according to the structure of formulas with the base case (i.e., the support of atoms) given by proof in a base. A base is a set of inference rules over atomic propositions, thought of as defining those atoms—an example is the set of rules above that define ‘Tammy is a vixen’. Though this approach is closely related to possible world semantics in the sense of Beth [2] and Kripke [17]—see, for example, Goldfarb [13] and Makinson [18]—it remains subtle. For example, there are several incompleteness results for intuitionistic logics—see, for example, Piecha et al. [20, 21, 23], Goldfarb [13], Sandqvist [27,28,29,30], Stafford [36]. Significantly, a sound and complete B-eS for IPL has been given by Sandqvist [29]. Gheorghiu and Pym [10] have shown that this B-eS captures the declarative content of P-tV.

Sandqvist’s B-eS for IPL is the point of departure for this paper. Fix a set of atomic propositions $\mathbb {A}$. Given a base $\mathscr {B}$, we write $\vdash _{\!\!\mathscr {B}} \textrm{p}$ to denote that $\textrm{p} \in \mathbb {A}$ can be derived in $\mathscr {B}$. Support in a base $\mathscr {B}$—denoted $\Vdash _{\!\!\mathscr {B}}$—is defined by the clauses of Fig. 1 in which $\mathrm {\Gamma }\ne \varnothing$. We desire to give an analogous semantics for intuitionistic multiplicative linear logic ($\mathrm IMLL$). We study this logic as it is the minimal setting in which we can explore how to set-up B-eS (and P-tS in general) for substructural logics, which enables extension to, for example, (intuitionistic) Linear Logic [11] and the logic of Bunched Implications [19]. Again, the aim is not simply to give a proof-theoretic interpretation of IMLL, which already exist, but to define the logical constants in terms of proofs.

Fig. 1.

Sandqvist’s Support in a Base

A compelling reading of $\mathrm IMLL$ is its resource interpretation, which is inherently proof-theoretic—see Girard [11]. Accordingly, looking at (Inf), we expect that $\varphi$ being supported in a base $\mathscr {B}$ relative to some multiset of formulas $\mathrm {\Gamma }$ means that the ‘resources’ garnered by $\mathrm {\Gamma }$ suffice to produce $\varphi$. We may express this by enriching the notion of support with multisets of resources P and U combined with multiset union—denoted . Then, that the resources garnered by $\mathrm {\Gamma }$ are given to $\varphi$ is captured by the following property:

Naively, we may define $\otimes$ as a resource-sensitive version of ($\wedge$); that is,

While the semantics is sound, proving completeness is more subtle. We aim to follow the method by Sandqvist [30], and this clause is not suitable because the following is not the case for $\mathrm IMLL$:

—a counter-example is the case where $\mathrm {\Gamma }$ is the (singleton) multiset consisting of $\varphi \otimes \psi$, which denies any non-trivial partition into smaller multisets. We therefore take a more complex clause, which is inspired by the treatment of disjunction in IPL, that enables us to prove completeness using the approach by Sandqvist [29].

There is an obvious difference between the B-eS for IPL and its standard possible world semantics by Kripke [17]—namely, the treatment of disjunction ($\vee$) and absurdity ($\bot$). The possible world semantics has the clause,

$$ \mathfrak {M},x \Vdash \varphi \vee \psi \qquad \text{ iff } \qquad \mathfrak {M},x \Vdash \varphi \text{ or } \mathfrak {M},x \Vdash \psi $$

If such a clause is taken in the definition of validity in a B-eS for IPL, it leads to incompleteness —see, for example Piecha and Schroeder-Heister  [20, 21]. To yield completeness, Sandqvist [30] uses a more complex form that is close to the elimination rule for disjunction in natural deduction (see Gentzen [37] and Prawitz [24])—that is,

$$ {\begin{array}{rcl} \Vdash _{\!\!\mathscr {B}} \varphi \vee \psi &{} \text { iff } &{} \text {for any } \mathscr {C} \text { such that } \mathscr {B} \subseteq \mathscr {C} \text { and any } \textrm{p} \in \mathbb {A}, \\ &{} &{} \text { if } \varphi \Vdash _{\!\!\mathscr {C}} \textrm{p} \text { and } \psi \Vdash _{\!\!\mathscr {C}} \textrm{p}, \text { then } \Vdash _{\!\!\mathscr {C}} \textrm{p} \end{array} } $$

One justification for the clauses is the principle of definitional reflection (DR) (see Hallnäs [14, 15] and Schroeder-Heister [31]):

whatever follows from all the premisses of an assertion also follows from the assertion itself

Taking the perspective that the introduction rules are definitions, DR provides an answer for the way in which the elimination rules follow. Similarly, it justifies that the clauses for the logical constants take the form of their elimination rules.

Why does the clause for conjunction ($\wedge$) not take the form given by DR? What DR gives is the generalized elimination rule,

We may modify the B-eS for IPL by replacing ($\wedge$) with the following:

We show in Sect. 2.3 that the result does indeed characterize IPL. Indeed, it is easy to see that the generalized elimination rule and usual elimination rule for $\wedge$ have the same expressive power.

Note, we here take the definitional view of the introduction rules for the logical constants of IPL, and not of bases themselves, thus do not contradict the distinctions made by Piecha and Schroeder-Heister [22, 34].

Taking this analysis into consideration, we take the following definition of the multiplicative conjunction that corresponds to the definitional reflection of its introduction rule:

We show in Sect. 4 that the result does indeed characterize $\mathrm IMLL{}$.

The paper is structured as follows: in Sect. 2, we review the B-eS for IPL given by Sandqvist [29]; in Sect. 3, we define $\mathrm IMLL$ and provide intuitions about its B-eS; in Sect. 4, we formally define the B-eS for $\mathrm IMLL$ and explain its soundness and completeness proofs. The paper ends in Sect. 5 with a conclusion and summary of results.

2 Base-Extension Semantics for IPL

In this section, we review the B-eS for IPL given by Sandqvist [29]. In Sect. 2.1, we give a terse but complete definition of the B-eS for IPL. In Sect. 2.2, we summarize the completeness proof. Finally, in Sect. 2.3, we discuss a modification of the treatment of conjunction. While IPL is not the focus of this paper, this review provides intuition and motivates the B-eS for $\mathrm IMLL$ in Sect. 3. Specifically, the analysis of the treatment of conjunction in IPL motivates the handling of the multiplicative conjunction in $\mathrm IMLL$.

Throughout this section, we fix a denumerable set of atomic propositions $\mathbb {A}$, and the following conventions: $\textrm{p}, \textrm{q}, \dots$ denote atoms; $\textrm{P}, \textrm{Q}, \dots$ denote finite sets of atoms; $\varphi , \psi , \theta , \dots$ denote formulas; $\mathrm {\Gamma }, \mathrm {\Delta }, \dots$ denote finite sets of formulas.

We forego an introduction to IPL, which is doubless familiar—see van Dalen [7]. For clarity, note that we distinguish sequents $\mathrm {\Gamma }\triangleright \varphi$ from judgements $\mathrm {\Gamma }\vdash _{\!\!} \varphi$ that say that the sequent is valid in IPL.

2.1 Support in a Base

The B-eS for IPL begins by defining derivability in a base. A (properly) second-level atomic rule—see Piecha and Schroeder-Heister [22, 34]— is a natural deduction rule of the following form, in which $q,q_1,...,q_n$ are atoms and $Q_1$,...,$Q_n$ are (possibly empty) sets of atoms:

Importantly, atomic rules are taken per se and not closed under substitution. They may be expressed inline as $\left( \textrm{Q}_1 \triangleright \textrm{q}_1, \dots , \textrm{Q}_n \triangleright \textrm{q}_n \right) \Rightarrow \textrm{q}$—note, the axiom case is the special case when the left-hand side is empty, $\Rightarrow \textrm{q}$. They are read as natural deduction rules in the sense of Gentzen [37]; thus, $\Rightarrow q$ means that the atom $\textrm{q}$ may be concluded whenever, while $\left( \textrm{Q}_1 \triangleright \textrm{q}_1, \dots , \textrm{Q}_n \triangleright \textrm{q}_n \right) \Rightarrow \textrm{q}$ means that one may derive q from a set of atoms S if one has derived $\textrm{q}_i$ from S assuming $\textrm{Q}_i$ for $i=1,...,n$.

A base is a set of atomic rules. We write $\mathscr {B}, \mathscr {C}, \dots$ to denote bases, and $\varnothing$ to denote the empty base (i.e., the base with no rules). We say $\mathscr {C}$ is an extension of $\mathscr {B}$ if $\mathscr {C}$ is a superset of $\mathscr {B}$, denoted $\mathscr {C} \supseteq \mathscr {B}$.

Definition 1

(Derivability in a Base). Derivability in a base $\mathscr {B}$ is the least relation $\vdash _{\!\!\mathscr {B}}$ satisfying the following:

• (Ref-IPL) $\textrm{S}, \textrm{q} \vdash _{\!\!\mathscr {B}} \textrm{q}$.

• (App-IPL) If atomic rule $\left( \textrm{Q}_1 \triangleright \textrm{q}_1, \dots , \textrm{Q}_n \triangleright \textrm{q}_n \right) \Rightarrow \textrm{q}$ is in $\mathscr {B}$, and $\textrm{S}, \textrm{Q}_i \vdash _{\!\!\mathscr {B}} \textrm{q}_i$ for all $i = 1, \dots , n$, then $\textrm{S} \vdash _{\!\!\mathscr {B}} \textrm{q}$.

This forms the base case of the B-eS for IPL:

Definition 2

(Sandqvist’s Support in a Base). Sandqvist’s support in a base $\mathscr {B}$ is the least relation $\Vdash _{\!\!\mathscr {B}}$ defined by the clauses of Fig. 1. A sequent $\mathrm {\Gamma }\triangleright \varphi$ is valid—denoted $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$—iff it is supported in every base,

$$ \mathrm {\Gamma }\Vdash _{\!\!} \varphi \qquad \text{ iff } \qquad \mathrm {\Gamma }\Vdash _{\!\!\mathscr {B}} \varphi \text{ holds } \text{ for } \text{ any } \mathscr {B} $$

Every base is an extension of the empty base ($\varnothing$), therefore $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$ iff $\mathrm {\Gamma }\Vdash _{\!\!\varnothing } \varphi$. Sandqvist [29] showed that this semantics characterizes IPL:

Theorem 1

(Sandqvist [29]).$\mathrm {\Gamma }\vdash _{\!\!} \varphi$ iff $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$

Soundness—that is, $\mathrm {\Gamma }\vdash _{\!\!}\varphi$ implies $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$—follows from showing that $\Vdash _{\!\!}$ respects the rules of Gentzen’s [37] $\textsf{NJ}$; for example, $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$ and $\mathrm {\Delta }\Vdash _{\!\!} \psi$ implies $\mathrm {\Gamma }, \mathrm {\Delta }\Vdash _{\!\!} \varphi \wedge \psi$. Completeness—that is, $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$ implies $\mathrm {\Gamma }\vdash _{\!\!} \varphi$—is more subtle. We present the argument in Sect. 2.2 as it motivates the work in Sect. 4.3.

2.2 Completeness of IPL

We require to show that $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$ implies that there is an $\textsf{NJ}$-proof witnessing $\mathrm {\Gamma }\vdash _{\!\!} \varphi$. To this end, we associate to each sub-formula $\rho$ of $\mathrm {\Gamma }\cup \{\varphi \}$ a unique atom $\textrm{r}$, and construct a base $\mathscr {N}$ such that $\textrm{r}$ behaves in $\mathscr {N}$ as $\rho$ behaves in $\textsf{NJ}$. Moreover, formulas and their atomizations are semantically equivalent in any extension of $\mathscr {N}$ so that support in $\mathscr {N}$ characterizes both validity and provability. When $\rho \in \mathbb {A}$, we take $\textrm{r} := \rho$, but for complex $\rho$ we choose r to be alien to $\mathrm {\Gamma }$ and $\varphi$.

Example 1

Suppose $\rho :=\textrm{p} \wedge \textrm{q}$ is a sub-formula of $\mathrm {\Gamma }\cup \{\varphi \}$. Associate to it a fresh atom $\textrm{r}$. Since the principal connective of $\rho$ is $\wedge$, we require $\mathscr {N}$ to contain the following rules:

We may write $(\textrm{p} \wedge \textrm{q})^\flat$ for $\textrm{r}$ so that these rules may be expressed as follows:

$\blacksquare$

Formally, given a judgement $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$, to every sub-formula $\rho$ associate a unique atomic proposition $\rho ^\flat$ as follows:

• if $\rho \not \in \mathbb {A}$, then $\rho ^\flat$ is an atom that does not occur in any formula in $\mathrm {\Gamma }\cup \{\varphi \}$;

• if $\rho \in \mathbb {A}$, then $\rho ^\flat = \rho$.

By unique we mean that $(\cdot )^\flat$ is injective—that is, if $\rho \ne \sigma$, then $\rho ^\flat \ne \sigma ^\flat$. The left-inverse of $(\cdot )^\flat$ is $(\cdot )^\natural$, and the domain may be extended to the entirety of $\mathbb {A}$ by identity on atoms not in the codomain of $(\cdot )^\flat$. Both functions act on sets pointwise—that is, $\varSigma ^\flat := \{\varphi ^\flat \mid \varphi \in \varSigma \}$ and $\textrm{P}^\natural := \{\textrm{p}^\natural \mid \textrm{p} \in \textrm{P} \}$. Relative to $(\cdot )^\flat$, let $\mathscr {N}$ be the base containing the rules of Fig. 2 for any sub-formulas $\rho$ and $\sigma$ of $\mathrm {\Gamma }$ and $\varphi$, and any $\textrm{p} \in \mathbb {A}$.

Fig. 2.

Atomic System $\mathscr {N}$

Sandqvist [29] establishes three claims that deliver completeness:

• (IPL-AtComp) Let $\textrm{S} \subseteq \mathbb {A}$ and $\textrm{p} \in \mathbb {A}$ and let $\mathscr {B}$ be a base: $\textrm{S} \Vdash _{\!\!\mathscr {B}} \textrm{p} \text { iff } \textrm{S} \vdash _{\!\!\mathscr {B}} \textrm{p}.$

• (IPL-Flat) For any sub-formula $\xi$ of $\mathrm {\Gamma }\cup \{\varphi \}$ and $\mathscr {N}' \supseteq \mathscr {N}$: $\Vdash _{\!\!\mathscr {N}'} \xi ^\flat \text { iff } \Vdash _{\!\!\mathscr {N}'} \xi$.

• (IPL-Nat) Let $\textrm{S} \subseteq \mathbb {A}$ and $\textrm{p} \in \mathbb {A}$: if $\textrm{S} \vdash _{\!\!\mathscr {N}} p \text {, then } \textrm{S}^\natural \vdash _{\!\!} p^\natural$.

The first claim is completeness in the atomic case. The second claim is that $\xi ^\flat$ and $\xi$ are equivalent in $\mathscr {N}$—that is, $\xi ^\flat \Vdash _{\!\!\mathscr {N}} \xi$ and $\xi \Vdash _{\!\!\mathscr {N}} \xi ^\flat$. Consequently,

$$ \mathrm {\Gamma }^\flat \Vdash _{\!\!\mathscr {N}'} \varphi ^\flat \qquad \text { iff } \qquad \mathrm {\Gamma }\Vdash _{\!\!\mathscr {N}'} \varphi $$

The third claim is the simulation statement which allows us to make the final move from derivability in $\mathscr {N}$ to derivability in $\textsf{NJ}$.

Proof

(Theorem 1—Completeness). Assume $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$ and let $\mathscr {N}$ be its bespoke base. By (IPL-Flat), $\mathrm {\Gamma }^\flat \Vdash _{\!\!\mathscr {N}} \varphi ^\flat$. Hence, by (IPL-AtComp), $\mathrm {\Gamma }^\flat \vdash _{\!\!\mathscr {N}} \varphi ^\flat$. Whence, by (IPL-Nat), $(\mathrm {\Gamma }^{\flat })^\natural \vdash _{\!\!} (\varphi ^{\flat })^\natural$, i.e. $\mathrm {\Gamma }\vdash _{\!\!} \varphi$, as required.$\square$

2.3 Base-Extension Semantics for IPL, Revisited

Goldfarb [13, 23] has also given a (complete) proof-theoretic semantics for IPL, but it mimics Kripke’s [17] semantics. What is interesting about the B-eS in Sandqvist [29] is the way in which it is not a representation of the possible world semantics. This is most clearly seen in ($\vee$), which takes the form of the ‘second-order’ definition of disjunction—that is,

$$ U+V = \forall X \left( (U \rightarrow X)\rightarrow (U \rightarrow X)\rightarrow X\right) $$

—see Girard [12] and Negri [41]. This adumbrates the categorical perspective on B-eS given by Pym et al. [26]. Proof-theoretically, the clause recalls the elimination rule for the connective restricted to atomic conclusions,

Dummett [9] has shown that such restriction in $\textsf{NJ}$ is without loss of expressive power. Indeed, all of the clauses in Fig. 1 may be regarded as taking the form of the corresponding elimination rules.

The principle of definitional reflection, as described in Sect. 1 justifies this phenomenon. According to this principle, an alternative candidate clause for conjunction is as follows:

Definition 3

The relation $\Vdash _{\!\!\mathscr {B}}^{*}$ is defined by the clauses of Fig. 1 with ($\wedge ^*$) in place of ($\wedge$). The judgement $\mathrm {\Gamma }\Vdash _{\!\!}^{*} \varphi$ obtains iff $\mathrm {\Gamma }\Vdash _{\!\!\mathscr {B}}^{*} \varphi$ for any $\mathscr {B}$.

The resulting semantics is sound and complete for IPL:

Theorem 2

$\mathrm {\Gamma }\Vdash _{\!\!}^{*} \varphi$ iff $\mathrm {\Gamma }\vdash _{\!\!} \varphi$.

Proof

We assume the following: for arbitrary base $\mathscr {B}$, and formulas $\varphi , \psi , \chi$,

• (IPL$^*$ -Monotone) If $\Vdash _{\!\!\mathscr {B}}^{*} \varphi$, then $\Vdash _{\!\!\mathscr {C}}^{*} \varphi$ for any $\mathscr {C}\supseteq \mathscr {B}$.

• (IPL$^*$ -AndCut) If $\Vdash _{\!\!\mathscr {B}}^{*} \varphi \wedge \psi$ and $\varphi , \psi \Vdash _{\!\!\mathscr {B}}^{*} \chi$, then $\Vdash _{\!\!\mathscr {B}}^{*} \chi$.

The first claim follows easily from (Inf). The second is a generalization of ($\wedge ^*$); it follows by induction on the structure of $\chi$—an analogous treatment of disjunction was given by Sandqvist [29].

By Theorem 1, it suffices to show that $\mathrm {\Gamma }\Vdash _{\!\!}^{*} \varphi$ iff $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$. For this it suffices to show $\Vdash _{\!\!\mathscr {B}}^{*} \theta$ iff $\Vdash _{\!\!\mathscr {B}} \theta$ for arbitrary $\mathscr {B}$ and $\theta$. We proceed by induction on the structure of $\theta$. Since the two relations are defined identically except in the case when the $\theta$ is a conjunction, we restrict attention to this case.

First, we show $\Vdash _{\!\!\mathscr {B}} \theta _1 \wedge \theta _2$ implies $\Vdash _{\!\!\mathscr {B}}^{*} \theta _1 \wedge \theta _2$. By ($\wedge ^*$), the conclusion is equivalent to the following: for any $\mathscr {C}\supseteq \mathscr {B}$ and $\textrm{p} \in \mathbb {A}$, if $\theta _1, \theta _2 \Vdash _{\!\!\mathscr {C}}^{*} \textrm{p}$, then $\Vdash _{\!\!\mathscr {C}}^{*} \textrm{p}$. Therefore, fix $\mathscr {C}\supseteq \mathscr {B}$ and $\textrm{p} \in \mathbb {A}$ such that $\theta _1, \theta _2 \Vdash _{\!\!\mathscr {C}}^{*} \textrm{p}$. By (Inf), this entails the following: if $\Vdash _{\!\!\mathscr {C}}^{*} \theta _1$ and $\Vdash _{\!\!\mathscr {C}}^{*} \theta _2$, then $\Vdash _{\!\!\mathscr {C}}^{*} \textrm{p}$. By ($\wedge$) on the assumption (i.e., $\Vdash _{\!\!\mathscr {B}} \theta _1 \wedge \theta _2$), we obtain $\Vdash _{\!\!\mathscr {B}} \theta _1$ and $\Vdash _{\!\!\mathscr {B}} \theta _2$. Hence, by the induction hypothesis (IH), $\Vdash _{\!\!\mathscr {B}}^{*} \theta _1$ and $\Vdash _{\!\!\mathscr {B}}^{*} \theta _2$. Whence, by (IPL$^*$-Monotone), $\Vdash _{\!\!\mathscr {C}}^{*} \theta _1$ and $\Vdash _{\!\!\mathscr {C}}^{*} \theta _2$. Therefore, $\Vdash _{\!\!\mathscr {C}}^{*} \textrm{p}$. We have thus shown $\Vdash _{\!\!\mathscr {B}}^{*} \theta _1 \wedge \theta _2$, as required.

Second, we show $\Vdash _{\!\!\mathscr {B}}^{*} \theta _1 \wedge \theta _2$ implies $\Vdash _{\!\!\mathscr {B}} \theta _1 \wedge \theta _2$. It is easy to see that $\theta _1, \theta _2 \Vdash _{\!\!\mathscr {B}}^{*} \theta _i$ obtains for $i = 1, 2$. Applying (IPL$^*$-AndCut) (setting $\varphi =\theta _1$, $\psi = \theta _2$) once with $\chi = \theta _1$ and once with $\chi =\theta _2$ yields $\Vdash _{\!\!\mathscr {B}}^{*} \theta _1$ and $\Vdash _{\!\!\mathscr {B}}^{*} \theta _2$. By the IH, $\Vdash _{\!\!\mathscr {B}} \theta _1$ and $\Vdash _{\!\!\mathscr {B}}\theta _2$. Hence, $\Vdash _{\!\!\mathscr {B}} \theta _1 \wedge \theta _2$, as required.$\square$

A curious feature of the new semantics is that the meaning of the context-former (i.e., the comma) is not interpreted as $\wedge$; that is, defining the context-former as

$$ \Vdash _{\!\!\mathscr {B}}^{*} \mathrm {\Gamma }, \mathrm {\Delta }\qquad \text{ iff } \qquad \Vdash _{\!\!\mathscr {B}}^{*} \mathrm {\Gamma } \text{ and } \Vdash _{\!\!\mathscr {B}}^{*} \mathrm {\Delta }$$

we may express (Inf)

$$ \mathrm {\Gamma }\Vdash _{\!\!\mathscr {B}}^{*} \varphi \qquad \text{ iff } \qquad \text{ for } \text{ any } \mathscr {C} \supseteq \mathscr {B}\text{, } \text{ if } \Vdash _{\!\!\mathscr {C}}^{*} \mathrm {\Gamma }\text{, } \text{ then } \Vdash _{\!\!\mathscr {C}}^{*} \varphi $$

The clause for contexts is not the same as the clause for $\wedge$ in the new semantics. Nonetheless, as shown in the proof of Theorem 2, they are equivalent at every base—that is, $\Vdash _{\!\!\mathscr {B}}^{*} \varphi , \psi$ iff $\Vdash _{\!\!\mathscr {B}}^{*} \varphi \wedge \psi$ for any $\mathscr {B}$.

This equivalence of the two semantics yields the following:

Corollary 1

For arbitrary base $\mathscr {B}$ and formula $\varphi$, $\Vdash _{\!\!\mathscr {B}} \varphi$ iff, for any $\mathscr {X}\supseteq \mathscr {B}$ and every atom $\textrm{p}$, if $\varphi \Vdash _{\!\!\mathscr {X}} \textrm{p}$, then $\Vdash _{\!\!\mathscr {X}} \textrm{p}$.

The significance of this result is that we see that formulas in the B-eS are precisely characterized by their support of atoms.

3 Intuitionistic Multiplicative Linear Logic

Having reviewed the B-eS for IPL, we turn now to intuitionistic multiplicative linear logic ($\mathrm IMLL$). We first define the logic and then consider the challenges of giving a B-eS for it. This motivates the technical work in Sect. 4. Henceforth, we abandon the notation of the previous section as we do not need it and may recycle symbols and conventions.

Fix a countably infinite set $\mathbb {A}$ of atoms.

Definition 4

(Formula). The set of formulas $( \textsf{Form}_\textrm{IMLL})$ is defined by the following grammar:

$$ \varphi , \psi {:}{:}= \textrm{p} \in \mathbb {A}\mid \varphi \otimes \psi \mid I\mid \varphi \mathrel {\multimap }\psi $$

We use $\textrm{p}, \textrm{q}, \dots$ for atoms and $\varphi , \psi , \chi , \dots$ for formulas. In contrast to the work on IPL, collections of formulas in $\mathrm IMLL$ are more typically multisets. We use $\textrm{P}, \textrm{Q}, \dots$ for finite multisets of atoms, and $\mathrm {\Gamma }, \mathrm {\Delta }, \ldots$ to denote finite multisets of formulas.

We use $[\,\cdot \,]$ to specify a multiset; for example, $[\varphi , \varphi , \psi ]$ denotes the multiset consisting of two occurrence of $\varphi$ and one occurrences of $\psi$. The empty multiset (i.e., the multiset with no members) is denoted $\varnothing$. The union of two multisets $\mathrm {\Gamma }$ and $\mathrm {\Delta }$ is denoted . We may identify a multiset containing one element with the element itself; thus, we may write instead of to denote the union of multiset $\mathrm {\Delta }$ and the singleton multiset $[ \psi ]$. Thus, when no confusion arises, we may write to denote $[\varphi _1,...,\varphi _n]$.

Definition 5

(Sequent). A sequent is a pair $\mathrm {\Gamma }\triangleright \varphi$ in which $\mathrm {\Gamma }$ is a multiset of formulas and $\varphi$ is a formula.

We characterize $\mathrm IMLL$ by proof in a natural deduction system. Since it is a substructural logic, we write the system in the format of a sequent calculus as this represents the context management explicitly. We assume general familiarity with sequent calculi—see, for example, Troelstra and Schwichtenberg [41].

Definition 6

(System $\textsf{NIMLL}{}$). The sequential natural deduction system for $\mathrm IMLL$, denoted $\textsf{NIMLL}$, is given by the rules in Fig. 3.

A sequent $\mathrm {\Gamma }\triangleright \varphi$ is a consequence of $\mathrm IMLL$—denoted $\mathrm {\Gamma }\vdash \varphi$—iff there is a $\textsf{NIMLL}$-proof of it.

Fig. 3.

The Sequential Natural Deduction System $\textsf{NIMLL}$ for IMLL

One may regard $\mathrm IMLL$ as IPL without the structural rules of weakening and contraction—see Došen [8]. In other words, adding the following rules to $\textsf{NIMLL}$ recovers a sequent calculus for IPL:

To stay close to the work in Sect. 2, it is instructive to consider the natural deduction presentation, too. The rule figures may be the same, but their application is not; for example,

Here, it is important that the context are multisets, not as sets.

The strict context management in $\mathrm IMLL$ yields the celebrated ‘resource interpretations’ of Linear Logic—see Girard [11]. The leading example of which is, perhaps, the number-of-uses reading in which a proof of a formula $\varphi \mathrel {\multimap }\psi$ determines a function that uses its arguments exactly once. This reading is, however, entirely proof-theoretic and is not expressed in the truth-functional semantics of $\mathrm IMLL$—see Girard [11], Allwein and Dunn [1], and Coumans et al. [6]. Though these semantics do have sense of ‘resource’ it is not via the number-of-uses reading, but instead denotational in the sense of the treatment of resources in the truth-functional semantics of the logic of Bunched Implications [19]. The number-of-uses reading is, however, reflected in the categorical semantics—see Seely [35] and Biermann [3, 4].

How do we render support sensitive to the resource reading? The subtlety is that for $\mathrm {\Gamma }\Vdash _{\!\!} \varphi$ (where $\mathrm {\Gamma }\ne \varnothing$), we must somehow transmit the resources captured by $\mathrm {\Gamma }$ to $\varphi$. From Corollary 1, we see that in B-eS the content of a formula is captured by the atoms it supports. Therefore, we enrich the support relation with an multiset of atoms P,

where

This completes the background on $\mathrm IMLL$.

4 Base-extension Semantics for $\mathrm IMLL$

In this section, we give a B-eS for $\mathrm IMLL$. It is structured as follows: first, we define support in a base in Sect. 4.1; second, we prove soundness in Sect. 4.2; finally, we prove completeness in Sect. 4.3.

4.1 Support in a Base

The definition of the B-eS proceeds in line with that for IPL (Sect. 2) while taking substructurality into consideration.

Definition 7

(Atomic Sequent). An atomic sequent is a pair $P \triangleright \textrm{p}$ in which P is a multiset of atoms and $\textrm{q}$ is an atom.

Definition 8

(Atomic Rule). An atomic rule is a pair $\mathcal {P} \Rightarrow \textrm{p}$ in which $\mathcal {P}$ is a (possibly empty) finite set of atomic sequents and $\textrm{p}$ in an atom.

Definition 9

(Base). A base $\mathscr {B}$ is a (possibly infinite) set of atomic rules.

Definition 10

(Derivability in a Base). The relation $\vdash _{\!\!\mathscr {B}}$ of derivability in $\mathscr {B}$ is the least relation satisfying the following:

• (Ref) $\textrm{p} \vdash _{\!\!\mathscr {B}} \textrm{p}$

• (App) If 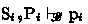for $i = 1, \dots , n$ and $\left( \textrm{P}_1 \triangleright \textrm{p}_1, \dots , \textrm{P}_n \triangleright \textrm{p}_n \right) \Rightarrow \textrm{p} \in \mathscr {B}$, then .

Fig. 4.

Base-extension Semantics for $\mathrm IMLL$

Note the differences between Definition 1 and Definition 10: first, in (Ref), no redundant atoms are allowed to appear, while in (Ref-IPL) they may; second, in (App), the multisets $\textrm{S}_1$,...,$\textrm{S}_n$ are collected together as a multiset, while in (App-IPL), there is one set. These differences reflect the fact in the multiplicative setting that ‘resources’ can neither be discharged nor shared.

Definition 11

(Support). That a sequent $\mathrm {\Gamma }\triangleright \varphi$ is supported in the base $\mathscr {B}$ using resources $\textrm{S}$—denoted $\mathrm {\Gamma }\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \varphi$—is defined by the clauses of Fig. 4 in which $\mathrm {\Gamma }$ and $\mathrm {\Delta }$ are non-empty finite multisets of formulas. The sequent $\mathrm {\Gamma }\triangleright \varphi$ is supported using resources S—denoted $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! \textrm{S} } \varphi$—iff $\mathrm {\Gamma }\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \varphi$ for any base $\mathscr {B}$. The sequent $\mathrm {\Gamma }\triangleright \varphi$ is valid—denoted $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi$—iff $\mathrm {\Gamma }\triangleright \varphi$ is supported using the empty multiset of resources (i.e., $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! \varnothing } \varphi$).

It is easy to see that Fig. 4 is an inductive definition on a structure of formulas that prioritizes conjunction ($\otimes$) over implication ($\mathrel {\multimap }$)—an analogous treatment in IPL with disjunction ($\vee$) prioritized over implication ($\rightarrow$) has been given by Sandqvist [29]. As explained in Sect. 3, the purpose of the multisets of atoms $\textrm{S}$ in the support relation $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} }$ is to express the susbtructurality of the logical constants. The naive ways of using multisets of formulas rather than multisets of atoms—for example, $\mathrm {\Gamma }\Vdash _{ \!\!\mathscr {B} }^{ \!\! \mathrm {\Delta } } \varphi$ iff —results in impredicative definitions of support.

We read (Inf) as saying that $\mathrm {\Gamma }\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \varphi$ (for $\mathrm {\Gamma }\ne \varnothing$) means, for any extension $\mathscr {X}$ of $\mathscr {B}$, if $\mathrm {\Gamma }$ is supported in $\mathscr {X}$ with some resources $\textrm{U}$ (i.e. $\Vdash _{ \!\!\mathscr {X} }^{ \!\! \textrm{U} } \mathrm {\Gamma }$), then $\varphi$ is also supported by combining the resources $\textrm{U}$ with the resources $\textrm{S}$ (i.e., ).

The following observation on the monotonicity of the semantics with regard to base extensions follows immediately by unfolding definitions:

Proposition 1

If $\mathrm {\Gamma }\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \varphi$ and $\mathscr {C}\supseteq \mathscr {B}$, then $\mathrm {\Gamma }\Vdash _{ \!\!\mathscr {C} }^{ \!\! \textrm{S} } \varphi$.

From this proposition we see the following: $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! \textrm{S} } \varphi$ iff $\mathrm {\Gamma }\Vdash _{ \!\!\varnothing }^{ \!\! \textrm{S} } \varphi$, and $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi$ iff $\mathrm {\Gamma }\Vdash _{ \!\!\varnothing }^{ \!\! \varnothing } \varphi$. As expected, we do not have monotonicity on resources—that is, $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! \textrm{S} } \varphi$ does not, in general, imply for arbitrary $\textrm{T}$. This exposes the different parts played by bases and the resources in the semantics: bases are the setting in which a formula is supported, resources are tokens used in that setting to establish the support.

A distinguishing aspect of support is the structure of (Inf). In one direction, it is merely cut, but in the other it says something stronger. The completeness argument will go through the atomic case (analogous to the treatment of IPL in Sect. 2.2), and the following proposition suggests that the setup is correct:

Proposition 2

The following two propositions are equivalent for arbitrary base $\mathscr {B}$, multisets of atoms $\textrm{P}, \textrm{S}$, and atom $\textrm{q}$, where we assume $\textrm{P} = [\textrm{p}_1, \dots , \textrm{p}_n]$:

• 1. .

• 2. for any $\mathscr {X}\supseteq \mathscr {B}$ and multisets of atoms $\mathrm {T_1}, \dots , \mathrm {T_n}$, if $\textrm{T}_i \vdash _{\!\!\mathscr {X}} \textrm{p}_i$ holds for all $i = 1, \dots ,n$, then .

It remains to prove soundness and completeness.

4.2 Soundness

Theorem 3

(Soundness). If $\mathrm {\Gamma }\vdash \varphi$, then $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi$.

The argument follows a typical strategy of showing that the semantics respects the rules of $\textsf{NIMLL}$—that is, for any $\mathrm {\Gamma }, \mathrm {\Delta }, \varphi , \psi ,$ and $\chi$:

These follow quickly from the fact that the clauses of each connective in Fig. 4 takes the form of its elimination rules. The only subtle cases are ($\otimes$E) and ($I$E).

To show ($I$E), suppose $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \chi$ and $\mathrm {\Delta }\Vdash _{ \!\! }^{ \!\! } I$. We require to show . By (Inf), we fix some base $\mathscr {B}$ and multisets of atoms $\textrm{P}$ and $\textrm{Q}$ such that $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{P} } \mathrm {\Gamma }$ and $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{Q} } \mathrm {\Delta }$. It remains to verify . When $\chi$ is atomic, this follows immediately from $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{P} } \chi$ and $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{Q} } I$ by ($I$). To handle non-atomic $\chi$, we require the following:

Lemma 1

For arbitrary base $\mathscr {B}$, multisets of atoms $\textrm{S}, \textrm{T}$, and formula $\chi$, if 1. $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } I$, 2. $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{T} } \chi$, then 3. .

This lemma follows by induction on the structure of $\chi$, with the base case given by ($I$). One cannot use this general form to define $I$ as it would result in an impredicative definition of support.

Similarly, we require the following to prove ($\otimes$E):

Lemma 2

For arbitrary base $\mathscr {B}$, multisets of atoms $\textrm{S}, \textrm{T}$, and formulas $\varphi , \psi , \chi$, if 1. $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \varphi \otimes \psi$, 2. , then 3. .

With these results, we may prove soundness:

Fig. 5.

Atomic System $\mathscr {M}$

Proof

(Theorem 3 —sketch). We demonstrate ($\otimes$I) and ($\otimes$E).

($\otimes$I). Assume $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi$ and $\mathrm {\Delta }\Vdash _{ \!\! }^{ \!\! } \psi$. We require to show . By (Inf), the conclusion is equivalent to the following: for any base $\mathscr {B}$, for any multisets of atoms $\textrm{T}$ and $\textrm{S}$ , if $\Vdash _{ \!\!\mathscr {B} }^{ \!\! T } \mathrm {\Gamma }$ and $\Vdash _{ \!\!\mathscr {B} }^{ \!\! S } \mathrm {\Delta }$, then . So we fix some $\mathscr {B}$ and $\textrm{T}$, $\textrm{S}$ such that $\Vdash _{ \!\!\mathscr {B} }^{ \!\! T } \mathrm {\Gamma }$ and $\Vdash _{ \!\!\mathscr {B} }^{ \!\! S } \mathrm {\Delta }$, and show that . By ($\otimes$), it suffices to show, for arbitrary $\mathscr {C}\supseteq \mathscr {B}$, multiset of atoms $\textrm{U}$, and atom $\textrm{p}$, if , then . So we fix some $\mathscr {C}\supseteq \mathscr {B}$, multiset of atoms $\textrm{U}$, and atom $\textrm{p}$ such that , and the goal is to show that . From the assumptions $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi$ and $\mathrm {\Delta }\Vdash _{ \!\! }^{ \!\! } \psi$, we see that obtains. Therefore, by monotonicity, obtains. By (Inf), this suffices for , to yield , as required.

($\otimes$E). Assume $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi \otimes \psi$ and . We require to show . By (Inf), it suffices to assume $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \mathrm {\Gamma }$ and $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{T} } \mathrm {\Delta }$ and show that . First, $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi \otimes \psi$ together with $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \mathrm {\Gamma }$ entails that $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \varphi \otimes \psi$. Second, by (Inf), is equivalent to the following:

Since $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{T} } \mathrm {\Delta }$, setting $\textrm{P} := \textrm{T}$ and $\textrm{Q} := \textrm{S}$, yields,

(1)

Now, given $\Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \varphi \otimes \psi$ and (1), we can apply Lemma 2 and conclude .$\square$

4.3 Completeness

Theorem 4

(Completeness). If $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi$, then $\mathrm {\Gamma }\vdash \varphi$.

The argument follows the strategy used by Sanqvist [29] for IPL—see Sect. 2.2. We explain the main steps.

Let $\varXi$ be the set of all sub-formulas of $\mathrm {\Gamma }\cup \{\varphi \}$. Let ${(\cdot )}^{\flat } :\varXi \rightarrow \mathbb {A}$ be an injection that is fixed on $\varXi \cap \mathbb {A}$—that is, ${\textrm{p}}^{\flat } = \textrm{p}$ for $\textrm{p}\in \varXi \cap \mathbb {A}$. Let ${(\cdot )}^{\natural }$ be the left-inverse of ${(\cdot )}^{\flat }$—that is ${\textrm{p}}^{\natural } = \chi$ if $\textrm{p}={\chi }^{\flat }$, and ${\textrm{p}}^{\natural } = \textrm{p}$ if $\textrm{p}$ is not in the image of ${(\cdot )}^{\flat }$. Both act on multisets of formulas pointwise; that is, ${\mathrm {\Delta }}^{\flat } {:}{=}[{\delta }^{\flat } \mid \delta \in \mathrm {\Delta }]$ and ${\textrm{P}}^{\natural } {:}{=}[{\textrm{p}}^{\natural } \mid \textrm{p} \in \textrm{P}]$.

We construct a base $\mathscr {M}$ such that ${\varphi }^{\flat }$ behaves in $\mathscr {M}$ as $\varphi$ behaves in $\textsf{NIMLL}{}$. The base $\mathscr {M}$ contains all instances of the rules of Fig. 5 when $\sigma$ and $\tau$ range over $\varXi$, and $\textrm{p}$ ranges over $\mathbb {A}$. We illustrate how $\mathscr {M}$ works with an example.

Example 2

Consider the sequent $\mathrm {\Gamma }\triangleright \varphi$ where and $\varphi = \textrm{q} \otimes \mathrm {p_1}$. By definition, $\varXi := \{ \textrm{p}_1, \textrm{p}_2, \textrm{p}_1 \otimes \textrm{p}_2 \mathrel {\multimap }\textrm{q}, \textrm{p}_1 \otimes \textrm{p}_2, \textrm{q}, \textrm{q} \otimes \textrm{p}_1 \}$, and, therefore, the image of ${(\cdot )}^{\flat }$ is $\{ \textrm{p}_1, \textrm{p}_2, \textrm{q}, {( \textrm{p}_1 \otimes \textrm{p}_2 \mathrel {\multimap }\textrm{q} )}^{\flat }, {( \textrm{p}_1 \otimes \textrm{p}_2 )}^{\flat }, {( \textrm{q} \otimes \textrm{p}_1 )}^{\flat } \}$.

That $\mathrm {\Gamma }\vdash \varphi$ obtains is witnessed by the following $\textsf{NIMLL}$-proof:

The base $\mathscr {M}$ is designed so that we may simulate the rules of $\textsf{NIMLL}$; for example, the $\otimes _\mathsf {{E}}$ is simulated by using (App) on $\otimes _\mathsf {{E}}^\flat$,

In this sense, the proof above is simulated by the following steps:

• (i) By (Ref), (1) $\textrm{p}_1 \vdash _{\!\!\mathscr {M}} \textrm{p}_1$; (2) $\textrm{p}_2 \vdash _{\!\!\mathscr {M}} \textrm{p}_2$; (3) ${\left( \textrm{p}_1 \otimes \textrm{p}_2 \mathrel {\multimap }\textrm{q} \right) }^{\flat } \vdash _{\!\!\mathscr {M}} {\left( \textrm{p}_1 \otimes \textrm{p}_2 \mathrel {\multimap }\textrm{q} \right) }^{\flat }$

• (ii) By (App), using $(\otimes _\mathsf {{I}})$ on (1) and (2), we obtain (4)

• (iii) By (App), using ${(\mathrel {\multimap }_\mathsf {{E}})}^{\flat }$ on (3) and (4), we obtain (5)

• (iv) By (App), using ${(\otimes _\mathsf {{I}})}^{\flat }$ on (1) and (5). we have .

Significantly, steps (i)–(iv) are analogues of the steps in the proof tree above.$\blacksquare$

Theorem 4 (Completeness) follows from the following three observations, which are counterparts to (IPL-AtComp), (IPL-Flat), and (IPL-Nat) from Sect. 2.2:

• (IMLL-AtComp) For any $\mathscr {B}$, $\textrm{P}$, $\textrm{S}$, and $\textrm{q}$, iff $\textrm{P} \Vdash _{ \!\!\mathscr {B} }^{ \!\! \textrm{S} } \textrm{q}$.

• (IMLL-Flat) For any $\xi \in \varXi$, $\mathscr {X}\supseteq \mathscr {M}$ and $\textrm{U}$, $\Vdash _{ \!\!\mathscr {X} }^{ \!\! \textrm{U} } {\xi }^{\flat }$ iff $\Vdash _{ \!\!\mathscr {X} }^{ \!\! \textrm{U} } \xi$.

• (IMLL-Nat) For any $\textrm{P}$ and $\textrm{q}$, if $\textrm{P} \vdash _{\!\!\mathscr {M}} \textrm{q}$ then ${\textrm{P}}^{\natural } \vdash {\textrm{q}}^{\natural }$.

(IMLL-AtComp) follows from Proposition 2 and is the base case of completeness. (IMLL-Flat) formalizes the idea that every formula $\xi$ appearing in $\mathrm {\Gamma }\triangleright \varphi$ behaves the same as ${\xi }^{\flat }$ in any base extending $\mathscr {M}$. Consequently, $\mathrm {\Gamma }^\flat \Vdash _{\!\!\mathscr {M}} \varphi ^\flat$ iff $\mathrm {\Gamma }\Vdash _{\!\!\mathscr {M}} \varphi$. (IMLL-Nat) intuitively says that $\mathscr {M}$ is a faithful atomic encoding of $\textsf{NIMLL}$, witnessed by ${(\cdot )}^{\natural }$. This together with (IMLL-Flat) guarantee that every $\xi \in \varXi$ behaves in $\mathscr {M}$ as ${\xi }^{\flat }$ in $\mathscr {M}$, thus as ${\left( {\xi }^{\flat } \right) }^{\natural } = \xi$ in $\textsf{NIMLL}$.

Proof

(Theorem 4 —Completeness). Assume $\mathrm {\Gamma }\Vdash _{ \!\! }^{ \!\! } \varphi$ and let $\mathscr {M}$ be the bespoke base for $\mathrm {\Gamma }\triangleright \varphi$. By (IMLL-Flat), $\mathrm {\Gamma }^\flat \Vdash _{ \!\!\mathscr {M} }^{ \!\! \varnothing } \varphi ^\flat$. Therefore, by (IMLL-AtComp), we have ${\mathrm {\Gamma }}^{\flat } \vdash _{\!\!\mathscr {M}} {\varphi }^{\flat }$. Finally, by (IMLL-Nat), ${\left( {\mathrm {\Gamma }}^{\flat } \right) }^{\natural } \vdash {\left( {\varphi }^{\flat } \right) }^{\natural }$, namely $\mathrm {\Gamma }\vdash _{\!\!} \varphi$.$\square$

5 Conclusion

Proof-theoretic semantics (P-tS) is the paradigm of meaning in logic based on proof, as opposed to truth. A particular form of P-tS is base-extension semantics (B-eS) in which one defines the logical constants by means of a support relation indexed by a base—a system of natural deduction for atomic propositions—which grounds the meaning of atoms by proof in that base. This paper provides a sound and complete base-extension semantics for intuitionistic multiplicative linear logic ($\mathrm IMLL$).

The B-eS for IPL given by Sandqvist [29] provides a strategy for the problem. The paper begins with a brief but instructive analysis of this work that reveals definitional reflection (DR) as an underlying principle delivering the semantics; accordingly, in Sect. 2.3, the paper modifies the B-eS for IPL to strictly adhere to DR and proves soundness and completeness of the result. Moreover, the analysis highlights that essential to B-eS is a transmission of proof-theoretic content: a formula $\varphi$ is supported in a base $\mathscr {B}$ relative to a context $\mathrm {\Gamma }$ iff, for any extension $\mathscr {C}$ of $\mathscr {B}$, the formula $\varphi$ is supported in $\mathscr {C}$ whenever $\mathrm {\Gamma }$ is supported in $\mathscr {C}$.

With this understanding of B-eS of IPL, the paper gives a ‘resource-sensitive’ adaptation by enriching the support relation to carry a multiset of atomic ‘resources’ that enable the transmission of proof-theoretic content. This captures the celebrated ‘resource reading’ of $\mathrm IMLL$ which is entirely proof-theoretic—see Girard [11]. The clauses of the logical constants are then delivered by DR on their introduction rules. Having set up the B-eS for $\mathrm IMLL$ in this principled way, soundness and completeness follow symmetrically to the preceding treatment of IPL.

To date, P-tS has largely been restricted to classical and intuitionistic propositional logics. This paper provides the first step toward a broader analysis. In particular, the analysis in this paper suggests a general methodology for delivering B-eS for other substructural logics such as, inter alia, (intuitionistic) Linear Logic [11] (LL) and the logic of Bunched Implications [19] (BI). While it is straightforward to add the additive connectives of LL, with the evident semantic clauses following IPL and with the evident additional cases in the proofs, it is less apparent how to handle the exponentials. For BI, the primary challenge is to appropriately account for the bunched structure of contexts, and to enable and confine weakening and contraction to the additive context-former.

Developing the P-tS for substructural logics is valuable because of their deployment in the verification and modelling of systems. Significantly, P-tS has shown the be useful in simulation modelling—see, for example, Kuorikoski and Reijula [16]. Of course, more generally, we may ask what conditions a logic must satisfy in order to provide a B-eS for it.