Abstract
This document describes the Coq formalisation accompanying the paper Definitional Functoriality for Dependent (Sub)Types, more specifically the content of section 4.
You have full access to this open access chapter, Download conference paper PDF
1 Organization of the Artefact and Other Resources
This document describes the Coq formalisation accompanying the paper Definitional Functoriality for Dependent (Sub)Types, more specifically the content of section 4. To complement this document, we also provide the following:
-
the REQUIREMENTS.md and INSTALL.md file with installation instructions;
-
the README.md file with a quick overview of the development with hyperlinks to the files of interest;
-
a DOCKER.md file, with installation and usage instructions for the provided docker image;
-
a Readme.v file, which gives a more in-depth overview of the development as a Coq file, using directly the main Coq definitions and theorems, and is roughly similar to the present PDF description;
-
a doc/dependency_graph.png file, showing the structure of the development.
We utilize the logical relation proof technique presented in Abel et al. [1] and build upon its Coq implementation due to Adjedj et al. [2]. This artefact contributes an extension of the formalisation with lists and definitional functor laws for lists. We refer to both articles for further details on the proof technique and the general setup of the formalisation.
2 Syntax
Terms (AutoSubst/Ast) The syntax of terms, along with the other files in the AutoSubst folder, are generated using the AutoSubst plugin. The definition of renaming and substitution are also automatically derived from the one of terms, and many boilerplate lemmas on them are too. Of particular interest are the constructors  and
and  , respectively corresponding to the type constructor for lists, the empty list, list consing, the (dependent) eliminator for lists, and the definitionally functorial map operation.
, respectively corresponding to the type constructor for lists, the empty list, list consing, the (dependent) eliminator for lists, and the definitionally functorial map operation.
NormalForms Weak-head normal forms  , neutrals
, neutrals  and compacted neutrals
and compacted neutrals  are defined as inductive predicate on terms, i.e. as function of type
are defined as inductive predicate on terms, i.e. as function of type  , corresponding to Fig. 4 and 10 from the paper. In particular, any compacted neutral is a normal form, and compacted neutrals can either consist of a map of a neutral, or simply of a neutral.
, corresponding to Fig. 4 and 10 from the paper. In particular, any compacted neutral is a normal form, and compacted neutrals can either consist of a map of a neutral, or simply of a neutral.
Reduction (UntypedReduction) Reduction, written  , is the transitive closure of one-step reduction
, is the transitive closure of one-step reduction  , defined as an inductive relation. In particular, we have the rules of Fig. 9, that is:
, defined as an inductive relation. In particular, we have the rules of Fig. 9, that is:

3 Typing and Conversion
GenericTyping Following Abel et al. [1],and Adjedj et al. [2], the definition of the logical relation is parametrized by a notion of generic typing, a common interface to be instantiated with both the declarative and algorithmic notions of typing. This interface features a family of judgments for context well-formation, typing, conversion but also a conversion of neutrals and a (typed) reduction relation. These judgements should satisfy properties, listed for each predicate with a record ( , etc.), and grouped together in the
, etc.), and grouped together in the  record. We use type-classes to automatically find these properties when needed, and attach generic notations (defined in Notations) to these type-classes too.
record. We use type-classes to automatically find these properties when needed, and attach generic notations (defined in Notations) to these type-classes too.
For lists, generic typing closely resembles declarative typing, as defined in Fig. 2. Generic conversion must contain reduction, which includes typed variants of the rules above. Moreover, we have congruence rules for constructors, for instance we have the following, where  stands for an arbitrary generic conversion:
stands for an arbitrary generic conversion:

Conversion is not constrained to be a congruence for destructors, but it must contain neutral conversion, which is a congruence for  and
and  , provided its main argument is too. Functor laws are also specified at the level of neutral conversion.
, provided its main argument is too. Functor laws are also specified at the level of neutral conversion.
DeclarativeTyping The definition of the declarative judgments, as inductive predicates, corresponds to Fig. 2, 3, and 9 - the latter being restricted to the case of lists. The corresponding instance of generic typing is defined in DeclarativeTypingInstance. Neutral comparison is instantiated simply with conversion,i.e. the declarative instance does not distinguish between the two notions. Typed reduction is instantiated as the conjunction of declarative conversion and untyped reduction. All other judgments are directly instantiated with the corresponding declarative one.
AlgorithmicTyping The raw algorithmic typing judgments, akin to Fig. 5 and 6, are again defined as inductive predicates. As we explain at the end of Section 2.3 in relation to Fig. 7, we must impose extra pre-conditions for these judgments to be well-behaved. The corresponding judgments, called bundled, are defined in BundledAlgorithmicTyping. In AlgorithmicConvProperties and AlgorithmicTypingProperties, we establish the properties of the conversion and typing judgments, to derive two new instances of generic typing. The first instance uses (bundled) algorithmic conversion, but declarative typing. It depends on consequences of the logical relation instantiated with the fully declarative instance. The second uses only bundled algorithmic judgments, but depends on consequences of the logical relation instantiated with the first, mixed instance.
4 The Logical Relation
The logical relation is built from two layers, first the reducibility layer attaching witnesses of reducibility to weak-head normal form and second the validity layer that closes reducibility under substitution.
Definition of reducibility (LogicalRelation) The reducibility layer describes the types  that are reducible in a given context
that are reducible in a given context  and level
and level  , noted
, noted  .Informally, a type is reducible when it weak-head reduces to a (weak-head) normal form, and the subterms of this normal form are themselves reducible. This weak-head normal form, when it exists, is unique by determinism of the weak-head reduction strategy. A witness of reducibility
.Informally, a type is reducible when it weak-head reduces to a (weak-head) normal form, and the subterms of this normal form are themselves reducible. This weak-head normal form, when it exists, is unique by determinism of the weak-head reduction strategy. A witness of reducibility  for the type
for the type  induce three subsequent predicates:
induce three subsequent predicates:
-
reducible conversion of a type
 to
to  , noted
, noted  ,
, -
reducibility of terms
 of type
of type  , noted
, noted  ,
, -
reducible conversion of terms
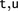 of type
of type  , noted
, noted 
These three predicates are packed in a single record  . Reducible types are characterized inductively together with their associated
. Reducible types are characterized inductively together with their associated  using an indexed inductive
using an indexed inductive  . This encoding of a seemingly inductive-recursive definition using the inductively generated graph of the functions is known as small-induction recursion. The actual content of the reducibility relation is defined independently for each type formers as well as the neutrals types. We focus here on the reducibility of lists and refer to [1, 2] for the other type formers.
. This encoding of a seemingly inductive-recursive definition using the inductively generated graph of the functions is known as small-induction recursion. The actual content of the reducibility relation is defined independently for each type formers as well as the neutrals types. We focus here on the reducibility of lists and refer to [1, 2] for the other type formers.
A type  is reducible as a list if it weak-head reduces to a type of shape
is reducible as a list if it weak-head reduces to a type of shape  where the parameter type
where the parameter type  is itself reducible in any weakening of the context
is itself reducible in any weakening of the context  . This Kripke-style quantification on all future (weakened) contexts
. This Kripke-style quantification on all future (weakened) contexts  is necessary for specifying reducibility in larger contexts.
is necessary for specifying reducibility in larger contexts.
Reducible terms of list type are defined inductively in two steps:  holds of canonical forms of type list (nil, cons and neutrals) with reducible arguments ;
holds of canonical forms of type list (nil, cons and neutrals) with reducible arguments ;  holds of terms that weak-head reduce to a reducible canonical form. The two inductive definitions must be mutual since the tail of a reducible
holds of terms that weak-head reduce to a reducible canonical form. The two inductive definitions must be mutual since the tail of a reducible  need not to be in weak-head normal form. A neutral term of list type is reducible if it is a well-typed neutral and moreover, if it is of shape
need not to be in weak-head normal form. A neutral term of list type is reducible if it is a well-typed neutral and moreover, if it is of shape  with
with  necessary neutral itself, then the body
necessary neutral itself, then the body  of
of  must be reducible in an extended context
must be reducible in an extended context  . In the latter case, the type
. In the latter case, the type  of the codomain of
of the codomain of  cannot be required to be reducible since that would lead to non-well-founded definition for the logical relation, but it is reducibly convertible to the reducible parameter type
cannot be required to be reducible since that would lead to non-well-founded definition for the logical relation, but it is reducibly convertible to the reducible parameter type  at which reducibility of lists is defined.
at which reducibility of lists is defined.
Reducible conversion between terms of list type follow a similar pattern. In order to account for the identity functor law, the additional reducibility datum needed to relate two neutral terms also depends on the shape of the terms:
-
if both terms are respectively of the shape
 and
and  , then the bodies of
, then the bodies of  and
and  must be reducibly convertible (congruence);
must be reducibly convertible (congruence); -
if only one of the term is of shape
 , then
, then  must be reducibly convertible to the identity function, i.e. its body must be reducibly convertible to the first variable in context
must be reducibly convertible to the identity function, i.e. its body must be reducibly convertible to the first variable in context  .
.
Properties of Reducibility In order to reason on reducibility, we derive the induction principle corresponding to the inductive-recursive definition of the logical relation in LogicalRelation/Induction. This induction principle is then employed to derive a variety of properties of reducibility in the LogicalRelation/ subdirectory: an inversion principle, irrelevance with respect to reducible conversion, reflexivity, symmetry and transitivity of reducible conversion, stability by weakening and by anti-reduction.
Validity and the Fundamental Lemma Validity closes reducibility by reducible substitution using another encoding of an inductive-recursive schema. The fundamental lemma then states that all components of a derivable declarative judgement are valid, in particular, terms well-typed for the declarative presentation are valid. The proof of the fundamental lemma proceed by an induction on declarative typing derivations, using that each declarative derivation step is admissible for the validity logical relation. These admissibility results are shown independently for each type former in the Substitution/Introductions/ subdirectory. Most type and term formers related to lists are in List, while the eliminator for lists is in ListElim. The proofs follow the description of the logical relation: first, we show that each type, term or conversion equation is reducible using the definition and properties of reducibility, and then that it is valid. To show that the functor laws are valid, we use that composition of functions (e.g. morphisms for list) is definitionally associative and unital.
5 Type-checker (Decidability folder)
Open Recursion for Partial Functions To side-step issues with the complex termination argument of the conversion checker, we define it in an open recursion fashion, relying on a form of free monad. The functions for reduction, conversion and type checking are defined in Decidability/Functions. The main change compared to Adjedj et al. [2] is the addition of compaction to weak-head evaluation. Evaluation is implemented using a stack machine, on which elimination forms are pushed as they are encountered. When the machine hits a variable, for Adjedj et al. [2] it means the whole term - the variable against the stack of eliminations - is a neutral. However, this is not the case for us: we want to compute a compacted neutral. Thus, we add an extra compaction pass, implemented by the  function, which merges successive \({{\,\mathrm{{\text {map}}}\,}}\) operations on the stack as we unpile them.
function, which merges successive \({{\,\mathrm{{\text {map}}}\,}}\) operations on the stack as we unpile them.
Correctness of the Functions Correctness of the implementations is shown in three steps. First, we show Soundness,i.e. that a positive answer of the checker implies the corresponding (algorithmic) judgment. Next, we show Completeness, i.e. that whenever an algorithmic judgment holds, then the corresponding checker answers positively. Finally, we show Termination,i.e. that the checkers always terminates when run on well-typed inputs. Again, the main innovation has to do with compaction. To reason about it, we need to make explicit the invariant that the stack is always “well-typed”, in a suitable sense, see  in Completeness.
in Completeness.
6 Main properties
The main properties we obtain from the logical relations and the certified checker are the following.First, every well-typed term and type are (weakly) normalising (proven in Normalisation):

Conversion and typing are decidable (proven in Decidability):

Finally, the type system seen as a logic is consistent, and canonicity holds at the type of natural numbers:

References
Andreas Abel et al. “Decidability of Conversion for Type Theory in Type Theory”. In:Proc. ACM Program. Lang. 2.POPL (Dec. 2017). https://doi.org/10.1145/3158111.
Arthur Adjedj et al. “Martin-Löf à la Coq”. In: Proceedings of the 13th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2024. 2024.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Laurent, T., Lennon-Bertrand, M., Maillard, K. (2024). Artifact Description. In: Weirich, S. (eds) Programming Languages and Systems. ESOP 2024. Lecture Notes in Computer Science, vol 14576. Springer, Cham. https://doi.org/10.1007/978-3-031-57262-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-031-57262-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57261-6
Online ISBN: 978-3-031-57262-3
eBook Packages: Computer ScienceComputer Science (R0)


 to
to  , noted
, noted  ,
, of type
of type  , noted
, noted  ,
,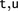 of type
of type  , noted
, noted 
 and
and  , then the bodies of
, then the bodies of  and
and  must be reducibly convertible (congruence);
must be reducibly convertible (congruence); , then
, then  must be reducibly convertible to the identity function, i.e. its body must be reducibly convertible to the first variable in context
must be reducibly convertible to the identity function, i.e. its body must be reducibly convertible to the first variable in context  .
.