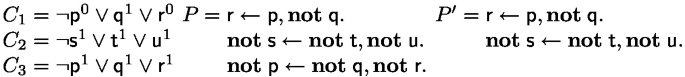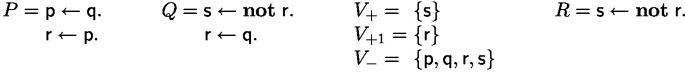1 Introduction

Answer set programming [3, 35, 50, 57, 60] is one of the major paradigms in knowledge representation. A problem is expressed declaratively as a logic program, a set of rules in the form of implications. An answer set solver returns representations of its answer sets or stable models [36, 49]. That is, minimal Herbrand models, where models with facts not properly justified in a non-circular way are excluded. Modern answer set solvers such as clingo [34] are advanced tools that integrate SAT technology.

Two logic programs can be considered as equivalent if and only if they have the same answer sets. However, if two equivalent programs are each combined with some other program, the results are not necessarily equivalent. Thus, it is of much more practical relevance to consider instead a notion of equivalence that guarantees the same answer sets even in combination with other programs: Two logic programs P, Q are strongly equivalent [54] if they can be exchanged in the context of any other program R without affecting the answer sets of the overall program. That is, P and Q are strongly equivalent if and only if for all logic programs R it holds that \(P \cup R\) and \(Q \cup R\) have the same answer sets.

Although it has been known that strong equivalence of logic programs under the stable model semantics can be translated into equivalence of classical logical formulas, e.g. [55], developments in the languages of answer set programming make this an issue of ongoing research [18, 25, 38, 39, 42, 53]. The practical objective is to apply first-order provers to determine the equivalence of two logic programs.

We now consider the situation where only a single program is given and a strongly equivalent one is to be synthesized automatically. For the new program the set of allowed predicates, including to some degree the position within rules in which they are allowed, is restricted to a given vocabulary. Not just “absolute” strong equivalence is of interest, but also strong equivalence with respect to some background knowledge expressed as a logic program. Thus, for given programs P and Q, and vocabulary V we want to find programs R in V such that \(P \cup R\) and \(P \cup Q\) are strongly equivalent.

Our question has two aspects: characterizing the existence of a program R for given P, Q, V and, if one exists, the effective construction of such an R. As we will show, existence can be addressed by Beth definability [7, 21] on the basis of Craig interpolation [20] for first-order logic. The construction can then be performed by extracting an interpolant from a proof of the first-order characterization of existence. We realize this practically with the first-order provers CMProver  [74, 75] and Prover9  [58] and an interpolation technique for clausal tableaux [76, 77].

To achieve this, we start from a known representation of logic programs in classical first-order logic for the purpose of verifying strong equality. We supplement it with a formal characterization to determine whether an arbitrary given first-order formula represents a logic program, and, if so, to extract a represented logic program from the formula. This novel “reverse translation” also has other potential applications in program transformation.

Beth definability and Craig interpolation play a key role for advanced tasks in other fields of knowledge representation, in particular for query reformulation in databases [5, 6, 59, 66, 72] and description logics as well as ontology-mediated querying [2, 16, 17, 73]. Our work aims to provide for these lines of research the bridge to answer set programming.

Structure of the Paper. After providing in Sect. 2 background material on strong equivalence as well as on interpolation and definability we develop in Sect. 3 our technical results. Our prototypical implementationFootnote 1 is then described in Sect. 4. We conclude in Sect. 5 with discussing related work and perspectives.

2 Background

2.1 Notation

We map between two formalisms: logic programs and formulas of classical first-order logic without equality (briefly formulas). In both formalisms we have atoms \(p(t_1,\ldots ,t_n)\), where p is a predicate and \(t_1,\ldots ,t_n\) are terms built from functions, including constants, and variables. We assume variable names as case insensitive to take account of the custom to write them uppercase in logic programs and lowercase in first-order logic. Predicates in logic programs are distinct from those in formulas, but with a correspondence: If p is a predicate for use in logic programs, then the two predicates \(p^0\) and \(p^1\), both with the same arity as p, are for use in formulas. Thus, predicates in formulas are always decorated with a 0 or 1 superscript. To emphasize this, we sometimes speak of 0/1-superscripted formulas.

A literal is an atom or a negated atom. A clause is a disjunction of literals, a clausal formula is a conjunction of clauses. The empty disjunction is represented by \(\bot \), the empty conjunction by \(\top \). On occasion we write a clause also as an implication.

A subformula occurrence in a formula has positive (negative) polarity if it is in the scope of an even (odd) number of possibly implicit negations. A formula is universal if occurrences of \(\forall \) have only positive polarity and occurrences of \(\exists \) have only negative polarity. Semantic entailment and equivalence of formulas are expressed by \(\models \) and \(\equiv \).

Let F be a formula. \(\mathcal {F} un (F)\) is the set of functions occurring in it, including constants, and \(\mathcal {P} red (F)\) is the set of predicates occurring in it. \(\mathcal {P} red ^{\pm }(F)\) is the set of pairs \(\langle pol , p \rangle \), where p is a predicate and \( pol \in \{{+},{-}\}\), such that an atom with predicate p occurs in F with the polarity indicated by \( pol \). We write \(\langle +, p\rangle \) and \(\langle -, p\rangle \) succinctly as \(+p\) and \(-p\). To map from the predicates occurring in a formula to predicates of logic programs we define . For logic programs P, we define \(\mathcal {F} un (P)\) and \(\mathcal {P} red (P)\) analogously as for formulas.

2.2 Strong Equivalence as First-Order Equivalence

We consider disjunctive logic programs with negation in the head [48, Sect. 5], which provide a normal form for answer set programs [12]. A logic program is a set of rules of the form

$$\begin{array}{l} A_1 ;\ldots ;A_k ;\textbf{not}\;A_{k+1} ;\ldots ;\textbf{not}\;A_l \leftarrow A_{l+1}, \ldots , A_{m}, \textbf{not}\;A_{m+1}, \ldots , \textbf{not}\;A_{n}., \end{array} $$

where \(A_1, \ldots , A_n\) are atoms, \(0 \le k \le l \le m \le n\). Recall from Sect. 2.1 that an atom can have argument terms with functions and variables. The positive/negative head of a rule are the atoms \(A_{1}, \ldots , A_{k}\) and \(A_{k+1}, \ldots , A_{l}\) respectively. Analogously the positive/negative body of a rule are \(A_{l+1}, \ldots , A_{m}\) and \(A_{m+1}, \ldots , A_{n}\) respectively. Answer sets with respect to the stable model semantics for this class of programs are for example defined in [32].

Next we review the definition of the translation \(\gamma \) used to express strong equivalence of two logic programs in classical first-order logic.Footnote 2 It makes use of the fact that strong equivalence can be expressed in the intermediate logic of here-and-there [54], which in turn can be mapped to classical logic [62]. For details and proofs we refer to [25, 38, 39]. Similar results appeared in [28, 55, 62, 63]. As stated in Sect. 2.1 we assume for each program predicate p two dedicated formula predicates \(p^0\) and \(p^1\) with the same arity. If A is an atom with predicate p, then \(A^0\) is A with \(p^0\) instead of p, and \(A^1\) is A with \(p^1\) instead of p.

Definition 1

For a rule

$$R = A_1 ;\ldots ;A_k ;\textbf{not}\;A_{k+1} ;\ldots ;\textbf{not}\;A_l \leftarrow A_{l+1}, \ldots , A_{m}, \textbf{not}\;A_{m+1}, \ldots , \textbf{not}\;A_{n}.$$

with variables \(\boldsymbol{x}\) define the first-order formulas \(\gamma ^0(R)\) and \(\gamma ^1(R)\) as

figure b

For a logic program P define the first-order formula \(\gamma (P)\) as

figure c

and define the first-order formula \(\textsf{S}_P\) as

figure d

where variables \(\boldsymbol{x}\) match the arity of p.

Using the transformation \(\gamma \) and the formula \(\textsf{S}_{P}\) we can express strong equivalence as an equivalence in first-order logic.

Proposition 2

([38]). Under the stable model semantics two logic programs P and Q are strongly equivalent iff the following equivalence holds in classical first-order logic \(\textsf{S}_{P \cup Q} \wedge \gamma (P) \equiv \textsf{S}_{P \cup Q} \wedge \gamma (Q)\).

2.3 Definition Synthesis with Craig Interpolation

A formula \(Q(\boldsymbol{x})\) is implicitly definable in terms of a vocabulary (set of predicate and function symbols) V within a sentence F if, whenever two models of F agree on values of symbols in V, then they agree on the extension of Q, i.e., on the tuples of domain members that satisfy Q. In the special case where Q has no free variables, this means that they agree on the truth value of Q. Implicit definability can be expressed as

$$\begin{aligned} F \wedge F' \models \forall \boldsymbol{x}\, (Q(\boldsymbol{x}) \leftrightarrow Q'(\boldsymbol{x})), \end{aligned}$$
(i)

where \(F'\) and \(Q'\) are copies of F and Q with all symbols not in V replaced by fresh symbols. This semantic notion contrasts with the syntactic one of explicit definability: A formula \(Q(\boldsymbol{x})\) is explicitly definable in terms of a vocabulary V within a sentence F if there exists a formula \(R(\boldsymbol{x})\) in the vocabulary V such that

$$\begin{aligned} F \models \forall \boldsymbol{x}\, (R(\boldsymbol{x}) \leftrightarrow Q(\boldsymbol{x})). \end{aligned}$$
(ii)

The “Beth property” [7] states equivalence of both notions and applies to first-order logic. “Craig interpolation” is a tool that can be applied to prove the “Beth property” [21], and, moreover to construct formulas R from given F, Q, V from a proof of implicit definability. Craig’s interpolation theorem [20] applies to first-order logic and states that if a formula F entails a formula G (or, equivalently, that \(F \rightarrow G\) is valid), then there exists a formula H, a Craig interpolant of F and G, with the properties that \(F \models H\), \(H \models G\), and the vocabulary of H (predicate and function symbols as well as free variables) is in the common vocabulary of F and G. Craig’s theorem can be strengthened to the existence of Craig-Lyndon interpolants [56] that satisfy the additional property that predicates in H occur only in polarities in which they occur in both F and G. In our technical framework this condition is expressed as \(\mathcal {P} red ^{\pm }(H) \subseteq \mathcal {P} red ^{\pm }(F) \cap \mathcal {P} red ^{\pm }(G)\).

Craig’s interpolation theorem can be proven by constructing H from a proof of \(F \models G\). This works on the basis of sequent calculi [68, 71] and analytic tableaux [29]. For calculi from automated first-order reasoning various approaches have been considered [10, 40, 44, 67, 76, 77]. A method [76] for clausal tableaux [46] performs Craig-Lyndon interpolation and operates on proofs emitted by a general first-order prover, without need to modify the prover for interpolation, and inheriting completeness for full first-order logic from it. Indirectly that method also works on resolution proofs expanded into trees [77].

Observe that the characterization of implicit definability (i) can also be expressed as \(F \wedge Q(\boldsymbol{x}) \models F' \rightarrow Q'(\boldsymbol{x})\). An “explicit” definiens \(R(\boldsymbol{x})\) can now be constructed from given F, \(Q(\boldsymbol{x})\) and V just as a Craig interpolant of \(F \wedge Q(\boldsymbol{x})\) and \(F' \rightarrow Q'(\boldsymbol{x})\). The synthesis of definitions by Craig interpolation was recognized as a logic-based core technique for view-based query reformulation in relational databases [5, 59, 66, 72]. Often strengthened variations of Craig-Lyndon interpolation are used there that preserve criteria for domain independence, e.g., through relativized quantifiers [5] or range-restriction [77].

3 Variations of Craig Interpolation and Beth Definability for Logic Programs

We synthesize logic programs according to a variation of Beth’s theorem justified by a variation of Craig-Lyndon interpolation. Craig-Lyndon interpolation “out of the box” is not sufficient for our purposes: To obtain logic programs as definientia we need as a basis a stronger form of interpolation where the interpolant is not just a first-order formula but, moreover, is the first-order encoding of a logic program, permitting to actually extract the program.

3.1 Extracting Logic Programs from a First-Order Encoding

We address the questions of how to abstractly characterize first-order formulas that encode a logic program, and how to extract the program from a first-order formula that meets the characterization. As specified in Sect. 2.1, we assume first-order formulas over predicates superscripted with 0 and 1. The notation \(\textsf{S}_P\) (Definition 1) is now overloaded for \(0/1\)-superscripted formulas F as , where variables \(\boldsymbol{x}\) match the arity of p. We introduce a convenient notation for the result of systematically renaming all 0-superscripted predicates to their 1-superscripted correspondence.

Definition 3

For \(0/1\)-superscripted first-order formulas F define \(\textsf{rename}_{0\mapsto 1}(F)\) as F with all occurrences of 0-superscripted predicates \(p^0\) replaced by the corresponding 1-superscripted predicate \(p^1\).

Obviously \(\textsf{rename}_{0\mapsto 1}\) can be moved over logic operators, e.g., \(\textsf{rename}_{0\mapsto 1}(F \wedge G) \equiv \textsf{rename}_{0\mapsto 1}(F) \wedge \textsf{rename}_{0\mapsto 1}(G)\), and \(\textsf{rename}_{0\mapsto 1}(\forall \boldsymbol{x}\, F) \equiv \forall \boldsymbol{x}\, \textsf{rename}_{0\mapsto 1}(F)\). Semantically, \(\textsf{rename}_{0\mapsto 1}\) preserves entailment and thus also equivalence.

Proposition 4

For \(0/1\)-superscripted first-order formulas F and G it holds that (i) If \(F \models G\), then \(\textsf{rename}_{0\mapsto 1}(F) \models \textsf{rename}_{0\mapsto 1}(G)\). (ii) If \(F \equiv G\), then \(\textsf{rename}_{0\mapsto 1}(F) \equiv \textsf{rename}_{0\mapsto 1}(G)\).

Observe that for all rules R it holds that \(\gamma ^1(R) = \textsf{rename}_{0\mapsto 1}(\gamma ^0(R))\) and for all logic programs P it holds that \(\gamma (P) \models \textsf{rename}_{0\mapsto 1}(\gamma (P))\). On the basis of \(\textsf{rename}_{0\mapsto 1}\) we define a first-order criterion for a formula encoding a logic program, that is, a first-order entailment that holds if and only if a given first-order formula encodes a logic program.

Definition 5

A \(0/1\)-superscripted first-order formula F is said to encode a logic program iff F is universal and \(\textsf{S}_{F} \wedge F \models \textsf{rename}_{0\mapsto 1}(F).\)

This criterion adequately characterizes that the formula represents a logic program on the basis of the translation \(\gamma \). The following theorem justifies this.

Theorem 6

(Formulas Encoding a Logic Program). (i) For all logic programs P it holds that \(\gamma (P)\) is a \(0/1\)-superscripted first-order formula that encodes a logic program. (ii) If a \(0/1\)-superscripted first-order formula F encodes a logic program, then there exists a logic program P such that \(\textsf{S}_F \models \gamma (P) \leftrightarrow F\), \(\mathcal {P} red (P) \subseteq \mathcal {P} red ^ LP (F)\) and \(\mathcal {F} un (P) \subseteq \mathcal {F} un (F)\). Moreover, such a program P can be effectively constructed from F.

Proof

(6.i) Immediate from the definition of \(\gamma \). (6.ii) Procedure 7 specified below and proven correct in Proposition 8 shows the construction of a suitable program.

   \(\square \)

Theorem 6.ii claims that the vocabulary of the program is only included in the respective vocabulary of the formula. This gives for the formula the freedom of a larger vocabulary with symbols that may be eliminated, e.g., by simplifications.

Procedure 7

(Decoding an Encoding of a Logic Program).

Input: A \(0/1\)-superscripted first-order formula F that encodes a logic program.

Method:

  1. 1.

    Bring F into conjunctive normal form matching \(\forall \boldsymbol{x}\, (M_0 \wedge M_1)\), where \(M_0\) and \(M_1\) are clausal formulas such that in all clauses of \(M_0\) there is a literal whose predicate has superscript 0 and in all clauses of \(M_1\) the predicates of all literals have superscript 1.

  2. 2.

    Partition \(M_1\) into two clausal formulas \(M_1'\) and \(M_1''\) such that

    $$\begin{aligned} \forall \boldsymbol{x}\, \textsf{rename}_{0\mapsto 1}(M_0) \models \forall \boldsymbol{x}\, M_1''. \end{aligned}$$

    A possibility is to take \(M_1' = M_1\) and \(M_1'' = \top \). Another possibility that often leads to a smaller \(M'\) is to consider each clause C in \(M_1\) and place it into \(M_1''\) or \(M_1'\) depending on whether there is a clause D in \(M_0\) such that \(\textsf{rename}_{0\mapsto 1}(D)\) subsumes C.

  3. 3.

    Let P be the set of rules

    $$A_1 ;\ldots ;A_k ;\textbf{not}\;A_{k+1} ;\ldots ;\textbf{not}\;A_l \leftarrow A_{l+1}, \ldots , A_{m}, \textbf{not}\;A_{m+1}, \ldots , \textbf{not}\;A_{n}$$

    for each clause \(\bigwedge _{i={l+1}}^{m} A^0_i \wedge \bigwedge _{i=m+1}^{n}\! \lnot A^1_i \rightarrow \bigvee _{i=0}^{k} A^0_i \vee \bigvee _{i=k+1}^{l}\! \lnot A^1_i\) in \(M_0 \wedge M_1'\).

Output: Return P, a logic program such that \(\textsf{S}_P \models \gamma (P) \leftrightarrow F\), \(\mathcal {P} red (P) \subseteq \mathcal {P} red ^ LP (F)\) and \(\mathcal {F} un (P) \subseteq \mathcal {F} un (F)\).

Proposition 8

Procedure 7 is correct.

Proof

For an input formula F and output program P the syntactic requirements \(\mathcal {P} red (P) \subseteq \mathcal {P} red ^ LP (F)\) and \(\mathcal {F} un (P) \subseteq \mathcal {F} un (F)\) are easy to see from the construction of P by the procedure. To prove the semantic requirement \(\textsf{S}_F \models \gamma (P) \leftrightarrow F\) we first note the following assumptions, which follow straightforwardly from the specification of the procedure.

  1. (1)

    \(\textsf{S}_{F} \wedge F \models \textsf{rename}_{0\mapsto 1}(F)\).

  2. (2)

    \(F \equiv \forall \boldsymbol{x}\, (M_0 \wedge M_1' \wedge M_1'')\).

  3. (3)

    \(\textsf{rename}_{0\mapsto 1}(\forall \boldsymbol{x}\, M_0) \models \forall \boldsymbol{x}\, M_1''\).

  4. (4)

    \(\gamma (P) \equiv \forall \boldsymbol{x}\, (M_0 \wedge \textsf{rename}_{0\mapsto 1}(M_0) \wedge M_1')\).

The semantic requirement \(\textsf{S}_F \models \gamma (P) \leftrightarrow F\) can then be derived as follows.

figure f

   \(\square \)

Some examples illustrate Procedure 7 and the encoding a logic program property.

Example 9

  1. (i)

    Consider the following clauses and programs.

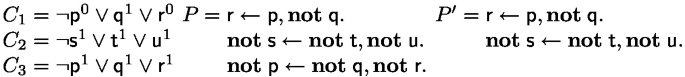
    figure g

    Assume as input of Procedure 7 the formula \(F = C_1 \wedge C_2 \wedge C_3\). Then \(M_0 = C_1\) and \(M_1 = C_2 \wedge C_3\). If in step 2 we set \(M_1' = M_1\) and \(M_1'' = \top \), then the extracted program is P. We might, however, also set \(M_1' = C_2\) and \(M_1'' = C_3\) and obtain the shorter strongly equivalent program \(P'\).

  2. (ii)

    For \(F = \lnot \textsf{p}^1 \vee \textsf{q}^1 \vee \textsf{r}^0\) we have to set \(M_1' = M_1'' = M_1 = \top \) and the procedure yields \(\{\textsf{r};\textbf{not}\;\textsf{p}\leftarrow \textbf{not}\;\textsf{q}.\}\).

  3. (iii)

    The formula \(F = \lnot \textsf{p}^0 \vee \textsf{q}^1 \vee \textsf{r}^0\) does not encode a logic program because \(\textsf{S}_{F} \wedge F \not \models \textsf{rename}_{0\mapsto 1}(F)\).

Remark 1

For the extracted program it is desirable that it is not unnecessarily large. Specifically it should not contain rules that are easily identified as redundant. Step 2 of Procedure 7 permits techniques to keep \(M'\) small. Other possibilities include well-known formula simplification techniques that preserve equivalence such as removal of tautological or subsumed clauses and may be integrated into classification, step 1 of the procedure. In addition, conversions that just preserve equivalence modulo \(\textsf{S}_F\) may be applied, conceptually as a preprocessing step, although in practice possibly implemented on the clausal form. Procedure 7 then receives as input not F but a universal first-order formula \(F'\) whose vocabulary is included in that of F with the property

$$\begin{aligned} \textsf{S}_F \models F' \leftrightarrow F. \end{aligned}$$
(iii)

Formula \(F'\) then also encodes a program: That \(\textsf{S}_{F'} \wedge F' \models \textsf{rename}_{0\mapsto 1}(F')\) follows from \(\textsf{S}_{F} \wedge F \models \textsf{rename}_{0\mapsto 1}(F)\), (iii) and Proposition 4.ii. Procedure 7 guarantees for its output \(\textsf{S}_{F'} \models \gamma (P) \leftrightarrow F'\), hence by (iii) it follows that \(\textsf{S}_F \models \gamma (P) \leftrightarrow F\).

Example 10

Consider the following clauses and programs.

figure h

Assume as input of Procedure 7 the formula \(F = C_1 \wedge C_2 \wedge C_3\). Then \(M_0 = C_1 \wedge C_2\) and \(M_1 = C_3\), and, aiming at a short program, we can set \(M_1' = \top \) and \(M_1'' = C_3\). The extracted program is then P. By preprocessing F according to Remark 1 we can eliminate \(C_2\) from F and obtain the shorter strongly equivalent program \(P'\).

3.2 A Refinement of Craig Interpolation for Logic Programs

With the material from Sect. 3.1 on extracting logic programs from formulas we can now state a theorem on LP-interpolation, where LP stands for logic program. It is a variation of Craig interpolation applying to first-order formulas that encode logic programs. The theorem states not only the existence of an LP-interpolant, but, moreover, also claims effective construction.

Theorem 11

(LP-Interpolation). Let F be a \(0/1\)-superscripted first-order formula that encodes a logic program and let G be a \(0/1\)-superscripted first-order formula such that \(\mathcal {F} un (F) \subseteq \mathcal {F} un (G)\) and \(\textsf{S}_{F} \wedge F \models \textsf{S}_{G} \rightarrow G\). Then there exists a \(0/1\)-superscripted first-order formula H, called the LP-interpolant of F and G, such that

  1. 1.

    \(\textsf{S}_{F} \wedge F \models H\).

  2. 2.

    \(H \models \textsf{S}_{G} \rightarrow G\).

  3. 3.

    \(\mathcal {P} red ^{\pm }(H) \subseteq S \cup \{+p^1 \mid +p^0 \in S\} \cup \{-p^1 \mid -p^0 \in S\}\), where \(S = \mathcal {P} red ^{\pm }(\textsf{S}_{F} \wedge F) \cap \mathcal {P} red ^{\pm }(\textsf{S}_G \rightarrow G)\).

  4. 4.

    \(\mathcal {F} un (H) \subseteq \mathcal {F} un (F)\).

  5. 5.

    H encodes a logic program.

Moreover, if existence holds, then an LP-interpolant H can be effectively constructed, via a universal Craig-Lyndon interpolant of \(F \wedge \textsf{S}_{F}\) and \(\textsf{S}_{G} \rightarrow G\).

Proof

We show the construction of a suitable formula H. Let \(H'\) be a Craig-Lyndon interpolant of \(\textsf{S}_{F} \wedge F\) and \(\textsf{S}_{G} \rightarrow G\). Since F and \(\textsf{S}_F\) are universal first-order formulas and we have the precondition \(\mathcal {F} un (F) \subseteq \mathcal {F} un (G)\), we may in addition assume that \(H'\) is a universal first-order formula. (This additional condition is guaranteed for example by the interpolation method from [76], which computes \(H'\) directly from a clausal tableaux proof, or indirectly from a resolution proof [77].) Define . Claims 2, 4 and 5 of the theorem statement are then easy to see. Claim 1 can be shown as follows. We may assume the following.

figure j

Claim 1 can then be derived in the following steps.

figure k

Claim 3 follows because since \(H'\) is a Craig-Lyndon interpolant it holds that \(\mathcal {P} red ^{\pm }(H') \subseteq \mathcal {P} red ^{\pm }(\textsf{S}_{F} \wedge F) \cap \mathcal {P} red ^{\pm }(\textsf{S}_G \rightarrow G)\). With the predicate occurrences in \(\textsf{rename}_{0\mapsto 1}(H')\), i.e., 1-superscripted predicates in positions of 0-superscripted predicates in \(H'\), we obtain the restriction of \(\mathcal {P} red ^{\pm }(H)\) stated as claim 3.    \(\square \)

For an LP-interpolant of formulas F and G, where F encodes a logic program, the semantic properties stated in claims 1 and 2 are those of a Craig or Craig-Lyndon interpolant of \(\textsf{S}_{F} \wedge F\) and \(\textsf{S}_{G} \rightarrow G\). The allowed polarity/predicate pairs are those common in \(\textsf{S}_{F} \wedge F\) and \(\textsf{S}_{G} \rightarrow G\), as in a Craig-Lyndon interpolant, and, in addition, the 1-superscripted versions of polarity/predicate pairs that appear only 0-superscripted among these common pairs. These additional pairs are those that might occur in the result of \(\textsf{rename}_{0\mapsto 1}\) applied to a Craig-Lyndon interpolant. In contrast to a Craig interpolant, functions are only constrained by the first given formula F. Permitting only functions common to F and G can result in an interpolant with existential quantification, which thus does not encode a program. Claim 5 states that the LP-interpolant indeed encodes a logic program as characterized in Definition 5. This property is, so-to-speak, passed through from the given formula F to the LP-interpolant.

3.3 Effective Projective Definability of Logic Programs

We present a variation of the “Beth property” that applies to logic programs with stable model semantics and takes strong equivalence into account. The underlying technique is our LP-interpolation, Theorem 11. It maps into Craig-Lyndon interpolation for first-order logic, utilizing that strong equivalence of logic programs can be expressed as first-order equivalence of encoded programs. This approach allows the effective construction of logic programs in the role of “explicit definitions” via Craig-Lyndon interpolation on first-order formulas. Our variation of the “Beth property” is projective as it is with respect to a given set of predicates allowed in the definiens. While our LP-interpolation theorem was expressed in terms of first-order formulas that encode logic programs, we now phrase definability entirely in terms of logic programs.Footnote 3

Theorem 12

(Effective Projective Definability of Logic Programs). Let P and Q be logic programs and let \(V \subseteq \mathcal {P} red (P) \cup \mathcal {P} red (Q)\) be a set of predicates. The existence of a logic program R with \(\mathcal {P} red (R) \subseteq V\), \(\mathcal {F} un (R) \subseteq \mathcal {F} un (P) \cup \mathcal {F} un (Q)\) such that \(P \cup R\) and \(P \cup Q\) are strongly equivalent is expressible as entailment between two first-order formulas. Moreover, if existence holds, such a program R can be effectively constructed, via a universal Craig-Lyndon interpolant of the left and the right side of the entailment.

Proof

The first-order entailment that characterizes the existence of a logic program R is \(\textsf{S}_{P} \wedge \textsf{S}_{Q} \wedge \gamma (P) \wedge \gamma (Q) \models \lnot \textsf{S}_{P'} \vee \lnot \textsf{S}_{Q'} \vee \lnot \gamma (P') \vee \gamma (Q')\), where the primed programs \(P'\) and \(Q'\) are like P and Q, except that predicates not in V are replaced by fresh predicates. If the entailment holds, we can construct a program R as follows: Let H be the LP-interpolant of \(\gamma (P) \wedge \gamma (Q)\) and \(\lnot \gamma (P') \vee \gamma (Q')\), as specified in Theorem 11, and extract the program R from H with Procedure 7. That R constructed in this way has the properties claimed in the theorem statement can be shown as follows. Since H is an LP-interpolant it follows that

  1. (1)

    \(\textsf{S}_{P} \wedge \textsf{S}_{Q} \wedge \gamma (P) \wedge \gamma (Q) \models H\).

  2. (2)

    \(H \models \lnot \textsf{S}_{P'} \vee \lnot \textsf{S}_{Q'} \vee \lnot \gamma (P') \vee \gamma (Q')\).

  3. (3)

    \(\mathcal {P} red ^ LP (H) \subseteq V\).

  4. (4)

    \(\mathcal {F} un (H) \subseteq \mathcal {F} un (P) \cup \mathcal {F} un (Q)\).

  5. (5)

    H encodes a logic program.

From the preconditions of the theorem and since R is extracted from H with Procedure 7 and thus meets the properties stated in Theorem 6.ii it follows that

  1. (6)

    \(V \subseteq \mathcal {P} red (P) \cup \mathcal {P} red (Q)\).

  2. (7)

    \(\textsf{S}_H \models \gamma (R) \leftrightarrow H\).

  3. (8)

    \(\mathcal {P} red (R) \subseteq \mathcal {P} red ^ LP (H)\).

  4. (9)

    \(\mathcal {F} un (R) \subseteq \mathcal {F} un (H)\).

The claimed properties of the theorem statement can then be derived as steps (10), (11) and (18) as follows.

figure l

Conversely, we have to show that if there exists a logic program R with the properties in the above theorem statement, then the characterizing entailment \(\textsf{S}_{P} \wedge \textsf{S}_{Q} \wedge \gamma (P) \wedge \gamma (Q) \models \lnot \textsf{S}_{P'} \vee \lnot \textsf{S}_{Q'} \vee \lnot \gamma (P') \vee \gamma (Q')\) does hold. We may assume

  1. (19)

    \(\mathcal {P} red (R) \subseteq V \subseteq \mathcal {P} red (P) \cup \mathcal {P} red (Q)\).

  2. (20)

    \(\mathcal {F} un (R) \subseteq \mathcal {F} un (P) \cup \mathcal {F} un (Q)\).

  3. (21)

    \(P \cup R\) and \(P \cup Q\) are strongly equivalent.

The characterizing entailment can then be derived as follows.

figure m

   \(\square \)

We now give some examples from the application point of view.

Example 13

The following examples show for given programs P, Q and sets V of predicates a possible value of R according to Theorem 12.

  1. (i)
    figure n

    In this first example we consider the special case where P is empty and thus not shown. Predicates \(\textsf{q}\) and \(\textsf{s}\) are redundant in Q, “absolutely” and not just relative to a program P. By Theorem 12, this is proven with the characterizing first-order entailment and, moreover, a strongly equivalent reformulation of Q without \(\textsf{q}\) and \(\textsf{s}\) is obtained as R.

  2. (ii)
    figure o

    Only \(\textsf{r}\) and \(\textsf{p}\) are allowed in R. Or, equivalently, \(\textsf{q}\) is redundant in Q, relative to program P. Again, this is proven with the characterizing first-order entailment and, moreover, a strongly equivalent reformulation of Q without \(\textsf{q}\) is obtained as R. It is the clause in Q with \(\textsf{q}\) that is redundant relative to P and hence is eliminated in R.

  3. (iii)
    figure p

    Only \(\textsf{r}\) and \(\textsf{p}\) are allowed in R. The negated literal with \(\textsf{q}\) in the body of the rule in Q is redundant relative to P and is eliminated in R.

  4. (iv)
    figure q

    The predicate \(\textsf{p}\) is not allowed in R. The idea is that \(\textsf{p}\) is a predicate that can be used by a client but is not in the actual knowledge base. Program P expresses a schema mapping from the client predicate \(\textsf{p}\) to the knowledge base predicates \(\textsf{q},\textsf{r},\textsf{s}\). The result program R is a rewriting of the client query Q in terms of knowledge base predicates. Only the first two rules of P actually describe the mapping. The other two rules complete them to a full definition, similar to Clark’s completion [19], but here yielding also a program. Such completed predicate specifications seem necessary for the envisaged reformulation tasks.

  5. (v)
    figure r

    In this example P is from Example 13.iv, while Q and R are also from that example but switched. The vocabulary allows only \(\textsf{p}\) and \(\textsf{t}\). While Example 13.iv realizes an unfolding of \(\textsf{p}\), this example realizes folding into \(\textsf{p}\).

  6. (vi)
    figure s

    Program P defines natural numbers recursively. Program Q has a rule whose body specifies the natural number 2 and whose head denies that 2 is a natural number. Because P implies that 2 is a natural number, this head is in R rewritten to the empty head, enforced by disallowing the predicate for natural numbers in R.

  7. (vii)
    figure t

    Program Q describes a transitive relation \(\textsf{r}\) using the helper predicate \(\textsf{c}\) to identify chains where transitivity needs to be checked. In R the use of \(\textsf{c}\) is not allowed, program P gives the definition of \(\textsf{c}\). Similar to Example 13.iv this realizes an unfolding of \(\textsf{c}\).

Definability according to Theorem 12 inherits potential decidability from the first-order entailment problem that characterizes it. If, e.g., in the involved programs only constants occur as function symbols, the characterizing entailment can be expressed as validity in the decidable Bernays-Schönfinkel class.

3.4 Constraining Positions of Predicates Within Rules

The sensitivity of LP-interpolation to polarity inherited from Craig-Lyndon interpolation and the program encoding with superscripted predicates offers a more fine-grained control of the vocabulary of definitions than Theorem 12 by considering also positions of predicates in rules. The following corollary shows this.

Corollary 14

(Position-Constrained Effective Projective Definability of Logic Programs). Let P and Q be logic programs and let \(V_{+},V_{+1},V_{-}\subseteq \mathcal {P} red (P) \cup \mathcal {P} red (Q)\) be three sets of predicates. Call a logic program R in scope of \(\langle V_{+},V_{+1},V_{-}\rangle \) if predicates p occur in R only as specified in the following table.

figure u

The existence of a logic program R in scope of \(\langle V_{+},V_{+1},V_{-}\rangle \) with \(\mathcal {F} un (R) \subseteq \mathcal {F} un (P) \cup \mathcal {F} un (Q)\) such that \(P \cup R\) and \(P \cup Q\) are strongly equivalent is expressible as entailment between two first-order formulas. Moreover, if existence holds, such a program R can be effectively constructed, via a universal Craig-Lyndon interpolant of the left and the right side of the entailment.

Proof

(Sketch). Like Theorem 12 but with applying the renaming of disallowed predicates not already at the program level but in the first-order encoding with considering polarity. Let \(V^{\pm }\) be the set of polarity/predicate pairs defined as . The corresponding entailment underlying definability and LP-interpolation is then \(\textsf{S}_{F} \wedge \textsf{S}_{Q} \wedge \gamma (P) \wedge \gamma (Q) \models \lnot \textsf{S}_{P}' \vee \lnot \textsf{S}_{Q}' \vee \lnot \gamma (P)' \vee \gamma (Q)' \vee \lnot Aux \), where the primed variations of formulas are obtained by replacing each predicate p that does not appear in \(V^{\pm }\) or appears in \(V^{\pm }\) with only a single polarity by a dedicated fresh predicate \(p'\). (Note that negation and priming commute.) With we define \( Aux \) as

$$\bigwedge _{+p \in V^{\pm }, -p \notin V^{\pm }, +p \in W} \forall \boldsymbol{x}\, (p(\boldsymbol{x}) \rightarrow p'(\boldsymbol{x}))\; \wedge \bigwedge _{-p \in V^{\pm }, +p \notin V^{\pm }, -p \in W} \forall \boldsymbol{x}\, (p'(\boldsymbol{x}) \rightarrow p(\boldsymbol{x})),$$

where \(\boldsymbol{x}\) matches the arity of the respective predicates p.    \(\square \)

In general, for first-order formulas F, G the second-order entailment \(F \models \forall p\, G\), where p is a predicate, holds if and only if the first-order entailment \(F \models G'\) holds, where \(G'\) is G with p replaced by a fresh predicate \(p'\). This explains the construction of the right side of the entailment in the proof of Corollary 14 as an encoding of quantification upon (or “forgetting about”) a predicate only in a single polarity. With predicate quantification this can be expressed, e.g., for positive polarity, as , where \(p'\) is a fresh predicate and \(G'\) is G with p replaced by \(p'\). We illustrate the specification of \( Aux \) with an example.

Example 15

Assume that \(+p \in V^{\pm }\) and \(-p \not \in V^{\pm }\). Let G stand for \(\textsf{S}_{P} \wedge \textsf{S}_{Q} \wedge \gamma (P) \wedge \lnot \gamma (Q)\) and let \(G'\) stand for G with all occurrences of p replaced by \(p'\). For now we ignore the restrictions of \( Aux \) by W as they only have a heuristic purpose. The following statements, which are all equivalent to each other, illustrate the specification of \( Aux \) in a step-by-step fashion. We start with expressing the required “forgetting”. Since it appears in a negation, we have to forget here the “allowed” \(+p\). (1) \(F \models \lnot \exists {+p}\, G\). (2) \(F \models \lnot \exists p'\, (G' \wedge \forall \boldsymbol{x}\, (p(\boldsymbol{x}) \rightarrow p'(\boldsymbol{x})))\). (3) \(F \models \forall p'\, (\lnot G' \vee \lnot \forall \boldsymbol{x}\, (p(\boldsymbol{x}) \rightarrow p'(\boldsymbol{x})))\). (4) \(F \models \lnot G' \vee \lnot \forall \boldsymbol{x}\, (p(\boldsymbol{x}) \rightarrow p'(\boldsymbol{x}))\). (5) \(F \models \lnot G' \vee \lnot Aux \).

Observing the restrictions by membership in W in the definition of \( Aux \) can result in a smaller formula \( Aux \). Continuing the example, this can be illustrated as follows. Assume \(+p \in V^{\pm }\) and \(-p \not \in V^{\pm }\) as before and in addition \(+p \notin W\). Since \(+p \notin W\) it follows that \(-p \notin \mathcal {P} red ^{\pm }(G)\). So “forgetting” about \(+p\) in G is then just \(\exists p'\, G'\) and the \( Aux \) component for p is not needed. (Also a further simplification, outlined in the remark below, is possible in this case.)

Remark 2

The view of “priming” as predicate quantification justifies a heuristically useful simplification of interpolation inputs for definability: If a predicate p occurs in a formula F only with positive (negative) polarity, then \(\exists p\, F\) is equivalent to F with all atoms of the form \(p(\boldsymbol{t})\) replaced by \(\top \) (\(\bot \)). Hence, if a predicate to be primed occurs only in a single polarity, we can replace all atoms with it by a truth value constant.

We now turn to application possibilities of Corollary 14. While it gives some control over the position of predicates, it does not allow to discriminate between allowing a predicate in negative heads and positive bodies. Predicates allowed in positive heads are also allowed in negative bodies. We give some examples.

Example 16

The following examples show for given programs P, Q and sets \(V_{+}, V_{+1}, V_{-}\) of predicates a possible value of R according to Corollary 14. In all the examples it is essential that a predicate is disallowed in R only in a single polarity. If it would not be allowed at all there would be no solution R.

  1. (i)
    figure y

    Here \(\textsf{q}\) is allowed in R in positive heads (and negative bodies) but not in positive bodies (and negative heads). Parentheses indicate constraints that apply but are not relevant for the example.

  2. (ii)
    figure z

    Here \(\textsf{p}\) is allowed in R in positive bodies (and negative heads) but not in negative bodies (and positive heads).

  3. (iii)
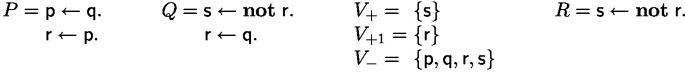
    figure aa

    Here \(\textsf{r}\) is allowed in R in negative bodies and but not in positive heads.

4 Prototypical Implementation

We implemented the synthesis according to Theorem 12 and Corollary 14 prototypically with the PIE (Proving, Interpolating, Eliminating) environment [74, 75], which is embedded in SWI-Prolog [78]. The implementation and all requirements are free software, see http://cs.christophwernhard.com/pie/asp.

For Craig-Lyndon interpolation there are several options, yielding different solutions for some problems. Proving can be performed by CMProver, a clausal tableaux/connection prover connection [8, 9, 46] included in PIE, similar to PTTP  [69], SETHEO  [47] and leanCoP  [61], or by Prover9  [58]. Interpolant extraction is performed on clausal tableaux following [76]. Resolution proofs by Prover9 are first translated to tableaux with the hyper property, which allows to pass range-restriction and the Horn property from inputs to outputs of interpolation [77]. Optionally also proofs by CMProver can be transformed before interpolant extraction to ensure the hyper property. With CMProver it is possible to enumerate alternate interpolants extracted from alternate proofs. More powerful provers such as E  [65] and Vampire  [43] unfortunately do not emit gap-free proofs that would be suited for extracting interpolants.

The organization of the implementation closely follows the abstract exposition in Sect. 3, with Prolog predicates corresponding to theorems. For convenience in some applications, the predicate that realizes Theorem 12 and Corollary 14 permits to specify the vocabulary also complementary, by listing predicates not allowed in the result. In general, if outputs are largely semantically characterized, simplifications play a key role. Solutions with redundancies should be avoided, even if they are correct. This concerns all stages of our workflow: preparation of the interpolation inputs, choice or transformation of the proof used for interpolant extraction, interpolant extraction, the interpolant itself, and the first-order representation of the output program, where strong equivalence must be preserved, possibly modulo a background program. Although our system offers various simplifications at these stages, this seems an area for improvement with large impact for practice. Some particular issues only show up with experiments. For example, for both CMProver and Prover9 a preprocessing of the right sides of the interpolation entailments to reduce the number of distinct variables that are Skolemized by the systems was necessary, even for relatively small inputs.

The application of first-order provers to interpolation for reformulation tasks is a rather unknown territory. Experiments with limited success are described in [4]. Our prototypical implementation covers the full range from the application task, synthesis of an answer set program for two given programs and a given vocabulary, to the actual construction of a result program via Craig-Lyndon interpolation by a first-order prover. At least for small inputs such as the examples in the paper it successfully produces results. We expect that with larger inputs from applications it at least helps to identify and narrow down the actual issues that arise for practical interpolation with current first-order proving technology. This is facilitated by the embedding into PIE, which allows easy interfacing to community standards, e.g., by exporting proving problems underlying interpolation in the TPTP [70] format.

5 Conclusion

We presented an effective variation of projective Beth definability based on Craig interpolation for answer set programs with respect to strong equivalence under the stable model semantics. Interpolation theorems for logic programs under stable models semantics were shown before in [1], where, however, programs are only on the left side of the entailment underlying interpolation, and the right side as well as the interpolant are just first-order formulas. Craig interpolation and Beth definability for answer set programs was considered in [31, 64], but with just existence results for equilibrium logic, which transfer to answer set semantics. The transfer of Craig interpolation and Beth definability from monotonic logics to default logics is investigated in [15], however, applicability to the stable model semantics and a relationship to strong equivalence are not discussed.

In [73] ontology-mediated querying over a knowledge base for specific description logics is considered, based on Beth definability and Craig interpolation. Interpolation is applied there to the Clark’s completion [19] of a Datalog program. Although completion semantics is a precursor of the stable model semantics, both agreeing on a subclass of programs, completion seems applied in [73] actually on program fragments, or on the “schema level”, as in our Examples 13.iv, 13.v and 13.vii. A systematic investigation of these forms of completion is on our agenda. Forgetting [22, 37] or, closely related, uniform interpolation and second-order quantifier elimination [30], may be seen as generalizing Craig interpolation: an expression is sought that captures exactly what a given expression says about a restricted vocabulary. A Craig interpolant is moreover related to a second given expression entailed by the first, allowing to extract it from a proof of the entailment.

We plan to extend our approach to classes of programs with practically important language extensions. Arithmetic expressions and comparisons in rule bodies are permitted in the language mini-gringo, used already in recent works on verifying strong equivalence [24, 26, 51]. We considered strong equivalence relative to a context program P. These contexts might be generalized to first-order theories that capture theory extensions of logic programs [13, 33, 41].

So far, our approach characterizes result programs syntactically by restricting allowed predicates and, to some degree, also their positions in rules. Can this be generalized? Restricting allowed functions, including constants, seems not possible: If a function occurs only in the left side of the entailment underlying Craig interpolation, the interpolant may have existentially quantified variables, making the conversion to a logic program impossible. From the interpolation side it is known that the Horn property and variations of range-restriction can be preserved [77]. It remains to be investigated, how this transfers to synthesizing logic programs, where in particular restrictions of the rule form and safety [14, 45], an important property related to range restriction, are of interest.

In addition to verifying strong equivalence, recent work addresses verifying further properties, e.g., uniform equivalence (equivalence under inputs expressed as ground facts) [24, 26, 52]. The approach is to use completion [19, 50] to express the verification problem in classical first-order logic. It is restricted to so-called locally tight logic programs [27]. Also forms of equivalence that abstract from “hidden” predicates are mostly considered for such restricted program classes, as relative equivalence [55], projected answer sets [23], or external behavior [24]. It remains future work to consider definability with uniform equivalence and hidden predicates, possibly using completion for translating logic programs to formulas (instead of \(\gamma \)), although it applies only to restricted classes of programs.

Independently from the application to program synthesis, our characterization of encodes a program and our procedure to extract a program from a formula suggest a novel practical method for transforming logic programs while preserving strong equivalence. The idea is as follows, where P is the given program: First-order transformations are applied to to obtain a first-order formula \(F'\) such that \(\textsf{S}_{F} \wedge F' \equiv \textsf{S}_{F} \wedge F\). For transformations that result in a universal formula, \(F'\) encodes a logic program, as argued in Remark 1. Applying the extraction procedure to \(F'\) then results in a program \(P'\) that is strongly equivalent to P. This makes the wide range of known first-order simplifications and formula transformations applicable and provides a firm foundation for soundness of special transformations. We expect that this approach supplements known dedicated simplifications that preserve strong equivalence [11, 23].

With its background in artificial intelligence research, answer set programming is a declarative approach to problem solving, where specifications are processed by automated systems. It is suitable for meta-level reasoning to verify properties of specifications and to synthesize new specifications. On the basis of a technique to verify an equivalence property of answer set programs we developed a synthesis technique. Our tools were Craig interpolation and Beth definability, fundamental insights about first-order logic that relate given formulas to further formulas characterized in certain ways. Practically realized with automated first-order provers, Craig interpolation and Beth definability become tools to synthesize formulas, and, as shown here, also answer set programs.