Local Intuitionistic Modal Logics and Their Calculi

Abstract

We investigate intuitionistic modal logics with locally interpreted $\square$ and $\lozenge$. The basic logic LIK is stronger than constructive modal logic WK and incomparable with intuitionistic modal logic IK. We propose an axiomatization of LIK and some of its extensions. Additionally, we present bi-nested calculi for LIK and these extensions, providing both a decision procedure and a procedure of finite countermodel extraction.

1 Introduction

Intuitionistic modal logic (IML) has a long history, starting from the pioneering work by Fitch [10] and Prawitz [16]. Along the time, two traditions have emerged. The first tradition, called intuitionistic modal logics [7,8,9, 15, 17], aims to define modalities justified by an intuitionistic meta-theory. In this tradition, the fundamental logic is IK, considered as the intuitionistic counterpart of the minimal normal modal logic K. The second tradition, known as constructive modal logics, is mainly motivated by computer science applications like Curry-Howard correspondence, verification and contextual reasoning, etc. In this tradition, the basic logics are CCDL [19] and CK [3].

However, there are other intuitionistic modal logics with natural interpretations of modalities that have received little interest and deserve to be studied. One approach can be to study intuitionistic modal logic on a common semantic ground in terms of a bi-relational model $(W,\le ,R,V)$ combining an intuitionistic pre-order $\le$ on states/worlds and an accessibility relation R for modalities. The present work aims to study several intuitionistic modal logics where, in a bi-relational model, the modal operators are classically interpreted:

(1) $x\Vdash \Box A$ iff for all y such that Rxy it holds $y \Vdash A$;

(2) $x\Vdash \Diamond A$ iff there exists y such that Rxy and $y \Vdash A$.

We call these forcing conditions “local” as they do not involve worlds $\le$-greater or $\le$-smaller than x. Meanwhile, we require that all the intuitionistic axioms remain valid in the full logic. This is conveyed by the hereditary property (HP), which says for any formula A, if A is forced by a world x, it will also be forced by any upper world of x. In order to ensure (HP), we need to postulate two frame conditions which relate $\le$ and R in a bi-relational model: the conditions of downward confluence (DC) and forward confluence (FC) [1, 4, 9, 17]. We call the basic K-style logic LIK by local IK.

In the literature, Božić and Došen [4] studied separately the $\Box$-fragment and the $\Diamond$-fragment of LIK and also considered a logic combining $\Box$ and $\Diamond$. However, the logic they obtained is stronger than LIK, since they considered a restricted class of frames. Moreover, in their setting, $\Diamond$ becomes definable in terms of $\Box$, which is inappropriate from an intuitionistic point of view. In other respect, Božić and Došen did not tackle the decidability issue. Besides, a logic related to LIK has been considered in [5] in the context of substructural logics. More recently, the S4-extension of LIK has been shown to be decidable [1].

In this paper, we consider LIK and some of its extensions with axioms characterizing seriality, reflexivity and transitivity of the accessibility relation R in a bi-relational model. We provide complete axiomatizations for them with respect to appropriate classes of models. The basic logic LIK is stronger than Wijesekera’s CCDL as well as another intuitionistic modal logic FIK which only assumes forward confluence on models [2]. But LIK is incomparable with IK. It is noteworthy that LIK fails to satisfy the disjunction property. However, unexpectedly, its extension with axioms characterizing either seriality or reflexivity of the accessibility relation possesses this property.

Turning to proof theory, we propose bi-nested sequent calculi for LIK and its extensions. A bi-nested calculus uses two kinds of nestings in the syntax: the first one is used for $\ge$-upper worlds proposed by Fitting in [11]. Recently a nested sequent calculus using Fitting’s nesting to capture an extension of CCDL has been presented in [6]. The second one is for R-successors, which is used in several nested sequent calculi for other IMLs [12, 14, 18]. A calculus for IK intended to combine the two nestings was also preliminarily considered in [13]. A bi-nested sequent calculus with the same bi-nested structure is proposed for the logic FIK in [2] where the frame condition of forward confluence is captured by a suitable “interaction” rule. A calculus for LIK can be obtained from the calculus for FIK by adopting a “local” $\Box$, or by adding another “interaction” rule capturing the downward confluence frame condition. Calculi for the extensions of LIK are defined by adding suitable modal rules.

We prove that these calculi provide a decision procedure for the logic LIK and some of its extensions. Moreover, we show the semantic completeness of these calculi: from a single failed derivation under a suitable strategy, it is possible to extract a finite countermodel for the given sequent at the root. In addition, for the extensions of LIK with (D) or (T), a syntactic proof of the disjunction property via the calculi is provided. These results demonstrate that bi-nested sequent calculus is a powerful and flexible tool which constitutes an alternative to other formalisms like labelled sequent calculus and is capable to treat uniformly various IMLs.¹

2 Local Intuitionistic Modal Logic

Let $\textbf{At}$ be a set (with members called atoms and denoted p, q, etc.).

Definition 1

(Formulas). Let $\mathcal {L}$ be the set (with members called formulas and denoted A, B, etc.) of finite words over $\textbf{At}\cup \{\supset , \top , \bot , \vee , \wedge , \square , \lozenge ,(,)\}$ defined by

$$A\ :\,\!:=\ p\mid (A\supset A)\mid \top \mid \bot \mid (A\vee A)\mid (A\wedge A)\mid \square A\mid \lozenge A$$

where p ranges over $\textbf{At}$. We follow the standard rules for omission of the parentheses. For all $A\in \mathcal {L}$, we write $\lnot A$ as $A\supset \bot$.

For all sets $\varGamma$ of formulas, let $\square \varGamma = \{A\in \mathcal {L}:\ \square A \in \varGamma \}$ and $\lozenge \varGamma =\{ \lozenge A\in \mathcal {L}:\ A\in \varGamma \}$.

Definition 2

(Frames). A frame is a relational structure $(W,\le ,R)$ where W is a nonempty set of worlds, $\le$ is a preorder on W and R is a binary relation on W. A frame $(W,\le ,R)$ is forward (resp. downward) confluent if $\ge \circ R\subseteq R \circ \ge$ (resp. $\le \circ R\subseteq R\circ \le$). For all $X\subseteq \{\textbf{D},\textbf{T},\textbf{4}\}$, an X-frame is a frame $(W,\le ,R)$ such that R is serial if $\textbf{D}\in X$, R is reflexive if $\textbf{T}\in X$ and R is transitive if $\textbf{4}\in X$. Let $\mathcal {C}_{\textbf{fdc}}^{X}$ be the class of forward and downward confluent X-frames. We write “$\mathcal {C}_{\textbf{fdc}}$” instead of “$\mathcal {C}_{\textbf{fdc}}^{\emptyset }$”.

We can see that $\mathcal {C}_{\textbf{fdc}}^{\textbf{ref}}\subseteq \mathcal {C}_{\textbf{fdc}}^{\textbf{ser}}\subseteq \mathcal {C}_{\textbf{fdc}}$.

Definition 3

(Valuations, Models and Truth Conditions). For all frames $(W,\le ,R)$, a subset U of W is $\le$ -closed if for all $s,t\in W$, if $s\in U$ and $s\le t$ then $t\in U$. A valuation on $(W,\le ,R)$ is a function $V: \textbf{At}\longrightarrow \wp (W)$ such that for all $p\in \textbf{At}$, V(p) is $\le$-closed. A model based on $(W,{\le },{R})$ is a model of the form $(W,{\le },{R},V)$. In a model $\mathcal {M}=(W,\le ,R,V)$, for all $x\in W$ and for all $A\in \mathcal {L}$, the satisfiability of Aat xin $\mathcal {M}$ (in symbols $\mathcal {M},x\Vdash A$) is defined as usual when A’s main connective is either $\top$, $\bot$, $\vee$ or $\wedge$ and as follows otherwise:

• $\mathcal {M},x\Vdash p$ if and only if $x\in V(p)$,

• $\mathcal {M},x\Vdash A \supset B$ if and only if for all $x'\in W$ with $x\le x'$, if $\mathcal {M},x'\Vdash A$ then $\mathcal {M},x'\Vdash B$,

• $\mathcal {M},x\Vdash \square A$ if and only if for all $y\in W$ such that Rxy, $\mathcal {M},y\Vdash A$,

• $\mathcal {M},x\Vdash \lozenge A$ if and only if there exists $y\in W$ such that Rxy and $\mathcal {M},y\Vdash A$.

When $\mathcal {M}$ is clear from the context, we simply write $x \Vdash A$. The notions of truth and validity are defined as usual.

Lemma 1

(Hereditary Property). Let $(W,\le ,R,V)$ be a forward and downward confluent model. For all $A \in \mathcal {L}$ and $x,x'\in W$, if $x\Vdash A$ and $x\le x'$ then $x'\Vdash A$.

Note that our definition of $\Vdash$ differs from the definitions proposed by Fischer Servi [9] and Wijesekera [19]. In both settings,

$x\Vdash \square A$ iff for all $x'\in W$ with $x\le x'$ and for all $y\in W$ with $Rx'y$, it holds $y \Vdash A$;

whereas in [19],

$x\Vdash \lozenge A$ iff for all $x'\in W$ with $x\le x'$, there exists $y\in W$ such that $Rx'y$ and $y\Vdash A$.

However, these satisfiability relations collapse on forward and downward confluent frames.

Proposition 1

In $\mathcal {C}_{\textbf{fdc}}$, our definition of $\Vdash$ determines the same satisfiability relation as the relations determined by definitions in [9] and [19].

From now on in this section, when we write frame (resp. model), we mean forward and downward confluent frame (resp. model).

Obviously, validity in $\mathcal {C}_{\textbf{fdc}}$ is closed under the following inference rules:

Moreover, the following axiom schemes are valid in $\mathcal {C}_{\textbf{fdc}}$:

$$ \begin{array}{ll} (\textbf{K}_{\square }) \ \square (A\supset B)\supset (\square A\supset \square B)\qquad \qquad &{} (\textbf{K}_{\Diamond }) \ \square (A\supset B)\supset (\Diamond A\supset \Diamond B) \\ (\textbf{DP}) \ \Diamond (A\vee B)\supset \Diamond A\vee \Diamond B\qquad \qquad &{} (\textbf{RV}) \ \square (A\vee B)\supset \Diamond A\vee \square B\\ (\textbf{N}) \ \lnot \Diamond \bot &{} \end{array} $$

In $\mathcal {C}_{\textbf{fdc}}^{\textbf{D}}$ (resp. $\mathcal {C}_{\textbf{fdc}}^{\textbf{T}}$, $\mathcal {C}_{\textbf{fdc}}^{\textbf{4}}$), modal axiom $\textbf{D}$ (resp. $\textbf{T}$, $\textbf{4}$) is valid:

$$ \begin{array}{ccc} (\textbf{D})\ \lozenge \top \quad & (\textbf{T})\ (\square A\supset A)\wedge (A\supset \lozenge A) \quad & (\textbf{4})\ (\square A\supset \square \square A)\wedge (\lozenge \lozenge A\supset \lozenge A) \end{array} $$

Axiom ($\textbf{RV}$) is also considered in [1] where it is called ($\textbf{CD}$) for constant domain, since it is related with the first-order formula $\forall x.(P(x)\vee Q(x))\supset \exists x.P(x)\vee \forall x.Q(x)$ which is intuitionistically valid when models with constant domains are considered.

Definition 4

(Axiom System). For all $X\subseteq \{\textbf{D},\textbf{T},\textbf{4}\}$, let LIK X be the axiomatic system consisting of all standard axioms of IPL, the inference rules ($\textbf{MP}$) and ($\textbf{NEC}$), the axioms $\textbf{K}_{\square }$, $\textbf{K}_{\Diamond }$, $\textbf{N}$, $\textbf{DP}$ and $\textbf{RV}$ and containing in addition the axioms from X. We write LIK for LIK $\emptyset$. Derivations are defined as usual. We write $\vdash _{\textbf{LIK}X}A$ when A is LIK X-derivable. The set of all LIK X-derivable formulas is also denoted as LIK X.

From now on in this section, let $X\subseteq \{\textbf{D},\textbf{T},\textbf{4}\}$.

Lemma 2

If $\textbf{D}\in X$ or $\textbf{T}\in X$ then $\square p\supset \lozenge p$ and $\lnot \square \bot$ are in LIK X.

Theorem 1

(Soundness). LIK X-derivable formulas are $\mathcal {C}_{\textbf{fdc}}^{X}$-validities.

Next we prove completeness, which is the converse of soundness, saying that every formula valid in $\mathcal {C}_{\textbf{fdc}}^{X}$ is LIK X-derivable. At the heart of our completeness proof lies the concept of theory. Let $\textbf{L}={\textbf {LIK}}X$.

Definition 5

(Theories). A theory is a set of formulas containing $\textbf{L}$ and closed with respect to MP. A theory $\varGamma$ is proper if $\bot \not \in \varGamma$. A proper theory $\varGamma$ is prime if for all formulas A, B, if $A\vee B\in \varGamma$ then either $A\in \varGamma$, or $B\in \varGamma$.

Lemma 3

If $\textbf{D}\in X$ or $\textbf{T}\in X$ then for all theories $\varGamma$, we have $\lozenge \square \varGamma \subseteq \varGamma$.

Definition 6

(Canonical Model). The canonical model $(W_{\textbf{L}},\le _{\textbf{L}},R_{\textbf{L}},V_{\textbf{L}})$ is a tuple where

• $W_{\textbf{L}}$ is the nonempty set of all prime theories,

• $\le _{\textbf{L}}$ is the partial order on $W_{\textbf{L}}$ defined by: $\varGamma \le _{\textbf{L}}\varDelta$ iff $\varGamma \subseteq \varDelta$,

• $R_{\textbf{L}}$ is the binary relation on $W_{\textbf{L}}$ defined by: $R_{\textbf{L}}\varGamma \varDelta$ iff $\square \varGamma \subseteq \varDelta$ and $\lozenge \varDelta \subseteq \varGamma$,

• $V_{\textbf{L}}$ is the valuation on $W_{\textbf{L}}$ defined by: $V_{\textbf{L}}(p)=\{\varGamma \in W_{\textbf{L}}:\ p\in \varGamma \}$.

Lemma 4

• 1. $(W_{\textbf{L}},\le _{\textbf{L}},R_{\textbf{L}},V_{\textbf{L}})$ is forward confluent,

• 2. $(W_{\textbf{L}},\le _{\textbf{L}},R_{\textbf{L}},V_{\textbf{L}})$ is downward confluent,

• 3. if $\textbf{D}\in X$ (resp. $\textbf{T}\in X$, $\textbf{4}\in X$) then $(W_{\textbf{L}},\le _{\textbf{L}},R_{\textbf{L}},V_{\textbf{L}})$ is serial (resp. reflexive, transitive).

The proof of the completeness is based on the following lemmas.

Lemma 5

(Existence Lemma). Let $\varGamma$ be a prime theory.

• 1. If $B\supset C\not \in \varGamma$ then there exists a prime theory $\varDelta$ such that $\varGamma \subseteq \varDelta$, $B\in \varDelta$ and $C\not \in \varDelta$,

• 2. if $\square B\not \in \varGamma$ then there exists a prime theory $\varDelta$ such that $R_{\textbf{L}}\varGamma \varDelta$ and $B\not \in \varDelta$,

• 3. if $\Diamond B\in \varGamma$ then there exists a prime theory $\varDelta$ such that $R_{\textbf{L}}\varGamma \varDelta$ and $B\in \varDelta$.

Lemma 6

(Truth Lemma). For all formulas A and all $\varGamma \in W_{\textbf{L}}$, we have $A\in \varGamma$ if and only if $(W_{\textbf{L}},\le _{\textbf{L}},R_{\textbf{L}},V_{\textbf{L}}),\varGamma \Vdash A$.

From Lemma 6, we conclude

Theorem 2

(Completeness). All $\mathcal {C}_{\textbf{fdc}}^{X}$-validities are LIK X-derivable.

In [17, Chapter 3], Simpson discusses the formal features that might be expected for an intuitionistic modal logic ${\textbf{L}}$:

• $\textbf{L}$ is conservative over Intuitionistic Propositional Logic,

• $\textbf{L}$ contains all substitution instances of axioms of Intuitionistic Propositional Logic and is closed under modus ponens,

• $\textbf{L}$ has the disjunction property: for each formula $A\vee B$, if $A{\vee }B$ is in $\textbf{L}$ then either A is in $\textbf{L}$, or B is in $\textbf{L}$,

• by adding the law of excluded middle to $\textbf{L}$ it yields modal logic $\textbf{K}$,

• ${\square }$ and ${\lozenge }$ are independent in $\textbf{L}$.

Now, we show that LIK X possesses the formal features that might be expected of an intuitionistic modal logic.

Proposition 2

• 1. LIK X is conservative over $\textbf{IPL}$,

• 2. LIK X contains all substitution instances of $\textbf{IPL}$ and is closed with respect to modus ponens,

• 3. LIK X has the disjunction property if and only if $\textbf{D}{\in }X$ or $\textbf{T}{\in }X$,

• 4. the addition of the law of excluded middle to LIK X yields modal logic $\textbf{K}$,

• 5. $\square$ and $\lozenge$ are independent in LIK X.

3 Bi-nested Sequent Calculi

In this section we present bi-nested calculi for LIK and its extensions LIKD  and LIKT. These calculi are called bi-nested in the sense that they make use of two kinds of nesting representing $\le$-upper worlds and R-successors in the semantics, similar to the calculus for FIK presented in [2]. In a basic system for LIK, two rules encoding forward and downward confluence are contained. We will show that the latter rule called $(\text {inter}_\downarrow )$ is admissible in a smaller system without it, thus by dropping out this rule we still have a complete calculus for LIK. However, as we will see, the $(\text {inter}_\downarrow )$ rule is required to prove the semantic completeness of the calculus and further allows us to obtain counter-model extraction. We also prove the disjunction property for LIKD and LIKT using the calculi.

In order to define the calculi we first give some preliminary notions.

Definition 7

(Bi-Nested Sequent). A bi-nested sequent S is defined as:

• The empty sequent $\Rightarrow$ is a bi-nested sequent;

• $\varGamma \Rightarrow \varDelta ,\langle T_1\rangle ,\ldots ,\langle T_n\rangle ,[S_1],\ldots ,[S_m]$ is a bi-nested sequent if both $\varGamma$ and $\varDelta$ are multisets of formulas, all the $S_1,\ldots ,S_m, T_1,\ldots , T_n$ are bi-nested sequents where $m,n\ge 0$.

We use S and T to denote a bi-nested sequent and simply call it “sequent" in the rest of this paper. The antecedent and consequent of a sequent S are denoted by Ant(S) and Con(S). Syntactic objects of the shape $\langle S\rangle$ and [T] are called implication and modal blocks respectively.

The notion of modal degree can be extended from a formula to a sequent.

Definition 8

(Modal Degree). Modal degree $\textit{md}(F)$ for a formula F is defined as usual. Let $\varGamma$ be a finite (multi)set of formulas, define $\textit{md}(\varGamma )=\textit{md}(\bigwedge \varGamma )$. For a sequent $S=\varGamma \Rightarrow \varDelta ,\langle T_1\rangle ,\ldots ,\langle T_n\rangle ,[S_1],\ldots ,[S_m]$, we define $\textit{md}(S)=\max \{\textit{md}(\varGamma ),\textit{md}(\varDelta ),\textit{md}(T_1),\ldots ,\textit{md}(T_n),\textit{md}(S_1)+1,\ldots ,\textit{md}(S_m)+1\}$.

Context is defined as usual in standard nested calculi which can be regarded as a placeholder to be filled by a sequent.

Definition 9

(Context). A context $G\{\ \}$ is inductively defined as follows:

• The empty context $\{\ \}$ is a context.

• if $\varGamma \Rightarrow \varDelta$ is a sequent and $G'\{\ \}$ is a context, then both $\varGamma \Rightarrow \varDelta , \langle G'\{\ \}\rangle$ and $\varGamma \Rightarrow \varDelta , [G'\{\ \}]$ are contexts.

Example 1

Given a context $G\{\ \}=p\wedge q, \square r\Rightarrow \Diamond p,\langle \square p\Rightarrow [\Rightarrow q]\rangle ,[\{\ \}]$ and a sequent $S=p\Rightarrow q\vee r,[r\Rightarrow s]$, we have $G\{S\}=p\wedge q, \square r\Rightarrow \Diamond p,\langle \square p\Rightarrow [\Rightarrow q]\rangle ,[p\Rightarrow q\vee r,[r\Rightarrow s]]$.

Definition 10

($\in ^{\langle \cdot \rangle }, \in ^{[\cdot ]}, \in ^+$-Relation). Let $\varGamma _1\Rightarrow \varDelta _1,\varGamma _2\Rightarrow \varDelta _2$ be two sequents. We denote $\varGamma _1\Rightarrow \varDelta _1 \in ^{\langle \cdot \rangle }_0\varGamma _2\Rightarrow \varDelta _2$ if $\langle \varGamma _1\Rightarrow \varDelta _1 \rangle \in \varDelta _2$ and let $\in ^{\langle \cdot \rangle }$ be the transitive closure of $\in ^{\langle \cdot \rangle }_0$. Relations $\in ^{[\cdot ]}_0$ and $\in ^{[\cdot ]}$ for modal blocks are defined similarly. Besides, let $\in ^+_0 =~\in ^{\langle \cdot \rangle }_0 \cup \in ^{[\cdot ]}_0$ and finally let $\in ^+$ be the reflexive-transitive closure of $\in ^+_0$.

When we say $S'\in ^+ S$, it is equivalent to say that $S = G\{S'\}$ for some context G.

As we will see, some rules in the calculi propagate formulas in the antecedent (“positive part”) or the consequent (“negative part”) of sequents into a modal block. The two operators in the following definition single out these formulas of a sequent.

Definition 11

($\flat$-Operator and $\sharp$-Operator). Let $\varLambda \Rightarrow \varTheta$ be a sequent and $Fm(\varTheta )$ the multiset of formulas directly belonging to $\varTheta$.

Let $\varTheta ^\flat =\emptyset$ if $\varTheta$ is $[\cdot ]$-free; $\varTheta ^\flat = [\varPhi _1\Rightarrow \varPsi _1^\flat ], \ldots , [\varPhi _k\Rightarrow \varPsi _k^\flat ]$, if $\varTheta =\varTheta _0,[\varPhi _1\Rightarrow \varPsi _1], \ldots , [\varPhi _k\Rightarrow \varPsi _k]$ and $\varTheta _0$ is $[\cdot ]$-free.

Dually let $\Rightarrow \varTheta ^\sharp = \ \Rightarrow Fm(\varTheta )$ if $\varTheta$ is $[\cdot ]$-free; $\Rightarrow \varTheta ^\sharp = \ \Rightarrow Fm(\varTheta _0), [\Rightarrow \varPsi _1^\sharp ], \ldots , [\Rightarrow \varPsi _k^\sharp ]$ if $\varTheta =\varTheta _0,[\varPhi _1\Rightarrow \varPsi _1], \ldots , [\varPhi _k\Rightarrow \varPsi _k]$ and $\varTheta _0$ is $[\cdot ]$-free.

Example 2

Consider the sequent $G\{S\}=p\wedge q, \square r\Rightarrow \Diamond p,\langle \square p\Rightarrow [\Rightarrow q]\rangle ,[p\Rightarrow q\vee r,[r\Rightarrow s]]$ of Example 1, denote $Ant(G\{S\})$ and $Suc(G\{S\})$ by $\varLambda$ and $\varTheta$ respectively, we can see by definition, $\varLambda \Rightarrow \varTheta ^\flat =p\wedge q, \square r\Rightarrow [p\Rightarrow [r\Rightarrow ]]$ while $\Rightarrow \varTheta ^\sharp = \ \Rightarrow \Diamond p,[\Rightarrow q\vee r,[\Rightarrow s]]$.

Definition 12

Rules for the basic logic LIK and its modal extensions are given in Fig. 1, which consists of the basic calculus $\textbf{C}_{{\textbf {LIK}}}$ and modal rules corresponding to axioms $({\textbf {D}})$, $({\textbf {T}}_\Diamond )$ and $({\textbf {T}}_\square )$. We define $\textbf{C}_{{\textbf {LIKD}}}$ = $\textbf{C}_{{\textbf {LIK}}}$ + $({\textbf {D}})$ and $\textbf{C}_{{\textbf {LIKT}}}$ = $\textbf{C}_{{\textbf {LIK}}}$ + $({\textbf {T}}_\square )$ + $({\textbf {T}}_\Diamond )$.

The notions of derivation and proof in a calculus are defined as usual. We say a formula A is provable if the sequent $\Rightarrow A$ has a proof in the calculus.

Fig. 1.

Bi-nested rules for local intuitionistic modal logics

Here are some remarks on the rules. First, the rule (id) which only concerns atoms can be easily generalized to arbitrary formulas. Reading the rule upwards, the rule ($\supset _R$) introduces an implication block $\langle \cdot \rangle$ while the rules ($\Diamond _L$) and ($\Box _R$) introduce a modal block $[\cdot ]$. Observe that the ($\Box _R$) rule corresponds to the “local” interpretation of $\Box$. The rule $(\text {inter}_{\rightarrow })$ is intended to capture Forward Confluence, whereas the rule ($\text {inter}_{\downarrow }$) Downward Confluence. Finally the (trans) rule captures the Hereditary Property. All the rules of $\textbf{C}_{{\textbf {LIK}}}$, except ($\Box _R$) and ($\text {inter}_{\downarrow }$) belong to the calculus $\textbf{C}_{{\textbf {FIK}}}$ for the logic FIK [2], we will discuss the relation between the two calculi later in the section.

We can verify that each axiom of LIK in Sect. 2 is provable in $\textbf{C}_{{\textbf {LIK}}}$. An example of axiom (RV) is given below.

Example 3

We show $\square (p\vee q)\Rightarrow \Diamond p\vee \square q$ is provable.

We now show that $\textbf{C}_{{\textbf {LIK}}}$ is sound with respect to the semantics. The first step is to extend the forcing relation $\Vdash$ to sequents and blocks therein.

Definition 13

Let $\mathcal {M}=(W,\le ,R,V)$ be a bi-relational model and $x\in W$. The satisfiability relation $\Vdash$ is extended to sequents as follows:

• $\mathcal {M}, x\not \Vdash \emptyset$

• $\mathcal {M}, x \Vdash [T]$ if for every y with Rxy, $\mathcal {M}, y \Vdash T$

• $\mathcal {M}, x \Vdash \langle T \rangle$ if for every $x'$ with $x\le x'$, $\mathcal {M}, x' \Vdash T$

• $\mathcal {M}, x \Vdash \varGamma \Rightarrow \varDelta$ if either $\mathcal {M}, x \not \Vdash A$ for some $A\in \varGamma$ or $\mathcal {M}, x \Vdash \mathcal{O}$ for some $\mathcal{O} \in \varDelta$, where $\mathcal{O}$ is a formula or a block.

We say S is valid in $\mathcal {M}$ iff $\forall w\in W$, we have $\mathcal {M},w\Vdash S$. We say S is valid iff it is valid in every model.

Definition 14

For a rule (r) of the form $\frac{G\{S_1\} \quad G\{S_2\}}{G\{S\}}$ or $\frac{G\{S_1\}}{G\{S\}}$, we say (r) is valid if the following holds: if for each i, $x\Vdash G\{S_i\}$, then it follows $x\Vdash G\{S\}$.

We can easily verify the validity of each rule and then obtain the soundness of $\textbf{C}_{{\textbf {LIK}}}$ by a standard induction on a derivation. The soundness of $\textbf{C}_{{\textbf {LIKD}}}$ and $\textbf{C}_{{\textbf {LIKT}}}$ can be proven similarly.

Theorem 3

(Soundness of $\textbf{C}_{{\textbf {LIK}}}$). If a formula A is provable in $\textbf{C}_{{\textbf {LIK}}}$, then it is valid in LIK.

Next, we show that the rule ($\text {inter}_{\downarrow }$) is admissible in the calculus $\textbf{C}_{{\textbf {LIK}}^-}$= $\textbf{C}_{{\textbf {LIK}}}$ $\backslash \{(\text {inter}_{\downarrow })\}$. The proof can be easily extended to the modal extensions as well. In order to prove this, we need some preliminary facts. First, weakening and contraction rules $(w_L)(w_R)(c_L)(c_L)$ defined as usual are height-preserving (hp) admissible in $\textbf{C}_{{\textbf {LIK}}^-}$, not only applied to formulas but also blocks. Moreover, extended weakening rules $\frac{S}{G\{S\}}$, $\frac{G\{\varGamma \Rightarrow \varDelta ^\flat \}}{G\{\varGamma \Rightarrow \varDelta \}}$, $\frac{G\{\varGamma \Rightarrow \varDelta ^\sharp \}}{G\{\varGamma \Rightarrow \varDelta \}}$ are hp-admissible as well.

Proposition 3

The $(\text {inter}_{\downarrow })$ rule is admissible in $\textbf{C}_{{\textbf {LIK}}^-}$. Consequently, a sequent S is provable in $\textbf{C}_{{\textbf {LIK}}}$ if and only if S is provable in $\textbf{C}_{{\textbf {LIK}}^-}$.

As mentioned above, all the rules in $\textbf{C}_{{\textbf {LIK}}}$, except ($\Box _R$) and ($\text {inter}_{\downarrow }$), belong to the calculus $\textbf{C}_{{\textbf {FIK}}}$ for the logic FIK [2]. As a difference with LIK, the logic FIK adopts the “global” forcing condition for $\Box$ as in [9, 17, 19] and only forward confluence on the frame. The ($\Box _R$) rule in $\textbf{C}_{{\textbf {FIK}}}$ is $\frac{G\{\varGamma \Rightarrow \varDelta ,\langle \Rightarrow [\Rightarrow A]\rangle \}}{G\{\varGamma \Rightarrow \varDelta ,\square A\}}$. It can be proved that this rule is admissible in $\textbf{C}_{{\textbf {LIK}}^-}$ and on the opposite direction, the “local” $(\Box _R)$ rule in $\textbf{C}_{{\textbf {LIK}}}$ is admissible in $\textbf{C}_{{\textbf {FIK}}}$+ ($\text {inter}_{\downarrow }$). Thus $\textbf{C}_{{\textbf {FIK}}}$+ ($\text {inter}_{\downarrow }$) can be regarded as another equivalent variant of $\textbf{C}_{{\textbf {LIK}}}$, which is obtained in a modular way from the one for FIK.

We end this section by considering the disjunction property. For simplicity, we only work in $\textbf{C}_{{\textbf {LIK}}^-}$ and its extensions. Let $\textbf{C}_{{\textbf {LIKD}}^-}$ = $\textbf{C}_{{\textbf {LIK}}^-}$ + (D) and $\textbf{C}_{{\textbf {LIKT}}^-}$ = $\textbf{C}_{{\textbf {LIK}}^-}$ + (${\textbf {T}}_\square$) + (${\textbf {T}}_\Diamond$). Consider the formula $\square \bot \vee \Diamond \top$ which is provable in $\textbf{C}_{{\textbf {LIK}}^-}$, but it is easy to see neither $\square \bot$ nor $\Diamond \top$ are provable.² However, this counterexample does not hold in LIKD or LIKT since $\Diamond \top$ is provable in both calculi. We show that the disjunction property indeed holds for both $\textbf{C}_{{\textbf {LIKD}}^-}$ and $\textbf{C}_{{\textbf {LIKT}}^-}$. The key fact is expressed by the following lemma:

Lemma 7

Suppose $S =\ \Rightarrow A_1, \ldots , A_m, \langle G_1\rangle , \ldots , \langle G_n\rangle ,[H_1],\ldots ,[H_l]$ is provable in $\textbf{C}_{{\textbf {LIKD}}^-}$ (resp. $\textbf{C}_{{\textbf {LIKT}}^-}$), where $A_i$’s are formulas, $G_j$ and $H_k$’s are sequents. Further assume that each $H_k$ is of the form $\Rightarrow \varTheta _k$ and for each sequent $T\in ^{[\cdot ]} H_k$, T has an empty antecedent. Then either $\Rightarrow A_i$ or $\Rightarrow \langle G_j\rangle$ or $\Rightarrow [H_k]$ is provable in $\textbf{C}_{{\textbf {LIKD}}^-}$ (resp. $\textbf{C}_{{\textbf {LIKT}}^-}$) for some $i\le m, j\le n, k\le l$.

We obtain the disjunction property by an obvious application of the lemma.

Proposition 4

(Disjunction Property for $\textbf{C}_{{\textbf {LIKD}}^-}$and $\textbf{C}_{{\textbf {LIKT}}^-}$). For any formulas A, B, if $\Rightarrow A \vee B$ is provable in $\textbf{C}_{{\textbf {LIKD}}^-}$ (resp. $\textbf{C}_{{\textbf {LIKT}}^-}$), then either $\Rightarrow A$ or $\Rightarrow B$ is provable $\textbf{C}_{{\textbf {LIKD}}^-}$ (resp. $\textbf{C}_{{\textbf {LIKT}}^-}$).

4 Termination

In this section we define decision procedure for LIK as well as its extensions LIKD and LIKT based on the calculi in Sect. 3. We treat first LIK, then at the end of the section we will briefly describe how to adopt the the procedure to the extensions. The terminating proof-search procedure is essential for the semantic completeness of the calculi, as well as for countermodel construction, as we will demonstrate in the following section.

We have introduced two calculi for LIK, namely $\textbf{C}_{{\textbf {LIK}}}$ and $\textbf{C}_{{\textbf {LIK}}^-}$. For $\textbf{C}_{{\textbf {LIK}}^-}$, we can obtain a terminating proof-search procedure by adapting the one in [2] for the calculus of FIK. Actually, the decision procedure for $\textbf{C}_{{\textbf {LIK}}^-}$ is remarkably simpler than that for FIK, as “blocking” is not needed to prevent loops. For $\textbf{C}_{{\textbf {LIK}}}$, however, some extra work needs to be done. Despite the equivalence of $\textbf{C}_{{\textbf {LIK}}}$ and $\textbf{C}_{{\textbf {LIK}}^-}$ in terms of provability, constructing a countermodel from a failed proof in $\textbf{C}_{{\textbf {LIK}}^-}$ poses a challenge due to the absence of a rule capturing downward confluence. Therefore, we need to explore a terminating proof-search procedure for $\textbf{C}_{{\textbf {LIK}}}$ to further advance our goal of proving semantic completeness.

Recall our ultimate aim is to build a countermodel from a failed derivation, in which the main ingredient is the pre-order relation $\le$ in the model construction. This relation is specified by the following notion of structural inclusion between sequents, which is also used in defining the saturation conditions required for termination.

Definition 15

(Structural Inclusion $\subseteq ^\textbf{S}$). Let $S_1=\varGamma _1\Rightarrow \varDelta _1,S_2=\varGamma _2\Rightarrow \varDelta _2$ be two sequents. We say that $S_1$ is structurally included in $S_2$, denoted by $S_1\subseteq ^{\textbf{S}} S_2$, when all the following holds:

• $\varGamma _1\subseteq \varGamma _2$;

• for each $[\varLambda _1\Rightarrow \varTheta _1]\in \varDelta _1$, there exists $[\varLambda _2\Rightarrow \varTheta _2]\in \varDelta _2$ such that $\varLambda _1\Rightarrow \varTheta _1\subseteq ^{\textbf{S}} \varLambda _2\Rightarrow \varTheta _2$;

• for each $[\varLambda _2\Rightarrow \varTheta _2]\in \varDelta _2$, there exists $[\varLambda _1\Rightarrow \varTheta _1]\in \varDelta _1$ such that $\varLambda _1\Rightarrow \varTheta _1\subseteq ^{\textbf{S}} \varLambda _2\Rightarrow \varTheta _2$.

It is easy to see $\subseteq ^\textbf{S}$ is both reflexive and transitive.

We now define an equivalent variant C $\textbf{C}_{{\textbf {LIK}}}$ of $\textbf{C}_{{\textbf {LIK}}}$ which adopts a cumulative version of the rules along with some bookkeeping. Moreover the $(\supset _{R})$ rule is modified in order to prevent loops. This calculus will be used as a base for the following decision procedure and then semantic completeness. At first we reformulate the $\sharp$-operator as below, annotating the generated $\sharp$-sequents by the full sequent where it comes from.

Definition 16

Let $Fm(\varTheta )$ be the multiset of formulas directly belonging to $\varTheta$. We define the $\sharp$-operator with annotation as follows:

• $\Rightarrow _{\varLambda \Rightarrow \varTheta }\varTheta ^\sharp = \ \Rightarrow Fm(\varTheta )$ if $\varTheta$ is $[\cdot ]$-free;

• $\Rightarrow _{\varLambda \Rightarrow \varTheta }\varTheta ^\sharp = \ \Rightarrow Fm(\varTheta _0), [\Rightarrow _{\varPhi _1\Rightarrow \varPsi _1}\varPsi _1^\sharp ], \ldots , [\Rightarrow _{\varPhi _k\Rightarrow \varPsi _k}\varPsi _k^\sharp ]$ if $\varTheta =\varTheta _0,[\varPhi _1\Rightarrow \varPsi _1], \ldots , [\varPhi _k\Rightarrow \varPsi _k]$ and $\varTheta _0$ is $[\cdot ]$-free.

The $\sharp$-sequents are generated only by applications of ($\text {inter}_{\downarrow }$), and we use the annotation (the subscript of $\Rightarrow$) to “track” the implication block from which a $\sharp$-sequent is generated. The annotation can be omitted and we simply write $\Rightarrow \varTheta ^\sharp$ whenever we do not need to track an ($\text {inter}_{\downarrow }$) application.

Definition 17

(The $\sharp$-Annotated Cumulative Calculus C $\textbf{C}_{{\textbf {LIK}}}$). The cumulative calculus C $\textbf{C}_{{\textbf {LIK}}}$ operates on set-based sequents, where a set-based sequent $S = \varGamma \Rightarrow \varDelta$ is defined as in definition 7, with the distinction that $\varGamma$ is a set of formulas and $\varDelta$ is a set of formulas and/or blocks (containing set-based sequents). The rules are as follows:

• $(\bot _L), \ (\top _R), \ (\text {id}),\ (\square _L),\ (\Diamond _R)$, $(\text {trans})$ and $(\text {inter}_{\rightarrow })$ as in $\textbf{C}_{{\textbf {LIK}}}$.

• $(\supset _R)$ is replaced by two rules for $A\in \varGamma$ or $A\notin \varGamma$:

  

• $(\text {inter}_{\downarrow })$ is replaced by the following annotated rule:

  

• The other rules in $\textbf{C}_{{\textbf {LIK}}}$ are modified by keeping the principal formula in the premises. For example, the cumulative versions of $(\wedge _L),\ (\square _R)$ are:

  

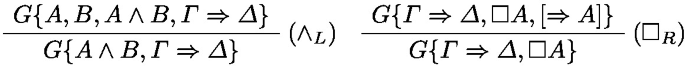
Given the admissibility of weakening and contraction in $\textbf{C}_{{\textbf {LIK}}}$, the following proposition is a direct consequence.

Proposition 5

A sequent S is provable in $\textbf{C}_{{\textbf {LIK}}}$  iff S is provable in C $\textbf{C}_{{\textbf {LIK}}}$.

Next, we introduce saturation conditions for each rule in C $\textbf{C}_{{\textbf {LIK}}}$. They are needed for both termination and counter-model extraction.

Definition 18

(Saturation Conditions). Let $S=\varGamma \Rightarrow \varDelta$ be a sequent. We say S satisfies the saturation condition on the top level with respect to

Saturation conditions for the other propositional rules are defined as usual.

We say a sequent is saturated with a rule (r) if it satisfies the saturation condition associated with (r). We say a backward application of a rule (r) to a sequent S is redundant if S already satisfies the corresponding saturation condition associated with (r).

Proposition 6

Let $S=\varGamma \Rightarrow \varDelta$ be a sequent. If S is saturated with $(\text {trans})$, $(\text {inter}_{\rightarrow })$ and $(\text {inter}_{\downarrow })$, then for $\langle \varSigma \Rightarrow \varPi \rangle \in \varDelta$, we have $\varGamma \Rightarrow \varDelta \subseteq ^\textbf{S}\varSigma \Rightarrow \varPi$.

In order to define a terminating proof-search strategy based on C $\textbf{C}_{{\textbf {LIK}}}$, we first impose the following constraints:

(i) No rule is applied to an axiom and (ii) No rule is applied redundantly.

However there is a problem: backward proof search only respecting these basic constraints does not necessarily ensure that any leaf of a derivation, to which no rule can be applied non-redundantly, satisfies all the saturation conditions of rules in C $\textbf{C}_{{\textbf {LIK}}}$. This is a significant difference from the calculus of FIK in [2]. The problematic case is the saturation condition for the ($\text {inter}_{\downarrow }$) rule.

Example 4

Let us consider the sequent $\square (p\vee q)\Rightarrow \square r\supset \square s$. After some preliminary steps, we obtain two sequents:

• (i). $\square (p\vee q)\Rightarrow \square r\supset \square s,\langle \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,p,r\Rightarrow s]\rangle$

• (ii). $\square (p\vee q)\Rightarrow \square r\supset \square s,\langle \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,q,r\Rightarrow s]\rangle$

Suppose we select (i) and then apply $(\text {inter}_\downarrow )$ obtaining (i’): $\square (p\vee q)\Rightarrow \square r\supset \square s,\langle \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,p,r\Rightarrow s]\rangle ,[\Rightarrow s]$. After applying $(\Box _L)$, $(\vee _L)$ and $(\text {inter}_{\rightarrow }$), we further obtain:

• (iii). $\square (p\vee q)\Rightarrow \square r\supset \square s,\langle \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,p,r\Rightarrow s]\rangle ,[p\vee q,p\Rightarrow s]$

• (iv). $\square (p\vee q)\Rightarrow \square r\supset \square s,\langle \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,p,r\Rightarrow s], [p\vee q,q\Rightarrow ]\rangle$, $[p\vee q,q\Rightarrow s]$

We can see that (iii) satisfies the saturation condition for ($\text {inter}_{\downarrow }$), as $p\vee q,p\Rightarrow s\subseteq ^\textbf{S} p\vee q,p,r\Rightarrow s$ but (iv) does not, since there is no $[\varPhi \Rightarrow \varPsi ]$ s.t. $\varPhi \Rightarrow \varPsi \subseteq ^{\textbf{S}} p\vee q,p,r\Rightarrow s$. Sequent (iv) would not give in itself a model satisfying (DC) and it is not obvious how to extend it in order to satisfy (DC).³ This example also shows the inadequacy of $\textbf{C}_{{\textbf {LIK}}^-}$ for semantic completeness, as sequent expansion in $\textbf{C}_{{\textbf {LIK}}^-}$ terminates with (i) and (ii), from which we do not know how to define a model satisfying (DC).

This means that certain branches in a derivation may lead to unprovable sequents from which we do not know how to build a “correct” counter-model directly. Hence, to obtain a “correct” counter-model, we require a mechanism that chooses the suitable branch which ensures the saturation condition for ($\text {inter}_{\downarrow }$). This is provided by the tracking mechanism and realization procedure defined below.

Definition 19

(Tracking Record Based on $\in ^{[\cdot ]}$). Let S be a set-based sequent which is saturated with respect to all the left rules in C $\textbf{C}_{{\textbf {LIK}}}$. Take an arbitrary set of formulas, denoted as $\varGamma$. Let $\varOmega =\{T~|~T=S~or~T\in ^{[\cdot ]}S\}$. For each $T\in \varOmega$, we define $\mathfrak {G}_S(T,\varGamma )$, the $\in ^{[\cdot ]}$-based tracking record of $\varGamma$ in S, which is a subset of Ant(T) as follows:

• $\mathfrak {G}_S(S,\varGamma )=\varGamma \cap Ant(S)$;

• If $T\in ^{[\cdot ]}_0 T'$ for some $T'\in \varOmega$, let $\mathfrak {G}_S(T,\varGamma )$ be the minimal set such that

  • if $\square A\in \mathfrak {G}_S(T',\varGamma )$, then $A\in \mathfrak {G}_S(T,\varGamma )$;

  • if $\Diamond A\in \mathfrak {G}_S(T',\varGamma )$ and $A\in Ant(T)$, then $A\in \mathfrak {G}_S(T,\varGamma )$;

  • if $A\wedge B\in \mathfrak {G}_S(T,\varGamma )$, then $A,B\in \mathfrak {G}_S(T,\varGamma )$;

  • if $A\vee B\in \mathfrak {G}_S(T,\varGamma )$ and $A\in Ant(T)$, then $A\in \mathfrak {G}_S(T,\varGamma )$;

  • if $A\supset B\in \mathfrak {G}_S(T,\varGamma )$ and $B\in Ant(T)$, then $B\in \mathfrak {G}_S(T,\varGamma )$.

Tracking record is used to control rule applications to and within a block created by ($\text {inter}_{\downarrow }$), preserving the saturation condition associated to it.

Definition 20

(Realization). Let $S=\varGamma \Rightarrow \varDelta ,\langle S_1\rangle ,[S_2]$, where $S_1=\varSigma \Rightarrow \varPi ,[\varLambda \Rightarrow \varTheta ]$, $S_2= \ \Rightarrow _{\varLambda \Rightarrow \varTheta }\varTheta ^\sharp$ and $\varGamma \subseteq \varSigma$. Moreover, we assume that $S_1$ is saturated with respect to all the left rules in C $\textbf{C}_{{\textbf {LIK}}}$. Using the $\in ^{[\cdot ]}$-based tracking record of $\varGamma$ in $S_1$, we define the realization of the block $[S_2]$ in S as follows:

• (i). First for each $T\in ^+ S_2$, define the realization function $f_{S_1}(T)$. By definition, T is of the form $\Rightarrow _{\varPhi \Rightarrow \varPsi }\varPsi ^\sharp$ for some $\varPhi \Rightarrow \varPsi \in ^+\varLambda \Rightarrow \varTheta$. $f_{S_1}(T)$ is defined inductively on the structure of $\varPsi ^\sharp$ as follows:

  • if $\varPsi ^\sharp$ is block-free, then $f_{S_1}(T)=\mathfrak {G}(\varPhi \Rightarrow \varPsi ,\varGamma )\Rightarrow \varPsi ^\sharp$.

  • otherwise $\varPsi ^\sharp = \varPsi _0, [T_1], \ldots , [T_k]$ where $\varPsi _0$ is a set of formulas, then $f_{S_1}(T)=\mathfrak {G}(\varPhi \Rightarrow \varPsi ,\varGamma )\Rightarrow \varPsi _0, [f_{S_1}(T_1)], \ldots , [f_{S_1}(T_k)]$.

• (ii). With $f_{S_1}(S_2)$, the realization of $[S_2]$ in S is $\varGamma \Rightarrow \varDelta ,\langle S_1\rangle ,[f_{S_1}(S_2)]$.

As the next proposition shows the expansion produced by a realization procedure is not an additional logical step; rather, it can be obtained by applying the rules of the calculus while selecting the appropriate branch.

Proposition 7

Let $S=\varGamma \Rightarrow \varDelta ,\langle S_1\rangle ,[S_2]$, where $S_1=\varSigma \Rightarrow \varPi ,[\varLambda \Rightarrow \varTheta ]$ and $S_2= \ \Rightarrow _{\varLambda \Rightarrow \varTheta }\varTheta ^\sharp$ and $\varGamma \subseteq \varSigma$. If $S_1$ is saturated with respect to all the left rules in C $\textbf{C}_{{\textbf {LIK}}}$, then for the sequent $S'=\varGamma \Rightarrow \varDelta ,\langle S_1\rangle ,[f_{S_1}(S_2)]$ which is obtained by the realization procedure in Definition 20, we have

• (i). $S'$ is saturated with respect to all the left rules applied to or within $[f_{S_1}(S_2)]$;

• (ii). $f_{S_1}(S_2)\subseteq ^\textbf{S} \varLambda \Rightarrow \varTheta$;

• (iii). $S'$ can be obtained by applying left rules of C $\textbf{C}_{{\textbf {LIK}}}$ to $[S_2]$ in S.

Example 5

We go back to sequent (i’) in Example 4. Let

$$ \begin{array}{lll} S &{} = &{} \square (p\vee q)\Rightarrow \square r\supset \square s,\langle \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,p,r\Rightarrow s]\rangle ,[\Rightarrow s]\\ S_1 &{} = &{} \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,p,r\Rightarrow s]\\ S_2 &{} = &{} \ \Rightarrow s,\,T= p\vee q,p,r\Rightarrow s \end{array} $$

Since $[S_2]$ is produced by ($\text {inter}_{\downarrow }$) from T, we have $S_2=\ \Rightarrow _T s$. We are intended to realize the block $[S_2]$ in S by the tracking record of Ant(S) in $S_1$. By definition, we have

$$ \begin{array}{ll} \mathfrak {G}_{S_1}(S_1,Ant(S)) &{} = Ant(S)=\{\square (p\vee q)\}\\ \mathfrak {G}_{S_1}(T,Ant(S)) &{} = \{p\vee q,p\} \end{array} $$

According to realization, by applying $f_{S_1}(\cdot )$ to $S_2$, we get $f_{S_1}(\Rightarrow _{T} s)=p\vee q,p \Rightarrow s$. Thus, the entire output sequent is

$$ \square (p\vee q)\Rightarrow \square r\supset \square s,\langle \square (p\vee q),\square r\Rightarrow \square s,[p\vee q,p,r\Rightarrow s]\rangle ,[p\vee q,p\Rightarrow s] $$

And this is just (iii) in Example 4, which is the right expansion of (i’).

In order to define the proof-search procedure, we first divide all the rules of C $\textbf{C}_{{\textbf {LIK}}}$ into four groups as (R1): all propositional and modal rules except $(\supset _R)$; (R2): (trans) and $(\text {inter}_{\rightarrow })$; (R3): $(\supset _R)$; and (R4): $(\text {inter}_{\downarrow })$.

Let $S=\varGamma \Rightarrow \varDelta$, we denote by $\bar{\varDelta }$ the sequent obtained by removing all the (nested) occurrences of $\langle \cdot \rangle$-blocks in $\varDelta$.⁴

Definition 21

(Saturation). Let $S =\varGamma \Rightarrow \varDelta$ be a sequent and not an axiom. S is called:

• R1-saturated if $\varGamma \Rightarrow \bar{\varDelta }$ satisfies all the saturation conditions of R1 rules;

• R2-saturated if S is R1-saturated and S satisfies saturation conditions of R2 rules for blocks $\langle S_1\rangle ,[S_2]$ s.t. $S_1 \in ^{\langle \cdot \rangle }_0 S$ and $S_2 \in ^{[\cdot ]}_0 S$;

• R3-saturated if S is R2-saturated and S satisfies saturation conditions of R3 rules for formulas $A\supset B\in \varDelta$;

• R4-saturated S is R3-saturated and S satisfies saturation conditions of R4 rule for each implication block $\langle \varSigma \Rightarrow \varPi ,[S_1]\rangle$ s.t. $\varSigma \Rightarrow \varPi ,[S_1]\in ^{\langle \cdot \rangle }_0 S$.

Definition 22

(Global Saturation). Let S be a sequent and not an axiom. S is called global-Ri-saturated if for each $T\in ^+S$, T is Ri-saturated where $i\in \{1,2,3\}$; global-saturated if for each $T\in ^+S$, T is R4-saturated.

Algorithm 1:

$\text {PROC}_0(S_0)$

In order to specify the proof-search procedure, we make use of the following four macro-steps that extend a given derivation $\mathcal {D}$ by expanding a leaf S. Each procedure applies rules non-redundantly to some $T=\varGamma \Rightarrow \varDelta \in ^+S$.

• ${\textbf {EXP1}}(\mathcal {D}, S, T)= \mathcal {D}'$ where $\mathcal {D}'$ is the extension of $\mathcal {D}$ obtained by applying R1-rules to every formula in $\varGamma \Rightarrow \bar{\varDelta }$.

• ${\textbf {EXP2}}(\mathcal {D}, S, T)= \mathcal {D}'$ where $\mathcal {D}'$ is the extension of $\mathcal {D}$ obtained by applying R2-rules to blocks $\langle T_i\rangle ,[T_j]\in \varDelta$.

• ${\textbf {EXP3}}(\mathcal {D}, S, T)= \mathcal {D}'$ where $\mathcal {D}'$ is the extension of $\mathcal {D}$ obtained by applying R3-rules to formulas $A\supset B\in \varDelta$.

• ${\textbf {EXP4}}(\mathcal {D}, S)= \mathcal {D}'$ where $\mathcal {D}'$ is the extension of $\mathcal {D}$ obtained by applying (i) R4-rule to each implication block $T'\in ^+S$ and (ii) realization procedures to modal blocks produced in (i). This step extends $\mathcal {D}$ by a single branch whose leaf is denoted by $S'$.

It can be proved that each of these four macro-steps terminates. The claim is almost obvious except for ${\textbf {EXP1}}$ (see [2, Proposition 46]).

Proposition 8

Given a finite derivation $\mathcal {D}$, a finite leaf S of $\mathcal {D}$ and $T\in ^+S$, then for $i\in \{1,2,3,4\}$, each ${\textbf {EXPi}}(\mathcal {D}, S, T)$ terminates by producing a finite expansion of $\mathcal {D}$ where all sequents are finite.

Now we define the procedure. We first demonstrate the preliminary procedure $\text {PROC}_0(S_0)$ (see Algorithm 1)which builds a derivation with root $S_0$ and only uses the macro-steps ${\textbf {EXP1}}(\cdot )$ to ${\textbf {EXP3}}(\cdot )$, thus only the rules in $\textbf{C}_{{\textbf {LIK}}^-}$are applied. It follows that $\text {PROC}_0(A)$ decides whether a formula A is valid in LIK. Additionally, the procedure $\text {PROC}_0(\cdot )$ is then used as a subroutine in the full procedure $\text {PROC}(\Rightarrow A)$ to obtain either a proof of A or a global-saturated sequent, see Algorithm 2.

Proposition 9

Given a sequent $S_0$, $\mathrm{PROC_0}(S_0)$ produces a finite derivation with all the leaves axiomatic or at least one global-R3-saturated leaf.

Algorithm 2:

$\text {PROC}(A)$

Lastly, we show that $\text {PROC}(A)$ terminates.

Theorem 4

(Termination for C $\textbf{C}_{{\textbf {LIK}}}$). Proof-search for a formula A in C $\textbf{C}_{{\textbf {LIK}}}$ terminates with a finite derivation in which either all the leaves are axiomatic or there is at least one global-saturated leaf.

We can also obtain decision procedures for $\textbf{C}_{{\textbf {LIKD}}}$ and $\textbf{C}_{{\textbf {LIKT}}}$ in a similar way. Consider a cumulative version C $\textbf{C}_{{\textbf {LIKD}}}$ and C $\textbf{C}_{{\textbf {LIKT}}}$ of the respective calculi and define suitable saturation conditions associated the extra modal rules, for a sequent $S=\varGamma \Rightarrow \varDelta$:

The saturation condition for (D) prevents a useless generation of infinitely nested empty blocks of the form $[ \Rightarrow [\ldots \Rightarrow [ \Rightarrow ]\ldots ]]$, which can be created by the backward application of the (D)-rule. The procedure $\textrm{PROC}_0(\cdot )$ integrates the rules for (D) or (T)’s accordingly: the rule (D) is applied immediately after each round of ${\textbf {EXP2}}(\cdot )$ while the two (T) rules are integrated in ${\textbf {EXP1}}(\cdot )$. As a result, we can obtain:

Theorem 5

(Termination for C $\textbf{C}_{{\textbf {LIKD}}}$ and C $\textbf{C}_{{\textbf {LIKT}}}$). Proof-search for a formula A in C $\textbf{C}_{{\textbf {LIKD}}}$ and C $\textbf{C}_{{\textbf {LIKT}}}$ terminates with a finite derivation in which either all the leaves are axiomatic or there is at least one global-saturated leaf.

5 Completeness

Using the decision procedure from the previous section, we show how to build a countermodel for an unprovable formula, which entails the completeness of C $\textbf{C}_{{\textbf {LIK}}}$. Subsequently, we adapt this construction to C $\textbf{C}_{{\textbf {LIKD}}}$ and C $\textbf{C}_{{\textbf {LIKT}}}$ as well.

Given a global-saturated sequent S in C $\textbf{C}_{{\textbf {LIK}}}$, we define a model $\mathcal {M}_S$ for it as below.

Definition 23

The model $\mathcal {M}_S=(W_S,\le _S,R_S,V_S)$ is a quadruple where

- $W_S=\{x_{\varPhi \Rightarrow \varPsi }~|~\varPhi \Rightarrow \varPsi \in ^+S\}$;

- $x_{S_1}\le _S x_{S_2}$ if $S_1\subseteq ^{\textbf{S}} S_2$;

- $R_Sx_{S_1}x_{S_2}$ if $S_2\in ^{[\cdot ]}_0S_1$;

- for each $p\in \textbf{At}$, let $V_S(p)=\{x_{\varPhi \Rightarrow \varPsi }~|~p\in \varPhi \}$.

Proposition 10

$\mathcal {M}_S$ satisfies (FC) and (DC).

Lemma 8

(Truth Lemma for C $\textbf{C}_{{\textbf {LIK}}}$). Let S be a global-saturated sequent in C $\textbf{C}_{{\textbf {LIK}}}$ and $\mathcal {M}_{S}=(W_S,\le _S,R_S,V_S)$ defined as above. (a). If $A\in \varPhi$, then $\mathcal {M}_{S},x_{\varPhi \Rightarrow \varPsi }\Vdash A$; (b). If $A\in \varPsi$, then $M_{S},x_{\varPhi \Rightarrow \varPsi }\nVdash A$.

By the truth lemma we obtain as usual the completeness of C $\textbf{C}_{{\textbf {LIK}}}$.

Theorem 6

(Completeness of C $\textbf{C}_{{\textbf {LIK}}}$). If A is valid in LIK, then A is provable in $\textbf{C}_{{\textbf {LIK}}}$.

Example 6

We show how to build a countermodel for the formula $(\Diamond p \supset \Box q) \supset \Box (p \supset q)$ which is not provable in C $\textbf{C}_{{\textbf {LIK}}}$. Ignoring the first step, we initialize the derivation with $\Diamond p \supset \Box q \Rightarrow \Box (p \supset q)$. By backward application of rules, one branch of the derivation ends up with the following saturated sequent

$$ S_0=\Diamond p\supset \square q\Rightarrow \square (p\supset q),\Diamond p,[\Rightarrow p\supset q,p,\langle p\Rightarrow q\rangle ] $$

and we further let $S_1= \ \Rightarrow p\supset q,p,\langle p\Rightarrow q\rangle$ while $S_2=p\Rightarrow q$. We then get the model $M_{S_0} = (W, \le , R, V)$ where

• $W=\{x_{S_0}, x_{S_1}, x_{S_2} \}$;

• $x_{S_1} \le x_{S_2}, x_{S_0} \le x_{S_0}, x_{S_1} \le x_{S_1}, x_{S_2} \le x_{S_2}$;

• $Rx_{S_0}x_{S_1}$;

• $V(p)=\{x_{S_2}\}$ and $V(q)=\varnothing$.

It is easy to see that $x_{S_0} \not \Vdash (\Diamond p \supset \Box q) \supset \Box (p \supset q)$.

Next, we consider the completeness of C $\textbf{C}_{{\textbf {LIKD}}}$ and C $\textbf{C}_{{\textbf {LIKT}}}$. We consider the model $\mathcal {M}_S=(W_S,\le _S,R_S,V_S)$ for a global-saturated sequent S in either calculi, where $W_S,\le _S$ and $V_S$ as in Definition 23, $R_S$ modified as follows:

• For C $\textbf{C}_{{\textbf {LIKD}}}$: $R_Sx_{S_1}x_{S_2}$ if $S_2\in ^{[\cdot ]}_0S_1$ or $Suc(S_1)$ is $[\cdot ]$-free and $x_{S_1} = x_{S_2}$;

• For C $\textbf{C}_{{\textbf {LIKT}}}$: $R_Sx_{S_1}x_{S_2}$ if $S_2\in ^{[\cdot ]}_0S_1$ or $x_{S_1} = x_{S_2}$.

Trivially the relation $R_S$ is serial or reflexive according to $\textbf{C}_{{\textbf {LIKD}}}$ or $\textbf{C}_{{\textbf {LIKT}}}$, moreover models for C $\textbf{C}_{{\textbf {LIKD}}}$ and C $\textbf{C}_{{\textbf {LIKT}}}$ still satisfy (FC) and (DC). Finally,

Theorem 7

(Completeness of C $\textbf{C}_{{\textbf {LIKD}}}$ and C $\textbf{C}_{{\textbf {LIKT}}}$). If A is valid in LIKD (resp. LIKT), then A is provable in C $\textbf{C}_{{\textbf {LIKD}}}$ (resp. C $\textbf{C}_{{\textbf {LIKT}}}$).

6 Conclusion

We studied LIK, the basic intuitionistic modal logic with locally defined modalities as well as some of its extensions. In further research, we intend to investigate both axiomatizations and calculi of extensions to the whole modal cube. For instance, we would like to provide a (terminating) calculus for the S4 extension of LIK (the logic is studied in [1]). Since LIK is incomparable with IK, we may also wonder what the “super” intuitionistic modal logic obtained by combining both is. Our broader goal is to establish a framework of axiomatization and uniform calculi for a wide range of IMLs, including other natural variants that have been little studied or remain entirely unexplored so far.