Abstract
The top-down solver (TD) is a local fixpoint algorithm for arbitrary equation systems. It considers the right-hand sides as black boxes and detects dependencies between unknowns on the fly—features that significantly increase both its usability and practical efficiency. At the same time, the recursive evaluation strategy of the TD, combined with the non-local destabilization mechanism, obfuscates the correctness of the computed solution. To strengthen the confidence in tools relying on the TD as their fixpoint engine, we provide a first machine-checked proof of the partial correctness of the TD. Our proof builds on the observation that the TD can be obtained from a considerably simpler recursive fixpoint algorithm, the plain TD, by applying an optimization that neither affects the termination behavior nor the computed result. Accordingly, we break down the proof into a partial correctness proof of the plain TD, which is only then extended to include the optimization. The backbone of our proof is a mutual induction following the solver’s computation trace. We establish sufficient invariants about the solver state to conclude the correctness of its optimization, i.e., the plain TD terminates if and only if the TD terminates, and they return the identical result. The proof is written using Isabelle/HOL and is available in the archive of formal proofs.
Y. Stade and S. Tilscher—Contributed equally to this research and are ordered alphabetically.
You have full access to this open access chapter, Download conference paper PDF
Keywords


1 Introduction
Fixpoint engines are at the heart of static program analyzers based on abstract interpretation [9]. An analysis introduces a set of unknowns and a domain of abstract values, which encode the properties of interest. Consider, e. g., the analysis of uninitialized variables as used by Java [13] or Kotlin [1]. Here, the unknowns are program points, while the abstract values are sets of local variables that have been initialized. The abstract value of an unknown may depend on the abstract values of preceding program points. These dependencies are formalized as an equation \(\textrm{x} = f_{\textrm{x}}\). The right-hand side \(f_{\textrm{x}}\) is the intersection of all sets of definitely initialized variables arriving at \(\textrm{x}\) via incoming edges. Such an incoming edge may be an assignment like \(\mathtt {a = 5}\), which adds the variable \(\texttt{a}\) to the set of initialized unknowns. Accordingly, the analysis of the program compiles it into a system of equations, cf. Example 1. A solution to this system approximates the concrete set of initialized variables when reaching a program point.
Solutions of equation systems can be computed using fixpoint iteration. Popular fixpoint algorithms are round-robin [14] and worklist iteration [20]. Both algorithms, though, have limitations. Round-robin iteration requires a fixed finite equation system; also, its running time depends on the evaluation order of unknowns. Worklist iteration is generally more efficient but, at least in the base setting, also suffers from the restriction that the dependencies between unknowns must be known beforehand. The latter short-coming is overcome by Vergauwen et al. [29], de Vilhena et al. [30] where the evaluation of right-hand side functions is enhanced with self-observation to dynamically detect the dependencies. More enhanced solvers recursively descend into queried unknowns to obtain their best values before the evaluation of a right-hand side proceeds. One instance of the latter is the recursive local descent solver (RLD) [16]. The unknowns, affected by an updated value, are collected in a local worklist for immediate re-evaluation.
This is in contrast to the top-down solver (TD) [21, 22, 28]. Like RLD, it relies on a recursive descent into queried unknowns combined with dynamic detection of dependencies. However, when an unknown changes its value, the influenced unknowns are not immediately scheduled for re-evaluation. Instead, all transitively influenced unknowns are marked as unstable so that, when queried again, their re-evaluation is triggered. The destabilization mechanism, combined with the delayed re-evaluation, potentially further increases the efficiency of the iteration but also obfuscates the correctness of the TD. Still, due to its conceptual simplicity, the TD opens possibilities for extensions, e.g., with widening and narrowing [4, 9, 10, 28] or side-effects [26], which otherwise are not so easy to incorporate [3]. This is one of the reasons why tools like the Ciao system [15] or Goblint [31] rely on variants of the TD as fixpoint engines. To strengthen the confidence in these tools, we formalize the TD with the interactive theorem prover Isabelle [24, 25] and prove it to be partially correct. Here, partial correctness means that assuming the TD terminates, it returns a partial solution of the equation system.
To accomplish the proof, we build on the observation [28] that the original TD, which we will also call TD for short, can be obtained from a significantly simpler fixpoint algorithm that we call the plain TD. The plain TD still uses a recursive descent into queried unknowns while using a set called to avoid infinite descent due to unknowns with cyclic dependencies. However, it neither keeps track of dependencies between unknowns nor maintains a set of stable unknowns whose value has already been computed. Adding these features to obtain the TD thus can be seen as an optimization of the plain TD. Accordingly, the proof is structured into two steps: In the first step, we show the partial correctness of the plain TD. As this algorithm consists of several mutually recursive functions, the proof consists of a mutual induction. To make the proof more comprehensible, we utilize the concept of a computation trace to explain its structure and to highlight important invariants. In the second step, the invariants of the plain TD are extended to obtain invariants for the TD. The extensions cover the correctness and modifications of the additional data structures that collect the already computed stable unknowns and the dependencies between unknowns. Additional effort is required to capture the effect of the non-local destabilization mechanism on those two data structures. Altogether, we prove that the TD and the plain TD are equivalent, i.e., the TD terminates if and only if the plain TD terminates and returns the same result whenever they terminate.
For our formalization, we use the function package with domain predicates and mutual recursion to define the solver algorithms in Isabelle. This allows for a clean proof structure. The combination of features is, however, not supported by the code generation framework provided by Isabelle. To obtain executable solver programs from our formalization we, therefore, refine the programs and use equivalent versions of the solver algorithms based on partial functions with options for the code generation. We extract executable code for both solvers and demonstrate their application on a small example. The formalization in Isabelle/HOL is publicly available in the archive of formal proofs [27].
2 Preliminaries
We first introduce some notation used throughout the paper. The powerset of a set \(M\) is denoted by \(\mathcal {P}\left( M\right) \), and the set difference of two sets \(A\) and \(B\) is written as \(A - B\). Given a mapping \(f:X\rightarrow Y\), the updated mapping \(f\oplus \left\{ x\mapsto y \right\} :X\rightarrow Y\) is defined by \(\left( f\oplus \left\{ x\mapsto y \right\} \right) \,x=y\) and \(\left( f\oplus \left\{ x\mapsto y \right\} \right) \,x'=f\,x'\) for all \(x'\ne x\). For a mapping \(f:X\rightarrow \mathcal {P}\left( X\right) \), the transitive closure is the mapping \(f^+:X\rightarrow \mathcal {P}\left( X\right) \) where \(f^+\,x\) is the minimal set such that \(f\,x\subseteq f^+\,x\) and \(f\,y\subseteq f^+\,x\) for all \(y\in f^+\,x\). Moreover, the reflexive and transitive closure is the mapping \(f^*:X\rightarrow \mathcal {P}\left( X\right) \) where \(f^*\,x\) is defined as \(f^*\,x:=\left\{ x \right\} \,\cup \,f^+\,x\).
For the remainder of this article, we consider some (possibly infinite) set \(\mathcal {U}\) of unknownsFootnote 1 and a domainFootnote 2 \(\mathbb {D}\) of abstract values. The set \(\mathbb {D}\) contains one special element \(\bot \) (bottom), used as the initial value for the fixpoint iteration. Elements from \(\mathbb {D}\) need to be comparable for equality, but there is no need to require a partial order or existence of least upper bounds. The equation system associates each unknown \(\textrm{x}\) (the left-hand side) with a right-hand side function \(f_{\textrm{x}}\), specifying other unknowns’ contribution to the left-hand side \(\textrm{x}\). Following Fecht and Seidl [11], the right-hand side function \(f_{\textrm{x}}\) is considered as a black box functional. The only requirement is that the right-hand side is pure [17], i. e., parametric in the solver state. That limitation has slightly been relaxed by de Vilhena et al. [30] to apparent purity, which allows functions to have internal side effects, e. g., logging important events or spawning a new thread—as long as two identical calls of a function return the same result. Here, we stick to the original notion of purity. For pure functionals in that sense, Hofmann et al. [17] prove that they can be represented as strategy trees. A strategy tree is composed of \(\texttt{Answer}\) nodes, the leaves of the tree, containing an element of \(\mathbb {D} \), and \(\texttt{Query}\) nodes that contain an unknown \(\textrm{y}\) to be queried together with a function g. Based on the value \(d_{\textrm{y}}\) of the queried unknown \(\textrm{y}\), the call \(g\,d_{\textrm{y}}\) returns the subtree to continue the evaluation of the right-hand side. In this work, we assume the depth of strategy trees to be finite, i.e., only finitely many unknowns may be queried in a right-hand side. As a shorthand, we write
 when evaluating the strategy tree
when evaluating the strategy tree

 using the mapping \(\sigma \).
using the mapping \(\sigma \).

Note that the strategy trees can describe right-hand sides with varying dependencies, which the TD can cope with. Further, their tree representation lends itself to a structural induction on the right-hand sides. A system of equations \(\mathcal {T}\) is then formally the function
that maps every unknown in \(\mathcal {U}\) to a strategy tree.
Example 1
Consider the following code snippet and the corresponding control-flow graph, where \(\texttt{a}\) and \(\texttt{b}\) are local program variables.

The domain for the variable initialization analysis is \(\mathbb {D} =\mathcal {P}\left( \left\{ \texttt{a},\texttt{b} \right\} \right) \), with \(\bot \) being the complete set \(\left\{ \texttt{a}, \texttt{b} \right\} \) and \(\top \) the empty set. A variable is added to the set of initialized variables whenever it occurs on the left-hand side of an assignment. Accordingly, we retrieve the following equation system and show its strategy tree representation in Fig. 1:
The figure shows the value table of \(\mathcal {T}\) from Example 1. Each unknown maps to a strategy tree with query nodes (Q) and answer nodes (A). The trees are defined over the domain \(\mathcal {P}\left( \left\{ a,b \right\} \right) \) where \(\bot \) represents the full set \(\left\{ a, b \right\} \) and \(\top \) the empty set.
For the remaining part, we fix some system of equations \(\mathcal {T}\) and assume that it is globally available. A total solution of such a system of equations is a mapping \(\sigma :\mathcal {U} \rightarrow \mathbb {D} \) from unknowns to values such that for all unknowns \(\textrm{x} \in \mathcal {U} \)
However, we are often not interested in a solution for the entire (potentially infinite) equation system, but rather in a partial solution. For an unknown \(\textrm{x} \in \mathcal {U} \) and a mapping \(\sigma :\mathcal {U} \rightarrow \mathbb {D} \), let the function \({\textsf{dep}} \,\textrm{x} \,\sigma \) return the set of all unknowns occurring in \(\mathcal {T} \,\textrm{x} \) when traversed with \(\sigma \), the so-called (direct) dependencies of \(\textrm{x}\). Then, the mapping \(\sigma :\mathcal {U} \rightarrow \mathbb {D} \) is a partial solution for a set \(s\subseteq \mathcal {U} \) ifFootnote 3

If \(\textrm{x}\) is in \({\textsf{dep}} ^+\textrm{x} \;\sigma \) for some \(\sigma \), i. e., the unknown \(\textrm{x}\) depends transitively on itself, we call the associated system of equations \(\mathcal {T} \) recursive (with respect to \(\sigma \)). In the proof, we argue about the subset of
 composed of all unknowns visited when solving some unknown \(\textrm{x}\). Such unknowns are reachable from \(\textrm{x}\) via the depends-relation without passing through (but including) unknowns of a set \(X\), where the recursive descent stops. Hence, we define the set \(R_X\) inductively for a given mapping \(\sigma :\mathcal {U} \rightarrow \mathbb {D} \) and an unknown \(\textrm{x}\) to contain all unknowns in \({\textsf{dep}} \,\sigma \;\textrm{x} \) if \(\textrm{x} \notin X\), and all unknowns in \({\textsf{dep}} \,\sigma \,\textrm{y} \) if \(\textrm{y} \in R_X-X\). We denote \(R_X\) by
composed of all unknowns visited when solving some unknown \(\textrm{x}\). Such unknowns are reachable from \(\textrm{x}\) via the depends-relation without passing through (but including) unknowns of a set \(X\), where the recursive descent stops. Hence, we define the set \(R_X\) inductively for a given mapping \(\sigma :\mathcal {U} \rightarrow \mathbb {D} \) and an unknown \(\textrm{x}\) to contain all unknowns in \({\textsf{dep}} \,\sigma \;\textrm{x} \) if \(\textrm{x} \notin X\), and all unknowns in \({\textsf{dep}} \,\sigma \,\textrm{y} \) if \(\textrm{y} \in R_X-X\). We denote \(R_X\) by

Note that
 holds. We extend the definitions of \({\textsf{dep}}\) and
holds. We extend the definitions of \({\textsf{dep}}\) and
 to strategy trees and use the same symbol for simplicity. This allows to compute both sets also for partial right-hand sides.
to strategy trees and use the same symbol for simplicity. This allows to compute both sets also for partial right-hand sides.
3 The Plain Top-Down Solver
The TD can be obtained from a considerably simpler fixpoint algorithm [28], which we call the plain TD. First, we prove the plain TD to be partially correct; second, we extend this proof to the original TD. Tilscher et al. [28], consider an even simpler version of the TD, the monadic base solver. It is, however, not as powerful as the TD since it does not track the set of called unknowns and thus cannot solve recursive equation systems. Therefore we excluded it from our layered approach.
The plain TD maintains a solver state that consists of the set of called unknowns \(\texttt{c}\) containing the unknowns that are already being evaluated, and a mapping \(\mathtt {\sigma }\) storing the current value of every unknown. The algorithm consists of three mutually recursive functions: \(\mathtt {iterate_{plain}}\), \(\mathtt {eval_{plain}}\), and \(\mathtt {query_{plain}}\). The function \(\mathtt {iterate_{plain}}\) iterates one unknown \(\textrm{x}\) until a fixpoint is reached for it, i. e., the newly computed value and the value from the previous iteration coincide. When the iteration continues because the value has changed, the mapping \(\sigma \) of unknowns to values is updated.

For the evaluation of \(\textrm{x}\) ’s right-hand side, the function \(\mathtt {eval_{plain}}\) is invoked. The function \(\mathtt {eval_{plain}}\) receives a right-hand side in the form of a strategy tree and traverses it top-down until reaching an answer node, whose value it returns.

The function \(\mathtt {query_{plain}}\) is called to determine the current value for \(\textrm{y}\) and thereby the subtree \(\mathtt {g\, d}\) in which to descend next, when \(\mathtt {eval_{plain}}\) is called for some query node \(\mathtt {Query\, y\, g}\). A call to \(\mathtt {query_{plain}}\) checks whether a call to \(\mathtt {query_{plain}}\) for the same unknown \(\textrm{y}\) already occurred in the current call stack. If this is the case, i. e., the unknown is contained in the set \(c\) of called unknowns, the current value of \(\textrm{y}\) is looked up in the mapping \(\sigma \). Otherwise, \(\mathtt {query_{plain}}\) invokes the function \(\mathtt {iterate_{plain}}\) with \(\textrm{y}\) added to \(c\) to start the fixpoint iteration for \(\textrm{y}\).

Finally, we have a function \(\mathtt {solve_{plain}}\) that wraps the initial call to \(\mathtt {iterate_{plain}}\) and provides it with the initial arguments, the singleton set \(\left\{ \textrm{x} \right\} \) as called unknowns, and the empty mapping
 that implicitly maps every unknown to \(\bot \).
that implicitly maps every unknown to \(\bot \).

A computation trace captures the execution of a solver’s run. It is a tree that contains a node for each function call, along with essential parameters and result values. The \(\mathtt {solve_{plain}}\) node constitutes its root node. Nested calls to other functions are added as children, while recursive calls (to the same function) are appended to the right as siblings.Footnote 4 In Figs. 2 and 4, we omit \(\mathtt {eval_{plain}}\) nodes for clarity since they essentially only add an intermediate node between \(\mathtt {iterate_{plain}}\) and \(\mathtt {query_{plain}}\) nodes. The backbone of the partial correctness proof is an induction over this computation trace, which can be conveniently implemented with the induction rules generated by Isabelle for the mutually recursive functions. The concept of a computation trace is illustrated in the following example.
Example 2
Consider the equation system from Example 1. We observe the execution of the TD when solving the unknown \(\textrm{z}\) and illustrate the occurring mutually recursive function calls as computation trace in Fig. 2.
The initial call \(\mathtt {solve_{plain}\,z}\) invokes the function \(\mathtt {iterate_{plain}}\) to iterate on the queried unknown \(\textrm{z}\). In \(\textrm{z}\) ’s first iteration, the call to \(\mathtt {eval_{plain}}\) queries the unknowns \(\textrm{y}\) and \(\textrm{w}\) to fully traverse the right-hand side of \(\textrm{z}\). The querying of \(\textrm{y}\) entails a call to \(\mathtt {iterate_{plain}}\) for its iteration which takes only one turn to stabilize. The evaluation of \(\textrm{y}\) ’s right-hand side only depends on the unknown \(\textrm{z}\), for which the call to \(\mathtt {query_{plain}}\) immediately returns since \(\textrm{z}\) is already being evaluated. The iteration of \(\textrm{w}\) entails no further queries because the strategy tree representing its right-hand side is an answer node.
The figure shows the computation trace of the plain TD for solving the unknown \(\textrm{z}\) from the equation system from Example 1. In dark, we highlight the function calls corresponding to unknowns in
 where \(\sigma \) is the final result. (Color figure online)
where \(\sigma \) is the final result. (Color figure online)
The computation trace reveals the information available during the solver’s computations. When the algorithm reaches a node \(v\) in the computation trace, (computations of) all nodes on the path to the root are in progress, and nodes in subtrees on the left of this path are already completed; we call this history the reaching left-context of \(v\). The solver’s state, i. e., the internal data structures maintained by the solver, can be seen as an abstraction of the (concrete) left-context. Since the algorithm always refers to the latest abstraction of the solver state, it could also be implemented as a reference to a mutable data structure.
For a subtree
 of the computation trace and \(\sigma '\) returned by the corresponding function call, the set
of the computation trace and \(\sigma '\) returned by the corresponding function call, the set

 \(\sigma '\) matches the unknowns occurring in the last iterations of
\(\sigma '\) matches the unknowns occurring in the last iterations of
 . Based on this, we introduce a set \(s\) that is an abstraction of the reaching left-context: it collects the unknowns of the last iterations in the reaching left-context, and unknowns under evaluation. A re-evaluation of \(\textrm{x} \in s\) returns the same value already stored in \(\sigma \) for \(\textrm{x}\). This holds specifically for unknowns in \(c\), a subset of \(s\), because the algorithm looks up their value instead of initiating a new iteration. Unknowns in \(s -c\) re-evaluate to the same value because they only depend on unknowns in \(s\); hence, we call them truly stable. Accordingly, the two milestones for proving the correctness of the plain TD are:
. Based on this, we introduce a set \(s\) that is an abstraction of the reaching left-context: it collects the unknowns of the last iterations in the reaching left-context, and unknowns under evaluation. A re-evaluation of \(\textrm{x} \in s\) returns the same value already stored in \(\sigma \) for \(\textrm{x}\). This holds specifically for unknowns in \(c\), a subset of \(s\), because the algorithm looks up their value instead of initiating a new iteration. Unknowns in \(s -c\) re-evaluate to the same value because they only depend on unknowns in \(s\); hence, we call them truly stable. Accordingly, the two milestones for proving the correctness of the plain TD are:
- (i):
-
defining the set
 to describe the set of unknowns queried in the last iterations for a subtree of the computation trace, and
to describe the set of unknowns queried in the last iterations for a subtree of the computation trace, and - (ii):
-
introducing the set \(s\) to collect unknowns that, when re-evaluated, evaluate to the same value.
Milestone (ii) is essential to ensure that the plain TD computes the same value for recurring occurrences of an unknown in a right-hand side.
For unknowns in \(s\) we show that \(\sigma \) is a partial solution after updating the value for the current unknown in \(\mathtt {iterate_{plain}}\).
Lemma 1
Assume \(\sigma \) is a partial solution for all \(\textrm{x} \in s-c\), the set \(s\) is closed under \({\textsf{dep}}\) except for elements that are in \(c\), i. e., \(\forall \textrm{y} \in s-c,\,{\textsf{dep}} \,\sigma \,\textrm{y} \subseteq s\), and \(\sigma \) and \(\sigma '\) are identical on \(s\), i. e., \(\forall \textrm{x} \in s.\,\sigma \,\textrm{x} =\sigma '\,\textrm{x} \). Then, \(\sigma '\) is also a partial solution for all \(\textrm{x} \in s-c\).
Recall that \(\sigma \) is a partial solution of all unknowns in the set \(s\). Within the \(\mathtt {iterate_{plain}}\) function, when the newly computed value for an unknown \(\textrm{x}\) and its old value stored in \(\sigma \) differ, we can conclude that \(\textrm{x}\) was not a member of \(s\) because the old \(\sigma \) would not have been a partial solution.
Lemma 2
Assume \(\mathcal {T} \,\textrm{x} \,\sigma \ne \sigma \,\textrm{x} \) and \(\sigma \) is a partial solution of all unknowns in a set \(s\). Then, \(\textrm{x}\) is not a member of \(s\).
The following definition summarizes the properties used as invariant for the partial correctness proof in one predicate.
Definition 1
(Plain TD Invariant). For \(c,s\subseteq \mathcal {U} \) and the mapping \(\sigma :\mathcal {U} \rightarrow \mathbb {D} \) the predicate \({\textsf{valid}_\textrm{plain}} \,c\,s\,\sigma \) is satisfied if
-
(i)
\(\forall \textrm{x} \in s-c.\,{\textsf{dep}} \,\sigma \,\textrm{x} \subseteq s\), i. e., the set \(s\) is closed under \({\textsf{dep}}\) except for unknowns that are also in \(c\), and
-
(ii)
\(\forall \textrm{x} \in s-c.\,\mathcal {T} \,\textrm{x} \,\sigma = \sigma \,\textrm{x} \), i. e., \(\sigma \) fulfills the equations for truly stable unknowns.
For \(c=\emptyset \), which holds after a call to \(\mathtt {solve_{plain}}\) terminated, the predicate implies that \(\sigma \) is a partial solution for \(s\). Using the predicate, we formulate the partial correctness theorem.
Theorem 1
(Partial Correctness of the plain TD). The theorem shows three mutual statements:
-
Assume \(\mathtt {query_{plain}} \,\,\textrm{x} \,\,\textrm{y} \,\,c\,\sigma =\left( d_{\textrm{y}}, \sigma '\right) \) is defined and \({\textsf{valid}_\textrm{plain}} \,\,c\,\,s\,\,\sigma \) holds. Then, we show (i) \({\textsf{valid}_\textrm{plain}} \,c\,s'\,\sigma '\), and (ii) \(\forall \textrm{u} \in s.\,\sigma \,\textrm{u} =\sigma '\,\textrm{u} \) where

-
Let \(c'=c-\left\{ x \right\} \). Assume \(\mathtt {iterate_{plain}} \,\textrm{x} \,c\,\sigma =\left( d_{\textrm{x}}, \sigma '\right) \) is defined, \(\textrm{x} \in c\), and \({\textsf{valid}_\textrm{plain}} \,c'\,s\,\sigma \) holds. Then, we show (i) \({\textsf{valid}_\textrm{plain}} \,c'\,s'\,\sigma '\), and (ii) \(\forall \textrm{u} \in s.\,\sigma \,\textrm{u} =\sigma '\,\textrm{u} \) where
 .
. -
Assume
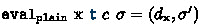 is defined, and \({\textsf{valid}_\textrm{plain}} \,\,c\,\,s\,\,\sigma \) holds. Then, we show (i) \({\textsf{valid}_\textrm{plain}} \,c\,s'\,\sigma '\), (ii) \(\forall \textrm{u} \in s.\,\sigma \,\textrm{u} =\sigma '\,\textrm{u} \), and (iii)
is defined, and \({\textsf{valid}_\textrm{plain}} \,\,c\,\,s\,\,\sigma \) holds. Then, we show (i) \({\textsf{valid}_\textrm{plain}} \,c\,s'\,\sigma '\), (ii) \(\forall \textrm{u} \in s.\,\sigma \,\textrm{u} =\sigma '\,\textrm{u} \), and (iii)
 where
where
 .
.
The figure illustrates exemplary for the Continue subcase in the Iterate case an induction step. First, the induction hypothesis (IH) for the nested \(\mathtt {query_{plain}}\) is instantiated, such that its premises are fulfilled. Its application then provides facts to reason that the premises of the IH for the recursive \(\mathtt {iterate_{plain}}\) call are satisfied.
Proof
This proof is more of a sketch to convey the proof idea; for a rigorous proof, see the Isabelle formalization [27]. We prove the statement by mutual induction. The induction rule derived from the three mutually recursive functions leads to three cases. Figure 3 illustrates an induction step in the computation trace exemplary for the iterate case.
Case 1
(Query). The first case reasons about a call to the \(\mathtt {query_{plain}}\) function. Let \(\textrm{x},\textrm{y} \in \mathcal {U},c\subseteq \mathcal {U},\sigma ,\sigma ':\mathcal {U} \rightarrow \mathbb {D} \), and \(d_{\textrm{y}}\in \mathbb {D} \) such that \(\mathtt {query_{plain}} \,\textrm{x} \,\textrm{y} \,c\,\sigma =\left( d_{\textrm{y}},\sigma '\right) \) is defined. We distinguish two subcases: the queried unknown can either be called or not, the former leading to a lookup and the latter to an iteration.
Subcase 1.1
(Lookup). This case is a base case since there are no further mutual recursive calls. In the computation trace, it corresponds to a query node as leaf. The proof goal follows directly from the premises since \(\sigma \) is not changed.
Subcase 1.2
(Iterate). In this case, the function \(\mathtt {iterate_{plain}}\) is called, and its result directly returned by the enclosing \(\mathtt {query_{plain}}\) function. Thus, \(\mathtt {iterate_{plain}} \textrm{y} \,\left( c\,\cup \,\left\{ \textrm{y} \right\} \right) \,\sigma =\left( d_{\textrm{y}},\sigma '\right) \) and the induction hypothesis for the \(\mathtt {iterate_{plain}}\) call can be applied. The proof goal follows immediately because the result of the call to \(\mathtt {iterate_{plain}}\) is returned without modifications.
Case 2
(Iterate). Let \(c\subseteq \mathcal {U},\textrm{x} \in c,\sigma ,\sigma ':\mathcal {U} \rightarrow \mathbb {D} \), and \(d_{\textrm{x}}\in \mathbb {D} \) such that \(\mathtt {iterate_{plain}} \,\textrm{x} \,c\,\sigma =\left( d_{\textrm{x}},\sigma '\right) \) is defined. We distinguish two subcases: either a fixpoint is reached or not. In either case, the function \(\mathtt {eval_{plain}}\) is invoked first, and the subcase depends on its result. Both subcases constitute two different induction steps, and both cases use the induction hypothesis for \(\mathtt {eval_{plain}}\).
Subcase 2.1
(Fixpoint). The induction hypothesis of \(\mathtt {eval_{plain}}\) provides all necessary facts, and since \(\sigma \) is not updated anymore, the proof goal follows.
Subcase 2.2
(Continue). Obtain \(d_{\textrm{x}}'\in \mathbb {D} \) and \(\sigma _1:\mathcal {U} \rightarrow \mathbb {D} \) such that the call \(\mathtt {eval_{plain}} \,\,{\textrm{x}}\,\left( \mathcal {T} \,\textrm{x} \right) \,c\,\sigma =\left( d_{\textrm{x}}',\sigma _1\right) \) is defined. The induction hypothesis for \(\mathtt {eval_{plain}}\) states (i) \({\textsf{valid}_\textrm{plain}} \,\,s'\,\,c\,\,\sigma _1\), (ii) \(\forall \textrm{y} \in s\,\cup \,\left\{ \textrm{x} \right\} .\,\sigma \,\textrm{y} =\sigma _1\,\textrm{y} \), and (iii) \(\mathcal {T} \,\textrm{x} \, \,\sigma _1=d_{\textrm{x}}'\) where
 . Since we are in the Continue case, we know that \(\sigma _1\,\textrm{x} \ne d_{\textrm{x}}'\). From Lemma 2 it follows \(\textrm{x} \notin s\). This allows us to show together with Lemma 1 that also \({\textsf{valid}_\textrm{plain}} \,s\,\left( c-\left\{ \textrm{x} \right\} \right) \left( \sigma _1\oplus \left\{ \textrm{x} \mapsto d_{\textrm{x}}' \right\} \right) \) holds. This is required to instantiate the induction hypothesis for the successive call to \(\mathtt {iterate_{plain}}\), which concludes the case.
. Since we are in the Continue case, we know that \(\sigma _1\,\textrm{x} \ne d_{\textrm{x}}'\). From Lemma 2 it follows \(\textrm{x} \notin s\). This allows us to show together with Lemma 1 that also \({\textsf{valid}_\textrm{plain}} \,s\,\left( c-\left\{ \textrm{x} \right\} \right) \left( \sigma _1\oplus \left\{ \textrm{x} \mapsto d_{\textrm{x}}' \right\} \right) \) holds. This is required to instantiate the induction hypothesis for the successive call to \(\mathtt {iterate_{plain}}\), which concludes the case.
Case 3
(Eval). The strategy tree passed to \(\mathtt {eval_{plain}}\) can either be a single answer node or a non-trivial strategy tree with a query node as a root.
Subcase 3.1
(Answer). This case is the second induction base of the entire induction and follows trivially.
Subcase 3.2
(Query). The proof follows from the facts retrieved from the induction hypotheses for both recursive calls to \(\mathtt {query_{plain}}\) and \(\mathtt {eval_{plain}}\) using the fact that \(\sigma \) remains unchanged for unknowns in \(s\). \(\square \)
The corollary below summarizes the results from this section. It follows directly from Theorem 1.
Corollary 1
(Partial Correctness of the plain TD). Assume the equality \(\mathtt {solve_{plain}} \,\textrm{x} =\sigma \) is defined. Then, \(\sigma \) is a partial solution for
 .
.
4 The Top-Down Solver
So far, we have proven partial correctness only for the plain TD. In the following, we extend the correctness statement to the original TD by showing that both fixpoint algorithms are equivalent. The TD improves the plain TD through more extensive self-observation. While the plain TD solely maintains a set of called unknowns to prevent non-termination in the case of recursive equation systems, the TD introduces two additional data structures for self-observation:
-
A set \({\texttt{stable}}\) collecting all unknowns that do not need to be re-evaluated, because they only depend on other stable unknowns whose value has not changed since their last evaluation.
-
An \({\texttt{infl}}\) map that dynamically records for each unknown \(\textrm{x}\) a set of unknowns influenced by \(\textrm{x}\). It, therefore, records the inverse of the \({\textsf{dep}}\) relationship.
The set \({\texttt{stable}}\) is similar to set \(s\) used in the proof of the plain TD; and indeed, \(s\) is in every step a subset of \({\texttt{stable}}\). However, \({\texttt{stable}}\) additionally collects unknowns that have been fully evaluated in earlier iterations but are not affected by any unknowns whose value changed in the meantime. Its additional maintenance allows skipping unnecessary re-evaluations of already stable unknowns.
Three modifications are necessary to integrate the new data structures and to keep them consistent. In the following code snippets, we highlight those changes. The function \(\texttt{eval}\) is only adapted marginally to facilitate the passing of the additional parameters (not highlighted).

At the end of a call to \(\texttt{query}\), the dependency is recorded in the map \({\texttt{infl}}\), i. e., the parent unknown is inserted into the set of unknowns influenced by the queried unknown.

The improvement to skip re-evaluations of unknowns in \({\texttt{stable}}\) is implemented in the function \(\texttt{iterate}\). If \(\texttt{iterate}\) is invoked for an unknown that is already in \({\texttt{stable}}\), its right-hand side is not evaluated; instead, its value is simply looked up in \(\sigma \). In case the current unknown is not yet stable, it is optimistically added to the set \({\texttt{stable}}\) when starting the evaluation of its right-hand side.

After the evaluation of the right-hand side of \(\textrm{x}\), \(\mathtt {iterate\; x}\) updates the value of \(\textrm{x}\) in \(\sigma \). If the value has changed, the values of unknowns that are (indirectly) influenced by \(\textrm{x}\) need to be recomputed. Instead of recomputing them immediately, all affected unknowns are removed from \({\texttt{stable}}\). This will trigger their re-evaluation in case they are queried again. To remove all indirectly influenced unknowns the additional function \(\texttt{destab}\) is provided. A call \(\mathtt {destab\; x}\) first removes all unknowns directly influenced by \(\textrm{x}\) from \({\texttt{stable}}\) and resets the set of influenced unknowns of \(\textrm{x}\) in \({\texttt{infl}}\) to the empty set, and then continues recursively to destabilize indirectly influenced unknowns of \(\textrm{x}\). Note that \(\mathtt {destab\; x}\) only removes \(\textrm{x}\) itself from the set \({\texttt{stable}}\) if \(\textrm{x}\) (transitively) depends on itself. If \(\textrm{x}\) does not depend on itself, \(\textrm{x}\) remains in \({\texttt{stable}}\), and the fixpoint iteration terminates after one iteration.Footnote 5

With those changes, the \(\texttt{solve}\) function of the TD is defined as follows, where \({\texttt{infl}} _0\) represents the empty mapping, i. e., where every unknown in \(\mathcal {U}\) maps to the empty set.

Calling \(\texttt{solve}\) for the unknown \(\textrm{x}\) and the equation system from Example 1 results in the computation trace shown in Fig. 4. The figure illustrates the effect of skipping superfluous computations. Nodes that belong to additional computations the plain TD would perform but which are skipped by the TD are indicated with small grey nodes. In this example, the TD saves more than half of the computations.
The figure shows the computation trace corresponding to the TD when solving the equation system from Example 1 for unknown \(\textrm{x} \). Some computation paths terminate because the queried unknown is called, others because the iterated unknown is already stable. The grey nodes below stable leaves indicate the additional computation steps that the plain TD would execute.
A crucial part of showing the correctness of the optimizations in the TD, is verifying that the destabilization preserves the essential properties of the solver’s state. This includes proving that destabilization is thorough enough to remove all unknowns possibly affected by a changed value from \({\texttt{stable}}\), such that no evaluation builds on possibly outdated values of stable unknowns. On the other hand, it also requires showing that destabilization is specific enough to not remove from \({\texttt{stable}}\) any unknown that was already stable before the iteration started. This ensures that the set of called unknowns remains a subset of \({\texttt{stable}}\) and thus invariants for \({\texttt{stable}}\) unknowns also hold for called unknowns where values are simply looked up without further descending. To guarantee these bounds of destabilization, we have found two invariants to be essential milestones:
- (i):
-
An invariant that the data structure \({\texttt{infl}}\) is complete, i. e., records all relevant dependencies, and
- (ii):
-
An invariant stating that, when evaluating an unknown \(\textrm{x}\), only influences to previously unstable unknowns or \(\textrm{x}\) itself, are recorded.
Similarly to Definition 1 for the plain TD, we define a predicate to describe valid input solver states.
Definition 2
(TD Invariant). For \(c,{\texttt{stable}} \subseteq \mathcal {U},\sigma :\mathcal {U} \rightarrow \mathbb {D} \) and \({\texttt{infl}}:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \) the predicate \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) is satisfied if:
-
(i)
\(c\subseteq {\texttt{stable}} \)
-
(ii)
\(\forall \textrm{x} \in {\texttt{stable}} -c.\,\mathcal {T} \,\textrm{x} \,\sigma =\sigma \,\textrm{x} \), i. e., the mapping \(\sigma \) fulfills the equations for all truly stable unknowns,
-
(iii)
\(\left\{ \textrm{x} \in \mathcal {U} \mid {\texttt{infl}} \,\textrm{x} \ne \emptyset \right\} \subseteq {\texttt{stable}} \), i. e., keys mapping to non-trivial values in \({\texttt{infl}}\) are members of \({\texttt{stable}}\), and
-
(iv)
\(\forall \textrm{y} \in {\texttt{stable}} -\,c.\,\forall \textrm{x} \in {\textsf{dep}} \,\sigma \,\textrm{y}.\,\textrm{y} \in {\texttt{infl}} \textrm{x} \), i. e., \({\texttt{infl}}\) stores the mapping “\(\textrm{x}\) influences \(\textrm{y}\) ” for all unknowns \(\textrm{x}\) on which any truly stable unknown \(\textrm{y}\) depends on.
Item (i) allows to conclude that \(\textrm{x}\) is not only in \(c\) but also in \({\texttt{stable}}\) when the unknown \(\textrm{x}\) is looked up in the \(\texttt{query}\) function. We remark that for the plain TD this can be implicitly concluded, for \(s\) respectively, from the fact that
 for the currently evaluated unknown \(\textrm{x}\). Item (iv) corresponds to milestone (i) and relates the map of influences to the dependencies of the equation system. It helps to show that \({\texttt{stable}}\) remains closed under \({\textsf{dep}}\) also after the application of \(\texttt{destab}\). With Item (ii) and (iii) the predicate \({\textsf{valid}} \) extends \({\textsf{valid}_\textrm{plain}} \) from Definition 1.
for the currently evaluated unknown \(\textrm{x}\). Item (iv) corresponds to milestone (i) and relates the map of influences to the dependencies of the equation system. It helps to show that \({\texttt{stable}}\) remains closed under \({\textsf{dep}}\) also after the application of \(\texttt{destab}\). With Item (ii) and (iii) the predicate \({\textsf{valid}} \) extends \({\textsf{valid}_\textrm{plain}} \) from Definition 1.
Lemma 3
Let \({\texttt{infl}}:\,\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \), and \(c,{\texttt{stable}} \subseteq \mathcal {U} \). Assume
-
\(\left\{ \textrm{u} \in \mathcal {U} \mid {\texttt{infl}} \,\textrm{u} \ne \emptyset \right\} \subseteq {\texttt{stable}} \) and
-
\(\forall \textrm{u} \in {\texttt{stable}} -\,c.\,\forall \textrm{v} \in {\textsf{dep}} \,\sigma \,\textrm{u}.\,\textrm{u} \in {\texttt{infl}} \textrm{v} \).
Then \(\forall \textrm{u} \in {\texttt{stable}} -\,c.\,{\textsf{dep}} \,\sigma \,\textrm{u}.\,\subseteq {\texttt{stable}} \). This immediately implies
Besides the predicate for valid solver states, we define a predicate relating the output solver state to the corresponding input state.
Definition 3
(Update relation). For \(\textrm{x} \in \mathcal {U},{\texttt{stable}},{\texttt{stable}} '\subseteq \mathcal {U} \), and \({\texttt{infl}},{\texttt{infl}} ':\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \) the predicate \({\textsf{update}} \,\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} \,{\texttt{infl}} '\,{\texttt{stable}} '\) is satisfied if
-
(i)
\({\texttt{stable}} \subseteq {\texttt{stable}} '\), i. e., the stable set is increasing,
-
(ii)
\(\forall \textrm{u}.\,\left( {\texttt{infl}} '\,\textrm{u} -{\texttt{infl}} \,\textrm{u} \right) \cap \,({\texttt{stable}} -\left\{ \textrm{x} \right\} ) = \emptyset \), i. e., only unknowns that were not previously stable (or \(\textrm{x}\)) are inserted into \({\texttt{infl}}\), and
-
(iii)
\(\forall \textrm{u} \in {\texttt{stable}}.\;{\texttt{infl}} \,\textrm{u} \subseteq {\texttt{infl}} ' \,\textrm{u} \), i. e., the set of influenced unknowns increases for all stable unknowns.
Item (i) is used to show that Definition 2 (i) still holds after destabilization (cf. Lemma 4). It also aids in deriving the appropriate variants of Item (ii) and Item (iii) in the induction steps. Definition 3 (ii) formalizes the earlier described milestone (ii) and allows to show that Item (i) still holds after destabilization. Item (iii) expresses that a dependency, recorded due to an unknown occurring in some right-hand side, persists till the end of this right-hand side’s evaluation. This is required to establish Definition 2 (iv).
Both defined predicates enable the formalization of the preservation of invariants by the destabilization mechanism.
Lemma 4
For \(\textrm{x} \in \mathcal {U},{\texttt{infl}}:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \), and \({\texttt{stable}} \subseteq \mathcal {U} \), let \({\texttt{infl}} ':\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \), and \({\texttt{stable}} '\subseteq \mathcal {U} \) such that \(\texttt{destab} \;\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} =\left( {\texttt{infl}} ', {\texttt{stable}} '\right) \) holds. Let \(c':=c-\left\{ x \right\} \) and \(\sigma ':=\sigma \oplus \left\{ \textrm{x} \mapsto d_{\textrm{x}} \right\} \).
-
(i)
Assume \(c \subseteq {\texttt{stable}} \) and \({\texttt{stable}} \subseteq {\texttt{stable}} '\). Then \(c \subseteq {\texttt{stable}} '\) holds.
-
(ii)
Assume
-
\(\forall \mathrm {\textrm{x}} \in {\texttt{stable}} -c.\,\mathcal {T} \,\textrm{x} \,\sigma =\sigma \,\textrm{x} \),
-
\(\mathcal {T} \,\mathrm {\textrm{x}} \,\sigma =d_{\textrm{x}}\), and
-
\(\forall \mathrm {\textrm{u}} \in {\texttt{stable}} -c'. \forall \textrm{v} \in {\textsf{dep}} \,\sigma \,u.\;\textrm{u} \in {\texttt{infl}} \,\textrm{v} \).
Then \(\forall \textrm{x} \in {\texttt{stable}} '-c'.\,\mathcal {T} \,\textrm{x} \,\sigma '=\sigma '\,\textrm{x} \) holds.
-
-
(iii)
Assume \(\left\{ \textrm{u} \in \mathcal {U} \mid {\texttt{infl}} \,\textrm{u} \ne \emptyset \right\} \subseteq {\texttt{stable}} \). Then \(\left\{ \textrm{u} \in \mathcal {U} \mid {\texttt{infl}} ' \,\textrm{u} \ne \emptyset \right\} \subseteq {\texttt{stable}} '\) holds.
-
(iv)
Assume \(\forall \textrm{u} \in {\texttt{stable}} -c'.\;\forall \textrm{v} \in {\textsf{dep}} \,\sigma \;\textrm{u}.\;\textrm{u} \in {\texttt{infl}} \,\textrm{v} \). Then \(\forall \textrm{u} \in {\texttt{stable}} '-c'.\;\forall \textrm{v} \in {\textsf{dep}} \,\sigma '\,\textrm{u}.\;\textrm{u} \in {\texttt{infl}} ' \,\textrm{v} \).
The TD skips re-evaluation of stable unknowns because it would yield the same value. The following lemma supports this and shows that the plain TD will return the same value as already computed if an unknown is stable.
Lemma 5
This lemma shows:
-
Assume \(\mathtt {query_{plain}} \,\textrm{x} \,\textrm{y} \,c\,\sigma =(d_{\textrm{y}},\sigma ')\) is defined, \({\textsf{valid}_\textrm{plain}} \,c\,s\,\sigma \) is satisfied, and \(\textrm{y} \in s\). Then \(\sigma \) and \(\sigma '\) are equal.
-
Assume \(\mathtt {iterate_{plain}} \,\textrm{x} \,c\,\sigma =(d_{\textrm{x}},\sigma ')\) is defined, \(\textrm{x} \in c\), \({\textsf{valid}_\textrm{plain}} \,(c-\left\{ \textrm{x} \right\} )\,s\,\sigma \) is satisfied, and \(\textrm{x} \in s\). Then \(\sigma \) and \(\sigma '\) are equal.
-
Assume
 is defined, \({\textsf{valid}_\textrm{plain}} \,c\,s\,\sigma \) is satisfied, and \({\textsf{dep}} \,t\,\sigma \subseteq s\). Then
is defined, \({\textsf{valid}_\textrm{plain}} \,c\,s\,\sigma \) is satisfied, and \({\textsf{dep}} \,t\,\sigma \subseteq s\). Then
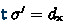 and \(\sigma =\sigma '\).
and \(\sigma =\sigma '\).
Following the auto-generated induction rules for the plain TD and the TD, we split the equivalence proof of both fixpoint algorithms into two directions. The first assumes the termination of the plain TD and shows that the TD terminates, yielding the same value, cf. Theorem 2. The second proves that the plain TD returns the same value as the TD under the assumption that the TD terminates, cf. Theorem 3. Both results are combined afterward in Corollary 2, and Corollary 3 concludes the correctness of the TD.
Theorem 2
(Equivalence I). The theorem shows:
-
Assume \(\mathtt {query_{plain}} \,\,\textrm{x} \,\,\textrm{y} \,\,c\,\,\sigma =\left( d_{\textrm{y}},\sigma '\right) \) is defined, and \({\textsf{valid}} \,\,c\,\,\sigma \,\,{\texttt{infl}} \,\,{\texttt{stable}} \) holds. Then there exist \({\texttt{infl}} ':\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \) and a set \({\texttt{stable}} '\subseteq \mathcal {U} \) such that
-
(i)
\(\texttt{query} \,\textrm{x} \,\textrm{y} \,c\,{\texttt{infl}} \,{\texttt{stable}} \,\sigma =\left( d_{\textrm{y}},{\texttt{infl}} ',{\texttt{stable}} ',\sigma '\right) \) is defined and
-
(ii)
\({\textsf{valid}} \,c\,\sigma '\,{\texttt{infl}} '\,{\texttt{stable}} '\) holds.
Furthermore, (iii) the statements \({\textsf{update}} \,\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} \,{\texttt{infl}} '\,{\texttt{stable}} '\), and (iv) \(\textrm{x} \in {\texttt{infl}} '\,\textrm{y} \) hold.
-
(i)
-
Assume \(\mathtt {iterate_{plain}} \,\,\textrm{x} \,\,c\,\,\sigma =\left( d_{\textrm{x}},\sigma '\right) \) is defined, \({\textsf{valid}} \,\,c'\,\,\sigma \,\,{\texttt{infl}} \,\,{\texttt{stable}} \) holds for \(c':=c-\left\{ \textrm{x} \right\} \), and \(\textrm{x} \in c\). Then there exist \({\texttt{infl}} ':\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \) and \({\texttt{stable}} '\subseteq \mathcal {U} \) such that
-
(i)
\(\texttt{iterate} \,\textrm{x} \,c\,{\texttt{infl}} \,{\texttt{stable}} \,\sigma =\left( d_{\textrm{x}},{\texttt{infl}} ',{\texttt{stable}} ',\sigma '\right) \) is defined and
-
(ii)
\({\textsf{valid}} \,c'\,\sigma '\,{\texttt{infl}} '\,{\texttt{stable}} '\) holds.
Furthermore, (iii) the statements \({\textsf{update}} \,\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} \,{\texttt{infl}} '\,{\texttt{stable}} '\), and (iv) \(\textrm{x} \in {\texttt{stable}} '\) hold.
-
(i)
-
Assume
 is defined, \({\textsf{valid}} \,\,c\,\,\sigma \,\,{\texttt{infl}} \,\,{\texttt{stable}} \) holds, and \(\textrm{x} \in {\texttt{stable}} \). Then there exist \({\texttt{infl}} ':\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \) and \({\texttt{stable}} '\subseteq \mathcal {U} \) such that
is defined, \({\textsf{valid}} \,\,c\,\,\sigma \,\,{\texttt{infl}} \,\,{\texttt{stable}} \) holds, and \(\textrm{x} \in {\texttt{stable}} \). Then there exist \({\texttt{infl}} ':\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) \) and \({\texttt{stable}} '\subseteq \mathcal {U} \) such that -
(i)
 is defined,
is defined, -
(ii)
\({\textsf{valid}} \,c\,\sigma '\,{\texttt{infl}} '\,{\texttt{stable}} '\) holds.
Furthermore, (iii) the statements \({\textsf{update}} \,\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} \,{\texttt{infl}} '\,{\texttt{stable}} '\), (iv)
 , and (v)
, and (v)
 hold.
hold. -
(i)
Proof
The complete proof is extensive, thus we only highlight pivotal steps and direct the reader to the formalization in Isabelle [27] for a detailed proof. The proof uses the same induction rules and covers the same cases as in Theorem 1.
Case 1
(Query). Let \(\textrm{x},\textrm{y} \in \mathcal {U},c\subseteq \mathcal {U},\sigma ,\sigma ':\mathcal {U} \rightarrow \mathbb {D},d_{\textrm{y}}\in \mathbb {D} \) such that the call \(\mathtt {query_{plain}} \,\textrm{x} \,\textrm{y} \,c\,\sigma =(d_{\textrm{y}},\sigma ')\) is defined. And let \({\texttt{infl}}:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) , {\texttt{stable}} \subseteq \mathcal {U} \) such that \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds.
Subcase 1.1
(Lookup). This case follows directly from the premises.
Subcase 1.2
(Iterate). Using the induction hypothesis, we obtain \({\texttt{infl}} _1\) and \({\texttt{stable}} _1\) such that \(\texttt{iterate} \,\,\textrm{y} \,\,c\,\,{\texttt{infl}} \,\,{\texttt{stable}} \,\,\sigma =(d_{\textrm{y}},{\texttt{infl}} _1,{\texttt{stable}} _1,\sigma ')\) is defined. The induction hypothesis for the \(\texttt{iterate}\) call provides the fact \(({\texttt{infl}} _1\,\textrm{u} -{\texttt{infl}} \,\textrm{u})\cap ({\texttt{stable}} -\left\{ \textrm{x} \right\} )=\emptyset \). Using the definition of \(\texttt{iterate}\), we can conclude that the subtraction of \(\left\{ \textrm{x} \right\} \) can be omitted, which aids in proving the subgoal.
Case 2
(Iterate). First, assume that \(\textrm{x} \in {\texttt{stable}} \). Lemma 5 implies that the plain TD returns \(\sigma \) unchanged, and the same holds for the TD since it skips computation altogether. Thus, the proof goals are trivially satisfied. Now, assume that \(\textrm{x} \notin {\texttt{stable}} \). Let \(\textrm{x} \in \mathcal {U},c\subseteq c,\sigma ,\sigma ':\mathcal {U} \rightarrow \mathbb {D},d_{\textrm{x}}\in \mathbb {D} \) such that \(\mathtt {iterate_{plain}} \,\textrm{x} \,c\,\sigma =(d_{\textrm{x}},\sigma ')\) is defined, and let \({\texttt{infl}}:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) , {\texttt{stable}} \subseteq \mathcal {U} \) such that \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds.
Subcase 2.1
(Fixpoint). The premises directly imply the subgoal.
Subcase 2.2
(Continue). Let \(d_{\textrm{x}}'\in \mathbb {D},\sigma _1:\mathcal {U} \rightarrow \mathbb {D} \) such that \(\mathtt {eval_{plain}} \,\,\textrm{x} \,\,(\mathcal {T} \,\,\textrm{x})\,\,c\,\,\sigma =(d_{\textrm{x}}',\sigma _1)\) is defined. According to the induction hypothesis for \(\texttt{eval}\), there exists \({\texttt{infl}} _1:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) , {\texttt{stable}} _1\subseteq \mathcal {U} \) such that
is defined. Let furthermore \({\texttt{infl}} _2:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) , {\texttt{stable}} _2\subseteq \mathcal {U} \) such that
Lemma 4 states that the predicate \({\textsf{valid}} \) is preserved for \({\texttt{infl}} _2\) and \({\texttt{stable}} _2\). This is key to applying the induction hypothesis for the tail call to \(\mathtt {iterate_{plain}}\). After that, one must show that
- (i):
-
\(\forall \textrm{u} \in {\texttt{stable}}.\;{\texttt{infl}} \,\textrm{u} \subseteq {\texttt{infl}} ' \,\textrm{u} \) and
- (ii):
-
\(\forall \textrm{u}.\,\left( {\texttt{infl}} '\,\textrm{u} -{\texttt{infl}} \,\textrm{u} \right) \cap \left( {\texttt{stable}} -\left\{ \textrm{x} \right\} \right) =\emptyset \).
For the first, we exploit the fact that we have previously shown that \({\texttt{stable}} \subseteq {\texttt{stable}} _2\) and that \(\texttt{destab}\) only removes key-value mappings with keys that are not in \({\texttt{stable}}\). For the second, we show similar to the Iterate subcase in the Query case above, that \(\left( {\texttt{infl}} '\,\textrm{u} -{\texttt{infl}} _2\,\textrm{u} \right) \cap \left( {\texttt{stable}} -\left\{ \textrm{x} \right\} \right) =\emptyset \) and \(\left( {\texttt{infl}} _1\,\textrm{u} -{\texttt{infl}} \,\textrm{u} \right) \cap \left( {\texttt{stable}} -\left\{ \textrm{x} \right\} \right) =\emptyset \). Together with the fact that \({\texttt{infl}} _2\,\textrm{u} \subseteq {\texttt{infl}} _1\,\textrm{u} \) for all \(\textrm{u}\), the statement follows.
Case 3
(Eval). Let \(\textrm{x} \in \mathcal {U},c\subseteq \mathcal {U},\sigma ,\sigma ':\mathcal {U} \rightarrow \mathbb {D},d_{\textrm{y}}\in \mathbb {D} \) and
 a strategy tree such that
a strategy tree such that
 is defined. Furthermore, let \({\texttt{infl}}:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) , {\texttt{stable}} \subseteq \mathcal {U} \) such that \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds.
is defined. Furthermore, let \({\texttt{infl}}:\mathcal {U} \rightarrow \mathcal {P}\left( \mathcal {U} \right) , {\texttt{stable}} \subseteq \mathcal {U} \) such that \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds.
Subcase 3.1
(Answer). This case follows directly from the premises.
Subcase 3.2
(Query). The main step here is to show, as in Theorem 1, that once a value for an unknown has been calculated, this value is preserved during the evaluation of the remaining right-hand side. To accomplish this, we use Lemma 3 to derive \({\textsf{valid}_\textrm{plain}} \,\,c\,\,{\texttt{stable}} \,\,\sigma \) and then use the value preserving property Theorem 1 (ii) of the plain TD. \(\square \)
A crucial part for the proof in the other direction is to show that when the TD reaches the Stable case, i. e., stops further descent because the iterated unknown is in \({\texttt{stable}}\), the plain TD terminates for the same parameters and returns the same value. Since the Stable case constitutes a base case of the induction using the rules for the TD, no induction hypotheses are available to conclude this fact. Hence, we add the obvious but vital premise that the set \({\texttt{stable}}\) is finite.
Lemma 6
Assume \(\textrm{x} \in c\), \(\textrm{x} \in {\texttt{stable}} \), \({\textsf{valid}_\textrm{plain}} \,(c-\left\{ \textrm{x} \right\} )\,{\texttt{stable}} \,\sigma \) holds, and the set \({\texttt{stable}} \) is finite. Then there exists \(d_{\textrm{x}}\in \mathbb {D} \) such that \(\mathtt {iterate_{plain}} \,\textrm{x} \,c\,\sigma =(d_{\textrm{x}},\sigma )\) is defined and \(d_{\textrm{x}}=\sigma \,\textrm{x} \).
This lemma holds since the resulting computation trace has finite width and height. The fixpoint iterations at any level terminate after one iteration since the input is already a solution. Also, the number of \(\texttt{query}\) nodes in a right-hand side is bounded, because we restrict strategy trees to be of finite height. Finally, its height is finite because one unknown is added to \(c\) at every second level and it is always a subset of \(s\). Formally, this lemma is proven by structural induction over \(s\). With the help of the lemma we can show the remaining direction of the equivalence:
Theorem 3
(Equivalence II). The theorem shows:
-
Assume \(\texttt{query} \,\textrm{x} \,\textrm{y} \,c\,{\texttt{infl}} \,{\texttt{stable}} \,\sigma =\left( d_{\textrm{y}},{\texttt{infl}} ',{\texttt{stable}} ',\sigma '\right) \) is defined, \(\textrm{x} \in {\texttt{stable}} \), \({\texttt{stable}}\) is finite, and \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds. Then
-
(i)
\(\mathtt {query_{plain}} \,\textrm{x} \,\textrm{y} \,c\,\sigma =\left( d_{\textrm{y}},\sigma '\right) \) is defined and
-
(ii)
\({\textsf{valid}} \,c\,\sigma '\,{\texttt{infl}} '\,{\texttt{stable}} '\) holds.
Furthermore, in this case (iii) \({\textsf{update}} \,\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} \,{\texttt{infl}} '\,{\texttt{stable}} '\) holds, (iv) \({\texttt{stable}} '\) is finite, and (v) \(\textrm{x} \in {\texttt{infl}} '\textrm{y} \).
-
(i)
-
Assume \(\texttt{iterate} \,\,\textrm{x} \,\,c\,\,{\texttt{infl}} \,\,{\texttt{stable}} \,\,\sigma =\left( d_{\textrm{x}},{\texttt{infl}} ',{\texttt{stable}} ',\sigma '\right) \) is defined, \(\textrm{x} \in c\), \({\texttt{stable}}\) is finite, and \({\textsf{valid}} \,c'\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds. Let \(c':=c-\left\{ \textrm{x} \right\} \). Then
-
(i)
\(\mathtt {iterate_{plain}} \,\textrm{x} \,c\,\sigma =\left( d_{\textrm{x}},\sigma '\right) \) is defined and
-
(ii)
\({\textsf{valid}} \,c'\,\sigma '\,{\texttt{infl}} '\,{\texttt{stable}} '\) holds.
Furthermore, in this case (iii) \({\textsf{update}} \,\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} \,{\texttt{infl}} '\,{\texttt{stable}} '\) holds, (iv) the set \({\texttt{stable}} '\) is finite, and (v) \(\textrm{x} \in {\texttt{stable}} '\).
-
(i)
-
Assume
 is defined, \(\textrm{x} \in {\texttt{stable}} \), \({\texttt{stable}}\) is finite, and \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds. Then
is defined, \(\textrm{x} \in {\texttt{stable}} \), \({\texttt{stable}}\) is finite, and \({\textsf{valid}} \,c\,\sigma \,{\texttt{infl}} \,{\texttt{stable}} \) holds. Then -
(i)
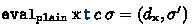 is defined and
is defined and -
(ii)
\({\textsf{valid}} \,c\,\sigma '\,{\texttt{infl}} '\,{\texttt{stable}} '\) holds.
Furthermore, in this case (iii) \({\textsf{update}} \,\textrm{x} \,{\texttt{infl}} \,{\texttt{stable}} \,{\texttt{infl}} '\,{\texttt{stable}} '\) holds, (iv) \({\texttt{stable}} '\) is finite, (v)
 , and (vi)
, and (vi)
 .
. -
(i)
Proof
This proof uses the induction rules for the TD; which results in an additional subcase Stabl in the Iterate case. This is the only case that differs significantly from the previous proof; it is proven using Lemma 6. \(\square \)
Both theorems combined establish the equivalence of the plain TD and the TD, which is expressed in the following corollary.
Corollary 2
(Equivalence of the TDs). The equation \(\mathtt {solve_{plain}} \,\textrm{x} =\sigma \) is defined for some \(\sigma \in \left\{ f:\mathcal {U} \rightarrow \mathbb {D} \right\} \) whenever \(\texttt{solve} \,\textrm{x} =\left( {\texttt{stable}}, \sigma '\right) \) is defined for some \({\texttt{stable}} \subseteq \mathcal {U} \) and \(\sigma ':\mathcal {U} \rightarrow \mathbb {D} \). In this case, \(\sigma \) and \(\sigma '\) are equal.
The following corollary reads identically to Corollary 1 but refers to the implementation of the TD. It is a straightforward consequence of Theorem 3.
Corollary 3
(Partial Correctness of the TD). Assume that the equation \(\texttt{solve} \,\textrm{x} =\left( {\texttt{stable}}, \sigma \right) \) is defined. Then the corollary shows that \(\sigma \) is a partial solution for \({\texttt{stable}}\) and \(x \in {\texttt{stable}} \).
5 Related Work
In the scope of verifying dataflow analyses, round-robin iteration [6] and variations of Kildall’s algorithm [5, 8, 23] have been verified. The latter maintain a global worklist for a chaotic iteration over the control-flow graph. Others formalize syntax-directed fixpoint iterators as part of their work on formalizing abstract interpreters [7, 12, 18]. Instead of iterating over the control-flow graph of a program, their abstract interpreters are guided by the program’s syntax. These dedicated solvers, however, are not generically applicable to all equation systems. Instead of dynamically detecting dependencies, the dependencies are derived directly from the program’s control flow.
The partial correctness of the local generic fixpoint solver RLD has been proven by Hofmann et al. [16]. This algorithm records dependencies dynamically to deal with changing dependencies between unknowns. In contrast to the TD, it locally destabilizes directly influenced unknowns when the value of the current unknown has been updated, and immediately triggers their re-evaluation through a local worklist. This may lead to different values being computed by the solver for repeated queries of the same unknown within a right-hand side. Extra mechanisms are required to avoid this undesired behavior [19]. In contrast, the TD relies on non-local destabilization to remove all unknowns from the set of stable unknowns that transitively depend on an updated unknown. The local worklist iteration of RLD is avoided and the same value is computed if the same unknown is queried multiple times within one right-hand side. In fact, the latter property constitutes an essential proof step in our formalization. Furthermore, the RLD solver always combines the old value for an unknown with its new value. This implies that the domain of values should provide some join operator, whereas our algorithm is fully generic by making no assumptions on the domain of values—except providing an element \(\bot \), and an equality operator.
De Vilhena et al. [30] use Iris to formalize a local generic solver and prove its partial correctness. Like the RLD, their solver detects dependencies between unknowns on the fly and can deal with a possibly infinite equation system. It does, however, not rely on recursive descent into encountered unknowns. Instead, it uses a worklist to iterate over the unknowns, which are either new or whose current values are possibly outdated. Similarly to the RLD, this does not require a non-local destabilization. In comparison, recursive descent into unknowns, as done by the TD, is likely to be more efficient than plain worklist iteration. Due to recursive descent, the evaluation of right-hand sides always uses the currently best values for encountered unknowns and thus may avoid useless computation. To prove that the results computed by their solver are part of an optimal least fixpoint, Vilhena et al. [30] assume that the domain of values is partially ordered and right-hand sides are monotonic. In practical applications such as interprocedural analysis, or the analysis of concurrent systems, though, monotonicity cannot always be assumed. This is why our solver is proven partially correct independent of any assumptions on ordering or monotonicity.
6 Conclusion
This work provides a formal proof of the partial correctness of the TD. We first proved the plain TD to be partially correct and then proved that the TD is equivalent to the plain TD. For complete lattices and monotonic right-hand sides, the computed partial solution agrees with the least solution of the equation system on all stable unknowns. A proof of this fact can be obtained by extending the given proof with further invariants. When the complete lattice additionally satisfies the ascending chain condition and the set of unknowns is finite, the TD is guaranteed to terminate. In this case, partial correctness turns into total correctness.
Another task for future work is to incorporate widening and narrowing [3, 28] into the solver and prove correctness. Widening and narrowing cannot be considered another semantics-preserving optimization. Even for complete lattices, the computed result is generally no longer the least solution. In case that narrowing is intertwined with widening as proposed by Seidl and Vogler [26] and right-hand sides are non-monotonic, the result need not be a (post-)solution. Further future work is to support side-effecting equation systems [2], where right-hand sides may not only contribute to the left-hand side but also contribute to other unknowns.
Notes
- 1.
We use the term unknown instead of variable because, in the context of program analysis, variables usually denote program variables, not unknowns in the equation system.
- 2.
In program analysis this is often a complete lattice of abstract values describing concrete program states.
- 3.
Recall,
 denotes the reflexive and transitive closure of \({\textsf{dep}}\).
denotes the reflexive and transitive closure of \({\textsf{dep}}\). - 4.
For the TD, the order of function calls during execution corresponds to the preorder traversal of the computation trace, because all recursive calls are tail calls.
- 5.
Recall that \(\textrm{x}\) is inserted optimistically into \({\texttt{stable}}\) before its iteration.
References
Akhin, M., Belyaev, M.: Variable initialization analysis (2020). https://kotlinlang.org/spec/control--and-data-flow-analysis.html#variable-initialization-analysis
Apinis, K., Seidl, H., Vojdani, V.: Side-effecting constraint systems: a Swiss army knife for program analysis. In: Jhala, R., Igarashi, A. (eds.) Programming Languages and Systems - 10th Asian Symposium, APLAS 2012, Kyoto, Japan, 11–13 December 2012. Proceedings. LNCS, vol. 7705, pp. 157–172. Springer, Cham (2012). https://doi.org/10.1007/978-3-642-35182-2_12
Apinis, K., Seidl, H., Vojdani, V.: How to combine widening and narrowing for non-monotonic systems of equations. In: Boehm, H., Flanagan, C. (eds.) ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2013, Seattle, WA, USA, 16–19 June 2013, pp. 377–386. ACM (2013). https://doi.org/10.1145/2491956.2462190
Apinis, K., Seidl, H., Vojdani, V.: Enhancing top-down solving with widening and narrowing. In: Probst, C.W., Hankin, C., Hansen, R.R. (eds.) Semantics, Logics, and Calculi - Essays Dedicated to Hanne Riis Nielson and Flemming Nielson on the Occasion of Their 60th Birthdays. LNCS, vol. 9560, pp. 272–288. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-27810-0_14
Bertot, Y., Grégoire, B., Leroy, X.: A structured approach to proving compiler optimizations based on dataflow analysis. In: Filliâtre, J., Paulin-Mohring, C., Werner, B. (eds.) Types for Proofs and Programs, International Workshop, TYPES 2004, Jouy-en-Josas, France, 15–18 December 2004, Revised Selected Papers. LNCS, vol. 3839, pp. 66–81. Springer, Cham (2004). https://doi.org/10.1007/11617990_5
Cachera, D., Jensen, T.P., Pichardie, D., Rusu, V.: Extracting a data flow analyser in constructive logic. In: Schmidt, D.A. (ed.) Programming Languages and Systems, 13th European Symposium on Programming, ESOP 2004, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2004, Barcelona, Spain, 29 March–2 April 2004, Proceedings. LNCS, vol. 2986, pp. 385–400. Springer, Cham (2004). https://doi.org/10.1007/978-3-540-24725-8_27
Cachera, D., Pichardie, D.: A certified denotational abstract interpreter. In: Kaufmann, M., Paulson, L.C. (eds.) Interactive Theorem Proving, First International Conference, ITP 2010, Edinburgh, UK, 11–14 July 2010, Proceedings. LNCS, vol. 6172, pp. 9–24. Springer, Cham (2010). https://doi.org/10.1007/978-3-642-14052-5_3
Coupet-Grimal, S., Delobel, W.: A uniform and certified approach for two static analyses. In: Filliâtre, J., Paulin-Mohring, C., Werner, B. (eds.) Types for Proofs and Programs, International Workshop, TYPES 2004, Jouy-en-Josas, France, 15–18 December 2004, Revised Selected Papers. LNCS, vol. 3839, pp. 115–137. Springer, Cham (2004). https://doi.org/10.1007/11617990_8
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Graham, R.M., Harrison, M.A., Sethi, R. (eds.) Conference Record of the Fourth ACM Symposium on Principles of Programming Languages, Los Angeles, California, USA, January 1977, pp. 238–252. ACM (1977). https://doi.org/10.1145/512950.512973
Cousot, P., Cousot, R.: Abstract interpretation frameworks. J. Log. Comput. 2(4), 511–547 (1992). https://doi.org/10.1093/LOGCOM/2.4.511
Fecht, C., Seidl, H.: A faster solver for general systems of equations. Sci. Comput. Program. 35(2), 137–161 (1999). https://doi.org/10.1016/S0167-6423(99)00009-X
Franceschino, L., Pichardie, D., Talpin, J.: Verified functional programming of an abstract interpreter. In: Dragoi, C., Mukherjee, S., Namjoshi, K.S. (eds.) Static Analysis - 28th International Symposium, SAS 2021, Chicago, IL, USA, 17–19 October 2021, Proceedings. LNCS, vol. 12913, pp. 124–143. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-88806-0_6
Gosling, J., et al.: Chapter 16. Definite Assignment, September 2023. https://docs.oracle.com/javase/specs/jls/se21/html/jls-16.html
Hecht, M.S., Ullman, J.D.: Analysis of a simple algorithm for global data flow problems. In: Proceedings of the 1st Annual ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, pp. 207–217, POPL 1973. Association for Computing Machinery, New York, NY, USA (1973). https://doi.org/10.1145/512927.512946
Hermenegildo, M.V., et al.: An overview of the Ciao system. In: Bassiliades, N., Governatori, G., Paschke, A. (eds.) Rule-Based Reasoning, Programming, and Applications - 5th International Symposium, RuleML 2011 - Europe, Barcelona, Spain, 19–21 July 2011. Proceedings. LNCS, vol. 6826, p. 2. Springer, Cham (2011). https://doi.org/10.1007/978-3-642-22546-8_2
Hofmann, M., Karbyshev, A., Seidl, H.: Verifying a local generic solver in Coq. In: Cousot, R., Martel, M. (eds.) Static Analysis - 17th International Symposium, SAS 2010, Perpignan, France, 14–16 September, 2010. Proceedings. LNCS, vol. 6337, pp. 340–355. Springer, Cham (2010). https://doi.org/10.1007/978-3-642-15769-1_21
Hofmann, M., Karbyshev, A., Seidl, H.: What is a pure functional? In: Abramsky, S., Gavoille, C., Kirchner, C., auf der Heide, F.M., Spirakis, P.G. (eds.) Automata, Languages and Programming, 37th International Colloquium, ICALP 2010, Bordeaux, France, 6–10 July 2010, Proceedings, Part II. LNCS, vol. 6199, pp. 199–210. Springer, Cham (2010). https://doi.org/10.1007/978-3-642-14162-1_17
Jourdan, J.: Verasco: a formally verified C static analyzer. (Verasco: un analyseur statique pour C formellement vérifié). Ph.D. thesis, Paris Diderot University, France (2016). https://tel.archives-ouvertes.fr/tel-01327023
Karbyshev, A.: Monadic parametricity of second-order functionals. Ph.D. thesis, Technische Universität München (2013). https://mediatum.ub.tum.de/1144371
Kildall, G.A.: A unified approach to global program optimization. In: Fischer, P.C., Ullman, J.D. (eds.) Conference Record of the ACM Symposium on Principles of Programming Languages, Boston, Massachusetts, USA, October 1973, pp. 194–206. ACM Press (1973). https://doi.org/10.1145/512927.512945
Le Charlier, B., Van Hentenryck, P.: A universal top-down fixpoint algorithm. Technical report CS-92-25, University of Namur and Brown University, May 1992
Muthukumar, K., Hermenegildo, M.V.: Compile-time derivation of variable dependency using abstract interpretation. J. Log. Program. 13(2 &3), 315–347 (1992). https://doi.org/10.1016/0743-1066(92)90035-2
Nipkow, T.: Verified bytecode verifiers. In: Honsell, F., Miculan, M. (eds.) Foundations of Software Science and Computation Structures, 4th International Conference, FOSSACS 2001 Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2001 Genova, Italy, 2–6 April 2001, Proceedings. LNCS, vol. 2030, pp. 347–363. Springer, Cham (2001). https://doi.org/10.1007/3-540-45315-6_23
Nipkow, T., Klein, G.: Concrete Semantics - With Isabelle/HOL. Springer, Cham (2014). ISBN 978-3-319-10541, https://doi.org/10.1007/978-3-319-10542-0
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL - A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Cham (2002). ISBN 3-540-43376, https://doi.org/10.1007/3-540-45949-9
Seidl, H., Vogler, R.: Three improvements to the top-down solver. Math. Struct. Comput. Sci. 31(9), 1090–1134 (2021). https://doi.org/10.1017/S0960129521000499
Stade, Y., Tilscher, S., Seidl, H.: Partial correctness of the top-down solver. Archive of Formal Proofs, May 2024. ISSN 2150-914x. https://isa-afp.org/entries/Top_Down_Solver.html. Formal proof development
Tilscher, S., Stade, Y., Schwarz, M., Vogler, R., Seidl, H.: The top-down solver—an exercise in A2I. In: Arceri, V., Cortesi, A., Ferrara, P., Olliaro, M. (eds.) Challenges of Software Verification, vol. 238, pp. 157–179. Springer, Singapore (2023). https://doi.org/10.1007/978-981-19-9601-6_9
Vergauwen, B., Wauman, J., Lewi, J.: Efficient fixpoint computation. In: Charlier, B.L. (ed.) Static Analysis, First International Static Analysis Symposium, SAS 1994, Namur, Belgium, 28–30 September 1994, Proceedings. LNCS, vol. 864, pp. 314–328. Springer, Cham (1994). https://doi.org/10.1007/3-540-58485-4_49
de Vilhena, P.E., Pottier, F., Jourdan, J.: Spy game: verifying a local generic solver in Iris. Proc. ACM Program. Lang. 4(POPL), 33:1–33:28 (2020). https://doi.org/10.1145/3371101
Vojdani, V., Apinis, K., Rõtov, V., Seidl, H., Vene, V., Vogler, R.: Static race detection for device drivers: the Goblint approach. In: Lo, D., Apel, S., Khurshid, S. (eds.) Proceedings of the 31st IEEE/ACM International Conference on Automated Software Engineering, ASE 2016, Singapore, 3–7 September 2016, pp. 391–402. ACM (2016). https://doi.org/10.1145/2970276.2970337
Acknowledgements
This work was supported by the German Research Foundation (DFG) - 378803395/2428 ConVeY and by Shota Rustaveli National Science Foundation of Georgia under the project FR-21-7973.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Stade, Y., Tilscher, S., Seidl, H. (2024). The Top-Down Solver Verified: Building Confidence in Static Analyzers. In: Gurfinkel, A., Ganesh, V. (eds) Computer Aided Verification. CAV 2024. Lecture Notes in Computer Science, vol 14681. Springer, Cham. https://doi.org/10.1007/978-3-031-65627-9_15
Download citation
DOI: https://doi.org/10.1007/978-3-031-65627-9_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-65626-2
Online ISBN: 978-3-031-65627-9
eBook Packages: Computer ScienceComputer Science (R0)




 to describe the set of unknowns queried in the last iterations for a subtree of the computation trace, and
to describe the set of unknowns queried in the last iterations for a subtree of the computation trace, and
 .
.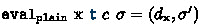 is defined, and
is defined, and  where
where
 .
.

 is defined,
is defined, 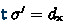 and
and  is defined,
is defined,  is defined,
is defined, , and (v)
, and (v)
 hold.
hold. is defined,
is defined, 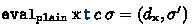 is defined and
is defined and , and (vi)
, and (vi)
 .
. denotes the reflexive and transitive closure of
denotes the reflexive and transitive closure of