Research on Dam Deformation Monitoring Model Based on BP + SVM Optimal Weighted Combination

Abstract

It is an important means to ensure the safe operation of dam to establish accurate and effective deformation monitoring data analysis and prediction model. In view of the complex conditions in dam safety monitoring, there are many unknown or uncertain factors, and they are difficult to have a single model to apply all problems. The optimal weighted combination method is constructed by combining neural network model and support vector machine model, which is used in the deformation monitoring analysis of concrete dam. The research shows that the prediction results of the optimal weighted combination model are highly consistent with the measured results, and have certain feasibility and practicability in the dam deformation monitoring work.

1 Introduction

The analysis and prediction model of deformation monitoring data are significant to dam safety monitoring [1]. At present, statistical model [2], deterministic model [3] and mixed model are usually used to process and analyze dam monitoring data. Different processing methods have different advantages and certain applications in practical engineering, but these methods also have certain limitations. In the actual work of monitoring data analysis, insufficient data samples or complex environmental factors have a great impact on the establishment of the model, and the model may have more errors and poor fitting effect, so the model cannot be applied to the actual work [4].

The paper mainly researches the BP neural network model and support vector machine model (SVM) [5]. These two models are organically combined and applied to the dam deformation analysis example [6]. The results show that the optimal weighted combination model can maximize the information of each monitoring model, reduce the mean square error of the prediction model, and improve the accuracy of dam deformation monitoring [7]. This paper can provide new ideas and reference for dam safety monitoring data analysis and prediction model.

2 BP Neural Network Model

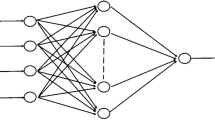
Artificial neural network (Ann) is a kind of distributed parallel information processing algorithm mathematical model which imitates the behavior characteristics of animal neural network [8]. The input signal x_i acts on the output node through the intermediate node (Hidden layer point), and the output signal Y_k is generated through nonlinear transformation [9]. Each sample of network training including the input vector x and the desired output t, network output value Y and t. By adjusting the w_ij which means connection strength between the input node and the hidden node, T_jk which means the connection strength between the hidden node and the output node, and the threshold, the error decreases along the gradient direction. After repeated learning and training, the training stops immediately when determining the network parameters (weights and thresholds) corresponding to the minimum error.

In the dam deformation monitoring system, we generally build the BP neural network of multi-layer perceptron composed of input layer, output layer and hidden layer, and determine the number of input layer node n, hidden layer node l, hidden layer excitation function f, and output layer node m. The connection weight w_ij and hidden layer threshold a_j between the input layer and hidden layer are initialized, so that we can determine parameters such as learning rate and activation function. After the sample data is sent to the input node and processed layer by layer through the hidden layer, the following formula is used to calculate the output H_j of the hidden layer.

$$ H_{j} = f\left( {\sum\limits_{i = 1}^{n} {w_{ij} x_{i} - a_{j} } } \right)\;\;\;j = 1,2,...,l $$

(1)

We initialize w_jk which is the weight between the hidden layer and the output layer, and also the output layer threshold b_k. Then the BP neural network will predict the output O_k._.

$$ O_{k} = \sum\limits_{j = 1}^{l} {H_{j} w_{jk} - b_{k} \;\;\;\;\;k = 1,2,...,m} $$

(2)

According to the network prediction we can output O_k and Y_k, and can press the following formula to calculate the network prediction error. This neural network will calculate the error value of each input sample data. If the error is relatively large, the error starts to reverse transmission, and adjust the neural network parameters until the system converges.

$$ e_{k} = Y_{k} - O_{k} \quad k = 1,2,...,m $$

(3)

Through network training, weights w_ij and w_jk which are updated according to network prediction error.

$$ w_{ij} = w_{ij} + \eta H_{j} \left( {1 - H_{j} } \right)x\left( i \right)\sum\limits_{k = 1}^{m} {w_{jk} e_{k} } \quad i = 1,2,...,n;\;j = 1,2,...,l $$

(4)

$$ w_{jk} = w_{jk} + \eta H_{j} e_{k} \quad j = 1,2,...,l;\;k = 1,2,...,m $$

(5)

Next update the network node thresholds a_j and b_k.

$$ a_{j} = a_{j} + \eta H_{j} \left( {1 - H_{j} } \right)x\left( x \right)\sum\limits_{k = 1}^{m} {w_{jk} e_{k} } \quad j = 1,2,...,l $$

(6)

$$ b_{k} = b_{k} + e_{k} \quad k = 1,2,...,m $$

(7)

If we determine the weights, we input the data into the model to predict the results.

3 SVM Support Vector Machine Model

Support vector machines are mostly used for classification problems, but they can also be used for regression, which is often referred to as support vector regression models [10]. The final model function is expressed as follows:

$$ f(x) = w^{{\text{T}}} x + b $$

(8)

W and b are the main coefficients required by the model.

For a given training sample $D = \{ (x_{1} ,y_{1} ),(x_{2} ,y_{2} ),...,(x_{m} ,y_{m} )\}$, traditional regression models usually calculate losses directly based on the difference between model output and true value, while SVR only calculates the loss when the difference between $f(x)$ and $y$ is greater than ${\upvarepsilon }$, and the parameters ${\upvarepsilon }$ is specified by the user. Therefore, according to other theories of support vector machine model, the optimization objective of SVR problem is written as follows.

$$ \mathop {\min }\limits_{w,b} \frac{1}{2}||w||^{2} + C\sum\limits_{i = 1}^{m} {l(f(x_{i} ) - y_{i} )} $$

(9)

The C is the loss coefficient, which can be specified by users or optimized by genetic algorithm. $l$ is ${\upvarepsilon }$’s insensitive loss function, calculating the loss only if the difference between f(x) and y is greater than $\varepsilon$.

$$ l(z) = \left\{ {\begin{array}{*{20}c} {0,} & {|z| \le \varepsilon } \\ {|z| - \varepsilon ,} & {|z| > \varepsilon } \\ \end{array} } \right. $$

(10)

Considering the relaxation variable ${\upxi }$ and ${\hat{\xi }}_{{\text{i}}}$, the above equation can be rewritten as follows:

$$ \mathop {\min }\limits_{{w,b,{\upxi }_{i} ,{\hat{\xi }}_{i} }} \frac{1}{2}||{\mathbf{w}}||^{2} + C\sum\limits_{i = 1}^{m} {\left( {{\upxi }_{i} + {\hat{\xi }}_{i} } \right)} $$

(11)

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {{\upxi }_{i} = y_{i} - \left( {f\left( {{\mathbf{x}}_{i} } \right) + {\upvarepsilon }} \right),} & {y_{i} > f(x_{i} ) + {\upvarepsilon }} \\ {\xi_{i} = 0,} & {y_{i} \le f(x_{i} ) - {\upvarepsilon }} \\ \end{array} } \right. \hfill \\ \left\{ {\begin{array}{*{20}c} {{\hat{\xi }}_{i} = \left( {f\left( {{\mathbf{x}}_{i} } \right) - {\upvarepsilon }} \right) - y_{i} } & {y_{i} < f(x_{i} ) - {\upvarepsilon }} \\ {{\hat{\xi }}_{i} = 0,} & {y_{i} \ge f(x_{i} ) - {\upvarepsilon }} \\ \end{array} } \right. \hfill \\ \end{gathered} $$

(12)

To solve the above problems, we first introduce the Lagrange multiplier: $u_{i} \ge 0,u_{i}^{*} \ge 0,{\upalpha }_{i} \ge 0,{\upalpha }_{i}^{*} \ge 0$

Construct the Lagrange function:

$$ \begin{aligned} L\left( {w,b,\upxi ,\hat{\upxi },\upalpha ,\upalpha ^{*} ,u,u^{*} } \right) & = \frac{1}{2}||w||^{2} + C\sum\limits_{{i = 1}}^{m} {\left( {\upxi _{i} + \hat{\upxi }_{i} } \right)} \\ & \quad + \sum\limits_{{i = 1}}^{m} {\upalpha _{i} \left( {f(x_{i} ) - y_{i} - \upvarepsilon - \upxi _{i} } \right)} \\ & \quad + \sum\limits_{{i = 1}}^{m} {\upalpha _{i}^{*} \left( {y_{i} - f(x_{i} ) - \upvarepsilon - \hat{\upxi }_{i} } \right)} \\ & \quad + \sum\limits_{{i = 1}}^{m} {u_{i} (0 - \upxi _{i} } ) + \sum\limits_{{i = 1}}^{m} {u_{i}^{*} \left( {0 - \hat{\upxi }_{i} } \right)} \\ \end{aligned} $$

(13)

In order to find the minimum value of this function for $w,b,{\upxi },{\hat{\xi }}$, the model take the partial derivative of $w,\,b,\,{\upxi },\,{\hat{\xi }}$ respectively, and let the partial derivative be 0.

So the dual problem corresponding to SVR is follows:

$$ \mathop {\max }\limits_{{{\upalpha },{\upalpha }^{*} ,u,u^{*} }} L\left( {w,b,{\upxi },{\hat{\xi }},{\upalpha },{\upalpha }^{*} ,u,u^{*} } \right) $$

(14)

We can solve the dual problem if the KKT condition is satisfied, and the KKT condition is as follows:

$$ \begin{gathered} w = \sum\limits_{i = 1}^{m} {\left( {{\upalpha }_{i}^{*} - {\upalpha }_{i} } \right)} x_{i} \hfill \\ 0 = \sum\limits_{i = 1}^{m} {\left( {{\upalpha }_{i}^{*} - {\upalpha }_{i} } \right)} \hfill \\ C = {\upalpha }_{i} + u_{i} \hfill \\ C = {\upalpha }_{i}^{*} + u_{i}^{*} \hfill \\ \end{gathered} $$

(15)

After taking partial derivatives, we substitute the various obtained into the dual formula and simplify, then can obtain the simplified dual formula.

$$ \mathop {\max }\limits_{{{\upalpha },{\upalpha }^{*} }} \sum\limits_{i = 1}^{m} {y_{i} \left( {{\upalpha }_{i}^{*} - {\upalpha }_{i} } \right) - } \varepsilon \left( {{\upalpha }_{i}^{*} + {\upalpha }_{i} } \right) - \frac{1}{2}\left( {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {\left( {{\upalpha }_{i}^{*} - {\upalpha }_{i} } \right)\left( {{\upalpha }_{i}^{*} - {\upalpha }_{j} } \right)} } x^{T}_{i} x_{j} } \right) $$

(16)

SMO (Sequential Minimal Optimization) algorithm can solve the problem. Before solving, a* and a_i should be converted into a coefficient, because SMO algorithm aims at the case that sample x_i only has one parameter a_i. It can be inferred from the first two expressions of the KKT (Karush–Kuhn–Tucker) condition that at least one of a_i and a^*_i is 0. If we assume that $\lambda_{i} = \alpha_{i} - \alpha_{{_{i} }}^{*}$, we can infer that $|\lambda_{i} | = {\upalpha }_{i} + {\upalpha }_{{_{i} }}^{*}$. Since the formula continues to be reduced to a form with only one variable, we can calculate through the SMO algorithm. We also can conclude the value of ${\upalpha } - {\upalpha }^{*}$ to calculate the w.

We can figure up that if $0 < {\upalpha }_{i} < C$ and ${\upalpha }_{i} (f(x_{i} ) - y_{i} - {\upvarepsilon } - {\upxi }_{i} ) = 0$, there will be ${\upxi }_{i} = 0$, so the calculation formula is as follows:

$$ b = y_{i} + {\upvarepsilon } - w^{T} x_{i} $$

(17)

In the concrete implementation, the algorithm calculates all samples that meet the condition $0 < {\upalpha }_{i} < C$ and takes the average of results.

4 Construction of Optimal Weighted Combination Model

In practice, suppose we construct m single dam deformation model k_i(i = 1, 2, …m), and construct a composite model K_q = φ(k₁, k₂, …k_n), n ≤ m and q is the number of model combination.

Let the weight vector of each single model in the combined model be $p = [p_{1} ,p_{2} , \ldots p_{n} ]$, $\sum\nolimits_{j = 1}^{n} {p_{j} } = 1$, then the combined prediction model is as follows:

$$ K = p_{1} \hat{K}_{1} + p_{2} \hat{K}_{2} + \cdots + p_{n} \hat{K}_{n} = \sum\limits_{j = 1}^{n} {p_{j} \hat{K}_{j} } $$

(18)

The fitting residual of a single model can be expressed as follows:

$$ e_{ti} = k_{ti} - \hat{K}_{tj} \quad \left( {j = 1,2,..., m;\quad t = 1,2,..., n} \right) $$

(19)

Then each single forecast model can form a fitting residual matrix:

$$ V = \left[ {\sum\nolimits_{t = 1}^{n} {e_{ti} } e_{tj} } \right]\quad \left( {i,j = 1,2,..., m} \right) $$

(20)

The objective function is solved according to the least square principle.

$$ \left\{ {\begin{array}{*{20}l} {Q = \sum\limits_{i = 1}^{n} {e_{i}^{2} = \min } } \hfill \\ {s.t = \sum\limits_{j = 1}^{n} {p_{j} = 1} } \hfill \\ \end{array} } \right. $$

(21)

If R = [1, 1, …,1]T, the formula above becomes as follows:

$$ \left\{ {\begin{array}{*{20}l} {Q = \sum\limits_{i = 1}^{n} {e_{i}^{2} = P^{T} VP = \min } } \hfill \\ {s.t = \sum\limits_{j = 1}^{n} {p_{j} = R^{T} P = 1} } \hfill \\ \end{array} } \right. $$

(22)

The optimal weight vector is obtained:

$$ P_{0} = \frac{{V^{ - 1} R}}{{R^{T} V^{ - 1} R}} $$

(23)

By using the optimal weight ratio obtained from the above equation, the combined model prediction can maximize the information of each deformation model and reduce the mean square error of the prediction model, thus improving the accuracy of dam deformation analysis (Fig. 1).

Fig. 1

Flow of BP-SVM combination model modeling

5 Analysis of Examples

The paper selects the monitoring data of PL02 measuring point from 2006/5/14 to 2019/12/20 and conducts modeling using the data from 2006 to 2018. Then, we use the 2019 causative data to predict the 2019 effect size data and compare with the measured data to verify the effectiveness of the model.

Factors such as water level, temperature and time mainly affect the displacement and deformation of concrete gravity dams, and Table 1 shows the setting of influencing selection factors.

Table 1 List of factor settings

In order to prove the effectiveness and superiority of the combined model proposed in this paper, the example trains data and predicts result through the combined model, BP model and SVM model. Each model uses the same training samples and test data as control variables. In data processing, the input factor of the model is water level, temperature and aging, and the output factor is the predicted dam displacement.

The correlation coefficient is the fitting accuracy evaluation index in the model analysis and comparison. Table 2 shows the calculation results of the overall modeling accuracy index for each model. It can be seen that the training and prediction correlation coefficients of the combined model are higher than those of other models, indicating its high accuracy and more suitable for dam deformation prediction.

Table 2 Summary of overall modeling accuracy indicators

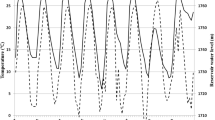
According to the modeling result and process line in Figs. 2 and 3, we can conclude that the monitoring data of PL02 measurement point from 2006 to 2018 are better modeled by the combined model.

Fig. 2

Comparison between calculated value of model and measured value

Fig. 3

The results of combination model and each sub-model are compared

Table 3 shows that the error of some calculated values in the optimal weighted combination model is larger than other models, the reason may be the influence of some abnormal points in the training process on the calculation results. In general, the calculation accuracy of the optimal weighted combination based on BP + SVM is higher than that of other models.

Table 3 Comparison between measured and predicted values of dam deformation

We can conclude from the above chart, that the fitting accuracy of BP model is lower than the SVM model. The combined model adopts the optimal weighted grouping method to reasonably determine the weight of the two models. Finally, the weight of the SVM model is higher, the BP is lower, and the relative relationship is reasonable. The fitting effect of the combined model is better than that of the sub-model, which indicates that the optimal weighted combination method is effective. It can be seen from Table 3 that the combined model is superior to the statistical model in all indicators of the training and prediction process, indicating that the optimization method adopted by the combined model is effective and further improves the calculation accuracy of the model.

6 Conclusion

Due to the complex dam working conditions and many influencing factors, a single analysis model is insufficient in stability. This paper adopts the optimal weighted combination method and organically combines the BP neural network model with support vector machine model (SVM), and the model can gain better and more stable modeling and prediction results. The model automatically determines the optimal weight, which improves the stability and prediction accuracy of the model and reduces the manual parameter adjustment.

The modeling and prediction results of the model are highly consistent with the measured results, and the overall accuracy of the model training results is good, indicating that the model is effective. From the results, the accuracy of the BP model is relatively low, while the accuracy of the SVM model is higher, and the combined model is better than other models. The optimal weighted combination method uses the best weight combination to ensure the reliability and stability of the final calculation results. When the model factors and options are not set properly, the optimal weighted combination model has stronger robustness and intelligence than the single model, which is helpful to obtain better calculation results.