Keywords

1 General Instructions

The safety of slope engineering (including dam slope and reservoir bank slope) is crucial to the safety of water conservancy projects. Slope stability analysis methods mainly include limit equilibrium method, limit analysis method and finite element method [1]. Generally speaking, the finite element method analysis methods are mainly divided into two categories, one method is to increase the gravity load, and the other method is to reduce the strength characteristics of the soil, i.e., the load increment method and the strength discount method. All the above-mentioned methods still use the traditional single factor of safety method, which is relatively easy to calculate, to assess the slope stability, but it is proved that this method does not effectively consider the uncertainty of the actual load and material parameters. Therefore, the introduction of the nonlinear stochastic finite element method, which takes into account the uncertainty, is more in line with the actual situation, and the improvement of computer performance and the continuous progress of numerical solution technology also makes the large-scale nonlinear and stochastic finite element analysis possible.

In the nonlinear stochastic finite element method, the selection of parameters related to soil spatial variability is extremely important, such as correlation distance, parameter mean value and variation coefficients. There are many ways to calculate the correlation distance, including Spatial average method, fitting sample autocorrelation function method, curve limit method, semi-variation function, mean average method and statistical simulation method, etc. [2]. However, in engineering practice, if it is not a particularly important slope project, the site survey data are always limited, and it is difficult to accurately estimate the relative distance of the soil parameters [3]. Song [4] summarized lots of soil parameters by the literatures and presented the corresponding value range. In the anisotropic soil, the vertical correlation distance ranges from 0.2 to 6 m, and the horizontal correlation distance ranges from 20 to 80 m. The specific correlation distance is related to the size of the model. Jiang [5] proposed that the value range of variation coefficients of internal friction angle and viscous force is [0.05, 0.2] and [0.2, 0.7].

To address the spatial variability of soil mechanical parameters in embankment dam projects, this paper combines the Monte-Carlo method with the nonlinear stochastic finite element method based on the viscoplastic method and the strength reduction method to propose a safety and stability analysis method in embankment dam projects, and develops a corresponding procedure to study the influence of the cohesion and internal friction angle variation coefficients on the distribution of FS, solves the reliability indexes using two different methods and comparative analysis is performed.

2 Slope Safety Analysis Method Based on Nonlinear Stochastic Finite Element Method

2.1 Local Average Method for Random Field Discretization

The common methods of random field discretization mainly include the center point method, the local average method, shape function interpolation method and so on. The center point method is simple and convenient and easy to program for uniform random field, whereas with low accuracy. Shape function interpolation method discretizes the original continuous random field into a still continuous function. It does not involve the calculation of the correlation between each unit caused by the random field. It only requires that the value of the random field at each node is known, so the calculation is relatively simple, more suitable for nonlinear and non-uniform random fields [6]. The local average method uses the local average value of each discrete unit to characterize the characteristics of each unit body, and the mutual covariance between discrete units can be used to characterize the correlation between them, which is more suitable for uniform random fields. Therefore, this paper adopts the local average method to discrete uniform random fields. For a two-dimensional continuous uniform random field α(x, y), the mean and variance are m and σ2, respectively, and the local average random field of element e is defined αe as [7]:

$$ \alpha_{e} \left( {x_{e} ,y_{e} } \right) = \frac{1}{{A_{e} }}\int\limits_{{\Omega_{e} }}^{{}} {\alpha (x,y)} {\text{d}}x{\text{d}}y $$
(1)

where \(A_{e}\) = area of element e; Ωe = domain of element e, the mean value of αe is:

$$ E(\alpha_{e} ) = E\left( {\frac{1}{{A_{e} }}\int\limits_{{\Omega_{e} }} {\alpha (x,y){\text{d}}x{\text{d}}y} } \right) = m $$
(2)

The covariance of any two elements is:

$$ Cov(\alpha_{e} ,\alpha_{{e^{^{\prime}} }} ) = \frac{{\sigma^{2} }}{{A_{e} A_{{e^{^{\prime}} }} }}\int\limits_{{\Omega_{e} }} {\int\limits_{{\Omega_{{e^{^{\prime}} }} }} {\rho (x - x^{^{\prime}} ,y - y^{^{\prime}} )} } {\text{d}}x{\text{d}}y{\text{d}}x^{^{\prime}} {\text{d}}y^{^{\prime}} $$
(3)

where ρ = autocorrelation function; σ = standard deviation. Do coordinate isoparametric transformation for integral of Eq. (3):

$$ x = \sum\limits_{i = 1}^{n} {N_{e}^{i} x_{e}^{i} } ,\;y = \sum\limits_{i = 1}^{n} {N_{e}^{i} y_{e}^{i} } $$
(4)

where n = number of nodes of element e; \(N_{e}^{i}\) = shape function of displacement pattern of element e; \(x_{e}^{i}\) and \(y_{e}^{i}\) = coordinate of nodes of element e. And do coordinate isoparametric transformation for integral of Eq. (3):

$$ Cov(\alpha_{e} ,\alpha_{e}^{^{\prime}} ) = \frac{{\sigma^{2} }}{{A_{e} A_{{e^{^{\prime}} }} }}\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\rho (r,s)\left| J \right|} } } } \left| {J^{^{\prime}} } \right|{\text{d}}\xi {\text{d}}\xi^{^{\prime}} {\text{d}}\eta {\text{d}}\eta^{^{\prime}} $$
(5)

where J = Jacobian matrix; ξ and η = variates of x and y after doing coordinate isoparametric transformation.

The random field correlation structure often uses autocorrelation functions in the form of triangular, exponential, second-order AR, Gaussian, etc. In this paper, the following two-dimensional Gaussian-type correlation functions are selected for calculation.:

$$ \rho (r,s) = \exp \left( { - \pi \left( {\frac{{r^{2} }}{{\theta_{h}^{2} }} + \frac{{s^{2} }}{{\theta_{v}^{2} }}} \right)} \right) $$
(6)

where θh = horizontal correlation distance; θv = vertical correlation distance; r and s = distance of two points in the horizontal direction and the distance of two points in the vertical direction.

2.2 Viscoplastic Method

There are two main methods for solving problems with material nonlinearity, which are “constant stiffness iterative method” and “variable stiffness method”. In this paper, the former method is adopted, which modifies the “load” vector on the right side of the stiffness equation during iteration to consider the nonlinearity of the problem. In each iteration of this method, the load vector is composed of external load and self-balancing “body load”. The viscoplastic method for generating body load is described below.

ZienKiewicz [8] proposed a variable load model that allowed the stress of the material to exceed the failure criterion within a limited “period”, which is the “time-step” derived by Cormeau [9] for numerical calculation of absolute stability, which was related to the assumed failure criterion. The time-step of materials Mohr–Coulomb widely used in geotechnical engineering is:

$$ \Delta t = \frac{{4(1 + v)(1 - 2v)}}{{E(1 - 2v + \sin ^{2} \phi )}} $$
(7)

If the viscoplastic strain rate is multiplied by a pseudo time step, the viscoplastic strain increment accumulated to the next time step can be obtained:

$$ \dot{\varepsilon }^{{{\text{VP}}}} { = }F\frac{\partial Q}{{\partial \sigma }} $$
(8)
$$ (\delta \varepsilon^{VP} )^{i} = \Delta t(\varepsilon^{.VP} )^{i} $$
(9)
$$ \left( {\Delta \varepsilon^{VP} } \right)^{i} = \left( {\Delta \varepsilon^{VP} } \right)^{i - 1} + \left( {\delta \varepsilon^{VP} } \right)^{i} $$
(10)

where \(\dot{\varepsilon }^{{{\text{VP}}}}\) = viscoplastic strain rate; \(\left( {\delta \varepsilon^{VP} } \right)^{i}\) = viscoplastic strain increment of time-step i; \(\left( {\Delta \varepsilon^{VP} } \right)^{i}\) = viscoplastic strain of time-step i; F = failure criterion function; Q = plastic potential function.

The body load is the result of adding up at each “time-step” within a strength reduction and integrating and summing over all elements containing Gaussian yield points as follows:

$$ P_{b}^{i} = P_{b}^{i - 1} + \sum\limits_{iel}^{nel} {\int {B^{T} D^{e} (\delta \varepsilon^{VP} )^{i} {\text{d}}\Omega } } $$
(11)

where \(P_{b}^{i}\) = body load at the i-th time-step; iel = element i, nel = number of elements; B = strain matrix; D = elastic matrix.

2.3 Strength Reduction Finite Element Method

Under the condition of constant external load, divide the slope soil strength parameters by the same reduction coefficient to obtain the cohesion and internal friction angle under the current reduction coefficient, and use the reduced soil parameters as the new the calculation parameters are substituted into the calculation. After several times of reductions, the slope soil reached a critical failure state and became unstable. The reduction coefficient at this time is defined as the FS of the slope, and the corresponding failure surface is the slippery surface of the slope instability. The strength parameter reduction formula is:

$$ c_{1} = \frac{{c_{0} }}{K} $$
(12)
$$ \varphi _{1} = \arctan \frac{{\tan \varphi _{0} }}{K} $$
(13)

where K = reduction coefficient; \(c_{0}\) and \(c_{1}\) = before and after reduced cohesive force; \( \varphi_{0}\) and \( \varphi_{1}\) = before and after reduced internal friction angle.

2.4 Criterion for Judging Slope Instability

Three methods are generally used to judge slope instability in finite element strength reduction analysis: (i) the numerical iteration of finite element does not converge; (ii) the displacement of characteristic points changes abruptly; (iii) the generalized plastic strain or equivalent plastic strain penetrates from the foot to the top of the slope.

Among them, the sudden change of displacement of characteristic points and plastic zone penetration usually need to be judged artificially after the post-processing of calculation results, and there is no better automatic computer identification technology or method at present because the stochastic finite element requires a large number of sampling calculations. In this paper, in order to facilitate a large number of sampling calculations, the method of numerical iterative non-convergence is used to determine the slope instability.

3 Example Analysis

3.1 A Calculation Example of Homogeneous Slope

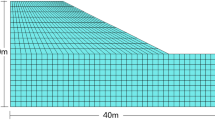
Using the homogeneous slope model in Dawson et al. [10] as the analysis object, the slope size is consistent with the literature, the slope height is 10 m, the slope angle is 45°, the horizontal constraint on both sides, the fixed constraint at the bottom, the weight is 20 kN/m3, the elastic modulus is 100 MPa, the Poisson’s ratio is 0.3, the cohesion is taken as 17.77 kPa, and the internal friction angle is 20°. The FS of the above parameters obtained by the limit equilibrium method in the software GeoStudio is 1.2, as shown in Fig. 3, which is consistent with the value of FS of grade 3 slopes under normal operation conditions in the specification. The calculation model and constraints are shown in Fig. 1. The background grid as shown in Fig. 2 is used for slope finite element analysis and random field dispersion.

Fig. 1
A slope model depicts an L-shaped structure with a 45 degrees slope and a section of 10 centimeters each at the base and the top of the slope.

Slope model and boundary conditions (M)

Full size image
Fig. 2
A random field and slope grid model depicts various grids on the surface of the structure.

Random field and slope grid division

Full size image
Fig. 3
An L-shaped structure with a slope between its two arms, and a distant point marked above it, labeled as 1200.

Calculation results of the limit equilibrium method

Full size image

3.2 A Calculation Example of Slope Considering Material Properties Random Field

In this section, on the basis of the homogeneous slope model and parameters in Sect. 3.1, the random field characteristics of cohesion and internal friction angle are considered, where the coefficient of variation of cohesion c and internal friction angle φ are taken as 0.2 and 0.05 respectively, and the horizontal and vertical correlation distances of both are taken as 5 m, and the correlation coefficients of both are taken as 0. The specific research ideas are as follows: (1) Firstly, the random field is sampled to get the corresponding random field of material properties, and then the slope displacement, stress and plastic zone results are calculated; (2) NMC times sampling of the random field; (3) Combined method M1: On the basis of (2), the reduction coefficients under each sample condition are obtained by strength reduction method and their distribution is calculated, and then the corresponding slope failure probability and reliability index are found; (4) MC direct method M2: On the basis of (2), the viscoplastic method is directly solved to determine the instability of the slope, and then the instability cases under all sample conditions are counted to obtain the failure probability and reliability index of the slope.

Calculation results of single sampling in random field

Based on the given random field parameters and the method in Sect. 2.1, the covariance matrix of the random field elements is obtained, and then the MC sampling of the random field is obtained using mathematical methods. By Fig. 4, normality of the once sampling results of the random field was examined, and the horizontal coordinate in the figure is the random field parameter values, and the vertical coordinates are the cumulative distribution probabilities of the parameter values in the horizontal coordinates. The distribution of points in the normal probability plots of the parameter random field is both approximated as a straight line, and their normal distribution properties can be verified accordingly.

Fig. 4
A graph plots probability versus random field value of C. The plot is nearly a straight line with a positive slope.

Normality verification of the cohesion distribution

Full size image

For this sampling, when the reduction coefficient is 1.28, the displacement changes abruptly, indicating that the FS of slope in this sample is 1.28. The calculation results of slope material characteristics and displacement under this reduction coefficient are shown in Figs. 5, 6, 7, 8 and 9. In Fig. 5, the maximum value and minimum value of cohesion are 18 kPa and 8 kPa respectively, and the mean value of cohesion after reduction is 13.83 kPa. In Fig. 6, the maximum value and minimum value of the internal friction angle are 17° and 14.2° respectively, and the mean value of the internal friction angle after reduction is 15.6°.

Fig. 5
The slope cohesion distribution plot for the structure depicts the maximum cohesion regions on the exposed top surfaces.

Slope cohesion distribution (Pa)

Full size image
Fig. 6
The internal friction angle distribution plot depicts scattered areas of high and low internal friction angle.

Distribution of internal friction angle of the slope (°)

Full size image
Fig. 7
The displacement distribution plot depicts scattered areas of high and low displacement. The displacement is maximum where the slope begins.

Displacement Ux (m)

Full size image
Fig. 8
The U y displacement plot depicts the high magnitude at the base of the structure and decreases as one moves up.

Displacement Uy (m)

Full size image
Fig. 9
A diagram depicts the plastic zone of the slope and where the slope begins, the magnitude is the greatest.

Plastic zone of the slope

Full size image

As shown in the figure, the maximum value of X-direction displacement is near the foot of the slope, which is 19 mm, and the displacement near the slope surface in the plastic zone is relatively large, between 16 and 19 mm; the maximum value of Y-direction displacement is at the top of the slope, which is 42 mm, and the overall trend of Y-direction displacement is larger at the top and smaller at the bottom; the plastic zone is shown in Fig. 9, plastic yielding occurs from the foot of the slope to the slip arc-like area in the middle of the slope.

Calculation of slope reliability based on combined method (M1)

MC strength reduction combined method to solve the reliability: the number of samples with the FS less than 1 in the strength reduction calculation after the random field sampling is considered as the number of slope failures Mf. The number of values of FS less than 1 in the distribution of FS and divided by the number of random field sampling NMC, the probability of failure can be obtained by Pf = Mf/NMC. When the basic variables are normally distributed, the reliability index is \(\beta = - \Phi^{ - 1} \left( {P_{f} } \right) = \Phi^{ - 1} \left( {1 - P_{f} } \right)\).

Figure 10 shows the statistical histogram distribution of the FS obtained by sampling random field for NMC times (NMC = 10,000). The corresponding probability cumulative distribution curve is shown in Fig. 11, and the specific description of each parameter in the figure is shown in Table 1. For this sampling, the mean value of the FS is 1.2467, slightly higher than 1.2 obtained by the limit equilibrium method. The values of FS are concentrated in [1.2, 1.3], and the highest frequency is about 1250. The failure probability obtained by M1 method is 0.0003, and the corresponding reliability index is 3.4316.

Fig. 10
A histogram plots the frequency of F S versus F S. The values taken into consideration are E subscript F S equals 1.2467, sigma subscript F S equals 0.0655, and N subscript M C equals 10000.

Frequency distribution of FS

Full size image
Fig. 11
A sigmoid curve depicts the cumulative distribution of F S.

Cumulative distribution of FS

Full size image
Table 1 Parameter values and calculation results
Full size table

Calculation of slope reliability based on MC direct sampling method (M2)

The calculation method of slope reliability based on MC direct sampling method: firstly, generate N groups of samples conforming to c and φ, and probability distribution and substitute into limit state function \(Z = g(c,\varphi )\) (when Z < 0, it means the slope fails; Z = 0,it is the limit state equation of the slope, which means the slope is in the limit state; Z > 0, it means the slope is in the reliable state and can meet the functional requirements), and Z1, Z2, …, ZN is a sample of the random variable Z with a capacity of N. If the number of samples in the failure zone is M, according to Bernoulli’s large number theorem, the failure probability can be approximately expressed as Pf = M/N. The reliability index is solved in the same way as in previous section.

When MC direct sampling method is used for slope stability analysis and calculation, the strength reduction is no longer considered, and the reduction coefficient is set as 1. The random field is sampled NMC times. The non-convergence of numerical iterations is taken as the criterion of slope instability, and the times of non-convergence are accumulated to obtain M, and the ratio of M to NMC is the failure probability.

3.3 Comparison of FS Distribution and Reliability Index Solution of M1 Method

On the basis of the slope calculations based on the random field in Sect. 3.2, the variation coefficients of c and φ is changed to analyze its influence on the distribution of FS. Material variability and calculation results of each group are shown in Table 1.

Note: The slight mutations in the distribution of Case3 and Case4 are caused by insufficient sampling, and the mutations will become smooth if the sampling number is increased.

It can be seen from Fig. 12 that, with the increase of COVc or COVφ, the reliability index gradually decreases, but in the ascending direction of COVc, the reliability index decreases at a faster speed and with a greater range. With different values of COVc (or COVφ), the distribution of the corresponding FS changes similarly when COVφ (or COVc) is changed, and the specific analysis is as follows: ① When COVc is set to 0.2: compare Figs. 10, 14 and 16, the mean value of FS decreases gradually with the increase of COVφ from 1.2467 to 1.2382, and the variance increases from 0.0655 to 0.093. The values of FS are concentrated in the area around 1.25, and the highest frequency is about 1250 times. ② When COVφ is set to 0.2: compare with Fig. 16 and Fig. 17, the distribution of FS becomes more dispersed after the COVc increase, and the smaller values of FS are more likely to appear. As shown in Fig. 16, values of FS are concentrated between [1.2, 1.25], with the highest frequency of about 1300 times. The values of FS of Fig. 17 are mainly distributed between [1.23, 1.25], and the highest frequency is only about 1000 times. ③ When the variability of φ is constant, the failure probability increases sharply with the increase of the variability of c, while the corresponding reliability index decreases rapidly. When the variability of c is kept constant, the failure probability increases relatively slowly with the increase of the variability of φ, and the reliability index decreases relatively slowly. Case1 has the lowest failure probability and the largest reliability index, which are 7 × 10−4 and 3.1947 respectively. ④ The variation trend of the mean value of FS is consistent with the reliability index, but opposite to the failure probability. While the mean value of FS decreases gradually, the reliability index also decreases gradually, and the failure probability increases gradually.

Fig. 12
A 3-D bar graph depicts the relationship between beta, C O V subscript c, and C O V subscript psi.

Relationship between material variability and reliability index

Full size image

The probability density and cumulative distribution curves of FS of each scheme are shown in Figs. 18 and 19: (1) when COVc is 0.2, the peak probability density of Case5 is the smallest \(\left( {PD_{\min }^{0.2} } \right)\). When COVc is 0.3, the peak probability density of Case2 is the highest \(\left( {PD_{\max }^{0.3} } \right)\). Where \(PD_{\min }^{0.2} > PD_{\max }^{0.3}\). (2) All schemes are sorted according to the descending order of the maximum probability density in the figure. The mean value of the probability density distribution graph decreases in this order, which shows that the normal distribution curve of each scheme moves to the left gradually. The variance of FS distribution increases in this order, which shows that the normal distribution curve and the cumulative distribution curve of each scheme gradually become more gentle.

3.4 Comparison Analysis of Reliability Indexes Obtained by M1 Method and M2 Method

In this section, MC direct sampling method (M2) is used to solve the slope failure probability and reliability indexes of the six groups of schemes in Sect. 3.3, and the results are compared with M1 method, as shown in Table 2:

Table 2 Comparison of the slope safety and reliability indexes obtained by different methods
Full size table

According to the above table and the results in Figs. 12, 13, 14, 15, 16 and 17, it can be found that: the reliability index obtained by M2 method is slightly smaller than that obtained by M1 method. In fact, the results are very similar, so it can be considered that the failure probability and reliability indexes obtained by using M1 method are reliable.

Fig. 13
A histogram plot of the frequency distribution of F S. The values taken into consideration are E subscript F S equals 1.2278, sigma subscript F S equals 0.1106, and N subscript M C equals 10000.

Frequency distribution of FS (Case2)

Full size image
Fig. 14
A histogram plot of the frequency distribution of F S. The values taken into consideration are E subscript F S equals 1.2445, sigma subscript F S equals 0.072, and N subscript M C equals 10000.

Frequency distribution of FS (Case3)

Full size image
Fig. 15
A histogram plot of the frequency distribution of F S. The values taken into consideration are E subscript F S equals 1.2246, sigma subscript F S equals 0.1184, and N subscript M C equals 10000.

Frequency distribution of FS (Case4)

Full size image
Fig. 16
A steep histogram plot of the frequency distribution of F S. The values taken into consideration are E subscript F S equals 1.2382, sigma subscript F S equals 0.093, and N subscript M C equals 10000.

Frequency distribution of FS (Case5)

Full size image
Fig. 17
A bell-shaped histogram plot of the frequency distribution of F S. The values taken into consideration are E subscript F S equals 1.2169, sigma subscript F S equals 0.1313, and N subscript M C equals 10000.

Frequency distribution of FS (Case6)

Full size image
Fig. 18
Hill-shaped probability density curves for 6 cases of F S.

Probability density of FS

Full size image
Fig. 19
Sigmoid cumulative density curves for 6 cases of F S.

Cumulative distribution of FS

Full size image

4 Conclusion

This paper proposes a slope safety analysis method based on the nonlinear stochastic finite element method, investigates the influence of the variability of the mechanical parameters of the slope soil on the distribution of FS, and uses two methods to solve and analyze the reliability index. The results shows that: the method can better simulate the spatial variability of materials; compared with the traditional single safety factor method, only a general empirical coefficient can be obtained, which cannot reflect the spatial variability of material parameters, the introduction of parameter random fields can reflect the spatial variability of material parameters in the mean, variance and distribution of the slope safety factor, and then combined with the reliability index to conduct a more comprehensive evaluation of the slope safety; the variability of soil parameters has a greater influence on the distribution of FS and reliability index, and as the variability of different parameters increases, the mean value of FS and slope reliability gradually decrease as the variability of different parameters increases.

In order to further improve the application effect of this method in actual engineering, the following research work is needed: the slope is regarded as a uniform random field in this slope calculation example, but there are different material partitions in actual engineering, and there is a certain correlation between different partitions, and the requirements for random field are more strict; the coefficient of variation of soil parameters and the correlation distance have significant effects on the calculation results, but there is less engineering information and lack of unified and clear standards for their values, so a large number of parameter experiments need to be carried out in the later stage to obtain reliable parameters for the distribution of soil properties.