Birkhoff Pseudospectral Method and Convex Programming for Trajectory Optimization

Abstract

Trajectory optimization, an optimal control problem (OCP) in essence, is an important issue in many engineering applications including space missions, such as orbit insertion of launchers, orbit rescue, formation flying, etc. There exist two kinds of solving methods for OCP, i.e., indirect and direct methods. For some simple OCPs, using the indirect methods can result in analytic solutions, which are not easy to be obtained for complicated systems. Direct methods transcribe an OCPs into a finite-dimensional nonlinear programming (NLP) problem via discretizing the states and the controls at a set of mesh points, which should be carefully designed via compromising the computational burden and the solution accuracy. In general, the larger number of mesh points, the more accurate solution as well as the larger computational cost including CPU time and memory [1]. There are many numerical methods have been developed for the transcription of OCPs, and the most common method is by using Pseudospectral (PS) collocation scheme [2], which is an optimal choice of mesh points in the reason of well-established rules of approximation theory [3]. Actually, there have several mature optimal control toolkits based PS methods, such as DIDO [4], GPOPS [5]. The resulting NLP problem can be solved by the well-known algorithm packages, such as IPOPT [6] or SNOPT [7]. However, these algorithms cannot obtain a solution in polynomial-time, and the resulting solution is locally optimal. Moreover, a good initial guess solution should be provided for complicated problems.

4.1 Introduction

Trajectory optimization, an optimal control problem (OCP) in essence, is an important issue in many engineering applications including space missions, such as orbit insertion of launchers, orbit rescue, formation flying, etc. There exist two kinds of solving methods for OCP, i.e., indirect and direct methods. For some simple OCPs, using the indirect methods can result in analytic solutions, which are not easy to be obtained for complicated systems. Direct methods transcribe an OCPs into a finite-dimensional nonlinear programming (NLP) problem via discretizing the states and the controls at a set of mesh points, which should be carefully designed via compromising the computational burden and the solution accuracy. In general, the larger number of mesh points, the more accurate solution as well as the larger computational cost including CPU time and memory [1]. There are many numerical methods have been developed for the transcription of OCPs, and the most common method is by using Pseudospectral (PS) collocation scheme [2], which is an optimal choice of mesh points in the reason of well-established rules of approximation theory [3]. Actually, there have several mature optimal control toolkits based PS methods, such as DIDO [4], GPOPS [5]. The resulting NLP problem can be solved by the well-known algorithm packages, such as IPOPT [6] or SNOPT [7]. However, these algorithms cannot obtain a solution in polynomial-time, and the resulting solution is locally optimal. Moreover, a good initial guess solution should be provided for complicated problems.

Convex optimization method provides a polynomial-time complexity for solving convex programming problem, and has been wildly used for solving OCP, especially for complicated space missions [8,9,10,11]. In convex optimization framework, the original OCP is converted into a second-order conic programming (SOCP) problem by using some convexification techniques and discretization on uniformly distributed points. To achieve sufficiently accurate solution, one way is to choose a large number of discretized points, which leads to extra computational burden, and an-other way is employing PS method [12,13,14]. In [15], the various discretization methods, including the zeroth order hold (ZOH), the first order hold (FOH), the classical Runge–Kutta fourth order integration method, and global PS methods (Chebyshev-Gauss-Lobatto, CGL, Legendre-Gauss-Radau, LGR) are considered in the convex optimization framework for solving the planetary powered landing trajectory optimization problem, and the authors con-clude that PS methods can provide more consistent solutions, which are less sensitive to the number of mesh points.

It is to note that only the cases of mesh points are considered in [15], while in some certain applications, especially aerospace applications, to achieve more accuracy, the more mesh points are required [16]. However, purely increasing will lead to ill-conditioned NLP problem [17], which is hard to solve or cannot to be solved. In order to overcome such ill-conditioned phenomenon, some well-conditioned PS methods for ordinary differential equations (ODEs) have been proposed in [17, 18], in which, Birkhoff PS method stemmed from Birkhoff interpolation [19] is introduced to solve higher-order ODEs. In [16, 19], the first-order Chebyshev Birkhoff PS (CBPS) method is proposed to transcribe general OCP into NLP, and the advantages of CBPS over other PS methods, especially for large mesh grids, is demonstrated by its application in solving an orbital transfer problem.

In this chapter, we apply PS methods using Bikrhoff polynomials to the convex optimization framework for OCPs, particularly, the first order and second-order Birkhoff PS (BPS) methods with LGL and CGL collocation schemes are applied to transcribe a class of cascaded second-order systems, which may be convex or not. The first-order BPS method in convex optimization framework is similar to that in [16], hence we focus on the PS transcription for convexified OCP by using second-order Birkhoff polynomials. The main contributions of this paper lie in two aspects: (1) the unified matrix formulation of OCP by using BPS method within the convex optimization framework is proposed and validated; and (2) the computational performances and solution accuracies resulted from various PS schemes are extensively exploited thereby a useful conclusion that, using BPS method renders the remarkable drops in the condition number for the generated programming problem therefore lowering the computational cost.

The remainder of this chapter is organized as follows. The preliminaries of convex programming and PS method for general convexified optimal control problems are presented in Sect. 4.2, then the proposed well-conditioned PS method via Birkhoff polynomials within the convex optimization framework is detailed in Sect. 4.3. The demonstrated examples of a simple cart problem as well as a rescue orbit searching problem for validating the effective-ness and efficiency of the proposed method are presented in Sect. 4.4 followed by the conclusions in Sect. 4.5.

4.2 Preliminaries of Convex Programming and PS Method for Optimal Control

In general, the free-final-time OCP can be converted into a fixed-final-time problem by normalizing the time into the domain of [0, 1], consequently, only the fixed-final-time problem is considered in this chapter. A typical OCP is given as the following problem G.

$$\begin{aligned} \mathrm{{Problem }}G \min J = \mathop \smallint \nolimits _{{t_0}}^{{t_f}} L(\mathbf{{x}},\mathbf{{u}})\mathrm{{d}}t \end{aligned}$$

(4.1)

$$\begin{aligned} \mathrm{{s}}{.\textrm{t}}{. }\ {\dot{\textbf{x}}} = \left[ \begin{array}{l} {\dot{\textbf{x}}}_1\\ {\dot{\textbf{x}}}_2 \end{array} \right] = \left[ \begin{array}{l} \mathbf{{x}}_2\\ \mathbf{{f}}(\mathbf{{x}}_1,\mathbf{{x}}_2,\textbf{u}) \end{array} \right] \buildrel \Delta \over = \mathbf{{F}}(\mathbf{{x}},\mathbf{{u}}) \end{aligned}$$

(4.2)

$$\begin{aligned} \mathbf{{P}}(\mathbf{{x}},\mathbf{{u}}) \le \mathbf{{0}} \end{aligned}$$

(4.3)

$$\begin{aligned} \mathbf{{x}}({t_0}) = {\mathbf{{x}}_0},{\boldsymbol{\psi }}(\mathbf{{x}}({t_f})) = \mathbf{{0}} \end{aligned}$$

(4.4)

where the prescribed time instants $t_0<t_f<\infty$, the state vector $\textbf{x}=[{\textbf{x}}_1^T,{\textbf{x}}_2^T]\in \mathbb {R}^{2n}$, the control vector $\textbf{u}\in \mathbb {R}^{m}$, ${\dot{\mathbf {x(t_0)}}}$ and ${\dot{\mathbf {x(t_f)}}}$ are specified with the boundary constraints (4.4), the nonlinear path constraints in (4.3) may be various form in terms of $\textbf{x}$ and $\textbf{u}$. The problem G is a kind of Lagrange problem, in which, the performance index (4.1) is the integral of Lagrange function [9] $L(\textbf{x},\textbf{u})$ on time domain $[t_0,t_f]$. According to the optimal control theory [20], other types including Mayer, Bollza, and Quadratic problems can be converted into a Lagrange problem. The nonlinear dynamics in (4.2) is a typical cascaded second-order system, which is widely used to formulate the linear motion of a spacecraft, such as the Mars landing [8], launch ascent [21], etc.

4.2.1 Convex Programming Method for OCP

To solve the general problem G by convex programming method, the performance index (4.1) and the constraints (4.2)$\sim$(4.4) should be the form of linear or second-order cone (SOC), thus the convexification techniques are required for converting the nonlinear or concave constraints to the corresponding convex formulation. The most important issue lies in the conversion process is to guarantee the solution of the converted problem is still that of the original problem.

For some typical problems with the form of G, which are relatively simple, one can introduce some auxiliary state and (or) control variables as well as some unique relaxation to obtain the convex versions of the original problems. Such procedure is called a lossless convexification technique, which can be found in [8, 9, 22, 23]. For general OCPs, successive convex programming (SCP) method is proposed for handling more general nonconvex constraints [10, 24,25,26]. The main idea of SCP is to solve a nonlinear and nonconvex problems via iteratively solving a series of local convex approximate problem using linearization on the solution of last iteration. Denote the solution of the $k\textrm{th}$ iteration to the original problem G as $\left\{ \textbf{x}^k,\textbf{u}^{k}\right\}$, thereby the following sequential convex version

$$\begin{aligned} \begin{aligned} \mathrm{{Problem }}SC:\min J = \mathop \smallint \nolimits _{{t_0}}^{{t_f}} \left[ {L({\mathbf{{z}}^k}) + {{\left[ {{L_z}({\mathbf{{z}}^k})} \right] }^T}(\mathbf{{z}} - {\mathbf{{z}}^k})} \right] dt\\ \quad \textrm{with}\quad \mathbf{{z}} = {[{\mathbf{{x}}^T},{\mathbf{{u}}^T}]^T}\\ \qquad s.t.\quad {{\dot{\textbf{x}}}_1} = {\mathbf{{x}}_\mathbf{{2}}}\\ \qquad \qquad \qquad {{\dot{\textbf{x}}}_2} = \mathbf{{a}}_1^k{\mathbf{{x}}_1} + \mathbf{{a}}_2^k{\mathbf{{x}}_2} + {\mathbf{{g}}^k}{} \mathbf{{u}} + {\mathbf{{c}}^k}\\ \mathrm{}{} \mathbf{{P}}({\mathbf{{z}}^k}) + \mathrm{{ }}{} \mathbf{{P}}_x^k(\mathbf{{z}} - {\mathbf{{z}}^k}) \le \mathbf{{0}}\\ \mathrm{}{} \mathbf{{x}}({t_0}) = {\mathbf{{x}}_\mathbf{{0}}}\\ \mathrm{}{\boldsymbol{\psi }}(\mathbf{{x}}_{{t_f}}^k) + {\boldsymbol{\psi }}_{{x_{tf}}}^k(\mathbf{{x}}({t_f}) - \mathbf{{x}}_{{t_f}}^k) = 0\\ \mathrm{}|\mathbf{{z}} - {\mathbf{{z}}^\mathbf{{k}}}| \le \varepsilon \end{aligned} \end{aligned}$$

(4.5)

which is a first-order approximation of the problem G, and the symbols denote the following:

(1) The performance index $L(\textbf{x},\textbf{u})$ is approximated by its Taylor first order expansion, and ${L_z}({\mathbf{{z}}^k}) = \partial L/\partial \mathbf{{z}}{|_{\mathbf{{z}} = {\mathbf{{z}}^k}}}$. Similarly the path constraints (4.3) and the boundary constraints (4.4) are first-orderly approximated, and

$$\begin{aligned} \mathbf{{P}}_z^k = \partial \mathbf{{P}}/\partial \mathbf{{z}}{|_{\mathbf{{z}} = {\mathbf{{z}}^\mathbf{{k}}}}},\mathbf{{\psi }}_{{x_{tf}}}^k = \partial \mathbf{{\psi }}/\partial {\mathbf{{x}}_{{\mathbf{{t}}_\mathbf{{f}}}}}{|_{{\mathbf{{x}}_{{\mathbf{{t}}_\mathbf{{f}}}}} = \mathbf{{x}}_{{\mathbf{{t}}_\mathbf{{f}}}}^\mathbf{{k}}}}. \end{aligned}$$

(2) The dynamic constraints (4.2) are linearized on the trajectory $\left\{ \textbf{x}^k,\textbf{u}^{k}\right\}$, and the linearizing coefficients are given by

$$\begin{aligned} \begin{array}{l} \mathbf{{a}}_1^k = \partial \mathbf{{f}}/\partial {\mathbf{{x}}_1}{|_{\mathbf{{x}} = {\mathbf{{x}}^k},\mathbf{{u}} = {\mathbf{{u}}^k}}},\mathbf{{a}}_2^k = \partial \mathbf{{f}}/\partial {\mathbf{{x}}_2}{|_{\mathbf{{x}} = {\mathbf{{x}}^k},\mathbf{{u}} = {\mathbf{{u}}^k}}}\\[2mm] {\mathbf{{g}}^k} = \partial \mathbf{{f}}/\partial \mathbf{{u}}{|_{\mathbf{{x}} = {\mathbf{{x}}^k},\mathbf{{u}} = {\mathbf{{u}}^k}}}\\[2mm] {\mathbf{{c}}^k} = \mathbf{{f}}({\mathbf{{x}}^k},{\mathbf{{u}}^k}) - \mathbf{{a}}_1^k\mathbf{{x}}_1^k - \mathbf{{a}}_2^k\mathbf{{x}}_1^k - {\mathbf{{g}}^k}{\mathbf{{u}}^k} \end{array} \end{aligned}$$

(4.6)

(3) The trust region constraints $|\mathbf{{z}} - {\mathbf{{z}}^\mathbf{{k}}}| \le \varepsilon$ are introduced in problem SC to ensure its solution is still that of original problem G, and the reason lies in that the first-order approximation is only reasonable within a small neighborhood around $\{ {\mathbf{{x}}^\mathbf{{k}}},{\mathbf{{u}}^\mathbf{{k}}}\}$.

For convex problem SC, one can use some appropriate discretizing methods, and let the states and controls on the discrete points be decision variables henceforth a convex programming problem (or an SOCP problem), which can be efficiently solved by the classical conjugate gradient method [13] or the popular primal-dual interior method, such as ECOS [27], Mosek [28].

Remark 1

Unlike the second-order approximations used in sequential quadratic programming (SQP) [29], the above procedure in the manner of first-order guarantees the approximations are convex and suitable be solved by efficient convex programming algorithms. In [10], the authors have presented a thoroughly theoretical analysis, and pointed out that, by introducing appropriate trust region constraints, the iterative solutions of the series problem SC will converge to that of the original problem G.

In this chapter, we concentrate on the PS method for problem SC, which contains various constraints and tedious bookkeeping, and may cause distractions. In fact, the emphasis of discretizing procedure is about the dynamic constraints, hence a distilled convex optimal control problem is given by

$$\begin{aligned} \mathrm{{Variables:}}{} \mathbf{{x}} = {[\mathbf{{x}}_1^T,\mathbf{{x}}_2^T]^T} \in {^{2n}},\mathbf{{u}} \in {^m},\tau \in [ - 1,1] \end{aligned}$$

(4.7)

$$\begin{aligned} \mathrm{{Problem }}C:\min J[\mathbf{{x}}( \cdot ),\mathbf{{u}}( \cdot )] = E(\mathbf{{x}}( - 1),\mathbf{{x}}(1)) \end{aligned}$$

(4.8)

$$\begin{aligned} \begin{aligned} s.t.\quad {{\dot{\textbf{ x}}}_1}(\tau ) = s{\mathbf{{x}}_2}(\tau )\\ \qquad {{\dot{\textbf{ x}}}_2}(\tau ) = s\left[ {{\mathbf{{a}}_1}{\mathbf{{x}}_1}(\tau ) + {\mathbf{{a}}_2}{\mathbf{{x}}_2}(\tau ) + \mathbf{{gu}}(\tau )} \right] \end{aligned} \end{aligned}$$

(4.9)

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \mathbf{{e}}(\mathbf{{x}}( - 1),\mathbf{{x}}(1)) = \mathbf{{0}} \end{aligned}$$

(4.10)

where the index function $E(\cdot )$ and the boundary constraints $\textbf{e}(\cdot )$ are reasonably supposed to be convex; the time mapping scale factor $s = dt/d\tau = ({t_f} - {t_0})/2$, which is resulted from that, the time dependent variable $t \in [{t_0},{t_f}]$ is converted into the PS time $\tau \in [ - 1,1]$ by using the mapping $t = ({t_f} - {t_0})\tau /2 + ({t_f} + {t_0})/2$.

In problem C, the dynamic constraint (4.9) and boundary constraint (4.9) are considered, while the path constraints $\textbf{P}(\cdot )$ are not considered for the convenience of subsequent discussions. It is a reasonable simplification, since the PS results generated for problem C can be easily recovered to problem SC as shown in [16, 30].

4.2.2 PS Method for Convex Optimal Control Problem

In PS optimal control techniques, any time signal $f(\cdot )$ can be expressed as a linear combination of a series of orthogonally Lagrange polynomials

$$\begin{aligned} f(\tau ) = \mathop \sum \limits _{i = 0}^N {f_i}\mathcal{L}{_i}(\tau ) \end{aligned}$$

(4.11)

where the spectral coefficient $f_i=f(\tau _i)$; ${\pi ^N}: = [{\tau _0},{\tau _1}, \ldots ,{\tau _N}]$ is the discrete point set such that $- 1 \le {\tau _0} \le {\tau _1} \le \cdots \le {\tau _{N - 1}} \le {\tau _N} \le 1$ and ${\mathcal{L}_i} \in {P_N}$ are the Lagrange orthogonally interpolating polynomials at the freedom of degree N, which satisfy the Kronecker relationship

$$\begin{aligned} {\mathcal{L}_j}({\tau _i}) = {\delta _{ij}} \end{aligned}$$

(4.12)

Differentiating (4.11) and evaluating $f(\tau )$ on the discrete points yields:

$$\begin{aligned} {\dot{f}}({\tau _i}) = \sum \limits _{j = 0}^N {{f_j}} \dot{\mathcal{L}}{_j}({\tau _i}) \buildrel \Delta \over = {\dot{\textbf{ f}}} = \mathcal{D}{} \mathbf{{f}} \end{aligned}$$

(4.13)

where the PS differentiation matrix (PSDM) $\mathcal{D} \in {^{(N + 1) \times (N + 1)}}$ is given by ${d_{ij}} = {\dot{\mathcal{L}}_j}({\tau _i})$ for $0 \le i,j \le N$ ; and $\mathbf{{f}} = {[{f_0}, \ldots ,{f_N}]^T}$. It’s to note that the higher-order differentiation matrix is given by [31]

$$\begin{aligned} {\mathcal{D}^{(k)}} = \mathcal{D}\mathcal{D} \ldots \mathcal{D} = {\mathcal{D}^k} \end{aligned}$$

(4.14)

Particularly for second differential of $f(\tau )$, we have

$$\begin{aligned} {\ddot{\textbf{f}}} = {\mathcal{D}^{(2)}}{} \mathbf{{f}} \end{aligned}$$

(4.15)

The best choices for $\mathcal{L}_i$ are the Legendre and Chebyshev polynomials [30] henceforth the Legendre and Chebyshev PS methods. When mesh points defined by ${\tau _i} \in ( - 1,1)$, the mesh points are Gauss points, while for Gauss-Labotto points, ${\tau _i} \in [ - 1,1]$ contain the two boundary points, and for Gauss-Radau points, ${\tau _i} \in ( - 1,1]$ or ${\tau _i} \in [ - 1,1)$. Since the boundary points must be constrained in many OCPs, Legend-Gauss-Labotto (LGL) and Chebyshev-Gauss-Labotto (CGL) collocation schemes are usually used in PS methods [32].

The PS transcription by using (4.13) for the general problem G can be found in [5, 33]. Here two types of PS transcription with matrix formulations for the convex problem C are presented as follows.

(1) Consider the dynamic constraints in problem C as a first-order system, and let

$$\begin{aligned} \begin{array}{l} \mathbf{{X}} = {[{\mathbf{{x}}_0},{\mathbf{{x}}_1}, \ldots ,{\mathbf{{x}}_N}]^T} = {[\mathbf{{x}}({\tau _0}),\mathbf{{x}}({\tau _1}), \ldots ,\mathbf{{x}}({\tau _N})]^T} \in {^{(N + 1) \times 2n}}\\ \mathbf{{U}} = {[{\mathbf{{u}}_0},{\mathbf{{u}}_1}, \ldots ,{\mathbf{{u}}_N}]^T} = {[\mathbf{{u}}({\tau _0}),\mathbf{{u}}({\tau _1}), \ldots ,\mathbf{{u}}({\tau _N})]^T} \in {^{(N + 1) \times m}} \end{array} \end{aligned}$$

(4.16)

Using (4.13) yields

$$\begin{aligned} \mathcal{D}{} \mathbf{{X}} = {\dot{\textbf{ X}}} \end{aligned}$$

(4.17)

For the convenience of representation, rewrite the dynamic constraint (4.9) in problem C as

$$\begin{aligned} {\dot{\textbf{ x}}}(\tau ) = \left[ {\begin{array}{*{20}{c}} {{{\dot{\textbf{ x}}}_1}(\tau )}\\ {{{\dot{\textbf{ x}}}_2}(\tau )} \end{array}} \right] = s\left[ {\begin{array}{*{20}{c}} \mathbf{{0}}&{}\mathbf{{I}}\\ {{\mathbf{{a}}_1}}&{}{{\mathbf{{a}}_\mathbf{{2}}}} \end{array}} \right] \mathbf{{x}}(\tau ) + s\left[ {\begin{array}{*{20}{c}} \mathbf{{0}}\\ \mathbf{{g}} \end{array}} \right] \mathbf{{u}}(\tau ) \buildrel \Delta \over = \mathbf{{F}}(\mathbf{{x}},\mathbf{{u}}) \end{aligned}$$

(4.18)

Denote

$$\begin{aligned} \mathcal{F}\left( {\mathbf{{X}},\mathbf{{U}}} \right) = {[{\mathbf{{F}}_0},{\mathbf{{F}}_1}, \ldots ,{\mathbf{{F}}_N}]^T} = {[\mathbf{{F}}(\mathbf{{x}}({\tau _0}),\mathbf{{u}}({\tau _0})),\mathbf{{F}}(\mathbf{{x}}({\tau _1}),\mathbf{{u}}({\tau _1})), \ldots ,\mathbf{{F}}(\mathbf{{x}}({\tau _N}),\mathbf{{u}}({\tau _N}))]^T} \end{aligned}$$

(4.19)

Thus, problem C can be transcribed as

$$\begin{aligned} \begin{array}{l} \mathrm{{Decision\ Variables}}:\mathbf{{X}} = \in {^{(N + 1) \times 2n}},\mathbf{{U}} \in {^{(N + 1) \times m}}\\ \mathrm{{Problem\ }}DPSC1:\min {J^N}[\mathbf{{X}},\mathbf{{U}}]: = E({\mathbf{{x}}_0},{\mathbf{{x}}_N})\\ \qquad \qquad s.t.\qquad \mathrm{{ }}\mathcal{D}{} \mathbf{{X}} = \mathcal{F}\left( {\mathbf{{X}},\mathbf{{U}}} \right) \\ \qquad \qquad \qquad \qquad \mathbf{{e}}({\mathbf{{x}}_0},{\mathbf{{x}}_N}) = \mathbf{{0}} \end{array} \end{aligned}$$

(4.20)

(2) An alternative PS method for problem C is taking its dynamic constraints as a second-order systems:

$$\begin{aligned} {{\ddot{\textbf{x}}}_1}(\tau ) = s{{\dot{\textbf{ x}}}_2}(\tau ) = {s^2}\left[ {{\mathbf{{a}}_1}{\mathbf{{x}}_1}(\tau ) + {\mathbf{{a}}_2}{{\dot{\textbf{ x}}}_\mathbf{{1}}}(\tau ) + \mathbf{{gu}}} \right] \buildrel \Delta \over = \mathbf{{f}}({\mathbf{{x}}_\mathbf{{1}}}(\tau ),{{\dot{\textbf{ x}}}_1}(\tau ),\mathbf{{u}}(\tau )) \end{aligned}$$

(4.21)

and let

$$\begin{aligned} {\mathbf{{X}}_1} = {[{\mathbf{{x}}_1}_0,{\mathbf{{x}}_1}_1, \ldots ,{\mathbf{{x}}_1}_N]^T} = {[{\mathbf{{x}}_1}({\tau _0}),{\mathbf{{x}}_1}({\tau _1}), \ldots ,{\mathbf{{x}}_1}({\tau _N})]^T} \in {^{(N + 1) \times n}} \end{aligned}$$

(4.22)

$$\begin{aligned} \mathcal{F}({\mathbf{{X}}_1},{{\dot{\textbf{ X}}}_1},\mathbf{{U}}) = {[{\mathbf{{f}}_0}, \ldots ,{\mathbf{{f}}_N}]^T} = {[\mathbf{{f}}({\mathbf{{x}}_1}({\tau _0}),{{\dot{\textbf{ x}}}_1}({\tau _0}),\mathbf{{u}}({\tau _0})) \ldots ,\mathbf{{f}}({\mathbf{{x}}_1}({\tau _N}),{{\dot{\textbf{ x}}}_1}({\tau _N}),\mathbf{{u}}({\tau _N}))]^T} \end{aligned}$$

(4.23)

thus, the system (4.18) can be transcribed as

$$\begin{aligned} \mathcal{D}{\mathbf{{X}}_1} = {{\dot{\textbf{ X}}}_1} = s{\mathbf{{X}}_2} = s{[{\mathbf{{x}}_{20}},{\mathbf{{x}}_{21}}, \ldots ,{\mathbf{{x}}_{2N}}]^T} = s{[{\mathbf{{x}}_2}({\tau _0}),{\mathbf{{x}}_2}({\tau _1}), \ldots ,{\mathbf{{x}}_2}({\tau _N})]^T} \end{aligned}$$

(4.24)

and

$$\begin{aligned} {\mathcal{D}^{(2)}}{\mathbf{{X}}_1} = {{\ddot{\textbf{X}}}_1} =\mathcal{F}({\mathbf{{X}}_1},{\dot{\textbf{ X}}_1},\mathbf{{U}})=\mathcal{F}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}}) \end{aligned}$$

(4.25)

Combining (4.21), (4.25), problem C can be transcribed as the following second-order form:

$$\begin{aligned} \begin{array}{l} \mathrm{{Decision\ Variables}}:{\mathbf{{X}}_1} \in {^{(N + 1) \times n}},\mathbf{{U}} \in {^{(N + 1) \times m}}\\ \mathrm{{Temporal\ Variable}}:\mathrm{{}}{\mathbf{{X}}_2} = \mathcal{D}{\mathbf{{X}}_1}/s\\ \mathrm{{Problem\ }}DPSC2:\min {J^N}[\mathbf{{X}},\mathbf{{U}}]: = E({\mathbf{{x}}_0},{\mathbf{{x}}_N}),\mathrm{{ }}{} \mathbf{{X}} = {[\mathbf{{X}}_1^T,{\mathbf{{X}}_\mathbf{{2}}}^T]^T}\\ \mathrm{{\qquad \qquad }}s.t.\mathrm{{\qquad \qquad \quad }}\mathcal{D}{^{(2)}}{\mathbf{{X}}_1} = \mathcal{F}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}})\\ \mathrm{{\qquad \qquad \qquad \qquad }}{} \mathbf{{e}}({\mathbf{{x}}_0},{\mathbf{{x}}_N}) = \mathbf{{0}} \end{array} \end{aligned}$$

(4.26)

where the temporal variable $\mathbf{{X}}_2$ is algebraically represented by the decision variable $\mathbf{{X}}_1$.

It is obviously that the number of decision variables in problem DPSC2 is only half of that in problem DPSC2, and this will reduce the scale of convexified problem and alleviate the requirement of computational memory. It is to note that such reduction of decision variables will make the transcribed problem denser, which will undermine the solving efficiency for some convex optimization solver. The PSDM $\mathcal{D}$ and $\mathcal{D}^{(2)}$ usually include large round-off error which is resulted from the large condition number [34], particularly, the condition numbers of the generated problems DPSC1 and DPSC2, irrespectively, dramatically grow in the manner of $\mathcal{O}(N^3)$ and $\mathcal{O}(N^4)$ (shown in Fig. in the subsequent of this chapter), where N is the number of mesh grids. The overlarge condition number will lead to an ill conditioned problem DPSC1 and DPSC2, which are difficult to solve since the numerically unstable phenomenon accompanying with the large condition number. Hence, the mesh grid number should be limited to alleviate numerical difficulties, meanwhile, the limited mesh grid number potentially undermines the pursuit of more accurate solution.

Actually, in order to reduce the condition number, there have many studies (see [17] and references therein) to find an appropriate preconditioner $\textbf{M}$ for PS method with the forms of (4.20) and (4.26), such that the discretized dynamic constrains can be written as

$$\begin{aligned} \mathbf{{M}}\mathcal{D}{} \mathbf{{X}} = \mathbf{{M}}\mathcal{F}(\mathbf{{X}},\mathbf{{U}}) \end{aligned}$$

(4.27)

for (4.20), or

$$\begin{aligned} \mathbf{{M}}{\mathcal{D}^{(2)}}{} \mathbf{{X}} = \mathbf{{M}}\mathcal{F}({\mathbf{{X}}_1},{\mathbf{{X}}_2}{} \mathbf{{U}}) \end{aligned}$$

(4.28)

for (4.26). The function of the matrix $\textbf{M}$ is to reduce the condition number of the matrix equations resulted by $\textbf{M}\mathcal{D}$ or $\mathbf{{M}\mathcal{D}^{(2)}}$. However, given a non-diagonal matrix $\textbf{M}$, the sparsity of the right hand of (4.27) and (4.28) will decrease therefore increasing the computational burden of the resulted mathematical programming problem [16]. An alternative method is show in the next section, in which, the use of Birkhoff interpolating polynomials [18] provides a new PS method by which solutions can be obtained over thousands of mesh points in a stable manner.

4.3 Well-Conditioned Second-Order Birkhoff PS Method

4.3.1 Birkhoff Interpolation at GL Points

Let $f(\tau )$ be a second-order continuously differentiable function on the interval $\tau \in [-1,1]$, then the second-order Birkhoff interpolation polynomial $f^{N}(\tau )$ is given as

$$\begin{aligned} {f^N}(\tau ): = f({\tau _0}){B_0}(x) + \sum \limits _{i = 1}^{N - 1} {\ddot{f}({\tau _i})} {B_i}(\tau ) + f({\tau _N}){B_N}(\tau ),\tau \in [ - 1,1] \end{aligned}$$

(4.29)

where ${\pi ^N} = [{\tau _0},{\tau _1}, \ldots ,{\tau _N}]$ with $\tau _0 = -1$ and $\tau _N = 1$ is a GL point grid, and ${B_i}(i = 0,\ldots ,N)$, the counterpart of the Lagrange basis polynomials $\left\{ \mathcal{L}\right\} _{i=0}^N$, are the Birkhoff interpolation basis polynomials of order N or less, meanwhile, the following interpolation condition on mesh points must be satisfied:

$$\begin{aligned} {\ddot{f}^N}({\tau _i}) = \ddot{f}({\tau _i})\,\,\mathrm{{ for }}\,\,1 \le i \le N - 1\,\,\mathrm{{and }}\,\,{f^N}( \pm 1) = f( \pm 1) \end{aligned}$$

(4.30)

If the interpolation (4.29) exists, then $B_i$ satisfy the following [18]

$$\begin{aligned} \begin{array}{l} {B_0}({\tau _0}) = 1,\mathrm{{ }}{B_N}({\tau _0}) = 0,\mathrm{{ }}{B_j}({\tau _0}) = 0, j = 1, \ldots ,N - 1\\ {B_0}({\tau _N}) = 0,\mathrm{{ }}{B_N}({\tau _N}) = 1,\mathrm{{ }}{B_j}({\tau _N}) = 0, j = 1, \ldots ,N - 1\\ {{\ddot{B}}_0}({\tau _i}) = 0,\mathrm{{ }}{{\ddot{B}}_N}({\tau _i}) = 0, {{\ddot{B}}_j}({\tau _i}) = {\delta _{ij}}\mathrm{{ }}i = 1, \ldots ,N - 1;j = 1, \ldots ,N - 1 \end{array} \end{aligned}$$

(4.31)

According to Theorem 3.1 proposed in [18], $B_i$ can be defined in terms of the Lagrange basis polynomials $\{ {\tilde{\mathcal{L}}_i}\} _{i = 1}^{N - 1}$ of degree $N-2$, therefore

$$\begin{aligned} \begin{array}{l} {B_0}(\tau ) = \frac{{1 - \tau }}{2}\\[2mm] {B_i}(\tau ) = \frac{{1 + \tau }}{2}\int _{ - 1}^1 {(\tau - 1)} {{\tilde{\mathcal{L}}}_i}(\tau )d\tau + \int _{ - 1}^\tau {(\tau - t)} {{\tilde{\mathcal{L}}}_i}(t)dt,j = 1, \ldots ,N - 1\\[2mm] {B_N}(\tau ) = \frac{{1 + \tau }}{2}. \end{array} \end{aligned}$$

(4.32)

Evaluate the Birkhoff basis interpolation polynomials on the given GL points $\pi ^{N}$, and let ${b_{ij}} = {B_j}({\tau _i})$, thus the second-order Birkhoff PS integration matrix (BPSIM) as

$$\begin{aligned} \begin{array}{l} \mathcal{B} = [{b_{ij}}]{|_{0 \le i,j \le N}} \in {^{(N + 1) \times (N + 1)}}\\ \mathcal{B}_{in}^{} = [{b_{ij}}]{|_{1 \le i,j \le N - 1}} \in {^{(N - 1) \times (N - 1)}} \end{array} \end{aligned}$$

(4.33)

Using the matrix defined in (4.33), rewrite (4.29) on, we henceforth have:

$$\begin{aligned} \mathcal{B}{{\tilde{\textbf{f}}}^{(2)}} = \mathbf{{f}} \end{aligned}$$

(4.34)

where ${{\tilde{\textbf{f}}}^{(2)}} {=} {[f({\tau _0}),\ddot{f}({\tau _1}), \ldots ,\ddot{f}({\tau _{N - 1}}),f({\tau _N})]^T},\mathbf{{f}} {=} {[f({\tau _0}),f({\tau _1}), \ldots , f({\tau _{N - 1}}),}{ f({\tau _N})]^T}$. In light of (4.13), differentiating two sides of (4.34) with respect to PS time yields

$$\begin{aligned} \mathcal{D}\mathcal{B}{{\tilde{\textbf{f}}}^{(2)}} = {\mathcal{B}^{(1)}}{{\tilde{\textbf{f}}}^{(2)}} = \mathcal{D}{} \mathbf{{f}} = {\dot{\textbf{ f}}} \end{aligned}$$

(4.35)

and, second-order differentiating has

$$\begin{aligned} {\mathcal{D}^{(2)}}\mathcal{B}{{\tilde{\textbf{f}}}^{(2)}} = {\mathcal{B}^{(2)}}{{\tilde{\textbf{f}}}^{(2)}} = {\mathcal{D}^{(2)}}{} \mathbf{{f}} = {\ddot{\textbf{f}}} \end{aligned}$$

(4.36)

The above equations can be generalized as [18]

$$\begin{aligned} {\mathcal{B}^{(k)}} = {\mathcal{D}^{(k)}}\mathcal{B} = {\mathcal{D}^k}\mathcal{B} = \mathcal{D}{\mathcal{B}^{(k - 1)}},k \ge 1 \end{aligned}$$

(4.37)

Recall (4.15), and replace the first row and the last row of $\mathcal{D}^{(2)}$ by ${\mathbf{{e}}_1} = [1,0, \ldots ,0]$ and ${\mathbf{{e}}_1} = [1,0, \ldots ,0]$, respectively, therefore a matrix denoted by ${\tilde{\mathcal{D}}}^{(2)}$. Then there has

$$\begin{aligned} {\widetilde{\mathcal{D}}^{2}}{} \mathbf{{f}} = {{\tilde{\textbf{f}}}^{2}} \end{aligned}$$

(4.38)

From (4.34) and (4.38), it is obvious that ${\widetilde{\mathcal{D}}^{2}}{} \mathbf{{f}} = {\widetilde{\mathcal{D}}^{2}}\mathcal{B}{{\tilde{\textbf{f}}}^{(2)}} = {\mathbf{{\widetilde{f}}}^{(2}}$, consequently, we have

$$\begin{aligned} {\widetilde{\mathcal{D}}^{2}}\mathcal{B} = {\mathbf{{I}}_{N + 1}},\mathrm{{ }}\mathcal{D}_{in}^{2}{\mathcal{B}_{in}} = {\mathbf{{I}}_{N - 1}} \end{aligned}$$

(4.39)

where $\mathcal{D}_{in}^{(2)}$ is a submatrix of ${\mathcal{D}^{(2)}}$, i.e, $\mathcal{D}_{in}^{2} = {[{d_{i,j}}]_{1 \le i,j \le N - 1}}$ ; and $\textbf{I}^{n}$ is an identity matrix.

According to (4.39), we can compute $\mathcal{B}$ by the inverse of ${\widetilde{\mathcal{D}}^{2}}$. Unfortunately, the condition number of ${\widetilde{\mathcal{D}}^{2}}$ will dramatically increase for the overlarge mesh points, and this will lead to the loss of accuracy for the matrix inverse computation. Consequently, it is necessary to formulate the Birkhoff integration matrix in accordance with (4.32), and the details for computing $\mathcal{B}$ can be found in [18].

Besides the second-order Birkhoff interpolation polynomial given by (4.29), one can easily obtain the first-order Birkhoff polynomial and the corresponding first-order BPSIM. The applications of first-order BPSIM for the OCP are demonstrated in [18, 35], in which, the OCP is transcribed into an NLP problem by first-order Birkhoff PS method. The interesting readers can found the details about first-order BPSIM in [35].

4.3.2 Preconditioned Birkhoff PS Method

It is possible to facilitate solving problem DPSC2 by using Birkhoff PSIM as preconditioners. Let the mesh grid ${\pi ^N} = [{\tau _0},\tau _{in}^N,{\tau _N}]$ where ${\pi }_{in}^{N}$ is the set of inner points except boundary points $\tau _0$ and $\tau _N$, and partition the algebraic equation $\mathcal{D}{^{(2)}}{\mathbf{{X}}_1} = \mathcal{F}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}})$ in (4.26) as

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {d_{0,0}^{(2)}}&{}{\mathbf{{d}}_{0,1:N - 1}^{(2)}}&{}{d_{0,N}^{(2)}}\\ {\mathbf{{d}}_{1:N - 1,0}^{(2)}}&{}{{\mathcal{D}_{in}}}&{}{\mathbf{{d}}_{1:N - 1,N}^{(2)}}\\ {d_{N,0}^{(2)}}&{}{\mathbf{{d}}_{N,1:N - 1}^{(2)}}&{}{d_{N,N}^{(2)}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{\mathbf{{X}}_{10}}}\\ {{\mathbf{{X}}_{1in}}}\\ {{\mathbf{{X}}_{1N}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathcal{F}_0}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}})}\\ {{\mathcal{F}_{in}}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}})}\\ {{\mathcal{F}_N}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}})} \end{array}} \right] \end{aligned}$$

(4.40)

where $d_{i,j}^{(2)}$ is the entry of the second PSDM ${\mathcal{D}^{(2)}}$. We henceforth have

$$\begin{aligned} {\mathcal{D}_{in}}{\mathbf{{X}}_{in}} = {\mathcal{F}_{in}}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}}) - \mathbf{{d}}_{1:N - 1,0}^{(2)}{\mathbf{{X}}_{10}} - \mathbf{{d}}_{1:N - 1,N}^{(2)}{\mathbf{{X}}_{1N}} \end{aligned}$$

(4.41)

Left-multiplying both sides of (4.41) by $\mathcal{B}^{in}$ and using (4.39) yield

$$\begin{aligned} {\mathbf{{X}}_{in}} = {\mathcal{B}_{in}}{\mathcal{F}_{in}}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}}) - {\mathcal{B}_{in}}{} \mathbf{{d}}_{1:N - 1,0}^{(2)}{\mathbf{{X}}_{10}} - {\mathcal{B}_{in}}{} \mathbf{{d}}_{1:N - 1,N}^{(2)}{\mathbf{{X}}_{1N}} \end{aligned}$$

(4.42)

Meanwhile, the boundary points at $\tau _0$ and $\tau _N$ are constrained by

$$\begin{aligned} \mathcal{D}_0^{(2)}{\mathbf{{X}}_1} = \mathcal{F}({\mathbf{{X}}_{10}},{\mathbf{{X}}_{20}},{\mathbf{{U}}_0}),\mathcal{D}_N^{(2)}{\mathbf{{X}}_1} = \mathcal{F}({\mathbf{{X}}_{1N}},{\mathbf{{X}}_{2N}},{\mathbf{{U}}_N}) \end{aligned}$$

(4.43)

where a matrix with subscript i represents the $i\textrm{th}$ row vector of the matrix.

Based on (4.41) (4.43), the preconditioned problem DPSC2 is given as follows

$$\begin{aligned} \begin{array}{l} \mathrm{{Decision Variables\ }}:{\mathbf{{X}}_1} \in {^{(N + 1) \times n}},\mathbf{{U}} \in {^{(N + 1) \times m}}\\ \mathrm{{Temporal Variable\ }}:\mathrm{{ }}{\mathbf{{X}}_2} = \mathcal{D}{\mathbf{{X}}_1}/s\\ \mathrm{{Problem\ }}P\mathrm{{ - }}DPSC2:\min {J^N}[\mathbf{{X}},\mathbf{{U}}]: = E({\mathbf{{x}}_0},{\mathbf{{x}}_N}),\mathrm{{ }}{} \mathbf{{X}} = {[\mathbf{{X}}_1^T,{\mathbf{{X}}_\mathbf{{2}}}^T]^T}\\ \mathrm{{\qquad \qquad \qquad }}s.t.\mathrm{{\quad }}\mathcal{D}_0^{(2)}{\mathbf{{X}}_1} = \mathcal{F}({\mathbf{{X}}_{10}},{\mathbf{{X}}_{20}},{\mathbf{{U}}_0}),\mathrm{{ }}\\ \mathrm{{ \qquad \qquad \qquad \qquad }}{\mathbf{{X}}_{in}} = {\mathcal{B}_{in}}{\mathcal{F}_{in}}({\mathbf{{X}}_1},{\mathbf{{X}}_2},\mathbf{{U}}) - {\mathcal{B}_{in}}{} \mathbf{{d}}_{1:N - 1,0}^{(2)}{\mathbf{{X}}_{10}} - {\mathcal{B}_{in}}{} \mathbf{{d}}_{1:N - 1,N}^{(2)}{\mathbf{{X}}_{1N}}\mathrm{{ }}\\ \mathrm{{ \qquad \qquad \qquad \qquad }}\mathcal{D}_N^{(2)}{\mathbf{{X}}_1} = \mathcal{F}({\mathbf{{X}}_{1N}},{\mathbf{{X}}_{2N}},{\mathbf{{U}}_N})\\ \mathrm{{ \qquad \qquad \qquad \qquad }}{} \mathbf{{e}}({\mathbf{{x}}_0},{\mathbf{{x}}_N}) = \mathbf{{0}} \end{array} \end{aligned}$$

(4.44)

4.3.3 Birkhoff PS Method for Convex Optimal Control

In order to apply the Birkhoff interpolates of the previous subsection to problem C. Denote the unknown optimization variables over the mesh grid ${\pi }^N$ by

$$\begin{aligned} \mathbf{{V}}^{N} = [\mathbf{{x}}_{10}, \mathbf{{x}}_{11},\ldots , \mathbf{{x}}_{1N}]^{T} = [ {\mathbf{{x}}_1}({\tau _0}), { {\ddot{\textbf{x}}}_1}({\tau _1}), \ldots , { {\ddot{\textbf{x}}}_{1(N-1)}}({\tau _{N-1}}), {\mathbf{{x}}_1}({\tau _N})]^{T}\in {\mathbb {R}}^{(N+1)\times n} \end{aligned}$$

(4.45)

correspondingly, over the inner points ${\tau }^{N}_{in}$ we have

$$\begin{aligned} \mathbf{{V}}^{N}_{in} = [\mathbf{{x}}_{11},\ldots , \mathbf{{x}}_{1(N-1)}]^{T} = [ { {\ddot{\textbf{x}}}_{1}}({\tau _{1}}), \ldots , { {\ddot{\textbf{x}}}_{1(N-1)}}({\tau _{N-1}})]^{T}\in {\mathbb {R}}^{(N+1)\times n} \end{aligned}$$

(4.46)

According to (4.34) (4.37) we have

$$\begin{aligned} {\mathbf{{X}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{X}}_{10}}}\\ {{\mathbf{{X}}_{1in}}}\\ {{\mathbf{{X}}_{1N}}} \end{array}} \right] = \mathcal{B}{} \mathbf{{V}} = \mathcal{B}\left[ {\begin{array}{*{20}{c}} {{\mathbf{{V}}_0}}\\ {{\mathbf{{V}}_{in}}}\\ {{\mathbf{{V}}_N}} \end{array}} \right] \end{aligned}$$

(4.47)

$$\begin{aligned} {\mathcal{B}^{(1)}}{} \mathbf{{V}} = \mathcal{D}\mathcal{B}{} \mathbf{{V}} = \mathcal{D}{\mathbf{{X}}_1} = {{\dot{\textbf{ X}}}_1} = s{\mathbf{{X}}_2} \end{aligned}$$

(4.48)

$$\begin{aligned} {\mathcal{B}^{(2)}}{} \mathbf{{V}} = {\mathcal{D}^2}\mathcal{B}{} \mathbf{{V}} = {\mathcal{D}^2}{\mathbf{{X}}_\mathbf{{1}}} = {{\ddot{\textbf{X}}}_1} \end{aligned}$$

(4.49)

where $\mathcal{B}_0$ and $\mathcal{B}_N$, respectively, are the first and last row of $\mathcal{B}$. Thus, for the dynamic constraints (4.21) we have

$$\begin{aligned} \mathcal{B}_{0 \cdot }^{(2)}{} \mathbf{{V}} = \mathcal{F}({\mathbf{{X}}_{10}},{{\dot{\textbf{X}}}_{10}},{\mathbf{{U}}_0}) \end{aligned}$$

(4.50)

$$\begin{aligned} {\mathbf{{V}}_{in}} = {\mathcal{F}_{in}}({\mathbf{{X}}_{1in}},{\dot{\textbf{ X}}_{1in}},{\mathbf{{U}}_{in}}) \end{aligned}$$

(4.51)

$$\begin{aligned} \mathcal{B}_{N \cdot }^{(2)}{} \mathbf{{V}} = \mathcal{F}({\mathbf{{X}}_{1N}},{\dot{\textbf{ X}}_{1N}},{\mathbf{{U}}_N}) \end{aligned}$$

(4.52)

The Birkhoff equality constraints (4.50) and (4.52) impose the differential equation (4.21) at the boundary point $\tau _0$ and $\tau _N$. The following proposition presents the equivalency between the above Birkhoff equality constraints and the differential equation via the Lagrange condition.

Proposition

Let ${\mathbf{{X}}_{1j}} = \mathbf{{x}}_{1j}^T = \mathbf{{x}}_1^T({\tau _j})$, At ${\tau }={\tau _0}$ and ${\tau }={\tau _N}$, the Lagrange and Birkhoff interpolants respectively satisfy the conditions

(4.53)

and

(4.54)

Proof

Recall the Birkhoff interpolation polynomial (4.29) and the Lagrange interpolants, we have

$$\begin{aligned} \begin{array}{l} {\mathbf{{X}}_1}(\tau ) = \sum \limits _{j = 0}^N {{\mathbf{{X}}_{1j}}\mathcal{L}(\tau )} = {\mathbf{{X}}_{10}}{B_0}(\tau ) + \sum \limits _{j = 1}^{N - 1} {{\mathbf{{V}}_i}} {B_i}(\tau ) + {\mathbf{{X}}_{1N}}{B_N}(\tau )\\ \mathrm{{ }} = {\mathbf{{V}}_1}{B_0}(\tau ) + \sum \limits _{j = 1}^{N - 1} {{\mathbf{{V}}_i}} {B_i}(\tau ) + {\mathbf{{V}}_N}{B_N}(\tau ) \end{array} \end{aligned}$$

(4.55)

where ${\mathbf{{V}}_i}$ denotes the ${i\textrm{th}}$ row of $\textbf{V}$. Differentiating (4.55) twice with respect to PS time ${\tau }$ yields

$$\begin{aligned} \begin{array}{l} \sum \limits _{j = 0}^N {{\mathbf{{X}}_{1j}}\ddot{\mathcal{L}}(\tau )} = {\mathbf{{V}}_0}{{\ddot{B}}_0}(\tau ) + \sum \limits _{j = 1}^{N - 1} {{\mathbf{{V}}_i}} {{\ddot{B}}_i}(\tau ) + {\mathbf{{V}}_N}{{\ddot{B}}_N}(\tau )\\ \mathrm{{ }} = \left[ {{{\ddot{B}}_0}(\tau ),{{\ddot{B}}_1}(\tau ), \ldots ,{{\ddot{B}}_N}(\tau )} \right] \mathbf{{V}} \end{array} \end{aligned}$$

(4.56)

Evaluating (4.56) at ${\tau = \tau _0}$ we henceforth have

$$\begin{aligned} \sum \limits _{j = 0}^N {{\mathbf{{X}}_{1j}}\ddot{\mathcal{L}}({\tau _0})} = \left[ {{{\ddot{B}}_0}({\tau _0}),{{\ddot{B}}_1}({\tau _0}), \ldots ,{{\ddot{B}}_N}({\tau _0})} \right] \mathbf{{V}} \end{aligned}$$

(4.57)

It is obvious that the first row of BPSIM is the evaluating value of ${B_j}(\tau )(j = 0, \ldots ,N)$ at ${\tau = \tau _0}$ in light of (4.33), further, the first row of ${\mathcal{B}^{(2)}}$ denoted by $\mathcal{B}_{0 \cdot }^{(2)} = \left[ {{{\ddot{B}}_0}({\tau _0}),{{\ddot{B}}_1}({\tau _0}), \ldots ,{{\ddot{B}}_N}({\tau _0})} \right]$. Thus (4.53) holds, and it is similar to (4.54). $\square$

Collecting the above relevant equation, the problem C can be transcribed as the follows

$$\begin{aligned} \begin{array}{l} \mathrm{{Decision Variables}}:\mathbf{{V}} \in {^{(N + 1) \times n}},\mathbf{{U}} \in {^{(N + 1) \times m}}\\ \mathrm{{Temporal Variables }} : {\mathbf{{X}}_\mathbf{{1}}} = \mathcal{B}{} \mathbf{{V}},\mathrm{{ }}{\mathbf{{X}}_2} = {\mathcal{B}^{(1)}}{} \mathbf{{V}}\\ \mathrm{{Problem }}BPSC2:\min {J^N}[\mathbf{{X}},\mathbf{{U}}]: = E({\mathbf{{x}}_0},{\mathbf{{x}}_N}),\mathrm{{ }}{} \mathbf{{X}} = {[\mathbf{{X}}_1^T,{\mathbf{{X}}_\mathbf{{2}}}^T]^T}\\ \mathrm{{ \qquad \qquad \qquad \qquad }}s.t.\mathrm{{ \quad }}\mathcal{B}_{0 \cdot }^{(2)}{} \mathbf{{V}} = \mathcal{F}({\mathbf{{X}}_{10}},{{\dot{\textbf{ X}}}_{10}},{\mathbf{{U}}_0})\\ \mathrm{{ \qquad \qquad \qquad \qquad \qquad }}{\mathbf{{V}}_{in}} = {\mathcal{F}_{in}}({\mathbf{{X}}_{1in}},{{\dot{\textbf{ X}}}_{1in}},{\mathbf{{U}}_{in}})\\ \mathrm{{ \qquad \qquad \qquad \qquad \qquad }}\mathcal{B}_{N \cdot }^{(2)}{} \mathbf{{V}} = \mathcal{F}({\mathbf{{X}}_{1N}},{{\dot{\textbf{ X}}}_{1N}},{\mathbf{{U}}_N})\\ \mathrm{{ \qquad \qquad \qquad \qquad \qquad }}{} \mathbf{{e}}({\mathbf{{x}}_0},{\mathbf{{x}}_N}) = \mathbf{{0}}. \end{array} \end{aligned}$$

(4.58)

4.4 Application Examples

To demonstrate the effectiveness of the proposed method for OCPs by using Birkhoff PS method and convex programming algorithms, two application examples are considered in this section. One is a simple cart problem with boundary position and velocity constraints, which is convex in nature. Another is an online rescue trajectory optimization problem for launch ascent to orbital insertion, which is concave and complicated, and SCP method by using successive linearization is required.

The following numerical results are obtained on a laptop computer with an Intel Core i7-1065G7 CPU @ 1.3GHz and 32G RAM. YALMIP [36] and ECOS [27, 37] are used for modeling and solving problems. YALMIP is a MATLAB toolbox for the rapid modeling for mathematical optimization problems, while ECOS is a light embedded toolkit based on the primal-dual interior-point algorithm. ECOS is designed to solve the following standard SOCP problem.

$$\begin{aligned} \begin{array}{l} \min {\mathbf{{c}}^T}{} \mathbf{{x}}\\ s.t.\mathrm{{ }}\mathcal{A}{} \mathbf{{x}} = \mathbf{{b}}\\ \mathrm{{ }}\mathcal{G}{} \mathbf{{x}} + \mathbf{{s}} = \mathbf{{h}},\mathrm{{ }}{} \mathbf{{s}} \in \mathcal{K} \end{array} \end{aligned}$$

(4.59)

where $\textbf{x}$ are decision variables to be optimized, s are the slack variables, and $\mathcal{K}$ are conic constraints. The previous problems of DPSC2, P-DPSC2, and BPSC2 are modeled by using YALMIP therefore a programming problem with the form of (4.59). The matrix $\mathcal{A}$ in equality constraints in (4.59) strongly depends on the collocation scheme, and the condition number of $\mathcal{A}$ will dramatically impacts on the efficiency of solving algorithms, although many special skills are proposed in ECOS to handle such phenomenon. Hence in the following numerical studies, the condition number of $\mathcal{A}$ is taken as an index to evaluate the performance of different PS schemes including the first-order and second-order methods.

In the remainder of this paper, three second-order methods refer to DPSC2 in (4.26), P-DPSC2 in (4.44) and BPSC2 in (4.58). While three first-order methods, respectively, are problem DPSC1 in (4.20), the preconditioned version denoted by P-DPSC1, and BPSC1 transcribed by using the first-order Birkhoff PS method. Note the formulations of P-DPSC1 and BPSC1 resulted from the first-order Birkhoff PS method are not presented in this paper, actually they are similar to P-DPSC2 and BPSC2, and the interested readers can find the details in [16]. Moreover, to demonstrate the effects of different collocation schemes, CGL and LGL collocation schemes are considered. The computation of BPSIM relating to Chebyshev and Legendre polynomials are given in [18].

4.4.1 Simple Cart Problem

An OCP of a simple cart system with fixed final time is given as follows [38]

$$\begin{aligned} \begin{array}{l} \min \mathrm{{ }}J = \mathop \smallint \nolimits _0^{{t_f}} {u^2}dt\\ s.t.\mathrm{{ }}{{\dot{x}}_1} = {x_2},\mathrm{{ }}{{\dot{x}}_2} = - {x_2} + u\\ \mathrm{{ }}{x_1}(0) = 0,{x_2}(0) = 0\\ \mathrm{{ }}a{x_1}({t_f}) + b{x_2}({t_f}) - c = 0 \end{array} \end{aligned}$$

(4.60)

where the parameters ${a = 1.0 , b = -2.694528 , c = -1.155356}$, the final time ${t_f = 2}$. Using the indirect method for (4.60) results the analytical solutions given as

$$\begin{aligned} \begin{array}{l} u(t) = \frac{1}{4}{e^t} - \frac{1}{2}\\ {x_1}(t) = - \frac{3}{8}{e^{ - t}} + \frac{1}{8}{e^t} - \frac{1}{2}t + \frac{1}{4}\\ {x_2}(t) = \frac{3}{8}{e^{ - t}} + \frac{1}{8}{e^t} - \frac{1}{2} \end{array} \end{aligned}$$

(4.61)

with the optimal performance index ${J_{ana} = 0.577678}$.

The problem (4.60) is convex in nature, hence the aforementioned six PS methods with convex programming can be directly used, and the convexifying operations are not required. Figure 4.1 presents the analytical solution as well as that of BPSC2 with LGL mesh grid. The interpolating curves based on the optimized values on mesh points via Lagrange polynomials at the freedom of degree almost identify with the analytical solution.

The comparison results are demonstrated by Tables 4.1 and 4.2, in which, six PS methods (DPSC1, P-DPSC1, BPSC1, DPSC2, P-DPSC2 and BPSC2) are implemented through CGL and LGL mesh grids (${N=5,20,60,120}$), respectively. Four different indices are listed as follows.

(1) Cond.$\mathcal{A}$ refers to the condition number of the matrix in equality constraint of (4.59).

(2) The integration error e in two tables is defined by

$$\begin{aligned} e = {\left\| {\mathbf{{x}} - {\mathbf{{x}}_{ana}}} \right\| _\infty } \end{aligned}$$

(4.62)

where ${\mathbf{{x}}_{ana}} = [{x_{1ana}},{x_{2ana}}]$ are given by (4.61), $\mathbf{{x}} = {[{x_1},{x_2}]^T}$ are the integration solution of simple cart system via 4-order Runge–Kuta algorithm with the control input u(t) which is interpolated from the optimized control variables $u^N$ on mesh nodes, and the step of Runge-Kuta integration is ${t_s = 0.001s}$.

(3) $\Delta J = |{J^N} - {J_{ana}}|$, where ${J_N}$ is resulted from optimized algorithms on different mesh grid N.

(4) Solve time in millisecond refer to the time consumed by ECOS.

Fig. 4.1

Optimal solution via BPSC2 with LGL collocation scheme and the analytical solution (mesh grid $N=5$)

Table 4.1 Comparison of condition numbers, integration error, performance index error and solve time for first-order PS methods

Table 4.2 Comparison of condition numbers, integration error, performance index error and solve time for second-order PS methods

Observe from Tables 4.1 and 4.2 that the proposed second-order BPSC methods provide a more stable performance than other methods while increasing the number of mesh grids N. The crucial reason lies that when the mesh grids increase, the condition number of $\mathcal{A}$ in DPSC2 will dramatically grows like $\mathcal{O}(N^4)$, and that in BPSC2 behaves like $\mathcal{O}(N)$. The growth of condition number of $\mathcal{A}$ resulted from DPSC1, DPSC2, BPSC1, and BPSC2 is clearly illustrated in Fig. 4.2 from which, CGL collocation scheme is slightly advantageous over than LGL. Meanwhile, the solver time consumptions of all mentioned methods provided in Tables 4.1 and 4.2 strongly relate to the condition number. It is also can be observed that when ${N \ge 60}$, DPSC2 and P-DPSC2 cannot provide a reasonable solution since the numerical instability aroused by the overlarge condition number. It can be seen that, preconditioned method using BPSIM according to the method in [16], and the main reason lies in the handling of boundary constraints. In [17], the authors proposed another preconditioning method, however, the method concentrates on solving general ODEs with boundary conditions, the control input cannot been considered. Moreover, comparing BPSC1 and BPSC2, the latter method demonstrates more efficiency while the increase of mesh grid number.

Fig. 4.2

Condition numbers of $\mathcal{A}$ resulted from DPSC1, DPSC2, BPSC1 and BPSC2

4.4.2 Rescue Orbit Searching Problem

The second illustrative problem is about launch insertion while thrust failure. When a thrust drop failure occurs during a launch mission, may the prescribed target orbit be reachable or not? This question can be addressed by searching a maximum-height circular orbit (MCO) in the orbital plane formed at the time of failure, and this is validated by [21], in which MCO is obtained by solving the following optimal control problem.

$$\begin{aligned} \mathrm{{Problem MCO: }}\min J = - {h_f} \end{aligned}$$

(4.63)

$$\begin{aligned} \begin{array}{l} \qquad \qquad s.t.\quad {\dot{\textbf{ r}}} = \mathbf{{v}}\\ \qquad \qquad \qquad \mathrm{{ }}{\dot{\textbf{ v}}} = - \frac{1}{{{r^3}}}{} \mathbf{{r}} + \frac{{\kappa T}}{m}{\mathbf{{i}}_\mathbf{{b}}},\ \mathrm{{ }}\left\| {{\mathbf{{i}}_b}} \right\| = 1 \end{array} \end{aligned}$$

(4.64)

$$\begin{aligned} {\dot{m}} = - \frac{{\kappa T}}{{{I_{sp}}{g_0}}} \end{aligned}$$

(4.65)

$$\begin{aligned} \mathrm{{ }}e({t_f}) = 0 \Leftrightarrow \left\{ \begin{array}{l} \mathbf{{r}}{({t_f})^T}{} \mathbf{{v}}({t_f}) = 0\\ r({t_f}){v^2}({t_f}) - \mu = 0 \end{array} \right. \end{aligned}$$

(4.66)

$$\begin{aligned} \mathrm{{ }}i({t_f}) = {i_{{t_f}}} \Leftrightarrow \left\{ \begin{array}{l} \mathbf{{r}}{({t_f})^T}{\mathbf{{i}}_{h\mathrm{{ref}}}} = 0\\ \mathbf{{v}}{({t_f})^T}{\mathbf{{i}}_{h\mathrm{{ref}}}} = 0 \end{array} \right. \end{aligned}$$

(4.67)

$$\begin{aligned} \mathbf{{r}}({t_0}) = {\mathbf{{r}}_0},\mathbf{{v}}({t_0}) = {\mathbf{{v}}_0} \end{aligned}$$

(4.68)

where $\textbf{r}$ and $\textbf{v}$ are the position and velocity vectors of the launch vehicle in the earth centered inertial (ECI) coordinate, respectively, normalized by the Earth radius $R_E$ and $\sqrt{R_{E} g_E}$, where $g_E$ is the gravitational acceleration at sea level, meanwhile their magnitudes defined by $r = ||\mathbf{{r}}||,v = ||\mathbf{{v}}||$; the dependent variable t is normalized by $\sqrt{{R_E}/{g_E}}$; the thrust direction is given by $\textbf{i}_b$; thrust failure factor ${\kappa }$ refers to the percentage of the failure thrust compared to the nominal thrust T normalized by ${m_0 g_E}$, where $m_0$ is the initial mass of vehicle; the mass m is scaled by $m_0$, and the rocket engine’s specific impulse $I_sp$ in seconds is scaled by $\sqrt{{R_E}/{g_E}}$; $g_0$ represents normalized gravitational acceleration by $g_E$;. The equations (4.66) and (4.67), respectively, impose constraints on the eccentricity e and the inclination angle i on the final time $t_f$. The reference normalized orbital angular moment is provided by

$$\begin{aligned} {\mathbf{{i}}_{h\mathrm{{ ref}}}}\mathrm{{ = [sin}}{\Omega _{ref}}\sin {i_{ref}}, - \cos {\Omega _{ref}}\sin {i_{ref}},\cos {i_{ref}}{]^T} \end{aligned}$$

(4.69)

where ${\Omega }_{ref}$ and $i_{ref}$ are the longitude of the ascending node (LAN) and the inclination angle, which are predefined by the nominal trajectory without any failure.

To solve problem MCO via convex programming method, an initial trajectory is necessary for linearizing and convexifying the non-convex constraints. However, a good initial trajectory, which can make solving procedure definitely converges, is hard to be obtained. In [22], through estimating the geocentric angle of injection point, a temporary orbital coordinate system (OCS) was established, then the maximum height searching was conducted in OCS, in which, the problem MCO is confined in 2-dimensional space. The solution obtained in OCS was converted into original inertial coordinate system, and was taken as the initial trajectory of problem MCO.

In this paper, a new procedure for solving problem MCO is presented. Note that the specific impulse $I_{sp}$ remains whatever unchanged, and the thrust magnitude is assumed being a known constant after the thrust drop. Hence the mass rate ${\dot{m}}$ as well as the remaining flight time ${t_{go}} = {m_{prop}}/\dot{m}$ can be calculated after thrust failure occurring, where $m_{prop}$ is the known remaining propellent. As a result, the mass variation equation in (4.65) can be replaced by an algebraic equation

$$\begin{aligned} m(t) = {m_0} - (t - {t_0})\dot{m},\mathrm{{ }}{t_0} \le t \le {t_0} + {t_{go}} \end{aligned}$$

(4.70)

Correspondingly, the acceleration magnitude in any time instant is given by

$$\begin{aligned} A(t) = \frac{{\kappa T}}{{m(t)}} \end{aligned}$$

(4.71)

Hence the dynamic constraints in (4.65) can be omitted in the subsequent optimization procedure, and the term of T/m in (4.64) can be replaced by A in (4.71).

The proposed iteratively solving procedure via SC algorithm is as follows.

Step 1. In the first iteration $k=0$, let the radius of vehicle ${r^0}(t)$ be a straight line from the vehicle’s current radius $r(t_0)$ and the prescribed radius $r(t_f)$ of the nominal trajectory. Irrespective of the constraints (4.66), we henceforth have the following simplified convex version of problem MCO.

$$\begin{aligned} \begin{array}{l} \mathrm{{Subproblem 0:}}\\ \min J = - {x_{of}}\\ s.t.\mathrm{{ }}{\dot{\textbf{ r}}} = \mathbf{{v}},{\dot{\textbf{ v}}} = - \mathbf{{r}}/{({r^0})^3} + A(t){\mathbf{{i}}_b}\\ \mathrm{{ }}{} \mathbf{{r}}{({t_f})^T}{\mathbf{{i}}_{h'}} = 0,\mathbf{{v}}{({t_f})^T}{\mathbf{{i}}_{h'}} = 0\\ \mathrm{{ }}{} \mathbf{{r}}({t_0}) = {\mathbf{{r}}_0},\mathrm{{ }}{} \mathbf{{v}}({t_0}) = {\mathbf{{v}}_0}\\ \mathrm{{ }}\left\| {{\mathbf{{i}}_b}} \right\| \le 1 \end{array} \end{aligned}$$

(4.72)

Here, the index performance

$$\begin{aligned} {x_{of}} = \left[ {1,0,0} \right] \mathbf{{T}}_{ECI}^{O'}{} \mathbf{{r}}\mathrm{{(}}{t_f}\mathrm{{)}} \end{aligned}$$

(4.73)

represents the position along the x-axis in a temporary OCS, which is defined by the LAN ${\Omega '}$ and the inclination angle $i'$ when the thrust failure occurs, as well as the prescribed argument of the perigee ${\omega }_{ref}$, thereby

$$\begin{aligned} \mathbf{{T}}_{ECI}^{O'} = \left[ {\begin{array}{*{20}{c}} {\cos \Omega '\cos {\omega _{ref}} - \sin \Omega '\sin {\omega _{ref}}\cos i'}&{}{\sin \Omega '\sin {\omega _{ref}} + \cos \Omega '\sin {\omega _{ref}}\cos i'}&{}{\sin {\omega _{ref}}\sin i'}\\ { - \cos \Omega '\sin {\omega _{ref}} - \sin \Omega '\cos {\omega _{ref}}\cos i'}&{}{ - \sin \Omega '\sin {\omega _{ref}} + \cos \Omega '\cos {\omega _{ref}}\cos i'}&{}{\cos {\omega _{ref}}\sin i'}\\ {\sin \Omega '\sin i'}&{}{ - \cos \Omega '\sin i'}&{}{\cos i'} \end{array}} \right] \end{aligned}$$

(4.74)

Note that ${\Omega '}$ and $i'$ can be calculated by the current position $\textbf{r}_0$ and velocity $\textbf{v}_0$ of the vehicle. Correspondingly, the desired terminal position and the velocity vectors are constrained by $\mathbf{{i}}_{h'}$ defined by

$$\begin{aligned} {\mathbf{{i}}_{h'}}\mathrm{{ = [sin}}\Omega '\sin i', - \cos \Omega '\sin ',\cos i'{]^T} \end{aligned}$$

(4.75)

Problem (4.72) can be solved by SOCP solver after discretization, thereby the solution denoted by $\{ {\mathbf{{r}}^1},{\mathbf{{v}}^1},\mathbf{{i}}_b^1\}$

Step 2. When $k \ge 1$, the constraints (4.64) and (4.66) in problem MCO can be linearized on the solution of last iteration $\{ {\mathbf{{r}}^k},{\mathbf{{v}}^k},\mathbf{{i}}_b^k\}$ thereby the convex subproblem 1 as follows

$$\begin{aligned} \begin{array}{l} \mathrm{{Subproblem 1:}}\\ \min J = - {\left( {r_f^k} \right) ^2} - 2r_f^k{\left( {\mathbf{{r}}_f^k} \right) ^T}({\mathbf{{r}}_f} - \mathbf{{r}}_f^k)\mathrm{{ }} \Leftarrow J = - {\left\| {{\mathbf{{r}}_f}} \right\| ^2}\\ s.t.\quad \mathrm{{ }}{\dot{\textbf{ r}}} = \mathbf{{v}},{\dot{\textbf{ v}}} = - \mathbf{{r}}/{({r^k})^3} + A(t){\mathbf{{i}}_b},\mathrm{{ }}{r^k}(t) = ||{\mathbf{{r}}^k}(t)||\mathrm{{ }}\\ \mathrm{{ }}{} \mathbf{{h}}(\mathbf{{r}}_f^k\mathbf{{v}}_f^k) + {\left. {\frac{{\partial \mathbf{{h}}}}{{\partial {\mathbf{{r}}_f}}}} \right| _{{\mathbf{{r}}_f} = \mathbf{{r}}_f^k,{\mathbf{{v}}_f} = \mathbf{{v}}_f^k}}({\mathbf{{r}}_f} - \mathbf{{r}}_f^k) + {\left. {\frac{{\partial \mathbf{{h}}}}{{\partial {\mathbf{{v}}_f}}}} \right| _{{\mathbf{{r}}_f} = \mathbf{{r}}_f^k,{\mathbf{{v}}_f} = \mathbf{{v}}_f^k}}({\mathbf{{v}}_f} - \mathbf{{v}}_f^k) = \mathbf{{0}}\\ \mathrm{{ }}{} \mathbf{{r}}{({t_f})^T}{\mathbf{{i}}_{h\mathrm{{ref}}}} = 0,\mathbf{{v}}{({t_f})^T}{\mathbf{{i}}_{h\mathrm{{ref}}}} = 0\\ \mathrm{{ }}{} \mathbf{{r}}({t_0}) = {\mathbf{{r}}_0},\mathrm{{ }}{} \mathbf{{v}}({t_0}) = {\mathbf{{v}}_0}\\ \mathrm{{ }}\left\| {{\mathbf{{i}}_b}} \right\| \le 1 \end{array} \end{aligned}$$

(4.76)

where the square of final radius, equivalent to the maximum height, is taken as the optimization objective, i.e. $J = - {\left\| {{\mathbf{{r}}_f}} \right\| ^2}$. In accordance with the convexification techniques provided by [10], the performance index J and the nonlinear equality constraints in (4.66), denoted by $\mathbf{{h}}({\mathbf{{r}}_f},{\mathbf{{v}}_f}) = 0$ in (4.76), are linearized on $\{ \mathbf{{r}}_f^k,\mathbf{{v}}_f^k\}$ which represent the final position and velocity vectors of the $k\textrm{th}$ iterative solution. Solving problem (4.76) yields the solution $\{ {\mathbf{{r}}^{k\mathrm{{ + }}1}},{\mathbf{{v}}^{k\mathrm{{ + }}1}},\mathbf{{i}}_b^{k\mathrm{{ + }}1}\}$.

Fig. 4.3

Flow chart for solving problem MCO via BPSC2

$\mathbf{{Step 3.}}$ Compute $error = ||{r^{k + 1}}(t) - {r^k}(t)||$. If $error \ge \delta$, where $\delta$ is a prescribed small positive number, then set $k=k+1$, and go to step 2; otherwise, terminate the iteration, and the optimal solution is found to be $\{ {\mathbf{{r}}^{k\mathrm{{ + }}1}},{\mathbf{{v}}^{k\mathrm{{ + }}1}},\mathbf{{i}}_b^{k\mathrm{{ + }}1}\}$., thus the maximum circular orbital height is given by ${h_{opt}} = ||\mathbf{{r}}_f^{k + 1}|| - {R_E}$.

The above solving procedures can be summarized as the flow chart shown in Fig. 4.3, in which, the BPSC2 method proposed in (4.58) is used to transcribe the subproblem 0 and subproblem 1. In accordance with the flow chart, one can easily use YALMIP to model and solve problem MCO.

Remark 2

In Step 1, since it is not easy to provide a three dimensional trajectory for initializing problem (4.72), only simply linear radius profile of the vehicle from the current position to the prescribed orbital insertion point is used for establishing problem (4.72). On this scenario, $\mathbf{{r}}_f$ and $\mathbf{{v}}_f$ on the final time cannot be initialized, hence the constraints (4.66), which enforce the orbital eccentricity be zero, are not considered. Further, the constraints (4.67), which confine the final orbit in the nominal orbital plane, are relaxed to confine the final states of vehicle in the current orbital plane, and this is effective demonstrated by the latter numerical results.

Remark 3

In Step 2, problem (4.76) is formulated by a very rough trajectory provided the first iteration in Step 1, in which, the terminal states $\mathbf{{r}}^{1}_{f}$ and $\mathbf{{v}}^{1}_{f}$ are hard to satisfy the constraints in (4.66), this results in that, directly linearizing (4.66) on $\mathbf{{r}}^{1}_{f}$ and $\mathbf{{v}}^{1}_{f}$ is not reasonable. Actually, the numerical studies reveal such linearizing manner cannot guarantee the convergence. Hence, the constraints (4.66) are relaxed as

$$\begin{aligned} {\left( {\mathbf{{r}}_f^k} \right) ^T}{} \mathbf{{v}}({t_f}) = 0r_f^k{v^2}({t_f}) - \mu = 0 \end{aligned}$$

(4.77)

which enforce the final velocity vector $\mathbf{{v}}(t_f)$ be perpendicular to the final position vector $\mathbf{{r}}^{k}_{f}$ provided by the last iteration solution, meanwhile, their magnitudes satisfy with the requirement of circular orbit. Such relaxations are reasonable in the above solving procedure, because in Step 3, when the iterative termination criterion is satisfied, we have $\mathbf{{r}}_f^{k\mathrm{{ + }}1} \rightarrow \mathbf{{r}}_f^k$, which means the relaxed constraints in (4.77) almost are equivalent to those in (4.66). Obviously, the degree of almost equivalence depends on the iterative termination condition $\delta$, which is set as $10_{-6}$ in the following numerical studies.

Fig. 4.4

Optimal height, velocity and control profiles by using GPOPS and BPSC2 ($N=10$, $\kappa = 0.85$)

According to the above procedure, the proposed DPSC1, BPSC1, and BPSC2 are used to solve problem MCO, and the aforementioned preconditioned methods (P-DPSC and P-DPSC2) are not considered since their poor performance demonstrated in the last subsection. Moreover, GPOPS is adopted to obtain a baseline solution for problem MCO.

Remark 4

The thrust direction $\mathbf{{i}}_b$ in problem MCO is constrained by $\left\| {{\mathbf{{i}}_b}} \right\| = 1$, which is non-convex and relaxed to a conic constraint $\left\| {{\mathbf{{i}}_b}} \right\| \ge 1$ in (4.72) and (4.76). Such relaxation is similar to that in [8, 25], and it can be proved that the optimal solution obtained by solving (4.76) will satisfy $\left\| {\mathbf{{i}}_b^*(t)} \right\| = 1,t \in [{t_0},{t_f}]$ as shown in Fig. 4.4.

Fig. 4.5

Iterative procedure of DPSC1 ($N=10$, $\kappa = 0.85$, 17 iterations, maximum height 165.0785 km, eccentricity 1.9445e-4)

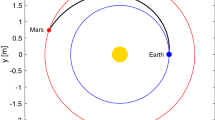
In the subsequent numerical studies, the vehicle parameters are same to those in the appendix A of [21]. Without loss of generality, the thrust drop occurs in the start of the second stage of vehicle. When the thrust failure factor, the optimized height and velocity trajectories by using GPOPS and BPSC2 are shown in Fig. 4.4, which reveals the results of two method are almost same. The results of DPSC1 and BPSC1 is similar to that of BPSC2, hence they are not presented in Fig. 4.4. DPSC2 cannot converge for any mesh grid, and DPSC1 converges only when mesh grid. It is to note that in DPSC1, the trust region constraints should be carefully selected, otherwise it cannot converge at all. Meanwhile, the trust region constraints can be discarded in BPSC1 and BPSC2, which are still converged. Figures 4.5 and 4.6, irrespectively, present the iterative procedures of DPSC1 and BPSC2, and it can be seen that BPSC2 is more efficient and accurate than DPSC1.

Fig. 4.6

Iterative procedure of DPSC1 ($N=10$, $\kappa = 0.85$, 17 iterations, maximum height 165.2726 km, eccentricity 7.0068e-07)

Table 4.3 presents the performance comparison between GPOPS, BPSC1 and BPSC2 for different thrust failure factor $\kappa$. CGL collocation scheme with $N=40$ is adopted in Birkhoff PS methods. The resulted trajectory profiles by using BPSC2 for different $\kappa$ and the nominal trajectory without any failure are presented in Fig. 4.7. Observing Table 4.3, for each scenario, the index of maximum height and the eccentricity provided by GPOPS are the best among three methods. The reason lies in that, GPOPS directly solves the original problem MCO, while BPSC1 and BPSC2 solve a series of convexified and relaxed problems. Particularly, the constraints on eccentricity of MCO are relaxed as (4.77) in our PS methods. However, BPSC1 and BPSC2 is more efficient than GPOPS, meanwhile, the optimized orbits with very small eccentricities are almost circular, and such performance is acceptable in practical engineering.

Further, the performances of BPSC1 and BPSC2 with different collocation schemes and different mesh grids are listed in Table 4.4. In general, the computational time consuming of BPSC2 is less than that of BPSC1 since the less decision variables used in BPSC2 thereby smaller scale of the transcribed SOCP problem. The growth of condition number of generated by CGL and LGL with respect to the mesh grid N is similar to Fig. 4.2, and CGL scheme is better than LGL to some degree.

Table 4.3 Comparison of GPOPS, BPSC1, and BPSC2 for different thrust failure factor

Table 4.4 Comparison of BPSC1 and BPSC2 for different mesh grid

Fig. 4.7

Height and velocity profiles via BPSC2 for different thrust failure factor and the nominal trajectory

4.5 Conclusions

In this chapter, Birkhoff polynomial based PS method is introduced to solve OCPs via convex programming algorithms. The constrained optimal control problem for a type of general second-order cascaded system is mainly considered. The matrix formulation of PS method with BPSIM under the convex programming framework for general OCPs is proposed, meanwhile, the solving procedure is generalized. Comparing to other PS methods using PSDM, the Birkhoff PS method renders a well-conditioned programming problem since the unique characteristics of BPSIM, which will alleviate the computational burden for the programming solvers. This advantage is remarkably demonstrated in the transcription of cascaded second-order systems, in which, the condition number of DPSC2 behaves like while that of BPSC2 like. Moreover, this allows us using more mesh points to improve accuracy of solution. From the view of application, BPSC and BPSC2 with LGL as well as CGL collocation scheme present similar performance while, however, for complicated problem, BPSC2 renders smaller scale of generated problem than that of BPSC1 while, consequently less computational time consuming. In general, for the typical cascaded second order, BPSC2 method is the best choice among the mentioned PS methods, and it can be potentially used in online trajectory optimization and guidance for ascent and recovery of launch vehicles.