The Potential Force Interface Tension Model in MPS Method for Stratification Simulation

Abstract

In the analysis of phenomenology of serious accident, stratification behavior is important in the late in-vessel stage of core melt. Traditional numerical methods have difficulties in analyzing stratification process accompanying with free surface, which need extra processes such as empirical correlations. The Moving Particle Semi-implicit (MPS) method has a natural advantage in calculating multiphase flows with free surface. In this paper, we apply the potential force surface tension model to the MPS program and extend the original surface tension model to the interface tension calculation of multiple flows. The improved MPS method is verified by a classical dam break problem. The surface tension model is verified by the cases of droplet oscillation, droplet on solid wall and floating droplet. Finally, the two-dimensional dam-break stratification experiment of silicone oil and salt water is simulated, and the simulation results agree with the experiment.

1 Introduction

Different fluids will be stratified by gravity. In the late in-vessel stage of core melt severe accident, stratification behavior is an important phenomenon. Like in the TIM accident [1], due to the decay heat of fission products, the molten corium is formed and collected in the lower head. And the molten corium may be separated into immiscible layers, usually thought of as two or three layers. For example, MASCA [2] experiment, which uses the prototypic core materials, indicate that the molten pool, initially a uniform mixture of components, separates into two layers with different densities. The process of melt stratification can influence the distribution of thermal load across the vessel wall and affect the process of severe accident [3].

Some system program, such as MAAP [4], MELCOR [5] and PECM [6], can calculate the thermo-hydraulics of the molten pool in lower head assuming stratified configuration with empirical correlations employed. For numerical simulation which does not rely on empirical correlations, the large deformation of interface and the interface tracking of stratification process is a challenging task. To model the interfaces between phases, some methods, like the Front Tracking Method, Level Set Method [7], or Immersed Boundary Method [8] are applied in CFD. These mesh methods have difficult in the simulation of large topology deformation, such as unphysical total mass change.

Except for grid methods, particle methods have natural advantages in dealing with free surface flow and large deformation of fluids. The Moving Particle Semi-implicit (MPS) method [9] is one of particle methods for incompressible flow with free surface flow. This method is widely applied in nuclear engineering [10]. In Lagrange system of particle methods, two major approaches have been adopted to model the surface tension, the continuum surface force (CSF) model [11] and the potential force (PF) model [12]. And the potential force model is much simpler and more stable compared to the continuum surface force model.

In this study, the potential force model is added to the original MPS method and extended to simulate the interface between different fluids for stratification calculation. The surface tension model and contact angle are verified by some droplet cases. And the modified method is validated by a two-dimensional dam-break stratification experiment.

2 Numerical Methods

2.1 The Basis MPS Method

The governing equations of MPS are the mass conservation equations and the momentum conservation equations for incompressible flow:

$$ \frac{{D{\varvec{\rho}}}}{Dt} + \rho \nabla \cdot {\varvec{u}} = 0 $$

(1)

$$ \frac{{D{\varvec{u}}}}{Dt} = - \frac{1}{\rho }\nabla p + \upsilon \nabla^{2} {\varvec{u}} + \frac{{\varvec{f}}}{\rho } + {\varvec{F}} $$

(2)

where the vectors u, f and F respectively are velocity, surface tension, and external force (gravity), t, ρ, p and υ respectively are time, density, pressure, and kinematic viscosity. For different fluids, the fluid properties of each particle don’t change.

Particle interactions are based on the kernel function:

$$ w\left( r \right) = \left\{ {\begin{array}{*{20}l} {\frac{{r_{e} }}{r} - 1 } \hfill & {(r < r_{e} )} \hfill \\ 0 \hfill & {\left( {r \ge r_{e} } \right)} \hfill \\ \end{array} } \right. $$

(3)

where r is the distance between particle i and particle j. The cut-off radius r_e, which determines the range of interaction, is usually set as 3.1d_p, where d_p is the initial particle diameter.

The particle number density is defined as the summation of neighboring kernel function:

$$ n_{i} = \sum\nolimits_{j \ne i} {w\left( {\left| {\vec{\user2{r}}_{ij} } \right|} \right)} $$

(4)

where n_i is the particle number density of particle i. For impressible fluid, the mass conservation is ensured by keeping the n_i as a constant.

The gradient and Laplacian terms could be discretized based on the weighted average of neighboring particles:

$$ \nabla \phi_{i} = \frac{d}{{n^{0} }}\sum\nolimits_{j \ne i} {\left[ {\frac{{\phi_{j} - \phi_{i} }}{{\left| {{\varvec{r}}_{j} - {\varvec{r}}_{i} } \right|^{2} }}\left( {{\varvec{r}}_{j} - {\varvec{r}}_{i} } \right)w\left( {\left| {{\varvec{r}}_{j} - {\varvec{r}}_{i} } \right|} \right)} \right]} $$

(5)

$$ \nabla^{2} \phi_{i} = \frac{2d}{{n^{0} \lambda }}\sum\nolimits_{j \ne i} {\left[ {\left( {\phi_{j} - \phi_{i} } \right)w\left( {\left| {{\varvec{r}}_{j} - {\varvec{r}}_{i} } \right|} \right)} \right]} $$

(6)

$$ \lambda = \frac{{\mathop \sum \nolimits_{j \ne i} \left| {{\varvec{r}}_{{\varvec{j}}} - {\varvec{r}}_{{\varvec{i}}} } \right|^{2} w\left( {\left| {{\varvec{r}}_{{\varvec{j}}} - {\varvec{r}}_{{\varvec{i}}} } \right|} \right)}}{{\mathop \sum \nolimits_{j \ne i} w\left( {\left| {{\varvec{r}}_{{\varvec{j}}} - {\varvec{r}}_{{\varvec{i}}} } \right|} \right)}} $$

(7)

where ϕ_i and ϕ_j is represent scalar, n⁰ is the constant particle density calculated in the initial state, d is the spatial dimension.

2.2 Boundary Condition

To preserve incompressible condition, the particle number density is kept constant in each time step. While for particles on the free surface, the number density will decrease. Using this property, the particles on free surface can be identified with a threshold value of particle number density. Then the Dirichlet boundary condition on free surface is applied in the pressure calculation. The threshold is set as follows:

$$ n_{i} < \beta n^{0} $$

(8)

where β is a constant value less than 1.0 and usually set as 0.97.

The wall boundary condition is the Norman boundary condition. The wall particles and dummy particles are arranged along the boundary. The wall particles are included in the pressure calculation and density calculation and the dummy particles are only included in density calculation. Then non-slip boundary condition is utilized for wall boundary.

2.3 The Potential Force Surface Tension Model

The potential function [13] is set similar to the molecular forces

$$ P\left( r \right) = \left\{ { \begin{array}{*{20}c} {\frac{C\_sur}{3}\left( {r - \frac{3}{2}r_{0} + \frac{1}{2}r_{e} } \right)\left( {r - r_{e} } \right)^{2} } & {(r < r_{e} )} \\ 0 & { \left( {r \ge r_{e} } \right)} \\ \end{array} } \right. $$

(9)

where r, r₀ and r_e respectively are the distance between particles, the distance between initial particles and the effective radius, which is generally set r_e as 3.2 r₀.

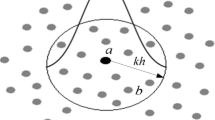
C_sur is a coefficient related to surface tension, which can be obtained by the surface energy between fluids:

$$ C_{f} = \frac{{3 \times 2\sigma r_{0}^{2} }}{{\mathop \sum \nolimits_{{i \in A,j \in B,\left| {r_{ij} } \right| < r_{e} }} \left( {r - \frac{3}{2}r_{0} + \frac{1}{2}r_{e} } \right)\left( {r - r_{e} } \right)^{2} }} $$

(10)

where σ is the coefficient of surface tension. The distribution of region A and B is shown in Fig. 1.

Fig. 1.

Schematic diagram of calculation of surface

The coefficient C_sur between fluid particles and solid particles can be derived from C_f:

$$ C_{fs} = \frac{{C_{f} }}{2}\left( {1 + \cos \theta } \right) $$

(11)

where θ is the contact angle.

The coefficient C_sur between different fluid particles can be derived in a similar way to a single fluid

$$ C_{f,AB} = \frac{{3\left( {\sigma_{f,A} + \sigma_{f,B} - \sigma_{f,AB} } \right)r_{0}^{2} }}{{\mathop \sum \nolimits_{i \in A,j \in B} \left( {r - \frac{3}{2}r_{0} + \frac{1}{2}r_{e} } \right)\left( {r - r_{e} } \right)^{2} }} $$

(12)

where σ_f,AB indicates the miscibility of fluid A and B, and θ_AB is defined as the hypothetical interface contact angle.

The interface tension coefficient can be calculated in a similar way to the coefficient between fluid particles and solid particles. Since the fluid A floats on the fluid B, ρ_f,A < ρ_f,B is presumed.

$$ C_{f,AB} = \frac{{C_{f,A} }}{2}\left( {1 + \cos \theta_{AB} } \right) $$

(13)

3 Model Verification

3.1 Dam Break

The dam break case has been widely used for liquid computing in CFD. In a rectangular container, the water column stands still on the left side of the container originally, and takes up 1/4 of the width of the container. Within 1s of the barrier being dropped, the water column is flowing rapidly due to gravity.

With the initial particle distance r₀ of 0.008 m and time step ∆t of 0.001 s, the process in 1s is simulated. The fluid front position was compared with the experiment [14] in Fig. 2. The trend of fluid front changing with time in MPS calculation is consistent with the experimental results, but the front motion changes slightly faster in simulation. Such a difference is reasonable considering that it takes time for the water column barrier to be extracted in the experiment. The simulation results of other scholars also reflected this difference.

Fig. 2.

Comparison of different fluid front positions

3.2 Droplet Oscillation

A square droplet is released in two-dimensional space in vacuo. The droplet oscillates periodically due to surface tension and the theoretical solution of the oscillation period can be calculated according to the physical properties. In this case, the droplet oscillation period is about 1.3 s and the numerical results are shown in Fig. 3.

Fig. 3.

Numerical results of droplet oscillation

The simulated oscillation period is close to the analytical result. The droplet shape rotates 45° at 0.7 s, and is close to the initial shape at 1.3 s. As numerical dissipation inhibits oscillation, eventually the droplet will approach the equilibrium sphere.

3.3 Droplet on Solid Wall

The droplet contacts the solid wall in initial state and is released. Figure 4 shows droplet morphology after 10.0s, when droplet movement almost stops and approaches steady state.

Fig. 4.

Numerical results of droplet behavior on solid wall

In Fig. 4, the larger potential force between fluid particles is, the smaller contact angle appears. The simulated solid-liquid contact angle is consistent with the set contact angle. When the contact angle is 180°, there is no attractive potential force between fluid and wall and the droplet separates from the wall.

3.4 Floating Droplet

For the case of two fluid interfaces, a case similar to the solid-liquid contact angle is selected. Fluid A and fluid B have the same physical properties and are immiscible. Fluid A is a droplet floating on fluid B. Figure 5 shows the calculation of different interface contact angles. It is considered that the calculated state is close to steady state after 10 s and the gravity is not calculated.

Fig. 5.

Numerical results of droplet behavior with different fluid-to-fluid interface angle

It can be seen from Fig. 5 that the contact angle θ_AB has a significant influence on the droplet interface shape. The contact area between fluid A and fluid B decreases as the contact angle increases. The principle is similar to the solid-liquid contact angle.

4 Model Validation

To validate the simulation of stratification process, Li et al. [15] carried out experiments similar to the dam break case. Two immiscible fluids, silicone oil and salt water, were chosen, and the density and viscosity of the two fluids could be adjusted. At the initial time, the baffle plate of the two liquids was removed and then the stratified flow process of the two liquids over time was recorded. The experimental schematic diagram is shown in Fig. 6.

Fig. 6.

Experiment container for stratification of two fluid columns

The comparison between the results simulated by MPS method and the experimental results under the same conditions is shown in Fig 7.

Fig. 7.

Side views of experiment (left), MPS without surface tension (middle) and MPS with surface tension (right)

It shows that the silicon oil with a lighter density flowed to the top of the salt water. The fluids flow quickly in the first 5s, because the pressure gradient of the fluid interface is larger. During the time after the fifth second, the fluid shape varied slowly and gradually reached steady state at 30 s. The density difference between fluids is the essential reason of stratification and the viscosity affects the time to steady state. The addition of the surface tension model makes the fluid interface smoother and more consistent with the actual situation.

5 Conclusions

The surface tension model based on potential function is added to the original MPS method and is extended to calculate the liquid-liquid interface in a way similar to solid-liquid contact angle. The new program is verified by a dam break case, and the surface tension model is verified by the cases of droplet oscillation, droplet on solid wall and floating droplet. Finally, the ability of the improved program is validated by a stratification experiment similar to the dam break experiment.

Density stratification is an important process of molten pool formation in severe accident analysis. The research in this paper can lay a foundation for the analysis of molten pool process in future.