Keywords

1 Introduction

In order to improve the efficiency of the Monte Carlo (MC) method, various variance reduction techniques have been proposed, such as geometrical importance, weight window, source biasing, etc. [1]. These methods perform well in most scenarios but require the users to set relevant parameters (such as geometrical importance, weight window boundary, and source sampling probability) which are strongly related to the problem. Therefore, high demands are put forward for the user's experience and ability to analyze problems. For the purpose of optimizing the selection of parameters and reducing the burden on users, a variety of automated methods which generate parameters for weight window and source biasing based on the importance distribution obtained by forward or adjoint transport calculation have been proposed. Among the above methods, the Consistent Adjoint Driven Importance Sampling (CADIS) method, which is proposed by Wagner [2] can automatically generate the parameters of weight window and source biasing for MC simulation based on the adjoint flux calculated by the discrete ordinate (SN) method. The CADIS method is proved to be effective in practical applications and is applied to the ADVANTG [3] and the MAVRIC [4], which is the shielding analysis tool of SCALE.

Most traditional CADIS implementations depend on the adjoint flux calculated by finite-difference SN code which can only model geometry with structural meshes. The structural meshes can only approximate the curve surfaces by reducing the mesh size thus considerable approximations will be introduced when modeling complex geometry through finite-difference code. Unstructured meshes are capable of modeling complex geometry with relatively lower approximations. Therefore, the adjoint flux obtained through unstructured meshes is more accurate, and can better describe the distribution of the importance of particles in space and energy, resulting in a more reasonable source biasing and weight window. The theoretical research and practical application of the traditional CADIS method based on structural mesh have been relatively mature [5], but the research on the unstructured-mesh CADIS method is rarely reported. The Finite Element method (FEM) can utilize unstructured meshes to perform transport calculations and the truncation error is inherently lower than the finite-difference method. Numerous researches on FEM have been carried out, including solving the second-order neutron transport equation through the continuous finite element method [6], solving the first-order neutron transport equation through stabilized finite element method [7], and solving the first-order neutron transport equation through discontinuous finite element method [8]. Among them, the numerical method which combines the SN method and the discontinuous FEM to discretize the first-order neutron transport equation in space and angle respectively shows strong stability in solving the problem with the internal vacuum region, and can effectively realize high-order angular expansion calculation, which makes it well applicable to the strong angular anisotropy problems such as shielding calculation.

In this paper, the parallel three-dimensional unstructured-mesh neutron-photon coupling transport calculation code NECP-SUN based on the discrete ordinate method and discontinuous finite element method is developed. Furtherly, the fully automatic unstructured-mesh CADIS method is implemented by embedding NECP-SUN into MC code NECP-MCX [9] and is applied to calculate the specific activity of the radiometric monitor in the cavity of the HBR-2 benchmark. The numerical results show that, compared with the traditional CADIS method, the unstructured-mesh CADIS method can obtain results that are closer to measurements with a lower relative statistical error, and its figure of merit (FOM) raised 3–4 orders compared to direct MC simulation.

2 Method and Implementation

2.1 Description of Unstructured-Mesh CADIS Method

The theoretical basis of the unstructured-mesh CADIS method includes the SN method and discontinuous FEM, as well as the source bias and weight window of the CADIS method. In this section, the local weighted residual form and global variational form of adjoint neutron transport equation are derived firstly, and then the basic theory of source biasing and weight window is briefly illustrated.

2.1.1 The Discretization of Aadjoint Transport Equation Through SN Method and FEM

The steady-state linear Boltzmann transport equation without fissile materials is:

$$\begin{aligned} & \user2{\varOmega }{\rm{\nabla }}\phi {\rm{(}}\user2{r},E,\user2{\varOmega }{\rm{)}} + \Sigma _{\rm{t}} {\rm{(}}\user2{r},E{\rm{)}}\phi {\rm{(}}\user2{r},E,\user2{\varOmega }) \\ & = \iint {\Sigma _{\rm{s}} (\user2{r},E',\user2{\varOmega }' \to E,\user2{\varOmega })\phi (\user2{r},E',\user2{\varOmega }')\rm{d}E'\rm{d}\user2{\varOmega }' + S(\user2{r},E,\user2{\varOmega })} \\ \end{aligned} $$
(1)

where \({\varvec{r}}\) is space, \(E\) is energy, \({\varvec{\varOmega}}\) is direction, Σt is total macro-cross section, \(\rm{cm}^{ - 1}\), \(\phi\) is forward flux, Σs is scattering macro-cross section, \(S\) is the forward source, \({\text{particle}} \cdot \rm{cm}^{ - 3} \cdot \rm{s}^{ - 1}\).

The adjoint equation of Eq. (1) can be constructed as Eq. (2):

$$\begin{aligned} &-{\varvec{\varOmega}}\rm{\nabla }\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}}\rm{)} + \Sigma_{\rm{t}} \rm{(}{\varvec{r}},E\rm{)}\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}}) \hfill \\ &= \iint {\Sigma_{\rm{s}} ({\varvec{r}},E,{\varvec{\varOmega}}\to E^{\prime},{\varvec{\varOmega}}^{\prime})\phi^{\rm{ * }} ({\varvec{r}},E^{\prime},{\varvec{\varOmega}}^{\prime})\rm{d}E^{\prime}\rm{d}{\varvec{\varOmega}}^{\prime}} + S^{*} ({\varvec{r}},E,{\varvec{\varOmega}}) \hfill \\ \end{aligned}$$
(2)

where \(\phi^{ * }\) is adjoint flux, \(S^{ * }\) is adjoint source.

The multi-group form adjoint transport equation can be obtained by integrating both sides of Eq. (2) over the energy interval [Eg, Eg-1]:

$$\begin{aligned} &-{\varvec{\varOmega}}\rm{\nabla }\phi_{g}^{*} ({\varvec{r}},{\varvec{\varOmega}}) + \Sigma_{\rm{t}}^{g} ({\varvec{r}})\phi_{g}^{*} ({\varvec{r}},{\varvec{\varOmega}}) \hfill \\& = \sum\limits_{g^{\prime} = g}^{\rm{1}} {\int {\Sigma_{\rm{s}}^{g \to g^{\prime}} ({\varvec{r}},{\varvec{\varOmega}}\to{\varvec{\varOmega}}^{\prime})\phi_{g^{\prime}}^{*} ({\varvec{r}},{\varvec{\varOmega}}^{\prime})\rm{d}{\varvec{\varOmega}}^{\prime}} } + S_{g}^{*} ({\varvec{r}},{\varvec{\varOmega}}) \hfill \\ \end{aligned}$$
(3)

The SN method can be introduced by integrating Eq. (3) on the region \(\Delta {\varvec{\varOmega}}_{m}\) near the selected discrete direction \({\varvec{\varOmega}}_{m} (\mu_{m} ,\eta_{m} ,\xi_{m} ),m = 1, \cdots ,M\):

$$\begin{aligned} &-{\varvec{\varOmega}}_{m} \rm{\nabla }\phi_{g}^{*} ({\varvec{r}},{\varvec{\varOmega}}_{m} ) + \Sigma_{\rm{t}}^{g} ({\varvec{r}})\phi_{g}^{*} ({\varvec{r}},{\varvec{\varOmega}}_{m} ) \hfill \\ &= \sum\limits_{{g^{^{\prime}} = g}}^{\rm{1}} {\Sigma_{\rm{s}}^{{g \to g^{^{\prime}} }} ({\varvec{r}},{\varvec{\varOmega}}_{m} \to{\varvec{\varOmega}}_{m}^{^{\prime}} )\phi_{{g^{^{\prime}} }}^{*} ({\varvec{r}},{\varvec{\varOmega}}_{m}^{^{\prime}} )} + S_{g}^{*} ({\varvec{r}},{\varvec{\varOmega}}_{m} ) \hfill \\ \end{aligned}$$
(4)

Expanding the scattering term with the spherical harmonics function and expressing the angular discretization as a subscript, the discrete ordinate form of the steady-state multi-group adjoint neutron transport equation without fissile materials can be described by Eq. (5):

$$\begin{aligned} &-{\varvec{\varOmega}}_{m} \rm{\nabla }\phi_{g,m}^{*} ({\varvec{r}}) + \Sigma_{\rm{t}}^{g} ({\varvec{r}})\phi_{g,m}^{*} ({\varvec{r}}) \hfill \\ &= \sum\limits_{g^{\prime} = g}^{\rm{1}} {\sum\limits_{l = 0}^{\infty } {\Sigma_{{\rm{s,}l}}^{g \to g^{\prime}} ({\varvec{r}})} \sum\limits_{n = - l}^{l} {Y_{l}^{n} ({\varvec{\varOmega}}_{m} )} } \sum\limits_{{m^{^{\prime}} = 0}}^{M} {w_{m^{\prime}} Y_{l}^{n} } ({\varvec{\varOmega}}_{m^{\prime}} )\phi_{g^{\prime},m^{\prime}}^{*} ({\varvec{r}}) + S_{g,m}^{*} ({\varvec{r}}) \hfill \\ \end{aligned}$$
(5)

Equation (5) only contains spatial-related unknown variables, which can be discretized in the spatial dimension by the discontinuous Galerkin method. Since the right-hand side of Eq. (5) can be regarded as a known function in SN calculation, it can be combined into a spatially related known function \(Q_{g,m}^{*} ({\varvec{r}})\):

$$-{\varvec{\varOmega}}_{m} {\nabla }\phi_{g,m}^{*} ({\varvec{r}}) + \Sigma_{{t}}^{g} ({\varvec{r}})\phi_{g,m}^{*} ({\varvec{r}}) = Q_{g,m}^{*} ({\varvec{r}})$$
(6)

The solution area can be divided into non-overlapping mesh elements and the dimensional approximation functions can be defined on them. Integrating the Eq. (6) on Dk(k = 1,…, K) with each term multiplied by the verification function \(\phi_{g,m}^{\rm{t}}\) which is arbitrarily selected from the aforementioned dimensional approximation functions:

$$\begin{aligned} \int_{{D^{k} }} { - \phi_{g,m}^{\rm{t}} ({\varvec{r}}){\varvec{\varOmega}}_{m} \rm{\nabla }\phi_{g,m}^{*} ({\varvec{r}})d{\varvec{r}}} \hfill \\ + \int_{{D^{k} }} {\phi_{g,m}^{\rm{t}} ({\varvec{r}})\Sigma_{\rm{t}}^{g} ({\varvec{r}})\phi_{g,m}^{*} ({\varvec{r}})\rm{d}{\varvec{r}}} \hfill \\ = \int_{{D^{k} }} {\phi_{g,m}^{\rm{t}} ({\varvec{r}})Q_{g,m}^{*} ({\varvec{r}})\rm{d}{\varvec{r}}} \hfill \\ \end{aligned}$$
(7)

After integrating the first term at the left-hand side of Eq. (7) by parts and applying the divergence theorem:

$$\begin{aligned} \int_{{D^{k} }} { - \phi_{g,m}^{\rm{t}} ({\varvec{r}}){\varvec{\varOmega}}_{m} \rm{\nabla }\phi_{g,m}^{*} ({\varvec{r}})\rm{d}{\varvec{r}}} \hfill \\ = - \int_{{\partial D^{k} }} {\rm{(}{\varvec{\varOmega}}_{m} \cdot {\varvec{n}}\rm{)}\phi_{g,m}^{\rm{t}} ({\varvec{r}})\phi_{g,m}^{*} ({\varvec{r}})\rm{d}s} \hfill \\ + \int_{{D^{k} }} {\phi_{g,m}^{*} ({\varvec{r}}){\varvec{\varOmega}}_{m} \rm{\nabla }\phi_{g,m}^{\rm{t}} ({\varvec{r}})\rm{d}{\varvec{r}}} \hfill \\ \end{aligned}$$
(8)

The local Galerkin weighted residual form of Eq. (6) can be obtained by substituting Eq. (8) into Eq. (7) and adopting the upwind flux, which is, finding the function \(\phi_{g,m}^{*}\) to make sure Eq. (9) is satisfied for any testing function \(\phi_{g,m}^{\rm{t}}\) in V(Dk):

$$\begin{aligned} (\phi_{g,m}^{*} ,({\varvec{\varOmega}}_{m} \cdot \nabla + \Sigma_{\rm{t}}^{g} )\phi_{g,m}^{\rm{t}} ) - \left\langle {\phi_{g,m}^{* - } ,\phi_{g,m}^{{\rm{t} - }} } \right\rangle_{{\partial D^{k + } }} \hfill \\ + \left\langle {\phi_{g,m}^{* - } ,\phi_{g,m}^{{\rm{t + }}} } \right\rangle_{{\partial D^{k - } }} = (\phi_{g,m}^{\rm{t}} ,Q_{g,m}^{*} ) \hfill \\ \end{aligned}$$
(9)

where,

$$(f,g)_{{D^{k} }} : = \int_{{D^{k} }} {f \cdot g\rm{d}{\varvec{r}}}$$
(10)
$$\left\langle {f,g} \right\rangle_{{\partial D^{k} }} : = \int_{{\partial D^{k} }} {\left| {{\varvec{\varOmega}}\cdot {\varvec{n}}} \right|f \cdot g\rm{d}s}$$
(11)
$$\left\{ {\begin{array}{*{20}c} {\phi_{g,m}^{ + } = \mathop {\lim }\limits_{{\varepsilon \to 0^{ + } }} \phi_{g,m} ({\varvec{r}} + \varepsilon{\varvec{\varOmega}}_{m} )} \\ {\phi_{g,m}^{ - } = \mathop {\lim }\limits_{{\varepsilon \to 0^{ - } }} \phi_{g,m} ({\varvec{r}} + \varepsilon{\varvec{\varOmega}}_{m} )} \\ \end{array} } \right.$$
(12)
$$\left\{ {\begin{array}{*{20}c} {\partial D^{k + } = \left\{ {{\varvec{r}} \in \partial D^{k} :{\varvec{\varOmega}}\cdot {\varvec{n}} \ge 0} \right\}} \\ {\partial D^{k - } = \left\{ {{\varvec{r}} \in \partial D^{k} :{\varvec{\varOmega}}\cdot \user2{n < }0} \right\}} \\ \end{array} } \right.$$
(13)

The global variational form of the steady-state SN adjoint transport equation in the direction of a single discrete angle of a single group can be obtained by summarizing the Eq. (9) over all elements, that is, finding \(\phi_{g,m}^{*}\) in \(V_{{D_{h} }}\) to make sure Eq. (14) is satisfied for any testing function \(\phi_{g,m}^{*}\) in \(V_{{D_{h} }}\):

(14)

where, \(\phi_{g,m}^{{\rm{upwind}}}\) is the value of upwind flux on the mesh interface, \(E_{h}\) is the set of mesh interfaces, and \(\phi_{g,m}^{inc}\) is the boundary condition.

2.1.2 Source Biasing and Weight Window

Based on the adjoint theory, the response of the target region can be determined by Eq. (15):

$$\begin{aligned} R = \int_{{V_{\rm{d}} }} {\rm{d}{\varvec{r}}} \int_{0}^{\infty } {\rm{d}E\int_{{4\uppi }} {\phi \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})\sigma_{\rm{d}} ({\varvec{r}},E,{\varvec{\varOmega}})d{\varvec{\varOmega}}} } \hfill \\ = \int_{{V_{\rm{s}} }} {\rm{d}{\varvec{r}}} \int_{0}^{\infty } {\rm{d}E\int_{{4\uppi }} {\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})S({\varvec{r}},E,{\varvec{\varOmega}})d{\varvec{\varOmega}}} } \hfill \\ \end{aligned}$$
(15)

where R is the response, Vd is the volume of the target region, cm3, σd is the response function, and Vs is the volume of the forward source, cm3.

It can be seen from Eq. (15) that the adjoint flux stands for the contribution of particles at a specific position, energy, and direction to the response of the target region. This is the theoretical basis for the CADIS method to generate parameters of source biasing and weight window based on adjoint flux.

With an appropriate bias function, the source biasing is able to sample more low-weight source particles in important space, energy, and angle ranges. The reducing factor of initial weight is determined by the increasing factor of source particles to ensure the result is unbiased. To minimize the variance of the response of the target region, the bias function shown in Eq. (16) is recommended:

$$\begin{aligned} \widehat{S}({\varvec{r}},E,{\varvec{\varOmega}}) = &\frac{{\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})S({\varvec{r}},E,{\varvec{\varOmega}})}}{R} \hfill \\ &= \frac{{\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})S({\varvec{r}},E,{\varvec{\varOmega}})}}{{\int_{{V_{\rm{s}} }} {d{\varvec{r}}} \int_{0}^{\infty } {dE\int_{{4\uppi }} {\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})S({\varvec{r}},E,{\varvec{\varOmega}})d{\varvec{\varOmega}}} } }} \hfill \\ \end{aligned}$$
(16)

The initial weight of the corresponding source particle should be determined by Eq. (17):

$$w = w_{0} \frac{{S({\varvec{r}},E,{\varvec{\varOmega}})}}{{\widehat{S}({\varvec{r}},E,{\varvec{\varOmega}})}} = w_{0} \frac{R}{{\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})}}$$
(17)

where w and w0 are the initial weight of source particles with and without an unbiased source, respectively.

Weight window is a synergistic application of split and Russian roulette, which can be applied separately or simultaneously to the dimensions of space, energy, and angle. The upper and lower bounds of the weight window are used as a trigger of split and Russian roulette to ensure that the population and weight of particles maintain at a reasonable level. To minimize the variance of the response of the target region, the weight of the particles generated by the weight window should be consistent with Eq. (17). Thus, the mean value of the weight window can be determined by Eq. (18):

$$\frac{{w_{\rm{t}} + w_{\rm{b}} }}{2} = w_{0} \frac{R}{{\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})}}$$
(18)

where wt and wb are the upper and lower bound of the weight window, respectively. Practical experience indicates that to ensure the validity and applicability of the weight window, the gap between its upper and lower bounds should neither be too large nor too small. Therefore, most MC codes provide a default upper and lower bound ratio for the weight window and recommend users to generate a weight window with the default ratio. Thus, the lower bound of the weight window in Eq. (18) can be determined by Eq. (19) with the aforementioned upper and lower bound ratio \(c_{u}\):

$$w_{\rm{b}} = w_{0} \frac{2R}{{(c_{\rm{u}} + 1)\phi^{\rm{ * }} \rm{(}{\varvec{r}},E,{\varvec{\varOmega}})}}$$
(19)

2.2 Implementation

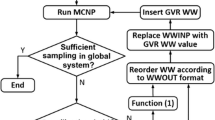
Based on the theoretical model in Sect. 2.1, the parallel three-dimensional unstructured-mesh neutron-photon coupled transport calculation code NECP-SUN, which is capable of performing adjoint transport calculation based on the unstructured mesh is developed independently. NECP-MCX [10] is a MC particle transport simulation code with independent intellectual property rights developed by the Nuclear Engineering Computational Physics (NECP) laboratory of Xi’an Jiaotong University. The traditional structural-mesh-based CADIS method has already been fulfilled by coupling the NECP-MCX with the finite-difference SN code NECP-Hydra [10]. To verify the method proposed in this paper, a coupling code based on unstructured-mesh CADIS is developed by embedding NECP-SUN into NECP-MCX as an adjoint transport solver. Figure 1 shows the flowchart of the unstructured-mesh CADIS method, which mainly consists of the following steps:

  • Step 1: Generate the unstructured mesh, the multi-group cross-section data, and the adjoint source which are required by FEM code based on the Constructive Solid Geometry (CSG) model, the continuous energy cross-section data, and the response characteristics of the tallied variable used in MC simulation, respectively.

  • Step 2: Obtain the distribution of adjoint flux on energy groups and unstructured meshes by performing the adjoint transport calculation based on the unstructured mesh, the multi-group cross-section data, and the adjoint source information generated in step 1.

  • Step 3: Perform forward MC simulation with the source biasing and weight window generated based on the distribution of adjoint flux provided by step 2 to obtain the response of the target region.

To implement the above processes, the following three problems need to be properly solved:

  1. 1)

    Building the computer-aided design (CAD) model corresponding to the CSG model,

  2. 2)

    Generating unstructured meshes,

  3. 3)

    Obtaining the adjoint source and cross-section data.

2.2.1 CSG-CAD Model Conversion

The unstructured mesh is generally generated based on the CAD model, thus it’s necessary to build a CAD model corresponding to the CSG model used in MC simulation. Boundary representation (BREP) is a relatively mature solid geometric representation method and is widely used in commercial CAD systems. A series of CSG-BREP conversion tools have been developed to generate CAD models based on the uniform surface-based basic Boolean operation. However, the geometric information for MC codes is often described by text, and complex nested customized expressions such as universe and lattice are added to effectively describe the complex characteristics of nuclear facilities. Moreover, the geometric description texts of different Monte Carlo codes are quite different in format. Therefore, to generate a CAD model utilizing the CSG-BREP conversion tools, it’s necessary to develop the analytic code for specific MC codes. The analytic code should be capable of parsing the geometric description text and translating the complex nested customized expression into uniform surface-based basic Boolean operations. The CSG-CAD conversion tool for NECP-MCX is developed and the specific processes are depicted in Fig. 2.

2.2.2 Unstructured Mesh Generation and the Local Mesh Refinement in the Target Region

The efficiency and accuracy of FEM calculation are determined by the quality of meshes. Many automatic mesh generation tools such as Gmsh and ICEM have been developed, which complete unstructured mesh generation within the global mesh size inputted by users. However, the following problems will occur when the automatically generated unstructured mesh is adopted in adjoint transport calculation: the size of the mesh in a specific region is determined by its geometric characteristics such as curvature and proximity. Unfortunately, the geometric characteristics are hardly irrelevant to the importance of particles, which will lead to serious memory waste and reduce the efficiency and accuracy of adjoint transport calculation. To solve this problem, the local mesh refinement for the target region based on face meshing control is implemented. After the global face meshing is completed, the face mesh in the target region will be regenerated with a smaller size, and then the volume mesh generation will be performed based on the updated face mesh. The above process is shown in Fig. 3, in which the size of global meshes and meshes in the target region is automatically determined based on CSG model information.

2.2.3 Determination of Adjoint Source and Generation of Multi-group Cross-section Data

Multi-group macro-cross section data are essential to carry out adjoint transport calculations with deterministic code. The coupling code automatically parses the nucleon density of nuclides in MC input and generates corresponding macro-cross sections based on the prefabricated bugle96 database.

The spatial and energetic distribution of the adjoint source is dependent on the location of the tallied region and the response function of the tallied variable. The coupling code automatically parses the tally information in MC input and then sets the adjoint source in deterministic code.

3 Numerical Results

To verify the variance-reduction capability of the update code, it is applied to calculate the specific activity of the radiometric monitor in the cavity of the HBR-2 benchmark problem. The CAD model of the HBR-2 benchmark is depicted in Fig. 4. The unstructured mesh generated automatically based on the CAD model and the structural mesh established by the finite difference discrete ordinate code are shown in Fig. 5 respectively.

To demonstrate the advantages of the unstructured-mesh CADIS method over the traditional CADIS method and illustrate the significant effect of local mesh refinement on improving the computational efficiency of unstructured-mesh CADIS, several cases are performed as follows:

  1. (1)

    Case1 performs MC simulation through NECP-MCX with unbiased source and energy cutoff, which is the base case.

  2. (2)

    Case2 obtains results through the traditional CADIS method which MC simulation is performed with source biasing and weight window generated based on adjoint flux calculated by finite-difference SN code NECP-Hydra.

  3. (3)

    Case3 obtains results through the unstructured-mesh CADIS method which MC simulation is performed with source biasing and weight window generated based on adjoint flux calculated by SN-FEM code NECP-SUN.

  4. (4)

    Case4 obtains results through the same method in case 3 with local mesh refinement for the target region implemented. The parameters of meshing control which are determined automatically are shown in Table 1 and the meshes of the radiometric monitor in case3 and case4 are shown in Fig. 6.

Fig. 1.
figure 1

Flowchart of unstructured-mesh CADIS method

Full size image
Fig. 2.
figure 2

Flowchart of CSG-CAD conversion

Full size image
Fig. 3.
figure 3

Flowchart of unstructured mesh generation

Full size image
Fig. 4.
figure 4

CAD model of HBR-2 benchmark

Full size image
Fig. 5.
figure 5

Structural-mesh and unstructured-mesh models for HBR-2 benchmark

Full size image
Table 1. Parameters for meshing control
Full size table
Fig. 6.
figure 6

Meshes of the radiometric monitor in case3 and case4

Full size image
Table 2. Dose rates and their C/E for different cases
Full size table
Table 3. Relative statistic error and FOM for different cases
Full size table

To ensure the comparability of the results, all 4 cases simulate 2 × 109 particles through 256 cores paralleled. For case2–4, the modeling and computing time of deterministic code is considered.

The dose rates of the radiometric monitor in the cavity and its ratio to measurements in all cases are shown in Table 2. From Table 2 we can conclude that the calculation of dose rates of the radiometric monitor in the cavity is a typical deep-penetration problem. Case1 can barely obtain reasonable results because of the dramatically low tally rate caused by the strong shielding effect between cavity and source. On the contrary, owing to the applications of the CADIS method, case2–4 obtain dose rates with acceptable error. Among them, cases in which unstructured-mesh CADIS is applied give out dose rates closer to measurements on the whole than in case2 the traditional CADIS method is applied. Furthermore, the C/E of all reaction channels in case4 is closer to 1 than in case3 because of the local mesh refinement in the radiometric monitor.

The relative statistical error and figure of merit (FOM) are listed in Table 3. It can be drawn from the results of the case1 that conventional MC simulation is incompetent since the unacceptable high variance. In certain reaction channels, the relative statistical error reaches 100% because of the zero tally rate, resulting in terrible FOM. By contrast, the relative statistical error is significantly reduced and the FOM is raised by 3–4 orders in case2–4 the CADIS method is implemented. Case2 and case4 demonstrate that the application of the unstructured-mesh CADIS method can further reduce the relative statistical error by up to 22% compared to the traditional CADIS method. Besides, case3 and case4 indicate that the local mesh refinement for the target region effectively improves the computational efficiency of the unstructured-mesh CADIS method, which is reflected in the reduction of relative statistical error and the boost of FOM.

4 Conclusions

The parallel three-dimensional unstructured-mesh neutron-photon coupled transport calculation code NECP-SUN based on the SN method and discontinuous FEM is developed and coupled with MC code NECP-MCX to study and implement the unstructured-mesh CADIS method. The coupled code automatically generates unstructured mesh based on the CSG model in MC input and performs adjoint transport calculation through the unstructured-mesh FEM, the adjoint flux obtained is utilized to generate the parameters of source bias and weight window for forward MC simulation. The numerical results of the HBR-2 benchmark obtained by the coupled code show that for deep-penetration problems, the unstructured-mesh CADIS method can obtain more accurate results with less relative statistical error (up to 22% reduction) than the traditional CADIS method, and the FOM is increased by up to 3–4 orders comparing to conventional MC simulation. Moreover, the efficiency and accuracy of the unstructured-mesh CADIS method can be further improved by applying the refinement of meshes in target regions.