Keywords

1 Introduction

Sparse representation of signals has attracted wide attention in recent years. The principle is to use a small number of atoms in a given supercomplete dictionary to represent seismic signals, and the original signals are expressed through a linear combination based on a small number of basic signals [1]. Sparse coding is also known as dictionary learning. This method seeks appropriate dictionaries for samples with common dense expression and converts the samples into appropriate sparse expression forms, thus simplifying the learning task and reducing the complexity of the model. The two main tasks of signal sparse representation are dictionary generation and signal sparse decomposition. The selection of dictionaries generally falls into two categories: dictionary analysis and dictionary learning.

In essence, Monte Carlo method is a very important numerical calculation method guided by the theory of probability and statistics. Monte Carlo method has been widely used in architecture, automation, computer software and other fields [2]. The Monte Carlo method is an effective method to find the numerical solution for the complicated problem. For large-scale image filtering, Chan et al. proposed a Monte Carlo local nonmean method (MCNLM) [3], which speeds up the classical nonlocal mean algorithm by calculating the subset of image block distance and randomly selecting the position of image block according to the preset sampling mode.

Monte Carlo thought has been widely applied. For example, in mechanical engineering, Rodgers et al. built a micro-structure prediction tool based on Monte Carlo thought, and explored the correlation between the average number of remelting cycles during construction and the generated cylindrical crystals by setting the correlation coefficient of the model [4].

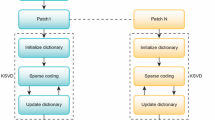
2 Dictionary Learning Theory

In theory, sparse dictionary learning includes two stages: dictionary construction stage and sparse dictionary representation sample stage. Learning every dimension of dictionary atoms requires training, and sparse representation is to represent the signal with as few atoms as possible in the over-complete dictionary. The trained dictionary is too large to be used in practice. The construction and training of the dictionary require a large number of training samples. The over-complete dictionary contains too many dimensions and is not practical and operable. The block theory can overcome this limitation and establish a training set. Data blocks can be extracted from noisy data or similar but non-noisy data as training sets.

The data is divided into small blocks and denoised separately, so the learning problem becomes [5, 6]:

$$ \left( {\hat{A},\,\hat{D}} \right) \in \,\arg \,\mathop {\min }\limits_{A,D} \sum\limits_{i,j} {0.5\left\| {{\text{R}}_{{\left( {{\text{i}},\left. {\text{j}} \right)} \right.}} \left( {\text{X}} \right) - {\text{Da}}_{{{\text{i}},{\text{j}}}} } \right\|^{2} + \lambda \left\| {{\text{a}}_{{\text{i,j}}} } \right\|}_{1} $$
(1)

Is the sparse decomposition of data blocks in the dictionary and is a parameter used to balance the fidelity of the data with the sparsity of the data representation in the dictionary. And are regarded as known quantities, and the variables in formula 1 correspond to the minimization of a single variable.

The update of sparse coding can be completed by the sparse matrix solver, which can find and solve the sparse representation of each training sample data in a fixed dictionary [7]:

$$ \hat{\upalpha }\, \in \,\arg \,\mathop {\min }\limits_{{\hat{\upalpha }}} \,\frac{1}{2}\left\| {{\text{x}}\, - \,{\text{D}}\alpha } \right\|^{2} \, + \,\lambda \,\left\| \upalpha \right\|_{1} $$
(2)

There are many algorithms to solve the problem of sparse representation of signal and decomposition in complete dictionary. In this paper, orthogonal matching tracking (OMP) is used.

Dictionary updates include minimizing data representation errors, i.e.

$$ \hat{D}\, \in \,\arg \,\mathop {{\text{min}}}\limits_{{\widehat{{{\text{D}} \in {\mathbf{D}}}}}} \left\| {{\text{P}} - {\text{D}}\upalpha \,} \right\|_{{\text{F}}}^{2} $$
(3)
$$ {\mathbf{D}} = \left\{ {{\text{d}}:\left\| {{\text{d}}_{{\text{j}}} } \right\|^{2} = \mathop \sum \nolimits_{{\text{i}}} \left| {{\text{d}}_{{\text{j}}} \left[ {\text{i}} \right]} \right|^{2} \le 1} \right\} $$
(4)

When the dictionary is retrieved in the set, the norm of the atom can become arbitrarily large, and the degree of variation of the coefficient can be arbitrarily small. Artificial reduction of energy minimizes the possibility of dictionary return [8].

The method adopted in this article is the MOD method, which essentially updates the dictionary by minimizing the mean residual. In the training with noisy data, the noise variance control parameters, first,

$$ \left\| {{\text{x}} - \,{\tilde{\text{x}}}} \right\|_{2} \, \le {\text{C}}\sigma \,\sqrt {\text{n}} $$
(5)

Formula 5 represents the level of noise. When the error between the vector and its sparse approximation meets the conditions, OMP calculation will be stopped. Among them, the gain factor C is used to balance the fidelity and sparsity, and the gain factor makes the sparse coding step more flexible. The denoising gain factor balances data fidelity and sparsity, and a larger gain factor will give a sparse and less accurate patch representation in the dictionary [9]. When learning on noiseless samples, a fixed number of coefficients estimated by OMP must be selected in advance.

After the dictionary is trained, the standard of formula 5 is used to calculate the sparse approximation in the dictionary, denoise each data block, and then calculate the average of the denoised data blocks to reconstruct the whole data.

3 Block Theory

Chunking is the theory that data is broken up into small chunks and processed before the dictionary is built. There are certain similarities in the data blocks, which may appear as coming from the same in-phase axis or signal edge region in the seismic data. When the similarity is not obvious, the whole data can be sparsely represented by a set of basis functions, and a new matrix is constructed after vectorization of the selected data blocks. The stacking of data blocks is called the overlap degree. In general, if the upper limit of the number of selected blocks is not set, the data size is fixed, the higher the overlap degree is, the more selected blocks are, the more samples are selected, and the more beneficial it is for dictionary construction and update. However, a large number of sample selection increases the calculation amount.

3.1 Regular and Random Chunking

Regular chunking and random chunking are both chunking methods that limit the upper limit of selected blocks and the degree of overlap. The selection of these two methods has nothing to do with the characteristics of the data itself.

The theory of regular block selection specifies the step size and direction of block selection in the process of selection. Formula 6 represents the regular block partitioning process of a 3 × 3 matrix with a block size of 2 ×  2:

$$ \left[ {\begin{array}{*{20}c} {{\text{x}}_{11} {\text{x}}_{12} {\text{x}}_{13} } \\ {{\text{x}}_{21} {\text{x}}_{22} {\text{x}}_{23} } \\ {{\text{x}}_{31} {\text{x}}_{32} {\text{x}}_{33} } \\ \end{array} } \right] \to \left[ {\begin{array}{*{20}c} {{\text{x}}_{11} } & {\begin{array}{*{20}c} {{\text{x}}_{12} } & {\begin{array}{*{20}c} {{\text{x}}_{12} } & {{\text{x}}_{13} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\text{x}}_{21} } \\ {\begin{array}{*{20}c} {{\text{x}}_{21} } \\ {{\text{x}}_{31} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{x}}_{22} } & {{\text{x}}_{22} } & {{\text{x}}_{23} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{x}}_{22} } & {{\text{x}}_{22} } & {{\text{x}}_{23} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\text{x}}_{32} } & {{\text{x}}_{32} } & {{\text{x}}_{33} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] $$
(6)

In seismic data, the process of regular block selection is uniform throughout the data. The difference between the random block theory and the regular block theory lies in that the block selection position of the random block is completely random, so the situation of data block cluster stacking may occur:

$$ \left[ {\begin{array}{*{20}c} {{\text{x}}_{11} } & {\begin{array}{*{20}c} {{\text{x}}_{12} } & {\begin{array}{*{20}c} {{\text{x}}_{13} } & {{\text{x}}_{14} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\text{x}}_{21} } \\ {\begin{array}{*{20}c} {{\text{x}}_{31} } \\ {{\text{x}}_{41} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{x}}_{22} } & {{\text{x}}_{23} } & {{\text{x}}_{24} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{x}}_{32} } & {{\text{x}}_{33} } & {{\text{x}}_{34} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\text{x}}_{42} } & {{\text{x}}_{43} } & {{\text{x}}_{44} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \to \left[ {\begin{array}{*{20}c} {{\text{x}}_{11} } & {\begin{array}{*{20}c} {{\text{x}}_{12} } & {\begin{array}{*{20}c} {{\text{x}}_{12} } & {{\text{x}}_{13} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\text{x}}_{21} } \\ {\begin{array}{*{20}c} {{\text{x}}_{21} } \\ {{\text{x}}_{31} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{x}}_{22} } & {{\text{x}}_{22} } & {{\text{x}}_{23} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{x}}_{22} } & {{\text{x}}_{33} } & {{\text{x}}_{34} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\text{x}}_{32} } & {{\text{x}}_{43} } & {{\text{x}}_{44} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] $$
(7)

Therefore, in seismic data, random blocks may be repeated selection of a large number of areas, obvious aggregation of data blocks, or no selection of data in some areas.

3.2 Monte Carlo Data Chunking

In dictionary learning, dictionary directly determines the quality and efficiency of denoising. In traditional data block and sample selection method is mostly random and selection rules, each sample is there, and we hope the dictionary thin enough, namely the limited samples can contain more useful information, can be enough to show the characteristics of complex data, so in the process of selecting data contains information should choose more blocks of data. If the variance of the set data block is associated with the contained valid information, set the standard we expect. When the variance is greater than the expected value, the corresponding data block will be retained, and then all the retained data blocks will undergo the next step of dictionary training. This selection method is called the Monte Carlo sample selection method.

Randomness to itself quality problem, usually need to probability of correct description and simulation process, for the deterministic randomness of itself is not quality problem, you need to build the probability of an artificial process, to a certain parameter set to solution of the problem, will not be the randomness of quality problem into a random. For example, using Monte Carlo method to estimate PI is a very classic problem. As shown in Fig. 1, the number of selected points n is 1000, and the calculated PI is 3.1568, with an error of about 0.048.

Fig. 1
A graph of y versus x plots an ellipse along with a dense concentration of points throughout the graph.

Calculation of π using Monte Carlo idea

Full size image

In seismic data, we want the data block to contain information about the same phase axis as much as possible. Therefore, variance can be used to determine whether the selected block region contains in-phase axis information or whether it contains enough effective information, which is defined as the complexity of the data block. If the amplitude of the in-phase axis does not change in the region selected from the noise-free data, the variance is 0. If the amplitude of the in-phase axis changes in the region, the variance will increase [10].

4 Examples of Measured Seismic Data

In order to explore the practical effect of Monte Carlo block theory dictionary learning, the dictionary learning method based on Monte Carlo block theory is applied to the processing of measured data. The data will be processed by random block theory dictionary learning, regular block theory dictionary learning and Monte Carlo block respectively. Moreover, the denoising effect is studied by marking the location of different block theory dictionary learning. Wherein, the iteration times of the dictionary learning algorithm is 50, the coincidence degree is 4, the noise variance is 0.2, and the size of a single data block selected is 9 × 9.

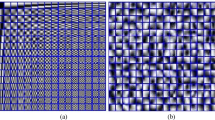
Figure 2. shows the data block selection diagram of the original data and its different block theory dictionary learning. Figure 2. a is the original data diagram of the data. There are a large number of weak amplitude signals, which are in obvious contrast with the in-phase axis of the main strong amplitude. From monte carlo block selection is shown in Fig. 2. b, data block is focused on the overall data of the upper signal strong area, compared with the signal is weak regional selection of data block is less, and most of the weak signal region selection data block in the subdivided by multiple axis gathered area, has the obvious and primary and secondary data without fine feature selection. As shown in Fig. 2. c, the data blocks selected by the rule are evenly spread over the entire data, which is close to the whole selection. However, due to the different proportions of data blocks in signal areas with different intensifies, it needs to be verified by the denoising process whether the dictionary can represent the data sparsely and accurately enough. In contrast, as shown in Fig. 2. d, the randomly selected data blocks are very messy, because randomness leads to a large number of selected data blocks in the blank area and a single area of the signal, and a small number of areas containing a lot of data feature information are not selected, which has an impact on later sparse representation and dictionary update.

Fig. 2
4 seismic data maps of time sampling numbers versus the trace number have light-shaded lines and gradient scales. Maps a to d are the original data diagram of real data 1, the Monte Carlo block selection diagram, the regular block selection diagram and the random block selection diagram with points.

Theoretical diagram of different blocks of realdata1 measured seismic data

Full size image

Figure 3. a shows the data with 20% noise added to the data, mainly strong signals with high amplitude. When 20% noise is added, most weak signals are submerged. Figure 3. b shows the Monte Carlo block denoising diagram, the SNR is 16.4 dB, the running time is 5.0 s, and the main horizontal in-phase axis is reconstructed with relatively complete denoising. Use a dictionary to learn the data sparse representation to rebuild and remove most of the noise, but some detail feature does not show it, the data distortion caused by Fig. 3. c denoising Fig. for the dictionary selection rules theory learning, denoising SNR is 14.9 dB, running time of 5.1 s, in Fig. 3. d random graph theory dictionary learning method, The signal-to-noise ratio of denoising is 15.5 dB and the running time is 5.5 s. The two methods have the most serious damage to the signal. From the perspective of running time, the previous speculation is verified. Since the Monte Carlo block selects the least data blocks, the running time is the shortest, and the processing efficiency of data denoising is relatively high.

Fig. 3
4 seismic data maps of time sampling number versus trace number have light-shaded lines and gradient scales, with corresponding S N R values. Maps a to d are the real data 1 denoised data map, Monte Carlo block denoising map, regular block denoising map, and random block denoising map.

Denoising results of realdata1 data dictionary learning with different block theory

Full size image

Figure 4. is the residuals of the data after denoising, and Fig. 4. a is the residuals of the Monte Carlo selection method. In the Fig. 4., except for some strong amplitude signals, there is basically no feature of weak signals, and they are mostly noise, indicating that the denoising is more thorough. Figure 4. b shows the residual signal-to-noise ratio selected by the rule, and weak signal features can be distinguished in the lower left and lower right parts. The random residual Fig. shown in Fig. 4 c shows that the signal features in the lower left part are more obvious, which indicates that in the original denoising process, the retention effect of data detail features in this area is poor. However, the residual graphs of the three methods can all see some features of the original data and have a certain degree of damage, while the Monte Carlo block theory dictionary learning denoising achieves better denoising results.

Fig. 4
3 seismic data maps of time sampling number versus trace number with gradient scales. The noisy maps a, b, and c are for Monte Carlo block residuals, regular block residuals, and random block residuals.

De-noising residuals of realdata1 data dictionary learning of different blocks theory

Full size image

Through this dictionary learning method based on monte carlo theory demonstrates how to applied to seismic data denoising, and the results with the stochastic block theory dictionary learning dictionary and rules of block theory, from the perspective of the denoising results of measured data, the dictionary to study seismic data denoising still has an obvious effect in the treatment of the complex seismic data. Comparing three methods, monte carlo block theory dictionary learning can be relatively better reconstructed seismic data, suppression of noise at the same time can effectively preserve the weak signal characteristics of seismic data, in smaller seismic data, the monte carlo block will priority selection signal strong area, weak signal area of less data, lead to appear weak in phase axis, the condition of the damaged However, when the data is large enough, the overall data de-noising and reconstruction is relatively complete and accurate, and the processing efficiency is fast, and a high signal-to-noise ratio is obtained. Random block theory dictionary learning and regular block theory dictionary learning are obviously inferior to Monte Carlo block theory dictionary learning in detail feature protection, and the processing efficiency is relatively poor, exposing a lot of disadvantages.

On the basis of data 1, we have conducted 6 comparative studies of measured data and 7 comparative studies and analyses to obtain the following tables and figures below.

Figure 5. for the three methods all data denoising SNR contrast Fig., it is not hard to see the monte carlo block theory in dealing with different types of data dictionary learning can obtain good denoising effect, is the most excellent in three ways. Table 1 is the running time of the three methods in seven data, Fig. 6. for three methods run time contrast Fig., it is not hard to see, Monte Carlo block theory dictionary learning has a higher signal-to-noise ratio and the shortest time. Due to its self-adaptability, it can use fewer data blocks to contain enough effective information and meet the requirements of dictionary construction denoising. Therefore, it is a more efficient denoising method.

Fig. 5
A multiline graph plots signal noise ratio versus data number. 3 lines decrease from real data 1 to 2 on the x-axis, peak at real data 3, decrease, and then increase gradually. The names of the lines are in a foreign language.

Comparison of SNR of different denoising methods

Full size image
Table 1 List of running time of different methods of measured data
Full size table
Fig. 6
A multiline graph plots time versus data number. 3 lines increase from real data 1 to 2 on the x-axis, decrease, peak at real data 5, decrease, and then increase steeply. The names of the lines are in a foreign language.

Compares the running time of different methods

Full size image

5 Conclusion

The data processing ability of dictionary learning and Monte Carlo block theory dictionary learning in complex cases is verified by the processing of actual data. By comparing the three methods, the method proposed in this paper achieves the highest signal-to-noise ratio and the highest processing efficiency, especially the weak features of the data are preserved. The results show that Monte Carlo block theory dictionary learning has a good performance of denoising under different conditions.

Because the dictionary directly determines the quality of the denoising result. Afterwards monte carlo block theory dictionary learning dictionary, selection rules of block theory and random selection rules of block theory dictionary learning, although three approaches to sparse coding, dictionary update and a series of core algorithm is consistent, but as a result of the selected data block, a higher effective information block of data of different, caused the denoising results of three methods there is a certain gap.

In this paper, dictionary learning based on a block theory provides a new attempt for seismic data of dictionary learning, and makes a certain breakthrough compared with the traditional methods. The dictionary learning algorithm itself is optimized to a certain extent. The advantage of dictionary learning lies in the extraction of the most essential features of data, which is of great significance in the research of data processing in the direction of geophysics.