Complex Frequency-Domain Oscillation Analysis of the Pumped-Storage Systems

Abstract

Hydraulic impedance, as an efficient frequency-domain analysis alternative, has been widely utilized in hydraulic transient analysis for decades. Since the mathematical expressions of hydraulic systems with complicated pipe networks are usually rather complex, it is difficult for the traditional continuous impedance method to obtain the analytical solutions to the system’s frequency responses directly. Therefore, an equivalent circuit modeling-based discrete impedance method is proposed to mathematically express the hydraulic systems of a pumped storage plant system with complicated pipe networks. Through drawing an analogy between various hydraulic facilities and different types of electrical circuits, the equivalent circuit topology of any hydraulic system can be obtained according to the circuit theory in electrical engineering. The oscillation analysis of the pumped-storage power plant is conducted, and influences of the pump-turbine impedance on the system’s oscillation characteristics have been discussed.

1 Introduction

The pumped-storage power plant is known as a multi-physics coupling system [1] and usually has a very complicated flow passage layout, so the investigation of the hydraulic features of pumped-storage systems is of great importance. Over the past decades, researchers have proposed different mathematical models of pumped-storage systems for better hydraulic description, and the mathematical analysis schemes are divided into two categories, i.e., time-domain models and frequency-domain models [2].

Time-domain models excel in simulating the time evolutions of the system states, e.g., the rotation speed, the head and the discharge [3]. Frequency-domain methods, such as the well-known transfer matrix [4] and hydraulic impedance [5], were extensively adopted in the stability criterion and the oscillation analysis of hydraulic systems. The hydraulic impedance [6] can explicitly express the relationship between head and discharge in complex domain. Existing literature has reported its applications in many practical water conveyance scenarios [7,8,9].

This paper introduces an equivalent circuit model-based discrete impedance method that can be applied to the complex frequency-domain analysis of pumped storage systems. The hydraulic transients in pipes are analogized with the electromagnetic characteristics in transmission lines. For a complex pumped storage plant system, the overall circuit topology can be obtained by combining the equivalent circuits of different hydraulic components according to the system structural layout. Oscillation analysis was performed in a pumped-storage power plant with a complex flow passage structure by applying the proposed discrete impedance model.

2 Methodology of the Equivalent Circuit Model

The Saint–Venant equations of the pressurized pipe [10, 11] are given as Eq. (1)

$$ \left\{ {\begin{array}{*{20}l} {\frac{\partial H}{{\partial t}} + v\frac{\partial H}{{\partial x}} + \frac{{a^{2} }}{gA}\frac{\partial Q}{{\partial x}} = 0} \hfill \\ {g\frac{\partial H}{{\partial x}} + \frac{1}{A}\frac{\partial Q}{{\partial t}} + \frac{v}{A}\frac{\partial Q}{{\partial x}} = g\left( {S_{0} - \frac{{n_{c}^{2} Q\left| Q \right|}}{{R_{a}^{4/3} A^{2} }}} \right)} \hfill \\ \end{array} } \right. $$

(1)

where, H and Q denote the pressurized head and discharge, respectively. n_c, $R_{a}$ and A represent the friction factor, the hydraulic radius and the cross-sectional flowing area of the pipe, respectively.

Since the value of wave propagation velocity a is bigger than that of flow velocity v, $v\frac{\partial H}{{\partial x}}$ is often ignored [11]. The hydraulic dynamics of the pipe can be modelled as a T-shaped equivalent circuit shown in Fig. 1, where $R_{e}$, $L_{e}$, $C_{e}$ are the circuit resistance, inductance and capacitance per unit length, respectively.

Fig. 1

The circuit of the transmission line per unit length

The equivalent resistance, inductance, and capacitance parameters can be obtained as $R_{e} = \frac{{n_{c}^{2} \left| Q \right|}}{{R^{4/3} A^{2} }} - \frac{{S_{0} }}{Q}{ + }\frac{1}{{gA^{2} }}\frac{\partial Q}{{\partial x}}$, $L_{e} = \frac{1}{gA}$, $C_{e} = \frac{gA}{{a^{2} }}$.

where, the partial differential term $\frac{1}{{gA^{2} }}\frac{\partial Q}{{\partial x}}$ corresponds to $v\frac{\partial h}{{\partial x}}$ in Eq. (2).

3 System Plant Introduction and its Modelling

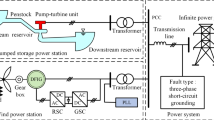
A pumped-storage power plant with a complex conduit system was taken as a case study. The flow passage comprises of a diversion tunnel, an upstream surge tank, a penstock, a volute, a draft tube and extension, a tailrace surge tank, and a tailrace tunnel. The structural schematic of the hydraulic system is illustrated in Fig. 2.

Fig. 2

Structural schematic of the pumped-storage power plant

According to the equivalent circuit modeling theory, the overall equivalent circuit topology of the flow passage of the pumped-storage plant is shown in Fig. 3.

Fig. 3

Equivalent circuit topology of the hydraulic structure of a pumped-storage plant

4 Simulation Result Analyses

The decay coefficients and eigen frequencies of the first ten orders of oscillation in free oscillation analysis with the proposed discrete model and the traditional continuous model are listed in Table 1. It shows that ECM can obtain very similar complex eigen frequency results to those of the traditional continuous impedance model. The modeling errors between the two models are quite small for low-frequency responses and gradually increase for higher frequency responses. The oscillation frequencies of the first two orders of oscillation are much lower than those of others. Compared with the classic theoretical oscillation frequencies of the surge tanks calculated by the equations in [10], the first two orders of oscillation are believed to coincide with the oscillation modes of the tailrace surge tank and upstream surge tank, respectively. While the 3^rd - 10^th order oscillations correspond to the os cillation modes of the system pipelines.

Table 1 The eigen mode analysis comparison of the two models

The change regulations of the decay coefficients of the 3^rd- to 10^th-order oscillations are depicted in Fig. 4. The decay coefficients of eight oscillation orders share the same variation trends and decrease at different rates as pump-turbine impedance increases. The 3^rd-order oscillation possesses the fastest decreasing rate, while the 5^th-order oscillation possesses the slowest. The decay coefficients are positive when Z_T < 0 and negative when Z_T > 0. When Z_T = 0, the decay coefficient equals zero, which means the oscillation pattern at this condition is a constant amplitude oscillation.

Fig. 4

Change regulations of the decay coefficients of the first eight orders that correspond to the pipelines

To further investigate the variation trend of the eigen frequency in each order of oscillation, the precise variation trends of the 3^rd- to 10^th- order of oscillation are displayed in Fig. 5 (a)–(h), respectively. It shows that the eigen frequencies of most oscillations vary along with the change of the pump-turbine impedance though the oscillation amplitudes are very small. Among the eight orders of oscillation, the frequencies of the 3^rd-, 4^th-, 9^th-, and 10^th- orders of oscillation decrease as the absolute value of the pump-turbine impedance increases, and the frequencies of the 6^th-, 7^th-, and 8^th- orders of oscillation increase as the absolute value of the pump-turbine impedance increases. the frequency of the 5^th- order oscillation remains constant as the pump-turbine impedance varies.

Fig. 5

The precise variation trend of the eigen frequency of each oscillation order that corresponds to the pipelines: (a) the 3rd- order; (b) the 4th- order; (c) the 5th- order; (d) the 6th- order; (e) the 7th- order; (f) the 8th- order; (g) the 9th- order; (h) the 10th- order

5 Conclusions

This work introduced an equivalent circuit modeling (ECM)-based discrete hydraulic impedance method in complex frequency-domain analysis of pumped storage systems. The proposed ECM-based impedance method can achieve satisfactory modeling accuracy. In the oscillation analysis of the pumped-storage power plant, numerical results showed that there exists a close relationship between the value of the pump-turbine impedance and the decay coefficients of the different orders of oscillation. However, the pump-turbine impedance can hardly affect the system’s eigen frequencies.