Study on Seepage Mechanism and Stability of Unsaturated Slope Based on Trefftz Method

Abstract

This paper proposes a space–time Trefftz method (STM) to study the seepage mechanism and stability of unsaturated slopes. The groundwater flow under transient conditions is important in engineering practice for solving practical problems such as assessing the stability of unsaturated soil slopes. Based on the transient groundwater equation, we derived the Trefftz basis functions by splitting the variables. The solutions are approximated using Trefftz basis functions in the space–time domain. The Stabl software is subsequently employed to analyze the stability of the slope under the rainfall recharge condition with the combined reservoir water level fall. The results demonstrate that the steeper the hydraulic slope drop under combined reservoir water level fall and rainfall infiltration, the more unstable the slope becomes.

1 Introduction

Slope instability occurs at the surface of the ground often affecting human activities and the building environment with catastrophic consequences. According to the results of geological hazard surveys in 290 counties and cities nationwide, slope instability accounts for 51% of geological hazards, while rainfall-induced landslides account for about 90% of the total [1]. Numerous scholars have studied unsaturated seepage [2] and slope stability analysis [3]. For reservoir bank slopes, the degree of influence of coupled rainfall effect on slope stability varies when the reservoir water level changes, and the unstable seepage of groundwater is the main factor affecting slope stability. Therefore, it is necessary to analyze and study the influence of precipitation-induced groundwater level change on the stability of soil slopes. At present, the experimental method and the numerical analysis method are mainly used for groundwater seepage in unsaturated soils [4]. Most of the traditional numerical methods for solving groundwater seepage problems are discretized by finite difference method [5], finite element method [6] to create meshes. Nevertheless, for complex study areas, such methods encounter the problem of difficult grid creation, and the problem boundary needs to be simplified to be analyzable [7]. In recent years, many scholars have studied meshless methods that are exempted from the establishment of a mesh [8], the collocation Trefftz method does not require the creation of a grid and integration of the boundary [9]. The basis function satisfies the control equation, and the points are only distributed on the boundary. The coefficient matrix satisfying the boundary conditions is obtained through the boundary points to solve the problem, which reduces the computational difficulty and ensures computational accuracy, has strong advantages for complex shape computational domain problems [10].

For solving the transient problem, this study instead of using the traditional time marching method, solves the problem based on the space–time coordinate system through the concept of space–time matching method, which effectively simplifies the calculation process and avoids error accumulation. In this paper, the groundwater seepage mechanism of unsaturated soil slopes under the action of rainfall is analyzed by using STM. The slope analysis model is established based on the limit equilibrium theory to calculate the safety coefficient at different water levels considering the influence of groundwater seepage, to investigate the influence of reservoir level changes combined with rainfall on the stability of unsaturated soil slopes.

2 Seepage Governing Equation and Unsaturated Slope Stability

2.1 Governing Equation

The governing equation for two-dimensional transient homogeneous isotropic seepage considering the complementary drainage effect of seepage is the Dupuit-Boussines equation as follows

$$ {{\partial^{{2}} h^{2} } \mathord{\left/ {\vphantom {{\partial^{{2}} h^{2} } {\partial^{{2}} x}}} \right. \kern-0pt} {\partial^{{2}} x}} + {{\partial^{{2}} h^{2} } \mathord{\left/ {\vphantom {{\partial^{{2}} h^{2} } {\partial^{{2}} y}}} \right. \kern-0pt} {\partial^{{2}} y}} + w = {{(1} \mathord{\left/ {\vphantom {{(1} D}} \right. \kern-0pt} D})({{\partial h^{{2}} } \mathord{\left/ {\vphantom {{\partial h^{{2}} } {\partial t}}} \right. \kern-0pt} {\partial t}}) $$

(1)

where D = k/S_s (m²/s) denotes hydraulic diffusion coefficient, h denotes total head (m), k is hydraulic conductivity, S_s is the volumetric specific storage, m/s), w = 2I/k expressed twice the ratio of subsurface subsidy rate and permeability coefficient for the dimensionless number, I indicates the aquifer unit time, unit area of vertical recharge and discharge, recharge is positive discharge is negative.

For simulating the transient flow of water in unsaturated soil slopes, the initial and boundary conditions are given as follows

$$ u(x,y,{0}) = h_{0}^{2} (x,y,t),\left( {x,y,t = 0} \right) \in \Omega_{t} $$

(2)

$$ u(x,y,t) = h_{D}^{2} (x,y,t),\left( {x,y,t} \right) \in \Gamma_{D} $$

(3)

$$\begin{array}{lll} \partial u(x,y,t)\big/\partial n & =& (\partial u(x,y,t)\big/ \partial x)n_{x} + (\partial u(x,y,t)\big/\partial y) n_{y}\\ &=& h_{N}^{2} (x,y,t),\left( {x,y,t}\right) \in \Gamma_{N}\end{array} $$

(4)

where h₀ is the initial total head, h_D is Dirichlet boundary data, h_N is Neumann boundary data, $\Omega_{t}$ donates the space–time domain, $\Gamma_{D}$ denotes the boundary that satisfies the Dirichlet boundary condition, $\Gamma_{N}$ denotes the boundary that satisfies the Neumann boundary condition, $\vec{n} = \left( {n_{x} ,n_{y} } \right)$ denotes the outward normal component.

2.2 Unsaturated Slope Stability

Janbu method was proposed by Janbu in 1973 to solve the safety coefficient by iteration. In this paper, we use the STABL program in (Janbu Circular) to calculate the slope stability, and use the two-dimensional limit equilibrium analysis to calculate the safety coefficient.

3 Numerical Algorithms

3.1 The Space–Time Trefftz Method

STM is to take time as a dimension, and the original N-dimensional space becomes (N + 1)-dimensional spatio-temporal domain. The transient seepage governing equation considering the complementary drainage effect is expressed in the polar coordinate system as follows

$$ \frac{{\partial^{{2}} u(r,\theta ,t)}}{{\partial r^{{2}} }} + \frac{1}{r}\frac{\partial u(r,\theta ,t)}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u(r,\theta ,t)}}{{\partial \theta^{2} }} + w = \frac{1}{D}\frac{\partial u(r,\theta ,t)}{{\partial t}},(r,\theta ,t) \in \Omega_{t} $$

(5)

where r is radius, t is time, $\theta$ is polar angle, The T-basis of the governing equation is obtained by using the variable separation method. To improve the order of STM and to eliminate the influence of the matrix pathology at the same time, the characteristic length $R_{0}$ is introduced, which effectively avoids the phenomenon of non-convergence of the basis function with the expansion of the level [11]. The T-basis of the simply domain of slope seepage under the Dirichlet boundary condition after adding the characteristic length as follow

$$ \begin{aligned} u(r,\theta ,t) = & \sum\limits_{{p = 1`}}^{m} {\sum\limits_{{q = 1`}}^{s} {\bar{\alpha }_{{pq}} T_{{qp}} (r,\theta ,t)} = 1 - \frac{{wr^{2} }}{4}\sum\limits_{{p = 1}}^{m} {\exp ( - Dp^{2} t)A_{p} J_{0} (\frac{{pr}}{{R_{0} }})} + \sum\limits_{{q = 1}}^{s} {B_{{2q}} (\frac{r}{{R_{0} }})^{{ - q}} \cos (q\theta )} } \\ & + \sum\limits_{{q = 1}}^{s} {B_{{3q}} (\frac{r}{{R_{0} }})^{{ - q}} \sin (q\theta )} + \sum\limits_{{p = 1}}^{m} {\sum\limits_{{q = 1}}^{s} {\exp ( - Dp^{2} t)J_{q} (\frac{{pr}}{{R_{0} }})(A_{{6pq}} \cos (q\theta ) + A_{{7pq}} \sin (q\theta ))} } \\ \end{aligned} $$

(6)

where J₀ and J_q denote the order 0 and q first class Bessel functions, respectively, $p = 1,2, \cdots m$ and $q = 1,2, \cdots ,s$ denote the order, m and s denote the order of T-basis function, ${\mathbf{T}}_{pq} (r,\theta ,t)$ denotes the basis function of Dirichlet boundary condition, ${\overline{\mathbf{\alpha }}}_{pq} = {{\varvec{\upalpha}}}$ denotes undetermined coefficient and $A_{1p}$, $B_{2q}$, $B_{3q}$, $A_{6pq}$, $A_{7pq}$ denote the coefficients to be determined. The basis function ${\mathbf{T^{\prime}}}_{pq} (r,\theta ,t)$ of Neumann boundary conditions as follow

$$ T_{{pq}} (r,\theta ,t) = \left\{ {\begin{array}{*{20}l} { - \frac{r}{2}w(\cos (\theta )n_{x} + \sin (\theta )n_{y} ), - \exp ( - Dp^{2} t)p\left( {J_{1} (\frac{{pr}}{{R_{0} }})\cos (\theta )n_{x} + J_{1} (\frac{{pr}}{{R_{0} }})\sin (\theta )n_{y} } \right),} \hfill \\ {q\left[ \begin{gathered} \left( {(\frac{r}{{R_{0} }})^{{q - 1}} \cos (q\theta )\cos (\theta ) + (\frac{r}{{R_{0} }})^{{q - 1}} \sin (q\theta )\sin (\theta )} \right)n_{x} + \hfill \\ \left( {(\frac{r}{{R_{0} }})^{{q - 1}} \cos (q\theta )\sin (\theta ) - (\frac{r}{{R_{0} }})^{{q - 1}} \sin (q\theta )\cos (\theta )} \right)n_{y} \hfill \\ \end{gathered} \right],q\left[ \begin{gathered} \left( {(\frac{r}{{R_{0} }})^{{q - 1}} \sin (q\theta )\cos (\theta ) - (\frac{r}{{R_{0} }})^{{q - 1}} \cos (q\theta )\sin (\theta )} \right)n_{x} + \hfill \\ \left( {(\frac{r}{{R_{0} }})^{{q - 1}} \sin (q\theta )\sin (\theta ) + (\frac{r}{{R_{0} }})^{{q - 1}} \cos (q\theta )\cos (\theta )} \right)n_{y} \hfill \\ \end{gathered} \right],} \hfill \\ {\exp ( - Dp^{2} t)\frac{q}{2}\left[ \begin{gathered} \left( {(J_{{q - 1}} (\frac{{pr}}{{R_{0} }}) - J_{{q + 1}} (\frac{{pr}}{{R_{0} }})\cos (q\theta )\cos (\theta ) + qJ_{q} (\frac{{pr}}{{R_{0} }})R_{0} \sin (q\theta )\frac{{\sin (\theta )}}{r}} \right)n_{x} + \hfill \\ \left( {J_{{q - 1}} (\frac{{pr}}{{R_{0} }}) - J_{{q + 1}} (\frac{{pr}}{{R_{0} }})\cos (q\theta )\sin (\theta ) - qJ_{q} (\frac{{pr}}{{R_{0} }})R_{0} \sin (q\theta )\frac{{\cos (\theta )}}{r}} \right)n_{y} \hfill \\ \end{gathered} \right],} \hfill \\ {\exp ( - Dp^{2} t)\frac{q}{2}\left[ \begin{gathered} \left( {(J_{{q - 1}} (\frac{{pr}}{{R_{0} }}) - J_{{q + 1}} (\frac{{pr}}{{R_{0} }})\sin (q\theta )\cos (\theta ) - qJ_{q} (\frac{{pr}}{{R_{0} }})R_{0} \cos (q\theta )\frac{{\sin (\theta )}}{r}} \right)n_{x} + \hfill \\ \left( {J_{{q - 1}} (\frac{{pr}}{{R_{0} }}) - J_{{q + 1}} (\frac{{pr}}{{R_{0} }})\sin (q\theta )\sin (\theta ) + qJ_{q} (\frac{{pr}}{{R_{0} }})R_{0} \cos (q\theta )\frac{{\cos (\theta )}}{r}} \right)n_{y} \hfill \\ \end{gathered} \right]} \hfill \\ \end{array} } \right\} $$

(7)

where J₁ and J_q-1 denote the order 1 and q-1 first class Bessel functions, respectively.

3.2 Slope Seepage and Stability Solving Process

In this paper, instead of solving the transient problem using the traditional time marching scheme, the problem is solved in the spatio-temporal coordinate system, combined with the concept of spatio-temporal matching points, the initial conditions are discretized as boundary conditions. 1) The governing equation is Eq. (5). 2) The boundary condition is Eqs. (2–4). 3) Initial and boundary condition discretization. The initial value of the study area is discretized into n_v points, and the boundary points are discretized into n points in the spatio-temporal coordinate system where the Dirichlet boundary points are n_f and the Neumann boundary points are n_g, n = n_{f +} n_g. As shown in Fig. 1, the solid circle point is the initial condition point and the hollow circle point is the boundary condition point. Depending on the boundary points, the boundary points are brought into the numerical solution of the governing equations of the Dirichlet and Neumann boundary conditions, respectively.

Fig. 1

Spatial and temporal distribution of the study area

The numerical solution of the initial conditions $V(r_{i} ,\theta_{i} ,t)$ into the basis function is expressed as follows

$$ V(r_{i} ,\theta_{i} ,t = 0) = \sum\limits_{p = 1}^{m} {\sum\limits_{q = 1}^{s} {{\overline{\mathbf{\alpha }}}_{pq} {\mathbf{T}}_{qp} (r_{i} ,\theta_{i} ,t = 0)} } $$

(8)

Numerical solutions satisfying Dirichlet boundary conditions $F(r_{i} ,\theta_{i} ,t_{i} )$ and Neumann boundary conditions $G(r_{i} ,\theta_{i} ,t_{i} )$ are expressed as follows

$$ F(r_{i} ,\theta_{i} ,t_{i} ) = \sum\limits_{p = 1}^{m} {\sum\limits_{q = 1}^{s} {{\overline{\mathbf{\alpha }}}_{pq} {\mathbf{T}}_{qp} (r_{i} ,\theta_{i} ,t_{i} ),\;G(r_{i} ,\theta_{i} ,t_{i} ) = \sum\limits_{p = 1}^{m} {\sum\limits_{q = 1}^{s} {{\overline{\mathbf{\alpha }}}_{pq} {\mathbf{T^{\prime}}}_{qp} (r_{i} ,\theta_{i} ,t_{i} )} } } } , $$

(9)

4) Solving undetermined coefficient. The system of linear algebraic equations consisting of initial and boundary conditions is expressed in the form of ${\mathbf{A\alpha }} = {\mathbf{B}}$. A matrix is a scale (n_v + n) (bb = 1 + 2 s + 3 + 2 ms) matrix formed by the Trefftz basis, the ${{\varvec{\upalpha}}}$ matrix is a scale bb = 1 + 2 s + 3 + 2 ms matrix of undetermined coefficient, and B matrix is a scale n_v + n matrix of boundary values formed by using the boundary conditions. A matrix is obtained by substituting the initial boundary conditions and boundary positions into the Trefftz basis, and B matrix is obtained by the boundary values, the matrix of undetermined coefficient is obtained by left division of the matrix by ${{\varvec{\upalpha}}} = {\mathbf{A}}^{ - 1} \;{\mathbf{B}}$. 5) Discrete for the study area. The internal distribution of the study area as shown in Fig. 1, the computational domain is discretized, the internal points satisfy the governing equations, and the coordinates of the computational points and the coefficients to be found are substituted into Eq. (6) to find the head values $h(r_{i} ,\theta_{i} ,t_{i} ) = \sqrt {u(r_{i} ,\theta_{i} ,t_{i} )}$ of the points in the computational study domain.

4 Numerical Results and Discussion

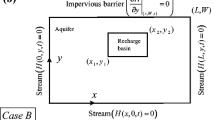
In this case, transient groundwater seepage with recharge is considered, the governing equation is as in Eq. (5), and the initial and boundary conditions are described below.

4.1 Calculation Model and Soil Parameters

The study area is as shown in Fig. 2. Figure 2 shows the slope of powdery clay with part of the foot of the slope cut off. The soil has a specific water storage coefficient of S_s = 6 × 10⁻⁵m⁻¹, saturation permeability coefficient k_s = 4 × 10⁻³mh⁻¹, saturation weight r_s = 20 kN/m³, dry weight γ = 18 kN/m³, cohesion c = 23 kPa, and internal friction angle φ = 65⁰. The bottom of the slope of the soil body is impermeable layer, the left side $ac$ is the reservoir water level boundary, and the right side $a^{\prime}c^{\prime}$ is the watershed.

Fig. 2

Schematic diagram of the study area

4.2 Impact of Rainfall Infiltration on Slope Stability

The left ac initial reservoir level is 30 m with continuous precipitation over a 24 h period. In order to increase the reservoir capacity, its reservoir level decreases from 30 m mean to 15 m within 24 h. The right side is a watershed with no flow boundary condition at the bottom.

Figure 3 shows that in the case of no rainfall infiltration, the reservoir water level decreases from 30 to 15 m in 24 h. The groundwater at the waterfront first decreases rapidly, and due to its hysteresis, the water level at the waterfront decreases faster and slower as the water level decreases into the slope. With the change of time, the slope drop gradually increases. As shown in Fig. 4, the vertical free aquifer recharge under rainfall infiltration is q = 1.2 × 10⁻⁴mh⁻¹. When the reservoir water level drops uniformly from 30 to 15 m in 24 h, the water level at the waterfront decreases rapidly with the reservoir water level, and the slope is near the slope with a gentler hydraulic slope drop. When the stabilization subsidy amount is large rain slope within the outflow water, the water level within the slope rises, but the outflow amount within the slope is close to the subsidy amount, the groundwater level rises slowly and tends to stabilize. The stability of the slope is analyzed by substituting the dynamic groundwater level with and without rainfall infiltration into STABL, which shows that the soil remains stable after 16 h without rainfall, and then the stability of the slope increases due to the effect of decreasing soil weight is greater than the effect of increasing slope drop on the slope. With rainfall, the hydraulic drop in the slope increases faster than without rainfall, and the stability decreases and tends to be unstable.

Fig. 3

Variation of free liquid level with time in the case of no replenishment

Fig. 4

Free liquid level versus time for precipitation recharge situation

4.3 Impact of Reservoir Water Level on Slope Stability

In the case of rainfall infiltration the vertical free aquifer recharge is q = 1.2 × 10⁻⁴mh⁻¹. The bottom is the no-flow boundary condition, and the right is the watershed; if the reservoir level is lowered to 15 m before the onset of rainfall and the internal seepage reaches a steady state, the reservoir level is kept constant at the onset of rainfall. As Fig. 5 shows that the infiltration of stable rainfall, the hydraulic slope drop in the slope increases. As Fig. 6 shows that the initial reservoir level on the left side at the onset of rainfall decreases uniformly from 25 to 15 m in 24 h, and the water level in the slope changes with time.

Fig. 5

Variation of free liquid level with time in the case of stable reservoir water level

Fig. 6

Free liquid level change pattern in uniform decline of reservoir water level

As shown in Fig. 7, the stability of its slope gradually decreases under constant rainfall conditions when the reservoir water level is lowered to 15 m in advance and is kept constant during the rainfall process. When the reservoir water level decreases uniformly from 25 to 15 m in 24 h, the safety coefficient of its side slope decreases steadily under the rainfall infiltration condition, and the rate of its decrease is approximately the same as the rate of decrease of the safety coefficient under the constant reservoir water level. Figure 8 shows the change of safety coefficient with time in Fig. 4 and Fig. 6, where the reservoir level decreases from 30 and 25 m to 15 m respectively in 24 h under the same rainfall infiltration conditions. The rate of decrease of safety coefficient with time is approximately the same for both conditions. However, the safety factor for the initial water level of 30 m is lower than that for the initial water level of 25 m.

Fig. 7

The effect of reservoir water level with time on slope stability

Fig. 8

Influence of initial reservoir water level on slope stability

5 Conclusion

• (1) The Space–Time Trefftz Method does not need to divide the grid, but only needs to lay points on the boundary. The Dupuit-Boussines equation is solved by STM to analyze the transient free liquid surface problem without iteration, saving a lot of time, and compared with traditional numerical methods, STM avoids the error accumulation problem caused by the time marching method.

• (2) The stability of the bank slope is significantly influenced by the combined effect of rainfall and reservoir water level change. To ensure the slope stability, the reservoir water level should be declined according to the predicted rainfall intensity and duration when the rainfall comes, to avoid the slope instability caused by the high reservoir water level due to rainfall or the rapid decline of reservoir water level during the rainfall.