Keywords

1 Introduction

Problems of calculation and design of fibrous composite materials began to be intensively studied in the 60 s–70 s of the last century [2, 3]. At present, the relevance of the problems has only increased [4]. For example, in connection with the development of hydrogen energy technologies, the problem arose of improving, creating and designing high-pressure vessels made of composite materials for storing hydrogen fuel. The hydrogen gas storage pressure is 5000–10,000 psi (340–680 atmospheres) [4,5,6]. It seems, the composite gas reservoirs are the best solution to the problem which attract attention both the engineers and researchers. An increase in the role of fibrous composites (in terms of the volume of their use as well as in terms of the responsibility of structural elements made from composites, is also observed in other areas of mechanical engineering. The prospect of mass use of products made of fibrous composite materials raises the question of testing of existing and developing new (in particular, based on the use of computers) methods for their calculation.

Reviewing the strength criteria of composite materials used in the modern design systems, one finds that the most of them are based on the motion of the local deformation modes of composite materials. The use of the concept of the local deformation modes of composite arose at the initial stages of the study of composites and was especially widely used in obtaining the classical criteria for the strength of composite materials in the 1960s-70 s [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

The notion of the deformation modes was based on the notes that the local stress–strain state in composite is strongly inhomogeneous. Naturally, the question arises: do exist any regularity in the inhomogeneous stress–strain state? Or the inhomogeneity is arbitrary and non-predictable? It was found that in many composites the stress–strain state has specific forms correlated with the local geometry and the local mechanical properties of the composite. These specific forms of the local stress–strain state were named the local deformation modes of composite. Note that the currently used theoretical criteria for the strength of fibrous composites, in fact, are based on taking into account certain modes of local stress–strain state [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. In [1], it was pointed out that the primary question is about local stress–strain state modes in a composite (the existence and characteristics of such modes), and the question about destruction modes is secondary, the solution of which follows from the solution of the first question.

The calculation of the local (microscopic) stress–strain state in composite material is a non-trivial problem because this requires solving a problem of the elasticity theory (the explicit solution to the problem is known only for layered composites [28]). Therefore, the desire of researchers to indicate the “basic” types of stress–strain state that determine the strength of the composite was understandable. Note that the question of the existence of such “basic” types of stress–strain states was usually not even raised. It was also not discussed how many “basic” types of stress–strain state can exist (if they exist) in composites in general and in composites of a particular type in particular.

In this paper, composites “hard fibers in a soft binder” of periodic structure are considered. Such kind composites have found wide application in engineering. For composites of periodic structure, methods of the homogenization theory are applicable [29,30,31]. In this case, it is necessary to indicate the multicomponent effect of the homogenization in contrast media predicted in [32, 33], whose numerical study showed that a very general type of stress–strain state occurs in the matrix of these composites.

In [1] (see also [34, 35]), a scheme for computation of the microscopic stress–strain state in the composites “hard fibers in a soft binder” was proposed for square cross-section fibers. In [1], there were listed the “main” types of the local stress–strain states – the local stress–strain state modes exist, which may exist in the fiber-reinforced composite made of pre-pregs. In addition, a method for their approximate calculation of the “main” stress–strain state nodes was proposed. True, the analysis in [1] was only possible for the square-section fibers. For fibers of other cross-section geometry (for example, circular), the local stress–strain state can only be computed numerically. The modes described in [1] included previously known modes [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] as well as new modes.

After the analysis presented in [1], questions arose: are all the deformation modes predicted in [1] realized and are there any other modes. In particular, what is the answer to this question for fibers of a cross-section other than considered in [1]?

For the reasons indicated above, an exhaustive answer to these questions can only be given by numerical calculations. Other, for example, experimental, study of local stress–strain state modes in cross-reinforced composites seems to the author practically unrealizable. Experimental methods (see, e.g., [36,37,38]) do not provide exhaustive information either on the types of modes or on the characteristic values ​​of the stress–strain state.

In numerical calculations, one encounters mathematical and programming problems. The main problem is related to the fact that the problem of constructing a periodic FEM mesh in regions of complex geometry, as far as the author knows, still remains practically unsolved [39,40,41].

The popular software systems used in the calculation of composites and the strength criteria used in them are given in Table 1 [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27, 36]. The strength criteria that the developers of the complexes indicated are also given; their list may vary depending on the development of software systems, changes in the composition of modules, as well as the licensing policy of developer firms, etc. We note that the listed in Table 1 strength criteria are based on the use of the local stress–strain state modes. One can verify this by looking through the corresponding references list [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

Table 1 The strength criteria used in popular software systems
Full size table

2 The Homogenization Method as Applied to an Orthogonally Fiber-Reinforced Composite

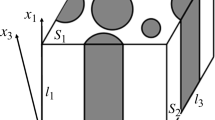
Let us describe the structure of the considered composite. The composite is obtained by stacking layers of unidirectional fibers - prepregs. In a layer, the fibers are parallel to each other. The layers are stacked parallel to each other (for definiteness, we assume the layers are perpendicular to the \(Ox_{2}\)-axis, see Fig. 1). The direction of fiber lying in the s-th layer is described by the direction vector \({\mathbf{v}}_{s}\). The fibers have diameter \(\varepsilon R\), half the distance between the fibers in the layers \(\varepsilon h\), half the distance between the layers of fibers \(\varepsilon \delta\), Fig. 1. The gaps between the fibers are filled with a binder that forms the matrix. In the work under consideration, the “ideal” connection between the fibers and the matrix is assumed.

Fig. 1
Two illustrations of the overlapping slanting fibers with an x, y, and z plane and a vertical cuboid structure with the labels h, delta, R, and h.

Orthogonally stacked fibers (two adjacent layers of fibers shown) and PC (fibers and binder) in “fast” variables

Full size image

The characteristic size \(\varepsilon\) is small compared to the size of the structure (material sample). It is usually assumed that the sample size is of the order of 1, then \(\varepsilon < < 1\). In addition to the original (macroscopic) variables, “fast” (microscopic) variables \({\mathbf{y}} = {\mathbf{x}}/\varepsilon\) are introduced.

Since the fibers in the layers and the layers are periodic, entire structure is periodic. Denote \(\varepsilon P\) the periodicity cell of composite. The periodicity cell may be chosen in different ways. One of the possible choices is displayed in Fig. 1. The periodicity cell (PC) has the form of a rectangle \(P = [0,h_{1} ] \times [0,h_{2} ] \times [0,h_{3} ]\). Faces of \(P\) are perpendicular to the \(Ox_{s}\)-axis. The faces are rectangles \(\Gamma_{s} = \{ {\mathbf{x}} \, : \, x_{s} = 0\}\) and \(\Gamma_{s} + h_{s} {\mathbf{e}}_{s}\). . Figures are given in “fast” (microscopic) variables. Let us consider the simplest composite obtained by stacking periodically alternating layers of orthogonally oriented fibers. We assume that the fibers in one layer are parallel to the Ox-axis, in the other - to the Oz-axis (\({\mathbf{v}}_{1} = {\mathbf{e}}_{1}\) and \({\mathbf{v}}_{1} = {\mathbf{e}}_{3}\); \({\mathbf{e}}_{1}\), \({\mathbf{e}}_{2}\), \({\mathbf{e}}_{3}\) - coordinate vectors), Fig. 1. We confine ourselves to considering the simplest packing, keeping in mind that this case allows to focus on the presentation of the mechanical aspects of the problem without cluttering them up with purely computational questions.

The solution to the elasticity theory problem of composite material in the framework of the homogenization theory [30, 31] is sought in the form

$${\mathbf{u}} = {\mathbf{u}}_{0} ({\mathbf{x}}) + \varepsilon {\mathbf{u}}_{1} ({\mathbf{x}}/\varepsilon ),$$
(1)

where \({\mathbf{u}}_{0} ({\mathbf{x}})\) is the homogenized (macroscopic, overall) solution, and \(\varepsilon {\mathbf{u}}_{1} ({\mathbf{x}}/\varepsilon )\) is the corrector (the function \({\mathbf{u}}_{1} ({\mathbf{y}})\) is periodic with PC \(P\)) [1]. The corrector makes a small contribution to displacements (1), but it makes not a small contribution to the local stresses [1]. It is proved in [30, 31] that the corrector has the form \(\varepsilon \frac{{\partial u_{0k} }}{{\partial x_{l} }}({\mathbf{x}}){\mathbf{N}}^{kl} ({\mathbf{x}}/\varepsilon )\), where \({\mathbf{N}}^{kl} ({\mathbf{y}})\) is the solution of the so-called periodicity cell problem (PCP) (see PCP problem (3) below).

We introduce the following function:

$$a_{ijkl} ({\mathbf{y}}) = \left\{ \begin{gathered} a_{ijkl}^{F} {\text{ in fibre}} \hfill \\ a_{ijkl}^{M} {\text{ in binder}} \hfill \\ \end{gathered} \right. \,$$
(2)

where \(a_{ijkl}^{F}\) - elastic constants of fibers, \(a_{ijkl}^{M}\) - elastic constant matrices. Formula (2) defines (in “fast” (microscopic) variables) the distribution of elastic constants over cell \(\varepsilon P\).

We consider a linear problem in the elasticity theory of composites. This is due, in particular, to the fact that the purpose of the article is to consider the deformation modes from [1] obtained for a linear problem. In this case, the PCP has the following form [1]: find the solution \({\mathbf{N}}^{kl} ({\mathbf{y}})\) to the following boundary value problem:

$$\left\{ \begin{gathered} (a_{ijkl} ({\mathbf{y}})N^{mn}_{k,ly} - a_{ijmn} ({\mathbf{y}}))_{,jy} = 0\;{\text{in}}\;P, \hfill \\ {\mathbf{N}}^{kl} ({\mathbf{y}})\;{\text{periodic}}\;{\text{in}}\;P \hfill \\ \end{gathered} \right.$$
(3)

The solutions to the problem (3) differ from each other by displacements of a rigid body. The differences can be excluded in different ways. In the homogenization theory, it is assumed that the average value of \({\mathbf{N}}^{kl} ({\mathbf{y}})\) over PC \(P\) is zero [30, 31]. In numerical computations, it is convenient to fix a proper point of PC. It is important that any method of excluding displacements of a rigid body from problem (3) leads to the same results when calculating local strains and stresses in composite, since these quantities depend on the derivatives of the function.

In (3) and below, indices \(mn =\)​​11, 22, 33 correspond to macroscopic tension (along the corresponding axis). Indices \(mn =\)​​12, 13, 23 correspond to macroscopic shear (in the corresponding plane).

We introduce the function \({\mathbf{Z}}^{mn} ({\mathbf{y}}) = \varepsilon_{mn}^{{}} ({\mathbf{x}})[{\mathbf{N}}^{mn} ({\mathbf{y}})({\mathbf{y}}) + y_{m} {\mathbf{e}}_{n} ]\) and write (3) in the form

$$\left\{ \begin{gathered} \left( {a_{ijkl} ({\mathbf{y}})Z_{k,ly}^{mn} } \right)_{,iy} = 0{\text{ in }}P, \hfill \\ {\mathbf{Z}}^{mn} ({\mathbf{y}}) - \varepsilon_{mn}^{{}} ({\mathbf{x}})y_{m} {\mathbf{e}}_{n} {\text{ periodic on }}P \hfill \\ \end{gathered} \right.$$
(4)

Denote \([f({\mathbf{y}})]_{s} = f({\mathbf{y}} + h_{s} {\mathbf{e}}_{s} ) - f({\mathbf{y}})\), where \({\mathbf{y}} \in \Gamma_{s}\) (\({\mathbf{y}} \in \Gamma_{s}\) and \({\mathbf{y}} \in \Gamma_{s} + h_{s} {\mathbf{e}}_{s}\) are the opposite faces of PC \(P\)). In this notation, we can write the periodicity condition in (3) in the form \([f({\mathbf{y}})]_{s} = 0\). . Then (4) can be rewritten in the following form

$$\left\{ \begin{gathered} \left( {a_{ijkl} ({\mathbf{y}})Z_{k,ly}^{mn} } \right)_{,iy} = 0{\text{ in }}P, \hfill \\ [{\mathbf{Z}}^{mn} ({\mathbf{y}})]_{s} = \varepsilon_{mn}^{{}} ({\mathbf{x}})[y_{m} {\mathbf{e}}_{n} ]_{s} \hfill \\ \end{gathered} \right.$$
(5)

(no sum in m, n in (5)).

The solutions to the PCs (problems (3), (4) or (5)) provide us with the detailed information about the local (microscopic) stress–strain state in composite. For example,

$$\sigma_{ik}^{mn} ({\mathbf{y}}) = a_{ijkl} ({\mathbf{y}})Z_{k,l}^{mn} ({\mathbf{y}})$$
(6)

are the local stress in the composite subjected to macroscopic deformations \(\varepsilon_{mn}^{{}} ({\mathbf{x}})\) [30, 31].

At the time of the writing of the works [1, 7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27], the computers available (in public domain for engineers) made it possible to solve a PC problem with a simple geometry. For example, for a system of unidirectional fibers (in this case, complex variables method can be used [42, 43], which also assume sufficient massive computations [42, 43]). But the mentioned computers had not sufficient to solve the problems corresponding to the cross-reinforced or particles-filled composites. At present, the power of computers has reached a level that allows solving a general type of problem. It should be noted that the progress in the field is restricted not only by the power of the computer, but also the theoretical programming problems, for example, the problem of the generation of periodic meshes. As an illustration of the current state of the art, we mention the recent monograph [42], which contains many programs for solving problems in the theory of composites. However, in relation to the PC of the form (5), [42] is limited only to the formulation of this problem. The solutions in [42] are given only for unidirectional fibers.

3 Numerical Analysis of the Local Stress–Strain State in the Periodicity Cell

For a cross-reinforced composite, even for the simplest reinforcement scheme under consideration, the local stress–strain state turns out to have a general form when any loads are applied to the composite (even loads of the simplest type). Let us consider the main types of the overall (the homogenized) deformations and present the calculations of the corresponding local deformations. Due to the symmetry of the problem, out of six cases (three axial and three shear deformations), only four types of averaged deformations listed below can be considered.

Let us present the results of the numerical solution of the PC for the case under consideration. The solution was carried out for a composite with the following characteristics. Fibers: Young's modulus \(E_{f}^{{}} = 1.7 \cdot 10^{11}\) Pa, Poisson's ratio \(\nu_{f}^{{}} = 0.3\). Binder: Young's modulus \(E_{b}^{{}} = 2 \cdot 10^{9}\) Pa, Poisson's ratio \(\nu_{b}^{{}} = 0.36\). These characteristics correspond to steel and epoxy resin.

In this paper, the theoretical problem of construction of FEM mesh is not considered, bearing in mind that the construction of a finite element mesh is carried out by predefined procedures. At the same time, the author had to develop an APDL program for setting periodic boundary conditions (an imperfection of ANSYS in this part is well known [42]). The convergence of the numerical solution of the finite element method for the elasticity theory problem is a well-known fact [21], the question in this case is the size of the finite elements. The selection of the finite elements size was carried out by dividing their characteristic size in half until the difference in the numerical solutions became less than 2–3%.

For the visual representation of the distribution of local stresses/strains, it is convenient to use the scalar characteristic of the stress tensor. The authors use the von Mises stress. Although the von Mises stress is often used in the formulation of the strength criterion [44, 45], here it is chosen as a visual scalar characteristic of the stress tensor. In combination with the image of the deformed periodicity cell, it makes it possible to clearly see the main type of local deformation.

If one wants to carry out strength calculations, one should keep in mind the discussion in the literature [36, 45,46,47] on the von Mises criterion, the Tresca criterion and the modification of the Mises and Drucker-Prager criteria for rubbers (including epoxy ones). In engineering calculations, apparently, the best is to use a criterion developed for a particular rubber [36] (if any) or an experimental criterion. Such criteria can be programmed and used together with other (in particular, with our proposed) methods.

3.1 Square Cross-Section Fibers

The model of a composite reinforced with square fibers was used in [1] in the analysis of typical types (modes) of local stresses in composites reinforced with fibers. Therefore, we will begin our consideration also with this type of fiber. For square cross-section fibers, stress concentrators appear near 90 degrees angles. It is inconvenient when analyzing the stress–strain state in the entire cell. To avoid these stress concentration, square fibers with fillet corners were considered.

In [1], the layers of fibers were placed one above the other and connected with a fragment of a matrix. The size of the matrix fragment in [1] coincides with the cross section of the fibers. As a result, it was possible to carry out numerical calculations for this case in the explicit form.

In the calculations, the cross section of the fibers \(H \times H\), filet radius \(R\). Other dimensions are the following: half the distance between the fibers \(h\), half the distance between the fiber layers \(\delta .\) Two types of periodicity cell were considered: «narrow» and «wide». For the «narrow» periodicity cell \(H = 0.96\), \(h = 0.07\), \(\delta = 0.02\), R = 0.25. For the «wide» \(H = 0.92\), \(h = 0.88\), \(\delta = 0.04\), R = 0.15. Note: indices 1, 2 and 3 of the tensor components correspond to the variables \(x\), \(y\), and \(z\) respectively.

Tension along Ox-axis. Macroscopic Deformations \(\varepsilon_{11}^{{}}\)

«Narrow» PC. The results of numerical calculations are presented in Fig. 2. Sections of fiber \(H \times H\), H = 0.96, fillet radius R = 0.25. Other dimensions - half the distance between the fibers \(h = 0.07\), half the distance between fiber layers \(\delta = 0.02.\) In calculations, the macroscopic strain \(\varepsilon_{11}^{{}} = 0.2/1.1 = 0.18\). Dimensions are given in dimensionless variables.

Fig. 2
A distribution graph of a fiber with a rectangular structure having depression at the top and bottom. The plotted data has values between 0.155 E + 09 and 0.606 E + 09 in the interiors, and between 0.126 E + 10 and 0.219 E + 10 in the periphery.

Stretching along the Ox-axis.

Full size image

«Wide» PC. The results of numerical calculations are presented in Fig. 2. Sections of fiber \(H \times H\), H = 0.92, fillet radius R = 0.15. Other dimensions - half the distance between the fibers \(h = 0.88\), half the distance between fiber layers \(\delta = 0.02.\) In calculations, the macroscopic strain \(\varepsilon_{11}^{{}} = 0.4/2.68 = 0.14\). The maximum stresses in the binder are observed between the fibers of one layer and are associated with a strong stretching of the matrix between the fibers, which are much more rigid than the matrix. These types of microscopic deformation of the binder are described in [1]

Tension along Oy-axis. Macroscopic Deformations \(\varepsilon_{22}^{{}}\)

«Narrow» PC. In calculations, the macroscopic strain \(\varepsilon_{22}^{{}} = 0.2/2 = 0.1\). Sections of fiber size \(0.96 \times 0.96\), fillet radius R = 0.25. Other sizes: \(h = 0.07\), \(\delta = 0.02.\) The results of numerical calculations are presented in Fig. 3. The maximum stresses in the binder are observed between the fibers of one layer and are associated with a strong stretching of the matrix between the rigid fibers.

Fig. 3
A distribution graph of a fiber with a rectangular structure with depression at the top and bottom has a scale ranging from 0.315 E + 08 to 0.304 E + 10. The values range at 0.315 E + 08 in the interior and between 0.365 E + 09 and 0.304 E + 10 in the depression areas.

Stretching along the Oy-axis

Full size image

«Wide» PC. In calculations, the macroscopic strain \(\varepsilon_{22}^{{}} = 0.4/2 = 0.2\). Fiber sections \(H \times H\) = \(0.92 \times 0.92\), fillet radius 0.15. Other sizes: \(h = 0.88\), \(\delta = 0.04\). The maximum stresses in the binder are observed between the fibers of one layer and are associated with a strong stretching of the matrix between the rigid fibers. The maximum stress according to Mises is 0.103E + 10 Pa.

Shift in Oxz-plane Macroscopic Deformations \(\varepsilon_{13}^{{}}\)

«Narrow» PC. In calculations, the macroscopice deformation \(\varepsilon_{13}^{{}} = 0.05\). Fiber sections size \(0.96 \times 0.96\), the fillet radius \(R = 0.25\). Other sizes: \(h = 0.07\), \(\delta = 0.02.\) The results of numerical calculations are presented in Fig. 4. The maximum stresses in the binder are observed between the fibers of one layer and are associated with the shear of the binder between the fibers of one layer. This case is described in [1].

Fig. 4
A distribution graph of a rectangular fiber structure with a depression at the top and bottom has a scale ranging from 0.769 E + 08 to 0.951 E + 09. The values range between 0.854 E + 09 and 0.951 E + 09 in the interiors and periphery, and between 0.174 E + 09 and 0.465 E + 09 at the depression.

Interfiber shear a layer of fibers

Full size image

«Wide» PC. In calculations, the macroscopic strain \(\varepsilon_{13}^{{}} = 0.4\). Fiber Sections \(0.92\; \times \;0.92\), fillet radius R = 0.15. Other sizes: \(h = 0.88\), \(\delta = 0.04\). The maximum stresses in the binder are observed between the fibers of one layer and are associated with the twisting of the binder between the fibers of different layers. The results of numerical calculations are presented in Fig. 5. This type of microscopic deformation of the binder is described in [1].

Fig. 5
Two distribution graphs of the multi-layered fibers have scales ranging from 0.483 E + 08 to 0.281 E + 10 and 0.980 E + 07 to 0.206 E + 10. The higher values are in the periphery and the lower values are in the interior in 1, and vice versa in 2.

Mutual rotation of the fibers and torsion of the binder between the layers of fibers («wide» PC)

Full size image

Shift in Oxy-plane.

«Narrow» PC. In calculations, the macroscopic strain \(\varepsilon_{12}^{{}} = 0.2\). Fiber Sections \(0.96\; \times \;0.96\), fillet radius \(R = 0.25\). Other sizes: \(h = 0.07\), \(\delta = 0.02.\) The maximum stresses in the binder are observed between the fibers of one layer and are associated with the twisting of the binder between the fibers of different layers.

«Wide» PC. In calculations, the macroscopic strain \(\varepsilon_{13}^{{}} = 0.8\). Fiber sections \(0.92\; \times \;0.92\), fillet radius R = 0.15. Other sizes: \(h = 0.88\), \(\delta = 0.04\). The maximum stresses in the binder are observed between the fibers of one layer and are associated with the twisting of the binder between the fibers of different layers.

3.2 Circular Cross-section Fibers

Fibers of various cross-sections are mentioned in the literature. Above, the fibers are rectangular in cross section. The most common are, however, fibers of a circular cross section. Let's see what types of local stresses are typical for a fiber with a circular cross section.

In the calculations, the distance between the fibers is taken \(h =\) 0.1, distance between fiber layers \(\delta = 0.1\). Cell dimensions \(h_{1} = 1.1\), \(h_{2} = 2\), \(h_{3} = 1.1\). Fiber radius 0.45. Since this problem depends only on the relative dimensions, all dimensions can be referred to the radius of the fibers.

Tension along Ox- axis. Macroscopic Deformations \(\varepsilon_{11}^{{}}\).

Figure 6 shows the von Mises stresses \(\sigma_{M}\). In calculations, the macroscopic strain \(\varepsilon_{11}^{{}} = 0.1/1.1\) = 0.091. Due to the linearity of the problem, \(\varepsilon_{11}^{{}}\) can be chosen arbitrarily. The choice of \(\varepsilon_{11}^{{}}\) = 0.091 (9.1%) here and below is due only to convenience for the programmer.

Fig. 6
Two distribution graphs of the multi-layered fibers with fiber z and fiber x in the first, and zone x and zone z in the second. 1. The lower values are in the periphery and higher values are in the interior. 2. The lower values are in the interior and higher values are in the periphery.

Local stresses in the fibers (left) and in the matrix (right) at macroscopic deformation \(\varepsilon_{11}^{{}}\) (stretching along the Ox-axis)

Full size image

In the binder, there is a stress–strain state of general type. The maximum von Mises stresse takes place in the fiber \(x\) and in the matrix in the zone \(x\), see Fig. 6 The maximum von Mises stress takes place in the zone where the distance between the fibers is minimal. The fibers are circular in cross section. As a result, the stress quickly decreases with distance from the zone \(x\). Thus, there is stress localization effect similar to one discussed theoretically in [48, 49] and demonstrated in numerical calculations [50,51,52] for rigid bodies in a soft binder.

The problem of stretching along the Oz-axis in this case is solved by rotating the PC around the Oy-axis.

Tension along Oy-axis. Macroscopic Deformations \(\varepsilon_{22}^{{}}\).

In calculations, the macroscopic strain \(\varepsilon_{22}^{{}} = 0.1/2\) = 0.05. According to the results of numerical computations, it can lead to the increasing of the von Mises stress in the fibers and the binder of one layer.

Shift in Oxz-plane Macroscopic Deformations \(\varepsilon_{13}^{{}}\).

The results of numerical calculations are presented in Fig. 7. In calculations, the macroscopic strain \(\varepsilon_{13}^{{}} = 0.1/1.1\) = 0.091. According to the results of the numerical computations, see Fig. 7, it leads to the increasing of von Mises stress in the fibers and the binder of one layer. This type of microscopic deformation of the binder is described in [1].

Fig. 7
A distribution graph of a fiber with zone x and zone z has a scale ranging from 0.647 E + 07 to 0.130 E + 10. Zone x in the periphery and zone z in the interior have higher values.

Local stresses in the matrix at macroscopic deformation \(\varepsilon_{13}^{{}}\) (shear in the Oxz-plane)

Full size image

In this case, the fibers in the layers rotate relative to each other, as predicted in [1]. However, in this case, no significant torsional deformations of the binder element connecting the fibers of different layers are observed. This is the result of a change in the shape of the cross-section of the fibers.

Shift in Oxy-plane.

The results of numerical calculations are presented in Fig. 8. Symmetric problem - shift in the Oyz-plane. In the calculations, the macroscopic strain \(\varepsilon_{12}^{{}} = 0.1\)

Fig. 8
A distribution graph of a fiber with depression in the top and bottom. The values increase from lower in the interior to higher in the periphery.

Local stresses in the matrix during macroscopic deformation \(\varepsilon_{12}^{{}}\) (shift in the Oyz-plane)

Full size image

4 Conclusions

The performed solutions of the periodicity cell problems of the homogenization theory showed that all potentially possible types (modes) of local deformation of the binder fibrous composite predicted in [1] are found in numerical calculations.

The local stress–strain state in the binder essentially depends on the cross-sectional shape of the fibers. So for a composite reinforced with circular fibers, some types of local deformation of the binder are small. If, in the case of square cross-section fibers, the stress–strain state estimation is possible using explicit formulas from [1], then for fibers of other cross-sections, it becomes necessary to use a computer to calculate the stress–strain state.

If a general macroscopic deformation \(\varepsilon_{ij}^{{}}\) is applied to the composite, then the local deformations \(\varepsilon_{kl}^{loc}\) in the binder are given by the linear combination

$$\varepsilon_{kl}^{loc} = \varepsilon_{kl}^{loc \, ij} \varepsilon_{ij}^{{}}$$
(7)

Here \(\varepsilon_{kl}^{loc \, ij}\) is the local deformations in the binder, corresponding to the application macroscopic deformation \(\varepsilon_{ij}^{{}}\). Examples of the deformation calculation \(\varepsilon_{kl}^{loc \, ij}\) are given above.

When the macroscopic strain \(\varepsilon_{ij}^{{}}\) applied to the composite is changed, the microscopic strains change \(\varepsilon_{kl}^{loc \, ij}\) quite difficultly, for example, they can go from one to another. When using computer technology, for example, the ANSYS software package [53], the calculation of quantities (7), after all \(\varepsilon_{kl}^{loc \, ij}\) are calculated, does not present a problem.

In this article, the author aimed to substantiate the maximum set of local stress–strain state modes in cross-reinforced composites of the type described above, predicted in [1].

The issue of composite fracture modes has been widely discussed and continues to be actively discussed, see, e.g., [4, 5, 7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27, 36]. In [1], it is indicated that the primary issue is the local stress–strain state modes in the composite (the existence and characteristics of such modes), and the issue of destruction modes is secondary, the solution of which follows from the solution of the first question. In [1], an example of obtaining a multimode strength criterion for a model composite is given.

The largest number of modes is observed in a composite reinforced with square cross-section fibers. In this case, the number of modes is six. For circular cross-section fibers, one mode weakens, up to the possibility of neglecting this mode. Accordingly, the number of modes becomes equal to five.

The alternative method of construction of the homogenized (macroscopic, overall) strength criteria is the numerical construction of the homogenized strength criteria [54,55,56].