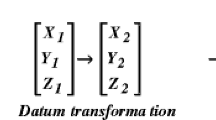Keywords

1 Introduction

A high-precision coordinate system is crucial for establishing a spatial data infrastructure and a paperless land administration system to promote long-term sustainable socio-economic growth [1, 2]. The satellite-based geodetic techniques have opened a new era for determining the high positional quality of points on the topographical surface in a geocentric three-dimensional system using precise observations of artificial celestial bodies. In the past, most national maps were produced by traditional surveying methods and relied on a non-geocentric local datum selected to deliver the best possible match of the earth's figure within a defined geographical area [3]. The global navigation satellite system (GNSS) is utilized to build more accurate geodetic control points and other applications within the mapping industry [4, 5]. Accordingly, developing a mathematical algorithm connecting two spatial reference frames is a critical challenge to guarantee the consistency of the coordinates. In reality, several researchers have extensively addressed the three-dimensional coordinate transformation in the literature to change between GNSS-derived coordinates and national terrestrial ones using the common points between two datasets [6,7,8,9,10,11,12]. In contrast, the discrepancies in triangulation stations are inevitable because a local datum is oriented astronomically at an initial point, the ellipsoidal surface is not earth-centered, and its rotational axis is not coincident with the earth's axis [13]. In addition, the horizontal control scale change generates a stretch in the related lines of the network [14].

Grid-on-grid transformation is applied to define a mathematical relationship between two sets of georeferenced spatial data obtained from separate sources with different grid reference systems [15]. It generally converts two-dimensional coordinates described by axes rotations, origin transitions, and a scale change [16]. Several methods have been investigated in the literature to address this issue by determining the parameters of the prediction model through control points in both systems [17,18,19]. The number of training sample data and their geographical distribution pattern significantly impact the accuracy of estimating algorithm parameters [20, 21]. As a result, redundant observations and the least-squares technique give the optimum solution for calculating polynomial coefficients and evaluating their accuracy and root mean square error (RMSE) of data points [22]. This research investigates different two-dimensional conformal transformation models to determine which algorithm performs best in this context and develops a spatial tool in the Microsoft Visual Studio environment to solve the addressed issue by minimizing the sum of errors’ squares. In addition, quantitative and qualitative methods are utilized to evaluate the findings by employing statistical analysis and descriptive illustrations.

2 Materials and Methods

It is necessary to cope with an increasingly broad spectrum of positioning information acquired from multi-sources such as terrestrial surveying and GNSS receiver observations. The location of a feature in space is related to a wide range of national and global datums. Hence, a comprehensive understanding of the various coordinate systems and their proper transformations is essential to guarantee an accurate evaluation of reference frame variations to deliver high-quality products in geospatial data processing activities. A transformation model is commonly applied to change GNSS-based coordinates to those in a national datum through two datasets of reference stations defined in both systems. Its parameters characterize the relationship between various spatial reference systems, significantly correlated with the diverse and local nature of deformations inherent in geodetic frameworks.

2.1 Case Study Description

The Swiss coordinate system (CH1903) is a geodetic reference frame for the national network in Switzerland for various mapping purposes. It is a cylindrical projection based on the Bessel ellipsoid and the Mercator projection. The geodetic network in Switzerland consists of several permanent control points on the earth's surface that have been accurately observed using traditional and advanced geodetic techniques. Figure 1 depicts the spatial distribution of first- and second-order Swiss triangulation points across Switzerland. The density and distribution of the points can significantly impact the data's accuracy, as well as the suitability of the data for different types of applications. The Federal Office of Topography swisstopo is responsible for maintaining and managing the geodetic network and the CH1903 coordinate system in Switzerland.

Fig. 1
A spatial distribution map of Switzerland has a dense cluster of connected training points, testing points, and the triangulation network. The scale range is 0 to 60 kilometers.

Spatial distribution of 1st and 2nd order Swiss triangulation points

Full size image

2.2 Grid-on-Grid Transformation

A coordinate transformation is a process of changing the point coordinates from one reference system to another [23], which can be broken into combining axes rotations, origin shifts, and scaling factors. The transformation parameters are initially calculated using the least-squares surface fitting approach. Hence, the other point coordinates are converted utilizing the interpolation algorithm. The two-dimensional conversion model is the most prevalent in surveying and mapping applications. On the other hand, geospatial data is acquired from various sources and georeferenced using a proper grid system. With the advent of artificial satellite positioning data, this issue has become critical for integrating GNSS observations and official spatial data to reduce the discrepancies between the physical reality and represented positions. The general formula of grid-on-grid transformation using the polynomial functions is presented in Eq. 1 [24].

$$ \begin{aligned} E^{\prime } & = \sum\limits_{{i{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}}^{u} {{\mkern 1mu} \sum\limits_{{j{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}}^{{u{\kern 1pt} - {\kern 1pt} i}} {a_{{i{\kern 1pt} j}} {\mkern 1mu} E^{i} {\mkern 1mu} N^{j} } } \\ N^{\prime } & = \sum\limits_{{i{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}}^{u} {{\mkern 1mu} \sum\limits_{{j{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}}^{{u{\kern 1pt} - {\kern 1pt} i}} {b_{{i{\kern 1pt} j}} {\mkern 1mu} E^{i} {\mkern 1mu} N^{j} } } \\ \end{aligned} $$
(1)

In which aij and bij are polynomial coefficients, and u its degree.

The six terms up to the first degree of the polynomials surface describe the well-known affine transformation in Eq. 1. Indeed, a conformal transformation of coordinates preserves local angles that can be satisfied by applying the Cauchy - Riemann conditions on the polynomials model [25]. The number of the conformal polynomial coefficients (m) is proportional to the polynomial degree. The fourth-degree conformal algorithms are given in Eq. 4, where first-order functions define the similarity (Helmert) transformation and the quantities beyond that, referred to as conformal deformation.

$$ \begin{aligned} \frac{{\partial {\mkern 1mu} E^{\prime } }}{{\partial {\mkern 1mu} E}} & \equiv \frac{{\partial {\mkern 1mu} N^{\prime } }}{{\partial {\mkern 1mu} N}} \\ \frac{{\partial {\mkern 1mu} E^{\prime } }}{{\partial {\mkern 1mu} N}} & \equiv - \frac{{\partial {\mkern 1mu} N^{\prime } }}{{\partial {\mkern 1mu} E}} \\ \end{aligned} $$
(2)
$$ m = 2 \times u + 2 $$
(3)
$$ \begin{aligned} E^{\prime } = & a_{o} + a_{1} {\mkern 1mu} E - b_{1} {\mkern 1mu} N \\ & + a_{2} {\mkern 1mu} \left( {E^{2} - N^{2} } \right) - 2{\mkern 1mu} b_{2} {\mkern 1mu} E{\mkern 1mu} N \\ & + a_{3} {\mkern 1mu} \left( {E^{3} - 3{\mkern 1mu} N^{2} {\mkern 1mu} E} \right){\mkern 1mu} + b_{3} {\mkern 1mu} \left( {N^{3} - 3{\mkern 1mu} E^{2} {\mkern 1mu} N} \right) \\ \end{aligned} $$
(4)
$$ \begin{aligned} N^{\prime } = & b_{o} + a_{1} {\mkern 1mu} N + b_{1} {\mkern 1mu} E \\ & + 2{\mkern 1mu} a_{2} {\mkern 1mu} E{\mkern 1mu} {\mkern 1mu} N + b_{2} {\mkern 1mu} \left( {E^{2} - N^{2} } \right) \\ & + b_{3} {\mkern 1mu} \left( {E^{3} - 3{\mkern 1mu} N^{2} {\mkern 1mu} E} \right){\mkern 1mu} - a_{3} {\mkern 1mu} \left( {N^{3} - 3{\mkern 1mu} E^{2} {\mkern 1mu} N} \right) \\ \end{aligned} $$
(5)

A linear scale factor and meridian convergence at any point are typically illustrated in the theory of map projections utilizing relations 6 and 7 [26].

$$ K = \sqrt {\,\left( {\frac{{\partial \,E^{\prime}}}{\partial \,E}} \right)^{2} + \left( {\frac{{\partial \,N^{\prime}}}{\partial \,E}} \right)^{2} } $$
(6)
$$ \tan \,\,\theta = - {{\frac{{\partial \,N^{\prime}}}{\partial \,E}} \mathord{\left/ {\vphantom {{\frac{{\partial \,N^{\prime}}}{\partial \,E}} {\frac{{\partial \,E^{\prime}}}{\partial \,E}}}} \right. \kern-0pt} {\frac{{\partial \,E^{\prime}}}{\partial \,E}}} $$
(7)

where

$$ \frac{{\partial \,E^{\prime}}}{\partial \,E} = a_{1} + 2\,a_{2} \,E - 2\,b_{2} \,N + 3\,a_{3} \,\left( {E^{2} - N^{2} } \right) - 6\,b_{3} \,E\,N $$
(8)
$$ \frac{{\partial \,N^{\prime}}}{\partial \,E} = b_{1} + 2\,a_{2} \,N + 2\,b_{2} \,E + 3\,b_{3} \,\left( {E^{2} - N^{2} } \right) + 6\,a_{3} \,E\,N $$
(9)

3 Results and Discussion

Errors in coordinate conversion can impact the mapping between target locations and pointing positions. Local distortion describes how the transformation from one coordinate system to another affects the spatial relationships between nearby points. It is an essential concept in geographic information systems (GIS) and spatial data analysis, as it helps to understand how changes in the coordinate system influence spatial data accuracy. Figure 2 describes the displacement vectors of distortion for control stations, with their original location serving as a starting point and the transformed position as an ending point. The vector's length illustrates the distance from the reference point to the point, whereas the vector's direction defines the direction of the displacement. As shown in Fig. 2, some points moved in the southeast direction and others in the northwest, indicating that the movement of the earth's crust (also known as tectonic movement) can cause displacement of points on the earth's surface.

Fig. 2
A map of Switzerland highlights the locations in a range of low, 0.00 meter and high, 1.20 meters. The lower values are in the interior and the higher values are in the periphery.

Displacement vectors of triangulation point between the original and transformed coordinates

Full size image

Figure 3 shows the displacement in the easting coordinates for three various polynomial transformation models of different degrees: first, second, and third. These models are utilized to describe the relationship between the displacement in the east–west direction and some other variables. As the polynomial degree increases, the displacement value tends to decrease for a given coordinate. This trend can be seen by comparing the curves representing the different models in the graph. This observation is also apparent when examining the displacement in the northing coordinates, as shown in Fig. 4, where the third-order polynomial model yields the lowest displacement values and the best fit to the data. Moreover, the results’ statistical distribution is investigated to understand further the influence of the polynomial degree on the displacement value. This is illustrated in the box plots depicted in Fig. 5, which show each model's range, median, and quartiles of displacement values. These plots demonstrate that the first-degree polynomial always yields the highest displacement values, indicating that it has the lowest performance among the three models. On the other hand, the third-order polynomial consistently provides the best capabilities for the northing and easting coordinates, with the lowest displacement values and the most.

Fig. 3
A graph of delta E versus observation number has some following estimated values. First order, (0, negative 0.20), (110, 0.50), (125, 0.10). Second order, (0, 0.00), (110, 0.20), (125, 0.10). Third order, (0, negative 0.18), (110, 0.10), (125, 0.10).

Differences in easting coordinates after applying addressed models

Full size image
Fig. 4
A graph of delta E versus observation number has some following estimated values. First order, (0, negative 0.20), (100, 0.60), (125, 0.00). Second order, (0, 0.20), (100, 0.50), (125, 0.10). Third order, (0, negative 0.18), (100, 0.60), (125, 0.14).

Differences in northing coordinates after applying addressed models

Full size image
Fig. 5
Two box and whisker plots of data for the first, second, and third orders. For delta E, medians are negative 0.10, negative 0.05, and negative 0.05, respectively. For delta N, medians are 0.10, 0.00, and negative 0.05, respectively. Values are estimated.

Displacement in easting and northing coordinates after applying addressed models

Full size image

4 Conclusion

This research investigates the effectiveness of conformal polynomial algorithms for making maps consistent with global coordinates using least-squares estimation to minimize the difference between the observed data and the model's predicted values. The study aims to determine the accuracy and reliability of these algorithms for map-matching with global coordinates and compare their performances. Based on the statements above, the following conclusions are drawn:

  1. (1)

    The grid-on-grid transformation method using conformal polynomial algorithms was effective in minimizing errors in converting geospatial data from multiple sources.

  2. (2)

    The study showed that increasing the polynomial degree decreased displacement values and improved performance.

  3. (3)

    The third-order polynomial model was the most accurate and reliable for easting and northing coordinates.

  4. (4)

    This approach is useful for harmonizing data from different reference systems and can be applied in any area with high accuracy.