Introductory remarks

Pressure transient analysis (PTA) offers a potentially attractive method to quantify compaction. It is a cost-effective way to estimate reservoir properties while under dynamic conditions. We propose a generalized well test model to estimate changes in permeability, porosity and/or thickness. The methodology depends on the assumption of exponential pressure functions for permeability, thickness and porosity. For clarity, we assume that the fluid properties also follow exponential pressure functions.

The proposed model is not rigorous. It is meant as a screening tool to warn against possible future problems. As such, it should primarily be used when more advanced models do not exist, or involve more work than justified for explorative calculations. We expect the majority application will be for new wells. In these, information about the rock properties is sparse and production history is too short for history matching. Some plausible results from special core analysis, correlations (e.g., Jones 1988; Raghavan and Chin 2004) or experience from similar formations are required.

Compaction may occur on widely different length scales. We consider the length scale of pores and fracture apertures (which we call micro), Mowars et al. (1995), and the length scale of reservoir thickness (which we call macro). The length scale of reservoir and larger falls outside the scope of this study. We recognize that the regional length scale may be important for responsible fluid extraction management.

Pressure signatures are non-unique in the sense that several models may give rise to the same pressure response. This problem is exacerbated for stress-sensitive reservoirs. Additional data from independent sources and careful analysis are necessary to discriminate between the many possible reservoir models, Jelmert and Toverud (2018).

Most reservoirs may be thought about as rigid within engineering accuracy. For some reservoirs, this assumption may not be valid. Terzaghi (1943) proposed an early theory of shrinking reservoirs. Most ensuing studies are based on his observations, including this work. Shrinking reservoirs could be low permeability, unconsolidated, deep, shallow, etc. A large thickness may also cause problems. Over-pressured reservoirs (a fluid pressure exceeds the hydrostatic) may give rise to macro-compaction. Many events may lead to overpressure, Poston and Berg (1997). Compaction because of fluid extraction could lead to reduced well integrity, subsidence and earthquakes, Doornhof et al. (2006), Guardian (2015) and Washington Post (2017). Furthermore, a study by National Academy of Science (2012) confirms that the danger of serious earthquakes is very real, even for fluid withdrawal. Such dramatic consequences are rare. They are costly to amend, if possible at all. In the majority of reservoirs, the effect of stress sensitivity is mild. Severe cases, however, have occurred many places around the world. Due to the environmental costs, possible problems should be identified and preventive actions are taken as soon as possible. A well test has the advantage that it may be conducted once a producing formation has been penetrated. Fluid injection with, or without, extraction may mitigate further damage. Fluid withdrawal at a reduced rate may have a palliative effect. Despite possible adverse consequences, the simultaneous effect of macro- and micro-changes due to compaction has received little attention.

A basic assumption of most well test models for stress-sensitive reservoirs is that results from core analysis somehow reflect the same properties on the length scale of well testing. This is a questionable proposition. Hence, most studies replace actual measurements by simplified pressure functions, but with unspecified parameter(s). The trial functions may be checked against results from core analysis by linear regression on a group of cores. Common choices are power law and exponential functions. Next, the chosen simplistic pressure functions are incorporated into the well test model, and then the unknown parameter(s) are quantified by matching the predicted pressure behavior to the observed pressure signature.

The classical method for PTA depends on matching analytical models to observed pressure behavior. Most nonlinear partial differential equations have no known analytical solutions. Approximate solutions, however, may be available, Al-Hussainy et al. (1966). They investigated the effect of gas withdrawal on pressure signatures. The authors derived a diffusivity equation of linear appearance by use of the Kirchhoff integral. The resulting equation, however, was still nonlinear. The problem was avoided (neglected) by evaluation of the pressure-dependent coefficient to the temporal pressure derivative at the initial condition. Then, they obtained a linear diffusivity equation in terms of the pseudo-potential (transformed variable). The important consequence is that known solutions for slightly compressible fluids are also available for gas wells, but in terms of the pseudo-potential. Since then, the pseudo-potential technique has been applied to PTA for many important problems, and stress-sensitive reservoirs included.

Since permeability and porosity reduction have more occurrences than reservoir shrinking, the micro-model may find more applications than the macro-model. The variation of permeability with pressure has an important influence on the flow capacity of the well, and as such an important impact on the economy. Hence, the effect of deteriorating permeability has been extensively researched.

Effect of restricted entry on well test theory

Nisle (1958) investigated the effect of partial penetration in an infinite-acting reservoir by integration of Kelvin’s instantaneous point source solution. He applied the theory to model the behavior of pressure drawdown and buildup. Brons and Marting (1961) investigated the productivity of restricted entry wells. Their work was based on Nisle’s work.

Hantush (1961) derived expressions for the pressure drawdown and buildup for restricted entry wells. He used the Laplace transform in the radial direction and the finite cosine transform in the vertical. The same approach has been applied more recently to stress-sensitive reservoirs, e.g., Yang and Yeh (2012), Zhao et al. (2014) and in this work.

Seth (1968) solved the Hantush (1961) equations for closed reservoirs. Kazemi and Seth (1969) extended Seth’s solution to account for directional permeabilities.

Gringarten and Ramey (1973) presented numerous solutions by combining Kelvin’s instantaneous source function with Newman’s product method. Ozkan and Raghavan (1991) extended the technique to the Laplace space. Then, variable rate and double porosity solutions became easily available.

Streltsova-Adams and McKinley (1981) analyzed the effect of partial penetration on the beginning of the formation straight line on a Horner plot.

Kuchuk and Kirwan (1987) discussed type curve matching for restricted entry wells by use of infinite conductivity wellbore models. They matched their type curves to real data from a reservoir in Prudhoe Bay. Their analysis included straight line techniques, e.g., Horner plots. They found that “if the final semi-log straight line is reached, the type curve may also be used to estimate the penetration ratio and hence the ultimate producing interval”. They used a composite (two-zone model in the radial direction).

Yang and Yeh (2012) investigated several different well tests in a confined aquifer. They used the Fourier cosine transform in the z-direction and the Laplace transform in the radial one. Zahn and Park (2003) investigated horizontal well responses in leaky aquifers.

Effect of pressure sensitivity

Advanced numerical models have the disadvantage of involving much work, especially during the history-matching phase. Analytical models need minimum work, but involve simplistic assumptions. For stress-sensitive reservoirs, the standard analytical technique is the pseudo-potential method.

Previous studies show that the approximate governing equation and the boundary conditions, in terms of the transformed variable (pseudo-potential) for stress-sensitive reservoirs, are also the same as for reservoirs without stress sensitivity. Hence, they share the same solution. The corresponding nonlinear pressure solution is called a zero-order perturbation solution. Any valid solution technique for the linear problem may be used, also for stress-sensitive reservoirs. We use the finite cosine transform in the vertical direction, and the Laplace transform in the radial, Hantush (1961).

Vairogs et al. (1971) proposed an early well test model for a low permeability gas reservoir with stress-sensitive permeability. They combined a rock mechanical model with a flow model. The models were coupled by a simple iteration scheme within each time step.

Yilmaz et al. (1985) presented an early study based on the permeability modulus approach. Since then, this approach has become a standard way to predict the effect of stress-sensitive permeability. Their approach depends on the assumption that the overburden pressure is reasonably constant.

Raghavan et al. (1972) proposed an analytical well test model for pressure-dependent rock and fluid properties based on the pseudo-potential approach. The resulting diffusivity equation had the same appearance as the traditional one without stress sensitivity, but with a pressure-dependent diffusivity. Their method allows for both arbitrary pressure functions and tabulated values to characterize the rock properties. Pedrosa (1986), used the same model, but he assumed an exponential relationship between permeability and fluid pressure. He showed that regular perturbations may improve the linearized (zero-order) pressure solution.

Kikani and Pedrosa (1991) matched the Pedrosa (1986) model results to real data. They showed that a constant dimensionless permeability modulus may be quantified by type curve analysis provided the initial permeability can be obtained. They found that the zero-order solution has sufficient accuracy for many problems of practical interest. Their conclusion has been confirmed by later studies.

An important advantage of using exponential permeability pressure functions is ease of application, Ali and Sheng (2015). (The first author works with Chesapeake Energy.) They investigated the production decline in shale gas reservoirs.

We find that a benefit of using exponential equations for all pressure-dependent variables is transparency. Then, the interaction between the pressure-dependent variables shows up as a sum modulus (Eq. 15). Furthermore, it is easy to invert the transformed variable by use of the generalized Pedrosa (1986) substitution (Eq. 39). The geometric average from routine core analysis may be generalized to account for exponential permeability functions, Jelmert and Selseng (1997). In addition, the authors showed that the logarithmic transformation method, as proposed by Pedrosa (1986), and the pseudo-pressure approach are equivalent to exponential pressure functions. They used normalized permeability change as dependent variable. They pointed out that a possible negative value of the permeability variable is unphysical. The logarithmic term in Eq. (39) cannot go negative. We find that this condition (for the generalized model) leads to a negative transmissibility, which is unphysical.

Ai and Yao (2012) argue that the porosity also depends on the fluid pressure. Based on results from previous studies, they recommend exponential decay for the pore compressibility. Their model is included in the generalized one.

The original work of Raghavan et al. (1972) and Pedrosa (1986) inspired many follow-up studies. Jelmert and Toverud (2016, 2017b) extended the Kikani and Pedrosa (1991) technique to macro-compaction. They found that the modulus to permeability and thickness might be predicted by use of type curves. Their technique has been extended to finite reservoirs and for the effect of wellbore storage and skin, Jelmert and Toverud (2018).

Zhao et al. (2014) extended the Kikani and Pedrosa (1991) technique to restricted entry horizontal wells in unconsolidated formations. Jelmert and Toverud (2017a, c) included the effect of macro-compaction for restricted entry vertical wells. They showed that any vertical distance, normalized to the thickness, is equal to its initial value. Then, the classical technique of Hantush (1961) becomes available. The generalized model depends on this property, which we call the initial value property, IVP.

Chin et al. (2000) proposed a flow model that was fully coupled (without iterations) to a rock mechanical model.

Theory

We consider a stress-sensitive reservoir with a restricted entry well.

Both the theory of stress-sensitive reservoirs by use of the Pedrosa (1986) technique and the theory of Hantush (1961) for restricted entry wells are well known. Hence, the theories will not be discussed here. The relevant equations are listed in Appendices.

This study includes all assumptions invoked by Raghavan et al. (1972). These are constant grain volume, the validity of Darcy’s law, instantaneous response to fluid pressure changes, constant overburden stress and that flow in the vertical direction due to compaction may be neglected. Under these conditions, the variation of the thickness with pressure becomes:

$$h(\Delta p) = \frac{{h_{\text{i}} \left( {1 - \varphi_{\text{i}} } \right)}}{{1 - \varphi \left( {\Delta p} \right)}}$$
(1)

We replace the porosity function (Eq. 1), by an exponential function of pressure.

$$h(\Delta p) = h_{\text{i}} e^{ - \xi \Delta p}$$
(2)

The coefficient, \(\xi\) which is the modulus of the thickness, is constant by assumption. Next, we replace the porosity term in the Raghavan et al. (1972) equations with the exponential thickness function.

We assume that the confining pressure in core analysis corresponds to drawdown in the reservoir. Furthermore, we assume that the permeability and porosity may be described by exponential functions of pressure.

$$k_{\text{n}} (\Delta p) = \frac{{k\left( {\Delta p} \right)}}{{k_{\text{i}} }} = e^{ - \gamma \Delta p} \quad \varphi_{\text{n}} (\Delta p) = \frac{\varphi (\Delta p)}{{\varphi_{\text{i}} }} = e^{{ - c_{\text{ma}} \Delta p}}$$
(3)

Index \({\text{n}}\) denotes normalized to the initial condition, and \(c_{\text{ma}}\) is the compressibility of the matrix.

Some experiments by special core analysis suggest that Eq. (3) may be inaccurate for large drawdowns. The values become negligible too quickly. Rather than that, they may approach a constant value, Wyble (1958). An intuitive explanation may be that that fracture roughness and infill material prevent complete closing. Still, the pressure function may have exponential characteristics. Wyble found that the similarity to an exponential function might improve if the asymptotical value was subtracted out of the decline equations.

Vairogs et al. (1971) completed a series of experiments on cores to generate data to be used with their coupled flow and rock mechanical model. They found that the decay occurs quickly for small values of confining pressure (drawdown) and slower for larger values. Many additional studies confirm this observation.

One objective of the present approach is to enable type curve matching. This dictates a few parameters in the pressure permeability and porosity functions. Otherwise, the analyst will run out of equations to obtain the unknown parameter(s). Note that the normalized functions (Eq. 3), depend on a single variable only. Other functions may have the same property.

The initial value property

Consider any vertical distance \(z\left( {\Delta p} \right)\) away from a horizontal boundary. Let primed variables denote normalized to the current reservoir thickness. Suppose a normalized function may be described by an arbitrary dimensionless function, \(f_{\text{n}} \left( {\Delta p} \right)\). Then,

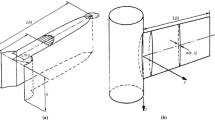
$$z^{\prime}\left( {\Delta p} \right) = \frac{{z\left( {\Delta p} \right)}}{{h\left( {\Delta p} \right)}} = \frac{{z_{\text{i}} f_{\text{n}} \left( {\Delta p} \right)}}{{h_{\text{i}} f_{\text{n}} \left( {\Delta p} \right)}} = \frac{{z_{\text{i}} }}{{h_{\text{i}} }} = z^{\prime}_{\text{i}}$$
(4)

In this study, the pressure functions are restricted to exponentials. Furthermore, let the wellbore be bounded by \(h_{\text{b}} \left( {\Delta p} \right) \le z\left( {\Delta p} \right) \le h_{\text{t}} \left( {\Delta p} \right)\) (indices t and b denote the top and bottom), as shown in Fig. 1.

Fig. 1
figure 1

Restricted entry well in an infinite-acting reservoir

Full size image

Then,

$$h^{\prime}_{\text{t}} \left( {\Delta p} \right) = \frac{{h_{\text{ti}} e^{ - \xi \Delta p} }}{{h_{\text{i}} e^{ - \xi \Delta p} }}{ = }\frac{{h_{\text{ti}} }}{{h_{\text{i}} }}\quad h^{\prime}_{\text{b}} \left( {\Delta p} \right) = \frac{{h_{\text{bi}} }}{{h_{\text{i}} }}\quad h^{\prime}_{\text{w}} \left( {\Delta p} \right) = \frac{{h_{\text{ti}} - h_{\text{bi}} }}{{h_{\text{i}} }} = h^{\prime}_{\text{wi}}$$
(5)

Hence, all fractional (primed) variables remain constant and equal to the initial value and at any reference pressure. For example, the pressure change could be the average one, \(\Delta p = p - \bar{p}\), rather than the initial, \(\Delta p = p - p_{\text{i}}\).

Figure 2 illustrates the initial value property. In this case, the penetration ratio, \(h^{\prime}_{\text{w}} \left( {\Delta p} \right)\), stays constant equal to one half.

Fig. 2
figure 2

a Length of well at initial pressure, b length of well at a reduced pressure

Full size image

The schematic also gives intuitive explanations of the conceptual model for deforming reservoirs. The flow capacity, permeability–thickness product, depends on fluid pressure.

Hence, the composite modulus, \(\tau = \gamma + c_{\text{l}} + \xi - \upsilon\), depends on the modulus to thickness; see Eq. (14)

Likewise, the volume of the reservoir has changed. The altered system compressibility includes the modulus to thickness, i.e., \(c_{\text{t}} = \left( {\xi + c_{\text{l}} + c_{\text{ma}} } \right)\) (Eq. 20). The zone of variable thickness is visualized as a skin zone in the area immediately adjacent to the well, as shown in Fig. 2b.

In case of negligible sum, \(c_{\text{t}} = \left( {\xi + c_{\text{l}} + c_{\text{ma}} } \right)\), the thickness and length of well remain as shown in Fig. 2a.

The directional permeability properties in stress-sensitive reservoir are difficult to quantify. Even the average directional permeability for a group of cores from the same formation is complex. Both the number of cores and the table readings for each core are limited. In light of the sparsity of the data, high accuracy is not required. However, if the permeability is stress sensitive in the radial direction, then it is reasonable to expect that it will be variable also in the vertical. It may be a mistake to neglect the anisotropy all together. Wyble (1958) found that the normalized permeability in the vertical and horizontal directions was decaying functions of pressure. He investigated sandstones. There was a steep decay initially, and then moderate decline later. The normalized permeabilities start out with the same value, \(k_{\text{nr}} \left( {p_{\text{i}} } \right) = k_{\text{nz}} \left( {p_{\text{i}} } \right) = 1\). Based on his work, we propose the following (very) approximate relationship:

$$k_{\text{zn}} \left( {\Delta p} \right) = k_{\text{rn}} \left( {\Delta p} \right) = e^{ - \gamma \Delta p}$$
(6)

The argument for use of Eq. (6) goes as follows: Initially, the permeability curves follow essentially the same path. For large pressures (or time), we expect the majority flow to be radial and horizontal. Then, the effect of anisotropy shows up as a constant pseudo-skin factor. The validity of Eq. (6) is uncertain.

We assume that Eq. (7) is correct. Then, the permeability (Eq. 3), obeys a similar equation as the thickness (Eq. 2). Hence, the permeability may also be simplified by the use of the initial value property ratio (Eq. 7).

$$k^{\prime}_{{{\text{z}},{\text{r}}}} \left( p \right) = \frac{{k_{\text{zi}} e^{ - \gamma \Delta p} }}{{k_{\text{ri}} e^{ - \gamma \Delta p} }} = \frac{{k_{\text{zi}} }}{{k_{\text{ri}} }}$$
(7)

As a result, the Hantush (1961) equations may be generalized to stress-sensitive anisotropic reservoirs in the same way as for a conventional reservoir, Kazemi and Seth (1969).

A possible permeability increase due to fracture generation is outside the scope of this study. This aspect has been discussed by Jelmert and Toverud (2018).

An inherent problem of traditional well test interpretation is non-unique responses and more variables than equations. Hence, the analyst has to rely on data from other sources. Core analysis, well logging, PVT analysis, etc., may help estimate the initial rock properties: permeability, porosity and thickness. In addition, fluid and matrix compressibility may be obtained. These techniques are useful, also for stress-sensitive reservoirs.

Infinite reservoirs

Hantush (1961) obtained an analytical solution for a vertical well with restricted entry (Eq. 45). The vertical space coordinates showed up as fractional quantities. As shown above, fractional space coordinates, with constant values, are valid also for the transformed variable in deforming reservoirs.

For small values of time, the sum term is negligible, and Eq. (45) reduces to the Ei solution. Then, the fluid withdrawal derives from a small region adjacent to the producing length of the well, \(h_{\text{w}}\).

Streltsova (1988) points out that the sum term in Eq. (45) may be regarded as a time-dependent pseudo-skin. With increasing time, the sum term will approach a constant value. A constant sum term (Eq. 47), defines the horizontal radial flow period. Furthermore, when either the wellbores open interval is at the top or bottom of the formation, the constant pseudo-skin factor simplifies to Eq. (48). The latter equation may be used to generate the Brons and Marting (1961) chart. They, Brons and Marting, used the Nisle (1958) source function to obtain their famous chart.

The conversion between the pseudo-pressure and pressure may be obtained by the Pedrosa (1986) substitution (Eq. 39).

The logarithmic derivative of the transformed variable was obtained by conventional derivation of Eq. (45):

$$\frac{{\partial \eta_{0} \left( {r_{\text{D}} ,t_{\text{D}} } \right)}}{{\partial \ln t_{\text{D}} }} = \frac{1}{2}\left\{ {e^{{ - \frac{{r_{\text{D}}^{2} }}{{4t_{\text{D}} }}}} + \frac{2}{{\pi h^{\prime}_{\text{wi}} }}\sum\nolimits_{n = 1}^{\infty } {\frac{1}{n}\left[ {\sin \left( {n\pi h^{\prime}_{\text{ti}} } \right) - \sin \left( {n\pi h^{\prime}_{\text{bi}} } \right)} \right]\cos \left( {n\pi z^{\prime}_{\text{i}} } \right)e^{{ - \left\{ {\frac{{r_{\text{D}}^{2} }}{{4t_{\text{D}} }} + \frac{{\beta^{2} t_{\text{D}} }}{{r_{\text{D}}^{2} }}} \right\}}} } } \right\}$$
(8)

Note that the logarithmic derivative approaches a constant value for large values of dimensionless time. Hence, Eq. (8) will show up as a single horizontal line, which highlights the late radial flow.

The logarithmic pressure derivative of the Pedrosa (1986) substitution, Eq. 39, becomes:

$$\frac{{\partial p_{\text{D}} }}{{\partial \ln t_{\text{D}} }} = \frac{1}{{1 - \tau_{\text{D}} \eta_{0} }} \, \frac{{\partial \eta_{0} }}{{\partial \ln t_{\text{D}} }}$$
(9)

The above equation shows that the logarithmic pressure derivative will not merge into a single horizontal line during the late radial flow. The logarithmic pressure derivative depends on the composite modulus. The coefficient to the temporal derivative will give the pressure derivative and upward lift since the denominator has a value less than unity (Eq. 9).

Suppose it may be possible to estimate the dimensionless moduli to thickness and permeability, Jelmert and Toverud (2016). Then, it is possible to obtain the variation of the thickness with time (Eq. 53).

The solution to the generalized Hantush (1961) equation (Eq. 45), may be improved by regular perturbations as explained by Zhao et al. (2014).

The transition from early radial to late radial flow

Spherical flow shows up when the flow is infinite acting, in both the horizontal and vertical directions. Hemispherical flow occurs when wellbore pressure is undisturbed by all external boundaries, except for a single horizontal one. A short producing interval, and/or a low value of the permeability ratio, vertical to horizontal (\(\frac{{k_{\text{zi}} }}{{k_{\text{ri}} }}\)), is favorable for spherical flow.

Special flow periods, e.g., linear, radial and spherical, may or may not show up in a given test. Each flow period gives some information. The classical interpretation technique depends on a combination of straight line analysis and type curves. In a short well test, the radial flow periods may not show up. Then, the spherical flow regime, if present, may provide the most reliable information. When plotted in a log–log coordinate system, the spherical flow period is characterized by a “negative half slope straight line” in the pressure derivative (Eq. 8).

Case studies

Kikani and Pedrosa (1991) and Zhao et al. (2014) found that the first-order perturbation of the transformed variable is the zero-order solution multiplied by \(\tau_{\text{D}}^{2}\) (Eq. 33). The dimensionless sum modulus usually assumes small values. In addition, they found that higher-order perturbations may be neglected for many engineering calculations. As such, we investigate the zero-order solutions (i.e., the pseudo-potential) only. If higher accuracy is required, the first- and second-order perturbation techniques may be obtained.

To check our restricted entry model, we reproduce the results from Streltsova (1988, p. 88, Fig. 3). A well, with a constant flow rate, is centrally located in an infinite reservoir. The figure shows calculated results for three penetration ratios, \(h^{\prime}_{\text{wi}} = 0.1, \, 0.2,{ 1} . 0\). The latter value corresponds to a fully penetrating well, i.e., the Ei solution. According to her, the restricted entry results show two radial flow periods, with a spherical one in between.

Figure 3 uses the same data as Streltsova, but is augmented with the corresponding nonlinear pressure solutions (red broken curves).

Fig. 3
figure 3

Comparison of dimensionless pressure, with and without stress sensitivity

Full size image

Our linear model results agree with Streltsova’s within visual accuracy. Responses without stress sensitivity show up as unbroken (blue) curves (Eq. 45). The nonlinear pressure responses (red curves) may be obtained from the linear solution by the Pedrosa (1986) substitution, i.e. Eq. (39). The nonlinear correction shows up as the vertical displacement between the unbroken and broken curves, \(p_{\text{DNonlinear}} - p_{\text{DLinear}}\).

Note that an increase in the penetration ratio leads to a decrease both in the linear dimensionless pressure and in the nonlinear correction.

The straight lines at the bottom are for a fully penetrating well, \(h^{\prime}_{\text{wi}} = 1. 0\) (the Ei solution). Then, the nonlinear correction is so small that it is difficult to distinguish between the linear and nonlinear responses. The latter observation may not be valid for larger values of \(\tau_{\text{D}}\), Jelmert and Toverud (2016).

Sidebar: It is well known that parameters on type curves may carry useful information.

Suppose the anisotropy assumption (Eq. 7) is valid. Then, it is possible to estimate the initial vertical to horizontal permeability ratio. Consider Fig. 3. From the matched curves, select corresponding values of \(t_{\text{D}}\) and \(p_{\text{D}}\). Obtain the appropriate \(r_{\text{D}}\) value, and calculate the initial permeability ratio by Eq. (29), i.e., \(r_{\text{D}} = \frac{{r_{\text{w}} }}{{h_{\text{i}} }}\sqrt {\frac{{k_{\text{zi}} }}{{k_{\text{ri}} }}}\). The value obtained can be compared against information from independent sources, e.g., a wireline formation tester or core analysis.

Figure 4 shows a diagnostic plot for a reservoir with and without stress sensitivity. The input data are as for the previous case.

Fig. 4
figure 4

Diagnostic plot

Full size image

Well test diagnostics can best be done on a log–log plot of the logarithmic derivative (diagnostic plot). Then, the linear response shows up as a horizontal line for radial flow and for spherical as a straight line with slope minus one half (Eq. 8). Both penetration ratios, \(h^{\prime}_{\text{wi}} = 0.1\,{\text{and}}\,0.2\), highlight two radial flow periods separated by a spherical one. For reference, an arbitrary negative half slope line (in black color) is included in the gridded part of Fig. 4.

The nonlinear response, for a reservoir with stress sensitivity (red broken curves), is more complicated (Eq. 9). The largest penetration ratio, \(h^{\prime}_{\text{wi}} = 0.2\), shows the existence of almost horizontal lines during both the early and late radial flow period. For the lower penetration ratio, there are no horizontal segments during the early radial flow period. Hence, the latter radial flow period could go undetected. Unlike the linear case, the nonlinear pressure derivative does not merge into a single curve during infinite acting radial flow. Failure to recognize the uplift property of the nonlinear correction may lead to incorrect well test interpretation. Regardless of flow period, the nonlinear derivative responses always fall above the linear ones.

Correct interpretation, however, depends on the identification of the right model. The logarithmic derivative of the pseudo-potential and the nonlinear pressure solutions highlights different aspects of the model. Hence, we recommend putting both methods into use for well test diagnostics.

Figure 5 shows the development of the estimated normalized thickness as a function of dimensionless time (Eq. 52).

Fig. 5
figure 5

Normalized thickness as a function of dimensionless time

Full size image

The plot shows that a decrease in the partial penetration ratio leads to increased shrinking.

The equation for the normalized permeability (Eq. 55), obeys a similar equation as for the thickness. Hence, a plot of the variation of the normalized permeability will be similar in shape to Fig. 5.

Figure 6 shows the pressure transient response for a faraway horizontal boundary. Streltsova (1988, p. 98, Fig. 6) points out that the linear pressure solution (Eq. 45), includes flow in a semi-infinite reservoir. We reproduce her plot as a benchmark. Linear responses are indicated by blue curves and nonlinear by red.

Fig. 6
figure 6

Early radial to hemispherical flow transition, \(t^{\prime}_{D} = \frac{{k_{ri} t}}{{\varphi_{i} \mu_{i} c_{ti} r^{2} }}\)

Full size image

When the producing interval is located close to a horizontal boundary and the other one is far away, a transition from early radial to hemispherical flow may develop. Equation (45) was used to compute the transformed variable \(\eta \left( {r_{\text{D}} ,t_{\text{D}} } \right)\) and Eq. (39) to compute the corresponding nonlinear dimensionless pressure.

Figure 6 depends on the following input data: \(h_{\text{ti}} = 0, \, h_{\text{bi}} = h_{\text{wi}} .\) Dimensionless time, \(t'_{\text{D}}\), is defined with basis in \(r\), rather than \(r_{\text{w}}\). This definition is useful for interference testing. For example, \(r\) could be the vertical distance between the open interval and a pressure probe for a wireline test. The dimensionless time is defined as \(t'_{\text{D}} = \frac{{k_{\text{ri}} t}}{{\varphi_{\text{i}} \mu_{\text{i}} c_{\text{ti}} r^{2} }}\). The dimensionless distance is given by: \(r_{\text{D}} = \frac{{r_{\text{w}} }}{{h_{\text{i}} }}\sqrt {\frac{{k_{\text{zi}} }}{{k_{\text{ri}} }}}\).

Model validation

The generalized model includes solutions without stress sensitivity as a limiting case for \(\tau \to 0\) in Eq. (39). Many sub-models, previously published, are included in the generalized model. Some authors have meticulously verified their models. Their verifications are relevant for this study. Hence, we provide a short discussion of some of these. The sub-models may be interrogated by simple changes in the input data.

Vairogs et al. (1971) investigated the effect of compaction on gas production. They proposed a model for stresses around a wellbore based on rock mechanics. The theory was based on the concepts of macro- and micro-stresses. The variation of in situ stresses does not control the mechanism of permeability changes. Hence, the necessity to add experimental results from core analysis to their theoretical rock mechanical model. Their flow model was the radial diffusivity equation for flow of an isothermal gas, but with pressure-dependent permeability. The geo-mechanical model and the flow model were coupled by a simple iteration scheme. Their model was verified by comparing results with previously published solutions and with the analytical semi-steady state solution. This approach (the forward problem) may be thought about as an extrapolation tool.

Kikani and Pedrosa (1991) matched results from the Pedrosa (1986) model to real data. Then, knowledge of underlying stress condition is not required. They present their matched curves on a Horner type curve, as shown in Fig. 5. This model (the generalized one) involves the same pressure equations, but with modified moduli in the transport and storage terms. The latter term has no influence on the type curve since the Horner ratio is dimensionless. As a result, predictions from the generalized model can be matched by the same procedure as proposed by Kikani and Pedrosa, see Fig. 7. Hence, the validity of the new model is supported by the analysis proposed by Kikani and Pedrosa. Due to non-unique pressure responses, none of the models can be considered completely verified.

Fig. 7
figure 7

Kikani and Pedrosa (1991) result reproduced by the generalized model, their results are indicated by symbol x

Full size image

The dimensionless sum modulus is given by Eq. (28), which is repeated below:

$$\tau_{\text{D}} = \frac{{q_{\text{sf}} \mu_{\text{i}} B_{\text{i}} \tau }}{{2\pi k_{\text{ri}} h_{\text{wi}} }}$$
(10)

Figure 7 is obtained under the assumption of a fully penetrating well, which is included in the generalized model (Eq. 49). In light of Eq. (10), Fig. 7 shows that a reduction in the sum modulus, \(\tau\), leads to a diminished drawdown. Both Eqs. (2) and (3) show that shrinking of thickness and permeability deterioration depends on the drawdown. A reduction of flow rate has the same effect. Thus, a reduced rate has a palliative effect on reservoir shrinking (Eq. 54), and decrease in permeability (Eq. 56). Likewise, an increase in radial permeability and/or well length has the same effect. Furthermore, a decrease in viscosity will also alleviate shrinking and/or decreasing permeability. The variation of the sand face thickness, for restricted entry wells, is given by Eq. (52). The intuitive explanation for the positive consequences is that the changes mentioned above will facilitate flow from remote regions of the drainage area.

Chin et al. (2000) proposed a fully coupled model for the combined effects of stress, fluid flow and fluid property changes on well responses in stress-sensitive reservoirs. They investigated elastic and plastic responses by a finite element/Galerkin reservoir simulator. Again, the rock mechanical model had to be supplemented by experimental data to capture the variation of permeability with pressure. The authors used the pseudo-pressure integral to simplify the nonlinear diffusivity equation. They proposed various normalized permeability functions used in the diffusivity equation.

Furthermore, Raghavan and Chin (2004) looked back to the previous model, Raghavan et al. (1972) for comparison. They found that if the normalized permeability is a function of pressure only, then in case of a line source well, the Boltzmann transformation leads to a constant value of the logarithmic pressure derivative. Hence, the pseudo-potential is a logarithmic function of time. Samaniego and Cinco-Ley (1989) concur. Both models, Raghavan and Chin (2004) and Raghavan et al. (1972), lead to the same result:

$$\frac{{\partial p_{\text{D}} }}{{\partial \ln t_{\text{D}} }} = \frac{1}{2}$$
(11)

We obtain the same result. For a fully penetrating well, the sine terms in Eq. (45) become zero. The result is the Ei solution for one-dimensional radial horizontal flow. Then, limiting equation for large values of time is given by Eq. (50). Hence, the logarithmic derivative is also given by Eq. (11). Our result is a generalization of the previous conclusions, since all the variables in Eq. (12) are functions of pressure.

As discussed previously (in case studies), our results agree with Streltsova’s (1988). Hence, the linear solution has been verified. The inversion of the transformed variable into the corresponding nonlinear solution is exact. Hence, the validity of our restricted entry nonlinear pressure solution has been justified.

Ai and Yao (2012) pointed out that the porosity, \(\varphi\), also depends on the fluid pressure. Based on similar studies, they decided for exponential decay (Eq. 12). The generalized model includes its model as a special case. They obtained the zero and first-order perturbation by use of the Boltzmann transformation and variation of parameters, respectively. In addition, they checked their model against a traditional finite difference numerical model. They concluded that the zero-order approximation is of sufficient accuracy.

Friedel and Voigt (2009) proposed new solutions for PTA during the infinite-acting reservoir period with constant rate and constant pressure boundary conditions. The authors applied the exponential and the linear permeability functions. They verified their model by numerical simulation and applied their model for well test analysis. According to them, their results are important in tight gas or coalbed methane reservoirs. The authors transformed the nonlinear partial differential equation into an ordinary differential equation by the Boltzmann transformation. The result was validated by a fully implicit commercial simulator, which incorporated pressure-dependent permeability. Their results are for fully penetrating wells.

Conclusions

Compaction may have serious environmental consequences. Ideally, early signs of shrinking should be identified and preventive or palliative actions started as soon as possible.

A new analytical model to predict changes in thickness and/or permeability has been proposed. The model has been validated against field data and previously published results.

The model will simplify many sub-models by simple changes in the input data.

The model is simplistic, but easy to apply and involves little work. History matching is not required. An advanced numerical model is the polar opposite.

Well test interpretation by the generalized model may be a useful screening tool for new wells. A test can be conducted once a formation has been penetrated.

A reduction of rate will alleviate shrinking and/or permeability deterioration. Likewise, an increase in radial permeability and/or well length has the same effect. Furthermore, a decrease in viscosity will also alleviate shrinking and/or decreasing permeability.

There is a possibility to estimate the variation of thickness and or permeability with time.

Well test diagnostic by the pseudo-potential and the nonlinear pressure highlights different aspects of the pressure signature. We recommend putting both techniques in use.

We find that any normalized vertical distance remains constant during reservoir shrinking. The restricted entry model depends on this initial value property.