Introduction

While earthquakes that occur naturally are typically the result of the gradual accumulation of tectonic stresses over geological time, they can also be triggered by relatively small stress perturbations if the affected region is already close to failure. Triggered seismicity refers to earthquakes triggered by human activities and typically falls into the latter category1,2,3. The past fifteen years have seen a rapid increase in triggered earthquakes. These events result from massive reinjection of waste fluids from oil and gas extraction4,5,6,7,8,9,10, or for the stimulation of reservoirs as hydraulic fracturing11 or hydraulic shearing12,13. The spatial proximity of the seismicity to such industrial operations and the fact that many of these events are preceded by months to years of high-volume fluid injection suggest a connection between the occurrence of seismicity and fluid injection14,15,16. Fluid injection triggers seismicity through two distinct mechanisms: (i) elevated pore pressures reduce the strength of a tectonically primed fault with the adjacent stress state remaining essentially unchanged, or (ii) far-field stresses are perturbed beyond the immediate region of pore pressure diffusion with fault strength remaining largely un-affected17,18,19.

Importantly, triggered earthquakes can be of substantial magnitude and highly destructive, such as the M-5.5 2017 Pohang earthquake in South Korea that resulted in significant infrastructure damage and civilian injuries12,13,20. As such, these occurrences pose a potential threat in many branches of energy production and utilization – particularly those for net-zero-carbon (e.g., EGS, hot sedimentary reservoirs, CO2 sequestration)21,22,23,24 and reduced-carbon (e.g., gas shale, coalbed methane) alternatives to conventional fossil fuels (i.e., coal and conventional oil)25. Such fluid-triggered earthquakes are observed to be causally linked to both overpressures and pressurization rates7,14,15,18,26,27, to evolve from both creeping slip28 and poroelastic stress projections3,11 and capable of characterization as both contained11,29,30,31 and runaway ruptures2,32,33,34. Laboratory experiments confirm various controls of pressure and pressurization rates35,36,37, pressure distributions38, evolution of permeability29,39, presence of asperities40 and the role of pre-stress29,31,37,38,41 in driving slip and influencing the magnitude of the largest anticipated earthquake - a key but elusive parameter in evaluating seismic hazard. To first order, seismic moment has been shown to scale with injection volume for both constrained17,29,30,31 and runaway ruptures2,32. These relationships link maximum seismic moment (M) to the product of the total injected fluid volume (∆V) and the shear modulus (G) of the affected zone as \({M}_{\max }={{\rm{\alpha }}}G\Delta {V}^{\beta }\) where \(\alpha\) and \(\beta\) represent the pre-stress (\(\alpha\)) and the form of the rupture as either constrained to within the overpressurized patch or runaway beyond it (\(\beta\)). Despite their differences, they broadly align with current observations of the \(M-\Delta V\) relationships within the range of 2 < M < 631 but remain equivocal in both defining the gradient of \({M}_{\max }={{\rm{\alpha }}}G\Delta {V}^{\beta }\) as a power of either \(\beta=1\) or \(3/2\), and in representing large events triggered by meager injection volumes such as the 2017 M-5.5 Pohang earthquake.

We define and quantify the role of pre-existing shear stress in controlling the form (gradient) and magnitude of the \(M-\Delta V\) relationship through a suite of experiments on laboratory faults constrained by end-member conditions of zero-displacement and constant stress and triggered by fluid overpressures. We define and observe a sigmoidal response in \(M-\Delta V\) space comprising pre-slip, slip then post slip phases whose magnitudes and gradients honor field observations. We explain our laboratory observations with a rupture model that accommodates pre-stress on a fault constrained to fail within the zone of fluid pressurization to allow parameterization of the model and extension to behavior at field scale.

Results and discussion

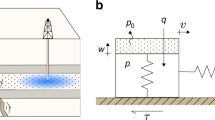
We performed shear reactivation experiments on laboratory faults pre-loaded close to failure and reactivated by the injection of fluid into the fault. The sample comprises a single-inclined-fracture (SIF) transecting a cylindrical sample (2.5-cm diameter by 5-cm long, Fig. 1) of Westerly granite with fluid pressure supplied to the fault by small conduits (drillholes) piercing the up-dip and down-dip extent of the fault. The artificial fault plane is inclined at 30° to the longitudinal axis of the core and polished with #60 grit grinding powder subsequently reworked through repeated shearing tests. The reactivation experiments introduce small-scale roughness on the fault surface, simulating the natural roughness of a fault that has experienced repeated slip events.

Fig. 1: Experimental configuration.
figure 1

The setup features three servo-controlled pumps (A, B, and C) for controlling axial pressure, confining pressure, and pore pressure, respectively. The enlarged sample assembly depicts the single-inclined-fracture (SIF) geometry.

Full size image

Injection-induced reactivation of laboratory faults

The sample assembly is jacketed in double latex sleeves and confined within a triaxial pressure vessel. The latex sleeves retain the structural arrangement of the core inside the pressure vessel, isolate the sample from the confining fluid and confine the fluid that fills the interior of the core. The pressure vessel provides independent control on axial stress (pump A), confining stress (pump B) and upstream pore pressure (pump C). Axial displacement rates are set through the volume rates of pump A and confirmed by a linear variable differential transducer (LVDT) connected to the axial loading piston. Shear displacement \(\varDelta u\) is then calculated as the along fracture component of displacement as \(\Delta u=\Delta {u}_{a}/\cos \theta\) where \({\varDelta u}_{a}\) is the axial displacement of the sample. Fault compaction/dilation-related displacements are neglected in this as their magnitudes are small relative to shear offset.

Two 1.3-mm boreholes drilled from each end of the cylindrical sample pierce the closest extent of the fault plane (along the sidewall) and allow fluid injection along the fault. Sealing the downstream exit port enables a uniform fluid pressure distribution to be applied, finely incremented (+/− 0.04 MPa) and measured both by the pump and a pressure transducer located downstream. Given the SIF configuration, the effective normal stress and shear stress can be recovered from the confining stress, axial stress and pore pressure as:

$${\sigma} ^{{\prime} }_{n}=\left({\sigma }_{3}-{P}_{p}\right)+\left({\sigma }_{1}-{\sigma }_{3}\right){\sin }^{2}\theta$$
(1)
$$\tau=\left({\sigma }_{1}-{\sigma }_{3}\right)\sin \theta \cos \theta$$
(2)

where \({\sigma }_{1}\) is axial stress, \({\sigma }_{3}\) is confining pressure stress, \({P}_{p}\) is pore pressure, and θ (30°) is the angle with respect to the longitudinal axis of the sample.

All experiments are at ambient temperature and follow a similar protocol. This involves (i) application of confining stresses (3 MPa) on the fault fully saturated with de-ionized water, followed by (ii) shear-mobilization through the increase of axial loading at a constant displacement rate until a post-peak steady-state condition is reached. (iii) The axial loading and related shear stress are reduced to a prescribed fraction of the peak steady-state frictional strength (typically 60% to 90%, representing intermediate to high magnitudes). (iv) Fault reactivation is triggered by stepwise increasing the pore pressure on the fault in 0.1 MPa increments held constant for 1–5-minutes. Uniform pressure on the fault is confirmed by the equilibration of the upstream and downstream pressure transducers and typically occurs in 1 to 20 secs – depending on the fault permeability, modulated by the applied fluid pressure.

This study considers two boundary conditions related to the in-situ stress state: constant shear stress (CSS) and zero-displacement (ZD). CSS represents a simplified model of a fault under constant tectonic shear stress, achieved by keeping the confining stress \(({\sigma }_{3})\) and axial stress \(({\sigma }_{1})\) constant, which results in a constant shear stress (τ). In contrast, ZD represents the case where the elastic strain energy in the (testing) system dissipates as the fault slips, causing the fault to relax and the axial/shear stress to decrease during displacement. The shearing of faults/fractures and associated stress relaxation are widely observed in episodes of seismicity or microseismicity34,42. To achieve ZD, the axial loading pump is locked, causing the differential stress (\({\sigma }_{d}={\sigma }_{1}-{\sigma }_{3}\)) acting on the sample to decrease significantly in response to the sample shortening with the gradual sliding of the fault, and therefore a decrease in shear stress. As apparent in Eq. (2), relaxation of the axial stress also results in a decrease in the effective normal stress \(({\sigma} ^{{\prime} }_{n})\), and thus a reduction in the fault frictional strength, which may promote slip. Slip will further reduce shear stress via system stiffness until the fault self-arrests. In other words, under ZD boundary conditions, the fault slip behavior is determined by the competition between the reduced fault strength that promotes slip and the reduced shear stress that limits slip.

Linking seismic moment to injected volume

The cumulative moment is recovered from the shear stress drop (\(\Delta \tau\)) driven at each reactivation within the sample of total volume \((V)\)43 as:

$$\sum M=\varDelta \tau V={\varDelta {uk}}_{t}V$$
(3)

where \({k}_{t}\) is the tangential system stiffness \(({k}_{t}=\varDelta \tau /\Delta u)\) calibrated from the elastic stiffness of a locked fault [Pa/m] and \(\Delta {{\rm{u}}}\) represents the tangential displacement (i.e., parallel to the fault). The loading tangential stiffness is measured during the initial phase of shear mobilization, when the axial stress is increased from a hydrostatic state to its peak strength (as illustrated in Fig. 2a–c).

Fig. 2: The stiffness of fracture.
figure 2

a Shear stress loading with time during initial shear stress loading. b Tangential displacement with time during initial shear stress loading. c The slope of shear stress loading vs. tangential displacement defines the tangential stiffness (ZD2 for zero-displacement boundary condition experiment #2). d Normal stress vs. aperture change with a slope equal to fracture/fault normal stiffness recovered through cyclic loading-unloading. Load (#1)-unload-load (#2) cycles are conducted in succession.

Full size image

Cumulative injection volume into the fault is estimated assuming a uniform dilation across the rigid fault wall as a function of the uniformly distributed fluid pressurization, and defined in terms of a constant normal stiffness, as:

$$\Delta V=A\varDelta a=\frac{A{\sigma ^{\prime} }_{n}}{{k}_{n}}=\frac{A\Delta p}{{k}_{n}}$$
(4)

where \(A\) is the area of the fault, \(\Delta a\) is the fracture aperture and \(\Delta p\) is the change in pore pressure. In the case of a pre-cut fault surface where there is no cohesion or tensile strength, the change in effective normal stress (\({\sigma} ^{{\prime} }_{n}\)) can be considered essentially equivalent to the change in pore pressure (\(\Delta p\)). Normal stiffness (\(({k}_{n})\) is measured through a cyclic loading-unloading test on an artificial fault plane cut perpendicular to the longitudinal axis. The axial loading is incremented in steps up to 3 MPa (the same magnitude as the prescribed confining stresses). Following this, the axial loading is decremented on the same schedule; then reloaded again (Fig. 2d). Applied normal stresses and longitudinal displacements measured by LVDT together yield the normal stiffness. The accuracy of the aforementioned indirect determination through normal stiffness has been validated against directly measured across-fault dilation in DDS configuration using the same method43.

Finally, Eqs. (3) and (4) enable both \(\sum M\) and \(\Delta V\) to be determined independently from direct experimental measurements of \(\varDelta u\) and \(\Delta p\). Thus, pore fluid injection modulates over-pressurization, and the measured shear displacement serves as a proxy for cumulative moment.

Additionally, the latex sleeves exert resistance when it is being stretched as faults slide in shear. We quantify this using a lubricated and polished SIF sample assumed frictionless that captures jacket restraint. This restraint is later removed from the total tangential system stiffness.

Observations

The experimental conditions and physical properties for each of the six experiments are listed in Table 1. During the initial shear-mobilization stage, we observe that frictional strength from all experiments exhibits a peak fault strength of 1.3 to 1.6 MPa (\({\tau }_{{peak}}\)), with the peak coefficient of friction \({\mu }_{p}\) (ratio of shear stress to effective normal stress) measured to be ~0.4 (see in supplementary Fig. 1). \({\tau }_{0}\) is the initial shear stress pre-slip, defined as a prescribed fraction (%) of peak steady-state frictional strength. Loading tangential stiffnesses are measured in each experiment, and the average \({k}_{{t\_loading}}\) is of \({6.4\times 10}^{-3}\) MPa/\({{\rm{\mu }}}{{\rm{m}}}\).

Table 1 Experimental conditions and properties
Full size table

A typical evolution of slip displacement, injection volume, and cumulative moment during the pressurization of test #CSS4 is shown in Fig. 3a for constant shear stress boundary conditions. The shear stress is fixed to ~89.7% of the peak strength and maintained constant throughout the experiment. As fluid is injected, the fault strength decreases due to the reduction in effective normal stress. The fault reactivates almost immediately after fluid pressurization (at a pore pressure of 0.4 MPa) since the fault is critically pre-stressed. Fault slip is rapid at the onset of reactivation, typically taking only a few seconds, but gradually slows towards the end of each pressurization step. In contrast, Fig. 3b presents the results for test #ZD2 under zero-displacement boundary conditions. Shear stress is again initially set to ~89% of the peak strength but allowed to relax during fault slip. As the shear displacement increases, there is an associated abrupt decline in shear stress (Fig. 3b).

Fig. 3: Typically observed fault displacement and cumulative moment over time as triggered by fluid pressurization.
figure 3

The reactivated laboratory faults are under boundary conditions of (a) constant shear stress (CSS) experiment #4 and (b) zero-displacement (ZD) experiment #2. Measured variables are color-coded to show the time evolution of shear stress, pore pressure, fault slip, injection volume and cumulative seismic event magnitude.

Full size image

In all experiments the cumulative moments (\(\sum M\)) and the injected fluid volume (\(\Delta V\)) are manifest as a two-stage scaling relation, regardless of the boundary conditions, and \(\sum M\) scales nearly linearly with \(\Delta V\) within each of the substages (Fig. 4). The first pre-slip stage represents a locked fault where incremented pore pressure promotes infinitesimal shear deformation through an effective-stress dependent tangential stiffness. Deformation is infinitesimal (Fig. 3) and seismic moment indiscernible on a natural scale (Fig. 3) but apparent in log \(M-\Delta V\) space (Fig. 4) at a slope of ~1:1. The second post-slip stage represents steady sliding activated through a constant frictional strength. The main fault rupture defines the transition between the two substages where the external shear stress exceeds the fault strength and shear reactivation is initiated (purple circles in Fig. 3). As the level of the pre-stress is increased and approaches the critical stress (CSS: 59% to 77% to 87%; ZD: 85% to 89%), the remobilization denoted by this up-step transition occurs at progressively lower pore fluid pressures and the ultimate cumulative seismic moment increases.

Fig. 4: Cumulative seismic moment versus total injection volume.
figure 4

a Constant shear stress boundary condition (experiments CSS1, CSS2 and CSS3); b Zero-displacement boundary condition (experiments ZD1 and ZD2).

Full size image

Scaling between cumulative moment (\(\sum {{\boldsymbol{M}}}\)) and injected fluid volume (\(\Delta {{\boldsymbol{V}}}\))

In cases where fault slip is limited to the fault area that has been pressurized, the maximum seismic moment (M) release is approximately bounded by the product of the total injected fluid volume (\(\Delta V\)) and the shear modulus (G) of the affected zone, i.e., \({M}_{\max }={G}\Delta V\)30. This assumes on average that each fault patch is approximately one half of a seismic stress drop below the yield stress and thus only requires approximately half the stress change imposed by the volume change to induce seismic slip. However, if the initial shear stress is closer to failure, a lower fluid pressure increases and hence less volume of fluid injection is required to trigger fault slip and to recover the full tectonic moment from the resulting earthquake. Clearly, the initial pre-stress is an important parameter for understanding the relationship between injected fluid volume and seismic moment of triggered earthquakes.

We consider a simplified model of a fault under constant tectonic shear stress. The initial shear stress magnitude is bounded by a peak stress, \({\tau }_{s}\), governed by the effective normal stress, \({\sigma} ^{\prime} _{n}\), and static frictional strength, \({\mu }_{s}\), as \({\tau }_{s}={\mu }_{s}{\sigma} ^{\prime} _{n}\). To quantify the initial stress – how close the fault is to failure before injection starts–we define a stress ratio (c) as the proportion of the static stress drop already accommodated by tectonic stressing, alternatively viewed as the proximity to failure (c ~ 0 to 99.9%), Thereby, initial shear stress acting on the fault, \({\tau }_{0}\), divides the stress budget between the change in fault strength required to cause slip on the fault, \(\left(1-c\right){\tau }_{s}\), and the stress liberated upon fault slip, \(c{\tau }_{s}\), as,

$${\tau }_{0}=c \, {\cdot }\, {\tau }_{s}.$$
(5)

If total stresses remain constant throughout, then the fluid pressurization by a uniform change in pressure, \(\Delta p\), results in a reduction in fault strength by,

$$\left(1-c\right){\tau }_{s}=\mu \Delta p$$
(6)

Here, \(\mu\) is a representative friction coefficient, intermediate in the small range between static and dynamic magnitudes. The pore pressure change driving rupture is related to the normalized volumetric dilatation, \(\Delta V/{V}_{P}\), and bulk modulus, \(K\), as

$$\Delta p=\frac{K\Delta V}{{V}_{P}}$$
(7)

where the volumetric dilation \(\Delta V\) is uniform and specifically restricted to the pressurized volume, \({V}_{P}.\,\)

Combining Eqs. (5), (6) and (7), the reduction in strength required to drive failure may be related to pore pressure or volumetric dilation as:

$${\tau }_{s}=\frac{\mu }{\left(1-c\right)}K\frac{\varDelta V}{{V}_{P}}$$
(8)

Concurrently, the strain energy that is released from the volume surrounding the rupturing fault is defined by the rupture volume, \({V}_{R}\). This defines the cumulative “seismic” moment as,

$$\sum M=c{\tau }_{s}{V}_{R}$$
(9)

where \({\tau }_{s}\) represents the total stress drop. Stress drop is bounded by the difference in static and dynamic friction coefficients and a near invariant normal effective stress for tectonic earthquakes. But for fluid injection triggered events, stress drop is conditioned by a near constant friction coefficient and an unbounded drop in effective stress responding to a large increase in pressure or injected volume (Eq. (8)). To simplify, the fault-bounded rupture volume is defined by the equiaxed footprint of the pressurized fault, as \({V}_{P}={V}_{R}\). Thus, substituting \({\tau }_{s}\) from Eq. (8), Eq. (9) yields,

$$\sum M=\frac{c}{(1-c)}\mu K\varDelta V$$
(10)

As shear modulus \((G)\) is related to bulk modulus \((K)\) through:

$$K=\frac{2G\left(1+\upsilon \right)}{3(1-2\upsilon )}$$
(11)

then Eq. (11) is rewritten as:

$$\sum M=\frac{c}{(1-c)}G\varDelta V$$
(12)

It may specifically be simplified by assuming \(\upsilon=0.25\), \(\mu\) = 0.6 (based on Byerlee’s law) to convert \(\mu K\) directly into \(G\). Thus, \(\sum M\) scales linearly with \(\Delta V\) and for this choice of parameters, directly through the shear modulus of the reservoir, since shear modulus controls the strain energy that is released. This defines the 1:1 trajectory of the cumulative seismic moment with parallel vertical offsets in log \(M-\Delta V\) space (final stage in Fig. 4) and is congruent with the trajectory observed in cumulative moment for a variety of triggered events27. This is exact for cumulative seismic moment.

Furthermore, the more useful maximum seismic moment \({M}_{\max }\) may be approximated from the cumulative seismic moment for an assumed coefficient of friction ~0.6 and b-value set of unity43 as:

$${M}_{\max }=\frac{1}{2}\sum M=\frac{c}{2(1-c)}G\varDelta V$$
(13)

offering an approximation from the cumulative seismic moment. Thus, Eqs. (12) and (13) establish a threshold for the cumulative and maximum triggered seismic moments as a function of the volume of fluid injected.

Note that this development and in particular Eqs. (12) and (13) assume that:

  1. i.

    The fluid injection zone is hydraulically connected to the seismogenic region, and that rupture is triggered by direct pressurization on the fault with the tectonic stress largely unchanged. Far-field poroelastic effects are not considered.

  2. ii.

    The rupture volume is restricted to the footprint of the fault that is uniformly pressurized by the fluid.

  3. iii.

    The failure criterion–that shear stress exceeds fault strength–does not differentiate between stability conditions for either seismic or aseismic rupture.

  4. iv.

    The mechanical and frictional properties are pre-defined as Poisson’s ratio \((\upsilon )=0.25\), coefficient of friction (μ) = 0.6 such that then \(\mu K \sim G\) in Eqs. (11) and (13).

These relations (Eqs. (12) and (13)) highlight the importance of the initial stress conditions on the resulting seismic moment. That is, as the proportion of the initial shear stress to strength ratio (c) increases, indicating proximity to failure before injection, both the maximum and cumulative seismic moment concomitantly increase. This is supported by our laboratory data showing an increase in post-slip seismic moment with an increase in the magnitude of the pre-stress (Fig. 5).

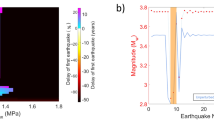
Fig. 5: Linkage between seismic moment and total injection volume for fluid-injection-triggered earthquakes.
figure 5

a Maximum seismic moment and magnitude as functions of total volume of injected fluid from the start of injection until the time of the largest triggered earthquake (modified from Li et al. 43). b Cumulative seismic moment and magnitude as functions of cumulative volume of injected fluid (modified from Bentz et al. 27) (c and d). Cumulative seismic moment versus total injection volume: c Constant shear stress boundary condition (experiments CSS1, CSS2 and CSS3); d Zero-displacement boundary condition (experiments ZD1 and ZD2). Black line defines the upper limit of the maximum (in a) and cumulative (in b, c and d) seismic moment with c values representing different pre-stress conditions (Eq. (12), assuming G = 24 GPa). Note that McGarr (1976)30 plots for c = 50%. Grey dashed lines represent maximum seismic moment with two different γ values, as proposed by Galis et al.,31.

Full size image

Relation to prior models

We clarify differences between contrasting assumptions in estimates of seismic moment (\(M={BG}\Delta V\)) as \(B=2\) (McGarr,30), \(B=\tfrac{1}{1-c}\) (Li et al.,43) and in this study as \(B=\tfrac{c}{1-c}\). Assuming that rupture liberates the strain energy accumulated within the full tectonic seismic cycle (\(1.{\tau }_{s}\)) after a strength reduction of \(\left(1-c\right){\tau }_{s}\) then the released moment scales as \(B=\tfrac{1}{1-c}\) (Li et al.,43). Where the increase in pore pressure required to trigger rupture is midway within the window defining stress/strength drop (\(c=0.5\)) then \(B=2\). This is congruent with the assumptions and outcome for McGarr,30, albeit without pre-stress. However, the fault will not accumulate stress (\(1.{\tau }_{s}\)) equivalent this full measure of strain energy – rather, this accumulated stress is equivalent to only \(c.{\tau }_{s}\) and thus \(B=\tfrac{c}{1-c}\) as noted in this study. The pre-factors, \(B\), conditioned by the different assumptions applied to the two pre-stressed conditions give essentially identical results – although Li et al.,43 slightly overestimates the anticipated seismic moment, especially at low magnitudes of pre-stress. As an extreme example, rupture triggered at the beginning of the seismic cycle where \(c=0\) would be incorrectly scaled as finite with \(B=2\) (McGarr,30) and \(B=1\) (Li et al.,43) but correctly as \(B=0\) in this study. We present this to note the consequences of different assumptions in the bounding magnitudes of these relations – but note that pre-stressing to high fractions of the strength/stress drop (\(c \, > \, 0.5\)) is a practical requirement for the hazard of such triggered events.

Impact of pre-stress

We plot for c = 10%, 90%, and 99.9% as the dot-dashed black lines in Fig. 5a together with our laboratory data and recent observations of injection-triggered earthquakes related to hydraulic fracturing, field pilot experiments, and enhanced geothermal stimulations. In this, the largest moment of a reported injection-triggered seismic event, the Pohang earthquake (indicated by the upper right red circle in Fig. 5a, is now capped by the updated upper limit where c = 99.9%. These same field observations of cumulative M-ΔV (Fig. 5b) are aligned at a gradient of 1:1 rather than 1:3/2, are vertically separated, and have components that transit to give very large moments for small injection volumes (e.g., Pohang)–all features that are observed in experiments, explained with our observations (Fig. 4), model and analysis and suggest a 1:1 rather than a 1:3/2 gradient for M-ΔV. Furthermore, laboratory observations with the pre-stress to strength ratios of ~60% to 90% (as shown in Fig. 5c, d) closely match predicted elevated moments for increasing pre-stress as in Eq. (12). The match is near-exact for the constant shear stress experiments (Fig. 5c) but is overestimated by Eq. (12) for the zero displacement experiments (Fig. 5d).

Comparing the two boundary conditions, zero-displacement boundary conditions characterize a scenario where elastic strain energy stored in the system dissipates as the fault slips, causing the shear stress to relax during that slip. Such stress relaxation is precluded under the constant shear stress boundary condition. Consequently, the cumulative shear displacement and therefore the seismic moment are both lower under zero-displacement boundary conditions compared to those measured under constant shear stress (as shown in Fig. 5b, c). Despite that, both boundary conditions are capable of linking event magnitude (M) with injected volume (ΔV). This suggests the general applicability of the constant shear stress boundary condition as an operationally simplified laboratory design that reliably captures the behavior of fault slip and triggered seismicity.

Based on this congruence between laboratory and field observations that span multiple decades in moment and injected volume, the restriction of considering rupture as confined to within the region of pressurization does not appear overly restrictive–at least based on the laboratory data, that is highly constrained in terms of the pre-stress. Thus, the scaling relation appears broadly applicable to a variety of environments subject to triggered seismicity, although confirmation of pre-stress in these environments is lacking. Nevertheless, precise estimation of seismic magnitude necessitates comprehension of fault or reservoir properties (e.g., from in-situ stress measurements and well logging).

Pre-rupture, rupture and post-rupture

The preceding analysis on the scaling relation linking maximum anticipated seismic moment (\(\sum M\)) and fluid injection volume (\(\Delta V\)) focuses on the condition of fault slip. However, linear correlations exist between \(\sum M\) and \(\Delta V\) both before (pre-rupture) and after (post-rupture) reactivation, as shown in Fig. 4. The two-stage relationship between \(\sum M-\Delta V\) is defined by two distinct mechanisms involved in the process. During the first stage, the observed infinitesimal shear displacement is possibly attributed to 1) elastic deformation on the locked fault and modulated by fault and system tangential stiffness; and 2) local inelastic deformation such as of micro-fractures. After exceeding fault strength - the transition point – the fault slips. This major slip event represents the release of the stored strain energy occasioned by slip, minus that pre-slip moment release due to the infinitesimal shear deformation of the embedded fault. Once static friction is fully mobilized, \(\sum M-\Delta V\) are again linearly related by a constant friction coefficient that is operated on by a pressure change increment that scales with volume injected – for a system of constant compressibility. Thus, additional fluid injection leads to a further reduction in fault strength. This similar two-stage scaling relation has been observed in other laboratory studies on triggered seismicity in natural fractures, where the total moment release initially increases slightly at the early stage of fluid injection, followed by a significant jump towards the upper bound47.

One intriguing possibility that arises when considering the observation of this transition step between pre-slip and slip is whether the timing of this event is foreseeable during fluid injection operations. Essentially, the point at which the relationship transitions between the two stages defines a critical injection volume that triggers fault reactivation. The critical injection volume \({V}_{c}\) is thereby determined by rewriting Eq. (8) as:

$${V}_{c}={\tau }_{s}\frac{1-c}{\mu }\frac{{V}_{P}}{K}$$
(14)

where this highlights the control of the initial stress conditions on the onset of fault reactivation. That is, where all other parameters remain constant, as the proportion of the initial shear stress to strength (c) increases, the amount of fluid required to reactivate the fault decreases. This is consistent with our laboratory observations where an increase in the magnitude of the pre-stress leads to a decrease in the critical injection volume, broadly regardless of the boundary conditions (Fig. 5b, c).

Implications at field scale

The ability to estimate seismic hazard and the onset of events triggered by fluid injection is important in mitigating triggered seismicity. We develop a scaling relation that considers initial pre-stress in the rupture of a rigid fault with rupture limited to the zone of pressurization. This cumulative event magnitude is defined as \(M=\frac{c}{1-c}G\Delta V\) with c defining the proportion of the static stress drop already accommodated by tectonic stressing, alternatively viewed as the proximity to failure. We confirm the validity of this model with laboratory experiments that trigger fluid injection-triggered reactivation using pore pressure pulses with measured shear displacement as a proxy for seismic moment. These observations document a two-stage relationship with seismic moment linearly related to fluid injection volume within each stage. The first stage represents the infinitesimal shear displacement likely due to 1) elastic deformation on the locked fault and modulated by fault and system tangential stiffness; and 2) local inelastic deformation such as that on micro-fractures. The limit to this response is driven by the onset of slip and defined by both injection volume/pressure and the magnitude of the pre-stress acting on the fault. Thus, the point at which the relationship transitions between stages defines a critical injection volume that, in turn, triggers fault reactivation. The second stage characterizes the fault rupture behaviors and is conditioned by the coefficient of friction on the fault. Faults loaded to different pre-existing shear stresses identify the dominant role of pre-existing shear stress in conditioning event magnitude. Laboratory observations confirm closely to the relationship \(M=\frac{c}{1-c}G\Delta V\) that broadly defines an increasing seismic moment with increasing pre-stress. Although not independently confirmed with pre-stress data from historic triggered earthquakes, the relationship appears broadly congruent over sixteen decades of seismic moment and injected volume. These observations suggest that with knowledge of the pre-existing stress state and reservoir properties from sources such as regional indicators, in situ stress measurements, and well logging, we may be better able to estimate the seismic hazard and the timing of events prior to any injection activities.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.