Forecasting House Prices through Credit Conditions: A Bayesian Approach

Abstract

As housing development and housing market policies involve many long-term decisions, improving house price predictions could benefit the functioning of the housing market. Therefore, in this paper, we investigate how house price predictions can be improved. In particular, the merits of Bayesian estimation techniques in enhancing house price predictions are examined in this study. We compare the pseudo out-of-sample forecasting power of three Bayesian models—a Bayesian vector autoregression in levels (BVAR-l), a Bayesian vector autoregression in differences (BVAR-d), and a Bayesian vector error correction model (BVECM)—and their non-Bayesian counterparts. These techniques are compared using a theoretical model that predicts the borrowing capacity of credit-constrained and unconstrained households to affect house prices. The findings indicate that the Bayesian models outperform their non-Bayesian counterparts, and within the class of Bayesian models, the BVAR-d is found to be more accurate than the BVAR-l. For the two winning Bayesian models, i.e., the BVECM and the BVAR-d, the difference in forecasting power is more ambiguous; which model prevails depends on the desired forecasting horizon and the state of the economy. Hence, both Bayesian models may be considered when conducting research on house prices.

1 Introduction

House price predictions are a fundamental part of informed decision-making in the built environment. For instance, the construction of houses is a time-consuming process.¹ Therefore, when contemplating whether to embark on a house-building project, one must consider future prices rather than current ones. The same rationale applies to housing market policies; the implementation of policies is a substantial undertaking, and their effects do not materialize immediately. Consequently, it may be prudent for policymakers to intervene or consider how to intervene before problems emerge. Moreover, house price forecasts can potentially reduce market uncertainty by providing guidance to the market at times when house prices are at a turning point. This is beneficial for banks and their regulators as it enables them to determine better capital requirements, thereby improving risk management. As such, in this paper, we compare different house price forecasts and test which provides more accurate house price predictions.

A frequently used method to forecast house prices is the ordinary least squares (OLS) technique. However, the problem with this estimation technique, for the use of forecasting house prices, is that it minimizes the sum of squares. While this technique results in the best fitting model (the model with the highest possible $R^2$), it can cause issues for forecasting as OLS models tend to explain variation that cannot be explained: they may overfit the data. That is, the model tries to attribute all variation to the model’s variables, while some variation observed in the data simply cannot be explained. This issue is especially relevant in the context of complex models that involve a large number of variables. Nonetheless, even for relatively parsimonious models, overfitting can occur (Giannone et al., 2015). This overfitting problem manifests itself as a poor out-of-sample performance, and hence it is particularly undesirable when forecasting.

Bayesian models can reduce this overfitting problem by utilizing prior information on the behavior of time series.² Therefore, Bayesian estimation techniques are often preferred to their OLS counterparts (Bańbura et al., 2010; Giannone et al., 2015; Koop et al., 2010b). In the literature, three Bayesian model specifications are frequently used to predict economic time series: a Bayesian vector autoregression in differences (BVAR-d), a Bayesian vector autoregression in levels (BVAR-l), and a Bayesian vector error correction model (BVECM). A point of criticism expressed regarding the first model (the BVAR-d), is that it does not take long-run—or cointegrating—relationships into account.³ Since the second model (the BVAR-l) is presented in levels, it does allow for (implicit) cointegrating relationships. The model does, however, include all potential long-run relationships and does not restrict variables to converge to their equilibrium in the long run. Consequently, the last model (the BVECM) might be more desirable than the previous two models as it includes a cointegration constraint that ties the variables together in the long run (Engle & Granger, 1987a).

The contribution of this study is twofold. Firstly, the literature lacks an empirical comparison of the forecasting ability of house prices for the three aforementioned Bayesian models. Although some studies have compared one or two of these Bayesian models to each other or their non-Bayesian counterparts, a systematic evaluation of all three models has not yet been undertaken. We conduct such a systematic comparison of the proposed Bayesian models and their non-Bayesian counterparts. Secondly, in the housing literature, a BVECM has, to the best of our knowledge, not been used to forecast house prices on a macroeconomic (or national) level, even though its model specification looks promising.⁴ Thus, our second contribution to the literature is to assess the merits of a BVECM to predict house prices on a national level.

Theoretical insights are required to incorporate long-run relationships into a BVECM. The long-run relationship we employ takes the importance of the financial sector into account by incorporating an equilibrium relationship between mortgage credit and house prices. This relationship is derived by Van der Drift et al. (2023) and relies on the notion that households spend a fixed fraction of their income on mortgage costs. The analysis is applied to the Dutch housing market as Dutch households generally purchase houses through mortgages, and thus, the proposed credit-based long-run equilibrium applies (Van der Drift et al., 2023).

The remainder of the paper is organized as follows. Section 2 briefly introduces the long-run model. Section 3 summarizes the econometric methods applied in this empirical analysis. Section 4 discusses how we evaluate each model’s performance, Sect. 5 presents the results, and the last section concludes the paper.

2 The Long-Run Model

The literature contains an abundance of papers on potential equilibrium relationships for house prices.⁵ In this paper, we focus on one equilibrium relationship: the relationship between mortgage credit and house prices. This equilibrium can be explained by the fact that, in most countries, houses are bought through a mortgage, and consequently, mortgage conditions are an important driver of house prices. Not only does it drive demand, but it can be used to assess whether the housing market is overvalued. This works as follows: if households spend an increasingly larger share of their income on housing, it could indicate potential default risk. That is, households simply are unable to spend a larger and larger fraction of their income on housing, and consequently, the demand for housing, and hence house prices, are likely to decrease shortly.

The credit-based equilibrium relationship employed in this paper incorporates the recent extension developed by Van der Drift et al. (2023). In contrast to previous equilibrium relationships, this relationship takes two types of households into account: lower-income and higher-income households. The first type, lower-income households, are assumed to be constrained in their borrowing behavior. This constraint could be caused by either a credit rationing bank or stringent financial regulation. Either way, due to the constraint, borrowers can only spend a certain share of their monthly income on mortgage costs (i.e., these households face a debt-service-to-income cap). In the model, these maximum monthly mortgage payments are discounted to receive the total amount a lower-income household can spend on housing $(b^{\max, c}_t$).⁶

The other category of consumers, higher-income households, may not be subject to lending regulations. However, these households might exhibit a preference for allocating a specific proportion of their income towards mortgage payments. This can be conceptualized as a household budget plan where housing, the largest expense, receives a set amount and the remaining funds are allocated towards other expenses such as food, transportation, and leisure activities. Again, the monthly values are discounted to reflect their ability (or desire) to pay for housing ($b^{cd, \, u}_t$).⁷

In Van der Drift et al. (2023), it is formally derived that this long-run equilibrium can be presented by:

$$\begin{aligned} \begin{aligned} {P}_{t}= \gamma {b^{\max, \, c}_t } +(1-\gamma ){\theta b^{cd, \, u}_t }. \end{aligned} \end{aligned}$$

(1)

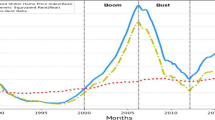
Thus, from Eq. (1) it follows that the purchase price of housing (${P}_{t}$) is explained by the maximum borrowing amount of constrained households ($b^{\max, c}_t$) and the ability to pay of unconstrained households ($b^{cd, \, u}_t$).⁸ Finally, $\gamma$ reflects the spending share of constrained households and the parameter $\theta$ reflects the fraction of income high-income households spend on mortgage costs.⁹ An overview of the data sources used to estimate Eq. (1) is presented in Table 1 and the data is plotted in Fig. 1.

Table 1 Data

While this equilibrium condition may provide a useful benchmark, the reality of the housing market is more complex. The housing market is a sluggish market and, due to speculative or psychological effects, it adjusts gradually to changing economic conditions. Consequently, house prices cannot be expected to always be at the long-run equilibrium relationship. As such, studies have found that lagged values of house prices yield substantial explanatory power over future values of house prices (Abraham & Hendershott, 1996; Hort, 1998; Malpezzi, 1999). Especially in the Netherlands, a country that displays minimal house price reversals, research has shown that house prices are past dependent (De Vries & Boelhouwer, 2009; Tu et al., 2017). To account for this phenomenon, we include four lags of each variable in the models.¹⁰

Fig. 1

Time series charts

3 Methodology

In the following subsections, we discuss each of the empirical models whose predictive power will be evaluated in this paper.

3.1 VAR

VARs are standard models to forecast time series, and they generally produce good forecasting results (Giannone et al., 2019). VARs can be viewed as a system of equations in which each dependent variable is explained by its own lags and the lags of explanatory variables, which themselves are the dependent variables in the system of equations (Sims, 1980). Due to this functional form, VARs are able to depict economic dependencies between own past values and lagged values of explanatory variables. Mathematically, the system of equations, in which all n variables are predicted, can be presented in the following way:

$$\begin{aligned} y_{t}=c+ \sum ^{p}_{i=1} \beta _i y_{t-i}+\varepsilon _{t}, \end{aligned}$$

(2)

where $y_{t}$ is an $n \times 1$ vector of variables. For the model presented in Sect. 2, $y_{t}$ is equal to the vector $P_t$, $b_t^{mac,c}$, and $b_t^{cd,u}$. p reflects the number of lags that are included in the regression and, as discussed in Sect. 2, in our research this term is equal to four. $\beta _i$ is an $n \times n$ matrix of parameters, and $\varepsilon _ {t}$ is an $n \times 1$ vector of disturbance terms or ‘noise’.

A prerequisite for the estimation of the above-presented VAR is that the analyzed time series are stationary.¹¹ House prices—and macroeconomic variables in general—usually fail to meet this requirement (Clayton, 1997; Koop et al., 2005; Wu et al., 2017). These time series are often non-stationary, and OLS-based inference breaks down; the autoregressive coefficients are biased and the t distributions are no longer approximately normally distributed.¹² Moreover, variables can appear to be related when in fact they are not, i.e., we might run a spurious regression.

In order to avoid invalid estimation, the data can be transformed into a stationary process by taking the differences between consecutive observations. If this first (second, third, etcetera) difference is stationary, we can run a VAR in differences (i.e., a VAR-d) without violating estimation assumptions. If we let $\Delta$ denote the difference operator, the VAR-d has the following functional form:

$$\begin{aligned} \Delta y_{t}=c+ \sum ^{p}_{i=1} \beta _i \Delta y_{t-i}+\varepsilon _{t}. \end{aligned}$$

(3)

For the model that will be estimated, i.e. the model described in the previous section, Eq. (3) can be written as:

$$\begin{aligned} \begin{aligned}&\Delta {P}_{t}&=c_1+ \sum ^{4}_{i=1} \beta _{1, \,1, \,i} \Delta {P}_{t-i} + \sum ^{4}_{i=1} \beta _{1, \,2, \,i} \Delta {b^{\max, \, c}_{t-i}}+ \sum ^{4}_{i=1} \beta _{1, \,3, \,i} \Delta {b^{cd, \, u}_{t-i}} +\varepsilon _{1, \,t}\\&\Delta b^{\max, \, c}_{t}&=c_2+ \sum ^{4}_{i=1} \beta _{2, \,1, \,i} \Delta {P}_{t-i} + \sum ^{4}_{i=1} \beta _{2, \,2, \,i} \Delta {b^{\max, \, c}_{t-i}}+ \sum ^{4}_{i=1} \beta _{2, \,3, \,i} \Delta {b^{cd, \, u}_{t-i}} +\varepsilon _{2, \,t}\\&\Delta b^{cd, \, u}_{t}&=c_3+ \sum ^{4}_{i=1} \beta _{3, \,1, \,i} \Delta {P}_{t-i} + \sum ^{4}_{i=1} \beta _{3, \,2, \,i} \Delta {b^{\max, \, c}_{t-i}}+ \sum ^{4}_{i=1} \beta _{3, \,3, \,i} \Delta {b^{cd, \, u}_{t-i}} +\varepsilon _{3, \,t}.\\ \end{aligned} \end{aligned}$$

(4)

Thus, from Eq. (4) it explicitly follows that each variable has its own equation. Thence, all explanatory variables in a VAR are endogenous variables, i.e., they are created within the model. This provides a major advantage in forecasting, as there is no need to obtain information on future values of the explanatory variables.

3.2 VECM

As discussed above, VARs generally have to be differenced in order for the variables to be stationary and the estimation to be valid. However, in case of a common stochastic trend (i.e., cointegration), we can provide a meaningful interpretation of the parameters in their levels without violating any of the estimation assumptions. When data are cointegrated there namely exist relationships between variables in levels, which can render these variables stationary without taking consecutive differences. So-called VECMs capture these relationships and, in the presence of cointegration, are expected to outperform VARs over longer forecasting horizons (Engle & Yoo, 1987).

These long-run relationships are especially important when predicting house prices, as the housing market tends to adapt sluggishly to changing economic conditions. Therefore, in the empirical housing market literature, models that capture these long-run relationships (VECMs) are often preferred over models that do not (VAR-d).¹³ Mathematically, a VECM can be presented by:

$$\begin{aligned} \Delta y_{t}= c+ \sum ^{p}_{i=1} \beta _i \Delta y_{t-i}+\Pi y_ {t-1}+\varepsilon _{t}. \end{aligned}$$

(5)

The only difference with a VAR-d (Eq. 3) is the error correction term $y_{t-1}$, which captures how variables change if one of the variables departs from its equilibrium value. The term’s parameter $\Pi$ represents the effect of the error-correction term on the short-run variables. This term is a $n \times r$ vector, where r is called the cointegration rank. r can be used to demonstrate the relationship between a VECM, a VAR-d, and a VAR-1. This works as follows: if r is zero, there are no cointegrating relationships, and the model reduces to a VAR-d as presented in Eq. (3). If r is larger than zero but smaller than n, cointegration is present and the model is best represented by a VECM (Eq. 5).¹⁴ Yet, if $r=n$, the variables are stationary, no cointegration is present, and the model can be validly estimated by a VAR-l (Eq. 2).

If the data are cointegrated (i.e., $0<r<n$), the parameter $\Pi$ can be further divided into two subterms: $\Pi =\alpha \beta '$. Where $\beta '$ can be interpreted as the distance of the variables from their equilibrium and $\alpha$ and describes the speed at which variables converge back to the equilibrium. In vector form, this error-correction term is rather abstract, yet for the model that will be estimated,¹⁵ the VECM can be written as:

$$\begin{aligned} \begin{aligned}&\Delta {P}_{t} \quad\;\;=c_1+ \sum ^{4}_{i=1} \beta _{1, \,1, \,i} \Delta {P}_{t-i} \; + \sum ^{4}_{i=1} \beta _{1, \,2, \,i} \Delta {b^{\max, \, c}_{t-i}}\;+ \sum ^{4}_{i=1} \beta _{1, \,3, \,i} \Delta {b^{cd, \, u}_{t-i}}+ \alpha _1 (P_{ t-1}-\beta '_1 b^{\max, \, c}_{t-1}-\beta '_2 b^{cd, \, u}_{t-1}) +\varepsilon _{1, \,t} \\&\Delta b^{\max, \, c}_{t} =c_2+ \sum ^{4}_{i=1} \beta _{2, \,1, \,i} \Delta {P}_{t-i}\;+ \sum ^{4}_{i=1} \beta _{2, \,2, \,i} \Delta {b^{\max, \, c}_{t-i}}\;+ \sum ^{4}_{i=1} \beta _{2, \,3, \,i} \Delta {b^{cd, \, u}_{t-i}}+\alpha _2 (P_{ t-1}-\beta '_1 b^{\max, \, c}_{t-1}-\beta '_2 b^{cd, \, u}_{t-1}) +\varepsilon _{2, \,t } \\&\Delta b^{cd, \, u}_{t} \;\;=c_3+ \sum ^{4}_{i=1} \beta _{3, \,1, \,i} \Delta {P}_{t-i} + \sum ^{4}_{i=1} \beta _{3, \,2, \,i} \Delta {b^{\max, \, c}_{t-i}}\;+ \sum ^{4}_{i=1} \beta _{3, \,3, \,i} \Delta {b^{cd, \, u}_{t-i}} +\alpha _3 (P_{ t-1}-\beta '_1 b^{\max, \, c}_{t-1}-\beta '_2 b^{cd, \, u}_{t-1})+\varepsilon _{3, \,t},\end{aligned} \end{aligned}$$

(6)

where $P_{ t-1}-\beta '_1 b^{\max, \, c}_{t-1}-\beta '_2 b^{cd, \, u}_{t-1}$ reflects the error-correction term. This term reflects how much the previous period deviated from the model’s long-run equilibrium. Its coefficient ($\alpha$), denotes how fast the equilibrium will be restored. Therefore, if variables are above (below) the long-run equilibrium they are expected to decrease (increase) shortly. Thus, in contrast to the VAR, this model incorporates an equilibrium mechanism and, when employed correctly, one can think of this equilibrium mechanism as a bubble buster.

3.3 BVAR

A drawback of the above-described models is that they contain numerous parameters that need to be estimated, while macroeconomic time series generally have a short length. To illustrate this argument: the simple three-variable VAR-d model presented in Eq. (4) already includes 39 parameters that have to be estimated. Particularly, when time series are relatively short, this can cause overfitting; i.e., a situation in which the in-sample fit of the model (i.e., the $R^2$) is excellent, but the model’s out-of-sample performance is poor.

Bayesian estimation techniques combat the overfitting problem by using Bayes’ rule to shrink the model’s parameters towards a benchmark that is known to have decent forecasting power (Doan et al., 1984; Litterman, 1979; Sims, 1980). This benchmark is called the prior and broadly speaking it reflects a loss function for implausible explanations. Therefore, the model does not optimize its in-sample fit completely, which reduces overfitting problems, decreases parameter uncertainty, and improves the model’s forecasting accuracy.

The Bayesian estimation method can be used to estimate the VAR-d as presented in Eq. (3), but it can also validly estimate a VAR-l as presented in Eq. (2). Thus, in contrast to an OLS-based VAR, having stationary data is not a requirement to estimate a BVAR (Phillips, 1991; Sims et al., 1990). That is the case as Bayesian estimation has the same shape regardless of whether the data are stationary or non-stationary, and consequently, one can validly estimate a BVAR-l.¹⁶

There is no consensus in the economic literature as to whether one should employ a BVAR-l or a BVAR-d. However, in the housing literature, the BVAR-l is used relatively more often.¹⁷ The popularity of the BVAR-l over the BVAR-d can presumably be explained by the fact that estimation in levels does not result in the information loss that is caused by differencing the data. Thence, similarly to a VECM, a BVAR-l includes information on variables in their levels. Yet, while a (B)VECM contains only stationary combinations of variables in levels, a BVAR-l simply contains all variables in their levels.¹⁸ Thence, the BVAR-l contains more potential long-run relationships that have to be estimated and does not restrict variables to converge to their equilibrium in the long run, and consequently, it is less efficient compared to a (B)VECM (Engle & Yoo, 1987).¹⁹ Furthermore, the BVAR-l includes non-stationary combinations of variables, while the (B)VECM only includes stationary combinations of variables, some of these non-stationary combinations might seem valid, but could turn out to be spurious.

For Bayesian models, it is common practice to utilize the Minnesota prior due to its ability to effectively forecast time series (Koop, 2017; Litterman, 1979). However, it is important to note that the prior specification for a BVAR-l differs from that of a BVAR-d as the former includes non-stationary variables, while the latter includes stationary variables. For non-stationary variables, the Minnesota prior incorporates the wisdom, that these time series generally follow a random walk. Therefore, it sets the prior mean of the first lag of own variables to one and it is set to zero for any other parameters (Koop & Korobilis, 2010a; Lütkepohl, 2005). As a result, this prior essentially mimics a random walk, which tends to forecast non-stationary variables quite well.²⁰ In contrast, for stationary variables, it is customary to set the prior mean of all variables to zero. This reduces the model’s parameters to white noise, which is known to accurately forecast stationary time series (Koop & Korobilis, 2010a).

The main merit of the Minnesota prior, that hence applies to the BVAR-d as well as the BVAR-l, is that the degree to which variables are shrunk differs per parameter. More distant lags of parameters (e.g., $y_{t-4}$) are expected to yield less information than more recent lags (e.g., $y_{t-1}$). This insight is incorporated by putting a stronger prior on more distant lags, hence shrinking these parameters relatively more. Moreover, the Minnesota prior includes the sensible notion that most of the variation in each of the variables is accounted for by own lags. This is enforced by putting a stronger prior on lags of other variables than on lags of the variable itself.²¹

3.4 BVECM

In the previous section we mentioned how a (B)VAR-l is different from VECM-like models; in essence, a VECM is a restricted VAR-l. These restrictions tie the variables together in the long run and make the VECM more efficient than an unrestricted VAR. Thence, imposing restrictions could result in a better forecasting accuracy.²² Yet, the Bayesian version of a VECM, the BVECM, has, to the best of our knowledge, not been used to forecast house prices at a macro level. The BVECM has only been used in a regional (spatial) model to capture price spillovers across housing markets (Gupta & Miller, 2012a; Nneji et al., 2015) and to predict house prices at the regional level (Gupta & Miller, 2012b).²³ Thence, the literature lacks an application and, more importantly, an evaluation of the forecasting power of the BVECM to predict house prices at the macro level.

The estimation of a BVECM is highly similar to that of a BVAR. The only difference is the need for a prior on the error correction term $\Pi$. This is, however, complicated by the fact that $\Pi$ involves a product of parameters $\Pi =\alpha \beta '$, which introduces identification issues.²⁴ Because of these identification issues using standard priors is problematic and can lead to an improper posterior distribution (Kleibergen & Van Dijk, 1994; Koop et al., 2005).

In order to avoid improper estimation, in the main body of the article, we use the cointegration space approach.²⁵ Since the cointegration space approach focuses on the space spanned by the vector of long-run parameters ($\beta '$)—rather than the values of the vector—the prior is able to tackle the above-mentioned identification issues (Koop et al., 2005, 2010b; Villani, 2005).²⁶ Moreover, as is customary for this approach, we put a noninformative prior on the speed of convergence ($\alpha$) (Koop et al., 2010b). And, in line with the estimation of our BVAR, for the short-run parameters ($\beta$) we employ a Minnesota prior with a prior mean of zero.

4 Model Evaluation

To evaluate each model’s predictive ability, we assess their out-of-sample—rather than in-sample—performance. This is because, as already hinted at in the introduction, in-sample errors are likely to underestimate forecasting errors (Makridakis et al., 1982). Method selection and estimation are namely designed to optimize the fit of the model on historical data, but history is unlikely to repeat itself, at least exactly. Thence, overfitting problems will only become apparent when looking at the out-of-sample performance of the models.

The entire dataset ranges from 1995 Q1 to 2020 Q4. However, to assess the out-of-sample performance of the models, we split the data into two parts: (1) the training set, which is used to estimate the parameters, and (2) the test set, which is used for model evaluation. We produce 1–40-quarter-ahead forecasts, starting with the training that ranges from 1995 Q1 to 2005 Q4. To eliminate the possibility that an arbitrary choice of sample split affects the model’s performance, we rely on a rolling-origin evaluation approach (Tashman, 2000). That is, we update the sample one quarter at a time, and repeat the procedure until the end of the sample in 2011 Q4. For each forecast, we calculate the Mean Absolute Percentage Error (MAPE) and we average them out to end up with our final result.²⁷

5 Results

In this section, we first present identification tests. Thereafter, the forecasting performance of the models is evaluated. Subsequently, the drivers of the two best-performing models are illustrated. Finally, the performance of these two winning models is assessed along the house price cycle.

5.1 Identification Tests

From Sect. 3, it followed that time series properties (i.e., stationarity and cointegration) are an important determinant of which empirical models can validly be estimated. Thence, the natural starting point of a forecasting exercise is to examine the time series properties of variables used herein.

We first assess whether the models’ variables are stationary. Please recall that one needs stationarity to properly estimate a VAR, while for BVARs stationarity is not a requirement. We utilize two non-stationarity tests: the Augmented Dickey-Fuller (ADF) and the Phillips-Perron (PP) test, as well as one stationarity test: the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test, to determine whether the variables are stationary. The test results are presented in Table 2, and they indicate that all variables are non-stationary.²⁸

Repeating the tests for the first-order difference, we found evidence that the first differences of these variables are stationary for all but one case. Specifically, only the ADF test for the first-order difference of house prices failed to reject the null hypothesis of non-stationarity. However, considering that all other tests indicate stationarity and the ADF test is known to have low power (Afriyie et al., 2020), it can be inferred that all the series are non-stationary but their first difference is stationary (i.e., all the time series are integrated of order one). Therefore, to prevent a spurious regression, we run the VAR in first differences.

Subsequently, the number of cointegrating relationships (or the cointegration rank) is tested. We need at least one cointegrating relationship to estimate a VECM. For a BVECM this test result is not a strict requirement, yet it is not uncommon to test for the number of cointegrating relationships. According to the results of the Johansen test presented in Table 3, both the trace and the eigenvalue test reject the null hypothesis of no cointegration, but the tests fail to reject the maximum of one cointegrating relationship at a 5% level. Thence, the Johansen test provides evidence on the existence of at least one cointegrating relationship and hence justifies the use of a (B)VECM.

Table 2 Non-stationarity & stationarity tests

Table 3 Johansen Cointegration test

5.2 Forecasting Power

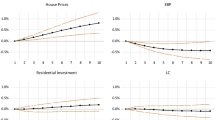
This section compares the predictive ability of the models discussed in Sect. 2. Figure 2 shows the forecasting errors of the models. Note that the same information is presented in tabular format in Appendix 1.

For ease of comparison, each subfigure displays a maximum of three models. As such, the BVAR-d model presented in subfigure b is identical to the BVAR-d model presented in subfigures c and d. When looking at all subfigures combined, we see a familiar pattern; i.e., for short-term forecasts, the forecasting errors are relatively small, but when forecasting further ahead the errors increase significantly. When forecasting ten years ahead the errors are severe, the model with the smallest forecasting error is on average off by circa 17 %. Thence, such long-term forecasts provide little valuable information. Nonetheless, for this research, it is interesting to include them as it is often argued that the benefits of a (B)VECM become apparent over longer forecasting horizons.

Fig. 2

Pseudo out-of-sample forecasting error

The first subfigure compares the predictive power of the two non-Bayesian models: the VAR and the VECM. It follows from the figure that the VAR performs slightly better at one-quarter-ahead forecasts, yet for all other forecasting horizons, the VECM prevails. This result is in line with economic theory (or practice), which states that VECMs are expected to outperform VARs over longer forecasting periods (Engle & Yoo, 1987). Note, however, that the VECM outperforms the VAR at relatively short forecasting horizons already. This is most likely the case as house prices do not drift off, they have a tendency to almost immediately move towards the long-run equilibrium (although it can still take a long time before the equilibrium is fully restored). Moreover, note that the difference in forecasting accuracy increases over the forecasting horizon, indicating that long-run relationships become more important when forecasting further ahead. Thus, modeling long-run relationships in VECM-form is especially beneficial when forecasting house prices more than one-quarter ahead, and this benefit becomes even more apparent on longer forecasting horizons.

Subsequently, in subfigure b, the forecasting accuracy of the VAR-d, BVAR-d, and BVAR-l are compared. At all forecasting horizons, the BVAR-d and BVAR-l outperform the VAR-d. When forecasting further ahead, this difference, in terms of forecasting accuracy, increases. Thus, the two Bayesian VARs always outperform the OLS VAR, indicating that using prior information improves the forecasting performance of the models significantly. When comparing the two BVARs, it is evident that their forecasting performance is comparable for predictions up to three and a half years ahead. However, as the forecasting horizon extends, the BVAR-d prevails over the BVAR-l. Thus, although a non-stationary BVAR is allowed, it does not seem to beat a stationary BVAR.

Subfigure c compares the VECM with the BVECM. For this comparison, we also find that at all forecasting horizons, the Bayesian model outperforms its non-Bayesian counterpart. However, in contrast to the VAR models (panel b), the difference in terms of forecasting accuracy is smaller. Moreover, the difference between the VECM and the BVECM stagnates after eight years (about 32 quarters). Overall, when we combine the results of panels b & c, we conclude that for both the VECM-like and VAR-like models, the Bayesian version outperforms its OLS counterpart, indicating that shrinking the models’ parameters towards a parsimonious benchmark is beneficial. Therefore, when forecasting house prices, Bayesian estimation techniques would be preferred over their OLS counterparts at all forecasting horizons.

Finally, in Panel d we compare the two winning Bayesian models: the BVECM and the BVAR-d. For these models, the results are less clear-cut: for forecasts up until three quarters ahead the BVAR-d slightly outperforms the BVECM, for forecasts from three quarters to seven years ahead the BVECM prevails, yet for forecasts further ahead the BVAR-d wins again. Since the results are more comparable, we use the Diebold–Mariano (DM) test in Appendix 1 to determine whether the two forecasts differ. Although the difference between the two models is not significant for all forecasting periods, the results of the DM test suggest that the BVAR-d outperforms in the short-run, the BVECM performs best for medium-term forecasts, and the BVAR-d wins again for long-term forecasts.²⁹ These results are seemingly in line with the notion that the benefits of a BVECM become apparent over longer forecasting horizons. However, in contrast to this notion, for long-term forecasts, the BVAR-d prevails.³⁰ This anomaly can most probably be explained by the fact that we fail to estimate the error-correction term adequately when forecasting this far ahead, leading to a poorer performance of the BVECM compared to the BVAR-d. All in all, for short-run forecasts, the BVAR-d appears to be the preferable option, while for medium-term forecasts the BVECM outperforms, and for long-term forecasts the BVAR-d is the more sensible choice.

5.3 Forecast Error Variance Decomposition

From the previous section, it followed that neither the BVECM nor the BVAR-d exhibited a clear advantage in terms of forecasting accuracy. Therefore, this subsection dives deeper into the differences between the BVECM and the BVAR-d. This exercise aims to provide a better understanding of what drives both models. In particular, we are interested in how much the models’ variables explain the variability of house prices over time. We formally assess each variable’s contribution by analyzing the effect of shocks in the models’ variables. This exercise is called a forecast error variance decomposition (FEVD), and it essentially reflects how important a shock is in explaining the variations of the variables in the model.³¹

Figure 3 reflects the FEVD of house prices for the BVECM and the BVAR-d. Up to one year ahead, the two subfigures are comparable. That is, variations in house prices are mainly determined by their past value. Thereafter, for the BVECM, the borrowing capacity of constrained households takes up a significant part of the explanation of house prices. Or, phrased differently, the error correction term gradually kicks in. For the BVAR-d this is not the case, this model mainly depends on variations in house prices. In particular, for the BVAR-d for forecasts ten years ahead, 90% of the variation in house prices comes from shocks in house prices, while this is only 70% for the BVECM. Thence, the BVAR-d resembles a simple autoregressive model that predicts that house prices tomorrow are merely explained by house prices today. The BVECM, on the other hand, incorporates an equilibrium relationship that includes the effect of changes in the borrowing capacity on house prices.

Fig. 3

Forecast error variance decomposition of house prices

5.4 Forecasting Power Along the House Price Cycle

Having a better understanding of the differences between the BVAR-d and the BVECM, we finally assess how well both perform during different economic seasons. Or, phrased differently, we compare the forecasting accuracy of the winning models over the house price cycle. This analysis is performed as forecasters might be more interested in predicting the timing of peaks and troughs (i.e., turning points) rather than the aggregated performance of a model over the boom-bust cycle (i.e., Sect. 5.2).

Nevertheless, since house prices experienced at most two turning points during the out-of-sample period, we do not attempt a formal analysis of the competing models’ ability to predict turning points. Instead, Our primary objective is to compare the forecasting accuracy of the models throughout the house price cycle. In particular, for this exercise, four different forecasting horizons are considered: one quarter ahead, half a year ahead, one year ahead, and two years ahead. We stop at two-years-ahead forecasts as predicting turning points is a difficult matter, and consequently, one can simply not expect a model to predict a turning point that lies more than two years ahead. Subsequently, these predictions are plotted against their actual outcomes to assess which model performs best when.

The first panel of Fig. 4 shows the results for one-quarter-ahead forecasts. Differences between the BVECM and BVAR-d are small. For the BVECM we see, however, slightly more outliers than for the BVAR-d. This is true over the entire sample and is not concentrated at a specific event or economic season, indicating the BVAR-d is the preferable option for one-quarter-ahead forecasts.

For half-a-year-ahead forecasts, the results are similar, but the differences between the BVECM and the BVAR-d are slightly larger. The BVAR-d seems to be better equipped to predict the temporary revival of house prices after the financial crisis (i.e., 2009). The BVECM, on the other hand, performs slightly better in the period of fast-rising house prices of 2015–2020. The latter is most likely the case as house prices increased rapidly in that period due to decreases in the interest rate. The lower interest rate increased households’ borrowing capacity ($b_{t}^{\max, \, c} \& \, b_{t}^{cd, \, u}$) and this allowed them to buy a more expensive home; as such, these house price increases are explained by their fundamentals (i.e., the long-run relationships). This equilibrium mechanism is incorporated in the BVECM, while the BVAR-d fails to disentangle speculative price movements from these founded price movements.

For one- and two-years-ahead forecasts, the differences between the models become even more apparent. From the two subfigures, it still follows that the BVECM exaggerated the bust caused by the financial recession. Strikingly, however, the revival of the housing market in 2014, is better captured by the BVECM than by the BVAR-d. The BVECM namely correctly pointed to a price increase in 2014, while the BVAR-d still predicted a decrease. In fact, the BVECM was able to predict the exact timing of this turning point. Thus, during a crisis, a BVAR-d may be more appropriate, while the BVECM might provide more accurate predictions after the crisis.

Fig. 4

Pseudo out-of-sample forecasts and actual house prices

6 Conclusion

This study investigated five empirical methods to predict house prices in the Netherlands. In particular, OLS-based estimation methods were compared to their Bayesian counterparts. The Bayesian models were expected to outperform, as they are able to tackle overfitting problems. Our findings substantiate this hypothesis: Bayesian models have a better forecasting performance compared to the OLS models. Notably, this finding was observed for the relatively parsimonious three-variable model, indicating that overfitting can occur even with a small number of variables. Therefore, when predicting house prices, it might be wise to opt for Bayesian models, particularly when the sample is relatively small and/or the model contains many parameters.

Within the class of Bayesian models, we compared three variants: a BVAR in levels, a BVAR in differences, and a BVECM. While the BVAR in levels is commonly utilized in the housing literature, it becomes apparent that the BVAR in differences consistently exhibits better performance than the BVAR in levels. As for the remaining models, namely the BVAR in differences and the BVECM, the results are less clear-cut. Which model performs best in terms of forecasting accuracy seems to depend on two things: (i) the forecasting horizon, and (ii) the economic season. The BVECM incorporates long-run relationships and this seems to be particularly beneficial for medium-term forecasts. However, in periods of market uncertainty, such as during a recession, incorporating these long-run equilibrium relationships might not provide as much insightful information. Instead, a more useful approach could involve predicting that tomorrow will likely resemble today. Incorporating long-run equilibrium relationships seems, however, especially valuable if one seeks to predict when the recession will end, or to forecast house prices in normal times (i.e., post-crisis). Therefore, a researcher interested in predicting house prices might consider applying both Bayesian models and carefully assess the models’ forecasting results in light of the current economic state and the desired forecasting horizon.

Nonetheless, it is important to acknowledge that while our study sheds light on the relative performance of these Bayesian models, the practical applicability of such models during crisis periods should be approached with caution. The lack of reliable prior information during crises and the potential for rapid and unforeseen changes in economic conditions could impact the models’ forecasting performance. Future research could explore alternative modeling approaches (e.g., regime-switching models) to better adapt to sudden economic shocks and identify optimal forecasting strategies during crisis periods.

Furthermore, it is essential to emphasize that this paper solely focuses on the Dutch housing market. In the Netherlands, mortgage debt is substantial, rendering mortgage conditions pivotal in determining house prices. Therefore, the long-term relationship used in the (B)VECM incorporates this insight. Our results support this equilibrium; in the short-run house prices are mainly driven by their lagged value, yet, this effect slowly fades away and the borrowing capacities take up a part of explaining house prices. Nevertheless, it is important to acknowledge that in countries where a greater share of properties are purchased outright or with minimal mortgage financing, the impact of mortgage conditions on house prices might be limited. For such contexts, integrating an alternate long-term relationship into a BVECM—potentially one based on wealth—could offer more insight. However, further research is necessary to delve into this subject.

Appendices

Appendix 1. Forecasting Errors

Table 4 shows the forecasting errors as presented in Fig. 2. Each row represents a different forecasting horizon, expressed in quarterly intervals. While not displayed in Fig. 2, the column labeled “RW" showcases the forecasting errors for a random walk model with drift. This random walk model serves as a baseline or reference point for evaluating the effectiveness of more complex forecasting models.

The column labeled “Min" indicates the model with the smallest forecasting error. As highlighted in the main text, the winning model is consistently either the BVAR-d or the BVECM. To test the differences in forecasting performance between the BVECM and BVAR-d, the “DM" column presents the results of the Diebold-Mariano test for absolute forecasting errors using Newey-West errors (Diebold & Mariano, 1995). The null hypothesis posits that the two models exhibit equivalent forecasting accuracy, while the alternative hypothesis suggests differences in their forecasting accuracies.

Table 4 Pseudo out-of-sample forecasting error

Appendix 2. The Combination Prior

Doan et al. (1984) and Sims (1993) suggested supplementing the Minnesota prior of a BVAR-l with additional priors that favor unit roots and cointegration. These additional priors are respectively known as the “sum-of-coefficients" and “dummy-initial-observation" prior and they were motivated by the desire to prevent an overly large share of the variation in the data from being explained by the deterministic component.

In the literature, it is common practice to combine the Minnesota prior with the sum-of-coefficients prior and the dummy-initial-observation prior, which is known as the “combination prior" (Giannone et al., 2015). Since this combination prior aligns with the common belief that macroeconomic data often exhibit unit roots and cointegration, it tends to improve the forecasting accuracy of a BVAR-l.

In the remaining part of this section, a model with combination prior, as proposed by Giannone et al. (2015), is estimated and compared to the forecasting results of the two winning Bayesian models, namely the BVAR-d and BVECM. When comparing the forecasting results of the model with the combination prior to those of the BVECM and BVAR-d, we find that their forecasting accuracy is highly similar for forecasts up to one year ahead See Fig. 5. However, in two instances, the combination prior demonstrates a slight advantage in forecasting power compared to the other models. Nevertheless, it is important to note that, as per the DM-test, this advantage does not translate into significantly better predictions in these cases. As we extend the forecasting horizon, the performance of the model with the combination prior deteriorates, and both the BVECM and BVAR-d significantly outperform it. Therefore, for this forecasting exercise, a model with a combination prior provides little improvement compared to a BVAR-d and/or BVECM.

Fig. 5

Pseudo out-of-sample forecasting error, combination prior

Appendix 3. Priors for the Long Run

According to Giannone et al. (2019), the BVECM specification used in the main text is too restrictive. The authors state that this model is not flexible enough as in practice it is difficult to identify whether data are stationary or integrated. The authors include these insights into the so-called “prior for the long run” (PLR). This model can be thought of as a BVAR which includes the BVECM specification as a special case.³² Unlike the BVECM, the PLR includes all potential long-run relationships and does not exclude any potentially non-stationary long-run relationships. However, the PLR utilizes economic theory to assign higher weights to more plausible long-run relationships and lower weights to less plausible relationships.

In this section, the forecasting performance of a PLR is compared with the two winning Bayesian models: the BVAR-d and BVECM.³³ From Fig. 6, it is evident that up until a 2.5-year forecasting horizon, the forecasting performance of the models is comparable. However, in five instances, the PLR demonstrates a slight advantage in forecasting power compared to the other models. Nevertheless, it is important to note that, as per the DM-test, this advantage does not translate into significantly better predictions in these five cases. As we extend the forecasting horizon, an interesting shift occurs. The PLR model begins to underperform significantly when compared to the BVECM and the BVAR-d. Thus, compared to the BVECM and the BVAR-d, the PLR yields little improvement. Therefore, one might argue that, in this case, it would be wiser to rely on a BVAR-d and a BVECM for forecasting house prices instead of combining them into one model (i.e., the PLR).

Fig. 6

Pseudo out-of-sample forecasting error, PLR