International Cooperation and Kantian Moral Behaviour: Complements or Substitutes?

Abstract

Faced with a global emissions problem such as climate change, we know that if countries’ emissions decisions are made in an independent and self-interested fashion the outcome can be very far from optimal. One proposed solution is to have countries enter international environmental agreements (IEAs) whereby individual countries’ emissions decisions are taken in the interests of all the participating countries and so reflect a degree of altruism. However, if the decision to co-operate is made in a self-interested fashion the standard non-cooperative model of IEAs yields the pessimistic conclusion that the more serious the environmental problem the smaller will be the equilibrium membership of an IEA. Our paper examines the implications for emissions, IEA membership and welfare of assuming that countries make both emissions and IEA membership decisions in the alternative moral fashion of acting as imperfect Kantians as defined by Alger and Weibull (Econometrica 81:2269–2302, 2013). We show that (i) the first-best can be achieved when countries either act as Perfect Kantians or by fully cooperating; (ii) in a more imperfect setting, these two forms of moral behaviour are complementary approaches to improving welfare outcomes in the sense that the greater the weights on Kantian behaviour the larger is the equilibrium coalition; (iii) the weights on Kantian behaviour that will induce full cooperation and hence the first-best are significantly less than 1; (iv) for given Kantian weights, our model generates higher equilibrium IEA membership, lower emissions and higher welfare than in the related paper by Eichner and Pethig (International environmental agreements when countries behave morally) which, we argue, does not fully capture the benefits of membership decisions.

1 Introduction

Climate scientists predict that with high probability there will be potentially catastrophic damage unless global emissions of greenhouse gases are rapidly reduced to net zero emissions per annum by 2050 (UNEP 2019). Economists emphasise that, in the absence of a global government, the global externality nature of the problem means that individual countries acting independently and in a purely self-interested fashion will make significantly smaller reductions in emissions than those required to achieve the global optimum. In this context pure self -interest means that (i) a country cares only about the welfare of its own citizens; (ii) it chooses the action that maximise this welfare treating the decisions of all other countries as given.

A long-standing proposal for addressing this problem has been the creation of an international environmental agreement (IEA) whereby countries act in a cooperative fashion and agree to set their individual emissions to achieve the best collective outcome for all participating countries. By making emissions decisions in this way countries are acting neither independently nor in the first sense of self-interest, so, in that sense, could be said to be acting more morally with regard to their emissions decisions. Indeed, it is well known that if all countries were to enter such an agreement, then the global optimum could be achieved since countries would be effectively internalising the externality.¹

The problem arises if countries make the decision to join an IEA in a self-interested fashion.² For then the workhorse two-stage non-cooperative game model,³ yields the pessimistic conclusion that the more serious is the environmental problem, (i.e. the greater is the gap between the non-cooperative and the fully cooperative outcomes) the smaller will be the size of a stable IEA. The intuition is that, for any membership size, fringe countries are always better off than coalition countries, and, the more serious is the environmental problem, the larger are the gains to fringe countries from free-riding on the emissions reductions of IEA members.⁴

There have been two approaches to obviating this pessimistic conclusion. The first explores richer forms of cooperative behaviour with respect to membership decisions. Chander and Tulkens (1997) study the γ-core, while de Zeeuw (2008), Diamantoudi and Sartzetakis (2015, 2018) study farsighted equilibria. Under both approaches it is possible to attain the social optimum.

The second approach continues to employ a non-cooperative Nash equilibrium to study membership decisions, but assumes that countries do not pursue their own self-interest but act in a moral fashion when making both their membership and emissions decisions.

A number of papers have studied how different forms of moral behaviour might allow IEAs to achieve better outcomes—in some cases the grand coalition. Specific forms of moral behaviour affecting IEAs include: modesty (Finus and Maus 2008); preference for equity (Lange and Vogt 2003; Vogt 2016; Rogna and Vogt 2020); altruism (van der Pol et al. 2012), reciprocity (Nyborg 2018; Bucholz et al. 2018). Much of the evidence for these forms of moral behaviour stem from social surveys or laboratory experiments.

However, this literature raises the question: which of these forms of moral behaviour is appropriate. We draw on the work of Alger and Weibull (2013, 2016, 2020) which demonstrates that imperfect Kantian behaviour is the only evolutionary stable form of moral behaviour. In this paper, we study non-cooperative IEAs when countries adopt this form of moral reasoning to both their emissions and their IEA membership decisions. An agent acting in an imperfect Kantian fashion gives a weight, $\upkappa , 0\le \upkappa \le 1$, to the Kantian categorical imperative⁵ (Kant 1785) to “act only according to that maxim through which you can at the same time will that it become a universal law”,⁶ which we call acting as a perfect Kantian, and the weight (1 − $\upkappa$) to acting in a self-interested fashion. With one exception which we mention below, this approach has not so far been studied in the context of IEAs.

To understand how outcomes in terms of emissions and welfare might depend on whether it is the emissions or IEA membership decision to which this calculus is applied we adopt the general approach of allowing countries to apply different Kantians weights to each type of decision. So ${\upkappa }_{\varepsilon }, 0\le {\upkappa }_{\varepsilon } \le 1$ (resp.${\upkappa }_{\mu }, 0\le {\upkappa }_{\mu } \le 1$) denotes the Kantian weight to the emissions (resp. membership) decision.

We are interested in the question of whether moral behaviour in the form of (imperfect) Kantian behaviour is a substitute or complement for co-operative behaviour. To address this question, we start with the second (emissions) stage of the game and analyse how equilibrium emissions of a coalition country, a fringe country, and an ‘average country’ vary with respect to the size of the coalition and the Kantian weight on emissions. We show that, if countries act as perfect Kantians, then, whatever the size of the coalition, the first-best is achieved, while, if there is full cooperation (the grand coalition) then, whatever the Kantian weight on emissions, once again, the first-best is achieved. In that sense they are substitute forms of behaviour. More generally we would expect average equilibrium emissions to decline with respect to both factors, and, we show that this is the case, albeit using specific functional forms.⁷

Turning to the first (membership) stage of the game we examine what values of the Kantian weights on emissions and membership will enable the grand coalition—and hence first-best to be achieved. We show that this can arise with Kantian weights that are positive but significantly less than one. So, in that sense, a Kantian form of behaviour promotes co-operation, so the two types of behaviour are complements.⁸

Our paper relates to the recent paper by Eichner and Pethig (2022). However, it differs in a number of respects. First, we explicitly capture the idea that coalition members have as their objective the total welfare of the coalition—and so are not self-interested in the first sense. Second, we employ the imperfect Kantian approach to the membership and emissions decisions in a nested fashion which allows each stage to be modelled using the binary imperfect Kantian payoff function derived by Alger and Weibull (2013, 2016, 2020). Thus, at Stage 1 countries make their membership decisions in an imperfect Kantian fashion, recognising that at Stage 2 both coalition and fringe countries will make their emissions decisions in an imperfect Kantian fashion.⁹

Given these differences in approach, we show that for the same values of Kantian weights, (a) our model results in higher equilibrium coalition membership and global welfare and lower equilibrium emissions than the model of Eichner and Pethig (2022); (b) consequently the grand coalition, and hence the first-best outcome, can be achieved with lower Kantian weights than in Eichner and Pethig (2022).

The structure of the paper is as follows. Section 2 presents the theoretical analysis. We first set out our basic model, some key benchmark equilibria, and then we analyse the non-cooperative equilibrium with Kantian behaviour. We then analyse our model of IEAs with imperfect Kantian behaviour. To complete this theoretical section, we briefly set out the model of Eichner and Pethig (2022), and show how it differs from our model. In Sect. 3 we study the special case of quadratic benefit function and damage cost functions. Our reason for using a quadratic damage cost function rather than the linear damage cost function used by Eichner and Pethig (2022) is that it allows marginal damage costs to rise with emissions, which better captures the serious risks associated with increasing emissions of gases linked to climate change. We first study the outcomes of our model and analyse the extent to which acting in a Kantian fashion and seeking to form an IEA are complements, and then compare the results from our general model with those derived from Eichner and Pethig (2022). Section 4 concludes with suggestions for further work.

2 Theoretical Results

There are n > 3 identical countries, $i\in N, N=\{1,\dots ,n\}$, where n is a large number. We denote by ${\text{e}}_{i}$ the level of emissions of country i of a global pollutant, such as greenhouse gases, and ${{\text{e}}}=({\text{e}}_{1},\dots {\text{e}}_{i},\dots {\text{e}}_{n})$ the vector of emissions by all countries. The associated level of welfare of country i is:

$${W}_{i}\left({\varvec{e}}\right)\equiv B\left({e}_{i}\right)-D\left[\sum_{j\in N}{e}_{j}\right].$$

(1)

B(e_i) is the level of net benefit (excluding environmental damages) country i derives from whatever production and consumption decisions give rise to its emissions e_i, and $D({\sum }_{j\in N}{e}_{j})$ is the level of damage costs it incurs from global emissions, ${\sum }_{j\in N}{e}_{j}$. We make the standard assumptions that $B\left(0\right)\ge 0, {B}^{\prime}\left(.\right)>0, {B}^{\prime \prime}\left(.\right)<0;\, D\left(0\right)=0,{D}^{\prime}\left(.\right)>0, {D}^{\prime \prime}(.)\ge 0$.

We begin by characterising three benchmark outcomes. The first-best, or social optimum, (which we denote by the suffix SO) is achieved when the emissions of each country’s emissions, ${e}_{i}^{SO}$, are chosen to maximise total welfare ${\sum }_{j\in N}{W}_{j}({\varvec{e}})$, giving rise to f.o.c.:

$${B}^{\prime}\left({e}_{i}^{SO}\right)=\sum_{j\in N}{D}^{\prime}\left(\sum_{k\in N}{e}_{k}^{SO}\right), i\in N$$

(2a)

Imposing symmetry, ${e}_{i}^{SO}={e}^{SO} \forall i$, where:

$${B}^{\prime}\left({e}^{SO}\right)=n{D}^{\prime}\left(n{e}^{SO}\right).$$

(2b)

The resulting common first-best, or socially-optimal, welfare is:

$${W}^{SO}=B\left({e}^{SO}\right)-D\left(n{e}^{SO}\right).$$

(2c)

If countries act in a fully-cooperative fashion (which we denote by the suffix FC) whereby each country chooses the emissions that would maximise total welfare of all countries, it is clear that, in our symmetric model, the fully-cooperative level of emissions for a country, ${e}^{FC}$, is identical to the social optimum, ${e}^{FC}={e}^{SO}$, with resulting welfare ${W}^{FC}={W}^{SO}$.

Finally, in the standard non-cooperative equilibrium (which we denote by the suffix NC), each country acts in a self-interested fashion and chooses its emissions to maximise its own welfare, taking as given the emissions of other countries. The resulting non-cooperative equilibrium emissions, ${e}_{i}^{NC}, i\in N$, satisfy:

$${B}^{\prime}\left({e}_{i}^{NC}\right)={D}^{\prime}\left(\sum_{j}{e}_{j}^{NC}\right), i\in N$$

(3a)

Imposing symmetry, ${e}_{i}^{NC}={e}^{NC}, i\in N$, yields:

$${B}^{\prime}\left({e}^{NC}\right)={D}^{\prime}(n{e}^{NC})$$

(3b)

with resulting non-cooperative welfare:

$${W}^{NC}=B\left({e}^{NC}\right)-D(n{e}^{NC})$$

(3c)

Given our assumptions, it is clear that ${e}^{NC}>{e}^{SO}, {W}^{NC}<{W}^{SO}$. Since we intend our analysis to apply to challenging global environmental issues such as climate change, we assume that these differences are large.

We now turn to the issue of how far the gaps in emissions and welfare between the non-cooperative equilibrium and the social optimum, i.e.$\left({e}^{NC}-{e}^{SO}\right), ( {W}^{SO-}{W}^{NC})$ might be closed by countries (a) acting in a more moral (Kantian) fashion; (b) seeking to form an IEA; (c) doing both.

2.1 Non-Cooperative Equilibrium When Countries Act in an Imperfect Kantian Fashion

In this equilibrium the only variable countries set is emissions. Following Alger and Weibull (2013, 2016, 2020), we denote by ${\upkappa }_{\varepsilon }, 0 \le {\upkappa }_{\varepsilon }\le 1$ the weight a country attaches to the payoff it would get if it acted as a perfect Kantian and a weight (1–${\upkappa }_{\varepsilon }$) to the payoff it would get if it acted in a self-interested fashion. A perfect Kantian (${\upkappa }_{\varepsilon }$ = 1) country i, acting non-cooperatively, asks what emissions it should set, on the Kantian hypothesis that all other countries choose the same level of emissions as it. Thus, the behaviour of a perfect Kantian country i acting non-cooperatively (which we denote by the suffix PKNC) can be characterised by saying it acts to maximise the perfect Kantian payoff function:

$${\Pi }_{i}^{PKNC}\left({\varvec{e}};1\right)=B\left({e}_{i}\right)-D\left(\sum_{j\in N}{e}_{i}\right)=B\left({e}_{i}\right)-D\left(n{e}_{i}\right).$$

(4)

However, just as it is unrealistic that independent countries would act in a fully cooperative fashion, it is also unrealistic to assume that countries act as perfect Kantians. Therefore, we explore the implications of having countries act non-cooperatively, but as imperfect Kantians. An imperfect Kantian country i seeks to maximise its non-cooperative imperfect Kantian payoff function:

$$ \begin{aligned} {\Pi }_{i}^{IKNC} \left( {{\varvec{e}};\upkappa_{\varepsilon } } \right) & = \upkappa_{\varepsilon } \left[ {B\left( {e_{i} } \right) - D\left( {\mathop \sum \limits_{j \in N} e_{i} } \right)} \right] + \left( {1 - \upkappa_{\varepsilon } } \right)\left\{ {B\left( {e_{i} } \right) - D\left[ {e_{i} + \mathop \sum \limits_{j \in N,j \ne i} e_{j} } \right]} \right\} \\ & = B\left( {e_{i} } \right) - \upkappa_{\varepsilon } D\left( {ne_{i} } \right) - \left( {1 - \upkappa_{\varepsilon } } \right)D\left[ {e_{i} + \mathop \sum \limits_{j \in N,j \ne i} e_{j} } \right] \\ \end{aligned} $$

(5a)

We emphasise that while the imperfect Kantian payoff function is used to characterise the behaviour of countries acting in an imperfect Kantian fashion, we will continue to assess the well-being of countries using their welfare functions defined in (1).

We denote the resulting equilibrium emissions by ${e}_{i}^{IKNC}({\upkappa }_{\varepsilon })$ which satisfies

$$ \begin{aligned} B^{\prime}\left[ {e_{i}^{IKNC} \left( {\upkappa_{\varepsilon } } \right)} \right] = & \upkappa_{\varepsilon } nD^{\prime}\left[ {ne_{i}^{IKNC} \left( {\upkappa_{\varepsilon } } \right)} \right] \\ & \quad + \left( {1 - \upkappa_{\varepsilon } } \right)D^{\prime}[e_{i}^{IKNC} \left( {\upkappa_{\varepsilon } } \right) + \mathop \sum \limits_{j \in N,j \ne i} e_{j}^{IKNC} \left( {\upkappa_{\varepsilon } } \right)] \forall i \\ \end{aligned} $$

(5b)

Imposing symmetry, the non-cooperative imperfect Kantian equilibrium level of emissions, which we denote ${e}^{IKNC}({\upkappa }_{\varepsilon })$, solves

$${B}^{\prime}\left[{e}^{IKNC}\left({\upkappa }_{\varepsilon }\right)\right]=\left[n{\upkappa }_{\varepsilon }+\left(1-{\upkappa }_{\varepsilon }\right)\right]{D}^{\prime}[n{e}^{IKNC}\left({\upkappa }_{\varepsilon }\right)]$$

(5c)

with the resulting imperfect Kantian non-cooperative equilibrium payoff and welfare, which we denote by ${\Pi }^{IKNC}\left({\upkappa }_{\varepsilon }\right), {W}^{IKNC}({\upkappa }_{\varepsilon })$ respectively:

$${\Pi }^{IKNC}\left({\upkappa }_{\varepsilon }\right)={W}^{IKNC}\left({\upkappa }_{\varepsilon }\right)=B\left[{e}^{IKNC}\left({\upkappa }_{\varepsilon }\right)\right]-D[n{e}^{IKNC}\left({\upkappa }_{\varepsilon }\right)]$$

(5d)

It is clear from (5c) that a country acting as a perfect Kantian would choose emissions ${e}^{IKNC}\left(1\right)={e}^{SO}$, while a country acting as a non-Kantian would choose emissions ${e}^{IKNC}\left(0\right)={e}^{NC}$. So, the first best can be achieved either by having all countries act in a fully cooperative fashion in setting emissions, or by having all countries acting non-cooperatively but as perfect Kantians. If countries are perfect Kantians, there is no need to try to form an IEA: seeking to get countries to act morally, as perfect Kantians, is a substitute to seeking to get all countries to join an IEA as an approach for tackling climate change.

Remark 1.

In the imperfect Kantian non-cooperative equilibrium, as ${\upkappa }_{\varepsilon }$ increases from 0 to 1,

• (i) ${{\text{e}}}^{{\text{IKNC}}}({\upkappa }_{\upvarepsilon })$ falls from the conventional non-Kantian non-cooperative level of emissions (${{\text{e}}}^{{\text{IKNC}}}\left(0\right)={{\text{e}}}^{{\text{NC}}})$ to the social optimum level of emissions (${{\text{e}}}^{{\text{IKNC}}}\left(1\right)={{\text{e}}}^{{\text{FC}}}={{\text{e}}}^{{\text{SO}}})$;

• (ii) the imperfect Kantian payoff and welfare, ${\Pi }^{{\text{IKNC}}}\left({\upkappa }_{\upvarepsilon }\right)={{\text{W}}}^{{\text{IKNC}}}\left({\upkappa }_{\upvarepsilon }\right)$, increases from the non-cooperative level (${\Pi }^{{\text{IKNC}}}\left(0\right)={{\text{W}}}^{{\text{IKIK}}}\left(0\right)={{\text{W}}}^{{\text{NC}}})$ to the social optimum level (${\Pi }^{{\text{IKNC}}}\left(1\right)={{\text{W}}}^{{\text{IKNC}}}\left(1\right)={{\text{W}}}^{{\text{SO}}})$.

2.2 IEAs with Imperfect Kantian Behaviour

We employ the two-stage non-cooperative model of IEAs, stemming from Carraro and Siniscalco (1993), Barrett (1994), in which Stage 1 solves for the equilibrium membership of a coalition or fringe while Stage 2 solves for equilibrium emissions for any possible membership. We denote by C (F), the set of countries which belong to the coalition (fringe) respectively in Stage 2, where $C\cup F=N$, and by ${C}_{-i} \left({F}_{-i}\right)$ the set of countries belonging to the coalition (fringe) excluding country i. For the case of identical countries, we denote by m the number of countries in the coalition, so, n–m is the number of countries in the fringe; if m = n, all countries are in the coalition, while if m = 1 all countries are in the fringe.

Before introducing our analysis of imperfect Kantian analysis of IEAs, we summarise the standard (non-Kantian) model when countries act in a self-interested, non-Kantian fashion (denoted NKIEA). In Stage 2, for any coalition of size, m, standard first-order conditions determine equilibrium Stage 2 emissions of a typical coalition and fringe country, ${\text{e}}_{i}^{NKIEA}\left(m\right), i=c,f$, and hence equilibrium Stage 2 payoffs:

$${W}_{i}^{NKIEA}\left(m\right)=B\left({\text{e}}^{i}\right)-D\left[m{\text{e}}^{c}\left(m\right)+\left(n-m\right){\text{e}}^{f}\left(m\right)\right] i=c.f$$

(6)

In Stage 1, the stability function $\sigma \left(m\right)={W}^{c}\left(m\right)-{W}^{f}\left(m-1\right), m=2,...,m$ is used to determine equilibrium membership, denoted ${m}^{NKIEA}$, satisfying $\sigma \left({m}^{NKIEA}\right)\ge 0, \sigma \left({m}^{NKIEA}+1\right)<0$, i.e.. no coalition country wishes to leave the coalition and no fringe country wishes to join. As we noted in Sect. 1, it is well known that, for a wide class of functional forms for benefit and damage cost functions, when countries act in a self-interested manner, we get the pessimistic conclusion that, because of the free-rider benefits accruing to fringe countries, the size of the stable IEA, is small.¹⁰ Applying this conclusion to problems like climate change involving a large number of countries, may seem to support the argument of Nowakowski and Oswald (2020) that environmental economists’ focus on how to secure an IEA to tackle climate change, rather than on changing individuals’ behaviour, may be misplaced.

Our model of IEAs with imperfect Kantian behaviour (which we denote by the suffix IKIEA) has two key features. First, we employ the imperfect Kantian approach to the membership and emissions decisions in a nested fashion which allows each stage to be modelled using the binary imperfect Kantian payoff function derived by Alger and Weibull (2013, 2016, 2020). By this we mean that, at Stage 1, countries make their membership decisions in an imperfect Kantian fashion with Kantian weight ${\upkappa }_{\mu }$, 0 ≤ κ_μ ≤ 1, recognising that at Stage 2 they will make their emissions decisions in an imperfect Kantian fashion with Kantian weight ${\upkappa }_{\varepsilon , } 0\le {\upkappa }_{\varepsilon }\le 1$¹¹The second key feature of our model concerns membership decisions, in which a coalition (fringe) country, acting as a perfect Kantian, assumes that all other countries make the same membership decision and choose the appropriate emissions for that assumption. By appropriate we mean that they take account of what they hypothesise about membership and the Kantian weight on emissions.

We now set out the payoff functions for coalition and fringe countries. It follows from the previous paragraph that it is necessary to distinguish between two sets of emission decisions, reflecting the difference between acting as imperfect Kantians with respect to emissions and with respect to membership. We denote by ${\text{e}}_{i}^{\varepsilon }$ the emissions of country i in the emissions game, and by ${\text{e}}_{i}^{\mu }$ the emissions country i would set in the membership game when it assumes that, hypothetically, all other countries have made the same membership decision. Although we distinguish between two sets of emissions, we note shortly that, in equilibrium, countries emit only one level of emissions which depends on the equilibrium membership. The payoff function is:

$$ \begin{aligned} {\Pi }_{i}^{IKIEA} \left( {{{\text{e}}}^{\varepsilon } ,{{\text{e}}}^{\mu } ;\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) & = \upkappa_{\mu } \{ \upkappa_{\varepsilon } [B\left( {{\text{e}}_{i}^{\mu } } \right) - D(\mathop \sum \limits_{j \in N} {\text{e}}_{i}^{\mu } )] + \left( {1 - \upkappa_{\varepsilon } } \right)[B\left( {{\text{e}}_{i}^{\mu } } \right) - D(\mathop \sum \limits_{j \in N} {\text{e}}_{j}^{\mu } )]\} \\ & \quad + \left( {1 - \upkappa_{\mu } } \right)\left\{ {\upkappa_{\varepsilon } [B\left( {{\text{e}}_{i}^{\varepsilon } } \right) - D(\mathop \sum \limits_{j \in N} {\text{e}}_{i}^{\varepsilon } )]} \right. \\ & \quad \left. { + \left( {1 - \upkappa_{\varepsilon } } \right)[B\left( {{\text{e}}_{i}^{\varepsilon } } \right) - D(\mathop \sum \limits_{j \in C} {\text{e}}_{i}^{\varepsilon } + \mathop \sum \limits_{k \in F} {\text{e}}_{k}^{\varepsilon } )]} \right\} i \in N \\ \end{aligned} $$

(7)

In (7), the two terms in the first curly brackets are the payoffs country i receives if it acts as a perfect Kantian with respect to membership, so assumes all other countries have made the same membership decision as country i. The first of these two terms, with weight ${\upkappa }_{\varepsilon }$, is the payoff it receives if it acts as a perfect Kantian with respect to emissions, while the second term, with weight $1-{\upkappa }_{\varepsilon }$, is the payoff it receives if it chooses emissions in a non-Kantian fashion. The two terms in the second curly bracket are the payoffs it receives if it acts as a non-Kantian with respect to membership. The first of these two terms, with weight ${\upkappa }_{\varepsilon }$, is the payoff it receives if it acts as a perfect Kantian with respect to emissions. The second term, with weight $1-{\upkappa }_{\varepsilon }$ is just the payoff country i would receive in the standard non-cooperative game with self-interested countries, depending whether it is in set C or set F. We note here that when countries act as imperfect Kantians with respect to emissions only, so κ_μ = 0, our model is identical to that used by Eichner and Pethig (2022), so the difference between our approaches is how we treat imperfect Kantian behaviour with respect to membership.

We now solve the game.

2.2.1 Stage 2-Equilibrium Emissions

We solve for equilibrium Stage 2 emissions, denoted by ${\widetilde{\text{e}}}_{\mu }^{i}(m;{\upkappa }_{\varepsilon }, {\upkappa }_{\mu })$, where i = c (f) denotes a typical coalition (fringe) country, m = 1,…,n denotes the size of coalition, and ${\upkappa }_{\varepsilon }$ (${\upkappa }_{\mu }$) denotes the value of the Kantian weight on emissions (membership).

We solve first for the equilibrium emissions, for any value of m, when countries act as perfect Kantians with respect to membership, so ${\upkappa }_{\mu }=1$. From (7), a coalition country i takes as given ${\text{e}}_{j}^{\mu }, j\ne i$, and chooses ${\text{e}}_{i}^{\mu }$ to maximise:

$$ \begin{gathered} \upkappa_{\varepsilon } \left\{ {B\left( {e_{i}^{\mu } } \right) - D\left( {ne_{i}^{\mu } } \right) + \mathop \sum \limits_{{j \in N_{ - i} }} \left[ {B\left( {e_{j}^{\mu } } \right) - D\left( {ne_{j}^{\mu } } \right)} \right]} \right\} \hfill \\ + \left( {1 - \upkappa_{\varepsilon } } \right)\left\{ {\mathop \sum \limits_{j \in N} [B\left( {e_{j}^{\mu } } \right) - D(\mathop \sum \limits_{k \in N} e_{k}^{\mu } )]} \right\}\;\;\; i \in C \hfill \\ \end{gathered} $$

(8a)

for which the first-order condition is:

$$ B^{\prime}\left( {e_{i}^{\mu } } \right) = \upkappa_{\varepsilon } nD^{\prime}\left( {ne_{i}^{\mu } } \right) + \left( {1 - \upkappa_{\varepsilon } } \right)\mathop \sum \limits_{j \in N} D^{\prime}(\mathop \sum \limits_{k \in N} e_{k}^{\mu } ) i \in C $$

(8b)

Imposing symmetry, equilibrium coalition emissions, ${\widetilde{\text{e}}}_{\mu }^{c}={\widetilde{{\text{e}}}}_{\mu }^{c}\left(m;{\upkappa }_{\varepsilon },1\right),$ solves:

$$ B^{\prime}\left( {\tilde{\text{e}}_{\mu }^{c} } \right) = nD^{\prime}\left( {n\tilde{\text{e}}_{\mu }^{c} } \right) \Rightarrow \tilde{\text{e}}_{\mu }^{c} = e^{SO} i \in C $$

(8c)

As we noted at the start of Sect. 2, when, for any actual coalition membership m = 2,…,n, a coalition country acting as a perfect Kantian with respect to membership, sets ${\widetilde{\text{e}}}_{\mu }^{c}\left(m;{\upkappa }_{\varepsilon },1\right),={\widetilde{\text{e}}}_{\mu }^{c}\left(n;{\upkappa }_{\varepsilon },1\right)$ = ${\text{e}}^{SO}$, the socially optimal (fully cooperative) level of emissions, irrespective of the Kantian weight on emissions.

A fringe country takes as given ${\text{e}}_{j}^{\mu }, j\ne i$, and chooses ${\text{e}}_{i}^{\mu }$ to maximise:

$$ \upkappa_{\varepsilon } [B\left( {e_{i}^{\mu } } \right) - D\left( {ne_{i}^{\mu } } \right)\left] { + \left( {1 - \upkappa_{\varepsilon } } \right)} \right[B\left( {e_{i}^{\mu } } \right) - D(\mathop \sum \limits_{j \in N} e_{j}^{\mu } )] i \in F $$

(8d)

for which the first-order condition is:

$$ B^{\prime}\left( {e_{i}^{\mu } } \right) = \upkappa_{\varepsilon } nD^{\prime}\left( {ne_{i}^{\mu } } \right) + \left( {1 - \upkappa_{\varepsilon } } \right)D^{\prime}(\mathop \sum \limits_{k \in N} e_{k}^{\mu } ) i \in F $$

(8e)

Imposing symmetry, equilibrium fringe emissions, ${\widetilde{\text{e}}}_{\mu }^{f}={\widetilde{\text{e}}}_{\mu }^{f}(m;{\upkappa }_{\varepsilon },1)$ solves:

$$ B^{\prime}\left( {\tilde{\text{e}}_{\mu }^{f} } \right) = [\upkappa_{\varepsilon } n + \left( {1 - \upkappa_{\varepsilon } } \right)]D^{\prime}\left( {n\tilde{\text{e}}_{\mu }^{f} } \right) \Rightarrow \tilde{\text{e}}_{\mu }^{f} = e^{IKNC} \left( {\upkappa_{\varepsilon } } \right) $$

(8f)

As we noted in Sect. 2.1, when, for any actual coalition membership m = 1,…,n–1, a fringe country acting as a perfect Kantian with respect to membership, sets ${\widetilde{\text{e}}}_{\mu }^{f}\left(m;{\upkappa }_{\varepsilon },1\right),={\widetilde{\text{e}}}_{\mu }^{f}\left(1;{\upkappa }_{\varepsilon },1\right)$ = ${\text{e}}^{IKNC}({\upkappa }_{\varepsilon })$, the non-cooperative Kantian equilibrium with Kantian weight on emissions, ${\upkappa }_{\varepsilon }$.

We now solve for the equilibrium emissions ${\text{e}}_{i}^{\varepsilon }$, when countries act as non-Kantians with respect to membership, so ${\upkappa }_{\mu }=0$. We deal first with the case where both C and F are non-empty (i.e. 2 ≤ m ≤ n–1). From (7), a coalition country i takes as given ${\text{e}}_{j}^{\varepsilon }, j\ne i$, and chooses ${\text{e}}_{i}^{\varepsilon }$ to maximise:

$$ \begin{aligned} & \upkappa_{\varepsilon } \left\{ {B\left( {e_{i}^{\varepsilon } } \right) - D\left( {ne_{i}^{\varepsilon } } \right) + \mathop \sum \limits_{{j \in N_{ - i} }} \left[ {B\left( {e_{j}^{\varepsilon } } \right) - D\left( {ne_{j}^{\varepsilon } } \right)} \right]} \right\} \\ & \quad + \left( {1 - \upkappa_{\varepsilon } } \right)\left\{ {\mathop \sum \limits_{j \in N} [B\left( {e_{j}^{\varepsilon } } \right) - D(\mathop \sum \limits_{k \in C} e_{k}^{\varepsilon } + \mathop \sum \limits_{l \in F} e_{l}^{\varepsilon } )]} \right\}\;\;\; i \in C \\ \end{aligned} $$

(9a)

for which the first-order condition is:

$$ B^{\prime}\left( {e_{i}^{\varepsilon } } \right) = \upkappa_{\varepsilon } nD^{\prime}\left( {ne_{i}^{\varepsilon } } \right) + \left( {1 - \upkappa_{\varepsilon } } \right)\mathop \sum \limits_{j \in C} D^{\prime}(\mathop \sum \limits_{k \in C} e_{k}^{\text{e}} + \mathop \sum \limits_{l \in F} e_{l}^{\varepsilon } ) i \in C $$

(9b)

A fringe country takes as given ${\text{e}}_{j}^{\varepsilon }, j\ne i$, and chooses ${\text{e}}_{i}^{\varepsilon }$ to maximise:

$$ \upkappa_{\varepsilon } [B\left( {e_{i}^{\varepsilon } } \right) - D\left( {ne_{i}^{\varepsilon } } \right)\left] { + \left( {1 - \upkappa_{\varepsilon } } \right)} \right[B\left( {e_{i}^{\varepsilon } } \right) - D(\mathop \sum \limits_{k \in C} e_{k}^{\varepsilon } + \mathop \sum \limits_{l \in F} e_{l}^{\varepsilon } )] i \in F $$

(9c)

for which the first-order condition is:

$$ B^{\prime}\left( {e_{i}^{\varepsilon } } \right) = \upkappa_{\varepsilon } nD^{\prime}\left( {ne_{i}^{\varepsilon } } \right) + \left( {1 - \upkappa_{\varepsilon } } \right)D^{\prime}(\mathop \sum \limits_{k \in C} e_{k}^{\varepsilon } + \mathop \sum \limits_{l \in F} e_{l}^{\varepsilon } ) i \in F $$

(9d)

Imposing symmetry, equilibrium coalition and fringe emissions, ${\widetilde{\text{e}}}_{\varepsilon }^{c}\equiv {\widetilde{\text{e}}}_{\varepsilon }^{c}(n;{\upkappa }_{\varepsilon },0)$, ${\widetilde{\text{e}}}_{\varepsilon }^{f}\equiv {\widetilde{\text{e}}}_{\varepsilon }^{f}(1;{\upkappa }_{\varepsilon },0)$, solve the simultaneous equations:

$$ B^{\prime}\left( {\tilde{\text{e}}_{\varepsilon }^{c} } \right) = \upkappa_{\varepsilon } nD^{\prime}\left( {n\tilde{\text{e}}_{\varepsilon }^{c} } \right) + \left( {1 - \upkappa_{\varepsilon } } \right)mD^{\prime} \left[ {m\tilde{\text{e}}_{\varepsilon }^{c} + \left( {m - n} \right)\tilde{\text{e}}_{\varepsilon }^{f} } \right] $$

(10a)

$$ B^{\prime}\left( {\tilde{\text{e}}_{\varepsilon }^{f} } \right) = \upkappa_{\varepsilon } nD^{\prime}\left( {n\tilde{\text{e}}_{\varepsilon }^{f} } \right) + \left( {1 - \upkappa_{\varepsilon } } \right)D^{\prime} \left[ {m\tilde{\text{e}}_{\varepsilon }^{c} + \left( {m - n} \right)\tilde{\text{e}}_{\varepsilon }^{f} } \right] $$

(10b)

It is clear that, when m = n, equilibrium coalition emissions when countries act as non-Kantians with respect to membership are the same as when they act as perfect Kantians with respect to membership, i.e. ${\widetilde{\text{e}}}_{\varepsilon }^{c}\left(n;{\upkappa }_{\varepsilon },0\right)={\widetilde{\text{e}}}_{\mu }^{c}(n;{\upkappa }_{\varepsilon },1)={\text{e}}^{SO}$, the socially optimal level of emissions. Similarly, when m = 1, equilibrium fringe emissions when countries act as non-Kantians with respect to membership are the same as when they act as perfect Kantians with respect to membership, i.e. ${\widetilde{\text{e}}}_{\varepsilon }^{f}\left(1;{\upkappa }_{\varepsilon },0\right)={\widetilde{\text{e}}}_{\mu }^{f}\left({1; \upkappa }_{\varepsilon },1\right)$. So, as we noted earlier in this section, in equilibrium, the distinction between emissions related to Kantian behaviour with respect to emissions and emissions related to Kantian behaviour with respect to membership is effectively redundant. Hence, for values of m = 1,…,n, we will refer simply to equilibrium Stage 2 imperfect Kantian IEA emissions: ${\text{e}}_{c}^{IKIEA}\left(m;{\upkappa }_{\varepsilon }\right), {\text{e}}_{f}^{IKIEA}\left(m;{\upkappa }_{\varepsilon }\right)$ for coalition and fringe countries. The associated equilibrium payoff functions with respect to emissions are:

$$ \begin{aligned} & {\text{for}}\;\;m = n:\;{\Pi }_{c}^{IKIEA} \left( {n;\upkappa_{\varepsilon } } \right) = B\left[ {e_{c}^{IKIEA} \left( {n;\upkappa_{\varepsilon } } \right)} \right] - D\left[ {ne_{c}^{IKIEA} \left( {n;\upkappa_{\varepsilon } } \right)} \right] = W^{SO} ; \\ & {\text{for}}\;\;{2} \le m \le n{-}{1}:\;{\Pi }_{j}^{IKIEA} \left( {m;\upkappa_{\varepsilon } } \right) = B\left[ {e_{j}^{IKIEA} \left( . \right)} \right] - \upkappa_{\varepsilon } D\left[ {ne_{j}^{IKIEA} \left( . \right)} \right] \\ & \quad - \left( {1 - \upkappa_{\varepsilon } } \right)D\left[ {me_{c}^{IKIEA} \left( . \right) + \left( {n - m} \right)e_{f}^{IKIEA} \left( . \right)} \right],\;\;j = c, \, f; \\ & {\text{for}}\;\;m = {1}:{\Pi }_{f}^{IKIEA} \left( {1;\upkappa_{\varepsilon } } \right) = B\left[ {e_{f}^{IKIEA} \left( {1;\upkappa_{\varepsilon } } \right)} \right] - D\left[ {ne_{f}^{IKIEA} \left( {1;\upkappa_{\varepsilon } } \right)} \right] = W^{IKNC} \left( {\upkappa_{\varepsilon } } \right). \\ \end{aligned} $$

The overall equilibrium payoff functions from Stage 2 are given by:

$$ {\Pi }_{c}^{IKIEA} \left( {m;\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) = \upkappa_{\mu } {\Pi }_{c}^{IKIEA} \left( {n;\upkappa_{\varepsilon } } \right) + \left( {1 - \upkappa_{\mu } } \right){\Pi }_{c}^{IKIEA} \left( {m;\upkappa_{\varepsilon } } \right) $$

(11a)

$$ {\Pi }_{f}^{IKIEA} \left( {m;\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) = \upkappa_{\mu } {\Pi }_{f}^{IKIEA} \left( {1;\upkappa_{\varepsilon } } \right) + \left( {1 - \upkappa_{\mu } } \right){\Pi }_{f}^{IKIEA} \left( {m;\upkappa_{\varepsilon } } \right) $$

(11b)

2.2.2 Stage 1: Equilibrium Membership

We now determine, for all values of ${\upkappa }_{\varepsilon },{\upkappa }_{\mu }$, the size of the equilibrium membership, ${m}^{IKIEA}={m}^{IKIEA}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$. The stability function is:

$$ \sigma \left( {m;\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) = {\Pi }_{c}^{IKIEA} \left( {m;\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) - {\Pi }_{f}^{IKIEA} \left( {m - 1;\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) $$

(12)

A coalition of size ${m}^{IKIEA}, 2\le {m}^{IKIEA} \le n-1$ is stable if $\sigma \left({m}^{IKIEA};{\upkappa }_{\varepsilon },{\upkappa }_{\mu }\right)\ge 0,$ and $\sigma \left({m}^{IKIEA}+1;{\upkappa }_{\varepsilon },{\upkappa }_{\mu }\right)\le 0$; the grand coalition is stable if $\sigma \left(n;{\upkappa }_{\varepsilon },{\upkappa }_{\mu }\right)\ge 0$.

With the general functional forms we use in Sect. 2, it is not possible to derive general results about the existence of an equilibrium coalition, whether it is unique, and how big it might be. However, we can draw an important implication of our model by writing the stability function as:

$$ \begin{aligned} \sigma \left( {m;\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) & = \upkappa_{\mu } \left[ {{\Pi }_{c}^{IKIEA} \left( {n;\upkappa_{\varepsilon } } \right) - {\Pi }_{f}^{IKIEA} \left( {1;\upkappa_{\varepsilon } } \right)} \right] \\ & \quad + \left( {1 - \upkappa_{\mu } } \right)\left[ {{\Pi }_{c}^{IKIEA} \left( {m;\upkappa_{\varepsilon } } \right) - {\Pi }_{f}^{IKIEA} \left( {m - 1;\upkappa_{\varepsilon } } \right)} \right] \\ & = \upkappa_{\mu } \left[ {W^{SO} - W^{IKNC} \left( {\upkappa_{\varepsilon } } \right)} \right] + \left( {1 - \upkappa_{\mu } } \right)\left[ {{\Pi }_{c}^{IKIEA} \left( {m,\upkappa_{\varepsilon } } \right) - {\Pi }_{f}^{IKIEA} \left( {m - 1;\upkappa_{\varepsilon } } \right)} \right] \\ \end{aligned} $$

(13)

The second term in square brackets on the RHS of (13) is the stability function when countries act as imperfect Kantians with respect to emissions only. As we noted above, in this special case our model is identical to that of Eichner and Pethig (2022), who noted that this payoff function is isomorphic to the payoff function of the standard model of IEAs presented in (6), and hence, for commonly employed functional forms for benefits and damage cost functions, this stability function becomes negative for values of m greater than a small number, typically no greater than 4. The first term in square brackets in (13) is the difference in welfare between the fully-co-operative equilibrium and the non-cooperative Kantian equilibrium with Kantian weight ${\upkappa }_{\varepsilon }$, and so, for κ_ε < 1 it is strictly positive. As ${\upkappa }_{\mu }$ increases, more weight is given to this positive first term and less to the possibly negative second term. Hence, the size of the stable IEA should increase as κ_μ increases. When ${\upkappa }_{\varepsilon }=1$, both terms in (13) are zero, so equilibrium emissions are the first-best (social optimum) and all coalition sizes are stable. When we wish to compare equilibrium coalition sizes across a range of parameters, we will apply the standard equilibrium selection criterion and select the grand coalition as the equilibrium coalition membership.

Remark 3:

For our general model of IEAs with Kantian behaviour towards emissions and membership, when countries are perfect Kantians with respect to emissions (${\upkappa }_{\varepsilon }=1)$, then, for any possible value of the Kantian weight on membership (${\upkappa }_{\mu }$), equilibrium emissions are socially optimal, e^SO, achieving the socially optimal level of welfare, W^SO.

2.2.3 Overall Equilibrium

Having derived equilibrium membership, ${m}^{IKIEA}\left({\upkappa }_{\varepsilon },{\upkappa }_{\mu }\right)$ of the IEA, we can derive the overall equilibrium emissions and welfare of a coalition or fringe country (i = c, f):

$$ e_{i}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) = e_{i}^{IKIEA} \left[ {m^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right),\upkappa_{\varepsilon } } \right] $$

(14a)

$$ W_{i}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) = B\left[ {e_{i}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)} \right] - D\left\{ {m^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)e_{c}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) + \left[ {n - m^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)} \right]e_{f}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)} \right\}$$

(14b)

As we have noted, to derive further results for our model, we need to turn to specific functional forms for the benefit and damage cost functions, which we do in Sect. 3.

2.2.4 Relationship Between Our Model and Eichner and Pethig (2022)

To complete this theory section, we note briefly how our model differs from that of Eichner and Pethig (2022). The payoff function employed by Eichner and Pethig (2022) can be written as¹²:

$$ \begin{aligned} {\Pi }^{EP} \left( {{\varvec{\text{e}}};\, \upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) & \equiv \upkappa_{\mu } \left[B\left( {e_{i} } \right) - D \left(\mathop \sum \limits_{j \in N} e_{j} \right)\right] + \upkappa_{\varepsilon } \left [ {B\left( {e_{i} } \right) - D\left( {ne_{i} } \right)} \right] \\ & \quad + \left( {1 - \upkappa_{\mu } - \upkappa_{\varepsilon } } \right)\left [B\left( {e_{i} } \right) - D \left(\mathop \sum \limits_{j \in C} e_{j} + \mathop \sum \limits_{k \in F} e_{k} \right)\right]. \\ \end{aligned} $$

(15)

The key difference is they do not distinguish between emissions chosen in an imperfect Kantian fashion at Stage 2 and emissions chosen at Stage 1 linked to imperfect Kantian analysis of membership decisions. This has two implications. First, this departs from the Alger and Weibull (2013, 2016, 2020) approach to modelling imperfect Kantian behaviour whereby the imperfect Kantian payoff function is a weighted average of the perfect Kantian payoff and the non-Kantian payoff. In (15) it a weighted average of the perfect Kantian payoff with respect to membership, the perfect Kantian payoff with respect to emissions and the non-Kantian payoff. The second implication of their approach is that they assume that $0\le {\upkappa }_{\varepsilon }+{\upkappa }_{\mu }\le 1$, whereas we assume that $0\le {\upkappa }_{\varepsilon },{\upkappa }_{\mu }\le 1$. In Sect. 3.2 we will use our special case to compare the implications of their approach and our approach for equilibrium emissions, membership and welfare.

3 Results for Specific Functional Forms

To derive more detailed results for the model we presented in Sect. 2 we assume that the benefit and damage cost functions are both quadratic.¹³ In Sect. 3.1 we present a range of results for our model of Imperfect Kantian IEAs, while in Sect. 3.2 we compare the results from our model with those derived from the model of Eichner and Pethig (2022), using the same quadratic benefit and damage cost functions, for 3 key metrics, and show that the results from our model outperform those from the model of Eichner and Pethig.

We assume that the benefit function takes the form $B\left({\text{e}}_{i}\right)=\beta {\text{e}}_{i}-0.5{\text{e}}_{i}^{2}$ and the damage cost function takes the form: $D[{\sum }_{j\in N}{\text{e}}_{j}]=0.5\delta {[{\sum }_{j\in N}{\text{e}}_{j}]}^{2}$. In the Online Appendix, we note first that to ensure non-negative emissions for coalition countries, the damage cost parameter must satisfy: $\delta <\overline{\delta }\equiv 4/{(n-1)}^{2}$. We also present key analytical results for this special case for: (i) the first-best emissions; (ii) the non-cooperative equilibria with self-interested and Kantian behaviour. Finally, for our model of IEAs with Kantian behaviour towards emissions and membership, the Online Appendix presents some analytical results, but only for equilibrium Stage 2 emissions.

The results we present in this section are derived numerically. We assume that the number of countries, n, equals 100 (which we take to be a ‘large’ number of countries), and we focus on a high value for the damage cost parameter: $\delta =0.9\overline{\delta }$ (in Ulph and Ulph 2023, we present results for lower values of δ). We employ a wide range of values of our key parameters $({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$.

For our model of IEAs with imperfect Kantian behaviour, it is useful to construct measures of equilibrium emissions and welfare of an average country defined as:

$$ \begin{aligned} e_{a}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) & \equiv \{ m^{IKIEA} \left( {\upkappa_{\text{e}} ,\upkappa_{\mu } } \right)e_{c}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) \\ & \quad + \left[ {n - m^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)} \right]e_{f}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)\} /n \\ \end{aligned} $$

(16a)

$$ \begin{aligned} W_{a}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) & \equiv \{ m^{IKIEA} \left( {\upkappa_{\text{e}} ,\upkappa_{\mu } } \right)W_{c}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) \\ & \quad + \left[ {n - m^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)} \right]W_{f}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)\} /n \\ \end{aligned} $$

(16b)

It will also be useful to construct measures of how far Imperfect Kantian non-cooperative behaviour, and Imperfect Kantian IEAs, with different Kantian weights, close the gaps between the non-cooperative non-Kantian levels of emissions and welfare (${\text{e}}^{NC}, {W}^{NC})$ and the social optimal levels of emissions and welfare (${\text{e}}^{SO}, {W}^{SO})$, where ${\text{e}}^{NC}> {\text{e}}^{SO}$ and ${W}^{SO}> {W}^{NC}$.

So, for the case of the Imperfect Kantian non-cooperative equilibrium, we define

$$ \widehat{{\hat{\text{e}}}}\left( {\upkappa_{\epsilon } } \right) \equiv \frac{{e^{NC} - e^{IKNC} \left( {\upkappa_{\varepsilon } } \right)}}{{e^{NC} - e^{SO} }} > 0; \;\;{\text{and}}\;\; \widehat{{\hat{W}}}\left( {\upkappa_{\varepsilon } } \right) \equiv \frac{{W^{IKNC} \left( {\upkappa_{\epsilon } } \right) - W^{NC} }}{{W^{SO} - W^{NC} }} > 0 $$

(16c)

as measures of the extent to which the equilibrium levels of emissions and welfare lie between their non-cooperative and socially optimal levels. Analogous measures that apply to the equilibrium values for emissions and welfare of a coalition country, a fringe country and an average country that arises with Imperfect Kantian IEAs are:

$$ \widetilde{{\tilde{\text{e}}}}^{j} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) \equiv \frac{{e^{NC} - e_{j}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right)}}{{e^{NC} - e^{SO} }};\; \widetilde{{\tilde{W}}}^{j} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) \equiv \frac{{W_{j}^{IKIEA} \left( {\upkappa_{\varepsilon } ,\upkappa_{\mu } } \right) - W^{NC} }}{{W^{SO} - W^{NC} }} \;j = c,f,a . $$

(16d)

As we will see, another benefit of employing these measures of emissions and welfare gaps in is that they are less dependent on some of parameters used in our specific functional forms.

3.1 Results from Our Model of Imperfect Kantian IEAs

We begin by presenting results for equilibrium membership, emissions and welfare of our model and then assess how far the Imperfect Kantian non-cooperative equilibrium and Imperfect Kantian IEAs close the emissions and welfare gaps between the non-cooperative and social optimal equilibria.

3.1.1 Equilibrium Membership

In Ulph and Ulph (2023), we show that with a linear damage cost function, the stability function is independent of δ and ${\upkappa }_{\varepsilon }$, and is decreasing in the size of IEA membership, m, so, for given parameters ${\upkappa }_{\varepsilon }, {\upkappa }_{\mu }$ there is a unique stable IEA.

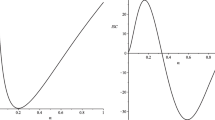
With quadratic damage costs, the stability function does depend on δ and ${\upkappa }_{\varepsilon }$, and is initially decreasing and then increasing in m. We illustrate the implications in Fig. 1 for ${\upkappa }_{\varepsilon }=0.05$. When ${\upkappa }_{\mu }=0.15$, the stability function intersects the horizontal axis once, so there is a unique stable IEA with 26 members. When ${\upkappa }_{\mu }=0.23$, the stability function intersects the horizontal axis twice; the lower value results in a stable IEA of size 41; the upper intersection, with m approximately 0.89, does not yield a stable IEA, but the grand coalition is a second stable IEA. As we did above, we again apply an equilibrium selection rule to choose the higher stable IEA, the grand coalition. With ${\upkappa }_{\mu }=0.3$, the stability function does not intersect the horizontal axis so the unique stable IEA is the grand coalition and social optimum.

Fig. 1

Stability function for different values of ${\upkappa }_{\upmu }$

More generally, the range of values of ${\upkappa }_{\mu }$ for which we get two stable IEAs ranges from (0.20–0.24) when ${\upkappa }_{\varepsilon }=0.0$, to (0.24–0.26) when ${\upkappa }_{\varepsilon }$= 0.1, becoming a singleton (0.28) when ${\upkappa }_{\varepsilon }=0.2.$

We now consider for different values of ${\upkappa }_{\varepsilon }$ what is the minimum value of ${\upkappa }_{\mu }$ needed to achieve the social optimum through securing the grand coalition. For our particular parameters, the grand coalition can now be achieved with values of ${\upkappa }_{\mu }=0.2$ when ${\upkappa }_{\varepsilon }=0.0$ tending to ${\upkappa }_{\mu }=0.5$ as ${\upkappa }_{\varepsilon }\hspace{0.17em}\to \hspace{0.17em}1.0$. The rationale is that an increase in ${\upkappa }_{\varepsilon }$ decreases the emissions that all countries would carry out in the absence of an IEA, reducing the conventional benefits of joining an IEA, so a higher weight on membership is needed to offset that effect.

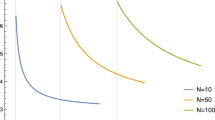
Finally, we determine the equilibrium size of IEA, which, for simplicity of notation in a diagram, we denote $\widetilde{m}\left({\upkappa }_{\varepsilon },{\upkappa }_{\mu }\right)$, for values of ${\upkappa }_{\mu }$ between 0 and 0.5 (we know the grand coalition is stable for ${\upkappa }_{\mu }>0.5$), and values of ${\upkappa }_{\varepsilon }$ = 0.1, 0.3, and 0.5. The results are shown in Fig. 2.

Fig. 2

Equilibrium IEA membership

We have already argued that, for any value of ${\upkappa }_{\varepsilon }$, the size of equilibrium IEA membership is increasing in the Kantian weight on membership, ${\upkappa }_{\mu }$. Comparing the curves for different values of ${\upkappa }_{\varepsilon }$ there are two factors at play: (i) as we argued above, for any given relatively low level of membership below about 40, an increase in ${\upkappa }_{\varepsilon }$ means countries would decrease emissions without any IEA, reducing the benefits of forming an IEA, which is offset by increasing the weight ${\upkappa }_{\mu }$; (ii) for low values of ${\upkappa }_{\varepsilon }$ we encounter the problem of two stable IEAs so the stable IEA jumps to the grand coalition.

We summarise these results as follows.

Remark 4:

With quadratic benefit and damage cost functions, there may be two stable IEAs, one being the grand coalition, which we select. ${{m}}^{{{IKIEA}}}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$ is increasing in ${\upkappa }_{\mu },$ but for values of ${\upkappa }_{\mu }$ above a critical level it is decreasing in ${\upkappa }_{\varepsilon }$. The grand coalition is always stable for ${\upkappa }_{\upmu }\ge 0.5$, but can be achieved for much smaller values, e.g. for ${\upkappa }_{\mu }=0.2$ when ${\upkappa }_{\upvarepsilon }=0.0$.

As we noted above, the rationale for the last result is that the lower the Kantian weight on emissions, the larger are emissions at Stage 2 and so the greater is the benefit of joining an IEA, so a quite modest Kantian weight on membership can be sufficient to induce the grand coalition and hence social optimum.

3.1.2 Closure of Emission and Welfare Gaps of Coalition and Fringe Countries

We consider first the closure of emission gaps, starting with the emissions gap for a coalition country. Values of ${\widetilde{\widetilde{\text{e}}}}^{c}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$, are plotted in Fig. 3a, using the same range of values for ${\upkappa }_{\varepsilon },{\upkappa }_{\mu }$ as for Fig. 2.

Fig. 3

a Closure of emissions gap of a coalition country, b Closure of emissions gap of a fringe country

For low values of ${\upkappa }_{\mu }$, the extent to which the coalition emission gap is closed is increasing in the two Kantian weights¹⁴${\upkappa }_{\varepsilon }, {\upkappa }_{\mu }$. However, there are two important differences for higher values of for higher values of ${\upkappa }_{\mu }$. First, it is now possible that$\frac{\partial {\widetilde{\widetilde{\text{e}}}}^{c}(.)}{\partial {\upkappa }_{\varepsilon }}<0$.¹⁵ The rationale is that, as we saw in 3.1.1, the grand coalition is achieved with smaller values of the Kantian weight on membership. Second, for sufficiently low values of ${\upkappa }_{\varepsilon }$, it is possible that ${\widetilde{\widetilde{\text{e}}}}^{c}\left(.\right)>100\%.$ This arises in Fig. 3a: when ${\upkappa }_{\varepsilon }$= 0.1, the grand coalition is achieved when ${\upkappa }_{\mu }$=0.24 so ${\widetilde{\widetilde{\text{e}}}}^{c}\left(\mathrm{0.1,0.24}\right)=110.00$; but when ${\upkappa }_{\mu }$=0.23, ${\widetilde{\widetilde{\text{e}}}}^{c}\left(0.1, 0.23\right)=100.45$. This does not arise for the higher values of ${\upkappa }_{\varepsilon }$ we have used.

The emissions gap for a fringe country, ${\widetilde{\widetilde{\text{e}}}}^{f}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$ is plotted in Fig. 3b.

While it may look as if ${\widetilde{\widetilde{\text{e}}}}^{f}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$ is independent of ${\upkappa }_{\mu }$¹⁶, in fact it declines slightly as ${\upkappa }_{\mu }$ increases. For example, ${\widetilde{\widetilde{\text{e}}}}^{f}(0.3,{\upkappa }_{\mu })$ falls from 65.89 to 65.57 as ${\upkappa }_{\mu }$ rises from 0.01 to 0.31 (the grand coalition is achieved when ${\upkappa }_{\mu }$ = 0.32). ${\widetilde{\widetilde{\text{e}}}}^{f}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$ falls sharply as ${\upkappa }_{\varepsilon }$ increases. Both results are due to free riding.

We now turn to closure of welfare gaps. Values of ${\widetilde{\widetilde{W}}}^{c}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$ are plotted in Fig. 4a. For high values of ${\upkappa }_{\varepsilon }$, 0.3 and 0.5, and low values of ${\upkappa }_{\mu }$ (< 0.2) coalition welfare can fall as ${\upkappa }_{\mu }$ increases.¹⁷ Values of ${\widetilde{\widetilde{W}}}^{f}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$ are plotted in Fig. 4b. For high values of ${\upkappa }_{\varepsilon }$ (0.3, 0.5) and ${\upkappa }_{\mu }$, ${\widetilde{\widetilde{W}}}^{f}({\upkappa }_{\varepsilon },{\upkappa }_{\mu })$ can exceed 100%, though not exceeding 103% for the values in Fig. 4a.¹⁸

Fig. 4

a Closure of welfare gap of a coalition country, b Closure of welfare gap of a fringe country

We summarise these findings in Result 5.

Remark 5:

With quadratic benefit function and quadratic damage cost function:

• (i) The emissions gap for a coalition country is decreasing in ${\upkappa }_{\mu }$, but, for large values of ${\upkappa }_{\mu }$, may be increasing in ${\upkappa }_{\varepsilon }$; emissions of a coalition country could fall below first-best for values of ${\upkappa }_{\mu }$ close to that which secures the grand coalition;

• (ii) The emissions gap for a fringe country is decreasing in ${\upkappa }_{\varepsilon }$ but is increasing, slightly, in ${\upkappa }_{\mu }$;

• (iii) The welfare gap for a coalition country decreases with increases in both Kantian weights, except for relatively high values of ${\upkappa }_{\upvarepsilon }$ (≥ 0.3) and low values of ${\upkappa }_{\mu }$ (< 0.2) when it increases in ${\upkappa }_{\mu }$;

• (iv) The welfare gap for a fringe country is decreasing in ${\upkappa }_{\varepsilon }, {\upkappa }_{\mu }$; while, because of its ability to free-ride, the welfare of a fringe country can sometimes exceed first-best; the size of the gap is smaller than with a linear damage cost function.

The intuition behind the latter result is that with increasing marginal damage free riding brings smaller net benefits than with constant marginal damages.

3.1.3 Is Acting in an Imperfect Kantian Fashion a Substitute or Complement to Forming an IEA

Finally, we address the question of the extent to which acting as an Imperfect Kantian is a substitute or complement to forming an IEA. Thus, we ask to what extent are average emissions and welfare gaps closed by countries acting in an Imperfect Kantian fashion in a non-cooperative equilibrium, and what additional contribution is made by countries seeking to form an IEA. The results are shown in Tables 1 and 2 for emissions and welfare respectively.

Table 1 Contribution of changing moral attitudes and negotiating IEAs to reducing global emissions

Table 2 Contribution of changing moral attitudes and negotiating IEAs to raising global welfare

The main result is that the Imperfect Kantian non-cooperative equilibrium makes significant contributions to closing the emissions and, particularly, welfare gaps,¹⁹ so the additional contribution of forming an IEA gets squeezed. This is particularly true for welfare where, for all three values of ${\upkappa }_{\varepsilon }$, the non-cooperative equilibrium contributes over 50% to closing the welfare gap. Nevertheless, it is still the case that changing moral attitudes and negotiating an IEA are complementary approaches to tackling climate change, not substitutes.

Remark 6:

Changing moral attitudes and negotiating an IEA are complementary approaches to seeking to reduce global emissions and hence raising global welfare, though the relative contributions vary significantly with the Kantian weights ${\upkappa }_{\varepsilon }$ and ${\upkappa }_{\mu }$.

3.2 Comparison of Results From Our Model With Those From Eichner and Pethig (2022)

In this section, we use our model with quadratic benefit and damage cost functions to compare results derived from our model of IEAs (denoted UU) with those derived from the model of IEAs in Eichner and Pethig (2022) (denoted EP), using the same quadratic benefit and damage cost functions. To make such comparison we need to choose parameter values for ${\upkappa }_{\varepsilon }, {\upkappa }_{\mu }$ which are applicable to both models. As we noted in sub-Sect. 2.2.4, EP effectively constrain ${\upkappa }_{\varepsilon }, {\upkappa }_{\mu }$ to satisfy $0\le {\upkappa }_{\varepsilon }+{\upkappa }_{\mu }\le$ 1, so we choose values of ${\upkappa }_{\varepsilon }, {\upkappa }_{\mu }$ that satisfy this constraint. We choose ${\upkappa }_{\varepsilon }=$ 0.1, 0.3 and 0.5, with ${\upkappa }_{\mu }$ ranging between 0.05 and 0.4.²⁰ We focus on 3 key measures of performance of these models: the size of the equilibrium IEA, and the extent to which the average equilibrium emissions and welfare gaps are closed. by the equilibrium IEA. The results are shown in Tables 3, 4, and5.

Table 3 Comparison of Size of Equilibrium IEA in Models UU and EP

Table 4 Comparison of % of emissions gap closed in models UU and EP

Table 5 Comparison of % of welfare gap closed in models UU and EP

So, comparing the model proposed in this paper (UU) with that employed by Eichner and Pethig 2022 (EP) we have the following:

Remark 7

For all three measures of the effectiveness of IEAs, and for all values of the Kantian weights satisfying $0 \le {\upkappa }_{\varepsilon }+{\upkappa }_{\mu }\le 1$: (i) whenever the EP model generates the grand coalition and hence the social optimum so too does UU; (ii) in all other cases UU produces more effective outcomes than EP.

We believe that these results arise because our model captures the full benefit of deciding to be a member of an IEA compared to being a member of the fringe by choosing emissions appropriate to those decisions.

4 Conclusions

This paper contributes to a literature which seeks to overcome the pessimistic conclusion drawn from standard non-cooperative two-stage game models of IEAs that the number of countries who join an IEA is small precisely when the potential gains from achieving the grand coalition are large. In the standard model, agents act in a self-interested manner. We draw on the important work of Alger and Weibull (2013, 2016, 2020) who used evolutionary game theory to demonstrate that, in a wide range of contexts, the evolutionary stable forms of behaviour derive from either self-interested motivation or application of the Kantian categorical imperative to “act only according to that maxim through which you can at the same time will that it become a universal law”. More generally, they suggest that individuals might act as imperfect Kantians, using an objective function which is a weighted average of the objective functions underlying the two stable forms of behaviour. In this paper we have explored the implications of assuming that countries act as imperfect Kantians in taking their decisions on emissions and membership.

Another motivation for this paper is the empirical observation that a growing number of people, notably young people, deliberately reduce their carbon footprint in an effort to do the morally right thing with regard to the imminent serious world-wide climate damage although they know that their emission reduction has hardly any effect on global emissions and reduces their non-Kantian utility. In their role as voters, they call on their governments to be serious about the reduction of domestic emissions and to play an active role towards an effective international climate agreement. Against this background, our paper also addresses the issue of whether trying to tackle problems such as climate change is best handled through government-level actions rather than persuading individuals, especially consumers, to make their choices in a more moral form. We posed this as a question whether seeking to encourage individuals to act more morally is a substitute or complement to government-level actions to join an IEA.

Our key findings are that when countries act as imperfect Kantians with respect only to emissions, the resulting IEA game is iso-morphic to the conventional model in which countries act in a self-interested fashion, with the same pessimistic conclusion about IEA membership. When countries also act as imperfect Kantians with respect only to membership, we show that it is always possible to achieve the grand coalition when the weight given to acting in a Kantian fashion never exceeds 0.5 and, for some cases, could be less than 25%. The important implication of this result is that trying to form IEAs and trying to encourage individuals and their governments to act more morally are complementary approaches to trying to achieve the first-best outcome, not substitutes.

There are a number of important areas for future research, and we note three. The first is that we have assumed that all countries are identical, and it would obviously be important to explore the implications of what would happen when countries differ some respect but seek to act in a Kantian fashion. An obvious source of difference between countries is their size, their benefit functions and damage cost functions. The assumption made in this paper that perfect Kantians do the same thing may not make sense when countries differ in such respects. Van Long (2021) cites the relevant literature and applies that to his study of dynamic models of exploitation of a renewable resource, and it might be appropriate to apply his approach to our two-stage game model of IEA formation. A further aspect of enriching the model in this way would be to recognise that damage costs experienced by a country can be moderated.

A second extension, motivated by the argument in de Zeeuw (2008) that it is important to study the implications of adopting a more cooperative model of government behaviour using a dynamic model of environmental damages, would be to study the implications of imperfect Kantian behaviour when damage costs depend on the stock of greenhouse gases, not the flow of such gases.

A final area for further development, which goes beyond the current IEA literature, is that we treat countries as a single entity, whereas emissions are the results of decisions by a large number of organisations (households, producers, retailers etc.) influenced, to different extents, by government policies. This may matter less given our assumption that countries are identical, but becomes important when countries differ in various respects. One important difference concerns the degree of democracy, where more autocratic governments can enforce policies in ways not available to more democratic governments.