Construction of some new traveling wave solutions to the space-time fractional modified equal width equation in modern physics

Abstract

Nonlinear fractional evolution equations are important for determining various complex nonlinear problems that occur in various scientific fields, such as nonlinear optics, molecular biology, quantum mechanics, plasma physics, nonlinear dynamics, water surface waves, elastic media and others. The space-time fractional modified equal width (MEW) equation is investigated in this paper utilizing a variety of solitary wave solutions, with a particular emphasis on their implications for wave propagation characteristics in plasma and optical fibre systems. The fractional-order problem is transformed into an ordinary differential equation using a fractional wave transformation approach. In this article, the polynomial expansion approach and the sardar sub-equation method are successfully used to evaluate the exact solutions of space-time fractional MEW equation. Additionally, in order to graphically represent the physical significance of created solutions, the acquired solutions are shown on contour, 3D and 2D graphs. Based on the results, the employed methods show their efficacy in solving diverse fractional nonlinear evolution equations generated across applied and natural sciences. The findings obtained demonstrate that the two approaches are more effective and suited for resolving various nonlinear fractional differential equations.

1 Introduction

From a mathematical perspective, nonlinear phenomena are among the most significant research areas that emerge in many domains of science, including solid-state and plasma physics, fluid mechanics, optical fibres, chemical kinematics and biology. Nonlinear evolution equations (NLEEs) are frequently produced by the mathematical modelling of nonlinear phenomena. To better understand the behaviour of these phenomena, it can be very useful to obtain the NLEE solutions Rezazadeh et al. (2020). The first researchers to explore fractional differential equations (FDEs) are Oldham and Spanier Oldham and Spanier (1974). Currently, fractional differential equations have an important role in a variety of academic disciplines, such as electricity, electronics biological control theory, systems verification, the field of finance, mechanics, engineering, signal analysis, random dynamic systems, plasma therapy physics and quantum systems Sagheer et al. (2019), Abdel-Aty et al. (2020), Kadkhoda and Jafari (2017), Tajadodi et al. (2021)), [7], Zidan et al. (2017), Zidan et al. (2019). The methods we have employed, the polynomial expansion approach and the Sardar sub-equation method, have never been used before in the context of the space-time fractional MEW equation. Previously, the governing model have been investigated by virous analytical approaches including the unified method Rafiq et al. (2022), the expansion method Ali et al. (2022), the improved Bernoulli sub-equation function method Zaman et al. (2023), the Kudryashov method Raslan et al. (2017) and several others.

Over the past few decades, a diverse range of researchers has successfully delved into the exploration of exact solutions and analytical approximations for NLEEs. Notably, various well-established methods have emerged in recent literature (Demirbilek and Mamedov 2023; Rasool et al. 2023; Pandir and Yasmin 2023) and also including the extended trial equation method Nawaz et al. (2017), the Hirota’s bilinear form Ma et al. (2018), the extended simplest equation scheme Torvattanabun et al. (2018), the improved F-expansion procedure Bashar and Islam (2020), the Adomian decomposition approach Ikram et al. (2019), the Riccati sub-equation technique Khodadad et al. (2017), the unified method Osman et al. (2018), the advanced auxiliary equation technique Bashar et al. (2022), etc. To obtain analytical solutions for FDEs, a number of reliable approaches have recently been developed. Examples of such techniques include the Kudryashov approach (Seadawy et al. 2017; Lu et al. 2018),  the generalized tanh-coth technique (Manafian and Lakestani 2017), the exponential rational function technique (Seadawy and Manafian 2018; Seadawy and El-Rashidy 2018), the simplest equation approach, the modified simple equation approach (Chen and Jiang 2018), the auxiliary equation technique (Khater et al. 2006), the improved F-expansion technique (Seadawy 2018), the first integral approach (Aminikhah et al. 2015) and many others (Alquran 2022; Jaradat and Alquran 2020, 2022; Alquran 2023; Alquran and Al Smadi 2023).

The selected techniques, the polynomial expansion approach and the Sardar sub-equation method, offer several advantages. These methods, being applied to the space-time fractional MEWE for the first time, have yielded several new solutions that can be utilized in various fields. The primary advantages include the ability to derive exact analytical solutions, providing clear insights into the behavior of the equation under different conditions. However, these methods have some limitations. Despite these limitations, once the necessary conditions are met, the methods can be successfully applied to several nonlinear equations, resulting in valuable new solutions.

2 The conformable fractional derivative

In contrast to the integer derivative, the fractional derivative exhibits global association and may provide a more accurate picture of the dynamic functions building processes. Fluid mechanics, applied mathematics, hydrodynamics, quasi-chaotic dynamical systems, system identification, finance, statistics, chaotic dynamical systems, ecology, solid-state biology, optical fibres, electric control theory, and many other topics are among those that can be formulated using fractional calculus. In contrast to conventional calculus, which only considers the current state of the problem, fractional derivatives, which are utilised in the mathematical modelling of these circumstances, provide a reasonable explanation for the nonlocal nature of these models. The purpose of this special issue is to bring together top academics from a variety of engineering disciplines, including applied mathematicians, and give them a forum to exchange their creative research findings (Jena and Chakraverty 2019; Seadawy et al. 2024; Kırcı et al. 2024; Tariq et al. 2024).

In literature, a variety of fractional derivatives are devised to characterize many crucial physical phenomena, For instance, the modified Riemann-Liouville derivative of Jumarie Jumarie (2006), for Riemann-Liouville derivative (Podlubny 1999), the conformable derivative of Atangana Wu et al. (2020), their Caputo derivative (Almeida 2017) or the Beta-derivative (Gurefe 2020), have been used in many applications in different fields of contemporary science and engineering; fractional-order derivatives provide a more suitable illustration (Bekir et al. 2021). Let $\psi$: $[0,\infty )\rightarrow R$, The conformable derivative fractional $\psi$ of an order $\beta$ is defined

$$\begin{aligned} {\mathcal {D}}_{x }^{\beta }\psi (x)= \lim _{\varepsilon \rightarrow 0} \frac{\psi \left( \varepsilon x^{1-\beta }+x\right) -\psi (x)}{\varepsilon }, \end{aligned}$$

for each $x> 0$ and $\beta \in (0,1)$. Additionally, a few characteristics of conformable fractional derivatives are provided

$$\begin{aligned} {\mathcal {D}}_x^{\beta }(x^{\gamma }) & = \lambda x ^{\gamma -\beta }, \forall \gamma \in R,\\ {\mathcal {D}}_x^{\beta }(\mu (x)+\upsilon (x)) & = {\mathcal {D}}_x^{\beta }\mu (x)+ {\mathcal {D}}_x^{\beta }\upsilon (x),\\ {\mathcal {D}}_x^{\beta }(\mu o \upsilon )(x) & = x^{1-\beta }\upsilon (x^{\beta -1})\upsilon '(t) {\mathcal {D}}_x^{\beta }(\mu (x))|_{x=\mu (x)}. \end{aligned}$$

3 The governing model

The fractional-order MEW equation, a nonlinear wave equation renowned for its relevance in describing wave phenomena in shallow water and plasmas, presents solutions featuring a distinctive interplay of positive and negative amplitudes. One intriguing characteristic of these solutions is the uniformity in their width. This peculiar aspect signifies that, while the amplitude may vary, the spatial extent of the waves remains unaltered. The space-time fractional MEW equation (Hosseini and Ayati 2016) takes the following format:

$$\begin{aligned} D_t^{\alpha }{\mathcal {L}}(x,t)+ \epsilon \text {D}_x^{\alpha }{\mathcal {L}}^3(x,t)-\mu \text {D}_{{xxt}}^{3 \alpha }{\mathcal {L}}(x,t)=0, \end{aligned}$$

(1)

where the actual parameters are $\mu$ and $\epsilon$ respectively. In the given scenario, x and t denote space and time coordinates, respectively. The function ${\mathcal {L}}(x,t)$ represents the amplitude of a wave. The space-time fractional MEW equation can lead to solutions that are either real-valued or complex-valued functions, depending on the specific parameters and initial or boundary conditions of the problem. The notation $D_t^{\alpha }$ symbolizes the conformable fractional derivative of ${\mathcal {L}}$ concerning time t with an order $\alpha$. In fluid dynamics, ${\mathcal {L}}$ shows how the water surface moves up and down due to long waves and in plasma physics, it represents the negative electric potential. It’s interesting how ${\mathcal {L}}$ can mean different things in different areas of science, like waves in water or electrical properties in plasmas. In recent years, scientists have been working on solving (1): Korkmaz (2017) found solutions using trigonometric and hyperbolic functions, Raslan et al. (2017) discovered new solutions with a modified method and Shallal et al. (2020) used a generalized expansion method. These findings help us better understand the MEW equation and how different mathematical methods can be applied to study it.

The space-time fractional MEW equation is a type of partial differential equation that includes fractional derivatives with respect to both space and time variables and it is modified to incorporate the equal width property. This equation has applications in various fields, particularly in the study of nonlinear waves and solitons. The MEW equation describes the evolution of nonlinear waves with fractional order derivatives. It is used to model the behavior of waves in different media, such as fluids, plasmas, or optical fibers, where the equal width property is relevant. This model can support soliton solutions, which are stable, localized, and self-reinforcing wave packets. Understanding the dynamics of solitons is crucial in fields like optics, where solitons play a role in signal transmission and information processing (Seadawy et al. 2021; Zafar 2019). Fractional differential equations, including the space-time fractional MEW equation, can be applied to model phenomena in biology, such as the spread of diseases or the diffusion of substances in biological tissues. The fractional order helps capture the memory and hereditary properties often present in biological systems. The governing model may find applications in plasma physics, where the behavior of charged particles in a plasma is modeled. Understanding the dynamics of plasma waves is crucial in areas like fusion research and space physics. Fractional differential equations can be used to model the transport properties of materials, including the diffusion of substances through porous media or the propagation of heat in materials with fractional properties (Raslan et al. 2017). The nonlinear structure can be relevant in the study of optical pulse propagation in fiber optics. Understanding how optical signals evolve in optical fibers is important for designing efficient and robust communication systems. This structure may also be applied to model the dynamics of waves and currents in geophysical fluids, such as ocean waves or atmospheric phenomena. The fractional derivatives help to capture the complex nature of these fluid systems Tariq et al. (2018).

The goal of this article is to explore novel and broad-spectrum soliton solutions for the time-fractional MEW equation. This investigation is conducted by employing the polynomial expansion approach and the Sardar sub-equation method. Furthermore, the article aims to analyze the dynamic behavior of these analytical solutions. The utilization of these mathematical methods provides a comprehensive exploration of soliton solutions and contributes to a deeper understanding of the dynamic characteristics described by the nonlinear model under consideration.

The remainder of the article is structured as follows: The Sardar sub-equation approach and the polynomial expansion approach is described in Sect. 2. The conformable derivative is used in Sect. 3 to produce a variety of new travelling wave solutions and stability analysis in Sect. 4. The graphical depictions of the solutions are elaborated in Sect. 5, while the conclusion is outlined in Sect. 6.

4 Methodology

Consider the nonlinear fractional differential equation shown below to demonstrate the fundamental concept of our approach

$$\begin{aligned} G\left( {\mathcal {L}}, D_t^{\alpha _1}{\mathcal {L}}, D_x^{2 \alpha _1}{\mathcal {L}}, D_{{tt}}^{2 \alpha _2}{\mathcal {L}}, D_{{xx}}^{2 \alpha _2}{\mathcal {L}}, D_t^{\alpha _1} D_t^{\alpha _2}{\mathcal {L}},\dots \right) , 0<\alpha _1,\alpha _2<1. \end{aligned}$$

(2)

Employing the fractional complex transformation

$$\begin{aligned} {\mathcal {L}}(x,t)={\mathcal {L}}(\mho ),~\mho =\frac{k }{(\alpha _2 +1) \Pi }x^{\alpha }-\frac{c }{(\alpha _1 +1) \Pi }t^{\alpha }-x_0, \end{aligned}$$

(3)

reduces (2) into an integer order nonlinear ordinary differential equations as follows, where k and c are nonzero constants, $x_0$ is an arbitrary constant and $\alpha _1$ and $\alpha _2$ are fractional orders.

$$\begin{aligned} H({\mathcal {L}},{\mathcal {L}}^{'},{\mathcal {L}}^{''},\dots )=0, \end{aligned}$$

(4)

where the derivatives are based on $\mho$.

4.1 The modified Sardar sub-equation approach

The solutions to Eq. (4) are viewed as a finite series, it is assumed

$$\begin{aligned} {\mathcal {L}}(\mho )=W_0+\sum _{b=1}^{ {N}} W_b {\mathcal {L}} ^b (\mho ),~W_{{N}}\ne 0. \end{aligned}$$

(5)

We give the integer value of N, which balances the greatest power nonlinear and highest derivative terms.

The following nonlinear ordinary equation can be resolved by the function ${\mathcal {L}} (\mho )$

$$\begin{aligned} {\mathcal {L}}'(\mho )^2=\psi _2 {\mathcal {L}}(\mho )^4+\psi _1 {\mathcal {L}}(\mho )^2+\psi _0. \end{aligned}$$

(6)

Additionally, the following are the general solutions to Eq. (6)

Step 1. $\text {If}~\psi _0=0,~\psi _1>0~\text {and}~ \psi _2\ne 0$, we have

$$\begin{aligned}{} & {} {\mathcal {L}}_1(\mho )=\pm \text {Sech} \sqrt{-\frac{\psi _1}{\psi _2}} \left( \sqrt{\psi _1} (\mho +\eta )\right) ,\\{} & {} {\mathcal {L}}_2(\mho )=\pm \text {Csch} \sqrt{-\frac{\psi _1}{\psi _2}} \left( \sqrt{\psi _1} (\mho +\eta )\right) . \end{aligned}$$

Step 2. If $\psi _0=0,\psi _1>0~\text {and}~\psi _2=4f_1f_2$, we have

$$\begin{aligned} {\mathcal {L}}_3(\mho )=\pm \frac{4 f_1 \sqrt{\psi _1}}{\left( 4 f_1^2-\psi _2\right) \sinh \left( \sqrt{\psi _1} (\mho +\eta )\right) +\left( 4 f_1^2-\psi _2\right) \cosh \left( \sqrt{\psi _1} (\mho +\eta )\right) }. \end{aligned}$$

Step 3. If $\psi _0=\frac{\psi _1^2}{4 \psi _2},~\psi _1<0~\text {and}~ \psi _2>0$, we have

$$\begin{aligned}{} & {} {\mathcal {L}}_4(\mho )=\pm \sqrt{-\frac{\psi _1}{2 \psi _2}} \tanh \left( \sqrt{-\frac{\psi _1}{2}} (\mho +\eta )\right) ,\\{} & {} {\mathcal {L}}_5(\mho )=\pm \sqrt{-\frac{\psi _1}{2 \psi _2}} \coth \left( \sqrt{-\frac{\psi _1}{2}} (\mho +\eta )\right) ,\\{} & {} {\mathcal {L}}_6(\mho )=\pm \sqrt{-\frac{\psi _1}{2 \psi _2}} \left( \tanh \left( \sqrt{-\frac{\psi _1}{2}} (\mho +\eta )\right) +i \text {sech}\left( \sqrt{-2 \psi _1} (\mho +\eta )\right) \right) ,\\{} & {} {\mathcal {L}}_7(\mho )=\pm \sqrt{-\frac{\psi _1}{8 \psi _2}} \left( \tanh \left( \sqrt{-\frac{\psi _1}{2}} (\mho +\eta )\right) +\coth \left( \sqrt{-\frac{\psi _1}{8}} (\mho +\eta )\right) \right) ,\\{} & {} {\mathcal {L}}_8(\mho )=\pm \frac{\sqrt{-\frac{\psi _1}{2 \psi _2}} \cosh \left( \sqrt{-2 \psi _1} (\mho +\eta )\right) }{\sinh \left( \sqrt{-2 \psi _1} (\mho +\eta )\right) +i}. \end{aligned}$$

Step 4. $\text {If}~\psi _0=0,~\psi _1<0,~\text {and}~ \psi _2\ne 0$, we have

$$\begin{aligned}{} & {} {\mathcal {L}}_9(\mho )=\pm \sqrt{-\frac{\psi _1}{\psi _2}} \sec \left( \sqrt{-\psi _1} (\mho +\eta )\right) ,\\{} & {} {\mathcal {L}}_{10}(\mho )=\pm \sqrt{-\frac{\psi _1}{\psi _2}} \csc \left( \sqrt{-\psi _1} (\mho +\eta )\right) . \end{aligned}$$

Step 5. $\text {If}~\psi _0=\frac{\psi _1^2}{4 \psi _2},~\psi _1>0~ {and}~\psi _2>0~\text {and}~G_1^2-G_2^2>0$, we have

$$\begin{aligned}{} & {} {\mathcal {L}}_{11}(\mho )=\pm \sqrt{\frac{\psi _1}{2 \psi _2}} \tan \left( \sqrt{\frac{\psi _1}{2}} (\mho +\eta )\right) ,\\{} & {} {\mathcal {L}}_{12}(\mho )=\pm \sqrt{\frac{\psi _1}{2 \psi _2}} \cot \left( \sqrt{\frac{\psi _1}{2}} (\mho +\eta )\right) ,\\{} & {} {\mathcal {L}}_{13}(\mho )=\pm \sqrt{\frac{\psi _1}{2 \psi _2}} \left( \tan \left( \sqrt{2 \psi _1} (\mho +\eta )\right) +\sec \left( \sqrt{2 \psi _1} (\mho +\eta )\right) \right) ,\\{} & {} {\mathcal {L}}_{14}(\tau )=\pm \sqrt{\frac{\psi _1}{8 \psi _2}} \left( \tan \left( \sqrt{\frac{\psi _1}{8}} (\mho +\eta )\right) -\cot \left( \sqrt{\frac{\psi _1}{8}} (\mho +\eta )\right) \right) ,\\{} & {} {\mathcal {L}}_{15}(\mho )=\pm \frac{\sqrt{\frac{\psi _1}{2 \psi _2}} \left( \sqrt{G_1^2-G_2^2}-e_1 \cos \left( \sqrt{2 \psi _1} (\mho +\eta )\right) \right) }{G_2+e_1 \sin \left( \sqrt{2 \psi _1} (\mho +\eta )\right) },\\{} & {} {\mathcal {L}}_{16}(\mho )=\pm \frac{\sqrt{\frac{\psi _1}{2 \psi _2}} \cos \left( \sqrt{2 \psi _1} (\mho +\eta )\right) }{\sin \left( \sqrt{2 \psi _1} (\mho +\eta )\right) -1}. \end{aligned}$$

Step 6. $\text {If}~\psi _0=0,~\psi _1>0$, we have

$$\begin{aligned}{} & {} {\mathcal {L}}_{17}(\mho )=\pm \frac{4 \psi _1 e^{\sqrt{\psi _1} (\mho +\eta )}}{e^{2 \sqrt{\psi _1} (\mho +\eta )}-4 \psi _1 \psi _2},\\{} & {} {\mathcal {L}}_{18}(\mho )=\pm \frac{4 \psi _1 e^{\sqrt{\psi _1} (\mho +\eta )}}{1-4 \psi _1 \psi _2 e^{2 \sqrt{\psi _1} (\mho +\eta )}}. \end{aligned}$$

Step 7. $\text {If}~\psi _0=0,~\psi _1=0~and~\psi _2>0$, we have

$$\begin{aligned}{} & {} {\mathcal {L}}_{19}(\mho )=\frac{1}{\sqrt{\psi _2} (\mho +\eta )},\\{} & {} {\mathcal {L}}_{20}(\mho )=\pm \frac{i}{\sqrt{\psi _2} (\mho +\eta )}. \end{aligned}$$

4.2 The polynomial expansion technique

The major steps in the procedure are briefly summarized in the section below:

Step 1: The solution to Eq. (4) can be stated as

$$\begin{aligned} {\mathcal {L}} (\mho ) & = \sum _{i=1}^N n_i \psi (\mho )^{-i}+\sum _{i=1}^N m_i \psi (\mho )^i+m_0, \end{aligned}$$

(7)

where N indicates a real variable and $m _i, n_ i$ are the unknowns, additionally, $\psi (\mho )$ fulfils

$$\begin{aligned} \psi '(\mho ) & = \nu \psi (\mho )+\Pi +\psi (\mho )^2, \end{aligned}$$

(8)

a real constant is represented by the sign $\mho$. According on the given variables, the equation displayed above has a variety of solutions.

Case I. If $\nu =0,~~\Pi =0$, the result is eventually determined as

$$\begin{aligned} \begin{aligned} \psi (\mho )=-\frac{1}{\mho }. \end{aligned} \end{aligned}$$

Case II. If $\nu \ne 0,~~\Pi =0$, the result is eventually determined as

$$\begin{aligned} \begin{aligned} \psi (\mho )=-\frac{\nu }{A_0 e^{-\nu \mho }-1}, \end{aligned} \end{aligned}$$

where $A_0$ is a integration constant.

Case III. If $\nu =0,~~\Pi \ne 0,~~\Pi >0$, the result is eventually determined as

$$\begin{aligned}{} & {} \psi (\mho )=\sqrt{\Pi } \tan \left( \sqrt{\Pi } \mho \right) ,\\{} & {} \psi (\mho )=-\sqrt{-\Pi } \cot \left( \sqrt{\Pi } \mho \right) . \end{aligned}$$

Case IV. If $\nu =0,~~\Pi \ne 0,~~\Pi <0$, the result is eventually determined as

$$\begin{aligned}{} & {} \psi (\mho )=-\sqrt{-\Pi } \tanh \left( \sqrt{-\Pi } \mho \right) ,\\{} & {} \psi (\mho )=\sqrt{-\Pi } \coth \left( \sqrt{-\Pi } \mho \right) . \end{aligned}$$

Case V. If $\Pi \ne 0,~~~\nu \ne 0$, the result is eventually determined as

$$\begin{aligned} \psi (\mho )=\frac{\psi _1-A_1 \psi _2 e^{\mho \left( \psi _1-\Theta _2\right) }}{1-A_1 e^{\mho \left( \psi _1-\psi _2\right) }}, \end{aligned}$$

a constant of integration is $A_1$. $\psi _1$ and $\psi _2$ is one of the roots of the equation $\psi ^2+\nu \psi +\Pi$ i.e.

$$\begin{aligned} \psi _1=\frac{-\nu +\sqrt{\nu ^2-4\Pi }}{2},~~~~~~~\psi _2=\frac{-\nu -\sqrt{\nu ^2-4\Pi }}{2}. \end{aligned}$$

Step 2: By applying Eqs. (7) and (8) to Eq. (4) and, if all of them were set to zero, we would obtain several mathematical equations by accumulating the same value of $\psi (\mho )$.

Step 3: As a result, in the last stage, one assesses the whole set of equations by combining the quantities obtained with the Eq. (7) and to the Eq. (8) response. This is necessary to properly obtain Eq. (1) accurate wave solutions.

5 Mathematical analysis

The following integer order nonlinear ordinary differential equation is created by transforming Eq. (1) using the fractional complex transformation Eq. (8)

$$\begin{aligned} -cg^{'}+\varepsilon k(g^3){'}+\mu ck^2g^{'''}=0, \end{aligned}$$

(9)

the result of once integrating Eq. (9) with respect to $\eta$

$$\begin{aligned} -cg+\varepsilon kg^3+\mu ck^2g^{''}=0, \end{aligned}$$

(10)

here,the integrating constant is considered as zero.

5.1 Applications of the modified sardar subequation technique

$g^{''}$ and $g^3$ are balanced in Eq. (10), which results in $N = 1$. When $N = 1$, the solution to Eq. (5) accepts the form

$$\begin{aligned} {\mathcal {L}}(\mho )=W_0+W_1 {\mathcal {L}}(\mho ), \end{aligned}$$

(11)

the following classes of solutions can be obtained by plugging Eq. (16), its second derivative, together with Eq. (6), into Eq. (10).

$$\begin{aligned} W_0^3 \epsilon \text {k}-c W_0=0,\\ -c W_1+W_1 \psi _1 \mu \text {ck}^2+3 W_0^2 W_1 \epsilon \text {k}=0,\\ 3 W_0 W_1^2 \epsilon \text {k}=0,\\ 2 W_1 \psi _2 \mu \text {ck}^2+W_1^3 \epsilon \text {k}=0. \end{aligned}$$

Family I

$$\begin{aligned} W_0= 0,~W_1= -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck}}{\sqrt{\epsilon \text {k}}},~c= \psi _1 \mu \text {ck}^2. \end{aligned}$$

Case I: $\text {If}~\psi _0=0,~\psi _1>0~\text {and}~ \psi _2\ne 0$, we have

$$\begin{aligned} {\mathcal {L}}_{1}(x,t) & = -\frac{i \sqrt{2} \text {Sech} \sqrt{\psi _1} \sqrt{\psi _2} \mu \text {ck} (\mho +\eta ) \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(12)

$$\begin{aligned} {\mathcal {L}}_{2}(x,t) & = -\frac{i \sqrt{2} \text {Csch} \sqrt{\psi _1} \sqrt{\psi _2} \mu \text {ck} (\mho +\eta ) \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) }{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(13)

Case II: $\text {If}~\psi _0=0,\psi _1>0~\text {and}~\psi _2=4f_1f_2$, we have

$$\begin{aligned} {\mathcal {L}}_{3}(x,t)=-\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{4 f_1 \sqrt{\psi _1}}{\left( 4 f_1^2-\psi _2\right) \sinh \left( \sqrt{\psi _1} (\mho +\eta )\right) +\left( 4 f_1^2-\psi _2\right) \cosh \left( \sqrt{\psi _1} (\mho +\eta )\right) }\right) }{\sqrt{\epsilon \text {k}}}.\nonumber \\ \end{aligned}$$

(14)

Case III: $\text {If}~\psi _0=\frac{\psi _1^2}{4 \psi _2},~\psi _1<0~\text {and}~ \psi _2>0$, we have

$$\begin{aligned} {\mathcal {L}}_{4}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \tanh \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(15)

$$\begin{aligned} {\mathcal {L}}_{5}(x,t) & = -\frac{i \sqrt{2} \sqrt{y_2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \coth \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(16)

$$\begin{aligned} {\mathcal {L}}_{6}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \left( \tanh \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) +i \text {sech}\left( \sqrt{2} \sqrt{-\psi _1} (\mho +\eta )\right) \right) }{\sqrt{\epsilon \text {k}}},\nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned} {\mathcal {L}}_{7}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{2 \sqrt{2}}\right) \left( \tanh \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) +\coth \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{2 \sqrt{2}}\right) \right) }{\sqrt{\epsilon \text {k}}},\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} {\mathcal {L}}_{8}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \cosh \left( \sqrt{2} \sqrt{-\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}} \left( \sinh \left( \sqrt{2} \sqrt{-\psi _1} (\mho +\eta )\right) +i\right) }. \end{aligned}$$

(19)

Case IV: $\text {If}~\psi _0=0,~\psi _1<0,~\text {and}~ \psi _2\ne 0$, we have

$$\begin{aligned} {\mathcal {L}}_{9}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) \sec \left( \sqrt{-\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(20)

$$\begin{aligned} {\mathcal {L}}_{10}(x,t)=-\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) \csc \left( \sqrt{-\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(21)

Case V: $\text {If}~\psi _0=\frac{\psi _1^2}{4 \psi _2},~\psi _1>0~ {and}~\psi _2>0~\text {and}~G_1^2-G_2^2>0$, we have

$$\begin{aligned} {\mathcal {L}}_{11}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \tan \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(22)

$$\begin{aligned} {\mathcal {L}}_{12}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \cot \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(23)

$$\begin{aligned} {\mathcal {L}}_{13}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \left( \tan \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) +\sec \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) \right) }{\sqrt{\epsilon \text {k}}},\nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} {\mathcal {L}}_{14}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{2 \sqrt{2}}\right) \left( \tan \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{2 \sqrt{2}}\right) -\cot \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{2 \sqrt{2}}\right) \right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(25)

$$\begin{aligned} {\mathcal {L}}_{15}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \left( \sqrt{G_1^2-G_2^2}-e_1 \cos \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) \right) }{\sqrt{\epsilon \text {k}} \left( G_2+e_1 \sin \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) \right) },\nonumber \\ \end{aligned}$$

(26)

$$\begin{aligned} {\mathcal {L}}_{16}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \cos \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}} \left( \sin \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) -1\right) }. \end{aligned}$$

(27)

Case VI: $\text {If}~\psi _0=0,~\psi _1>0$, we have

$$\begin{aligned} {\mathcal {L}}_{17}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{4 \psi _1 e^{\sqrt{\psi _1} (\mho +\eta )}}{e^{2 \sqrt{\psi _1} (\mho +\eta )}-4 \psi _1 \psi _2}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(28)

$$\begin{aligned} {\mathcal {L}}_{18}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{4 \psi _1 e^{\sqrt{\psi _1} (\mho +\eta )}}{1-4 \psi _1 \psi _2 e^{2 \sqrt{\psi _1} (\mho +\eta )}}\right) }{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(29)

Case VII: $\text {If}~\psi _0=0,~\psi _1=0~and~\psi _2>0$, we have

$$\begin{aligned} {\mathcal {L}}_{19}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{1}{\sqrt{\psi _2} (\mho +\eta )}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(30)

$$\begin{aligned} {\mathcal {L}}_{20}(x,t) & = -\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{i}{\sqrt{\psi _2} (\mho +\eta )}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(31)

where $\mho =\frac{k }{(\alpha +1) \Pi }x^{\alpha }-\frac{c }{(\alpha +1) \Pi }t^{\alpha }-x_0$.

Family II:

$$\begin{aligned} W_0= 0,~W_1=\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck}}{\sqrt{\epsilon \text {k}}},~W_2= 0,~c= \psi _1 \mu \text {ck}^2. \end{aligned}$$

Case I: $\text {If}~\psi _0=0,~\psi _1>0~\text {and}~ \psi _2\ne 0$, we have

$$\begin{aligned} {\mathcal {L}}_{21}(x,t) & = \frac{i \sqrt{2} \text {Sech} \sqrt{\psi _1} \sqrt{\psi _2} \mu \text {ck} (\mho +\eta ) \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(32)

$$\begin{aligned} {\mathcal {L}}_{22}(x,t) & = \frac{i \sqrt{2} \text {Csch} \sqrt{\psi _1} \sqrt{\psi _2} \mu \text {ck} (\mho +\eta ) \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) }{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(33)

Case II: $\text {If}~\psi _0=0,\psi _1>0~\text {and}~\psi _2=4f_1f_2$, we have

$$\begin{aligned} {\mathcal {L}}_{23}(x,t)=\frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{4 f_1 \sqrt{\psi _1}}{\left( 4 f_1^2-\psi _2\right) \sinh \left( \sqrt{\psi _1} (\mho +\eta )\right) +\left( 4 f_1^2-\psi _2\right) \cosh \left( \sqrt{\psi _1} (\mho +\eta )\right) }\right) }{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(34)

Case III: $\text {If}~\psi _0=\frac{\psi _1^2}{4 \psi _2},~\psi _1<0~\text {and}~ \psi _2>0$, we have

$$\begin{aligned} {\mathcal {L}}_{24}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \tanh \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(35)

$$\begin{aligned} {\mathcal {L}}_{25}(x,t) & = \frac{i \sqrt{2} \sqrt{y_2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \coth \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(36)

$$\begin{aligned} {\mathcal {L}}_{26}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \left( \tanh \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) +i \text {sech}\left( \sqrt{2} \sqrt{-\psi _1} (\mho +\eta )\right) \right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(37)

$$\begin{aligned} {\mathcal {L}}_{27}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{2 \sqrt{2}}\right) \left( \tanh \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{\sqrt{2}}\right) +\coth \left( \frac{\sqrt{-\psi _1} (\mho +\eta )}{2 \sqrt{2}}\right) \right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(38)

$$\begin{aligned} {\mathcal {L}}_{28}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \cosh \left( \sqrt{2} \sqrt{-\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}} \left( \sinh \left( \sqrt{2} \sqrt{-\psi _1} (\mho +\eta )\right) +i\right) }. \end{aligned}$$

(39)

Case IV: $\text {If}~\psi _0=0,~\psi _1<0,~\text {and}~ \psi _2\ne 0$, we have

$$\begin{aligned} {\mathcal {L}}_{29}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) \sec \left( \sqrt{-\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(40)

$$\begin{aligned} {\mathcal {L}}_{30}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \sqrt{-\frac{\psi _1}{\psi _2}}\right) \csc \left( \sqrt{-\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(41)

Case V: $\text {If}~\psi _0=\frac{\psi _1^2}{4 \psi _2},~\psi _1>0~ {and}~\psi _2>0~\text {and}~G_1^2-G_2^2>0$, we have

$$\begin{aligned} {\mathcal {L}}_{31}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \tan \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(42)

$$\begin{aligned} {\mathcal {L}}_{32}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{-\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \cot \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{\sqrt{2}}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(43)

$$\begin{aligned} {\mathcal {L}}_{33}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \left( \tan \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) +\sec \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) \right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(44)

$$\begin{aligned} {\mathcal {L}}_{34}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{2 \sqrt{2}}\right) \left( \tan \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{2 \sqrt{2}}\right) -\cot \left( \frac{\sqrt{\psi _1} (\mho +\eta )}{2 \sqrt{2}}\right) \right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(45)

$$\begin{aligned} {\mathcal {L}}_{35}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \left( \sqrt{G_1^2-G_2^2}-e_1 \cos \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) \right) }{\sqrt{\epsilon \text {k}} \left( G_2+e_1 \sin \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) \right) }, \end{aligned}$$

(46)

$$\begin{aligned} {\mathcal {L}}_{36}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{\sqrt{\frac{\psi _1}{\psi _2}}}{\sqrt{2}}\right) \cos \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) }{\sqrt{\epsilon \text {k}} \left( \sin \left( \sqrt{2} \sqrt{\psi _1} (\mho +\eta )\right) -1\right) }. \end{aligned}$$

(47)

Case VI: $\text {If}~\psi _0=0,~\psi _1>0$, we have

$$\begin{aligned} {\mathcal {L}}_{37}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{4 \psi _1 e^{\sqrt{\psi _1} (\mho +\eta )}}{e^{2 \sqrt{\psi _1} (\mho +\eta )}-4 \psi _1 \psi _2}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(48)

$$\begin{aligned} {\mathcal {L}}_{38}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{4 \psi _1 e^{\sqrt{\psi _1} (\mho +\eta )}}{1-4 \psi _1 \psi _2 e^{2 \sqrt{\psi _1} (\mho +\eta )}}\right) }{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(49)

Case VII: $\text {If}~\psi _0=0,~\psi _1=0~and~\psi _2>0$, we have

$$\begin{aligned} {\mathcal {L}}_{39}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{1}{\sqrt{\psi _2} (\mho +\eta )}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(50)

$$\begin{aligned} {\mathcal {L}}_{40}(x,t) & = \frac{i \sqrt{2} \sqrt{\psi _2} \mu \text {ck} \left( \pm \frac{i}{\sqrt{\psi _2} (\mho +\eta )}\right) }{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(51)

where $\mho =\frac{k }{(\alpha +1) \Pi }x^{\alpha }-\frac{c }{(\alpha +1) \Pi }t^{\alpha }-x_0$.

5.2 Applications of the polynomial expansion technique

$g^{''}$ and $g^3$ are balanced in Eq. (10), which results in $N = 1$. When $N = 1$, the solution to Eq. (7) accepts the form

$$\begin{aligned} {\mathcal {L}}(\mho )=m_0+m_1 \psi (\mho )+n_1 \frac{1}{\psi (\mho )}, \end{aligned}$$

(52)

the following classes of solutions can be obtained by plugging Eq. (52), its second derivative, together with Eq. (8), into Eq. (10).

$$\begin{aligned} 6 m_1 m_0 n_1 \epsilon \text {k}-m_0 c+m_1 \nu \Pi \mu \text {ck}^2+m_0^3 \epsilon \text {k}+n_1 \nu \mu \text {ck}^2=0,\\ 2 n_1 \Pi ^2 \mu \text {ck}^2+n_1^3 \epsilon \text {k}=0,\\ 3 m_0 n_1^2 \epsilon \text {k}+3 n_1 \nu \Pi \mu \text {ck}^2=0,\\ 3 m_1 n_1^2 \epsilon \text {k}+3 m_0^2 n_1 \epsilon \text {k}-n_1 c+n_1 \nu ^2 \mu \text {ck}^2+2 n_1 \Pi \mu \text {ck}^2=0,\\ 3 m_1^2 n_1 \epsilon \text {k}-m_1 c+m_1 \nu ^2 \mu \text {ck}^2+2 m_1 \Pi \mu \text {ck}^2+3 m_0^2 a_1 \epsilon \text {k}=0,\\ 3 m_1 \nu \mu \text {ck}^2+3 m_0 m_1^2 \epsilon \text {k}=0,\\ m_1^3 \epsilon \text {k}+2 m_1 \mu \text {ck}^2=0. \end{aligned}$$

The algebraic set of problems described above can be resolved using the Mathematica.

Family I:

$$\begin{aligned} a_0=-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}},~a_1=0,~b_1=-\frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c}}{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}},~\nu =-\frac{\sqrt{2} \sqrt{2 \Pi \mu \text {ck}^2-c}}{\mu \text {ck}}. \end{aligned}$$

When we input the mentioned results into Eq. (52), distinct sets of solutions for traveling waves are generated.

Case I.

$$\begin{aligned} {\mathcal {L}}_{41}(x,t)=\frac{\sqrt{2} \mho \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c}}{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(53)

Case II.

$$\begin{aligned} {\mathcal {L}}_{42}(x,t)=\frac{\sqrt{2} \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \left( K_0 e^{-\mho \Pi }-1\right) }{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(54)

Case III.

$$\begin{aligned} {\mathcal {L}}_{43}(x,t) & = -\frac{\sqrt{2} \sqrt{\Pi } \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \cot \left( \mho \sqrt{\Pi }\right) }{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(55)

$$\begin{aligned} {\mathcal {L}}_{44}(x,t) & = \frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \tan \left( \mho \sqrt{\Pi }\right) }{\sqrt{-\Pi } \sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(56)

Case IV.

$$\begin{aligned} {\mathcal {L}}_{45}(x,t) & = \frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \coth \left( \mho \sqrt{-\Pi }\right) }{\sqrt{-\Pi } \sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(57)

$$\begin{aligned} {\mathcal {L}}_{46}(x,t) & = -\frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \tanh \left( \mho \sqrt{-\Pi }\right) }{\sqrt{-\Pi } \sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(58)

Case V.

$$\begin{aligned} {\mathcal {L}}_{47}(x,t)=-\frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \left( 1-K_1 e^{\mho \left( \varrho _1-\varrho _2\right) }\right) }{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2} \left( \varrho _1-K_1 \varrho _2 e^{\mho \left( \varrho _1-\varrho _2\right) }\right) }-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(59)

where $\mho =\frac{k }{(\alpha +1) \Pi }x^{\alpha }-\frac{c }{(\alpha +1) \Pi }t^{\alpha }-x_0$.

Family II:

The results for the second category are provided below,

$$\begin{aligned} a_0=-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}},~a_1=0,~b_1=\frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c}}{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}},~\nu =\frac{\sqrt{2} \sqrt{2 \Pi \mu \text {ck}^2-c}}{\mu \text {ck}}. \end{aligned}$$

When we input the mentioned results into Eq. (52), distinct sets of solutions for traveling waves are generated.

Case I.

$$\begin{aligned} {\mathcal {L}}_{48}(x,t)=-\frac{\sqrt{2} \mho \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c}}{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(60)

Case II.

$$\begin{aligned} {\mathcal {L}}_{49}(x,t)=-\frac{\sqrt{2} \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \left( K_0 e^{-\mho \Pi }-1\right) }{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(61)

Case III.

$$\begin{aligned} {\mathcal {L}}_{50}(x,t) & = \frac{\sqrt{2} \sqrt{\Pi } \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \cot \left( \mho \sqrt{\Pi }\right) }{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(62)

$$\begin{aligned} {\mathcal {L}}_{51}(x,t) & = -\frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \tan \left( \mho \sqrt{\Pi }\right) }{\sqrt{-\Pi } \sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(63)

Case IV.

$$\begin{aligned} {\mathcal {L}}_{52}(x,t) & = -\frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \coth \left( \mho \sqrt{-\Pi }\right) }{\sqrt{-\Pi } \sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(64)

$$\begin{aligned} {\mathcal {L}}_{53}(x,t) & = \frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \tanh \left( \mho \sqrt{-\Pi }\right) }{\sqrt{-\Pi } \sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2}}-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}. \end{aligned}$$

(65)

Case V.

$$\begin{aligned} {\mathcal {L}}_{54}(x,t)=\frac{\sqrt{2} \Pi \mu \text {ck} \sqrt{2 \Pi \mu \text {ck}^2-c} \left( 1-K_1 e^{\mho \left( \varrho _1-\varrho _2\right) }\right) }{\sqrt{\epsilon \text {k}} \sqrt{c-2 \Pi \mu \text {ck}^2} \left( \varrho _1-K_1 \varrho _2 e^{\mho \left( \varrho _1-\varrho _2\right) }\right) }-\frac{\sqrt{c-2 \Pi \mu \text {ck}^2}}{\sqrt{\epsilon \text {k}}}, \end{aligned}$$

(66)

where $\mho =\frac{k }{(\alpha +1) \Pi }x^{\alpha }-\frac{c }{(\alpha +1) \Pi }t^{\alpha }-x_0$.

6 Stability analysis

In Eq. (1), we establish the Hamiltonian and momentum for the described strategy, providing a clear definition for these parameters (Alhefthi et al. 2024; Rizvi et al. 2024)

$$\begin{aligned} S=\frac{1}{2}\int _{-\infty }^{\infty } {\mathcal {H}} ^2 \, d\psi , \end{aligned}$$

(67)

the electrical potential, denoted by ${\mathcal {H}}$, and momentum represented by S, are key elements for stabilizing solitary waves is

$$\begin{aligned} \frac{\partial S}{\partial \sigma }>0, \end{aligned}$$

(68)

Therefore, $\sigma$ represents frequency. We derive Eq. (67), incorporating the traveling wave solution from Eq. (15)

$$\begin{aligned} S=\frac{1}{2}\int _{-10 }^{10}\left( -\frac{i c \sqrt{-\frac{y_1}{y_2}} \sqrt{y_2} \mu \tanh \left( \frac{\sqrt{-y_1} \left( -c y_1 \mu +\eta +\frac{x}{2}-1\right) }{\sqrt{2}}\right) }{\sqrt{\epsilon }}\right) ^2 dx, \end{aligned}$$

(69)

after simplification, we obtain

$$\begin{aligned} S=\frac{c^2 \sqrt{y_1} \mu ^2 \left( 10 \sqrt{y_1}-\sqrt{2} \left( \tan \left( \frac{\sqrt{y_1} \left( c y_1 \mu -\eta +6\right) }{\sqrt{2}}\right) +\tan \left( \frac{\sqrt{y_1} \left( -c y_1 \mu +\eta +4\right) }{\sqrt{2}}\right) \right) \right) }{\epsilon }. \end{aligned}$$

(70)

Applying the stabilization condition for solitary waves, we conclude that a stable nonlinear model is represented by Eq. (1).

7 Physical description of the solutions

We discuss about how the space-time fractional MEW equation’s conclusions should be interpreted physically. The solutions obtained here include those for soliton waves, bright and dark solitons, multi-solitons, periodic solitary waves, rational functions, and elliptic functions for certain relevant parameter values. In this research, we have applied two innovative methods namely the polynomial expansion approach and the Sardar sub-equation method to the space-time fractional MEWE. These methods, which have not been previously employed for this equation, offer new insights and analytical solutions that contribute to the broader understanding of fractional PDEs. The nature of nonlinear waves created from Eq. (1) is visualised in the 3D, contour and 2D graphs. Figures display the graphical representations of some of the solutions that were obtained. Below are the physical explanations for these figures.

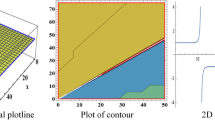
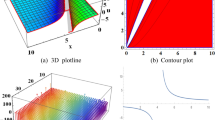
Figure 1 show how dark soliton solutions emerge under specific parameter values $\alpha =1,~c=1.2,~\Gamma =1.22,~\eta =1,~k=1.1,~x_0=1.23,~ y_1=0.11,~ y_2=0.5,~\epsilon =1,~\mu =1$. In Figs. 2, 7, 9, 10 the solution’s behavior is represented by a distinct bell-shaped pattern, influenced by specific parameters $y_1=1,~y_2=1.5,~\mu =1,~c=1.02,~k=1.1,~\eta =-1,~x_0=1.23,~\alpha =0.02,~\Gamma =1.22,~\epsilon =1$ and $\omega =2,~\nu =0.001,~\mu =1,~c=2,~k=2,~\Omega =-2,~x_0=1.02,~\Gamma =1,~\alpha =1.3,~\epsilon =1$ and $\omega =1,~\nu =0.001,~\mu =1,~c=-1,~k=2,~\Pi =-1,~x_0=1.02,~\Gamma =1,~\alpha =1.3,~\epsilon =1$. For the set of appropriate values $y_1=1,~y_2=4 f_1 f_2,~\mu =1,~c=1.02,~k=1.1,~\eta =0.1,~f_1=-1,~f_2=1,~x_0=1.23,~\alpha =2,~\Gamma =1.22,~\epsilon =1$, bright typed soliton is represented in Fig. 3, whereas Fig. 5 produces a W-shaped solution for different constant values $y_1=-1,~y_2=1,~y_0=\frac{y_1^2}{4 y_2},~\mu =1,~c=1.02,~k=1.1,~\eta =-1,~f_1=0.1,~f_2=1,~x_0=1.23,~\alpha =2,~\Gamma =1.22,~\epsilon =1$. For the set of appropriate values $y_1=1,~y_2=2,~\mu =2,~c=1.6,~k=2.1,~\eta =2,~x_0=2,~\alpha =1,~\Gamma =0.5,~\epsilon =1$, the parabolic wave solution is represented in Fig. 8. Furthermore, for different constant values $\omega =3.3,~\nu =0.001,~\mu =2,~c=1,~k=2,~\Pi =-1,~x_0=2,~\Gamma =1,~\alpha =1.3,~\epsilon =2$ and $\omega =1,~\nu =0.001,~\mu =2,~c=3.3~,k=2,~\Pi =-0.5,~x_0=1.02,~\Gamma =1,~\alpha =1.3,~\epsilon =1$, represents dark type structure soliton solutions are shown in Figs. 11, 12.

Fig. 1

a Represents 3D plot of a v-shaped dark soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{1}(x,t)$ highlighting specific values $\alpha =1,~c=1.2,~\Gamma =1.22,~\eta =1,~k=1.1,~x_0=1.23,~ y_1=0.11,~ y_2=0.5,~\epsilon =1,~\mu =1$

Fig. 2

a Represents the solution 3D plot of a bell shaped singular soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{2}(x,t)$ highlighting specific values $y_1=1,~y_2=1.5,~\mu =1,~c=1.02,~k=1.1,~\eta =-1,~x_0=1.23,~\alpha =0.02,~\Gamma =1.22,~\epsilon =1$

Fig. 3

a Represents the solution 3D plot of a bell shaped bright soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{3}(x,t)$ highlighting specific values $y_1=1,~y_2=4 f_1 f_2,~\mu =1,~c=1.02,~k=1.1,~\eta =0.1,~f_1=-1,~f_2=1,~x_0=1.23,~\alpha =2,~\Gamma =1.22,~\epsilon =1$

Fig. 4

a Represents the solution 3D plot of a double peaked singular soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{4}(x,t)$ highlighting specific values $y_1=-1,~y_2=1,~y_0=\frac{y_1^2}{4 y_2},~\mu =1,~c=1.02,~k=1.1,~\eta =0.1,~f_1=-1,~f_2=1,~x_0=1.23,~\alpha =2,~\Gamma =1.22,~\epsilon =1$

Fig. 5

a Represents the solution 3D plot of a multiple peaked bright soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{5}(x,t)$ highlighting specific values $y_1=-1,~y_2=1,~y_0=\frac{y_1^2}{4 y_2},~\mu =1,~c=1.02,~k=1.1,~\eta =-1,~f_1=0.1,~f_2=1,~x_0=1.23,~\alpha =2,~\Gamma =1.22,~\epsilon =1$

Fig. 6

a Represents the solution 3D plot of a $\mu$ shaped bright soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{15}(x,t)$ highlighting specific values $y_1=1,`y_2=2,~y_0=\frac{y_1^2}{4 y_2},~G_1=3,~G_2=2,~\mu =0.1,~c=1.6,~k=2.1,~\eta =-1,~x_0=1,~\alpha =1,~\Gamma =1.22,~\epsilon =1,~e_1=1.5$

Fig. 7

a Represents the solution 3D plot of a bright singular soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{18}(x,t)$ highlighting specific values $y_1=1,~y_2=2,~y_0=\frac{y_1^2}{4 y_2},~\mu =0.1,~c=1.6,~k=2.1,~\eta =-1,~x_0=1,~\alpha =1,~\Gamma =1.22,~\epsilon =1$

Fig. 8

a Represents the solution 3D plot of a v-shaped singular periodic soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{34}(x,t)$ highlighting specific values $y_1=1,~y_2=2,~\mu =2,~c=1.6,~k=2.1,~\eta =2,~x_0=2,~\alpha =1,~\Gamma =0.5,~\epsilon =1$

Fig. 9

a Represents the solution 3D plot of a solitary wave soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{44}(x,t)$ highlighting specific values $\omega =2,~\nu =0.001,~\mu =1,~c=2,~k=2,~\Pi =-2,~x_0=1.02,~\Gamma =1,~\alpha =1.3,~\epsilon =1$

Fig. 10

a represents the solution 3D plot of a singular bright soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{45}(x,t)$ highlighting specific values $\omega =1,~\nu =0.001,~\mu =1,~c=-1,~k=2,~\Pi =-1,~x_0=1.02,~\Gamma =1,~\alpha =1.3,~\epsilon =1$

Fig. 11

a Represents the solution 3D plot of a dark singular soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{46}(x,t)$ highlighting specific values $\omega =3.3,~\nu =0.001,~\mu =2,~c=1,~k=2,~\Pi =-1,~x_0=2,~\Gamma =1,~\alpha =1.3,~\epsilon =2$

Fig. 12

a Represents the solution 3D plot of a bell shaped dark soliton in x, t and  ${\mathcal {L}}(x,t)$ dimensions. In b, there’s a contour plot offering a different view, while c simplifies the depiction with a 2D plot of the solution for ${\mathcal {L}}_{53}(x,t)$ highlighting specific values $\omega =1,~\nu =0.001,~\mu =2,~c=3.3,~k=2,~\Pi =-0.5,~x_0=1.02,~\Gamma =1,~\alpha =1.3,~\epsilon =1$

8 Conclusion

In the context of the ongoing research, the modified Sardar sub-equation approach and the polynomial expansion method were used in this study to provide exact solutions for the conformable space-time fractional MEW problem, encompassing bright and dark soliton, periodic solitons and various other solution types. The Sardar sub-equation method is generally more effective due to its accuracy, stability, efficiency, simplicity, and versatility. However, the polynomial expansion approach can still be valuable for specific types of solutions where it excels in accuracy. Employing two distinct methodologies, we were able to directly and effectively acquire these solutions, contributing to a comprehensive understanding of the behavior and dynamics described by the fractional differential equations. Studying fractional nonlinear problems is essential for enhancing our understanding and modeling of complex systems, improving predictive capabilities, and developing new mathematical tools and techniques. The article presents new solutions to the nonlinear evolution equation by employing these techniques. With the help of the Mathematica software, every calculation in this work has been performed and verified by back substitution (Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12).